Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends
Abstract
1. Introduction
- RQ1: What is the distribution of financial options pricing research from 2002 to 2022 based on the total number of publications and citations generated annually and the various research areas?
- RQ2: In the field of research that focuses on financial options pricing, who are some of the most prominent authors, institutions, countries, high impact journals and notable publications?
- RQ3: What advancements have been made in co-citation studies, and what significant clusters have emerged, specifically concerning the study’s research area?
- RQ4: What are the most active research fields, the new research trends and the emerging themes in financial option pricing?
2. Materials and Methods
3. Results
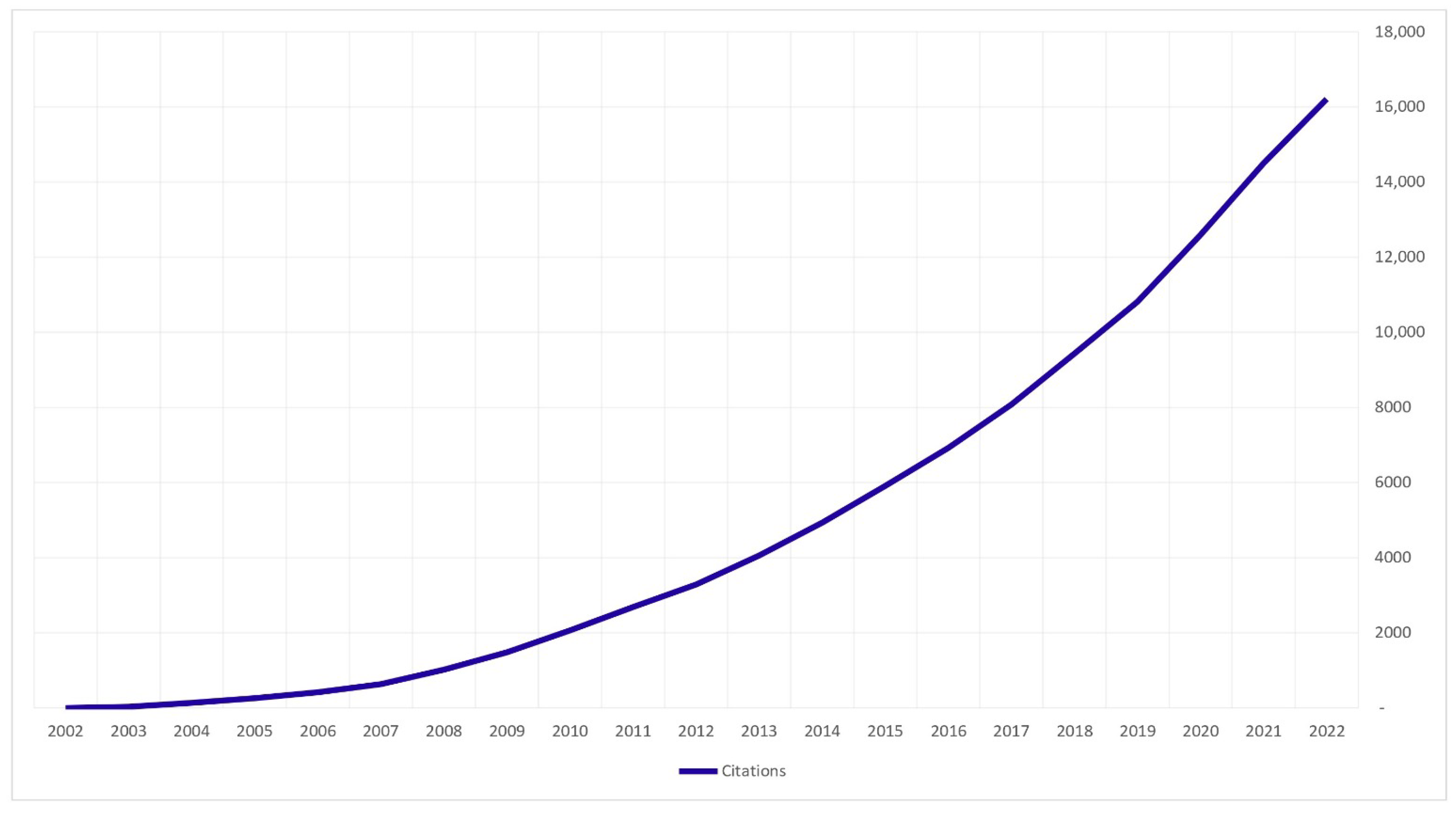
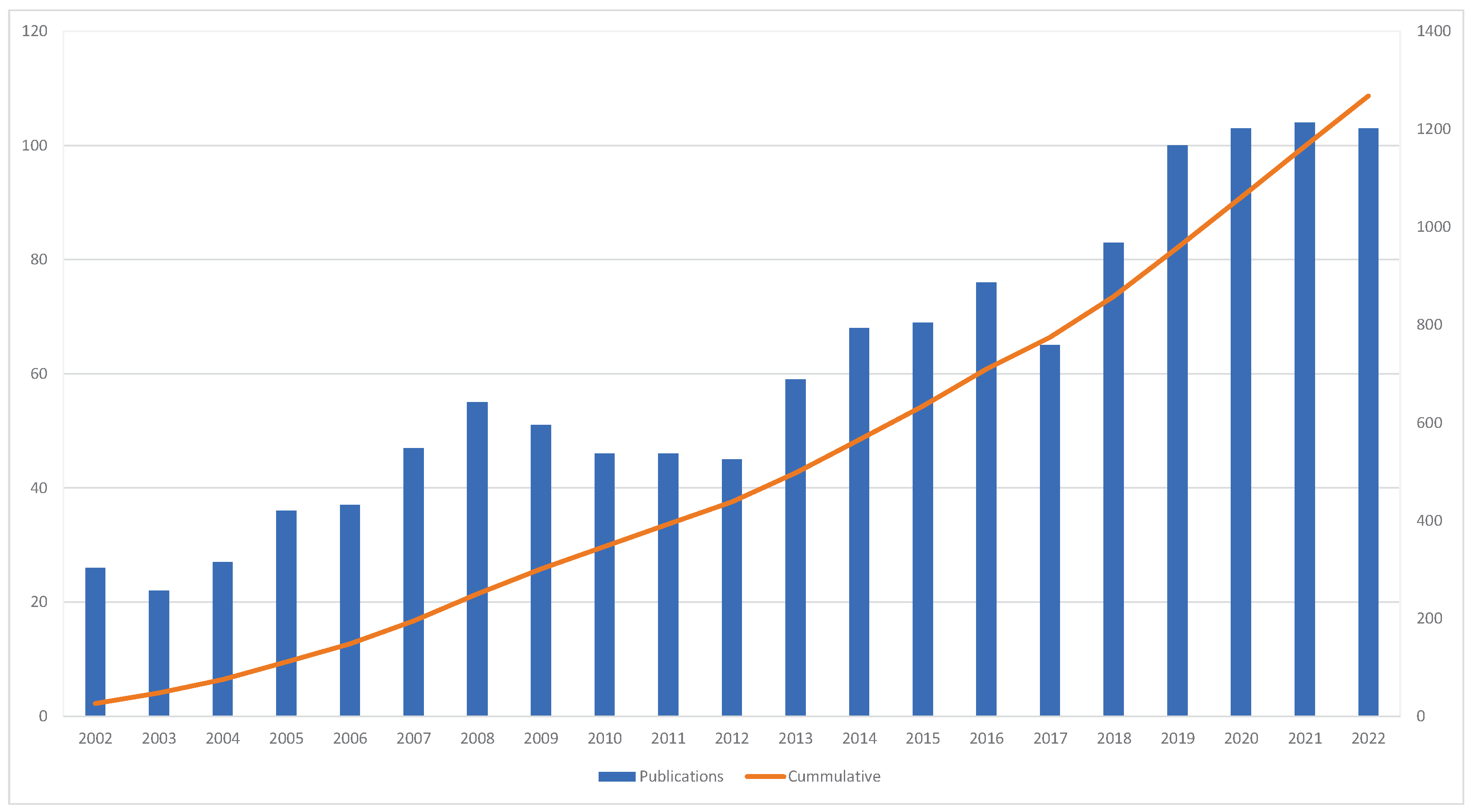
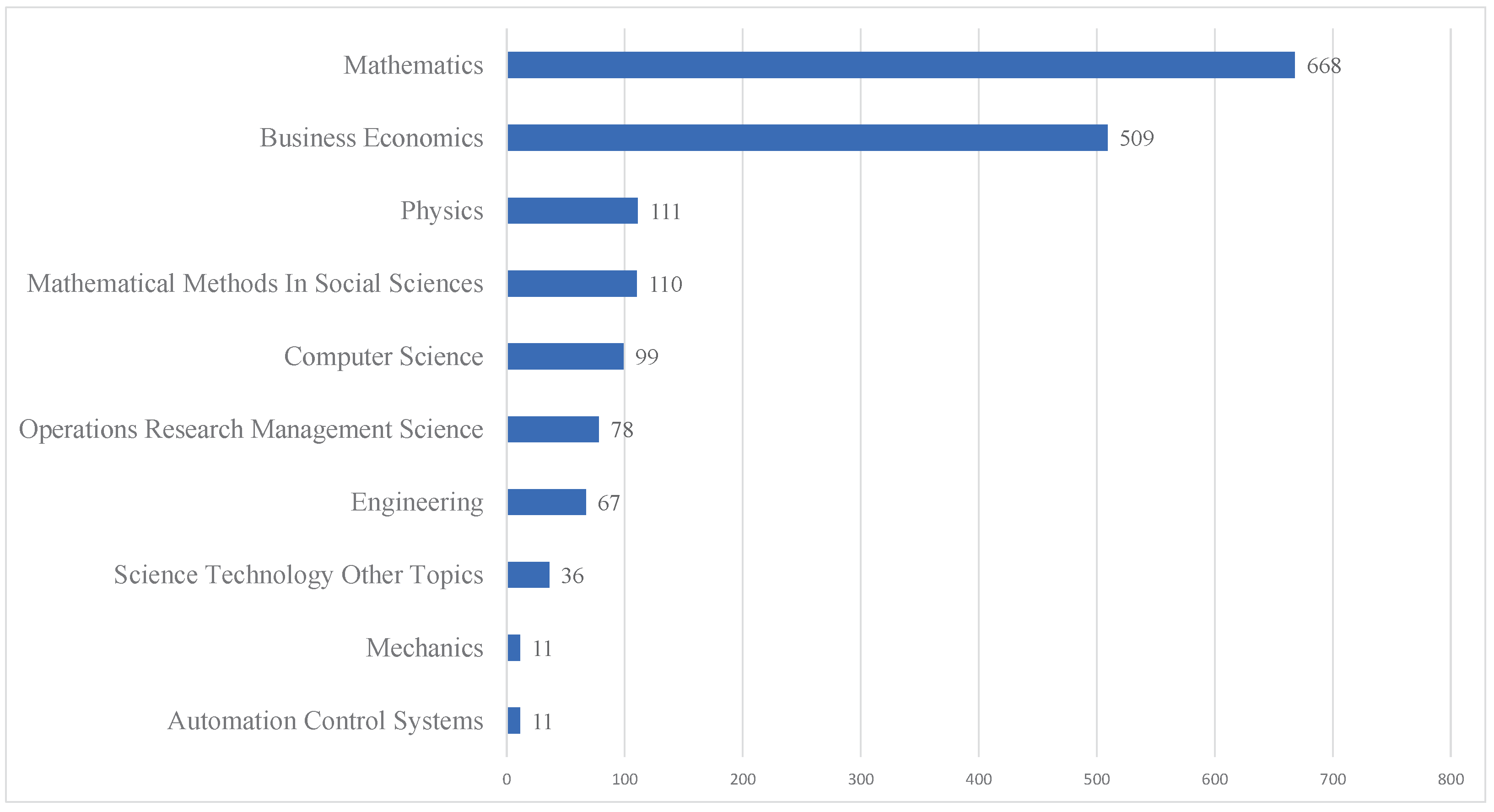
3.1. Descriptive Statistics
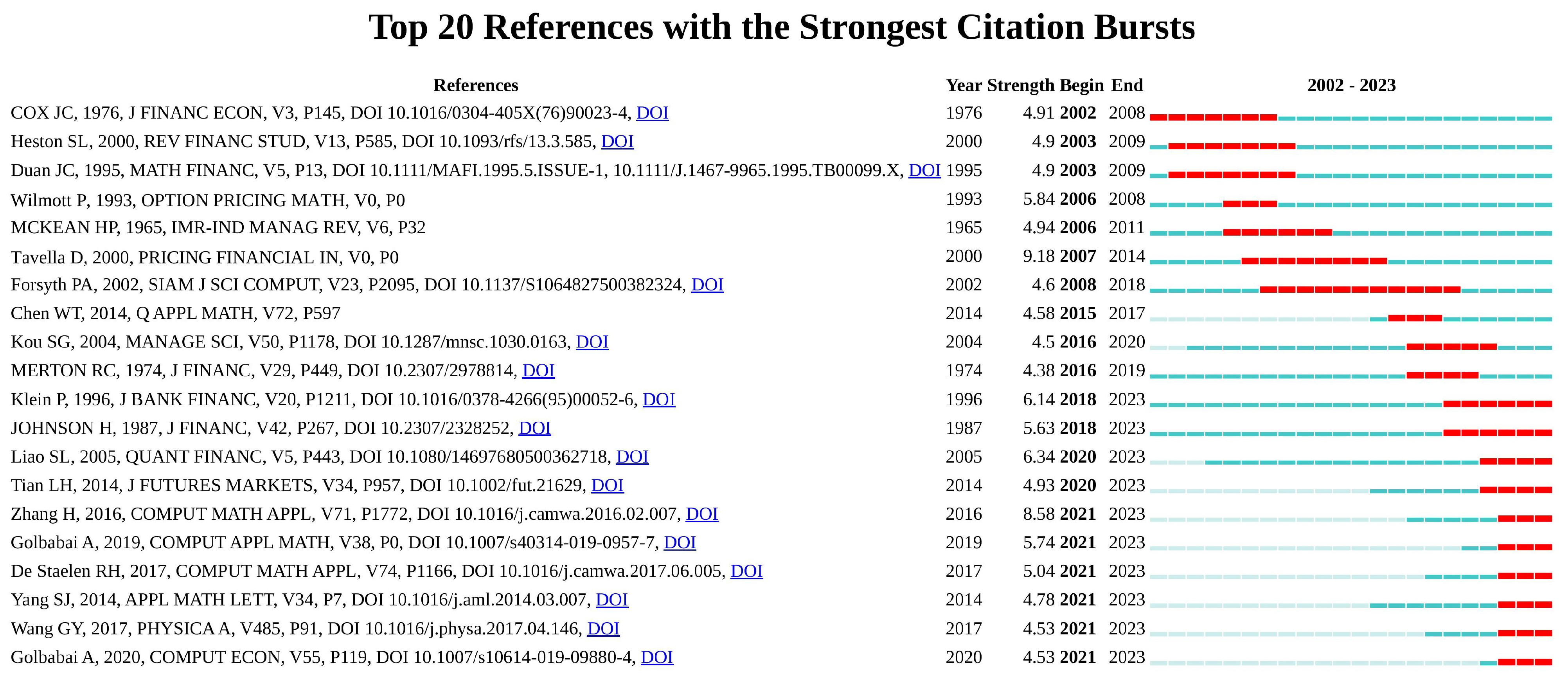
3.2. Citation Network Analysis
3.3. Co-Citation Analysis
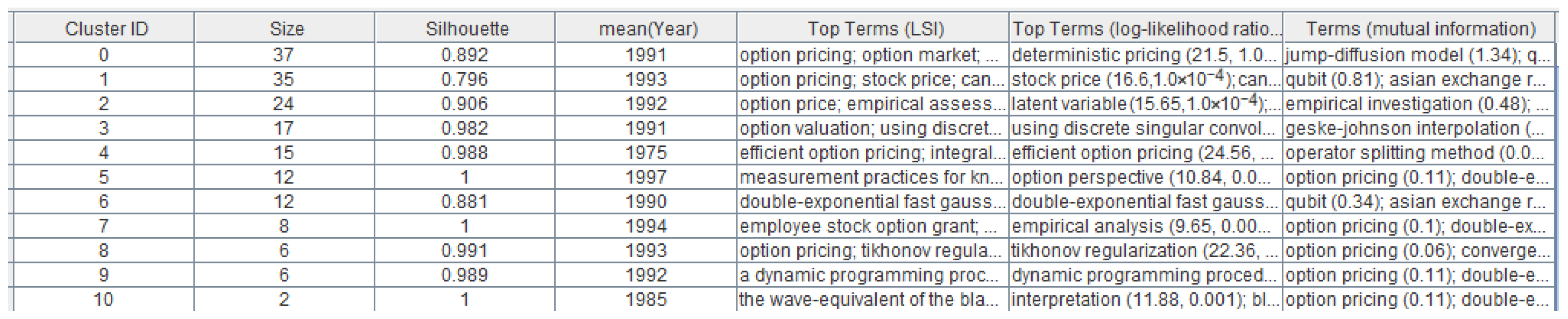
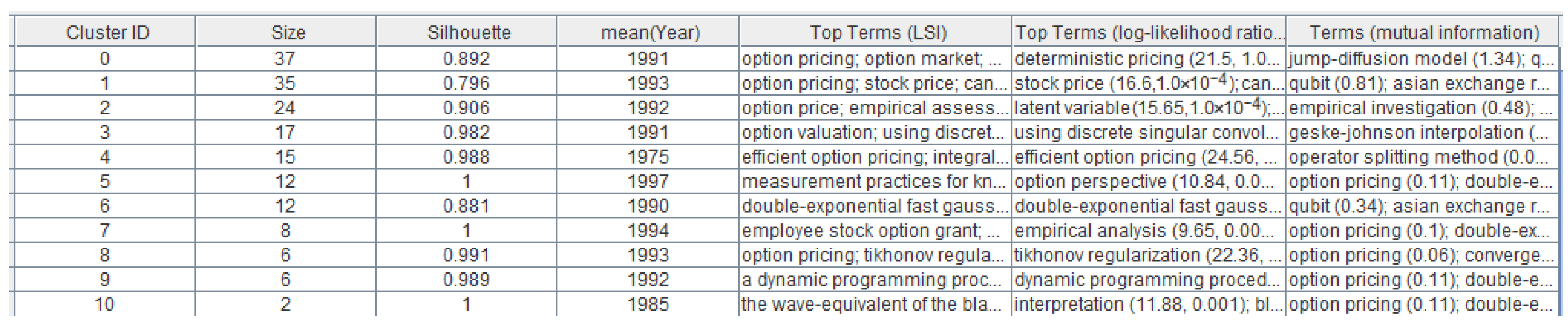
3.3.1. Clustering
3.3.2. Content Analysis
- Cluster 0: Deterministic Pricing
- Cluster 1: Stock Price
- Cluster 2: Latent Variable
- Cluster 3: Discrete Singular Convolution
- Cluster 4: Efficient Option Pricing
- Cluster 6: Double-Exponential Fast Gaussian Transform
- Cluster 8: Tikhonov Regularization
- Cluster 9: Dynamic Programming
3.4. Research Trends, Active Research Areas and Emerging Themes
4. Discussion
5. Limitations and Future Research
- The research was based on an analysis of 1713 papers published on options pricing in the financial industry over the previous two decades. The research used a combination of keywords, and it is possible that various combinations of keywords would have produced different findings.
- We acknowledged that relying solely on the Web of Science (WoS) may omit relevant studies indexed in Scopus. Therefore, future studies could combine two or three of the major indexing databases, such as Farooq (2023) and Sánchez et al. (2017).
- In subsequent research on this subject, all ten clusters mentioned above should be included. As a result of these findings, additional investigation into this subject area is required.
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aït-Sahalia, Y., & Lo, A. W. (1998). Nonparametric estimation of state-price densities implicit in financial asset prices. The Journal of Finance, 53(2), 499–547. [Google Scholar] [CrossRef]
- Alshater, M. M., Atayah, O. F., & Hamdan, A. (2021). Journal of sustainable finance and investment: A bibliometric analysis. Journal of Sustainable Finance & Investment, 13(3), 1131–1152. [Google Scholar] [CrossRef]
- Anderson, D., & Ulrych, U. (2023). Accelerated american option pricing with deep neural networks. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4000756 (accessed on 1 February 2025).
- Ansari, Y., Albarrak, M. S., Sherfudeen, N., & Aman, A. (2022). A study of financial literacy of investors—A bibliometric analysis. International Journal of Financial Studies, 10(2), 36. [Google Scholar] [CrossRef]
- Ashok Naarayan, A., & Parpas, P. (2024, November 14–17). Stable multilevel deep neural networks for option pricing and xvas using forward-backward stochastic differential equations. ACM Transactions on Modeling and Computer Simulation (TOMACS), Brooklyn, NY, USA. [Google Scholar] [CrossRef]
- Bachelier, L. (1900). Théorie de la spéculation. In Annales scientifiques de l’école normale supérieure (Vol. 17, pp. 21–86). Gauthier-Villars. [Google Scholar]
- Baker, H. K., Kumar, S., & Pandey, N. (2020). A bibliometric analysis of managerial finance: A retrospective. Managerial Finance, 46(11), 1495–1517. [Google Scholar] [CrossRef]
- Barone-Adesi, G., Engle, R. F., & Mancini, L. (2008). A GARCH option pricing model with filtered historical simulation. The Review of Financial Studies, 21(3), 1223–1258. [Google Scholar] [CrossRef]
- Ben-Ameur, H., Breton, M., & L’Ecuyer, P. (2002). A dynamic programming procedure for pricing American-style Asian options. Management Science, 48(5), 625–643. [Google Scholar] [CrossRef]
- Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654. [Google Scholar] [CrossRef]
- Blanco-Mesa, F., Merigó, J. M., & Gil-Lafuente, A. M. (2017). Fuzzy decision making: A bibliometric-based review. Journal of Intelligent & Fuzzy Systems, 32(3), 2033–2050. [Google Scholar] [CrossRef]
- Bollerslev, T., Gibson, M., & Zhou, H. (2011). Dynamic estimation of volatility risk premia and investor risk aversion from option-implied and realized volatilities. Journal of Econometrics, 160(1), 235–245. [Google Scholar] [CrossRef]
- Borland, L. (2002). Option pricing formulas based on a non-Gaussian stock price model. Physical Review Letters, 89(9), 098701. [Google Scholar] [CrossRef] [PubMed]
- Boubaker, S., Goodell, J. W., Kumar, S., & Sureka, R. (2023). COVID-19 and finance scholarship: A systematic and bibliometric analysis. International Review of Financial Analysis, 85, 102458. [Google Scholar] [CrossRef]
- Broadie, M., Chernov, M., & Johannes, M. (2009). Understanding index option returns. The Review of Financial Studies, 22(11), 4493–4529. [Google Scholar] [CrossRef]
- Broadie, M., & Yamamoto, Y. (2003). Application of the fast Gauss transform to option pricing. Management Science, 49(8), 1071–1088. [Google Scholar] [CrossRef]
- Broadie, M., & Yamamoto, Y. (2005). A double-exponential fast Gauss transform algorithm for pricing discrete path-dependent options. Operations Research, 53(5), 764–779. [Google Scholar] [CrossRef]
- Carr, P., & Wu, L. (2004). Time-changed Lévy processes and option pricing. Journal of Financial Economics, 71(1), 113–141. [Google Scholar] [CrossRef]
- Cartea, A., & del Castillo-Negrete, D. (2007). Fractional diffusion models of option prices in markets with jumps. Physica A: Statistical Mechanics and Its Applications, 374(2), 749–763. [Google Scholar]
- Chen, C. (2014). The citespace manual. College of Computing and Informatics, 1, 1–84. [Google Scholar]
- Chen, C., Ibekwe-SanJuan, F., & Hou, J. (2010). The structure and dynamics of cocitation clusters: A multiple-perspective cocitation analysis. Journal of the American Society for Information Science and Technology, 61(7), 1386–1409. [Google Scholar] [CrossRef]
- Cheng, T.-Y., Ho, S. Y.-C., Chien, T.-W., Chow, J. C., & Chou, W. (2023). A comprehensive approach for clustering analysis using follower-leading clustering algorithm (FLCA): Bibliometric analysis. Medicine, 102(42), e35156. [Google Scholar] [CrossRef]
- Chiaramonte, L., Dreassi, A., Piserà, S., & Khan, A. (2023). Mergers and acquisitions in the financial industry: A bibliometric review and future research directions. Research in International Business and Finance, 64, 101837. [Google Scholar] [CrossRef]
- Christoffersen, P., Heston, S., & Jacobs, K. (2009). The shape and term structure of the index option smirk: Why multifactor stochastic volatility models work so well. Management Science, 55(12), 1914–1932. [Google Scholar] [CrossRef]
- Christoffersen, P., & Jacobs, K. (2004). The importance of the loss function in option valuation. Journal of Financial Economics, 72(2), 291–318. [Google Scholar] [CrossRef]
- Cox, J. C., & Ross, S. A. (1976). A survey of some new results in financial option pricing theory. The Journal of Finance, 31(2), 383–402. [Google Scholar] [CrossRef]
- Cox, J. C., Ross, S. A., & Rubinstein, M. (1979). Option pricing: A simplified approach. Journal of financial Economics, 7(3), 229–263. [Google Scholar] [CrossRef]
- Crepey, S. (2003). Calibration of the local volatility in a generalized black–scholes model using tikhonov regularization. SIAM Journal on Mathematical Analysis, 34(5), 1183–1206. [Google Scholar] [CrossRef]
- Culnan, M. J. (1987). Mapping the intellectual structure of MIS, 1980–1985: A co-citation analysis. Mis Quarterly, 11(3), 341–353. [Google Scholar] [CrossRef]
- Donthu, N., Kumar, S., Mukherjee, D., Pandey, N., & Lim, W. M. (2021). How to conduct a bibliometric analysis: An overview and guidelines. Journal of Business Research, 133, 285–296. [Google Scholar] [CrossRef]
- Duan, J.-C. (1995). The GARCH option pricing model. Mathematical Finance, 5(1), 13–32. [Google Scholar] [CrossRef]
- Egger, H., & Engl, H. W. (2005). Tikhonov regularization applied to the inverse problem of option pricing: Convergence analysis and rates. Inverse Problems, 21(3), 1027. [Google Scholar] [CrossRef]
- Farooq, R. (2023). Knowledge management and performance: A bibliometric analysis based on Scopus and WOS data (1988–2021). Journal of Knowledge Management, 27(7), 1948–1991. [Google Scholar] [CrossRef]
- Figlewski, S., & Gao, B. (1999). The adaptive mesh model: A new approach to efficient option pricing. Journal of Financial Economics, 53(3), 313–351. [Google Scholar] [CrossRef]
- Glasserman, P., & Yu, B. (2004). Number of paths versus number of basis functions in American option pricing. The Annals of Applied Probability, 14, 2090–2119. [Google Scholar] [CrossRef]
- Goodell, J. W., Kumar, S., Lahmar, O., & Pandey, N. (2023). A bibliometric analysis of cultural finance. International Review of Financial Analysis, 85, 102442. [Google Scholar] [CrossRef]
- Goodell, J. W., Kumar, S., Li, X., Pattnaik, D., & Sharma, A. (2022). Foundations and research clusters in investor attention: Evidence from bibliometric and topic modelling analysis. International Review of Economics & Finance, 82, 511–529. [Google Scholar] [CrossRef]
- Goodell, J. W., Kumar, S., Lim, W. M., & Pattnaik, D. (2021). Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. Journal of Behavioral and Experimental Finance, 32, 100577. [Google Scholar] [CrossRef]
- Guo, J., Kang, W., & Wang, Y. (2023). Option pricing under sub-mixed fractional Brownian motion based on time-varying implied volatility using intelligent algorithms. Soft Computing, 27, 15225–15246. [Google Scholar] [CrossRef]
- Hall, B. J., & Murphy, K. J. (2002). Stock options for undiversified executives. Journal of Accounting and Economics, 33(1), 3–42. [Google Scholar] [CrossRef]
- Harrison, J. M., & Kreps, D. M. (1978). Speculative investor behavior in a stock market with heterogeneous expectations. The Quarterly Journal of Economics, 92(2), 323–336. [Google Scholar] [CrossRef]
- Heston, S. L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies, 6(2), 327–343. [Google Scholar] [CrossRef]
- Heston, S. L., & Nandi, S. (2000). A closed-form GARCH option valuation model. The Review of Financial Studies, 13(3), 585–625. [Google Scholar] [CrossRef]
- Horvath, B., Muguruza, A., & Tomas, M. (2021). Deep learning volatility: A deep neural network perspective on pricing and calibration in (rough) volatility models. Quantitative Finance, 21(1), 11–27. [Google Scholar] [CrossRef]
- Ikonen, S., & Toivanen, J. (2004). Operator splitting methods for American option pricing. Applied Mathematics Letters, 17(7), 809–814. [Google Scholar] [CrossRef]
- Jackwerth, J. C., & Rubinstein, M. (1996). Recovering probability distributions from option prices. The Journal of Finance, 51(5), 1611–1631. [Google Scholar] [CrossRef]
- Jang, H., & Lee, J.-H. (2019). Generative Bayesian neural network model for risk-neutral pricing of American index options. Quantitative Finance, 19(11), 1783–1797. [Google Scholar] [CrossRef]
- Jarrow, R., & Rudd, A. (1982). Approximate option valuation for arbitrary stochastic processes. Journal of Financial Economics, 10(3), 347–369. [Google Scholar] [CrossRef]
- Kairys, J. P., Jr., & Valerio, N., III. (1997). The market for equity options in the 1870s. The Journal of Finance, 52(4), 1707–1723. [Google Scholar] [CrossRef]
- Khan, A., Goodell, J. W., Hassan, M. K., & Paltrinieri, A. (2022). A bibliometric review of finance bibliometric papers. Finance Research Letters, 47, 102520. [Google Scholar] [CrossRef]
- Knopf, J. D., Jr., Nam, J., & Thornton, J. H., Jr. (2002). The volatility and price sensitivities of managerial stock option portfolios and corporate hedging. The Journal of Finance, 57(2), 801–813. [Google Scholar] [CrossRef]
- Kolani, K., Wang, Y., Zhou, D., Nouyep Tchitchui, J. U., & Okolo, C. V. (2023). Passive building design for improving indoor thermal comfort in tropical climates: A bibliometric analysis using CiteSpace. Indoor and Built Environment, 32(6), 1095–1114. [Google Scholar] [CrossRef]
- Kou, S. G. (2002). A jump-diffusion model for option pricing. Management Science, 48(8), 1086–1101. [Google Scholar] [CrossRef]
- Kou, S. G., & Wang, H. (2004). Option pricing under a double exponential jump diffusion model. Management Science, 50(9), 1178–1192. [Google Scholar] [CrossRef]
- Kumar, S., Rao, S., Goyal, K., & Goyal, N. (2022). Journal of behavioral and experimental finance: A bibliometric overview. Journal of Behavioral and Experimental Finance, 34, 100652. [Google Scholar] [CrossRef]
- Kwok, Y. K., Leung, K. S., & Wong, H. Y. (2011). Efficient options pricing using the fast Fourier transform. In Handbook of computational finance (pp. 579–604). Springer. [Google Scholar]
- Li, K., Rollins, J., & Yan, E. (2018). Web of Science use in published research and review papers 1997–2017: A selective, dynamic, cross-domain, content-based analysis. Scientometrics, 115(1), 1–20. [Google Scholar] [CrossRef]
- Liu, D. (2022). Studies of issues on hybrid neural networks for pricing financial options. AI in Applications, 2(3), 331–339. [Google Scholar] [CrossRef]
- Liu, W. (2019). The data source of this study is web of science core collection? Not enough. Scientometrics, 121(3), 1815–1824. [Google Scholar] [CrossRef]
- Madureira, B., Pinto, T., Fernandes, F., & Vale, Z. (2017, June 18–22). Context analysis in energy resource management residential buildings. 2017 IEEE Manchester PowerTech (pp. 1–6), Manchester, UK. [Google Scholar]
- Market Watch. (2025). 2024 was another record-breaking year for options trading—What’s on tap for the industry in 2025? Available online: https://www.marketwatch.com/story/2024-was-another-record-breaking-year-for-options-trading-whats-on-tap-for-the-industry-in-2025-8f4a097c (accessed on 1 September 2025).
- Merigó, J. M., Yang, J.-B., & Xu, D.-L. (2015). A bibliometric overview of financial studies. In Scientific methods for the treatment of uncertainty in social sciences (pp. 245–254). Springer International Publishing. [Google Scholar]
- Merton, R. C. (1973). Theory of rational option pricing. The Bell Journal of Economics and Management Science, 141–183. [Google Scholar] [CrossRef]
- Migliavacca, M., Goodell, J. W., & Paltrinieri, A. (2023). A bibliometric review of portfolio diversification literature. International Review of Financial Analysis, 90, 102836. [Google Scholar] [CrossRef]
- Mordecki, E. (2002). Optimal stopping and perpetual options for Lévy processes. Finance and Stochastics, 6, 473–493. [Google Scholar] [CrossRef]
- Myneni, R. (1992). The pricing of the American option. The Annals of Applied Probability, 1–23. [Google Scholar] [CrossRef]
- Nasir, A., Farooq, U., & Khan, A. (2021). Conceptual and influential structure of Takaful literature: A bibliometric review. International Journal of Islamic and Middle Eastern Finance and Management, 14(3), 599–624. [Google Scholar] [CrossRef]
- Paltrinieri, A., Hassan, M. K., Bahoo, S., & Khan, A. (2023). A bibliometric review of sukuk literature. International Review of Economics & Finance, 86, 897–918. [Google Scholar] [CrossRef]
- Randhawa, K., Wilden, R., & Hohberger, J. (2016). A bibliometric review of open innovation: Setting a research agenda. Journal of Product Innovation Management, 33(6), 750–772. [Google Scholar] [CrossRef]
- Rubinstein, M. (1994). On the accounting valuation of employee stock options. Institute of Business and Economic Research, University of California, Berkeley. [Google Scholar]
- Samuelson, P. (1965). Rational theory of warrant pricing. Industrial Management Review, 6, 13–32. [Google Scholar]
- Samuelson, P. A. (1960). The St. Petersburg paradox as a divergent double limit. International Economic Review, 1(1), 31–37. [Google Scholar] [CrossRef]
- Sánchez, A. D., Del Río, M. d. l. C., & García, J. Á. (2017). Bibliometric analysis of publications on wine tourism in the databases Scopus and WoS. European Research on Management and Business Economics, 23(1), 8–15. [Google Scholar] [CrossRef]
- Small, H. (1973). Co-citation in the scientific literature: A new measure of the relationship between two documents. Journal of the American Society for information Science, 24(4), 265–269. [Google Scholar] [CrossRef]
- Trujillo, C. M., & Long, T. M. (2018). Document co-citation analysis to enhance transdisciplinary research. Science Advances, 4(1), e1701130. [Google Scholar] [CrossRef]
- Van Eck, N., & Waltman, L. (2010). Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics, 84(2), 523–538. [Google Scholar] [CrossRef]
- Vogel, R., & Güttel, W. H. (2013). The dynamic capability view in strategic management: A bibliometric review. International Journal of Management Reviews, 15(4), 426–446. [Google Scholar] [CrossRef]
- Wang, S. (2004). A novel fitted finite volume method for the Black–Scholes equation governing option pricing. IMA Journal of Numerical Analysis, 24(4), 699–720. [Google Scholar] [CrossRef]
- Wei, G. (1999). Discrete singular convolution for the solution of the Fokker–Planck equation. The Journal of Chemical Physics, 110(18), 8930–8942. [Google Scholar] [CrossRef]
- Wu, Y.-C. J., & Wu, T. (2017). A decade of entrepreneurship education in the Asia Pacific for future directions in theory and practice. Management Decision, 55(7), 1333–1350. [Google Scholar] [CrossRef]
- Xu, S., Liu, J., Zhai, D., An, X., Wang, Z., & Pang, H. (2018). Overlapping thematic structures extraction with mixed-membership stochastic blockmodel. Scientometrics, 117(1), 61–84. [Google Scholar] [CrossRef]
- Xu, X., Chen, X., Jia, F., Brown, S., Gong, Y., & Xu, Y. (2018). Supply chain finance: A systematic literature review and bibliometric analysis. International Journal of Production Economics, 204, 160–173. [Google Scholar] [CrossRef]
- Yamamoto, Y. (2005). Double-exponential fast Gauss transform algorithms for pricing discrete lookback options. Publications of the Research Institute for Mathematical Sciences, 41(4), 989–1006. [Google Scholar] [CrossRef]
- Zhang, J., Quoquab, F., & Mohammad, J. (2023). What do we know about plastic pollution in coastal/marine tourism? Documenting its present research status from 1999 to 2022. Sage Open, 13(4), 21582440231211706. [Google Scholar] [CrossRef]
- Zhao, S., & Wei, G.-W. (2005). Option valuation by using discrete singular convolution. Applied Mathematics and Computation, 167(1), 383–418. [Google Scholar] [CrossRef]
- Zhu, S.-P. (2006). An exact and explicit solution for the valuation of American put options. Quantitative Finance, 6(3), 229–242. [Google Scholar] [CrossRef]

| Top Authors | Top Institutions | Top Countries | ||||||
|---|---|---|---|---|---|---|---|---|
| Authors | TP | TC | Institution | TP | TC | Country | TP | TC |
| Zhu, Song-Ping | 17 | 441 | University Wollongong | 32 | 535 | China | 248 | 2296 |
| Wang, Xingchun | 15 | 104 | University of International Business and Economics | 17 | 108 | USA | 203 | 6449 |
| Wang, Song | 14 | 215 | Iran University of Science and Technology | 16 | 229 | Australia | 104 | 1524 |
| He, Xin-Jiang | 11 | 70 | University Mauritius | 13 | 199 | England | 87 | 1530 |
| Chen, Wenting | 10 | 187 | Columbia University | 11 | 1670 | Taiwan | 73 | 909 |
| Kim, Jeong-Hoon | 10 | 98 | Jilin University | 11 | 123 | Republic of Korea | 72 | 435 |
| Ballestra, Luca Vincenzo | 7 | 205 | Southwestern University of Finance and Economics | 11 | 102 | Iran | 70 | 566 |
| Company, Rafael | 7 | 140 | Zhejiang University | 11 | 191 | Italy | 67 | 900 |
| Company, R. | 6 | 72 | The University of Tabriz | 10 | 24 | Germany | 59 | 744 |
| Jodar, L. | 6 | 72 | University of Western Australia | 9 | 344 | Canada | 50 | 1007 |
| Lu, Xiaoping | 6 | 62 | Polytechnic University of the Marches | 8 | 213 | India | 48 | 309 |
| Zhang, Kai | 6 | 50 | Islamic Azad University | 7 | 44 | France | 43 | 475 |
| Bhuruth, M. | 5 | 166 | University of Naples Federico II | 7 | 224 | Spain | 29 | 435 |
| Jodar, Lucas | 5 | 77 | Fuzhou University | 5 | 160 | Belgium | 24 | 332 |
| Xu, Xiang | 5 | 156 | Queensland University of Technology | 5 | 160 | Mauritius | 13 | 199 |
| Journal Name | TP | TC | CPP | JIF | JCI |
|---|---|---|---|---|---|
| Physica A-Statistical Mechanics and Its Applications | 61 | 936 | 15 | 3.3 | 0.9 |
| Journal of Computational and Applied Mathematics | 48 | 874 | 18 | 2.4 | 1.4 |
| Journal of Futures Markets | 44 | 457 | 10 | 1.9 | 0.6 |
| Quantitative Finance | 44 | 619 | 14 | 1.3 | 0.5 |
| Computational Economics | 26 | 188 | 7 | 2.0 | 0.6 |
| Computers & Mathematics with Applications | 26 | 677 | 26 | 2.9 | 1.7 |
| Applied Mathematics and Computation | 25 | 335 | 13 | 4.0 | 2.3 |
| North American Journal of Economics and Finance | 24 | 112 | 5 | 3.6 | 1.1 |
| Chaos Solitons & Fractals | 19 | 170 | 9 | 7.8 | 2.5 |
| International Journal of Computer Mathematics | 17 | 119 | 7 | 1.8 | 0.9 |
| Journal of Computational Finance | 17 | 120 | 7 | 0.9 | 0.3 |
| Journal of Economic Dynamics & Control | 12 | 274 | 23 | 1.9 | 0.6 |
| Applied Mathematics Letters | 9 | 223 | 25 | 3.7 | 2.3 |
| Mathematical Methods in The Applied Sciences | 9 | 25 | 3 | 2.9 | 1.5 |
| Management Science | 8 | 1719 | 215 | 5.4 | 1.2 |
| Reference | Article Title | Journal | Times Cited (WoS) |
|---|---|---|---|
| (Kou, 2002) | A jump-diffusion model for option pricing | Management Science | 955 |
| (Hall & Murphy, 2002) | Stock options for undiversified executives | Journal Of Accounting & Economics | 545 |
| (Carr & Wu, 2004) | Time-changed Levy processes and option pricing | Journal of Financial Economics | 301 |
| (Kou & Wang, 2004) | Option pricing under a double exponential jump diffusion model | Management Science | 300 |
| (Christoffersen et al., 2009) | The Shape and Term Structure of the Index Option Smirk: Why Multifactor Stochastic Volatility Models Work So Well | Management Science | 267 |
| (Cartea & del Castillo-Negrete, 2007) | Fractional diffusion models of option prices in markets with jumps | Physica A-Statistical Mechanics and Its Applications | 208 |
| (Knopf et al., 2002) | The volatility and price sensitivities of managerial stock option portfolios and corporate hedging | Journal of Finance | 196 |
| (Bollerslev et al., 2011) | Dynamic estimation of volatility risk premia and investor risk aversion from option-implied and realized volatilities | Journal of Econometrics | 173 |
| (Zhu, 2006) | An exact and explicit solution for the valuation of American put options | Quantitative Finance | 173 |
| (Borland, 2002) | Option pricing formulas based on a non-Gaussian stock price model | Physical Review Letter | 162 |
| (Wang, 2004) | A novel fitted finite volume method for the Black-Scholes equation governing option pricing | IMA Journal of Numerical Analysis | 129 |
| (Mordecki, 2002) | Optimal stopping and perpetual options for Levy processes | Finance and Stochastics | 129 |
| (Ikonen & Toivanen, 2004) | Operator splitting methods for American option pricing | Applied Mathematics Letters | 127 |
| (Barone-Adesi et al., 2008) | A GARCH option pricing model with filtered historical simulation | Review of Financial Studies | 125 |
| (Broadie et al., 2009) | Understanding Index Option Returns | Review of Financial Studies | 119 |
| Theme | Description | References |
|---|---|---|
| Deep Learning and Hybrid Neural Networks | Deep learning models (DNN, LSTM, FBSDE) are widely used to price and hedge options under frictions. They offer improved calibration and performance over traditional models. | (Ashok Naarayan & Parpas, 2024; Horvath et al., 2021) |
| Stochastic and Rough Volatility Modeling | Incorporates rough paths, fractional Brownian motion and stochastic processes with ML to better match observed volatility surfaces. | (Guo et al., 2023; Jang & Lee, 2019) |
| Market Frictions and xVA Adjustments | Modern pricing accounts for bid-ask spreads, liquidity constraints and valuation adjustments using neural strategies. | (Anderson & Ulrych, 2023; D. Liu, 2022) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alokley, S.A. Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. J. Risk Financial Manag. 2025, 18, 513. https://doi.org/10.3390/jrfm18090513
Alokley SA. Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. Journal of Risk and Financial Management. 2025; 18(9):513. https://doi.org/10.3390/jrfm18090513
Chicago/Turabian StyleAlokley, Sara Ali. 2025. "Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends" Journal of Risk and Financial Management 18, no. 9: 513. https://doi.org/10.3390/jrfm18090513
APA StyleAlokley, S. A. (2025). Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. Journal of Risk and Financial Management, 18(9), 513. https://doi.org/10.3390/jrfm18090513






