Performance of Pairs Trading Strategies Based on Various Copula Methods
Abstract
1. Introduction
2. Literature Review
2.1. Distance Method
- Foundational Studies
- International Evidence
- Methodological Innovations
2.2. Copula Method
- Early Applications of Copulas in Pairs Trading
- Expanded Empirical Studies and Comparisons
- Advanced Extensions of Copula Approaches
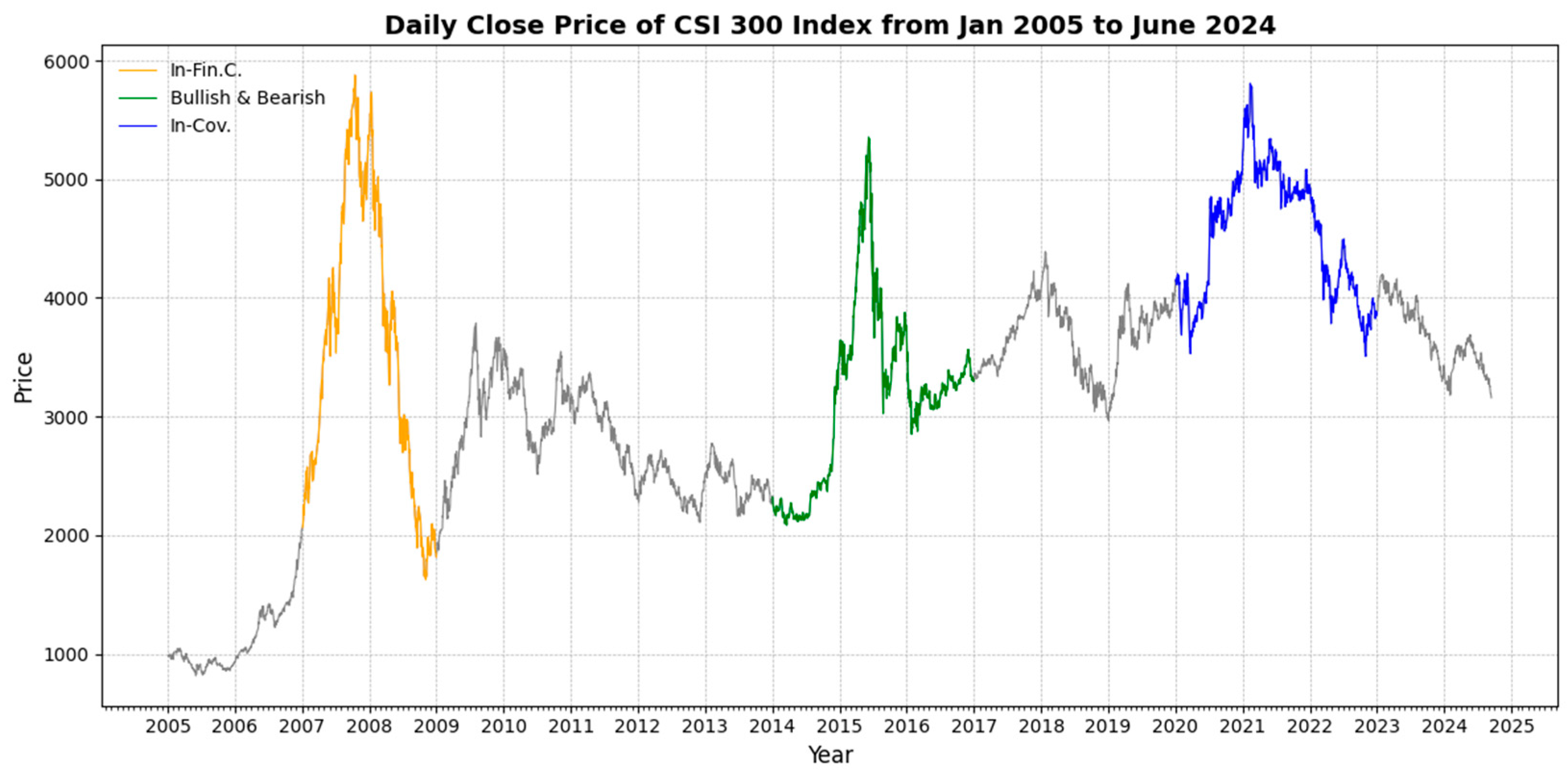
3. Data
4. Methodology
4.1. The Distance Method
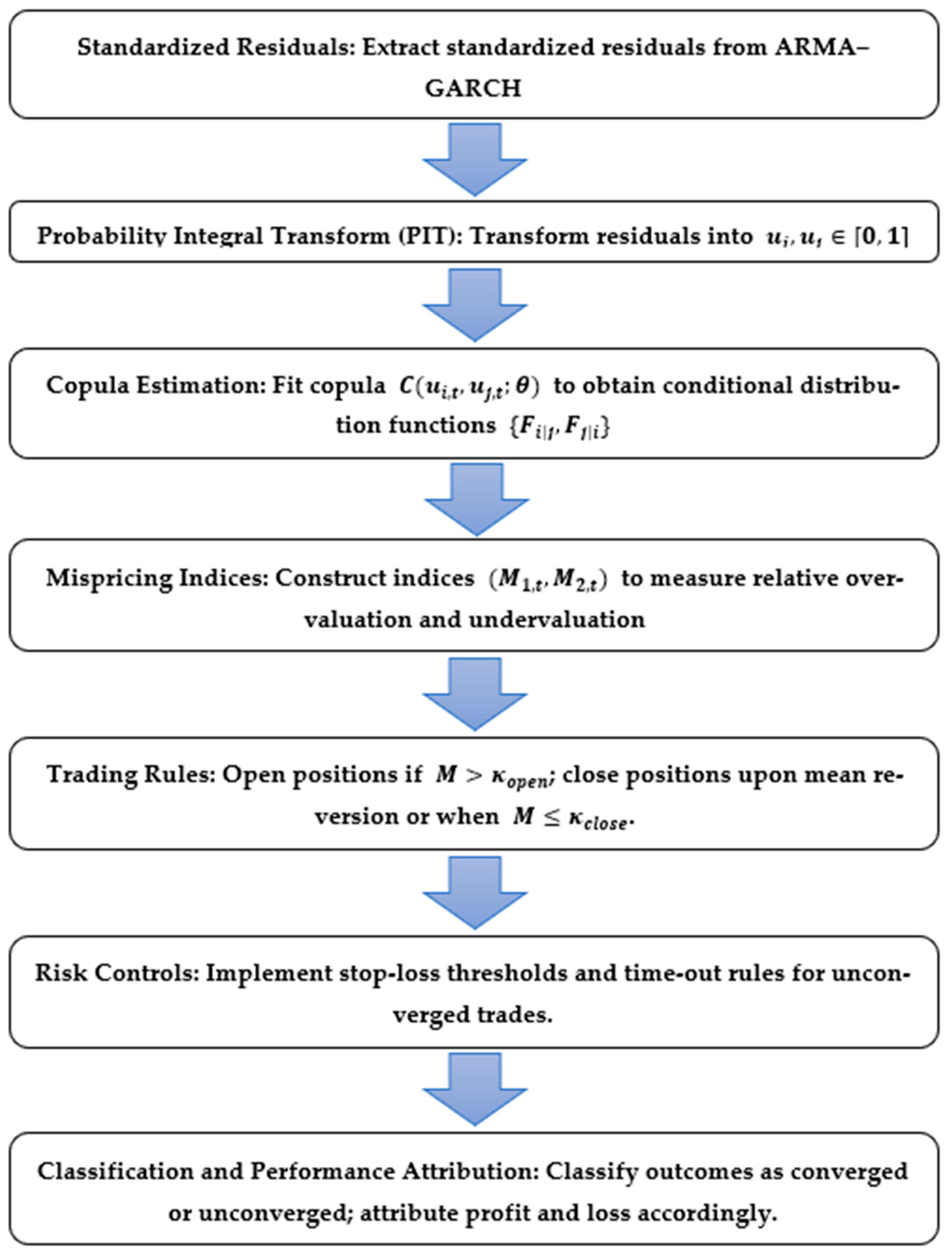
4.2. The Mispricing Index Copula Method
4.2.1. Method Framework Overview
4.2.2. Trading Strategy
4.3. The Optimal Copula Method
4.3.1. Method Framework Overview
4.3.2. Trading Strategy
4.4. The Mixed Copula Method
4.4.1. Method Framework Overview
4.4.2. Estimation of Mixed Copula Parameters
4.5. Transaction Costs
4.6. Return Calculation
5. Results
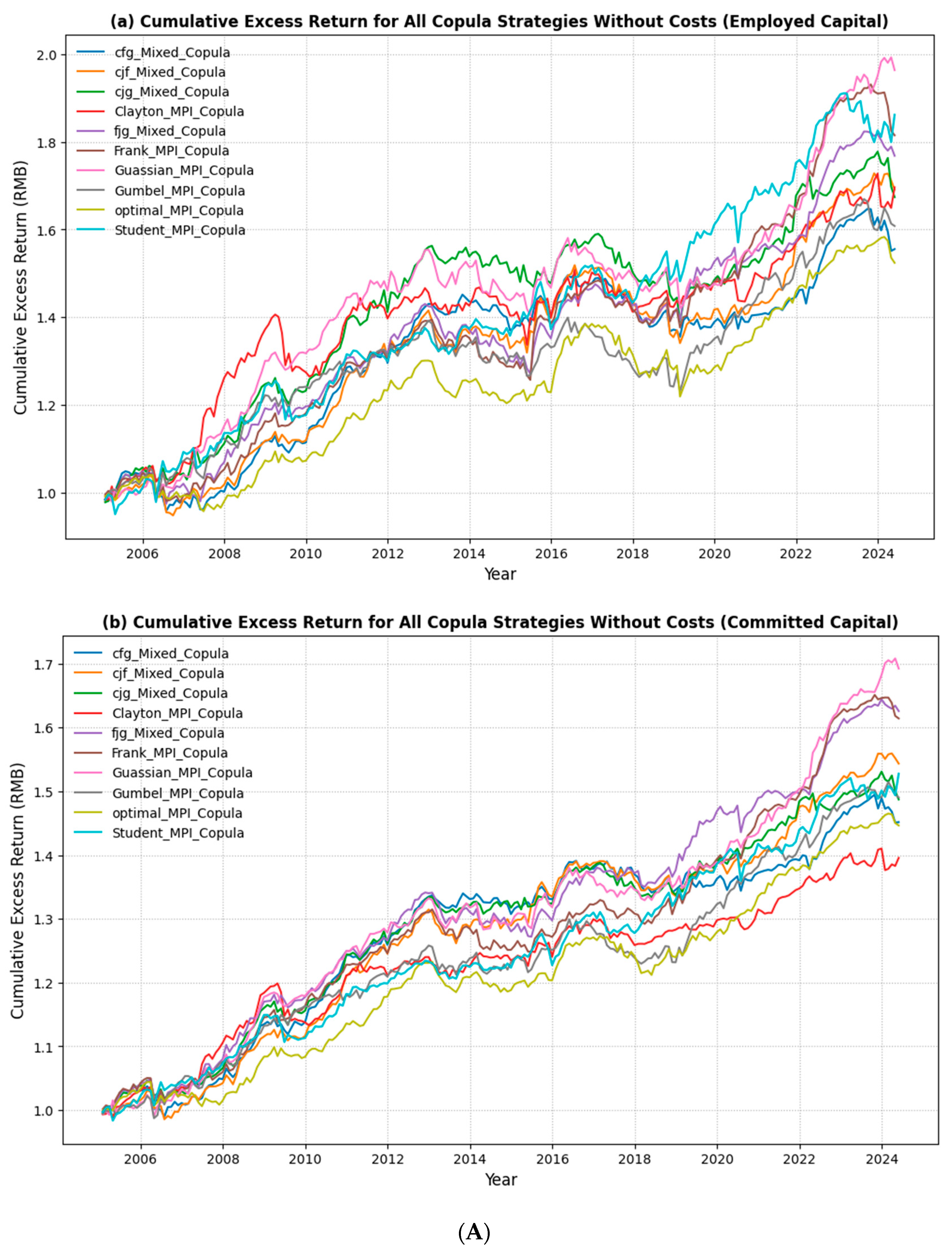
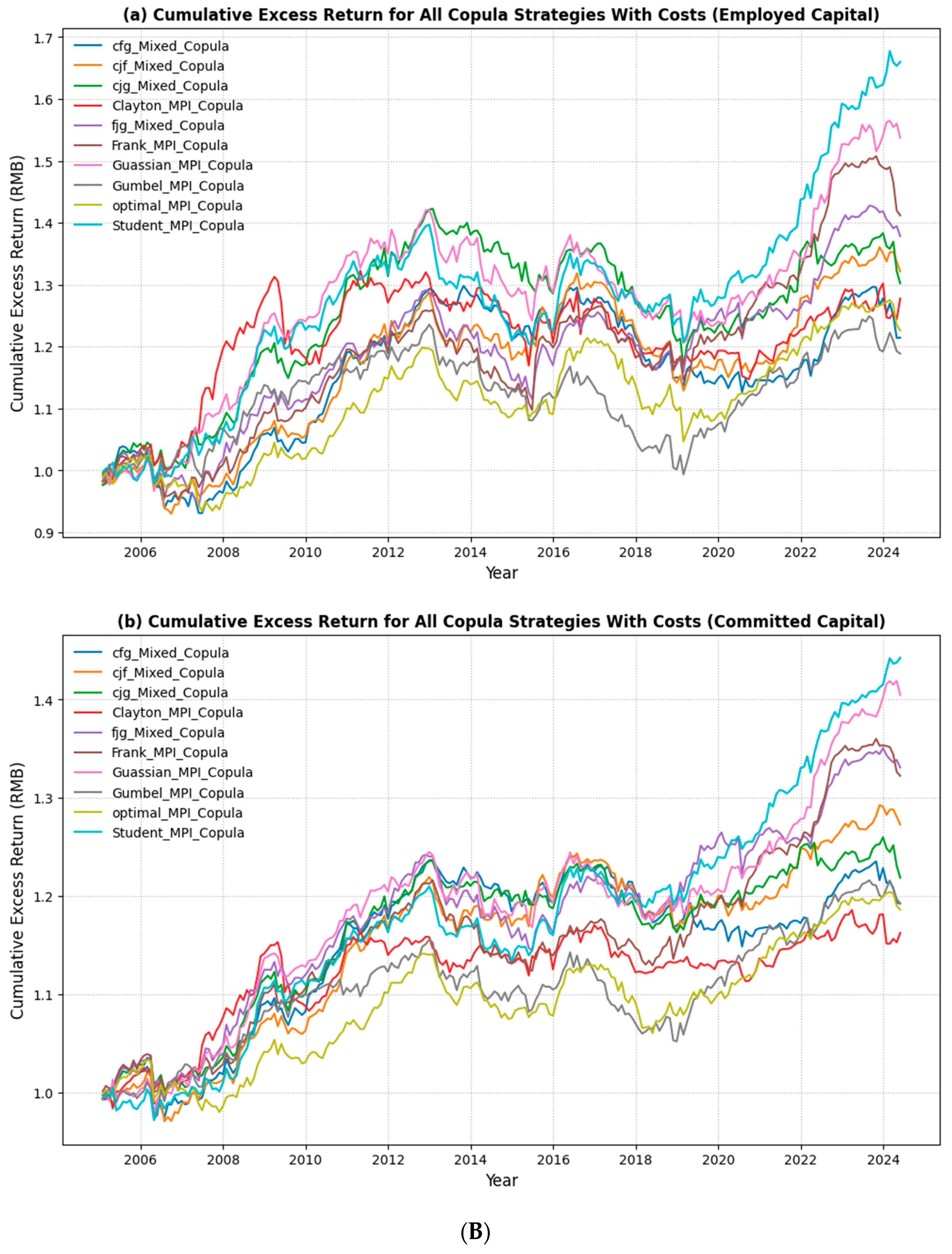
5.1. Profitability of the Strategies
Statistical Significance Tests
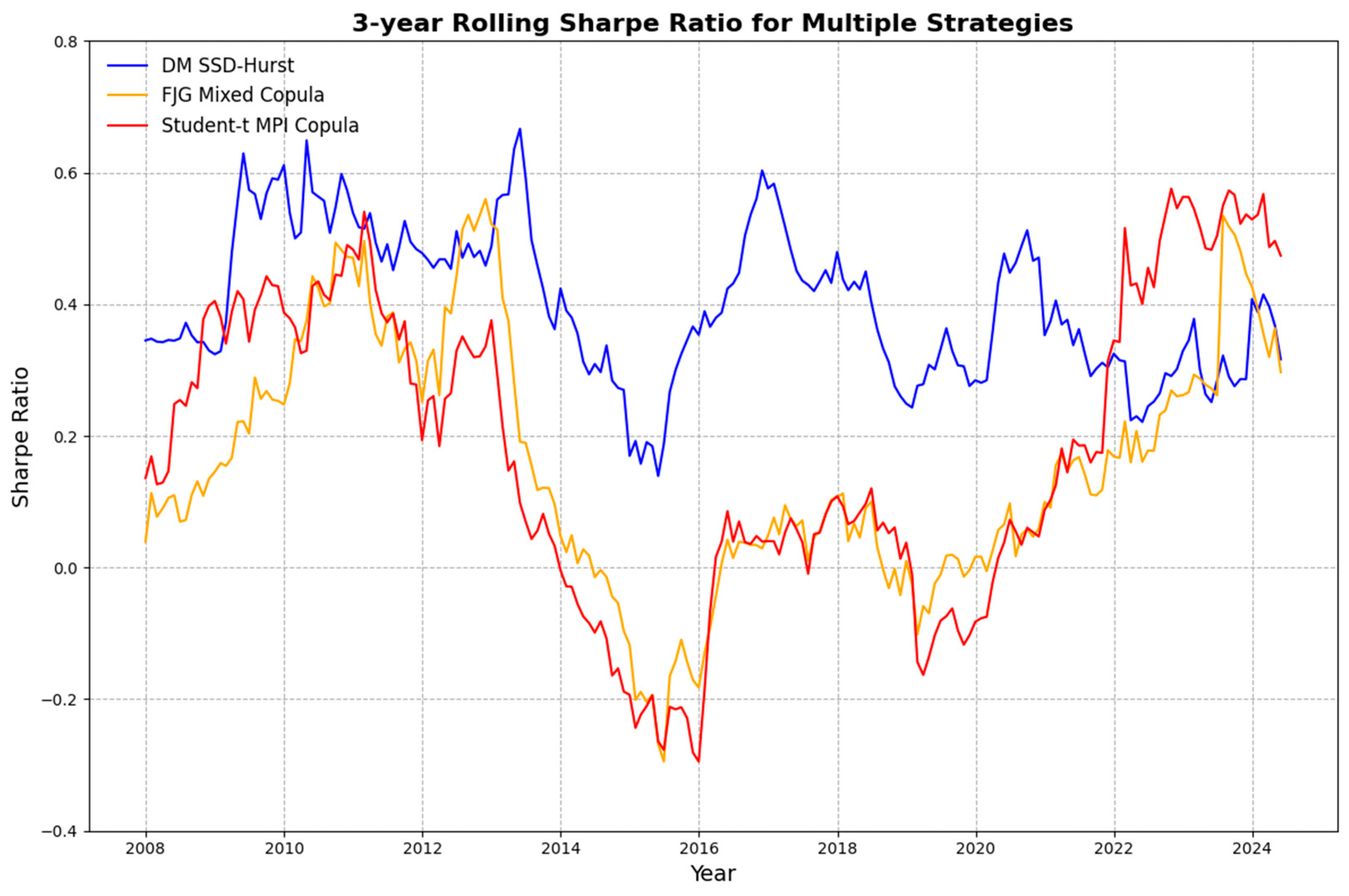
5.2. Risk Adjusted Performance
5.3. Risk Characteristics of Pairs Trading Strategies
5.4. Robustness and Sensitivity Analysis
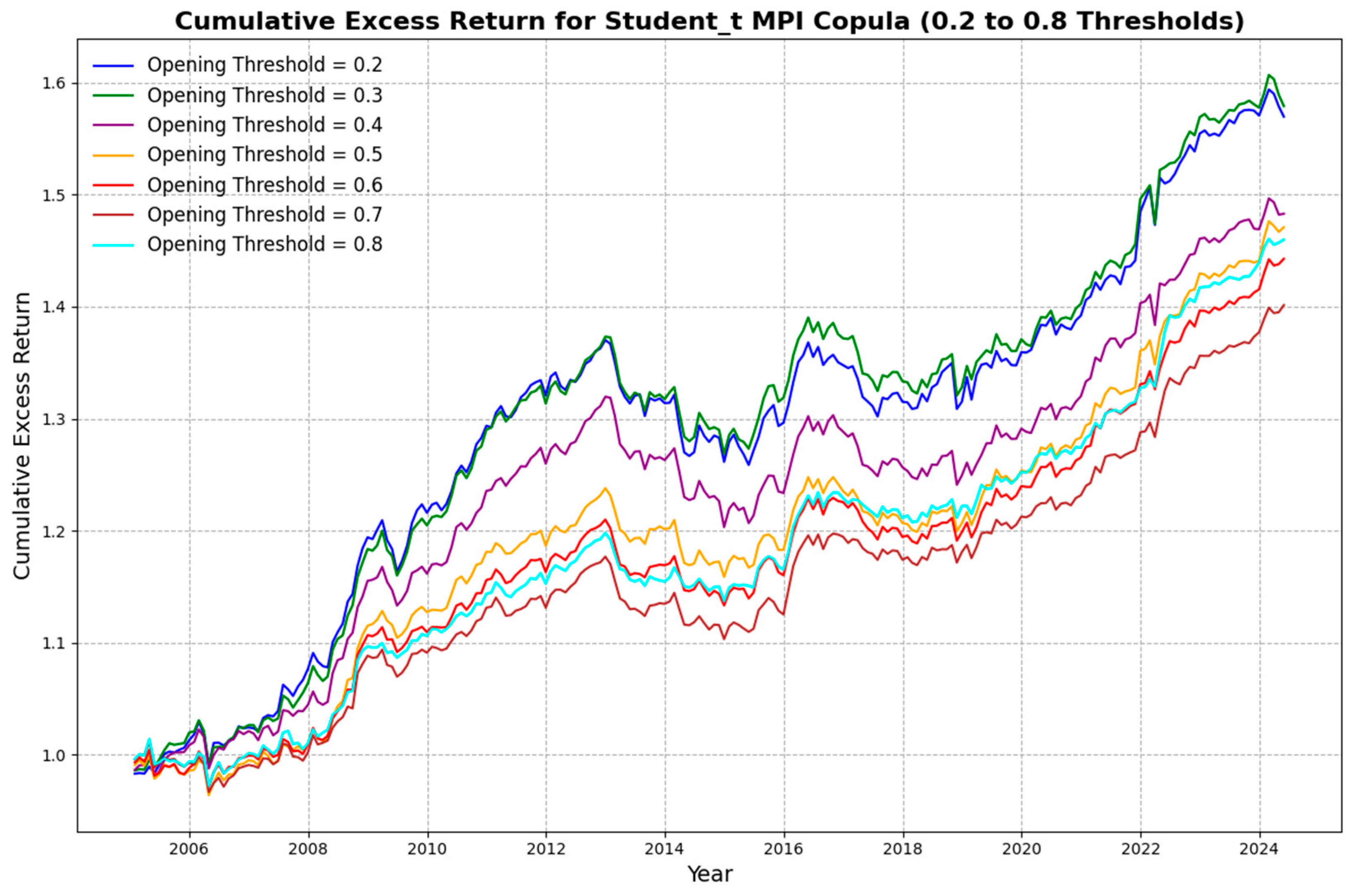
5.4.1. Varying Opening Thresholds
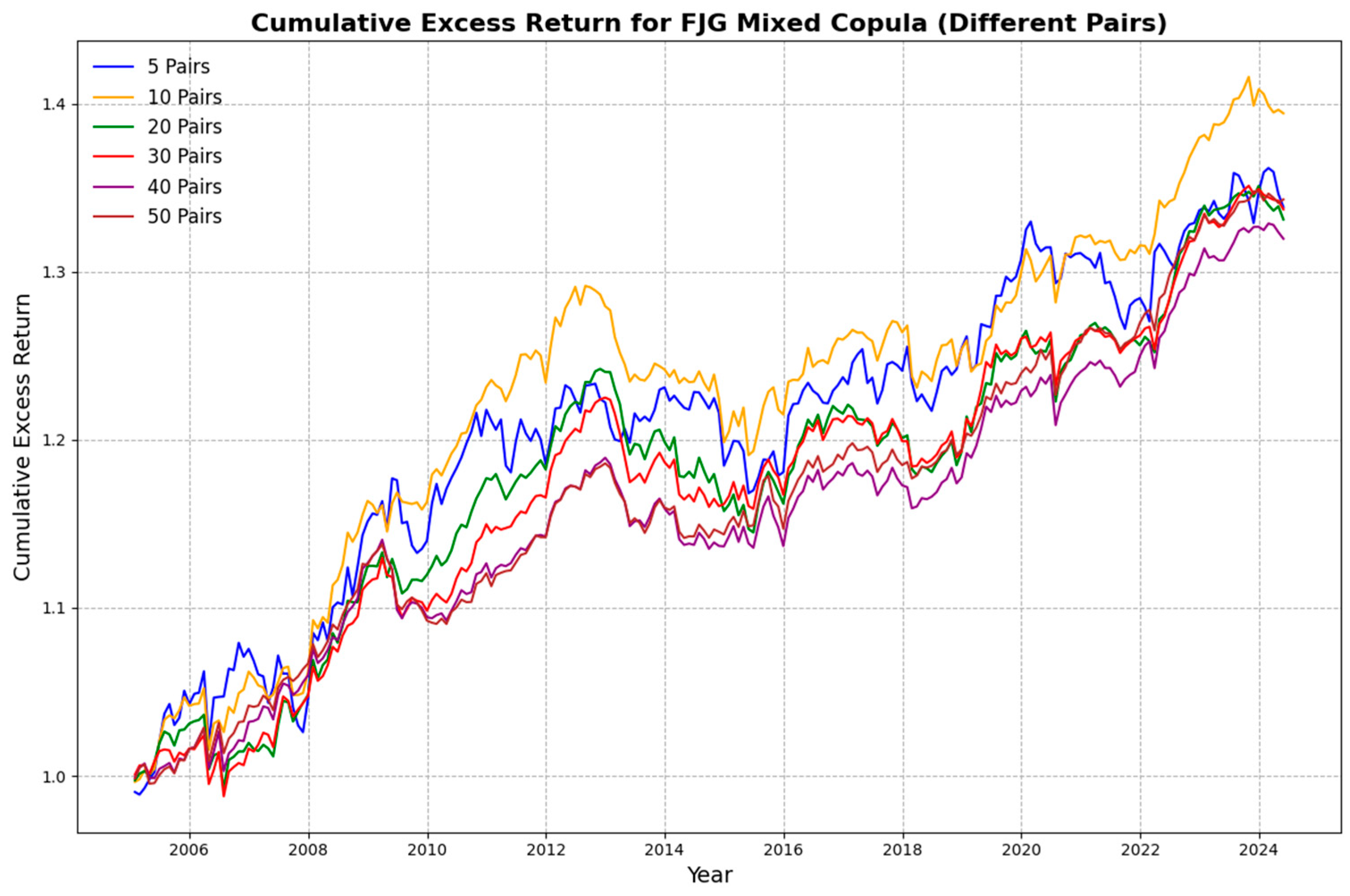
5.4.2. Varying Number of Pairs Traded
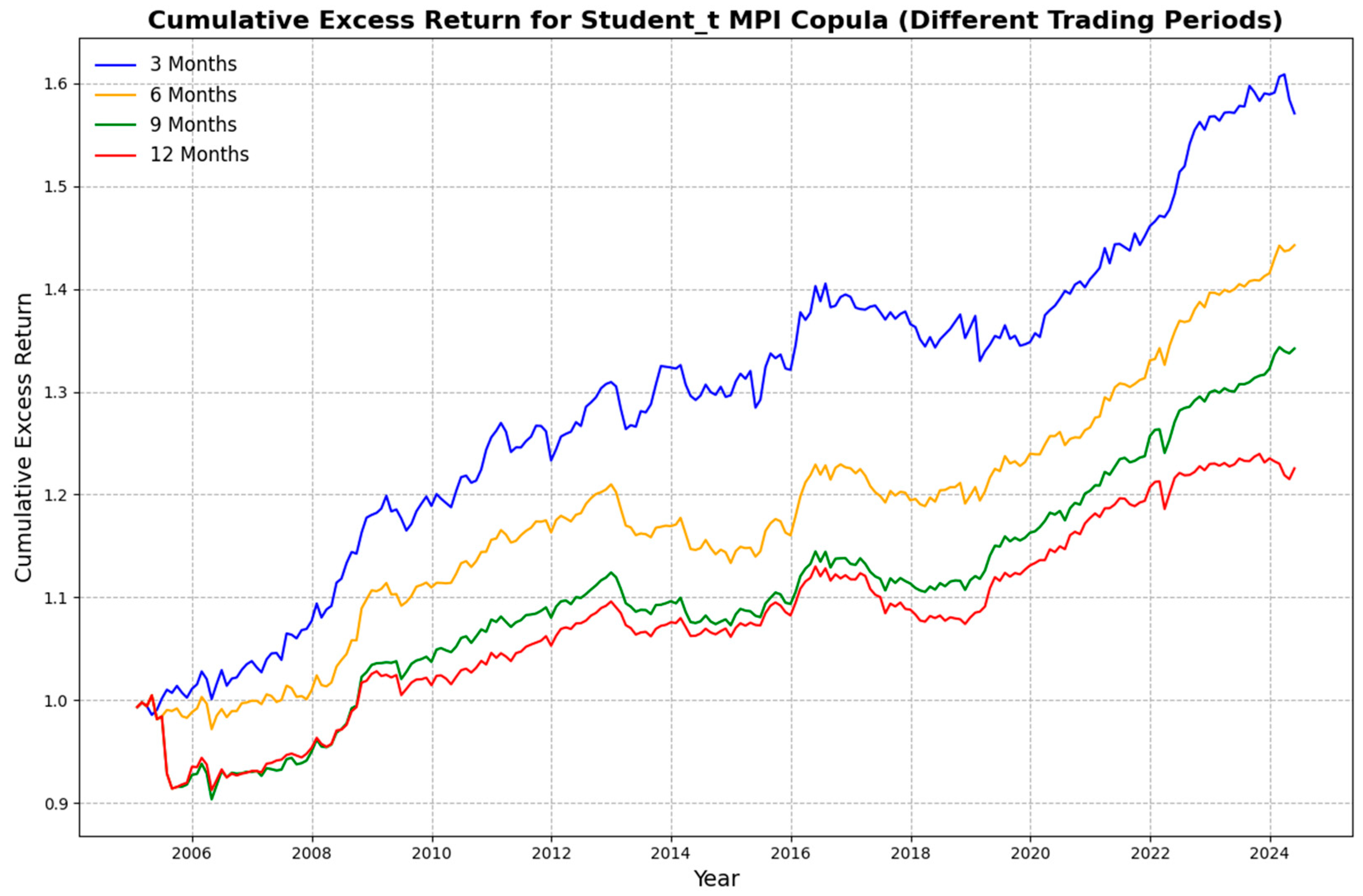
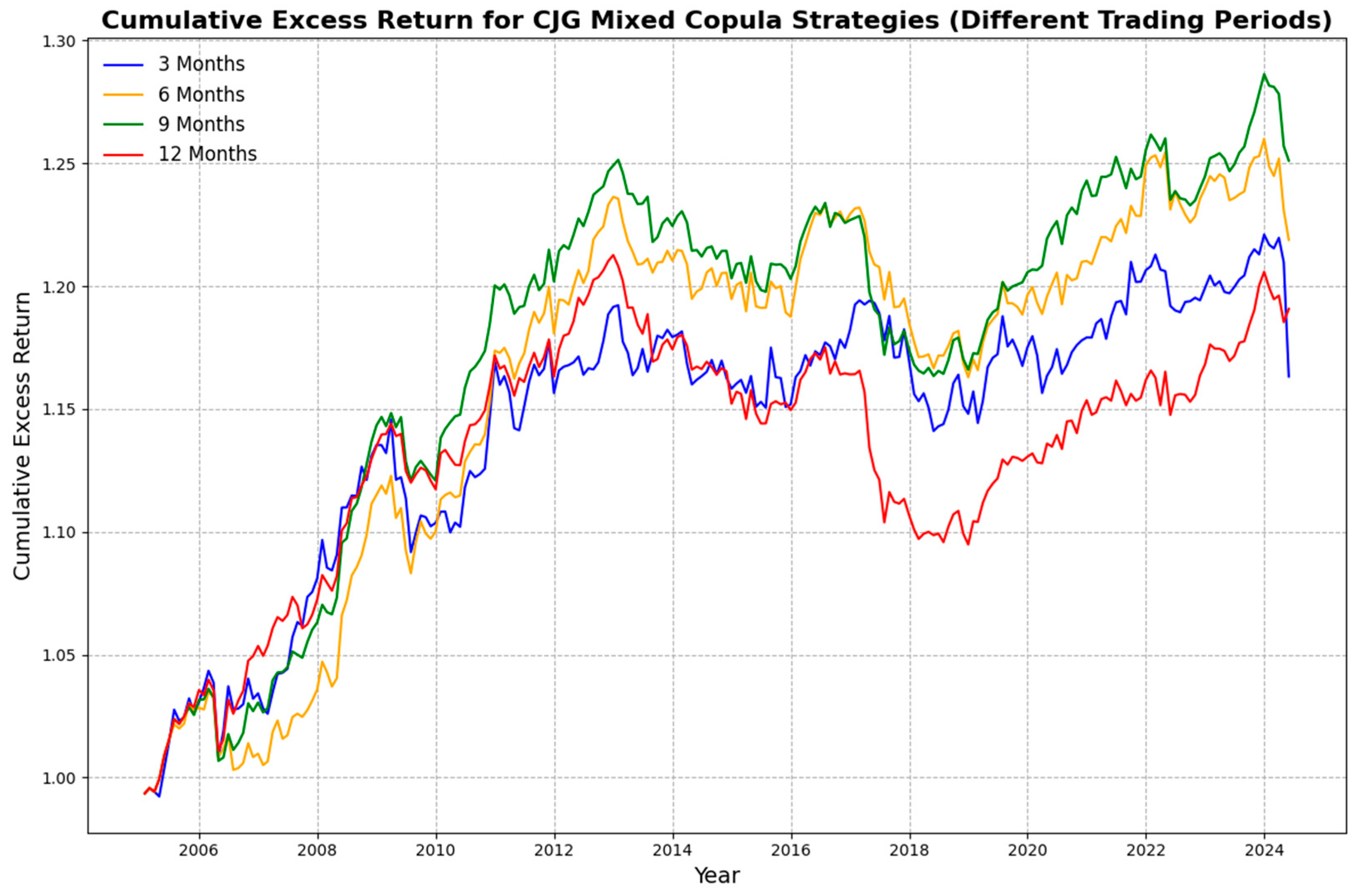
5.4.3. Varying Trading Period
5.4.4. Varying Market Capitalization
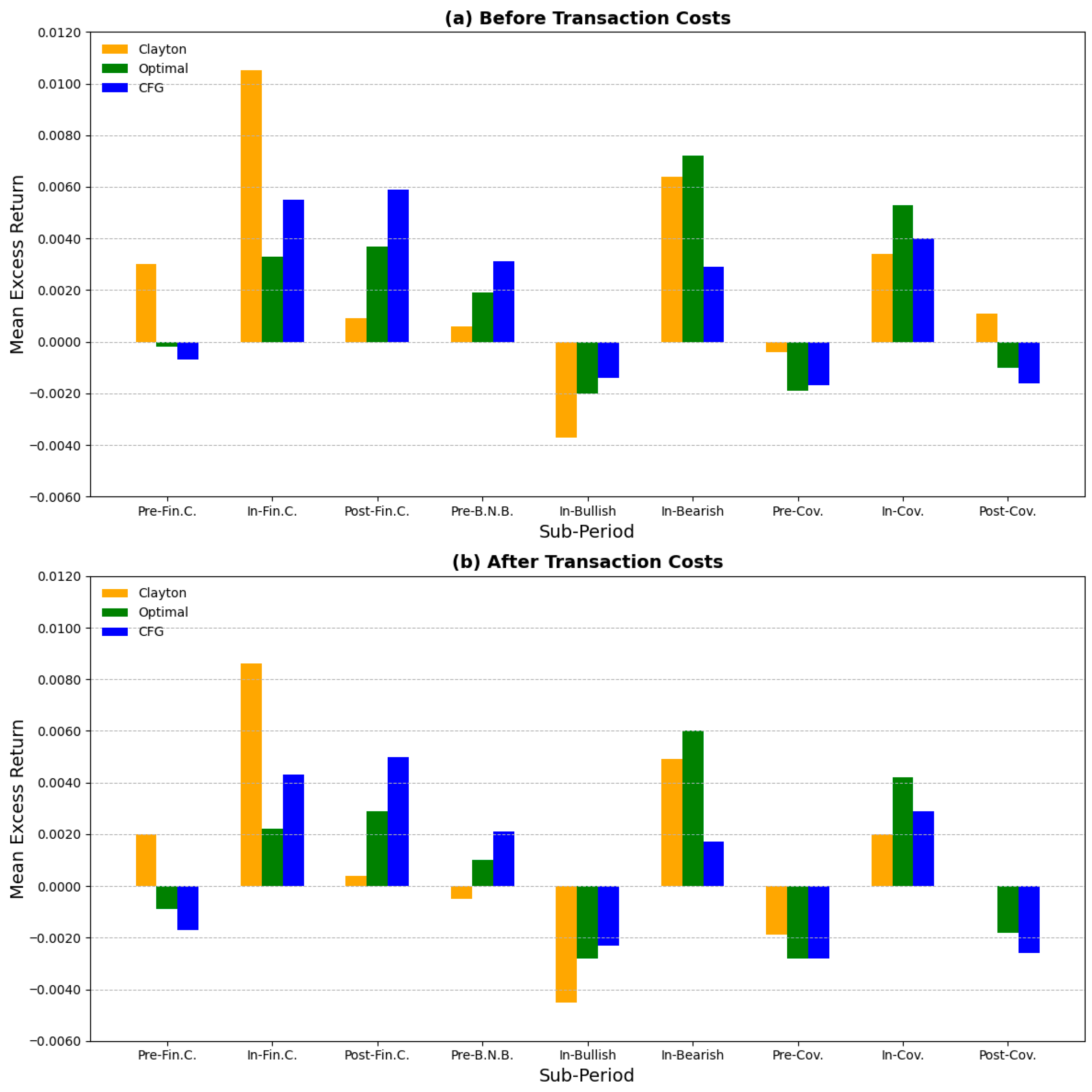
5.5. Sub-Period Performance Analysis
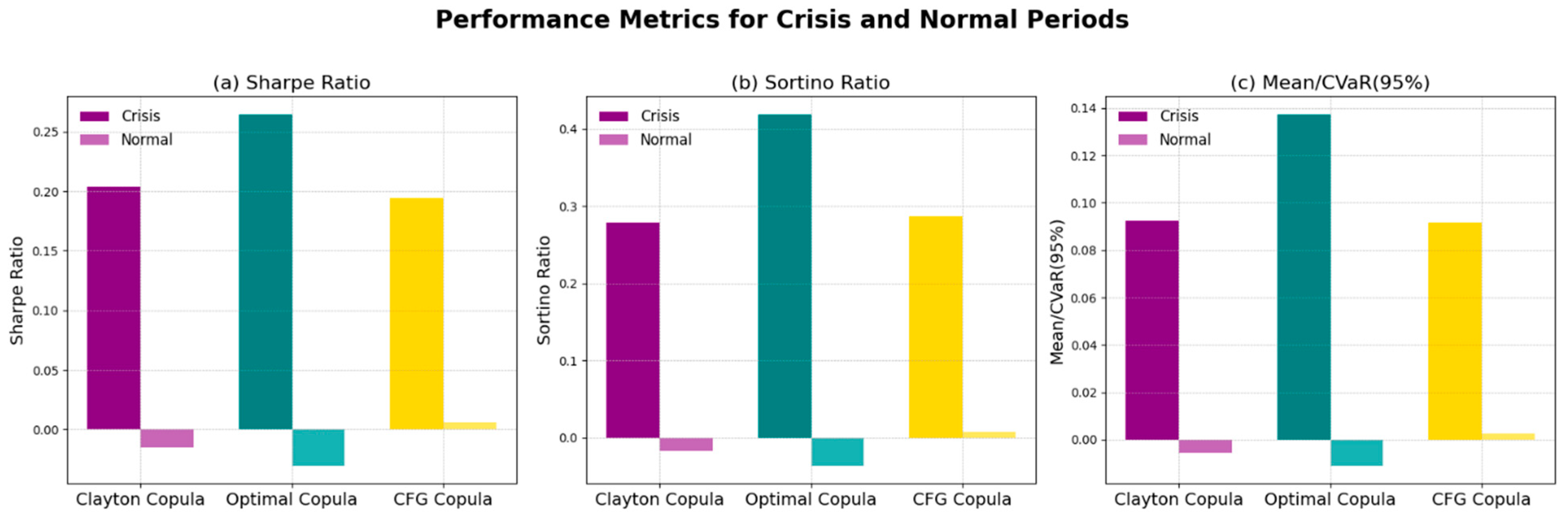
5.6. Crisis Versus Non-Crisis
6. Discussion
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Dimension | Distance Method (DM) | Copula-Based Approaches |
|---|---|---|
| Underlying Principle | Spread-based mean reversion; pairs selected by minimizing SSD; trades triggered when spread deviates from historical mean. | Dependence modeling; separates marginals from dependence structure; uses copulas to model joint behavior of returns. |
| Dependence Structure | Linear correlation; symmetric mean-reversion. | Nonlinear, asymmetric, and tail dependence; captures extreme co-movements. |
| Modeling Flexibility | Rigid, correlation-driven; limited for higher-order dependence. | Flexible, distribution-free; adapts to diverse dependence patterns. |
| Computational Requirements | Low; simple and efficient. | Higher; requires marginal modeling and parameter estimation (e.g., likelihood, EM). |
| Strengths | Transparent, intuitive, historically profitable; natural benchmark. | Richer dependence modeling; potentially more robust in volatile/crisis periods. |
| Limitations | Declining profitability; ignores nonlinearities and tail risk. | Computationally intensive; risk of overfitting; sensitive to copula choice. |
| Practical Relevance | Widely used baseline in practice. | Advanced framework; attractive to sophisticated investors seeking robustness. |
| Study | Sample Period | Market | Method | Main Findings |
|---|---|---|---|---|
| Gatev et al. (2006) | 1962–2002 | U.S. (CRSP) | Distance Method | DM generates significant excess returns; ~1.3% monthly; robust after re-testing. |
| Do and Faff (2010, 2012) | 1962–2009 | U.S. | Distance Method | Profitability peaked in 1970s–80s; declined post-1990s; still positive in bear markets; eroded by transaction costs. |
| Andrade et al. (2005) | 1990–2002 | U.S. Treasury bond futures | Distance Method | Pairs trading generates consistent abnormal profits in futures markets. |
| Perlin (2009) | 1995–2002 | Brazil (BOVESPA) | Distance Method | Strategy yields significant excess returns in an emerging market setting. |
| Broussard and Vaihekoski (2012) | 1926–2010 | Finland | Distance Method | DM profitable over long horizons; profitability varies by regime and transaction costs. |
| Jacobs and Weber (2015) | 34 countries | Global | Distance Method | DM yields positive returns; profitability varies with investor over/under-reaction. |
| Miao and Laws (2016) | 12 countries | Global | Distance Method | Profitable in most countries, even in bear markets; returns deteriorate under high costs. |
| Bogomolov (2013) | 2004–2012 | U.S. Australia | Distance + Technical (Renko, Kagi) | Non-parametric extension; monthly returns up to 3.65%. |
| Zeng and Lee (2014) | 2009–2012 | U.S. | Distance + OU process | Optimized thresholds improve performance. |
| Liew and Wu (2013) | 2000–2009 | U.S. | Copula (Gumbel, Clayton, t) | Copulas capture tail dependence, outperform DM; limited dataset. |
| Stander et al. (2013) | 1999–2009 | U.S. | Conditional Copulas | Profitable signals, but profits eroded by equity costs; futures improve feasibility. |
| Xie et al. (2016) | 2003–2012 | U.S. utilities | Copula | Outperforms DM; fewer negative-return trades; limited horizon. |
| Rad et al. (2016) | 1962–2014 | U.S. | DM, Cointegration, Copula | DM > Copula in raw returns, but copulas more stable in later years; computationally costly. |
| Stübinger et al. (2018) | 1990–2015 | U.S. (S&P 500) | Vine Copula | Annualized returns 9.25%, Sharpe 1.12; robust under crises. |
| Keshavarz Haddad and Talebi (2023) | 2017–2020 | Canada (TSX) | DM, Cointegration, Copula | Copula highest profitability; robust during COVID-19. |
| He et al. (2024) | 2010–2022 | China (A-shares) | Multivariate and Mixture Copula | Trivariate copulas improve dependence modeling, reduce false signals. |
| Period | Commission | Stamp Duty | Market Impact and Slippage | Do and Faff (2012) | Zhang (2018) |
|---|---|---|---|---|---|
| Pre-Fin.C.: Jan 2005–Dec 2006 | Ranged 0.1–0.3%. Selection criterion: 0.2% (buy and sell). | 24 January 2005: Stamp duty reduced from 0.2 to 0.1%, applied to both buying and selling. Selection criterion: 0.2% (buy and sell) | Refer Do and Faff (2012) Assign a market impact cost of 0.3%. | 1963–2009: commission + market impact of 0.60% (i.e., 0.34% + 0.26%) (60 bps). | SHSE 2005: 0.62% SZSE 2005: 0.73% SHSE 2006: 0.79% SZSE 2006: 0.82% |
| In-Fin.C.: Jan 2007–Dec 2008 | Remained 0.1–0.3%. Selection criterion: 0.2% (buy and sell). | 30 May 2007: Stamp duty increased from 0.1 to 0.3% (buys and sells). 24 April 2008: Reduced to 0.1%. 19 September 2008: applied to sales only at 0.1%. Selection criterion: 0.2% (buy and sell). | Based on historical experience, the slippage is set to a fixed value of 0.3%. | - | SHSE 2007: 0.92% SZSE 2007: 1.01% SSE 2008: 0.86% SZSE 2008: 0.87% |
| Post-Fin.C.: Jan 2009–Dec 2010 | Ranged 0.05–0.2%. Selection criterion: 0.2% (buy and sell). | Maintained at 0.1%, sales only. Selection criterion: 0.1% (buy and sell). | - | - | SHSE 2009: 0.78% SZSE 2009: 0.81% SSE 2010: 0.68% SZSE 2010: 0.75% |
| Pre-B.N.B.: Jan 2011–Dec 2013 | Ranged 0.05–0.1%. Selection criterion: 0.2% (buy and sell). | Maintained at 0.1%, sales only. Selection criterion: 0.1% (buy and sell). | - | - | SHSE 2011: 0.56% SZSE 2011: 0.60% SSE 2012: 0.52% SZSE 2012: 0.61% |
| In-Bullish: Jan 2014–May 2015 | Remained 0.05–0.1%. Selection criterion: 0.2% (buy and sell). | Maintained at 0.1%, sales only. Selection criterion: 0.1% (buy and sell). | - | - | SHSE 2013: 0.64% SZSE 2013: 0.74% SSE 2014: 0.65% SZSE 2014: 0.73% |
| In-Bearish: June 2015–Dec 2016 | Remained 0.05–0.1%. Selection criterion: 0.2% (buy and sell). | Maintained at 0.1%, sales only. Selection criterion: 0.1% (buy and sell). | - | - | SHSE 2015: 0.95% SZSE 2015: 0.93% SHSE 2016: 0.62% SZSE 2016: 0.68% |
| Pre-Cov.: Jan 2017–Dec 2019 | Mostly 0.02–0.05%. Selection criterion: 0.05% (buy and sell). | Continued at 0.1%, sales only. Selection criterion: 0.1% (buy and sell). | - | - | - |
| In-Cov.: Jan 2020–Dec 2022 | Around 0.02–0.03%. Selection criterion: 0.05% (buy and sell). | Maintained at 0.1%. Selection criterion: 0.1% (buy and sell). | - | - | - |
| Post-Cov.: Jan 2023–Jun 2024 | Expected 0.02–0.03%. Selection criterion: 0.05% (buy and sell). | Expected to remain at 0.1%. Selection criterion: 0.1% (buy and sell). | - | - | - |
| Test | t-Statistic | p-Value | Conclusion |
|---|---|---|---|
| Panel I-A: Return on employed capital without costs | |||
| ANOVA | 0.1736 | 0.9966 | , no mean differences. |
| Kruskal–Wallis | 1.9354 | 0.9924 | No significant distributional differences. |
| Friedman | 4.7450 | 0.8559 | No rank differences. |
| Levene | 1.2525 | 0.2581 | No evidence of heteroskedasticity. |
| Welch ANOVA | 0.1826 | 0.9959 | , no mean differences. |
| Panel I-B: Return on committed capital without costs | |||
| ANOVA | 0.3302 | 0.9653 | , no mean differences. |
| Kruskal–Wallis | 4.0392 | 0.9088 | No significant distributional differences. |
| Friedman | 6.2713 | 0.7125 | No rank differences. |
| Levene | 0.6023 | 0.7961 | No evidence of heteroskedasticity. |
| Welch ANOVA | 0.3245 | 0.9671 | , no mean differences. |
| Panel II-A: Return on employed capital with costs | |||
| ANOVA | 0.3274 | 0.9662 | , no mean differences. |
| Kruskal–Wallis | 2.0585 | 0.9905 | No significant distributional differences. |
| Friedman | 4.9191 | 0.8413 | No rank differences. |
| Levene | 0.8954 | 0.5285 | No evidence of heteroskedasticity. |
| Welch ANOVA | 0.3289 | 0.9656 | , no mean differences. |
| Panel II-B: Return on committed capital with costs | |||
| ANOVA | 0.5299 | 0.8538 | , no mean differences. |
| Kruskal–Wallis | 5.1239 | 0.8234 | No significant distributional differences. |
| Friedman | 12.7813 | 0.1728 | No rank differences. |
| Levene | 0.5623 | 0.8288 | No evidence of heteroskedasticity. |
| Welch ANOVA | 0.5193 | 0.8612 | , no mean differences. |
| Group1 | Group2 | MeanDiff | p-Adj | Lower | Upper | Reject |
|---|---|---|---|---|---|---|
| CFG_Mixed_Copula | CJF_Mixed_Copula | 0.0004 | 1.0000 | −0.0032 | 0.0040 | FALSE |
| CFG_Mixed_Copula | CJG_Mixed_Copula | 0.0003 | 1.0000 | −0.0033 | 0.0039 | FALSE |
| CFG_Mixed_Copula | Clayton_Copula | 0.0003 | 1.0000 | −0.0034 | 0.0039 | FALSE |
| CFG_Mixed_Copula | FJG_Mixed_Copula | 0.0006 | 1.0000 | −0.0031 | 0.0042 | FALSE |
| CFG_Mixed_Copula | Frank_Copula | 0.0007 | 0.9999 | −0.0030 | 0.0043 | FALSE |
| CFG_Mixed_Copula | Guassian_Copula | 0.0010 | 0.9964 | −0.0026 | 0.0047 | FALSE |
| CFG_Mixed_Copula | Gumbel_Copula | −0.0001 | 1.0000 | −0.0037 | 0.0035 | FALSE |
| CFG_Mixed_Copula | Optimal_Copula | 0.0000 | 1.0000 | −0.0036 | 0.0037 | FALSE |
| CFG_Mixed_Copula | Student_t_Copula | 0.0014 | 0.9742 | −0.0023 | 0.0050 | FALSE |
| CJF_Mixed_Copula | CJG_Mixed_Copula | −0.0001 | 1.0000 | −0.0037 | 0.0036 | FALSE |
| CJF_Mixed_Copula | Clayton_Copula | −0.0001 | 1.0000 | −0.0037 | 0.0035 | FALSE |
| CJF_Mixed_Copula | FJG_Mixed_Copula | 0.0002 | 1.0000 | −0.0034 | 0.0038 | FALSE |
| CJF_Mixed_Copula | Frank_Copula | 0.0003 | 1.0000 | −0.0033 | 0.0039 | FALSE |
| CJF_Mixed_Copula | Guassian_Copula | 0.0007 | 0.9999 | −0.0030 | 0.0043 | FALSE |
| CJF_Mixed_Copula | Gumbel_Copula | −0.0004 | 1.0000 | −0.0041 | 0.0032 | FALSE |
| CJF_Mixed_Copula | Optimal_Copula | −0.0003 | 1.0000 | −0.0040 | 0.0033 | FALSE |
| CJF_Mixed_Copula | Student_t_Copula | 0.0010 | 0.9975 | −0.0026 | 0.0046 | FALSE |
| CJG_Mixed_Copula | Clayton_Copula | −0.0001 | 1.0000 | −0.0037 | 0.0036 | FALSE |
| CJG_Mixed_Copula | FJG_Mixed_Copula | 0.0002 | 1.0000 | −0.0034 | 0.0039 | FALSE |
| CJG_Mixed_Copula | Frank_Copula | 0.0003 | 1.0000 | −0.0033 | 0.0040 | FALSE |
| CJG_Mixed_Copula | Guassian_Copula | 0.0007 | 0.9998 | −0.0029 | 0.0043 | FALSE |
| CJG_Mixed_Copula | Gumbel_Copula | −0.0004 | 1.0000 | −0.0040 | 0.0032 | FALSE |
| CJG_Mixed_Copula | Optimal_Copula | −0.0003 | 1.0000 | −0.0039 | 0.0033 | FALSE |
| CJG_Mixed_Copula | Student_t_Copula | 0.0010 | 0.9961 | −0.0026 | 0.0047 | FALSE |
| Clayton_Copula | FJG_Mixed_Copula | 0.0003 | 1.0000 | −0.0033 | 0.0039 | FALSE |
| Clayton_Copula | Frank_Copula | 0.0004 | 1.0000 | −0.0032 | 0.0040 | FALSE |
| Clayton_Copula | Guassian_Copula | 0.0008 | 0.9996 | −0.0028 | 0.0044 | FALSE |
| Clayton_Copula | Gumbel_Copula | −0.0003 | 1.0000 | −0.0039 | 0.0033 | FALSE |
| Clayton_Copula | Optimal_Copula | −0.0002 | 1.0000 | −0.0038 | 0.0034 | FALSE |
| Clayton_Copula | Student_t_Copula | 0.0011 | 0.9939 | −0.0025 | 0.0047 | FALSE |
| FJG_Mixed_Copula | Frank_Copula | 0.0001 | 1.0000 | −0.0035 | 0.0037 | FALSE |
| FJG_Mixed_Copula | Guassian_Copula | 0.0005 | 1.0000 | −0.0031 | 0.0041 | FALSE |
| FJG_Mixed_Copula | Gumbel_Copula | −0.0006 | 0.9999 | −0.0042 | 0.0030 | FALSE |
| FJG_Mixed_Copula | Optimal_Copula | −0.0005 | 1.0000 | −0.0041 | 0.0031 | FALSE |
| FJG_Mixed_Copula | Student_t_Copula | 0.0008 | 0.9995 | −0.0028 | 0.0044 | FALSE |
| Frank_Copula | Guassian_Copula | 0.0004 | 1.0000 | −0.0033 | 0.0040 | FALSE |
| Frank_Copula | Gumbel_Copula | −0.0007 | 0.9998 | −0.0044 | 0.0029 | FALSE |
| Frank_Copula | Optimal_Copula | −0.0006 | 0.9999 | −0.0042 | 0.0030 | FALSE |
| Frank_Copula | Student_t_Copula | 0.0007 | 0.9998 | −0.0029 | 0.0043 | FALSE |
| Guassian_Copula | Gumbel_Copula | −0.0011 | 0.9940 | −0.0047 | 0.0025 | FALSE |
| Guassian_Copula | Optimal_Copula | −0.0010 | 0.9974 | −0.0046 | 0.0026 | FALSE |
| Guassian_Copula | Student_t_Copula | 0.0003 | 1.0000 | −0.0033 | 0.0039 | FALSE |
| Gumbel_Copula | Optimal_Copula | 0.0001 | 1.0000 | −0.0035 | 0.0037 | FALSE |
| Gumbel_Copula | Student_t_Copula | 0.0014 | 0.9634 | −0.0022 | 0.0051 | FALSE |
| Optimal_Copula | Student_t_Copula | 0.0013 | 0.9793 | −0.0023 | 0.0049 | FALSE |
References
- Aas, K., Czado, C., Frigessi, A., & Bakken, H. (2009). Pair-copula constructions of multiple dependence. Insurance: Mathematics and Economics, 44(2), 182–198. [Google Scholar] [CrossRef]
- Andrade, S., Di Pietro, V., & Seasholes, M. (2005). Understanding the profitability of pairs trading [Unpublished working paper]. UC Berkeley, Northwestern University. [Google Scholar]
- Bogomolov, T. (2013). Pairs trading based on statistical variability of the spread process. Quantitative Finance, 13(9), 1411–1430. [Google Scholar] [CrossRef]
- Bookstaber, R. (2007). A demon of our own design. Wiley. [Google Scholar]
- Bowen, D. A., & Hutchinson, M. C. (2016). Pairs trading in the UK equity market: Risk and return. The European Journal of Finance, 22(14), 1363–1387. [Google Scholar] [CrossRef]
- Broussard, J. P., & Vaihekoski, M. (2012). Profitability of pairs trading strategy in an illiquid market with multiple share classes. Journal of International Financial Markets, Institutions and Money, 22(5), 1188–1201. [Google Scholar] [CrossRef]
- Cai, Z., & Wang, X. (2014). Selection of mixed copula model via penalized likelihood. Journal of the American Statistical Association, 109(506), 788–801. [Google Scholar] [CrossRef]
- Chang, K. L. (2023). The low-magnitude and high-magnitude asymmetries in tail dependence structures in international equity markets and the role of bilateral exchange rate. Journal of International Money and Finance, 133, 102839. [Google Scholar] [CrossRef]
- Chen, X., Huang, Z., & Yi, Y. (2021). Efficient estimation of multivariate semi-nonparametric GARCH filtered copula models. Journal of Econometrics, 222(1), 484–501. [Google Scholar] [CrossRef]
- Chu, B. (2011). Recovering copulas from limited information and an application to asset allocation. Journal of Banking & Finance, 35(7), 1824–1842. [Google Scholar] [CrossRef]
- Cortese, F. P. (2019). Tail dependence in financial markets: A dynamic copula approach. Risks, 7(4), 116. [Google Scholar] [CrossRef]
- Creamer, G., & Freund, Y. (2010). Automated trading with boosting and expert weighting. Quantitative Finance, 10(4), 401–420. [Google Scholar] [CrossRef]
- Da Silva, F. A. S., Ziegelmann, F. A., & Caldeira, J. F. (2023). A pairs trading strategy based on mixed copulas. The Quarterly Review of Economics and Finance, 87, 16–34. [Google Scholar] [CrossRef]
- Dempster, M. A. H., & Jones, C. M. (2001). A real-time adaptive trading system using genetic programming. Quantitative Finance, 1(4), 397–413. [Google Scholar] [CrossRef]
- Do, B., & Faff, R. (2010). Does simple pairs trading still work? Financial Analysts Journal, 66(4), 83–95. [Google Scholar] [CrossRef]
- Do, B., & Faff, R. (2012). Are pairs trading profits robust to trading costs? Journal of Financial Research, 35(2), 261–287. [Google Scholar] [CrossRef]
- Dong, X., Li, C., & Yoon, S. M. (2020). Asymmetric dependence structures for regional stock markets: An unconditional quantile regression approach. The North American Journal of Economics and Finance, 52, 101111. [Google Scholar] [CrossRef]
- Easton, A., van Dalen, O., Goeb, R., & Di Bucchianico, A. (2022). Bivariate copula monitoring. Quality and Reliability Engineering International, 38(3), 1272–1288. [Google Scholar] [CrossRef]
- Eling, M. (2008). Does the measure matter in the mutual fund industry? Financial Analysts Journal, 64(3), 54–66. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (2015). A five-factor asset pricing model. Journal of Financial Economics, 116(1), 1–22. [Google Scholar] [CrossRef]
- Fritzsch, S., Timphus, M., & Weiss, G. (2024). Marginals versus copulas: Which account for more model risk in multivariate risk forecasting? Journal of Banking & Finance, 158, 107035. [Google Scholar]
- Fu, J., & Wu, L. (2021). Regime-switching herd behavior: Novel evidence from the Chinese A-share market. Finance Research Letters, 39, 101652. [Google Scholar] [CrossRef]
- Gatev, E., Goetzmann, W. N., & Rouwenhorst, K. G. (2006). Pairs trading: Performance of a relative-value arbitrage rule. The Review of Financial Studies, 19(3), 797–827. [Google Scholar] [CrossRef]
- Genest, C., Okhrin, O., & Bodnar, T. (2024). Copula modeling from Abe Sklar to the present day. Journal of Multivariate Analysis, 201, 105278. [Google Scholar] [CrossRef]
- He, F., Yarahmadi, A., & Soleymani, F. (2024). Investigation of multivariate pairs trading under copula approach with mixture distribution. Applied Mathematics and Computation, 472, 128635. [Google Scholar] [CrossRef]
- Hu, X., Zhu, B., Zhang, B., & Zeng, L. (2024). Extreme risk spillovers between US and Chinese agricultural futures markets in crises: A dependence-switching copula-CoVaR model. PLoS ONE, 19(3), e0299237. [Google Scholar] [CrossRef] [PubMed]
- Huang, N., Huang, Z., & Wang, W. (2019). The dynamic extreme co-movement between Chinese stock market and global stock markets. Emerging Markets Finance and Trade, 55(14), 3241–3257. [Google Scholar] [CrossRef]
- Huck, N. (2009). Pairs selection and outranking: An application to the S&P 100 index. European Journal of Operational Research, 196(2), 819–825. [Google Scholar] [CrossRef]
- Huck, N. (2010). Pairs trading and outranking: The multi-step-ahead forecasting case. European Journal of Operational Research, 207(3), 1702–1716. [Google Scholar] [CrossRef]
- Jacobs, H., & Weber, M. (2015). On the determinants of pairs trading profitability. Journal of Financial Markets, 23, 75–97. [Google Scholar] [CrossRef]
- Joe, H. (1997). Multivariate models and dependence concepts. Chapman & Hall. [Google Scholar]
- Jondeau, E., & Rockinger, M. (2006). The copula-garch model of conditional dependencies: An international stock market application. Journal of International Money and Finance, 25(5), 827–853. [Google Scholar] [CrossRef]
- Keshavarz Haddad, G., & Talebi, H. (2023). The profitability of pair trading strategy in stock markets: Evidence from Toronto stock exchange. International Journal of Finance & Economics, 28(1), 193–207. [Google Scholar]
- Ko, V., Hjort, N. L., & Hobæk Haff, I. (2019). Focused information criteria for copulas. Scandinavian Journal of Statistics, 46(4), 1117–1140. [Google Scholar] [CrossRef]
- Liew, R. Q., & Wu, Y. (2013). Pairs trading: A copula approach. Journal of Derivatives & Hedge Funds, 19(1), 12–30. [Google Scholar] [CrossRef]
- Lo, A. W. (2002). The statistics of Sharpe ratios. Financial Analysts Journal, 58(4), 36–52. [Google Scholar] [CrossRef]
- Longin, F., & Solnik, B. (1995). Is the correlation in international equity returns constant: 1960–1990? Journal of International Money and Finance, 14(1), 3–26. [Google Scholar] [CrossRef]
- Low, R. K. Y., Alcock, J., Faff, R., & Brailsford, T. (2013). Canonical vine copulas in the context of modern portfolio management: Are they worth it? Journal of Banking & Finance, 37(8), 3085–3099. [Google Scholar] [CrossRef]
- Lowenstein, R. (2000). When genius failed: The rise and fall of long-term capital management. Random House. [Google Scholar]
- Markowitz, H. (1952). Portfolio selection. The Journal of Finance, 7(1), 77–91. [Google Scholar]
- Miao, J., & Laws, J. (2016). Profitability of a simple pairs trading strategy: Recent evidences from a global context. International Journal of Theoretical and Applied Finance, 19(4), 1650023. [Google Scholar] [CrossRef]
- Oh, D. H., & Patton, A. J. (2017). Modeling dependence in high dimensions with factor copulas. Journal of Business & Economic Statistics, 35(1), 139–154. [Google Scholar] [CrossRef]
- Okimoto, T. (2014). Asymmetric increasing trends in dependence in international equity markets. Journal of Banking & Finance, 46, 219–232. [Google Scholar] [CrossRef]
- Patton, A. J. (2004). On the out-of-sample importance of skewness and asymmetric dependence for asset allocation. Journal of Financial Econometrics, 2(1), 130–168. [Google Scholar] [CrossRef]
- Patton, A. J. (2006). Modelling asymmetric exchange rate dependence. International Economic Review, 47(2), 527–556. [Google Scholar] [CrossRef]
- Perlin, M. S. (2009). Evaluation of pairs-trading strategy at the Brazilian financial market. Journal of Derivatives & Hedge Funds, 15(2), 122–136. [Google Scholar] [CrossRef]
- Pesaran, M. H., & Timmermann, A. (1995). Predictability of stock returns: Robustness and economic significance. The Journal of Finance, 50(4), 1201–1228. [Google Scholar] [CrossRef]
- Rad, H., Low, R. K. Y., & Faff, R. (2016). The profitability of pairs trading strategies: Distance, cointegration and copula methods. Quantitative Finance, 16(10), 1541–1558. [Google Scholar] [CrossRef]
- Rodriguez, J. C. (2007). Measuring financial contagion: A copula approach. Journal of Empirical Finance, 14(3), 401–423. [Google Scholar] [CrossRef]
- Siburg, K. F., Stoimenov, P., & Wei, G. N. F. (2015). Forecasting portfolio-Value-at-Risk with nonparametric lower tail dependence estimates. Journal of Banking & Finance, 54, 129–140. [Google Scholar]
- Stander, Y., Marais, D., & Botha, I. (2013). Trading strategies with copulas. Journal of Economic and Financial Sciences, 6(1), 83–107. [Google Scholar] [CrossRef]
- Stübinger, J., Mangold, B., & Krauss, C. (2018). Statistical arbitrage with vine copulas. Quantitative Finance, 18(11), 1831–1849. [Google Scholar] [CrossRef]
- Sun, T., Cheng, Y., & Ding, Y. (2023). An information ratio-based goodness-of-fit test for copula models on censored data. Biometrics, 79(3), 1713–1725. [Google Scholar] [CrossRef]
- Tsoku, J. T., & Moroke, N. D. (2018). Pairs trading in JSE financial sector. Journal of Statistics and Management Systems, 21(5), 877–899. [Google Scholar] [CrossRef]
- Wang, Y., Ding, X., Wang, P., & Huang, Z. (2024). Impact of global crisis events on the dependence and risk spillover between gold and crude oil: A regime-switching copula approach. Humanities and Social Sciences Communications, 11(1), 1–10. [Google Scholar] [CrossRef]
- Wei, G. N. F., & Scheffer, M. (2015). Mixture pair-copula-constructions. Journal of Banking & Finance, 54, 175–191. [Google Scholar] [CrossRef]
- Xie, W., Liew, R. Q., Wu, Y., & Zou, X. (2016). Pairs Trading with Copulas. The Journal of Trading, 2016, 41–52. [Google Scholar] [CrossRef]
- Yang, S. Y., Qiao, Q., Beling, P. A., Scherer, W. T., & Kirilenko, A. A. (2015). Gaussian process-based algorithmic trading strategy identification. Quantitative Finance, 15, 1–21. [Google Scholar] [CrossRef]
- Zeng, Z., & Lee, C. G. (2014). Pairs trading: Optimal thresholds and profitability. Quantitative Finance, 14(11), 1881–1893. [Google Scholar] [CrossRef]
- Zhang, Q. (2018). The performance of China stock market, based on the analysis of implicit transaction cost. American Journal of Industrial and Business Management, 8(4), 1050. [Google Scholar] [CrossRef][Green Version]



| Copula | ||
| Student-t | ||
| Clayton | ||
| Frank | ||
| Gumbel | ||
| Gaussian |
| Strategy | Mean | t-Stat | Std. Dev. | Sharpe | z-Stat | Skewness | Kurtosis | VaR (95%) | CvaR (95%) | JB Test (p-Value) |
|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Return on employed capital | ||||||||||
| SSD-Hurst | 0.0084 | 2.26 ** | 0.0399 | 0.21 | 2.25 ** | 10.1033 | 120.5140 | −0.0090 | −0.0207 | 0 |
| SSD-NZC | 0.0082 | 2.44 ** | 0.0408 | 0.20 | 2.43 ** | 9.0968 | 106.0665 | −0.0174 | −0.0336 | 0 |
| Clayton | 0.0024 | 2.61 *** | 0.0143 | 0.17 | 2.60 *** | −0.4138 | 2.9655 | −0.0214 | −0.0344 | 0 |
| Frank | 0.0026 | 3.03 *** | 0.0128 | 0.21 | 3.02 *** | 0.5756 | 6.8005 | −0.0150 | −0.0272 | 0 |
| Gaussian | 0.0030 | 3.63 *** | 0.0129 | 0.23 | 3.62 *** | −0.1911 | 1.1780 | −0.0180 | −0.0258 | 0 |
| Gumbel | 0.0021 | 2.90 *** | 0.0129 | 0.16 | 2.90 *** | −0.4994 | 1.3553 | −0.0213 | −0.0296 | 0 |
| Student-t | 0.0028 | 3.41 *** | 0.0146 | 0.19 | 3.42 *** | −0.5746 | 2.2493 | −0.0220 | −0.0357 | 0 |
| Optimal | 0.0019 | 2.33 ** | 0.0116 | 0.16 | 2.32 ** | −0.9099 | 3.2471 | −0.0174 | −0.0273 | 0 |
| CFG | 0.0020 | 2.33 ** | 0.0114 | 0.17 | 2.32 ** | −0.4443 | 0.8605 | −0.0181 | −0.0257 | 0 |
| CJF | 0.0023 | 2.79 *** | 0.0125 | 0.19 | 2.78 *** | −0.4243 | 2.6056 | −0.0183 | −0.0279 | 0 |
| CJG | 0.0023 | 2.82 *** | 0.0127 | 0.18 | 2.82 *** | −0.2754 | 1.6407 | −0.0218 | −0.0290 | 0 |
| FJG | 0.0025 | 3.07 *** | 0.0124 | 0.20 | 3.06 *** | −0.3048 | 2.1104 | −0.0150 | −0.0263 | 0 |
| Panel B: Return on committed capital | ||||||||||
| SSD-Hurst | 0.0082 | 2.21 ** | 0.0395 | 0.21 | 2.20 ** | 10.1453 | 121.1081 | −0.0088 | −0.0204 | 0 |
| SSD-NZC | 0.0081 | 2.39 ** | 0.0407 | 0.20 | 2.38 ** | 9.1478 | 106.8560 | −0.0174 | −0.0335 | 0 |
| Clayton | 0.0015 | 3.10 *** | 0.0068 | 0.21 | 3.09 *** | −0.6681 | 3.5863 | −0.0099 | −0.0160 | 0 |
| Frank | 0.0021 | 4.32 *** | 0.0068 | 0.30 | 4.31 *** | −0.8892 | 3.2254 | −0.0086 | −0.0146 | 0 |
| Gaussian | 0.0023 | 4.81 *** | 0.0072 | 0.32 | 4.80 *** | −0.3102 | 1.5599 | −0.0097 | −0.0145 | 0 |
| Gumbel | 0.0017 | 4.04 *** | 0.0072 | 0.24 | 4.04 *** | −0.4528 | 1.8285 | −0.0110 | −0.0155 | 0 |
| Student-t | 0.0018 | 4.37 *** | 0.0073 | 0.25 | 4.37 *** | −0.8609 | 2.7959 | −0.0110 | −0.0178 | 0 |
| Optimal | 0.0016 | 3.62 *** | 0.0062 | 0.26 | 3.61 *** | −0.9754 | 4.4947 | −0.0087 | −0.0125 | 0 |
| CFG | 0.0016 | 3.37 *** | 0.0067 | 0.24 | 3.36 *** | −0.5552 | 1.8233 | −0.0105 | −0.0146 | 0 |
| CJF | 0.0019 | 4.17 *** | 0.0067 | 0.28 | 4.16 *** | −0.3788 | 1.6577 | −0.0085 | −0.0136 | 0 |
| CJG | 0.0017 | 3.86 *** | 0.0065 | 0.26 | 3.85 *** | −0.3094 | 1.3252 | −0.0100 | −0.0137 | 0 |
| FJG | 0.0021 | 4.43 *** | 0.0072 | 0.29 | 4.42 *** | −0.7207 | 2.6422 | −0.0095 | −0.0158 | 0 |
| Strategy | Mean | t-Stat | Std. Dev. | Sharpe | z-Stat | Skewness | Kurtosis | VaR (95%) | CvaR (95%) | JB Test (p-Value) |
|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Return on employed capital | ||||||||||
| SSD-Hurst | 0.0081 | 2.16 ** | 0.0397 | 0.20 | 2.15 ** | 10.2231 | 122.1875 | −0.0095 | −0.0199 | 0 |
| SSD-NZC | 0.0077 | 2.29 ** | 0.0407 | 0.19 | 2.28 ** | 9.1010 | 106.1485 | −0.0179 | −0.0342 | 0 |
| Clayton | 0.0011 | 1.33 | 0.0138 | 0.08 | 1.32 | −0.4373 | 2.8047 | −0.0223 | −0.0342 | 0 |
| Frank | 0.0016 | 1.84 * | 0.0125 | 0.12 | 1.83 * | 0.4745 | 6.3886 | −0.0158 | −0.0278 | 0 |
| Gaussian | 0.0019 | 2.37 ** | 0.0126 | 0.15 | 2.36 ** | −0.1816 | 0.9517 | −0.0193 | −0.0264 | 0 |
| Gumbel | 0.0008 | 1.14 | 0.0126 | 0.07 | 1.14 | −0.5245 | 1.2660 | −0.0219 | −0.0300 | 0 |
| Student-t | 0.0023 | 2.69 *** | 0.0125 | 0.18 | 2.68 *** | −0.1109 | 0.4397 | −0.0193 | −0.0249 | 0 |
| Optimal | 0.0009 | 1.20 | 0.0113 | 0.08 | 1.19 | −0.8492 | 2.7027 | −0.0171 | −0.0272 | 0 |
| CFG | 0.0009 | 1.08 | 0.0111 | 0.08 | 1.08 | −0.5046 | 0.8898 | −0.0188 | −0.0261 | 0 |
| CJF | 0.0013 | 1.55 | 0.0122 | 0.10 | 1.54 | −0.4444 | 2.4726 | −0.0191 | −0.0281 | 0 |
| CJG | 0.0012 | 1.50 | 0.0124 | 0.10 | 1.49 | −0.2420 | 1.5668 | −0.0222 | −0.0291 | 0 |
| FJG | 0.0015 | 1.82 * | 0.0120 | 0.12 | 1.82 * | −0.4066 | 1.9814 | −0.0164 | −0.0269 | 0 |
| Panel B: Return on committed capital | ||||||||||
| SSD-Hurst | 0.0078 | 2.10 ** | 0.0395 | 0.20 | 2.09 ** | 10.1688 | 121.4783 | −0.0092 | −0.0208 | 0 |
| SSD-NZC | 0.0075 | 2.24 ** | 0.0407 | 0.18 | 2.23 ** | 9.1522 | 106.9420 | −0.0178 | −0.0341 | 0 |
| Clayton | 0.0007 | 1.41 | 0.0069 | 0.10 | 1.41 | −0.7092 | 3.5148 | −0.0110 | −0.0169 | 0 |
| Frank | 0.0012 | 2.52 ** | 0.0069 | 0.18 | 2.51 ** | −0.9186 | 3.2798 | −0.0096 | −0.0156 | 0 |
| Gaussian | 0.0015 | 3.09 *** | 0.0072 | 0.21 | 3.09 *** | −0.3482 | 1.5314 | −0.0105 | −0.0154 | 0 |
| Gumbel | 0.0008 | 1.80 * | 0.0072 | 0.11 | 1.80 * | −0.5171 | 1.8396 | −0.0121 | −0.0168 | 0 |
| Student-t | 0.0016 | 3.39 *** | 0.0070 | 0.23 | 3.38 *** | −0.2295 | 1.7032 | −0.0101 | −0.0144 | 0 |
| Optimal | 0.0008 | 1.67 * | 0.0063 | 0.12 | 1.67 * | −1.0113 | 4.5703 | −0.0095 | −0.0135 | 0 |
| CFG | 0.0008 | 1.60 | 0.0067 | 0.12 | 1.60 | −0.5918 | 1.8551 | −0.0115 | −0.0157 | 0 |
| CJF | 0.0011 | 2.31 ** | 0.0068 | 0.16 | 2.30 ** | −0.4156 | 1.6426 | −0.0095 | −0.0146 | 0 |
| CJG | 0.0009 | 1.92 * | 0.0066 | 0.13 | 1.91 * | −0.3344 | 1.3441 | −0.0108 | −0.0147 | 0 |
| FJG | 0.0013 | 2.60 *** | 0.0073 | 0.17 | 2.59 ** | −0.7415 | 2.6566 | −0.0104 | −0.0167 | 0 |
| Lower Partial Moments Measures | Drawdown Measures | ||||||
|---|---|---|---|---|---|---|---|
| Omega | Sortino Ratio | Kappa 3 | Max D. | Calmar Ratio | Sterling Ratio | Burke Ratio | |
| Panel A: Before transaction costs | |||||||
| SSD-Hurst | 5.0290 | 0.7395 | 0.6951 | −0.0831 | 1.2767 | 7.1608 | 0.4977 |
| SSD-NZC | 3.4930 | 0.4769 | 0.4428 | −0.0963 | 1.0745 | 4.1353 | 0.2782 |
| Clayton | 1.5983 | 0.1558 | 0.1637 | −0.1005 | 0.2870 | 0.9600 | 0.0577 |
| Frank | 1.7884 | 0.2171 | 0.2312 | −0.0988 | 0.3258 | 1.1411 | 0.0704 |
| Gaussian | 1.8122 | 0.2307 | 0.2610 | −0.1014 | 0.3590 | 1.0808 | 0.0685 |
| Gumbel | 1.5314 | 0.1558 | 0.1688 | −0.1208 | 0.2135 | 0.7163 | 0.0440 |
| Student-t | 1.6723 | 0.1762 | 0.1900 | −0.0730 | 0.4637 | 1.4738 | 0.0917 |
| Optimal | 1.5375 | 0.1444 | 0.1509 | −0.1197 | 0.1901 | 0.5929 | 0.0374 |
| CFG | 1.5689 | 0.1635 | 0.1816 | −0.0953 | 0.2497 | 0.6288 | 0.0393 |
| CJF | 1.6587 | 0.1738 | 0.1891 | −0.1171 | 0.2424 | 0.7158 | 0.0460 |
| CJG | 1.6131 | 0.1699 | 0.1906 | −0.1258 | 0.2217 | 0.9192 | 0.0546 |
| FJG | 1.7169 | 0.2053 | 0.2150 | −0.1112 | 0.2765 | 1.0946 | 0.0656 |
| Panel B: After transaction costs | |||||||
| SSD-Hurst | 4.7299 | 0.7982 | 0.7966 | −0.0675 | 1.4971 | 6.2675 | 0.4372 |
| SSD-NZC | 3.2149 | 0.4462 | 0.4099 | −0.0973 | 0.9916 | 3.6369 | 0.2368 |
| Clayton | 1.2642 | 0.0795 | 0.0794 | −0.1326 | 0.1045 | 0.2431 | 0.0145 |
| Frank | 1.4204 | 0.1282 | 0.1334 | −0.1284 | 0.1470 | 0.5225 | 0.0306 |
| Gaussian | 1.4832 | 0.1495 | 0.1670 | −0.1516 | 0.1542 | 0.4257 | 0.0247 |
| Gumbel | 1.1852 | 0.0603 | 0.0639 | −0.1960 | 0.0506 | 0.1553 | 0.0086 |
| Student-t | 1.5929 | 0.1805 | 0.2079 | −0.1382 | 0.1982 | 0.5405 | 0.0319 |
| Optimal | 1.2470 | 0.0759 | 0.0766 | −0.1379 | 0.0822 | 0.2501 | 0.0141 |
| CFG | 1.2379 | 0.0739 | 0.0806 | −0.1320 | 0.0818 | 0.1961 | 0.0113 |
| CJF | 1.3254 | 0.0956 | 0.1016 | −0.1439 | 0.1068 | 0.2917 | 0.0173 |
| CJG | 1.2967 | 0.0901 | 0.0999 | −0.1788 | 0.0818 | 0.2418 | 0.0143 |
| FJG | 1.3761 | 0.1174 | 0.1210 | −0.1362 | 0.1288 | 0.4162 | 0.0245 |
| Strategy | Alpha | MKT | SMB | HML | RMW | CMA | MOM | REV |
|---|---|---|---|---|---|---|---|---|
| Panel A: Before transaction costs | ||||||||
| SSD-Hurst | 0.0052 | 0.0049 | 0.1828 | 0.1314 | 0.0465 | −0.2632 | −0.0729 | −0.0486 |
| SSD-NZC | 0.0055 | 0.0028 | 0.1851 | 0.1573 | 0.0729 | −0.2967 * | −0.0663 | −0.0251 |
| Clayton | −0.0006 | −0.0041 | 0.2059 ** | 0.1080 | 0.1016 | −0.1966 * | 0.0042 | 0.0126 |
| Frank | 0.0011 | −0.0202 | 0.1178 | 0.0438 | 0.1051 | −0.0702 | −0.0127 | 0.0244 |
| Gaussian | 0.0011 | −0.0078 | 0.1126 | 0.0917 | 0.0538 | −0.1167 | 0.0284 | 0.0231 |
| Gumbel | 0.0001 | −0.0097 | 0.1345 | 0.0674 | 0.1057 | −0.1160 | 0.0024 | 0.0147 |
| Student-t | 0.0009 | 0.0075 | 0.0691 | 0.0280 | 0.0359 | −0.1030 | −0.0243 | 0.0093 |
| Optimal | −0.0003 | −0.0156 | 0.1721 * | 0.0945 | 0.0981 | −0.1220 | 0.0065 | 0.0233 |
| CFG | 0.0001 | −0.0088 | 0.1418 | 0.0080 | 0.0812 | −0.0861 | −0.0010 | 0.0278 |
| CJF | 0.0001 | −0.0036 | 0.1585 | 0.0662 | 0.1182 | −0.1029 | −0.0119 | 0.0188 |
| CJG | 0.0000 | −0.0092 | 0.1815 * | 0.0761 | 0.0963 | −0.0951 | 0.0037 | 0.0205 |
| FJG | 0.0005 | −0.0199 | 0.1506 | 0.0436 | 0.1096 | −0.1086 | −0.0045 | 0.0257 |
| Panel B: After transaction costs | ||||||||
| SSD-Hurst | 0.0048 | 0.0046 | 0.1811 | 0.1314 | 0.0457 | −0.2652 | −0.0705 | −0.0476 |
| SSD-NZC | 0.0049 | 0.0025 | 0.1865 | 0.1577 | 0.0725 | −0.2973 * | −0.0653 | −0.0238 |
| Clayton | −0.0018 | −0.0028 | 0.1993 ** | 0.0998 | 0.0988 | −0.1881 * | 0.0053 | 0.0133 |
| Frank | 0.0000 | −0.0182 | 0.1181 | 0.0421 | 0.1044 | −0.0717 | −0.0125 | 0.0245 |
| Gaussian | 0.0000 | −0.0075 | 0.1123 | 0.0915 | 0.0507 | −0.1207 | 0.0257 | 0.0236 |
| Gumbel | −0.0013 | −0.0097 | 0.1366 | 0.0704 | 0.1010 | −0.1240 | 0.0028 | 0.0142 |
| Student-t | 0.0004 | −0.0129 | 0.1234 | 0.0458 | 0.0954 | −0.0782 | 0.0055 | 0.0263 |
| Optimal | −0.0013 | −0.0119 | 0.1682 * | 0.0891 | 0.0964 | −0.1173 | 0.0042 | 0.0241 |
| CFG | −0.0010 | −0.0077 | 0.1446 | 0.0094 | 0.0831 | −0.0883 | −0.0003 | 0.0275 |
| CJF | −0.0010 | −0.0026 | 0.1602 * | 0.0651 | 0.1178 | −0.1043 | −0.0133 | 0.0178 |
| CJG | −0.0011 | −0.0064 | 0.1825 * | 0.0783 | 0.0943 | −0.1011 | 0.0041 | 0.0204 |
| FJG | −0.0006 | −0.0186 | 0.1516 | 0.0414 | 0.1123 | −0.1076 | −0.0045 | 0.0256 |
| Strategy | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
|---|---|---|---|---|---|---|---|---|
| Clayton | Mean | 0.0001 | 0.0003 | 0.0003 | 0.0005 | 0.0007 | 0.0008 | 0.0007 |
| Min | −0.0415 | −0.0401 | −0.0360 | −0.0339 | −0.0323 | −0.0351 | −0.0323 | |
| Max | 0.0240 | 0.0304 | 0.0261 | 0.0199 | 0.0239 | 0.0231 | 0.0242 | |
| Std. Dev. | 0.0088 | 0.0087 | 0.0080 | 0.0072 | 0.0069 | 0.0067 | 0.0062 | |
| Frank | Mean | 0.0014 | 0.0015 | 0.0015 | 0.0013 | 0.0012 | 0.0013 | 0.0011 |
| Min | −0.0491 | −0.0427 | −0.0442 | −0.0378 | −0.0355 | −0.0331 | −0.0348 | |
| Max | 0.0214 | 0.0258 | 0.0203 | 0.0178 | 0.0154 | 0.0167 | 0.0165 | |
| Std. Dev. | 0.0085 | 0.0084 | 0.0080 | 0.0071 | 0.0069 | 0.0067 | 0.0063 | |
| Gaussian | Mean | 0.0016 | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0015 | 0.0015 |
| Min | −0.0384 | −0.0344 | −0.0336 | −0.0323 | −0.0276 | −0.0270 | −0.0248 | |
| Max | 0.0363 | 0.0334 | 0.0320 | 0.0307 | 0.0244 | 0.0235 | 0.0223 | |
| Std. Dev. | 0.0093 | 0.0087 | 0.0082 | 0.0078 | 0.0072 | 0.0069 | 0.0065 | |
| Gumbel | Mean | 0.0004 | 0.0007 | 0.0007 | 0.0007 | 0.0008 | 0.0007 | 0.0006 |
| Min | −0.0433 | −0.0432 | −0.0404 | −0.0342 | −0.0305 | −0.0302 | −0.0266 | |
| Max | 0.0249 | 0.0364 | 0.0326 | 0.0295 | 0.0269 | 0.0211 | 0.0150 | |
| Std. Dev. | 0.0090 | 0.0089 | 0.0085 | 0.0074 | 0.0072 | 0.0068 | 0.0063 | |
| Student-t | Mean | 0.0020 | 0.0020 | 0.0017 | 0.0017 | 0.0016 | 0.0015 | 0.0016 |
| Min | −0.0304 | −0.0296 | −0.0279 | −0.0283 | −0.0248 | −0.0252 | −0.0257 | |
| Max | 0.0301 | 0.0325 | 0.0268 | 0.0249 | 0.0294 | 0.0302 | 0.0261 | |
| Std. Dev. | 0.0087 | 0.0084 | 0.0080 | 0.0073 | 0.0070 | 0.0067 | 0.0063 | |
| Optimal | Mean | 0.0012 | 0.0010 | 0.0009 | 0.0008 | 0.0008 | 0.0007 | 0.0005 |
| Min | −0.0490 | −0.0431 | −0.0458 | −0.0379 | −0.0368 | −0.0336 | −0.0367 | |
| Max | 0.0212 | 0.0195 | 0.0182 | 0.0177 | 0.0133 | 0.0163 | 0.0133 | |
| Std. Dev. | 0.0080 | 0.0077 | 0.0074 | 0.0066 | 0.0063 | 0.0059 | 0.0056 | |
| CFG | Mean | 0.0009 | 0.0010 | 0.0008 | 0.0009 | 0.0008 | 0.0009 | 0.0007 |
| Min | −0.0422 | −0.0371 | −0.0376 | −0.0320 | −0.0297 | −0.0258 | −0.0273 | |
| Max | 0.0267 | 0.0233 | 0.0212 | 0.0222 | 0.0201 | 0.0166 | 0.0152 | |
| Std. Dev. | 0.0087 | 0.0083 | 0.0078 | 0.0070 | 0.0067 | 0.0062 | 0.0058 | |
| CJF | Mean | 0.0012 | 0.0011 | 0.0010 | 0.0011 | 0.0011 | 0.0011 | 0.0010 |
| Min | −0.0407 | −0.0352 | −0.0291 | −0.0278 | −0.0260 | −0.0262 | −0.0269 | |
| Max | 0.0281 | 0.0234 | 0.0221 | 0.0220 | 0.0216 | 0.0203 | 0.0174 | |
| Std. Dev. | 0.0086 | 0.0082 | 0.0076 | 0.0072 | 0.0068 | 0.0063 | 0.0058 | |
| CJG | Mean | 0.0014 | 0.0013 | 0.0012 | 0.0010 | 0.0009 | 0.0008 | 0.0008 |
| Min | −0.0364 | −0.0327 | −0.0264 | −0.0236 | −0.0233 | −0.0239 | −0.0251 | |
| Max | 0.0247 | 0.0237 | 0.0201 | 0.0236 | 0.0247 | 0.0173 | 0.0166 | |
| Std. Dev. | 0.0086 | 0.0084 | 0.0078 | 0.0071 | 0.0066 | 0.0060 | 0.0057 | |
| FJG | Mean | 0.0014 | 0.0016 | 0.0015 | 0.0014 | 0.0013 | 0.0014 | 0.0012 |
| Min | −0.0468 | −0.0409 | −0.0425 | −0.0362 | −0.0313 | −0.0296 | −0.0304 | |
| Max | 0.0274 | 0.0252 | 0.0243 | 0.0231 | 0.0198 | 0.0194 | 0.0167 | |
| Std. Dev. | 0.0092 | 0.0089 | 0.0085 | 0.0079 | 0.0073 | 0.0067 | 0.0062 |
| Strategy | 5 Pairs | 10 Pairs | 20 Pairs | 30 Pairs | 40 Pairs | 50 Pairs | |
|---|---|---|---|---|---|---|---|
| Clayton | Mean | 0.0008 | 0.0008 | 0.0007 | 0.0010 | 0.0010 | 0.0012 |
| Min | −0.0092 | −0.0195 | −0.0323 | −0.0314 | −0.0481 | −0.0541 | |
| Max | 0.0082 | 0.0174 | 0.0239 | 0.0275 | 0.0394 | 0.0494 | |
| Std. Dev. | 0.0024 | 0.0041 | 0.0069 | 0.0085 | 0.0108 | 0.0134 | |
| Frank | Mean | 0.0009 | 0.0013 | 0.0012 | 0.0013 | 0.0014 | 0.0017 |
| Min | −0.0154 | −0.0263 | −0.0355 | −0.0512 | −0.0555 | −0.0571 | |
| Max | 0.0093 | 0.0123 | 0.0154 | 0.0248 | 0.0305 | 0.0336 | |
| Std. Dev. | 0.0027 | 0.0041 | 0.0069 | 0.0094 | 0.0120 | 0.0137 | |
| Gaussian | Mean | 0.0011 | 0.0013 | 0.0015 | 0.0015 | 0.0020 | 0.0025 |
| Min | −0.0065 | −0.0128 | −0.0276 | −0.0398 | −0.0468 | −0.0560 | |
| Max | 0.0092 | 0.0128 | 0.0244 | 0.0329 | 0.0385 | 0.0448 | |
| Std. Dev. | 0.0027 | 0.0043 | 0.0072 | 0.0098 | 0.0118 | 0.0139 | |
| Gumbel | Mean | 0.0008 | 0.0006 | 0.0008 | 0.0008 | 0.0008 | 0.0011 |
| Min | −0.0068 | −0.0147 | −0.0305 | −0.0446 | −0.0514 | −0.0575 | |
| Max | 0.0100 | 0.0219 | 0.0269 | 0.0298 | 0.0348 | 0.0408 | |
| Std. Dev. | 0.0024 | 0.0043 | 0.0072 | 0.0098 | 0.0122 | 0.0147 | |
| Student-t | Mean | 0.0012 | 0.0011 | 0.0016 | 0.0018 | 0.0020 | 0.0023 |
| Min | −0.0075 | −0.0139 | −0.0248 | −0.0369 | −0.0528 | −0.0597 | |
| Max | 0.0112 | 0.0169 | 0.0294 | 0.0307 | 0.0432 | 0.0480 | |
| Std. Dev. | 0.0028 | 0.0043 | 0.0070 | 0.0095 | 0.0123 | 0.0147 | |
| Optimal | Mean | 0.0010 | 0.0010 | 0.0008 | 0.0007 | 0.0010 | 0.0013 |
| Min | −0.0154 | −0.0264 | −0.0368 | −0.0527 | −0.0583 | −0.0599 | |
| Max | 0.0087 | 0.0127 | 0.0133 | 0.0215 | 0.0301 | 0.0412 | |
| Std. Dev. | 0.0026 | 0.0040 | 0.0063 | 0.0091 | 0.0112 | 0.0134 | |
| CFG | Mean | 0.0007 | 0.0009 | 0.0008 | 0.0007 | 0.0007 | 0.0010 |
| Min | −0.0367 | −0.0291 | −0.0297 | −0.0282 | −0.0245 | −0.0205 | |
| Max | 0.0457 | 0.0271 | 0.0201 | 0.0180 | 0.0144 | 0.0147 | |
| Std. Dev. | 0.0108 | 0.0077 | 0.0067 | 0.0061 | 0.0058 | 0.0054 | |
| CJF | Mean | 0.0007 | 0.0006 | 0.0011 | 0.0009 | 0.0008 | 0.0009 |
| Min | −0.0342 | −0.0276 | −0.0260 | −0.0243 | −0.0253 | −0.0208 | |
| Max | 0.0373 | 0.0232 | 0.0216 | 0.0211 | 0.0179 | 0.0150 | |
| Std. Dev. | 0.0104 | 0.0076 | 0.0068 | 0.0065 | 0.0061 | 0.0055 | |
| CJG | Mean | 0.0004 | 0.0009 | 0.0009 | 0.0008 | 0.0008 | 0.0008 |
| Min | −0.0440 | −0.0218 | −0.0233 | −0.0229 | −0.0265 | −0.0224 | |
| Max | 0.0358 | 0.0246 | 0.0247 | 0.0220 | 0.0180 | 0.0155 | |
| Std. Dev. | 0.0109 | 0.0077 | 0.0066 | 0.0062 | 0.0060 | 0.0055 | |
| FJG | Mean | 0.0013 | 0.0015 | 0.0013 | 0.0013 | 0.0012 | 0.0013 |
| Min | −0.0405 | −0.0349 | −0.0313 | −0.0284 | −0.0241 | −0.0214 | |
| Max | 0.0375 | 0.0291 | 0.0198 | 0.0164 | 0.0158 | 0.0150 | |
| Std. Dev. | 0.0100 | 0.0077 | 0.0073 | 0.0066 | 0.0062 | 0.0057 |
| Strategy | Trading Periods | 3 Months | 6 Months | 9 Months | 12 Months |
|---|---|---|---|---|---|
| Clayton | Mean | 0.0014 | 0.0007 | 0.0011 | 0.0012 |
| Min | −0.0194 | −0.0323 | −0.0196 | −0.0187 | |
| Max | 0.0199 | 0.0239 | 0.0157 | 0.0178 | |
| Std. Dev. | 0.0070 | 0.0069 | 0.0056 | 0.0052 | |
| Frank | Mean | 0.0011 | 0.0012 | 0.0012 | 0.0011 |
| Min | −0.0300 | −0.0355 | −0.0277 | −0.0289 | |
| Max | 0.0212 | 0.0154 | 0.0191 | 0.0165 | |
| Std. Dev. | 0.0084 | 0.0069 | 0.0063 | 0.0060 | |
| Gaussian | Mean | 0.0014 | 0.0015 | 0.0012 | 0.0010 |
| Min | −0.0335 | −0.0276 | −0.0269 | −0.0266 | |
| Max | 0.0293 | 0.0244 | 0.0220 | 0.0220 | |
| Std. Dev. | 0.0086 | 0.0072 | 0.0065 | 0.0064 | |
| Gumbel | Mean | 0.0005 | 0.0008 | 0.0007 | 0.0005 |
| Min | −0.0339 | −0.0305 | −0.0579 | −0.0579 | |
| Max | 0.0338 | 0.0269 | 0.0242 | 0.0207 | |
| Std. Dev. | 0.0091 | 0.0072 | 0.0076 | 0.0073 | |
| Student-t | Mean | 0.0020 | 0.0016 | 0.0013 | 0.0009 |
| Min | −0.0320 | −0.0248 | −0.0565 | −0.0565 | |
| Max | 0.0247 | 0.0294 | 0.0283 | 0.0239 | |
| Std. Dev. | 0.0086 | 0.0070 | 0.0077 | 0.0075 | |
| Optimal | Mean | 0.0009 | 0.0008 | 0.0010 | 0.0010 |
| Min | −0.0288 | −0.0368 | −0.0280 | −0.0286 | |
| Max | 0.0204 | 0.0133 | 0.0141 | 0.0154 | |
| Std. Dev. | 0.0076 | 0.0063 | 0.0056 | 0.0054 | |
| CFG | Mean | 0.0010 | 0.0008 | 0.0011 | 0.0012 |
| Min | −0.0260 | −0.0297 | −0.0303 | −0.0331 | |
| Max | 0.0276 | 0.0201 | 0.0196 | 0.0184 | |
| Std. Dev. | 0.0077 | 0.0067 | 0.0064 | 0.0062 | |
| CJF | Mean | 0.0013 | 0.0011 | 0.0012 | 0.0008 |
| Min | −0.0301 | −0.0260 | −0.0301 | −0.0293 | |
| Max | 0.0257 | 0.0216 | 0.0204 | 0.0158 | |
| Std. Dev. | 0.0079 | 0.0068 | 0.0063 | 0.0060 | |
| CJG | Mean | 0.0007 | 0.0009 | 0.0010 | 0.0008 |
| Min | −0.0384 | −0.0233 | −0.0249 | −0.0237 | |
| Max | 0.0213 | 0.0247 | 0.0209 | 0.0173 | |
| Std. Dev. | 0.0077 | 0.0066 | 0.0058 | 0.0058 | |
| FJG | Mean | 0.0013 | 0.0013 | 0.0012 | 0.0010 |
| Min | −0.0304 | −0.0313 | −0.0302 | −0.0320 | |
| Max | 0.0221 | 0.0198 | 0.0197 | 0.0144 | |
| Std. Dev. | 0.0084 | 0.0073 | 0.0066 | 0.0061 |
| Strategy | CSI100 | CSI200 | CSI500 | All | |
|---|---|---|---|---|---|
| Clayton | Mean | 0.0009 | 0.0011 | 0.0012 | 0.0007 |
| Min | −0.0258 | −0.0925 | −0.0143 | −0.0323 | |
| Max | 0.0240 | 0.3134 | 0.0263 | 0.0239 | |
| Std. Dev. | 0.0065 | 0.0226 | 0.0061 | 0.0069 | |
| Frank | Mean | 0.0004 | −0.0003 | 0.0017 | 0.0012 |
| Min | −0.0340 | −0.0352 | −0.0241 | −0.0355 | |
| Max | 0.0139 | 0.0194 | 0.0247 | 0.0154 | |
| Std. Dev. | 0.0059 | 0.0077 | 0.0073 | 0.0069 | |
| Gaussian | Mean | 0.0008 | 0.0003 | 0.0016 | 0.0015 |
| Min | −0.0289 | −0.1093 | −0.0344 | −0.0276 | |
| Max | 0.0214 | 0.0904 | 0.0227 | 0.0244 | |
| Std. Dev. | 0.0061 | 0.0120 | 0.0072 | 0.0072 | |
| Gumbel | Mean | 0.0001 | −0.0001 | 0.0009 | 0.0008 |
| Min | −0.0327 | −0.0998 | −0.0182 | −0.0305 | |
| Max | 0.0183 | 0.0478 | 0.0202 | 0.0269 | |
| Std. Dev. | 0.0060 | 0.0111 | 0.0067 | 0.0072 | |
| Student-t | Mean | 0.0005 | 0.0012 | 0.0016 | 0.0016 |
| Min | −0.0297 | −0.0311 | −0.0359 | −0.0248 | |
| Max | 0.0230 | 0.0980 | 0.0254 | 0.0294 | |
| Std. Dev. | 0.0061 | 0.0110 | 0.0074 | 0.0070 | |
| Optimal | Mean | 0.0005 | 0.0004 | 0.0015 | 0.0008 |
| Min | −0.0389 | −0.0302 | −0.0210 | −0.0368 | |
| Max | 0.0224 | 0.0931 | 0.0219 | 0.0133 | |
| Std. Dev. | 0.0065 | 0.0101 | 0.0067 | 0.0063 | |
| CFG | Mean | 0.0011 | 0.0009 | 0.0019 | 0.0008 |
| Min | −0.0412 | −0.0999 | −0.0201 | −0.0297 | |
| Max | 0.0250 | 0.2987 | 0.0254 | 0.0201 | |
| Std. Dev. | 0.0065 | 0.0218 | 0.0064 | 0.0067 | |
| CJF | Mean | 0.0009 | 0.0008 | 0.0013 | 0.0011 |
| Min | −0.0214 | −0.1014 | −0.0191 | −0.0260 | |
| Max | 0.0207 | 0.2809 | 0.0274 | 0.0216 | |
| Std. Dev. | 0.0060 | 0.0210 | 0.0066 | 0.0068 | |
| CJG | Mean | 0.0008 | 0.0007 | 0.0013 | 0.0009 |
| Min | −0.0224 | −0.0851 | −0.0161 | −0.0233 | |
| Max | 0.0211 | 0.2040 | 0.0258 | 0.0247 | |
| Std. Dev. | 0.0062 | 0.0163 | 0.0064 | 0.0066 | |
| FJG | Mean | 0.0005 | 0.0007 | 0.0017 | 0.0013 |
| Min | −0.0342 | −0.0350 | −0.0231 | −0.0313 | |
| Max | 0.0188 | 0.1419 | 0.0215 | 0.0198 | |
| Std. Dev. | 0.0063 | 0.0120 | 0.0070 | 0.0073 |
| Strategy | Period | Pre-Fin.C. | In-Fin.C. | Post-Fin.C. | Pre-B.N.B. | In-Bullish | In-Bearish | Pre-Cov. | In-Cov. | Post-Cov. |
|---|---|---|---|---|---|---|---|---|---|---|
| Timeline | Jan 2005–Dec 2006 | Jan 2007–Dec 2008 | Jan 2009–Dec 2010 | Jan 2011–Dec 2013 | Jan 2014–May 2015 | June 2015–Dec 2016 | Jan 2017–Dec 2019 | Jan 2020–Dec 2022 | Jan 2023–Jun 2024 | |
| Panel A: Before Transaction Costs | ||||||||||
| Clayton | Mean | 0.0030 | 0.0105 | 0.0009 | 0.0006 | −0.0037 | 0.0064 | −0.0004 | 0.0034 | 0.0011 |
| Std. Dev. | 0.0156 | 0.0160 | 0.0179 | 0.0095 | 0.0109 | 0.0228 | 0.0084 | 0.0097 | 0.0155 | |
| Frank | Mean | −0.0002 | 0.0067 | 0.0046 | 0.0012 | −0.0038 | 0.0083 | 0.0002 | 0.0067 | −0.0021 |
| Std. Dev. | 0.0155 | 0.0125 | 0.0091 | 0.0094 | 0.0109 | 0.0198 | 0.0131 | 0.0099 | 0.0090 | |
| Gaussian | Mean | 0.0018 | 0.0094 | 0.0044 | 0.0014 | −0.0037 | 0.0046 | −0.0012 | 0.0071 | 0.0020 |
| Std. Dev. | 0.0147 | 0.0133 | 0.0075 | 0.0123 | 0.0125 | 0.0160 | 0.0128 | 0.0112 | 0.0094 | |
| Gumbel | Mean | 0.0030 | 0.0056 | 0.0019 | 0.0014 | −0.0034 | 0.0041 | −0.0002 | 0.0050 | −0.0002 |
| Std. Dev. | 0.0165 | 0.0139 | 0.0104 | 0.0108 | 0.0124 | 0.0113 | 0.0151 | 0.0110 | 0.0105 | |
| Student-t | Mean | 0.0039 | 0.0105 | 0.0045 | 0.0012 | 0.0010 | 0.0075 | 0.0017 | 0.0086 | 0.0040 |
| Std. Dev. | 0.0215 | 0.0142 | 0.0160 | 0.0082 | 0.0087 | 0.0150 | 0.0143 | 0.0139 | 0.0157 | |
| Optimal | Mean | −0.0002 | 0.0033 | 0.0037 | 0.0019 | −0.0020 | 0.0072 | −0.0019 | 0.0053 | −0.0010 |
| Std. Dev. | 0.0132 | 0.0119 | 0.0099 | 0.0095 | 0.0080 | 0.0129 | 0.0153 | 0.0083 | 0.0076 | |
| CFG | Mean | −0.0007 | 0.0055 | 0.0059 | 0.0031 | −0.0014 | 0.0029 | −0.0017 | 0.0040 | −0.0016 |
| Std. Dev. | 0.0138 | 0.0121 | 0.0107 | 0.0092 | 0.0077 | 0.0117 | 0.0113 | 0.0105 | 0.0116 | |
| CJF | Mean | −0.0006 | 0.0054 | 0.0051 | 0.0022 | −0.0019 | 0.0073 | −0.0017 | 0.0047 | 0.0007 |
| Std. Dev. | 0.0153 | 0.0099 | 0.0100 | 0.0126 | 0.0112 | 0.0158 | 0.0129 | 0.0108 | 0.0074 | |
| CJG | Mean | 0.0019 | 0.0075 | 0.0047 | 0.0028 | −0.0021 | 0.0034 | −0.0016 | 0.0041 | −0.0015 |
| Std. Dev. | 0.0129 | 0.0130 | 0.0120 | 0.0119 | 0.0123 | 0.0102 | 0.0136 | 0.0125 | 0.0115 | |
| FJG | Mean | 0.0010 | 0.0066 | 0.0039 | 0.0014 | −0.0038 | 0.0071 | 0.0012 | 0.0043 | −0.0002 |
| Std. Dev. | 0.0160 | 0.0143 | 0.0086 | 0.0095 | 0.0124 | 0.0144 | 0.0119 | 0.0123 | 0.0057 | |
| Panel B: After Transaction Costs | ||||||||||
| Clayton | Mean | 0.0020 | 0.0086 | 0.0004 | −0.0005 | −0.0045 | 0.0049 | −0.0019 | 0.0020 | 0.0000 |
| Std. Dev. | 0.0150 | 0.0151 | 0.0176 | 0.0094 | 0.0105 | 0.0219 | 0.0083 | 0.0093 | 0.0148 | |
| Frank | Mean | −0.0014 | 0.0053 | 0.0037 | 0.0003 | −0.0048 | 0.0070 | −0.0009 | 0.0056 | −0.0030 |
| Std. Dev. | 0.0150 | 0.0118 | 0.0089 | 0.0094 | 0.0107 | 0.0190 | 0.0129 | 0.0094 | 0.0090 | |
| Gaussian | Mean | 0.0008 | 0.0083 | 0.0035 | 0.0004 | −0.0048 | 0.0036 | −0.0021 | 0.0058 | 0.0004 |
| Std. Dev. | 0.0144 | 0.0126 | 0.0074 | 0.0122 | 0.0126 | 0.0156 | 0.0122 | 0.0109 | 0.0094 | |
| Gumbel | Mean | 0.0017 | 0.0040 | 0.0010 | 0.0003 | −0.0048 | 0.0026 | −0.0014 | 0.0036 | −0.0016 |
| Std. Dev. | 0.0160 | 0.0136 | 0.0103 | 0.0106 | 0.0122 | 0.0108 | 0.0146 | 0.0109 | 0.0101 | |
| Student-t | Mean | 0.0006 | 0.0081 | 0.0030 | 0.0000 | −0.0049 | 0.0055 | −0.0011 | 0.0061 | 0.0025 |
| Std. Dev. | 0.0126 | 0.0142 | 0.0105 | 0.0109 | 0.0111 | 0.0147 | 0.0128 | 0.0107 | 0.0089 | |
| Optimal | Mean | −0.0009 | 0.0022 | 0.0029 | 0.0010 | −0.0028 | 0.0060 | −0.0028 | 0.0042 | −0.0018 |
| Std. Dev. | 0.0129 | 0.0118 | 0.0096 | 0.0094 | 0.0077 | 0.0126 | 0.0145 | 0.0081 | 0.0075 | |
| CFG | Mean | −0.0017 | 0.0043 | 0.0050 | 0.0021 | −0.0023 | 0.0017 | −0.0028 | 0.0029 | −0.0026 |
| Std. Dev. | 0.0135 | 0.0116 | 0.0103 | 0.0088 | 0.0075 | 0.0114 | 0.0109 | 0.0102 | 0.0114 | |
| CJF | Mean | −0.0015 | 0.0043 | 0.0041 | 0.0012 | −0.0026 | 0.0059 | −0.0027 | 0.0035 | −0.0005 |
| Std. Dev. | 0.0150 | 0.0102 | 0.0097 | 0.0122 | 0.0107 | 0.0154 | 0.0126 | 0.0106 | 0.0072 | |
| CJG | Mean | 0.0006 | 0.0070 | 0.0039 | 0.0016 | −0.0033 | 0.0023 | −0.0027 | 0.0027 | −0.0023 |
| Std. Dev. | 0.0127 | 0.0123 | 0.0117 | 0.0116 | 0.0119 | 0.0102 | 0.0131 | 0.0124 | 0.0107 | |
| FJG | Mean | −0.0002 | 0.0052 | 0.0031 | 0.0005 | −0.0048 | 0.0056 | 0.0002 | 0.0032 | −0.0010 |
| Std. Dev. | 0.0156 | 0.0144 | 0.0083 | 0.0094 | 0.0121 | 0.0134 | 0.0116 | 0.0119 | 0.0052 | |
| Strategy | Sharpe Ratio | Sortino Ratio | Mean/CvaR (95%) |
|---|---|---|---|
| Panel A: Average monthly performance in crisis period | |||
| SSD-Hurst | 0.4749 | 0.8386 | 0.3052 |
| SSD-NZC | 0.3969 | 0.6701 | 0.2237 |
| Clayton | 0.2038 | 0.2788 | 0.0926 |
| Frank | 0.2961 | 0.5967 | 0.1924 |
| Gaussian | 0.3065 | 0.5248 | 0.1687 |
| Gumbel | 0.1632 | 0.2494 | 0.0757 |
| Student-t | 0.3384 | 0.6686 | 0.2213 |
| Optimal | 0.2649 | 0.4197 | 0.1376 |
| CFG | 0.1943 | 0.2867 | 0.0917 |
| CJF | 0.2576 | 0.4533 | 0.1478 |
| CJG | 0.2138 | 0.3473 | 0.1106 |
| FJG | 0.2030 | 0.3183 | 0.1062 |
| Panel B: Average monthly performance in normal period | |||
| SSD-Hurst | 0.1920 | 1.1439 | 0.4672 |
| SSD-NZC | 0.1798 | 0.5460 | 0.2267 |
| Clayton | −0.0147 | −0.0177 | −0.0055 |
| Frank | −0.0104 | −0.0126 | −0.0037 |
| Gaussian | 0.0323 | 0.0443 | 0.0139 |
| Gumbel | −0.0010 | −0.0013 | −0.0004 |
| Student-t | 0.0561 | 0.0767 | 0.0235 |
| Optimal | −0.0305 | −0.0365 | −0.0111 |
| CFG | 0.0061 | 0.0079 | 0.0024 |
| CJF | −0.0007 | −0.0008 | −0.0003 |
| CJG | 0.0163 | 0.0208 | 0.0064 |
| FJG | 0.0508 | 0.0636 | 0.0202 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y. Performance of Pairs Trading Strategies Based on Various Copula Methods. J. Risk Financial Manag. 2025, 18, 506. https://doi.org/10.3390/jrfm18090506
Sun Y. Performance of Pairs Trading Strategies Based on Various Copula Methods. Journal of Risk and Financial Management. 2025; 18(9):506. https://doi.org/10.3390/jrfm18090506
Chicago/Turabian StyleSun, Yufei. 2025. "Performance of Pairs Trading Strategies Based on Various Copula Methods" Journal of Risk and Financial Management 18, no. 9: 506. https://doi.org/10.3390/jrfm18090506
APA StyleSun, Y. (2025). Performance of Pairs Trading Strategies Based on Various Copula Methods. Journal of Risk and Financial Management, 18(9), 506. https://doi.org/10.3390/jrfm18090506






