From Pandemic Shock to Sustainable Recovery: Data-Driven Insights into Global Eco-Productivity Trends During the COVID-19 Era
Abstract
1. Introduction
2. Methods
2.1. Input-Oriented Slack-Based Measure (IO-SBM) Model
- is the input vector for the evaluated country;
- is the desirable output (GDP);
- is the undesirable output (CO2 emissions);
- represents input excess (slacks);
- denotes the shortfall in desirable outputs;
- represents excess undesirable outputs;
- λ is the intensity vector.
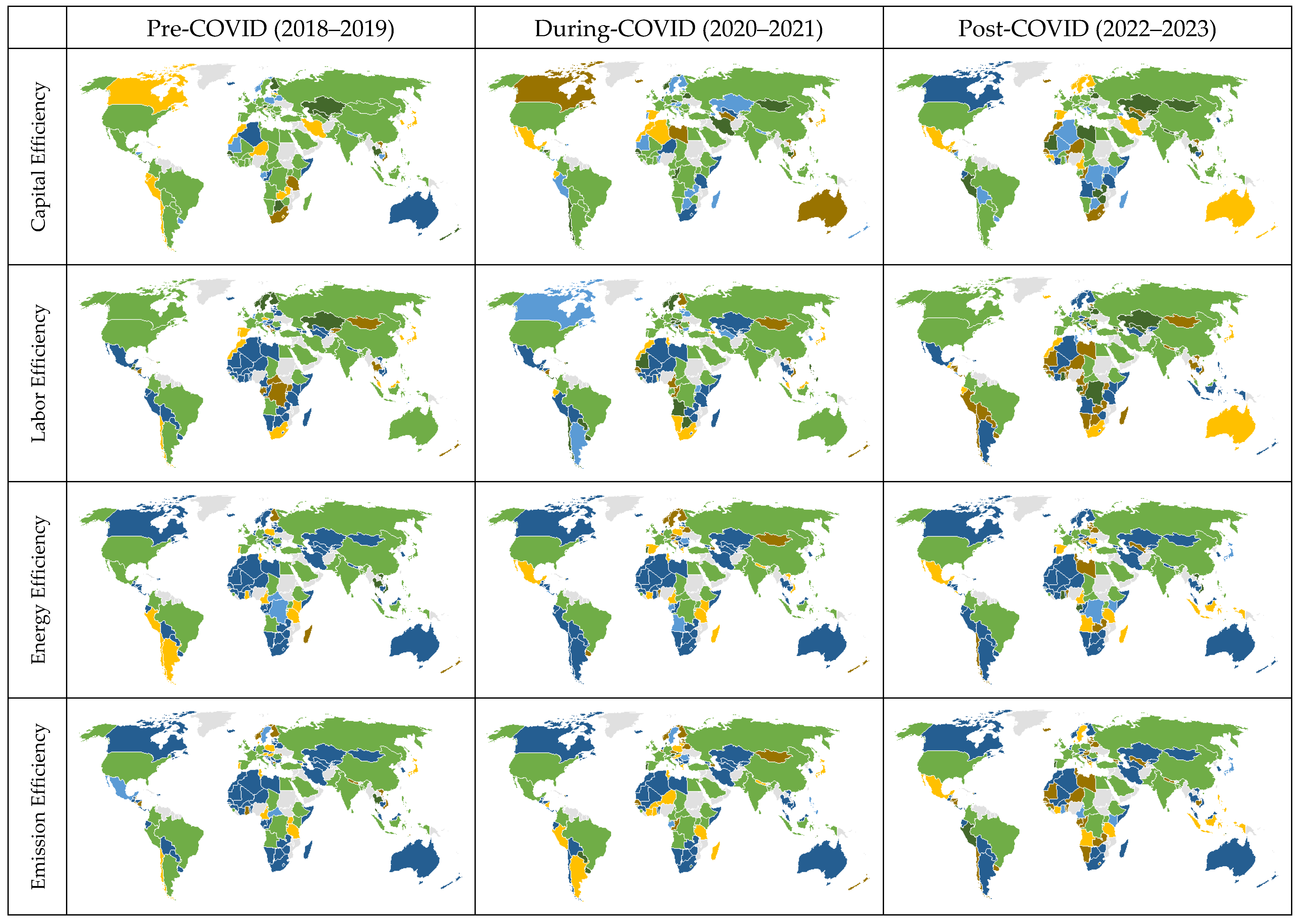
- Capital Efficiency (KE): Measures how close a country’s actual use of gross fixed capital formation (GFCF) is to its optimal frontier target. A higher score indicates that capital is being used with minimal waste.
- Labor Efficiency (LE): Reflects how effectively labor force inputs are transformed into GDP relative to their target values. Countries with low scores use more labor than necessary compared to efficient peers.
- Energy Efficiency (EE): captures how far a country’s energy consumption is from its frontier target, indicating the potential to achieve the same GDP with less energy.
- Carbon Efficiency (CE): indicates the gap between actual CO2 emissions and the frontier benchmark, showing the extent to which emissions could be reduced without lowering GDP.
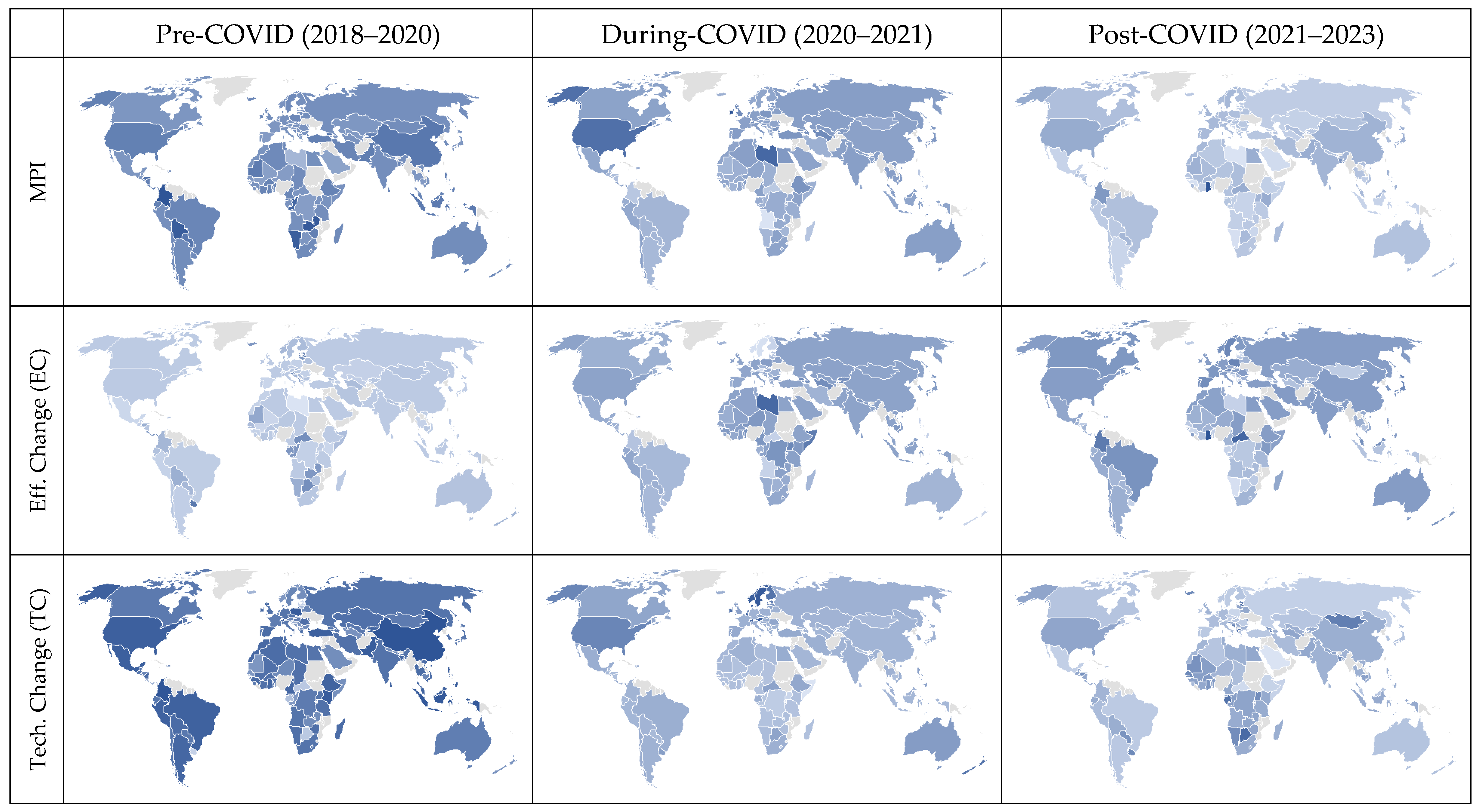
2.2. Malmquist Productivity Index (MPI) Model
- Efficiency Change (EC): This component, often referred to as the “catch-up” effect, quantifies the change in a DMU’s relative efficiency between periods and . It indicates whether the DMU has moved closer to the efficiency frontier (, an improvement in efficiency), further away (, a deterioration in efficiency), or maintained its relative position (). It is calculated as follows:
- Technological Change (TC): This component, also known as the “frontier-shift” effect, measures the displacement of the efficiency frontier itself between the two periods. It captures technological progress if the frontier shifts outward (), technological regress if it shifts inward (), or no change in the frontier (). The formula is as follows:
2.3. Sensitivity Analysis of the Model and Variables
2.3.1. Sensitivity Analysis of the Model
- Input-oriented CCR (IO-CCR) Model: DEA is a non-parametric mathematical programming methodology used to assess the relative efficiency of a homogeneous set of DMUs that convert multiple inputs into multiple outputs. The seminal model in this field is the CCR model, introduced by Charnes et al. (1978), which operates under the assumption of constant returns to scale (CRS). The input-oriented CCR model emphasizes input minimization, evaluating the technical efficiency of a DMU by identifying the maximum feasible proportional reduction in its input vector while maintaining its current output levels. This model is particularly suited for settings where inputs can be controlled or reduced, offering a benchmark for identifying inefficiencies and guiding resource optimization. The overall technical efficiency score () of a DMU is calculated as follows:
- Input-Oriented BCC (IO-BCC) Model: The input-oriented BCC model, introduced by Banker et al. (1984), is a crucial extension of the original DEA framework that enhances efficiency evaluation by replacing the CRS assumption of the CCR model with the more adaptable VRS. This modification enables the BCC model to differentiate between technical inefficiency and scale inefficiency, providing a more accurate assessment of performance across DMUs operating at various scales. Specifically, the input-oriented BCC model assesses pure technical efficiency (PTE) by determining the maximum proportional reduction in a DMU’s input usage while maintaining its current output levels. It constructs a convex envelopment frontier against which each DMU is benchmarked relative to peers of similar scale. A DMU achieves an efficiency score of one if it operates on this frontier, indicating best-practice performance regardless of any scale-related advantages or disadvantages. The overall PTE score () of a DMU is calculated as follows:
- Input-Oriented SBM (IO-SBM) Model under CRS: The IO-SBM model under CRS, introduced by Tone (2001), is a non-radial DEA approach that provides a more detailed and rigorous assessment of technical efficiency by directly incorporating input slacks. Unlike traditional radial models such as the CCR, which assume proportional input reductions, the IO-SBM model quantifies specific excesses for each input, allowing it to identify inefficiencies that radial models may overlook. Operating under CRS, the IO-SBM model evaluates a DMU’s efficiency relative to a production possibility set that assumes proportional scalability. A DMU is considered fully efficient, with a score of one, only if it exhibits zero slacks across all inputs, indicating that it lies on the efficient frontier with no further potential for non-proportional input reductions. This approach offers a more nuanced and comprehensive measure of inefficiency, making it particularly valuable for performance diagnostics and resource optimization. The IO-SBM model under CRS is formulated as follows for a DMU :
2.3.2. Sensitivity Analysis of the Variables
3. Data and Variables
3.1. Input Variables
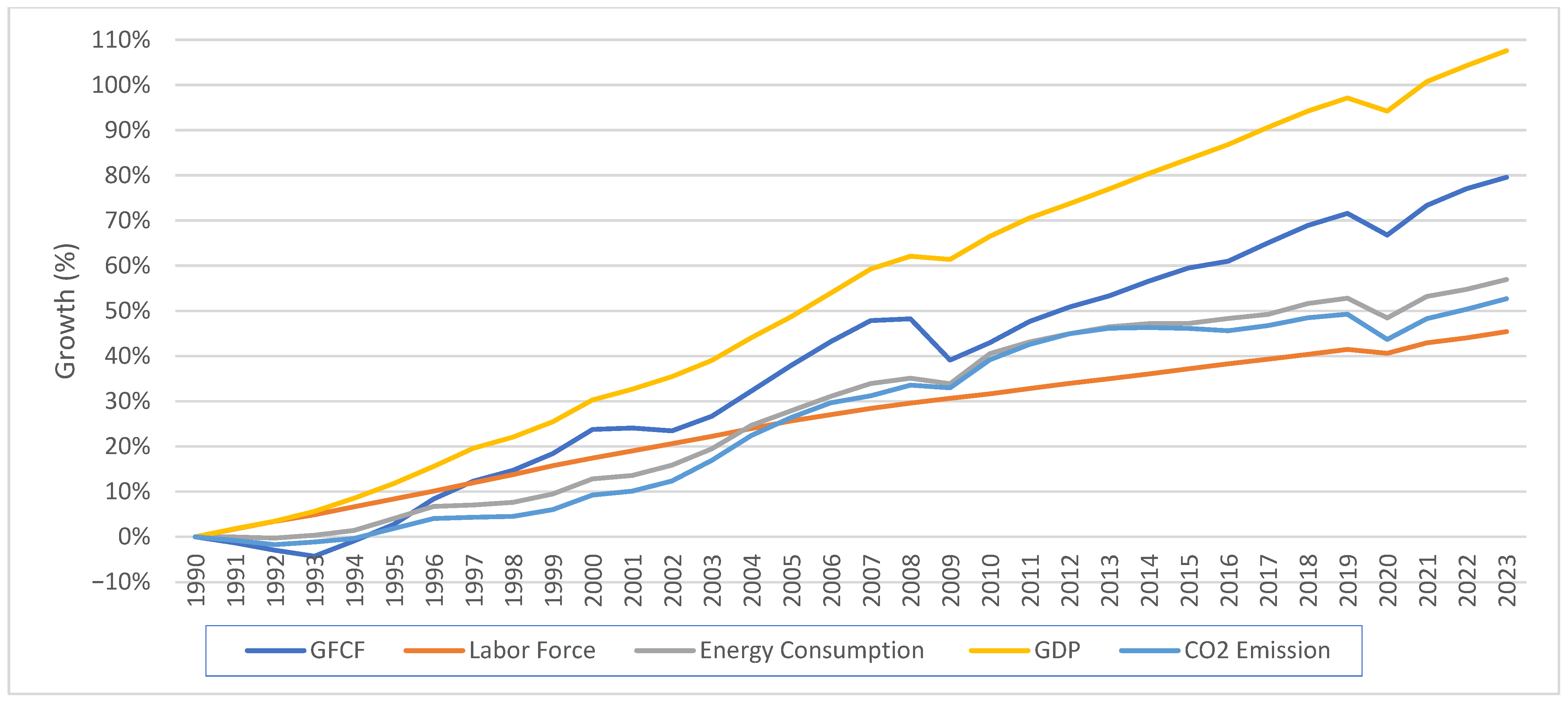
- GFCF reflects country-level investment in physical assets such as infrastructure, machinery, equipment, and facility construction—key drivers of long-term economic growth and technological progress. Between 2018 and 2023, the average GFCF across countries was approximately USD 167.97 billion, with values ranging from USD 134 million to over USD 7.49 trillion, underscoring the wide disparity in investment capacity. As a capital input, GFCF indicates an economy’s capacity to expand its productive frontier. The dataset reveals a significant global contraction in GFCF in 2020, coinciding with the peak of COVID-19-related economic disruptions. The extent of the decline and the subsequent recovery varied considerably across income levels and regions. Advanced and upper-middle-income economies typically experienced a sharp rebound from 2021 onward, supported by large-scale stimulus measures and improved investor confidence. In contrast, many low-income and commodity-dependent countries faced slower recoveries due to limited fiscal capacity and ongoing structural challenges. Understanding these investment patterns is crucial for grasping differences in capital efficiency and the level of economic resilience during recovery.
- Labor force represents the total number of individuals who are either employed or actively seeking work, serving as a proxy for human capital input. Labor force participation reflects not only demographic trends but also institutional factors such as labor regulations, social safety nets, and the adaptability of labor markets. Over the study period, the average labor force size was approximately 23.1 million, with values ranging from 57,484 to over 781 million. The global labor market experienced significant turbulence as a result of the COVID-19 pandemic. In 2020, many countries recorded a decline in labor force size due to pandemic-related shutdowns, mobility restrictions, and health-related absences. While labor force levels began to recover in 2021, the pace and completeness of recovery varied. High-income countries, with robust public health systems and labor protections, generally returned to pre-pandemic levels more quickly. Meanwhile, several developing countries exhibited slower or irregular labor force recovery, impacted by long-term scarring effects and vulnerabilities in the informal sector. These disparities have direct implications for assessing labor productivity and identifying gaps in labor market resilience.
- Energy consumption serves as a vital indicator of an economy’s industrial activity scale, transportation demand, and overall production processes. As a physical input, energy use is closely tied to both output levels and environmental externalities, making it a dual-purpose variable in efficiency and sustainability assessments. The average energy consumption from 2018 to 2023 was 3.84 quadrillion BTU, with minimum and maximum values ranging from 0.0031 to 161.9 quadrillion BTU. The data reveal a sharp decline in energy consumption in 2020 across most countries, driven by widespread lockdowns, reduced economic activity, and supply chain disruptions. The rebound in energy demand from 2021 onward varied by structural characteristics: energy-intensive and export-oriented economies displayed a strong resurgence, while more diversified or energy-efficient countries showed gradual increases in demand. The evolution of energy consumption during this period reflects shifting production patterns and policy choices aimed at balancing recovery with environmental commitments. This variable is particularly relevant for interpreting eco-efficiency and the broader implications of resource use in the post-pandemic recovery landscape.
3.2. Output Variables
- Gross domestic product (GDP) serves as the primary measure of economic output in this analysis, capturing the total economic value generated by a country through the production of goods and services. As a widely accepted indicator of economic performance, GDP reflects the productive capacity and market activity that underpin national development. Over the 2018–2023 period, the average GDP between 2018 and 2023 was approximately USD 893 billion, with values ranging from a minimum of USD 0.97 billion to a maximum of USD 27.31 trillion. GDP trends reveal significant disruptions and asymmetries driven by the COVID-19 pandemic. While most countries experienced a sharp contraction in 2020 due to lockdowns, supply chain disruptions, and reduced consumer demand, the scale and pace of recovery in subsequent years varied widely. Advanced economies often showed strong rebounds fueled by fiscal and monetary interventions, whereas many developing countries faced prolonged stagnation or slower growth due to structural constraints. These variations in GDP trajectories are crucial for evaluating changes in output efficiency across different phases of the pandemic and for understanding how national economies responded to post-crisis conditions.
- Carbon dioxide (CO2) emissions are included as an undesirable output to capture the environmental externalities associated with economic activity and energy use. As a key driver of climate change, CO2 emissions serve as a critical indicator of the environmental cost of production, making their inclusion essential for evaluating eco-efficiency. Over the 2018–2023 period, the average annual CO2 emissions across countries were approximately 241 MMt CO2, with individual country values ranging from 0.22 MMt CO2 to 12,196 MMt CO2. CO2 emission patterns closely mirrored the economic and mobility disruptions brought on by the COVID-19 pandemic. Most countries recorded a noticeable decline in emissions in 2020, reflecting reduced industrial output, transportation activity, and energy consumption during lockdowns. However, emissions rebounded in many economies as restrictions eased and production resumed in 2021 and 2022, although the magnitude of the recovery differed based on the energy structure, policy responses, and decarbonization commitments. By accounting for CO2 emissions as an undesirable output, this study integrates sustainability into the efficiency framework, enabling a more comprehensive assessment of how countries balanced economic recovery with environmental impact in the post-pandemic period.
4. Results
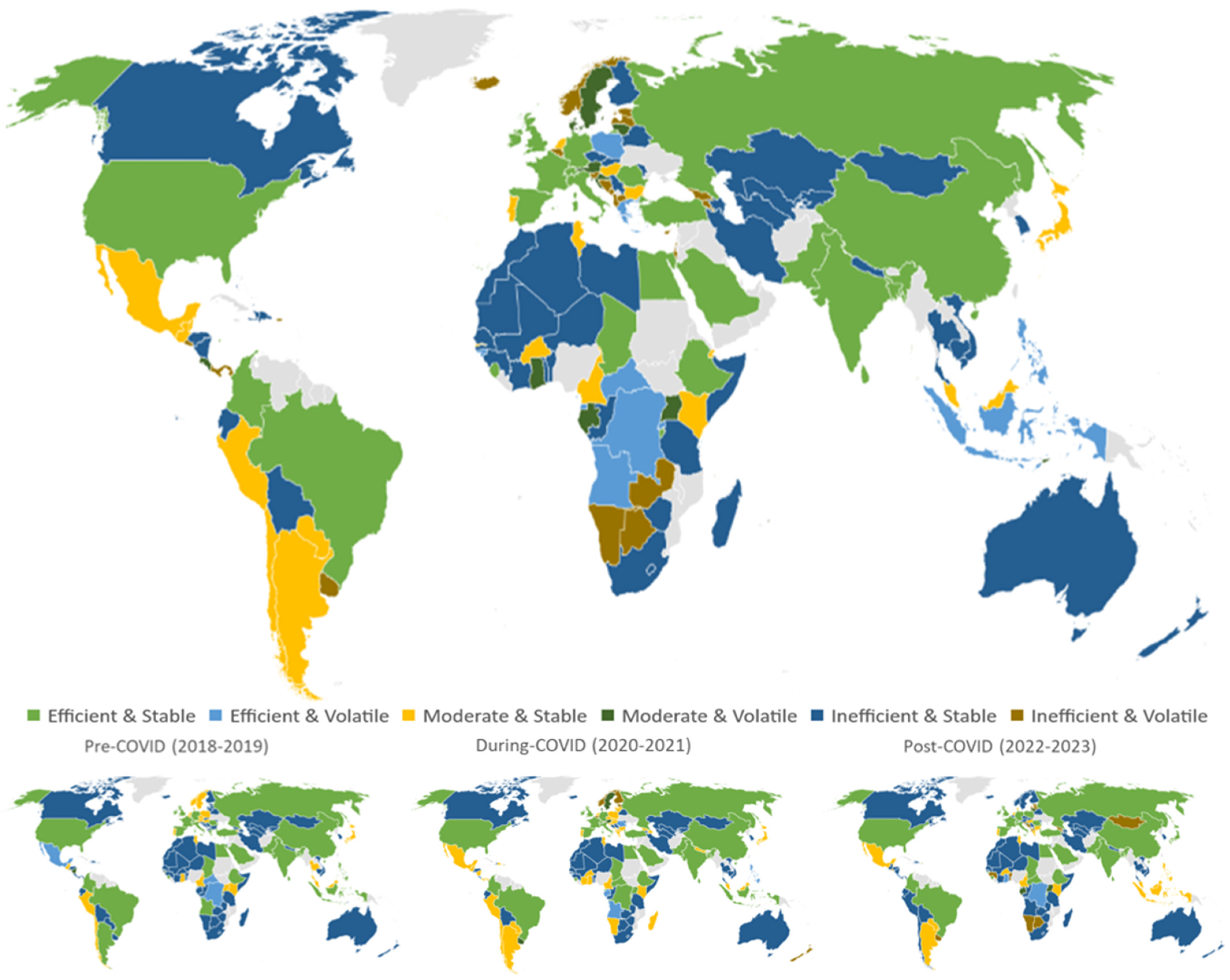
4.1. Uneven Efficiency Trajectories in Response to COVID-19: IO-SBM Analysis
4.2. Cross-Country Dynamics in Sustainability Performance Indicators Across the COVID-19 Period (2018–2023)
4.3. Temporal Decomposition of Eco-Productivity in the COVID-19 Context: MPI, EC, and TC Results
4.4. Sensitivity Analysis
4.4.1. Sensitivity Analysis Results of the Model
4.4.2. Sensitivity Analysis of the Input Variables
4.5. Statistical Analysis
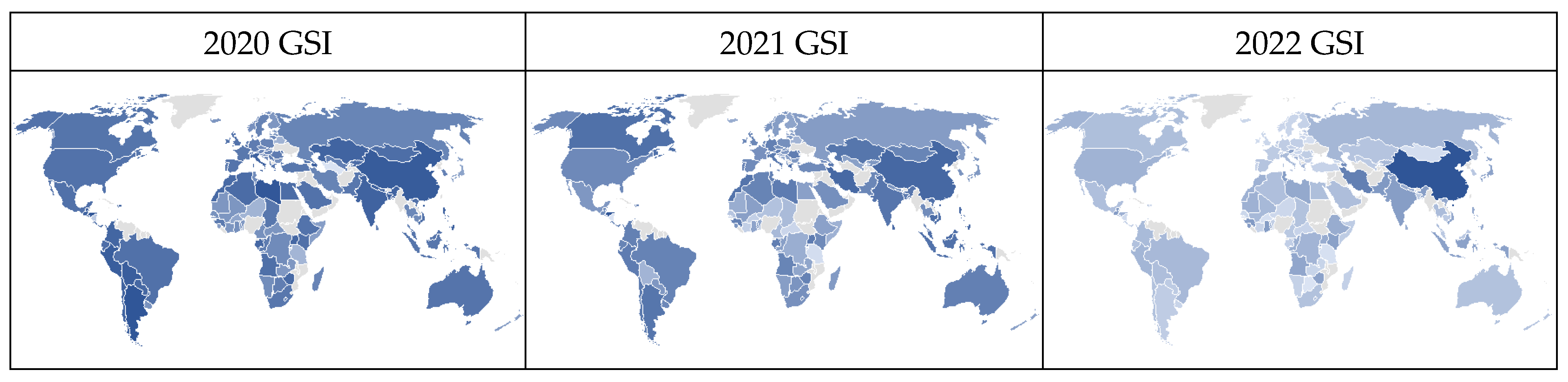
4.5.1. Government Stringency Index (GSI)
4.5.2. Non-Parametric Tests for World Bank Income Groups and Efficiency Scores
5. Discussions
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aghion, P., Antonin, C., & Bunel, S. (2021). The power of creative destruction: Economic upheaval and the wealth of nations. Harvard University Press. [Google Scholar]
- Apergis, N., Aye, G. C., Barros, C. P., Gupta, R., & Wanke, P. (2015). Energy efficiency of selected OECD countries: A slacks based model with undesirable outputs. Energy Economics, 51, 45–53. [Google Scholar] [CrossRef]
- Banker, R. D., Charnes, A., & Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30(9), 1078–1092. [Google Scholar] [CrossRef]
- Brockett, P. L., Golany, B., & Li, S. (1999). Analysis of intertemporal efficiency trends using rank statistics with an application evaluating the macro economic performance of OECD nations. Journal of Productivity Analysis, 11, 169–182. [Google Scholar] [CrossRef]
- Camanho, A. S., Silva, M. C., Piran, F. S., & Lacerda, D. P. (2024). A literature review of economic efficiency assessments using Data Envelopment Analysis. European Journal of Operational Research, 315(1), 1–18. [Google Scholar] [CrossRef]
- Chang, T. P., & Hu, J. L. (2010). Total-factor energy productivity growth, technical progress, and efficiency change: An empirical study of China. Applied Energy, 87(10), 3262–3270. [Google Scholar] [CrossRef]
- Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444. [Google Scholar] [CrossRef]
- Chien, T., & Hu, J. L. (2007). Renewable energy and macroeconomic efficiency of OECD and non-OECD economies. Energy Policy, 35(7), 3606–3615. [Google Scholar] [CrossRef]
- Choi, Y., Zhang, N., & Zhou, P. (2012). Efficiency and abatement costs of energy-related CO2 emissions in China: A slacks-based efficiency measure. Applied Energy, 98, 198–208. [Google Scholar] [CrossRef]
- Cohen, W. M., & Levinthal, D. A. (1990). Absorptive capacity: A new perspective on learning and innovation. Administrative Science Quarterly, 35(1), 128–152. [Google Scholar] [CrossRef]
- Deliktas, E., & Balcilar, M. (2005). A comparative analysis of productivity growth, catch-up, and convergence in transition economies. Emerging Markets Finance and Trade, 41(1), 6–28. [Google Scholar] [CrossRef]
- Demiral, E. E., & Sağlam, Ü. (2021). Eco-efficiency and Eco-productivity assessments of the states in the United States: A two-stage Non-parametric analysis. Applied Energy, 303, 117649. [Google Scholar] [CrossRef]
- Demiral, E. E., & Sağlam, Ü. (2023). Sustainable production assessment of the 50 US states. Journal of Cleaner Production, 419, 138086. [Google Scholar] [CrossRef]
- Färe, R., Grosskopf, S., Norris, M., & Zhang, Z. (1994). Productivity growth, technical progress, and efficiency change in industrialized countries. The American Economic Review, 84(1), 66–83. [Google Scholar]
- Forstner, H., & Isaksson, A. (2002). Productivity, technology, and efficiency: An analysis of the world technology Frontier; when memory is infinite. Statistics and Information Networks Branch of UNIDO. [Google Scholar]
- Hale, T., Angrist, N., Goldszmidt, R., Kira, B., Petherick, A., Phillips, T., Webster, S., Cameron-Blake, E., Hallas, L., Majumdar, S., & Tatlow, H. (2021). A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nature Human Behaviour, 5(4), 529–538. [Google Scholar] [CrossRef]
- Hsieh, C. T., & Klenow, P. J. (2018). The reallocation myth. Center for Economic Studies Working Paper, 18, 1–25. [Google Scholar]
- Hu, J. L., & Kao, C. H. (2007). Efficient energy-saving targets for APEC economies. Energy Policy, 35(1), 373–382. [Google Scholar] [CrossRef]
- Hu, J. L., & Wang, S. C. (2006). Total-factor energy efficiency of regions in China. Energy Policy, 34(17), 3206–3217. [Google Scholar] [CrossRef]
- Iftikhar, Y., He, W., & Wang, Z. (2016). Energy and CO2 emissions efficiency of major economies: A non-parametric analysis. Journal of Cleaner Production, 139, 779–787. [Google Scholar] [CrossRef]
- Kaüger, J. J., Cantner, U., & Hanusch, H. (2000). Total factor productivity, the East Asian miracle, and the world production frontier. Weltwirtschaftliches Archiv, 136(1), 111–136. [Google Scholar] [CrossRef]
- Lin, B., & Du, K. (2015). Modeling the dynamics of carbon emission performance in China: A parametric Malmquist index approach. Energy Economics, 49, 550–557. [Google Scholar] [CrossRef]
- Loayza, N. (2018). Informality: Why is it so widespread and how can it be reduced? World Bank research and policy briefs No. 133110. Available online: https://ssrn.com/abstract=3360124 (accessed on 1 July 2025).
- Moutinho, V., Fuinhas, J. A., Marques, A. C., & Santiago, R. (2018). Assessing eco-efficiency through the DEA analysis and decoupling index in the Latin America countries. Journal of Cleaner Production, 205, 512–524. [Google Scholar] [CrossRef]
- Moutinho, V., Madaleno, M., & Robaina, M. (2017). The economic and environmental efficiency assessment in EU cross-country: Evidence from DEA and quantile regression approach. Ecological Indicators, 78, 85–97. [Google Scholar] [CrossRef]
- Park, Y. S., Lim, S. H., Egilmez, G., & Szmerekovsky, J. (2018). Environmental efficiency assessment of US transport sector: A slack-based data envelopment analysis approach. Transportation Research Part D: Transport and Environment, 61, 152–164. [Google Scholar] [CrossRef]
- Rodrik, D. (2016). Premature deindustrialization. Journal of Economic Growth, 21(1), 1–33. [Google Scholar] [CrossRef]
- Sağlam, Ü. (2017a). A two-stage data envelopment analysis model for efficiency assessments of 39 state’s wind power in the United States. Energy Conversion and Management, 146, 52–67. [Google Scholar] [CrossRef]
- Sağlam, Ü. (2017b). Assessment of the productive efficiency of large wind farms in the United States: An application of two-stage data envelopment analysis. Energy Conversion and Management, 153, 188–214. [Google Scholar] [CrossRef]
- Sağlam, Ü. (2018). A two-stage performance assessment of utility-scale wind farms in Texas using data envelopment analysis and Tobit models. Journal of Cleaner Production, 201, 580–598. [Google Scholar] [CrossRef]
- Sağlam, Ü. (2019). The effects of electricity prices on productive efficiency of states’ wind power performances in the United States. Economics Bulletin, 39(2), 866–875. [Google Scholar]
- Sağlam, Ü. (2025). Beyond GDP: COVID-19’s effects on macroeconomic efficiency and productivity dynamics in OECD countries. Econometrics, 13(3), 29. [Google Scholar] [CrossRef]
- Sueyoshi, T., Mo, F., & Wang, D. D. (2022). Sustainable development of countries all over the world and the impact of renewable energy. Renewable Energy, 184, 320–331. [Google Scholar] [CrossRef]
- Tone, K. (2001). A slacks-based measure of efficiency in data envelopment analysis. European Journal of Operational Research, 130(3), 498–509. [Google Scholar] [CrossRef]
- Tone, K. (2004). Malmquist productivity index: Efficiency change over time. In Handbook on data envelopment analysis (pp. 203–227). Springer US. [Google Scholar]
- Tone, K. (2010). Variations on the theme of slacks-based measure of efficiency in DEA. European Journal of Operational Research, 200(3), 901–907. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration (EIA). (2024a). Emissions by fuel—World. Available online: https://www.eia.gov/international/data/world/other-statistics/emissions-by-fuel (accessed on 1 April 2025).
- U.S. Energy Information Administration (EIA). (2024b). Gross domestic product by country—World. Available online: https://www.eia.gov/international/data/world/other-statistics/gross-domestic-product-by-country (accessed on 1 May 2025).
- U.S. Energy Information Administration (EIA). (2024c). Total energy consumption—World. Available online: https://www.eia.gov/international/data/world/total-energy/total-energy-consumption (accessed on 1 April 2025).
- Wang, C. N., Hsu, H. P., Wang, Y. H., & Nguyen, T. T. (2020). Eco-efficiency assessment for some European countries using slacks-based measure data envelopment analysis. Applied Sciences, 10(5), 1760. [Google Scholar] [CrossRef]
- Wang, C. N., Nguyen, T. T. T., Dang, T. T., & Hsu, H. P. (2023). Exploring economic and environmental efficiency in renewable energy utilization: A case study in the Organization for Economic Cooperation and Development countries. Environmental Science and Pollution Research, 30(28), 72949–72965. [Google Scholar] [CrossRef]
- Wang, K., Yu, S., & Zhang, W. (2013). China’s regional energy and environmental efficiency: A DEA window analysis based dynamic evaluation. Mathematical and Computer Modelling, 58(5–6), 1117–1127. [Google Scholar] [CrossRef]
- Wei, C., Ni, J., & Sheng, M. (2011). China’s energy inefficiency: A cross-country comparison. The Social Science Journal, 48(3), 478–488. [Google Scholar] [CrossRef]
- World Bank. (2024a). Gross fixed capital formation (constant 2015 US$). Available online: https://data.worldbank.org/indicator/NE.GDI.FTOT.KD (accessed on 1 April 2025).
- World Bank. (2024b). Labor force, total. Available online: https://data.worldbank.org/indicator/SL.TLF.TOTL.IN (accessed on 1 April 2025).
- Zhang, X. P., Cheng, X. M., Yuan, J. H., & Gao, X. J. (2011). Total-factor energy efficiency in developing countries. Energy Policy, 39(2), 644–650. [Google Scholar] [CrossRef]
- Zhou, P., & Ang, B. W. (2008). Linear programming models for measuring economy-wide energy efficiency performance. Energy Policy, 36(8), 2911–2916. [Google Scholar] [CrossRef]
- Zhou, P., Ang, B. W., & Han, J. Y. (2010). Total factor carbon emission performance: A Malmquist index analysis. Energy Economics, 32(1), 194–201. [Google Scholar] [CrossRef]


| Reference | Measure | Methods | DMUs | Input Variables | Output Variables | Period |
|---|---|---|---|---|---|---|
| Färe et al. (1994) | Total-factor productivity | MPI | 17 OECD countries | K, L | GDP | 1979–1988 |
| Brockett et al. (1999) | Productivity | DEA | 17 OECD countries | K, L | GDP | 1979–1988 |
| Kaüger et al. (2000) | Total-factor productivity | MPI | 87 countries | K, L | GDP | 1960–1990 |
| Forstner and Isaksson (2002) | Technology frontier | MPI | 57 countries | K, L | GDP | 1980–1990 |
| Deliktas and Balcilar (2005) | Macroeconomic performance | MPI | 25 countries | K, L | GDP | 1991–2000 |
| Chang and Hu (2010) | Total-factor energy productivity | DDF | China’s 29 Provinces | K, L | Real GDP | 2000–2004 |
| Hu and Wang (2006) | Total-factor energy efficiency | DEA | China’s 29 Provinces | K, L, E | Real GDP | 1995–2002 |
| Hu and Kao (2007) | Energy efficiency | DEA | 17 APEC countries | K, L, E | GDP | 1991–2000 |
| Chien and Hu (2007) | Technical efficiency | DEA | 45 countries | K, L, E | GDP | 2001, 2002 |
| Zhang et al. (2011) | Total-factor energy efficiency | DEA | 23 countries | K, L, E | GDP | 1980–2005 |
| Wei et al. (2011) | Total-factor energy efficiency | DEA | 156 countries | K, L, E | GDP | 1950–2007 |
| Lin and Du (2015) | Emission efficiency | MPI | China’s 30 Provinces | K, L | GDP, CO2 | 2000–2010 |
| Zhou and Ang (2008) | Energy efficiency | DEA | 21 OECD countries | K, L, E | GDP, CO2 | 1997–2001 |
| Zhou et al. (2010) | Total-factor emission efficiency | MPI | Top 18 CO2 emitters | K, L, E | GDP, CO2 | 1995–2004 |
| Choi et al. (2012) | Energy efficiency | SBM | China’s 30 Provinces | K, L, E | GDP, CO2 | 2001–2010 |
| K. Wang et al. (2013) | Energy and environmental efficiency | DEA-window | China’s 30 Provinces | K, L, E | GDP, CO2 | 2006–2010 |
| Apergis et al. (2015) | Energy efficiency | SBM, MCMC-GLMM | OECD countries | K, L, E | GDP, CO2 | 1985–2011 |
| Iftikhar et al. (2016) | Energy and emission efficiency | SBM | 26 major economies | K, L, E | GDP, CO2 | 2013–2014 |
| Moutinho et al. (2017) | Environmental efficiency | DEA, QR | 26 European countries | K, L, E | GDP, GHG | 2001–2012 |
| Moutinho et al. (2018) | Eco-efficiency | MPI | 16 Latin American countries | K, L, E | GDP, CO2 | 1994–2013 |
| Park et al. (2018) | Environmental and emission efficiency | SBM | The US’s 50 states | K, L, E | GDP, CO2 | 2004–2012 |
| C. N. Wang et al. (2020) | Eco-efficiency | SBM | 17 European countries | K, L, E | GDP, CO2 | 2013–2017 |
| Demiral and Sağlam (2021) | Eco-efficiency, Eco-productivity | SBM-DEA | The US’s 50 states | K, L, E | GDP, CO2 | 2018 |
| Sueyoshi et al. (2022) | Unified efficiency, Natural disposability | DEA | 121 countries | K, L, E | GDP, CO2 | 1990–2014 |
| Demiral and Sağlam (2023) | Eco-efficiency, Eco-productivity | SBM-DEA, MPI | The US’s 50 states | P, K, L, E | GDP, CO2 | 1997–2018 |
| C. N. Wang et al. (2023) | Economic efficiency, Environmental efficiency | SBM-DEA | 20 OECD countries | K, L, E | GDP, CO2 | 2015–2020 |
| Research Gaps: |
| |||||
| This Study | Eco-efficiency, Eco-productivity | SBM-DEA, MPI | 141 countries | K, L, E | GDP, CO2 | 2018–2023 |
| Contributions: |
| |||||
| Input Variables | Output Variables | ||||
|---|---|---|---|---|---|
| Capital | Labor | Energy | GDP | Emission | |
| Model 1 | X | X | X | X | X |
| Model 2 | X | X | X | X | |
| Model 3 | X | X | X | X | |
| Model 4 | X | X | X | X | |
| GFCF | Labor Force | Energy Consumption | GDP | |
| Labor Force | 0.984 (0.000) | |||
| Energy Consumption | 0.980 (0.000) | 0.987 (0.000) | ||
| GDP | 0.993 (0.000) | 0.983 (0.000) | 0.985 (0.000) | |
| CO2 Emission | 0.964 (0.000) | 0.977 (0.000) | 0.997 (0.000) | 0.970 (0.000) |
| Input Variables | Desirable Output | Undesirable Output | ||||
|---|---|---|---|---|---|---|
| GFCF (Billion 2015 USD) | Labor Force (Million People) | Energy Consumption (Quadrillion BTU) | GDP (Billion 2015 USD PPP) | CO2 Emissions (Million Metric Tons) | ||
| 2018 | Mean | 152.861 | 22,590.507 | 3.769 | 843.959 | 240.067 |
| StDev | 636.156 | 80,741.076 | 14.597 | 2622.763 | 1024.673 | |
| Minimum | 0.175 | 67.026 | 0.003 | 1.090 | 0.278 | |
| Q1 | 3.594 | 1591.688 | 0.093 | 34.966 | 5.688 | |
| Median | 11.573 | 4873.299 | 0.292 | 119.661 | 18.872 | |
| Q3 | 79.912 | 13,608.204 | 1.745 | 543.064 | 99.522 | |
| Maximum | 5953.000 | 776,868.988 | 136.574 | 21,317.630 | 10,601.870 | |
| 2019 | Mean | 156.314 | 22,831.280 | 3.819 | 869.326 | 242.168 |
| StDev | 656.418 | 81,070.190 | 14.922 | 2732.846 | 1048.783 | |
| Minimum | 0.151 | 64.684 | 0.003 | 1.139 | 0.220 | |
| Q1 | 3.636 | 1606.570 | 0.097 | 36.685 | 5.706 | |
| Median | 11.999 | 4904.458 | 0.309 | 123.332 | 18.999 | |
| Q3 | 75.446 | 13,975.088 | 1.763 | 554.217 | 100.040 | |
| Maximum | 6115.052 | 775,928.449 | 142.096 | 22,614.990 | 10,983.970 | |
| 2020 | Mean | 152.969 | 22,606.234 | 3.656 | 844.288 | 228.972 |
| StDev | 664.262 | 80,247.533 | 14.704 | 2719.089 | 1031.439 | |
| Minimum | 0.134 | 61.844 | 0.004 | 1.104 | 0.261 | |
| Q1 | 3.373 | 1578.075 | 0.092 | 34.482 | 5.428 | |
| Median | 11.985 | 4980.288 | 0.274 | 107.201 | 16.887 | |
| Q3 | 68.574 | 14,626.913 | 1.658 | 529.581 | 99.023 | |
| Maximum | 6240.247 | 763,830.073 | 144.442 | 23,136.770 | 11,046.936 | |
| 2021 | Mean | 175.236 | 23,154.782 | 3.833 | 901.431 | 239.796 |
| StDev | 769.980 | 82,261.422 | 15.442 | 2921.965 | 1073.958 | |
| Minimum | 0.172 | 59.595 | 0.005 | 1.025 | 0.303 | |
| Q1 | 3.902 | 1612.577 | 0.095 | 37.189 | 5.485 | |
| Median | 13.946 | 4937.106 | 0.309 | 120.250 | 18.450 | |
| Q3 | 80.236 | 14,862.735 | 1.794 | 564.236 | 103.444 | |
| Maximum | 7475.906 | 781,187.865 | 151.637 | 25,123.270 | 11,442.165 | |
| 2022 | Mean | 181.715 | 23,525.328 | 3.900 | 933.984 | 245.053 |
| StDev | 794.447 | 82,511.177 | 15.661 | 3013.175 | 1082.020 | |
| Minimum | 0.161 | 57.627 | 0.005 | 0.971 | 0.305 | |
| Q1 | 4.197 | 1621.653 | 0.099 | 38.674 | 5.397 | |
| Median | 14.980 | 5012.404 | 0.309 | 130.544 | 19.318 | |
| Q3 | 87.636 | 15,522.682 | 1.820 | 589.285 | 106.559 | |
| Maximum | 7493.288 | 770,113.477 | 153.520 | 25,910.600 | 11,484.335 | |
| 2023 | Mean | 188.706 | 23,909.350 | 3.983 | 966.245 | 250.777 |
| StDev | 805.480 | 83,816.668 | 16.237 | 3150.574 | 1134.404 | |
| Minimum | 0.172 | 57.484 | 0.005 | 1.049 | 0.313 | |
| Q1 | 4.445 | 1634.355 | 0.101 | 41.900 | 5.890 | |
| Median | 15.702 | 5089.291 | 0.307 | 133.211 | 19.203 | |
| Q3 | 94.166 | 16,078.729 | 1.945 | 604.609 | 108.603 | |
| Maximum | 7356.190 | 774,607.590 | 161.897 | 27,313.920 | 12,195.657 | |
| Model | Years | Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum | MPI (2018–2023) |
|---|---|---|---|---|---|---|---|---|---|
| IO-SBM (under VRS) | 2018–2019 | 1.0183 | 0.0688 | 0.6055 | 0.9900 | 1.0208 | 1.0503 | 1.2301 |  |
| 2019–2020 | 1.0168 | 0.1096 | 0.4944 | 0.9761 | 1.0066 | 1.0460 | 1.8194 | ||
| 2020–2021 | 0.9869 | 0.0837 | 0.7091 | 0.9441 | 0.9839 | 1.0128 | 1.3308 | ||
| 2021–2022 | 1.0028 | 0.0680 | 0.8288 | 0.9640 | 1.0065 | 1.0434 | 1.3188 | ||
| 2022–2023 | 0.9971 | 0.0926 | 0.7897 | 0.9576 | 0.9892 | 1.0186 | 1.5109 | ||
| 2018–2023 | 1.0152 | 0.1603 | 0.6602 | 0.9217 | 1.0044 | 1.0801 | 1.8649 | ||
| IO-SBM (under CRS) | 2018–2019 | 1.0233 | 0.0804 | 0.8653 | 0.9803 | 1.0139 | 1.0532 | 1.2946 |  |
| 2019–2020 | 1.0174 | 0.0973 | 0.4920 | 0.9775 | 1.0059 | 1.0574 | 1.2940 | ||
| 2020–2021 | 0.9795 | 0.0782 | 0.7241 | 0.9435 | 0.9756 | 1.0057 | 1.2936 | ||
| 2021–2022 | 0.9972 | 0.0683 | 0.7006 | 0.9682 | 1.0039 | 1.0405 | 1.1993 | ||
| 2022–2023 | 0.9914 | 0.1004 | 0.7526 | 0.9476 | 0.9879 | 1.0134 | 1.5447 | ||
| 2018–2023 | 1.0024 | 0.1665 | 0.5342 | 0.9016 | 0.9959 | 1.0608 | 1.9774 | ||
| IO-CCR | 2018–2019 | 1.0143 | 0.0555 | 0.8440 | 0.9828 | 1.0140 | 1.0407 | 1.2161 |  |
| 2019–2020 | 1.0106 | 0.0859 | 0.4997 | 0.9742 | 1.0018 | 1.0474 | 1.2561 | ||
| 2020–2021 | 0.9808 | 0.0735 | 0.7953 | 0.9407 | 0.9783 | 1.0098 | 1.2802 | ||
| 2021–2022 | 0.9961 | 0.0547 | 0.8336 | 0.9624 | 1.0044 | 1.0370 | 1.1350 | ||
| 2022–2023 | 0.9922 | 0.0844 | 0.7451 | 0.9576 | 0.9882 | 1.0161 | 1.5796 | ||
| 2018–2023 | 0.9879 | 0.1209 | 0.7031 | 0.9185 | 0.9810 | 1.0487 | 1.4683 | ||
| IO-BCC | 2018–2019 | 1.0173 | 0.0621 | 0.8332 | 0.9865 | 1.0173 | 1.0355 | 1.4391 | 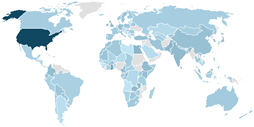 |
| 2019–2020 | 1.0124 | 0.0847 | 0.4928 | 0.9753 | 1.0062 | 1.0562 | 1.2451 | ||
| 2020–2021 | 0.9904 | 0.0846 | 0.7870 | 0.9514 | 0.9871 | 1.0171 | 1.4859 | ||
| 2021–2022 | 0.9966 | 0.0597 | 0.8157 | 0.9634 | 1.0036 | 1.0371 | 1.1629 | ||
| 2022–2023 | 0.9974 | 0.0836 | 0.7967 | 0.9588 | 0.9929 | 1.0208 | 1.5490 | ||
| 2018–2023 | 1.0117 | 0.1790 | 0.7030 | 0.9279 | 0.9966 | 1.0658 | 2.5454 |
| IO-SBM (Under VRS) | IO-SBM (Under CRS) | IO-CCR | |
|---|---|---|---|
| IO-SBM (under CRS) | 0.902 (0.000) | ||
| IO-CCR | 0.845 (0.000) | 0.908 (0.000) | |
| IO-BCC | 0.928 (0.000) | 0.841 (0.000) | 0.888 (0.000) |
| Model | Years | Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum | MPI (2018–2023) |
|---|---|---|---|---|---|---|---|---|---|
| Model 1 (IO-SBM) | 2018–2019 | 1.0183 | 0.0688 | 0.6055 | 0.9900 | 1.0208 | 1.0503 | 1.2301 | 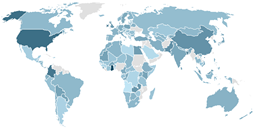 |
| 2019–2020 | 1.0168 | 0.1096 | 0.4944 | 0.9761 | 1.0066 | 1.0460 | 1.8194 | ||
| 2020–2021 | 0.9869 | 0.0837 | 0.7091 | 0.9441 | 0.9839 | 1.0128 | 1.3308 | ||
| 2021–2022 | 1.0028 | 0.0680 | 0.8288 | 0.9640 | 1.0065 | 1.0434 | 1.3188 | ||
| 2022–2023 | 0.9971 | 0.0926 | 0.7897 | 0.9576 | 0.9892 | 1.0186 | 1.5109 | ||
| 2018–2023 | 1.0152 | 0.1603 | 0.6602 | 0.9217 | 1.0044 | 1.0801 | 1.8649 | ||
| Model 2 (excludes K) | 2018–2019 | 1.0129 | 0.0840 | 0.5604 | 0.9815 | 1.0134 | 1.0391 | 1.5330 | 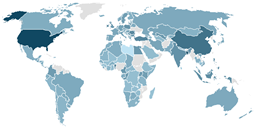 |
| 2019–2020 | 1.0057 | 0.1287 | 0.5305 | 0.9633 | 0.9927 | 1.0342 | 1.9202 | ||
| 2020–2021 | 1.0228 | 0.0956 | 0.6658 | 0.9834 | 1.0236 | 1.0551 | 1.4682 | ||
| 2021–2022 | 1.0205 | 0.1082 | 0.7241 | 0.9863 | 1.0218 | 1.0517 | 1.7963 | ||
| 2022–2023 | 1.0184 | 0.0848 | 0.5534 | 0.9929 | 1.0157 | 1.0419 | 1.6500 | ||
| 2018–2023 | 1.0759 | 0.2024 | 0.5001 | 0.9656 | 1.0500 | 1.1799 | 2.0293 | ||
| Model 3 (excludes L) | 2018–2019 | 1.0251 | 0.0775 | 0.8341 | 0.9871 | 1.0205 | 1.0575 | 1.4740 |  |
| 2019–2020 | 1.0324 | 0.1090 | 0.4087 | 0.9840 | 1.0242 | 1.0683 | 1.5289 | ||
| 2020–2021 | 0.9747 | 0.09358 | 0.6781 | 0.9292 | 0.9736 | 1.0138 | 1.3620 | ||
| 2021–2022 | 1.0029 | 0.0810 | 0.6799 | 0.9520 | 1.0027 | 1.0557 | 1.1772 | ||
| 2022–2023 | 1.0021 | 0.1164 | 0.7866 | 0.9566 | 0.9935 | 1.0279 | 2.0336 | ||
| 2018–2023 | 1.0329 | 0.2175 | 0.6289 | 0.9060 | 1.0208 | 1.1192 | 2.4739 | ||
| Model 4 (excludes E) | 2018–2019 | 1.0184 | 0.0631 | 0.8013 | 0.9891 | 1.0162 | 1.0414 | 1.3191 |  |
| 2019–2020 | 1.0044 | 0.0986 | 0.5300 | 0.9576 | 0.9963 | 1.0463 | 1.5351 | ||
| 2020–2021 | 0.9846 | 0.0814 | 0.6635 | 0.9337 | 0.9889 | 1.0205 | 1.2864 | ||
| 2021–2022 | 0.9952 | 0.0758 | 0.4922 | 0.9671 | 1.0003 | 1.0372 | 1.1963 | ||
| 2022–2023 | 0.9984 | 0.1382 | 0.6498 | 0.9439 | 0.9822 | 1.0168 | 2.2096 | ||
| 2018–2023 | 0.9917 | 0.1593 | 0.6051 | 0.9067 | 0.9649 | 1.0558 | 1.8123 |
| Models | N | Median | Sum of Ranks | |||
|---|---|---|---|---|---|---|
| Model 1 | 141 | 0.99947 | 336.0 | Null hypothesis: H0: All treatment effects are zero | ||
| Model 2 | 141 | 1.05860 | 423.0 | Alternative hypothesis: H1: Not all treatment effects are zero | ||
| Model 3 | 141 | 1.01054 | 355.0 | |||
| Model 4 | 141 | 0.98046 | 296.0 | DF | Chi-Square | p-Value |
| Overall | 564 | 1.01227 | 3 | 35.92 | 0.000 | |
| Term | Coef | SE Coef | T-Value | p-Value | VIF | Term | Coef | SE Coef | T-Value | p-Value | VIF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Constant | 1.0077 | 0.0460 | 21.91 | 0.000 | Constant | 0.9982 | 0.0370 | 27.00 | 0.000 | ||
| GSI2020 | −0.0006 | 0.0012 | −0.53 | 0.598 | 1.88 | GSI2020 | −0.0001 | 0.0009 | −0.11 | 0.911 | 1.88 |
| GSI2021 | −0.0007 | 0.0010 | −0.68 | 0.498 | 2.04 | GSI2021 | −0.0013 | 0.0008 | −1.61 | 0.110 | 2.04 |
| GSI2022 | 0.0026 | 0.0010 | 2.63 | 0.010 | 1.20 | GSI2022 | 0.0030 | 0.0008 | 3.86 | 0.000 | 1.20 |
| Efficiency | Group 1 | Group 2 | U-Statistic | p-Value |
|---|---|---|---|---|
| AVG IO-SBM | Lower-middle-income countries | High-income countries | 668.5 | 0.0765 |
| AVG LE | Upper-middle-income countries | Lower-middle-income countries | 987 | 0.0025 |
| AVG LE | Upper-middle-income countries | High-income countries | 725 | 0.0724 |
| AVG LE | Lower-middle-income countries | High-income countries | 438 | 0.0001 |
| AVG LE | High-income countries | Low-income countries | 519 | 0.0984 |
| AVG EE | Upper-middle-income countries | Low-income countries | 167 | 0.0035 |
| AVG EE | Lower-middle-income countries | Low-income countries | 206 | 0.0571 |
| AVG EE | High-income countries | Low-income countries | 271 | 0.0413 |
| AVG CDE | Upper-middle-income countries | Low-income countries | 178 | 0.0064 |
| AVG CDE | Lower-middle-income countries | Low-income countries | 204.5 | 0.0535 |
| AVG ECOP | Upper-middle-income countries | Lower-middle-income countries | 994 | 0.0020 |
| AVG ECOP | Lower-middle-income countries | High-income countries | 449 | 0.0002 |
| AVG ECOE | Upper-middle-income countries | Low-income countries | 171 | 0.0043 |
| AVG ECOE | Lower-middle-income countries | Low-income countries | 209 | 0.0653 |
| AVG ECOE | High-income countries | Low-income countries | 288 | 0.0741 |
| AVG MPI | Lower-middle-income countries | Low-income countries | 404 | 0.0632 |
| AVG MPI | High-income countries | Low-income countries | 572 | 0.0147 |
| AVG EC | Upper-middle-income countries | High-income countries | 576.5 | 0.0022 |
| AVG EC | Lower-middle-income countries | High-income countries | 558 | 0.0056 |
| AVG TC | Upper-middle-income countries | Low-income countries | 519 | 0.0009 |
| AVG TC | Lower-middle-income countries | Low-income countries | 465 | 0.0025 |
| AVG TC | High-income countries | Low-income countries | 569 | 0.0166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sağlam, Ü. From Pandemic Shock to Sustainable Recovery: Data-Driven Insights into Global Eco-Productivity Trends During the COVID-19 Era. J. Risk Financial Manag. 2025, 18, 473. https://doi.org/10.3390/jrfm18090473
Sağlam Ü. From Pandemic Shock to Sustainable Recovery: Data-Driven Insights into Global Eco-Productivity Trends During the COVID-19 Era. Journal of Risk and Financial Management. 2025; 18(9):473. https://doi.org/10.3390/jrfm18090473
Chicago/Turabian StyleSağlam, Ümit. 2025. "From Pandemic Shock to Sustainable Recovery: Data-Driven Insights into Global Eco-Productivity Trends During the COVID-19 Era" Journal of Risk and Financial Management 18, no. 9: 473. https://doi.org/10.3390/jrfm18090473
APA StyleSağlam, Ü. (2025). From Pandemic Shock to Sustainable Recovery: Data-Driven Insights into Global Eco-Productivity Trends During the COVID-19 Era. Journal of Risk and Financial Management, 18(9), 473. https://doi.org/10.3390/jrfm18090473






