The Good, the Bad, and the Bankrupt: A Super-Efficiency DEA and LASSO Approach Predicting Corporate Failure

Abstract

Corporate failure prediction remains a major topic in the literature. Numerous methodologies have been established for its assessment, while data envelopment analysis (DEA) has received particular attention. This study contributes to the literature, establishing a new approach in the construction process of prediction models based on the combination of logistic LASSO and an advanced version of data envelopment analysis (DEA). We adopt the modified slacks-based super-efficiency measure (modified super-SBM-DEA), following the “Worst practice frontier” approach, and focus on the selection process of predictive variables, implementing the logistic LASSO regression. A balanced sample with one-to-one matching between forty-five firms that filed for reorganization under U.S. bankruptcy law during the period 2014–2020 and forty-five non-failed firms of a similar size from the U.S. energy economic sector has been used for the empirical analysis. The proposed methodology offers superior results in terms of corporate failure prediction accuracy. For the dynamic assessment of failure, Malmquist DEA has been implemented during the five fiscal years prior to the event of failure, offering insights into financial distress before the event of a default. The model outperforms alternatives by achieving higher overall prediction accuracy (85.6%), the better identification of failed firms (91.1%), and the improved classification of non-failed firms (80%). Compared to prior DEA-based models, it demonstrates superior predictive performance with lower Type I and Type II errors and higher sensitivity as well as specificity. These results highlight the model’s effectiveness as a reliable early warning tool for bankruptcy prediction.

1. Introduction

Corporate failure prediction remains a significant topic in the economic literature since the event of a bankruptcy severely affects various stakeholders and the economy as a whole. The social, political, and economic dimensions of failure elevate it as one of the most popular issues in accounting and finance. As pointed out by Premachandra et al. (2009) and Sueyoshi and Goto (2009), relevant studies suggest that the direct costs of corporate failure may be as low as 5% (Warner, 1977), but when also taking indirect costs into account the total costs can reach 28% (Altman, 1984). The traditional literature (Beaver, 1966; Altman, 1968; Dimitras et al., 1996) defines the term corporate failure according to a firm’s financial status, focusing on issues such as profitability, insolvency level, and quality of management. However, bankruptcy is more complicated, and relevant research has established a framework of joint factors and conditions that illustrate bankruptcy. Mousavi et al. (2015) claimed that corporate failure may result from a combination of factors, including internal ones like managerial errors caused by lack of experience, risk-taking behavior, lack of commitment, and failure to adapt to changing circumstances. Also, external factors like economic conditions, changes in laws, and industry decline also play a significant role. Understanding the aforementioned causes of failure and identifying early warning signals can guide strategic decisions that prevent or mitigate financial distress. Corrective measures may include operations and financial restructuring, innovative strategy adoption, and market diversification, as well as targeted interventions by policymakers to stabilize vulnerable industries. Thus, predicting potential failures can serve as an early warning system, enabling timely decision-making and the appropriate allocation of resources (Xu et al., 2014), increasing the practical relevance and feasibility of corporate failure prediction models.

This research establishes a corporate failure prediction model using data from the US energy sector. In the last decade, significant changes in the world energy market occurred due to the rise in competition among producing countries and the changes in international political and economic contexts. Another significant element is the shift towards renewable energy sources and the turn to the production of alternative energy products and new technologies. Moreover, the significant decline in oil and gas prices caused by reduced demand and oversupply due to the COVID-19 pandemic also played a crucial role. The USA keeps a significant part of the global energy production, which demonstrates the significance of the energy sector for the American economy. Under this framework, improving the accuracy of corporate failure prediction models in this industry has both sector-specific and broader economic significance.

Over the last six decades, several studies have contributed to the development of corporate failure prediction models, offering advanced methodological instruments and a strong theoretical framework relevant to the causes of firms’ failure. The relevant research was deployed in most sectors, comparing findings among alternative methodologies and hypotheses (Premachandra et al., 2009) and focusing on specific issues, such as financial, corporate, and macroeconomic conditions (F. Lin et al., 2010; Tinoco & Wilson, 2013). During the last two decades, the use of data envelopment analysis (DEA) has also received particular attention. A crucial part of corporate failure prediction is the appropriate selection of variables. However, the selection of the variables incorporated in previous corporate failure prediction studies that implemented DEA is mostly based on the literature and expert judgment (Cielen et al., 2004; Premachandra et al., 2009, 2011; Shetty et al., 2012), leaving room for more systematic approaches that reduce subjectivity.

This study contributes to the literature, establishing a new approach in the construction process of corporate failure prediction models based on the combination of logistic least absolute shrinkage and selection operator (LASSO) and an advanced version of data envelopment analysis (DEA). We adopt the modified slacks-based super-efficiency measure (super-SBM-DEA) by R. Lin et al. (2019) that addresses the existence of negative data in financial ratios, following the “Worst practice frontier” approach, and focus on the selection process of predictive variables, implementing the logistic LASSO regression. The modified super-SBM-DEA is used for the first time to establish a corporate failure prediction model following the “Worst practice frontier” approach. The findings of the empirical analysis indicate that the model with the logistic LASSO-selected variables had superior results in terms of corporate failure prediction accuracy. For the dynamic assessment of failure, Malmquist DEA with a VRS input-oriented modified super-SBM-DEA model following the “Worst Practice Frontier” approach has been implemented during the five fiscal years before the event of failure, offering insights into financial distress prior to the event of a default, which can support firms in anticipating and addressing financial vulnerabilities in a timely manner.

The rest of the paper is organized as follows: Section 2 includes a critical overview of the relative literature, highlighting the methods already proposed for predicting corporate failure, as long as the variables used and the variable selection techniques implemented in the previous literature. The steps of the methodology and the sample selection are deployed in Section 3. Section 4 covers the empirical analysis stages, starting with the predictive variable selection through logistic LASSO implementation, and proceeding with a comparison of the results of the modified super-SBM-DEA model with logistic LASSO-selected variables with those of the modified super-SBM-DEA model with a different set of variables, a comparison with logistic regression as an alternative corporate failure prediction model, and a discussion of the results of Malmquist DEA. The concluding remarks and suggestions for future research are presented in Section 5.

2. Literature Review

In this section, we provide a critical overview of the current literature, also focusing on the use of DEA as a prediction tool, and on the variables’ selection in the stage of prediction model establishment.

2.1. Overview of Previous Corporate Failure Prediction Models

Beaver (1966) and Altman (1968) mark the beginning of the development of corporate failure prediction models. Beaver (1966) suggested the use of univariate discriminant analysis, which was later enhanced by Altman (1968) with the introduction of multivariate discriminant analysis (MDA). The strict statistical assumptions of MDA, such as the distribution of the values of the independent variables following the multivariate normal distribution, which is not valid in the case of financial ratios (Dimitras et al., 1996), led to a considerable amount of research focusing on the proposal of other methods for corporate failure prediction that address these limitations. Ohlson (1980) and Zmijewski (1984) proposed the use of Logit and Probit models, respectively, for bankruptcy prediction. MDA, Logit, and Probit models comprise the first category of methods proposed for bankruptcy prediction, named as the statistical approaches. Despite the limitations of statistical approaches, the application of MDA and Logit dominates the field of corporate failure prediction (Aziz & Dar, 2006).

The second category includes models of machine learning and artificial intelligence. Odom and Sharda (1990) proposed the use of neural networks. However, the complexity of neural networks and the requirement of a large dataset for training make their use limited. Min and Lee (2005) and Shin et al. (2005) proposed the use of support vector machines (SVMs). The results of Min and Lee (2005) indicated that SVMs overperform MDA and Logit. The third category consists of methods stemming from operational research, such as data envelopment analysis (DEA) first proposed by Charnes et al. (1978) and multi-criteria decision-making (Doumpos et al., 2002). DEA is a non-parametric linear programming technique that offers more flexibility regarding the selection of the variables incorporated in the model compared to statistical approaches.

The fourth category includes stochastic methods that belong to the family of hazard models (Shumway, 2001), such as the panel Logit model (Tinoco & Wilson, 2013) and the complementary log-log model (Mare, 2012) for the dynamic assessment of corporate failure during the years before the event of a default. Christopoulos et al. (2019a) also applied a dynamic Logit model for the investigation of firms’ financial distress, incorporating profitability and liquidity ratios in their analysis. Hazard models differentiate from the previous categories due to the incorporation of macroeconomic and market variables, as opposed to financial ratios only. Finally, the fifth category consists of contingent claims analysis (CCA) models, also referred to as Black–Scholes–Merton (BSM)-based models (Hillegeist et al., 2004; Bharath & Shumway, 2008), stemming from option pricing theory (Mousavi et al., 2023) and utilizing market-based variables, which can strengthen the corporate failure prediction framework, reflecting not only financial statement information but also expectations about future cash flows (Mousavi et al., 2015). However, the reliance of CCA on market prices limits its applicability for firms lacking highly traded securities (Das et al., 2009). On the other hand, whereas models like DEA do not provide a market-driven risk assessment, they bring a firm-level operational perspective. Failure can be examined through the assessment of how changes in inefficiency and productivity can contribute to bankruptcy risk, leveraging publicly available accounting information, without the limitations often associated with market data. This fact highlights the added value of using efficiency-based models. A detailed analysis of corporate failure prediction models can be found in the studies of Aziz and Dar (2006), Balcaen and Ooghe (2006), Veganzones and Severin (2021), and Mousavi et al. (2023).

2.2. Corporate Failure and DEA

During the last two decades, the use of DEA for corporate failure prediction has received particular attention mainly due to its methodological strengths compared to statistical approaches with strict requirements to be met. As pointed out by Premachandra et al. (2009, 2011), DEA is a distribution-free approach in the sense that inputs and outputs incorporated in the model do not need to be normally distributed. This is an advantage when financial ratios are incorporated into an analysis since they can be highly skewed and not normally distributed (Dimitras et al., 1996).

The first idea of the “Worst Practice” DEA, instead of the traditional efficiency one, came from Paradi and Simak (2004), by placing the worst-performing decision-making units (DMUs) at the frontier. Paradi and Simak (2004) also introduced a layering approach for the classification of bankrupt and non-bankrupt firms, instead of using a traditional fixed cut-off point for the efficiency scores, where the worst-performing units that appeared each time at the frontier were removed from the sample and the method was rerun, resulting in a new set of worst-performing units placed at the frontier. Each layer defined a different level of bankruptcy risk. Cielen et al. (2004) also proposed the use of DEA for bankruptcy prediction in the banking sector using a CCR (radial) DEA model. Their findings showed that a model based on the DEA approach is more accurate compared to the linear programming method and decision trees method. However, the CCR DEA model cannot deal with the negative data often present in financial ratios due to the absence of a translation invariance property, thus the DEA approach proposed by Cielen et al. (2004) has limited use. To address the issue of negative data, Premachandra et al. (2009) proposed the use of a non-radial model (i.e., the additive model), where the translation invariance property is present, also following the “Worst Practice Frontier” approach. The additive DEA results were compared with those from logistic regression (LR) and showed that DEA overperformed LR bankruptcy prediction. Sueyoshi and Goto (2009) also applied an additive DEA model and compared their results with DEA-DA. Their results indicated that, in alignment with Premachandra et al. (2009), DEA is a useful tool for bankruptcy assessment, whereas DEA-DA can offer insights into the dynamic process of failure before reaching the final stage of bankruptcy. Premachandra et al. (2011) proposed the use of the additive super-efficiency DEA, together with the development of a corporate failure assessment index that combined both the efficient and inefficient frontiers. Paradi et al. (2014) utilized the input-oriented slacks-based measure (SBM) proposed by Tone (2001) in their analysis, due to the advantageous properties of the SBM compared to traditional DEA approaches (Tone, 2001). Based on the analysis of five years of DEA scores prior to the event of a default, firms were categorized into safe, gray, and distressed statuses, using appropriate cut-off points (Paradi et al., 2014). The methodological framework of Mousavi et al. (2015) also incorporated the SBM models proposed by Tone (2001, 2002). The SBM model (Tone, 2001) and the super-efficiency SBM (Tone, 2002) cannot deal with the negative data often present in financial ratios.

Most of the previous studies that incorporated DEA as a tool for failure prediction were mostly focused on cross-sectional analysis (Cielen et al., 2004; Paradi & Simak, 2004; Premachandra et al., 2009, 2011; Shetty et al., 2012). However, corporate failure is a dynamic process and the evolution of changes in efficiency over the years before bankruptcy can offer insights into financial distress prior to the event of a default. Li et al. (2017) proposed the use of Malmquist DEA for the dynamic evaluation of financial distress in combination with a discrete hazard model. To dynamically assess bank efficiency, Li et al. (2022) proposed the use of Malmquist DEA utilizing the modified SBM model by Sharp et al. (2007) in combination with the “Worst Practice Frontier” approach.

2.3. Variable Selection Techniques

The selection of the variables incorporated into corporate failure prediction models was mostly based on literature and expert judgment (Cielen et al., 2004; Premachandra et al., 2009, 2011; Shetty et al., 2012). The selected variables play a significant role in the reliability status of a prediction model. This fact contributed to the establishment of various selection methods. F. Lin et al. (2011) applied data mining techniques and Xu et al. (2014) proposed a parameter reduction method (novel soft set theory (NSS)) for the identification of financial ratios useful for business failure prediction, integrating statistical logistic regression into traditional soft set theory. NSS proved to have superior forecasting performance compared to support vector machines (SVMs), neural network (NN), and logistic regression. NSS, introduced by Xu et al. (2014), may be difficult to implement due to its complexity. Moreover, there is a possibility of overfitting when identifying the critical value, c, that is used in creating the tabular representation of soft sets. This value determines the effectiveness of NSS. The least absolute shrinkage and selection operator (LASSO) has also been proposed as a method for corporate failure prediction variable selection. LASSO is not only a state-of-the-art variable selection method but also deals well with the multicollinearity that is often present in financial ratios, is stable even when minor data changes occur, and is also computationally efficient (Tian et al., 2015).

Amendola et al. (2011) introduced LASSO as a method for corporate failure prediction, taking into consideration only accounting variables. Tian et al. (2015), apart from applying LASSO, also offered insights into the significance of accounting-based variables compared to market-based ones. Pereira et al. (2016) applied logistic LASSO and ridge regression for corporate failure prediction and compared their results with statistical stepwise methods. Tian and Yu (2017) applied the adaptive-LASSO for the selection of variables for default prediction, and the results of their research indicate that, compared to the traditional Z score model by Altman (1968), the selected variables had superior predictive power in out-of-sample evaluation. Recently, Cao et al. (2022) combined LASSO with a Bayesian network model for bankruptcy prediction and their model outperformed logistic regression, decision trees, and support vector machines. LASSO has also been combined with DEA by Lee and Cai (2020), Chen et al. (2021), and Mokrišová and Horváthová (2023). Lee and Cai (2020) combined LASSO with sign-constrained convex non-parametric least squares (SCNLS) to deal with the problem of dimensionality in DEA, and Chen et al. (2021) revisited the approach proposed by Lee and Cai (2020) by combining elastic net LASSO and DEA. Mokrišová and Horváthová (2023) compared the performance of VRS DEA regarding corporate failure prediction, under the use of domain knowledge and LASSO features, and reached the conclusion that whereas the DK + DEA model achieved slightly better performance metrics, the number of firms at the “Worst Practice Frontier” under the LASSO + DEA model deviated less.

3. Steps of the Methodology

Section 3 provides a description of the firm sample and the proposed methodology, emphasizing the context and utility of logistic LASSO, the modified super-SBM-DEA model as a prediction tool, logistic regression as a comparative corporate failure prediction methodology, and the Malmquist Productivity Index (MPI) for the dynamic assessment of failure.

3.1. Sample

The sample includes nighty listed firms in two a priori groups: failed and non-failed. Data were selected from only one sector under the assumption that an essential component of the proposed methodology is the implementation of the MPI for the dynamic assessment of failure. The group of failed firms consisted of forty-five firms from the energy sector that filed for reorganization (Chapter 11) under U.S. bankruptcy law during the period 2014–2020. The accounting firms’ data were received from the REFINITIV EIKON database. Every firm included in the failure sample was matched with a non-failed one that belonged to the same Thomson Reuters Business Classification industry, making the total sample consist of nighty firms. The natural logarithm of total assets at the fiscal year before the event of a default, as an indication of firm size, has been used as a criterion for matching the firms. Apart from the firm size, no other criteria have been set for the non-failed firms.

During the period 2014–2020, several events had a negative impact on the financial performance of energy firms, leading those already facing financial difficulties or having a substantial amount of debt on their balance sheet to go bankrupt. Twelve of the forty-five bankrupt firms filed for Chapter 11 during 2020. The primary reason for bankruptcy filings was the significant decline in oil and gas prices caused by reduced demand and oversupply due to the COVID-19 pandemic, which in turn had a severe negative impact on the firms’ revenues, making it difficult for firms to serve their debt obligations. Of the remaining thirty-three failed firms, four filed for bankruptcy in 2019, four in 2018, six in 2017, nine in 2016, six in 2015, and four in 2014. Most of the firms had a significant amount of debt on their balance sheet, which had been increasing every year due to a combination of factors, such as the decline in oil and natural gas prices, a shift towards renewable energy sources, high operating costs, and capital expenditure.

3.2. Logistic LASSO Regression

The least absolute shrinkage and selection operator (LASSO), first introduced by Tibshirani (1996), is a state-of-the-art variable selection method for identifying the most important predictors. LASSO deals well with multicollinearity, which is often present when financial ratios are used in an analysis.

LASSO makes use of the $L_1$ penalty to the sum of the absolute value of the regression coefficients, forcing some of the coefficient estimates to be equal to zero when the tuning parameter, λ, is sufficiently large, thus performing variable selection (James et al., 2013). The best value of the tuning parameter, λ, is selected by using a machine learning technique known as cross-validation. Under k-fold cross-validation, the dataset is separated into k subsets (Hastie et al., 2009). One of them is treated as the validation dataset and the remaining ones are used as the training datasets. The process is repeated k times until all the subsets have been selected as validation datasets. The optimum value for the tuning parameter, λ, is the one that maximizes the log-likelihood function (Pereira et al., 2016).

Corporate failure status is a binary outcome. To assess the relationship between the corporate failure status of the firms included in the sample and the predictor variables, logistic LASSO is implemented. The binary variable defining whether the firm is in failure or non-failure status is defined as follows:

$$y_i=\left\{\begin{array}{c}1 if the status of the i^{th} firm is failure\\ 0 otherwise \end{array}\right. i=1,\dots ., n$$

For logistic LASSO, the log-likelihood function takes the following form (Hastie et al., 2009, formula 4.31 in Section 4.4.4):

$$\sum _{i=1}^n\left[y_i\left({\beta }_0+ {\beta }^T{x}_i\right)-\mathit{log}\left(1+ e^{{\beta }_0+ {\beta }^T{x}_i}\right)\right]-\lambda \sum _{j=1}^p\left|{\beta }_j\right|$$

where $x_i$, $i=1,\dots .,n$ is the i-th row of an nxp matrix where the number of rows, n, is the number of observations (firms) included in the sample and the number of columns, p, is the number of independent variables incorporated in the model, ${\beta }_0$ is the constant term, ${\beta }^T$ is the regression coefficient row vector, $y_i$, $i=1,\dots .,n$ is the binary dependent variable, λ is the tuning parameter that controls the amount of shrinkage, and ${\sum }_{j=1}^p\left|{\beta }_j\right|$ is the $L_1$ LASSO penalty that is applied to all coefficients except the intercept.

3.3. Data Envelopment Analysis (DEA)

DEA is a non-parametric linear programming technique proposed by Charnes et al. (1978) for the assessment of the relative efficiency of decision-making units (DMUs). Traditional approaches such as the CCR model cannot deal with negative data due to the absence of a translation invariance property (Sueyoshi & Sekitani, 2009). The existence of negative data is a common issue when financial ratios are used as inputs or outputs in DEA. The initial SBM model proposed by Tone (2002) and the super-SBM model proposed by Fang et al. (2013) cannot deal with negative data, while the MSBM model proposed by Sharp et al. (2007) deals with negative data, but it is not a super-efficiency model. R. Lin et al. (2019) proposed a modified slacks-based super-efficiency measure (modified super-SBM) under the condition of variable returns to scale (VRS) that addresses successfully the existence of negative data in DEA. In addition, it is also monotonous, unit-invariant, and translation-invariant for both inputs and outputs. In essence, the proposed model constitutes an advanced approach compared with previous studies that also implemented DEA for corporate failure prediction, presented in the literature review section.

Assume that there is a set of n DMUs with m inputs and s outputs. For each DMU j (j = 1, …, n), let $x_{ij}$ denote its i-th ($i=1,\dots ,m)$ input and $y_{rj}$ denote its r-th ($r=1,\dots ,s)$ output. Assume that for each DMU k ($k=1,\dots ,n)$, there is $r_0\in \left\{1,\dots ,s\right\}$ satisfying the following condition:

$${\displaystyle \frac{1}{n-1}} \sum _{j=1, j\ne k }^n{y}_{r_{0}j}> \underset{j}{\mathit{min}}\left\{y_{r_{0}j}\right\}$$

Also, the following input and output ranges of the RAM (Cooper et al., 1999) are adopted:

$$P_i^{-}= \underset{j}{\mathit{max}}\left\{x_{ij}\right\}- \underset{j}{\mathit{min}}\left\{x_{ij}\right\}, i=1, \dots , m,$$

$$P_r^{+}= \underset{j}{\mathit{max}}\left\{y_{rj}\right\}- \underset{j}{\mathit{min}}\left\{y_{rj}\right\}, r=1, \dots , s$$

The modified super-SBM-DEA model that deals with negative data includes two-stage modeling. In the first stage, the following model is applied:

$$\mathit{min}{\displaystyle \frac{1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-}/P_i^{-}}{1- {\sum }_{r \in \mathbb{O}}{v}_r{w}_r^{+}/P_r^{+}}}$$

subject to

$$x_{ik} \ge \sum _{j=1, j\ne k }^n{x}_{ij}{\lambda }_j- w_i^{-}, i \in \mathbb{I},$$

$$y_{ik} \le \sum _{j=1,j\ne k }^n{y}_{rj}{\lambda }_j- w_r^{+}, r \in \mathbb{O},$$

$$\sum _{j=1,j\ne k }^n{\lambda }_j=1, {\lambda }_j \ge 0, j = 1, \dots , n, j \ne k,$$

$$w_r^{+} \le P_r^{+}, r \in \mathbb{O},$$

$$w_r^{+}, w_i^{-} \ge 0, \forall r \in \mathbb{O},i \in \mathbb{I}.$$

The model of the second stage is formulated as follows:

$$\mathit{min}{\displaystyle \frac{1- {\sum }_{i \in \mathbb{I}}{\mu }_i{s}_i^{-}/P_i^{-}}{1+ {\sum }_{r \in \mathbb{O}}{v}_r{s}_r^{+}/P_r^{+}}}$$

subject to

$$x_{ik}= \sum _{j=1, j\ne k }^n{x}_{ij}{\lambda }_j- w_i^{-*}+s_i^{-}, i \in \mathbb{I},$$

$$y_{rk}= \sum _{j=1,j\ne k }^n{y}_{rj}{\lambda }_j+ w_r^{+*}- s_r^{+}, r \in \mathbb{O},$$

$$\sum _{j=1,j\ne k }^n{\lambda }_j=1, {\lambda }_j \ge 0, j = 1, \dots , n, j \ne k,$$

$$s_r^{+}, s_i^{-} \ge 0, \forall r \in \mathbb{O},i \in \mathbb{I},$$

where $\mathbb{I}=\left\{i|P_i^{-}>0,i=1,\dots ,m\right\},\mathbb{O}=\left\{r|P_r^{+}>0,r=1,\dots ,s\right\},$ ${\mu }_i$ and $v_r$ are known positive weights satisfying ${\sum }_{i\in \mathbb{I}}{\mu }_i=1$ and ${\sum }_{r\in \mathbb{O}}{v}_r=1$, $w_i^{-\mathrm{*}}$ are the input savings, $w_r^{+\mathrm{*}}$ are the output surpluses, $s_i^{-}$ are the possible input excesses, and $s_r^{+}$ are the possible output shortfalls. The $w_r^{{+}^{\mathrm{*}}}$, $w_i^{{-}^{\mathrm{*}}}$, and ${\lambda }_j^{\mathrm{*}}$ are the optimal variables of the first model, and $s_i^{-\mathrm{*}}$, $s_r^{+\mathrm{*}}$, and ${\tilde{\lambda }}_j^{\mathrm{*}}$ are the optimal variables of the second model. For a DMU k, the super-efficiency score is defined as follows:

$${\theta }^{*}=\left\{\begin{array}{c}{\displaystyle \frac{1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-*}/P_i^{-}}{1- {\sum }_{r \in \mathbb{O}}{v}_r{w}_r^{+*}/P_r^{+}}} if {\displaystyle \frac{1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-*}/P_i^{-}}{1- {\sum }_{r \in \mathbb{O}}{v}_r{w}_r^{+*}/P_r^{+}}}>1,\\ {\displaystyle \frac{1- {\sum }_{i \in \mathbb{I}}{\mu }_i{s}_i^{-*}/P_i^{-}}{1+ {\sum }_{r \in \mathbb{O}}{v}_r{s}_r^{+*}/P_r^{+}}} otherwise\end{array}\right.$$

If ${\theta }^{\mathrm{*}}>1$, DMU k is super-efficient and has at least one input saving or output surplus. If ${\theta }^{\mathrm{*}}=1,$ for DMU k there are no input savings, no output surpluses, and neither input excesses nor output shortfalls, and is characterized as efficient. Finally, if ${\theta }^{\mathrm{*}}<1,$ DMU k is inefficient and has either input excesses or output shortfalls. R. Lin et al. (2019) provide a detailed analysis of all the properties satisfied by the modified super-SBM-DEA model.

The input-oriented modified super-SBM-DEA model is the numerator of the modified super-SBM-DEA model with a proper adjustment of the model constraints, and is formulated as follows:

First model:

$$\mathit{min}1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-}/P_i^{-}$$

subject to

$$x_{ik} \ge \sum _{j=1, j\ne k }^n{x}_{ij}{\lambda }_j- w_i^{-}, i \in \mathbb{I},$$

$$y_{ik} \le \sum _{j=1,j\ne k }^n{y}_{rj}{\lambda }_j, r \in \mathbb{O},$$

$$\sum _{j=1,j\ne k }^n{\lambda }_j=1, {\lambda }_j \ge 0, j = 1, \dots , n, j \ne k,$$

$$w_i^{-} \ge 0, \forall r \in \mathbb{O},i \in \mathbb{I}.$$

Second model:

$$\min 1- {\sum }_{i \in \mathbb{I}}{\mu }_i{s}_i^{-}/P_i^{-}$$

subject to

$$x_{ik}= \sum _{j=1, j\ne k }^n{x}_{ij}{\lambda }_j- w_i^{-*}+s_i^{-}, i \in \mathbb{I},$$

$$y_{rk}\le \sum _{j=1,j\ne k }^n{y}_{rj}{\lambda }_j, r \in \mathbb{O},$$

$$\sum _{j=1,j\ne k }^n{\lambda }_j=1, {\lambda }_j \ge 0, j = 1, \dots , n, j \ne k,$$

$$s_i^{-} \ge 0, \forall r \in \mathbb{O},i \in \mathbb{I}.$$

For a DMU k, the super-efficiency score is defined as follows:

$${\theta }^{*}=\left\{\begin{array}{c}1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-*}/P_i^{-} if 1+ {\sum }_{i \in \mathbb{I}}{\mu }_i{w}_i^{-*}/P_i^{-}>1,\\ 1- {\sum }_{i \in \mathbb{I}}{\mu }_i{s}_i^{-*}/P_i^{-} otherwise\end{array}\right.$$

If ${\theta }^{\mathrm{*}}>1$, DMU k is super-efficient and has at least one input saving. If ${\theta }^{\mathrm{*}}=1,$ for DMU k there are neither input savings nor input excesses, and is characterized as efficient. Finally, if ${\theta }^{\mathrm{*}}<1,$ DMU k is inefficient and has input excesses.

Our research utilizes the “Worst Practice Frontier” DEA approach, introduced by Paradi and Simak (2004). This approach differs from the traditional DEA efficiency frontier one, by placing the worst-performing DMUs at the frontier instead of the efficient ones through the appropriate selection of inputs and outputs.

3.4. Logistic Regression (LR)

Logistic regression (Ohlson, 1980) has been selected as a comparative methodology for corporate failure prediction to assess the performance of the modified super-SBM-DEA model as a corporate failure prediction tool. The selection of logistic regression was based on the fact that, together with MDA, it dominates the field of corporate failure prediction (Aziz & Dar, 2006).

The binary variable defining whether a firm is in failure or non-failure status is defined as follows:

$$y_i=\left\{\begin{array}{c}1 if the status of the i^{th} firm is failure\\ 0 otherwise \end{array}\right. i=1,\dots ., n$$

In logistic regression, the probability that a firm will fail is given by the following equation:

$$P \left(y=1\right)= {\displaystyle \frac{1}{1+exp\left(-{\mathit{\beta }}^T\mathit{x}\right)}}$$

where

$${\mathit{\beta }}^T\mathit{x}={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_m{x}_m$$

where $x_i,i=1,\dots m$ denote the variables included in the model, and ${\beta }_i$ coefficients are estimated by the maximum likelihood estimator, measuring the effect of each variable on y.

3.5. Malmquist Productivity Index (MPI)

To assess the efficiency change in a DMU between two periods, the MPI has been incorporated. As per Färe et al. (1994), the input-oriented MPI for two consecutive periods (t and t + 1) is determined by the distance function ratio of each period with respect to a common technology, as follows (Färe et al., 1998):

$${MPI}_0^t = {\displaystyle \frac{d_0^t\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^t\left(y_0^t,x_0^t\right)}}$$

where $\left(y_0^{t+1},x_0^{t+1}\right)$ and $\left(y_0^t,x_0^t\right)$ are two consecutive production points, $d_0^t\left(y_0^{t+1},x_0^{t+1}\right)$ and $d_0^{t+1}\left(y_0^t,x_0^t\right)$ are two mixed period input distance functions for the firm under evaluation indicated by the zero subscript, and measured against the technology of period t. If the base period is t + 1, then the MPI is defined as follows:

$${MPI}_0^{t+1} = {\displaystyle \frac{d_0^{t+1}\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^{t+1}\left(y_0^t,x_0^t\right)}}$$

Moreover, ${MPI}_0$ can be expressed as the geometric mean of the two indices, evaluated for period t and period t + 1 technologies as follows:

$${MPI}_0= \sqrt{ {\displaystyle \frac{d_0^t\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^t\left(y_0^t,x_0^t\right)}} . {\displaystyle \frac{d_0^{t+1}\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^{t+1}\left(y_0^t,x_0^t\right)}}}$$

Under the variable returns to scale (VRS) assumption, the MPI from period t to period t + 1 can be further decomposed to pure efficiency change (PEFFCH) and technical change (TECH) as follows:

$$\begin{gathered} {MPI}_t^{t+1}=PEFFCH \times TECH \\ = {\displaystyle \frac{d_0^{t+1}\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^t\left(y_0^t,x_0^t\right)}} \times \sqrt{ {\displaystyle \frac{d_0^t\left(y_0^t,x_0^t\right)}{d_0^{t+1}\left(y_0^t,x_0^t\right)}} . {\displaystyle \frac{d_0^t\left(y_0^{t+1},x_0^{t+1}\right)}{d_0^{t+1}\left(y_0^{t+1},x_0^{t+1}\right)}}} \end{gathered}$$

In our research, Malmquist DEA with the VRS input-oriented modified super-SBM model following the “Worst Practice Frontier” approach is implemented for corporate failure assessment during five fiscal years before the event of a failure.

4. Empirical Analysis

The structure of this section includes the stages of empirical analysis, starting with the predictive variables’ selection. This process is based on logistic LASSO implementation according to the framework presented in the previous section. In the second stage, the proposed analysis provides the findings from implementing the modified super-SBM-DEA model incorporating the proposed inputs and outputs from the stage of logistic LASSO. Additionally, a second modified super-SBM-DEA model was introduced, using a different set of variables, to establish a comparative process relative to the predictive power of the two models. At stage 3, a comparison between DEA and logistic regression results is performed, as a comparative corporate failure prediction methodology. Finally, at stage 4, Malmquist DEA is implemented for the dynamic assessment of failure.

4.1. Variable Selection with Logistic LASSO (Stage 1)

In our research, 43 financial ratios (

Table 1. Initial pool of financial ratios.

No	Financial Ratios
1	Current Ratio (CACL)	23	Total Equity to Total Liabilities (TETL)
2	Acid Test Ratio (ATR)	24	Net Working Capital to Non-Current Liabilities (WCNCL)
3	Cash Ratio (CR)	25	Equity plus Non-Current Liabilities to Non-Current Assets (ENCLNCA)
4	Cash Flow to Total Assets (CFTA)	26	Working Capital to Total Liabilities (WCTL)
5	Sales to Total Assets (STA)	27	Total Equity to Non-Current Assets (TENCA)
6	Total Assets Turnover (TAT)	28	Non-Current Assets to Non-Current Liabilities (NCANCL)
7	Fixed Assets Turnover (FATR)	29	Financial Leverage (FL)
8	Account Receivables Turnover (ART)	30	Total Liabilities to Total Assets plus Total Equity (TLTATE)
9	Net Proft Margin (NPM)	31	Total Liabilities to EBITDA (TLEBITDA)
10	Net Income to Total Assets (NITA)	32	Total Liabilities to Total Assets (TLTA)
11	Pretax Margin (PTM)	33	Earnings Per Share (EPS)
12	Operating Profit Margin (OPM)	34	Cash from Operating Activities to Total Liabilities (CFOTL)
13	EBITDA Margin (EBITDAM)	35	Earnings Before Interest and Taxes to Total Assets (EBITTA)
14	Return on Assets (ROA)	36	Retained Earnings to Total Assets (RETA)
15	Gross Profit Margin (GPM)	37	Working Capital to Sales (WCA)
16	Working Capital to Total Assets (WCTA)	38	Current Liabilities to Sales (CLS)
17	Current Assets to Total Assets (CATA)	39	Quick Assets to Sales (QAS)
18	Quick Assets to Total Assets (QATA)	40	Operating Expenses to Total Revenue (OER)
19	Current Liabilities to Total Assets (CLTA)	41	Cash Flow to Total Liabilities (CFTL)
20	Working Capital to Current Assets (WCCA)	42	Cash Flow to Sales (CFS)
21	Total Equity to Total Assets (TETA)	43	Net Income to Weighted Average Common Shares Outstanding (NIWACSO)
22	Current Liabilities to Total Liabilities (CLTL)

) have been selected as an initial pool of corporate failure predictors. The selection of most of these ratios was based on the literature (Beaver, 1966; Altman, 1968; Ohlson, 1980; Premachandra et al., 2009; Premachandra et al., 2011; F. Lin et al., 2011; Xu et al., 2014; Christopoulos et al., 2019b). As pointed out by Tian et al. (2015), financial ratios can also possess valuable additional information about potential default risks in the future. Previous studies also utilized financial ratios in their analyses (Cielen et al., 2004; Premachandra et al., 2009, 2011; Shetty et al., 2012; Paradi et al., 2014; Mousavi et al., 2015).

In the first step of the variable selection process, an independent sample non-parametric test (Mann–Whitney U) has been implemented for the 43 financial ratios included in Table 1, to assess whether there were statistically significant differences between the financial ratios of failed and non-failed firms. A non-parametric independent sample test has been selected due to the fact that none of the financial ratios were normally distributed. Based on the results of the Mann–Whitney U test, for 28 out of the 43 financial ratios included in the initial pool of financial ratios, there was statistically significant evidence of difference between the two groups of firms, since their p-values were less than 0.05. Those 28 financial ratios are displayed in

Table 2. Mann–Whitney independent sample test results—financial ratios used for logistic LASSO implementation.

No	Financial Ratios	Sig. *
1	Current Ratio (CACL)	0.002
2	Acid Test Ratio (ATR)	0.003
3	Net Profit Margin (NPM)	0.000
4	Net Income to Total Assets (NITA)	0.000
5	Pretax Margin (PTM)	0.000
6	Operating Profit Margin (OPM)	0.000
7	EBITDA Margin (EBITDAM)	0.026
8	Return on Assets (ROA)	0.000
9	Working Capital to Total Assets (WCTA)	0.001
10	Current Liabilities to Total Assets (CLTA)	0.000
11	Working Capital to Current Assets (WCCA)	0.002
12	Total Equity to Total Assets (TETA)	0.000
13	Total Equity to Total Liabilities (TETL)	0.000
14	Net Working Capital to Non-Current Liabilities (WCNCL)	0.000
15	Equity plus Non-Current Liabilities to Non-Current Assets (ENCLNCA)	0.001
16	Working Capital to Total Liabilities (WCTL)	0.000
17	Total Equity to Non-Current Assets (TENCA)	0.000
18	Total Liabilities to Total Assets plus Total Equity (TLTATE)	0.000
19	Total Liabilities to Total Assets (TLTA)	0.000
20	Earnings Per Share (EPS)	0.001
21	Cash from Operating Activities to Total Liabilities (CFOTL)	0.000
22	Earnings Before Interest and Taxes to Total Assets (EBITTA)	0.008
23	Retained Earnings to Total Assets (RETA)	0.000
24	Working Capital to Sales (WCA)	0.002
25	Current Liabilities to Sales (CLS)	0.001
26	Operating Expenses to Total Revenue (OER)	0.000
27	Cash Flow to Total Liabilities (CFTL)	0.008
28	Net Income to Weighted Average Common Shares Outstanding (NIWACSO)	0.001

* Asymptotic significance (p-value) is displayed. The significance level is 0.050.

, together with the results of the Mann–Whitney U test.

The 28 financial ratios included in Table 2 were used for the implementation of logistic LASSO through the statistical software ‘STATA’(version 17) to identify the most important predictors of corporate failure. For the selection of the best value of the tuning parameter, λ, 10-fold cross-validation has been applied. The results are presented in

Table 3. Logistic LASSO—optimal tuning parameter lambda (λ) selection.

ID	Description	Lambda	No. of Nonzero Coef.	CV Mean Deviance
1	First lambda	0.288631	0	1.402111
14	Lambda before	0.0861173	4	1.101192
* 15	Selected lambda	0.0784669	5	1.099664
16	Lambda after	0.0714961	5	1.100356
19	Last lambda	0.0540842	6	1.109833

* Lambda selected by 10-fold cross-validation.

. For the selected λ (0.0784669), the lowest CV mean deviance has been achieved.

As presented in Table 3, under the selected λ, the estimated coefficients were non-zero for five financial ratios. Those financial ratios were identified as important for corporate failure prediction and are the following: Return on Assets (ROA), Working Capital to Total Liabilities (WCTL), Total Equity to Non-Current Assets (TENCA), Cash from Operating Activities to Total Liabilities (CFOTL), and Current Liabilities to Total Assets (CLTA). The financial interpretation of each one of those financial ratios is as follows:

Return on Assets (ROA) is a profitability ratio offering information regarding total asset performance. The higher the ratio, the more income is generated by a given level of total assets, thus lowering the possibility of corporate failure status.

Working Capital to Total Liabilities (WCTL) indicates to what extent a firm’s total liabilities can be covered by the net working capital.

Total Equity to Non-Current Assets (TENCA), indicates the participation level of a firm’s total equity to non-current asset financing.

Cash from Operating Activities to Total Liabilities (CFOTL) can be used to determine how long it will take a firm to cover its total liabilities, in case all cash from operating activities is utilized. To the best of our knowledge, this ratio has not been recognized again as an important predictor for corporate failure assessment.

Current Liabilities to Total Assets (CLTA) is a measure of financial flexibility, and high values indicate potential challenges in meeting short-term obligations.

Apart from the logistic LASSO-selected variables and to assess the prediction accuracy of the modified super-SBM-DEA model by R. Lin et al. (2019), from the remaining 23 financial ratios, 8 were also selected based on the criterium not to be highly correlated (the correlation matrix is presented in

Table 4. Spearman correlation coefficient matrix for the second set of variables.

	CACL	NPM	EBITDAM	TLTA	EBITTA	RETA	CLS	CFTL
CACL	1.000	0.208	−0.166	−0.420	−0.040	0.425	−0.749	0.205
NPM	0.208	1.000	0.249	−0.354	0.474	0.496	−0.227	0.066
EBITDAM	−0.166	0.249	1.000	−0.146	0.770	0.056	0.013	0.091
TLTA	−0.420	−0.354	−0.146	1.000	−0.141	−0.693	0.526	−0.523
EBITTA	−0.040	0.474	0.770	−0.141	1.000	0.176	−0.036	−0.146
RETA	0.425	0.496	0.056	−0.693	0.176	1.000	−0.531	0.325
CLS	−0.749	−0.227	0.013	0.526	−0.036	−0.531	1.000	−0.394
CFTL	0.205	0.066	0.091	−0.523	−0.146	0.325	−0.394	1.000

): Current Ratio (CR), Net Profit Margin (NPM), Earnings Before Interest and Taxes, Depreciation and Amortization Margin (EBITDAM), Retained Earnings to Total Assets (RETA), Earnings Before Interest and Taxes to Total Assets (EBITTA), Cash Flow to Total Liabilities (CFTL), Total Liabilities to Total Assets (TLTA), and Current Liabilities to Sales (CLS). The financial interpretation of each one of these financial ratios is as follows:

Current Ratio (CACL) is a fundamental liquidity measure indicating the ability of a firm to satisfy its current liabilities using its current assets.

Net Profit Margin (NPM) is a profitability measure that indicates a firm’s performance in effectively managing assets and operational expenses.

Earnings Before Interest and Taxes, Depreciation and Amortization Margin (EBITDAM) is a profitability measure indicating a firm’s ability to manage operating expenses and generate profit.

Retained Earnings to Total Assets (RETA) indicates to what extent a firm relies on leverage to fund its assets.

Earnings Before Interest and Taxes to Total Assets (EBITTA) measures the income-generating ability of a firm’s assets.

Cash Flow (net income plus depreciation, depletion, and amortization) to Total Liabilities (CFTL), can be used to determine how long it will take a firm to cover its total liabilities, in case all net income plus depreciation, depletion, and amortization is utilized.

Total Liabilities to Total Assets (TLTA) is one of the most frequently accounting-based variables adopted in numerous studies (Beaver, 1966; Deakin, 1972; Ohlson, 1980; Zmijewski, 1984; Shumway, 2001; Ding et al., 2008; Martens et al., 2008; Premachandra et al., 2009, 2011; F. Lin et al., 2011; Xu et al., 2014; Christopoulos et al., 2019b). As pointed out by Premachandra et al. (2009), increased levels of leverage are positively correlated with the probability of corporate failure.

Current Liabilities to Sales (CLS) is used for the evaluation of the financial position of a firm.

The implementation of DEA requires first the classification of the financial ratios included in the two sets, to inputs and outputs. This research follows the “Worst Practice Frontier” approach, introduced by Paradi and Simak (2004) and also applied in the work of Premachandra et al. (2009, 2011). This approach is, in fact, the opposite of the traditional DEA efficiency frontier one. Under the traditional DEA efficiency frontier approach, larger is better for outputs and lower is better for inputs, and the model orientation defines whether emphasis will be given, for example, to the maximization of outputs (output orientation) for a given level of inputs, or to the minimization of inputs (input orientation) for a given level of outputs. When the traditional efficiency frontier of DEA is being converted to a “Worst Practice Frontier”, the nature of inputs and outputs is opposite. Thus, this conversion is achieved through the appropriate classification of the financial ratios to inputs and outputs, also taking into consideration the contribution of the financial interpretation of the financial ratios to the assessment of the financial status of firms, based on the theory of the field of financial analysis. Under this framework, the financial ratios for which a decrease in their values can be conceptually linked with an increased possibility of financial distress for firms are categorized as inputs. Under the same logic, the financial ratios for which an increase in their values can be conceptually linked with an increased possibility of financial distress for firms are categorized as outputs. The final classification of the five financial ratios to inputs and outputs is presented in

Table 5. Input and output classification.

Inputs (Lower the Worst)	Outputs (Higher the Worst)
Logistic LASSO-Selected Variables
Return on Assets (ROA)	Current Liabilities/Total Assets (CLTA)
Working Capital/Total Liabilities (WCTL)
Total Equity/Non-Current Assets (TENCA)
Cash from Operating Activities/Total Liabilities (CFOTL)
Other selected variables
Current Ratio (CACL)	Total Liabilities/Total Assets (TLTA)
Net Profit Margin (NPM)	Current Liabilities/Sales (CLS)
EBITDA Margin (EBITDAM)
Retained Earnings/Total Assets (RETA)
Earnings Before Interest and Taxes/Total Assets (EBITTA)
Cash Flow/Total Liabilities (CFTL)

.

4.2. Modified Super-SBM-DEA Model Performance Evaluation (Stage 2)

In this stage, the first part of our analysis consists of the assessment of the efficiency results of the input-oriented modified super-SBM-DEA model following the “Worst Practice Frontier” approach for the fiscal year before the event of a default. For the assessment of the results, the actual status of firms included in the sample was taken into account.

The results of the modified super-SBM model following the “Worst Practice Frontier” approach with logistic LASSO-selected variables were compared with the results of a modified super-SBM-DEA model following the “Worst Practice Frontier” approach with a different set of variables. This comparison facilitated the assessment of whether the results of the modified super-SBM model following the “Worst Practice Frontier” approach are improved in terms of corporate failure prediction accuracy when a variable selection process with the implementation of logistic LASSO is performed. For the calculation of the results of both models, ‘MaxDEA X’ software (version 12.1) has been utilized.

Previous studies for corporate failure prediction (Paradi et al., 2014; Premachandra et al., 2011) suggest that an appropriate cut-off should be set for the efficiency scores to classify firms into failed and non-failed status. Following the approach of Paradi et al. (2014), potential cut-off points have been tested in the range of 0 to 1. In our research, the optimal cut-off point for each model was selected based on the overall prediction accuracy, also taking into consideration sensitivity and specificity. The results for all tested cut-off points are presented in

Table 6. Optimal cut-off point selection.

Cut-Off Point	Model 1 Overall Prediction Accuracy	Model 1 Sensitivity	Model 1 Specificity	Model 2 Overall Prediction Accuracy	Model 2 Sensitivity	Model 2 Specificity
0.55	57%	100%	13%	61%	76%	47%
0.6	64%	100%	29%	62%	73%	51%
0.61	64%	100%	29%	62%	71%	53%
0.62	66%	100%	31%	61%	67%	56%
0.63	66%	100%	31%	64%	67%	62%
0.64	67%	100%	33%	63%	64%	62%
0.65	70%	100%	40%	64%	64%	64%
0.66	71%	100%	42%	64%	64%	64%
0.67	72%	100%	44%	64%	64%	64%
0.68	76%	98%	53%	64%	64%	64%
0.69	76%	96%	56%	64%	62%	67%
0.7	74%	93%	56%	67%	62%	71%
0.71	81%	93%	69%	68%	60%	76%
0.72	82%	93%	71%	67%	56%	78%
0.73	86%	91%	80%	67%	53%	80%
0.74	84%	89%	80%	68%	49%	87%
0.75	83%	82%	84%	70%	49%	91%
0.76	82%	78%	87%	71%	49%	93%
0.8	77%	64%	89%	69%	40%	98%
0.85	66%	38%	93%	61%	24%	98%
0.9	58%	22%	93%	59%	20%	98%
0.95	57%	18%	96%	59%	20%	98%
1	57%	18%	96%	59%	20%	98%

Model 1: modified super-SBM-DEA with logistic LASSO-selected variables. Model 2: modified super-SBM-DEA with other variables.

.

Considering the actual status of the firms included in our sample, sensitivity was defined as the number of actually failed firms with an efficiency score higher than the cut-off point (true positives) divided by the total number of actually failed firms, and is an indication of the ability of a model to correctly identify firms in failure status. Specificity was calculated as the number of actually non-failed firms with efficiency scores less than the cut-off point (true negatives) divided by the total number of actually non-failed firms, and is an indication of the ability of a model to correctly identify firms in non-failure status. The overall prediction accuracy was defined as the ratio of the number of firms correctly classified as failed and non-failed (true positives and true negatives) to the total number of firms included in the analysis.

Based on the efficiency scores of the modified super-SBM-DEA model following the “Worst Practice Frontier” approach with the logistic LASSO-selected variables, regarding the end of the fiscal year before the event of a default, for a cut-off point in the range of 0 to 0.67, sensitivity was 100%, but the maximum level of specificity was 44%, reducing the overall prediction accuracy of the model to 72%. Considering the trade-off between sensitivity and specificity together with the overall prediction accuracy, the optimal cut-off point for the modified super-SBM-DEA model with the logistic LASSO-selected variables has been set to 0.73. Under this cut-off point, the overall prediction accuracy of the model is 86%, sensitivity is 91%, and specificity is 80%.

The selection of the optimal cut-off point for the modified super-SBM-DEA model following the “Worst Practice Frontier” approach with a different set of variables was performed similarly. For a cut-off point of 0.73, which was the optimal one for the modified super-SBM-DEA model with the logistic LASSO-selected variables, the overall prediction accuracy for the modified super-SBM-model with a different set of variables was 67%, driven by 53% sensitivity and 80% specificity. The maximum overall prediction accuracy of up to 71% was achieved with a cut-off point of 0.76, but this result was mostly driven by the correct classification of non-failed firms (93%). Sensitivity was only 49% at this cut-off point level. Since for bankruptcy prediction the correct classification of failed firms is more important than non-failed ones, and also considering the trade-off between sensitivity and specificity together with the overall prediction accuracy, the optimal cut-off point has been set to 0.63, where the overall prediction accuracy is 64%, sensitivity is 67%, and specificity is 62%.

Based on the optimal cut-off point, the firms’ efficiency scores of the modified super-SBM-DEA model with logistic LASSO-selected variables and the results of the modified super-SBM-DEA model with a different set of variables were assessed, taking into consideration the overall prediction accuracy, sensitivity, specificity, and Type I as well as II errors. Type I errors occur when an actually failed firm is misclassified as being non-failed, while the occurrence of Type II errors is when a non-failed firm is misclassified as failed. The complements of Type I and II errors are sensitivity and specificity.

The results presented in

Table 7. Estimation accuracy assessment of the two DEA models relative to the optimal cut-off point at the end of the fiscal year immediately preceding the year of failure.

Model	Sensitivity	Specificity	Overall Prediction Accuracy	Type I Error	Type II Error
Modified super-SBM-DEA with logistic LASSO-selected variables	91.1%	80%	85.6%	8.9%	20%
Modified super-SBM-DEA with other variables	66.7%	62.2%	64.4%	33.3%	37.8%

indicate that the modified super-SBM-DEA with logistic LASSO-selected variables is superior compared to the modified super-SBM-DEA with a different set of variables, under the “Worst Practice Frontier” approach, since it has lower Type I and Type II errors, together with higher sensitivity, specificity, and overall prediction accuracy.

4.3. Comparison with Logistic Regression (Stage 3)

Logistic regression (Ohlson, 1980) has been selected as a comparative methodology for corporate failure prediction to assess the performance of the modified super-SBM-DEA model with logistic LASSO-selected variables as a corporate failure prediction tool. The same set of logistic LASSO-selected variables has also been used for logistic regression implementation (Return on Assets (ROA), Working Capital to Total Liabilities (WCTL), Total Equity to Non-Current Assets (TENCA), Cash from Operating Activities to Total Liabilities (CFOTL), and Current Liabilities to Total Assets (CLTA)) to ensure a proper comparison between the two corporate failure prediction methodologies.

The results presented in

Table 8. Estimation accuracy assessment of logistic regression at the end of the fiscal year immediately preceding the year of failure.

Model	Sensitivity	Specificity	Overall Prediction Accuracy	Type I Error	Type II Error
LR with logistic LASSO-selected variables	82.2%	77.8%	80%	17.8%	22.2%

indicate the superiority of the modified super-SBM-DEA with logistic LASSO-selected variables as a corporate failure prediction model compared to logistic regression. The modified super-SBM-DEA with logistic LASSO-selected variables had lower Type I and Type II errors, together with higher sensitivity, specificity, and overall prediction accuracy.

4.4. Productivity Analysis—Malmquist DEA (Stage 4)

In our research, Malmquist DEA with a VRS input-oriented modified super-SBM-DEA model following the “Worst Practice Frontier” approach is implemented for corporate failure assessment during five fiscal years before the event of a failure. Thus, values of the MPI larger than one indicate productivity decline (instead of productivity progress), values less than one indicate productivity progress (instead of productivity decline), and values equal to one indicate no change. Consecutive periods used for the MPI implementation are defined as follows: periods one, two, three, and four are defined as the periods four, three, two, and one year(s) prior to the end of the fiscal year immediately preceding the year of failure. Finally, period five is the end of the fiscal year immediately preceding the year of failure.

Based on the MPI results, it was found that the percentage of failed firms with values of MPI indicating productivity decline was higher than the percentage of the respective non-failed firms between all consecutive periods, apart from period two to period three, where the percentages were quite similar for both groups of firms. Notably, between period four and period five, 89% of actually failed firms had MPI values larger than one. The respective percentage for the non-failed firms was 55.6%. As also pointed out by Paradi and Simak (2004), the non-failed firms are not necessarily in excellent financial condition, and possibly there are also firms that might file for bankruptcy in the coming years. In Figure 1, the percentage of firms in failure and non-failure status with an MPI larger than one between all consecutive periods under investigation is presented.

Under the VRS assumption, the MPI from period t to period t + 1, t = 1, …, 4 was further decomposed to pure efficiency change (PEFFCH) and technical change (TECH), to provide more insights into the drivers of changes in productivity based on whether firms moved closer or further away from the “Worst Practice Frontier” (PEFFCH) or shifts on the frontier itself were observed (TECH).

Table 9. Summary of the average values of MPI and its components between all consecutive periods.

Failure Status		Period One–Period Two	Period Two–Period Three	Period Three–Period Four	Period Four–Period Five
Yes	MPI	1.03	1.01	1.02	1.12
	%	3	1	2	12
	PEFFCH	1.11	1.10	0.98	1.04
	%	11	10	−2	4
	TECH	0.93	0.92	1.04	1.07
	%	−7	−8	4	7
No	MPI	0.97	1.05	1.09	1.06
	%	−3	5	9	6
	PEFFCH	1.03	1.14	0.99	0.92
	%	3	14	−1	−8
	TECH	0.93	0.92	1.08	1.15
	%	−7	−8	8	15

provides the average values of MPI and its components between all consecutive periods.

Based on the results presented in Table 9, among failed firms, the strongest deterioration in productivity was observed between periods four and five (MPI = 1.12), which were also the closest to the year of failure. This confirms that productivity decline accelerates in the years immediately preceding bankruptcy. That deterioration was jointly driven by efficiency decline (PEFFCH = 1.04) and technological regression (TECH = 1.07). In contrast, non-failed firms also experienced technological regression (TECH = 1.15) between periods four and five, but they managed to partially offset it through efficiency progress (PEFFCH = 0.92). As a result, their overall productivity decline (MPI = 1.06) was less severe than that of failed firms (MPI = 1.12). This indicates that non-failed firms were better at adjusting operations and managing their resources more effectively in the short run, which cushioned the overall productivity decline. In contrast, failed firms lacked this adjustment mechanism, losing ground in managerial and operational efficiency, resulting in steeper deterioration.

The fact that TECH values are persistently below 1 both for failed and non-failed firms in early periods suggests that the technological environment was improving. However, this trend has been interrupted as we move to later periods, indicating an industry-wide deterioration in new technology investments. Regarding PEFFCH, non-failed firms performed better in general, whereas the results for failed ones reflect poorer managerial and operational performance, and occasional short-term gains (PEFFCH < 1 between periods three and four) were insufficient to offset the prevailing decline in efficiency.

Based on the results, another finding (

Table 10. Cumulative results of MPI values and its components.

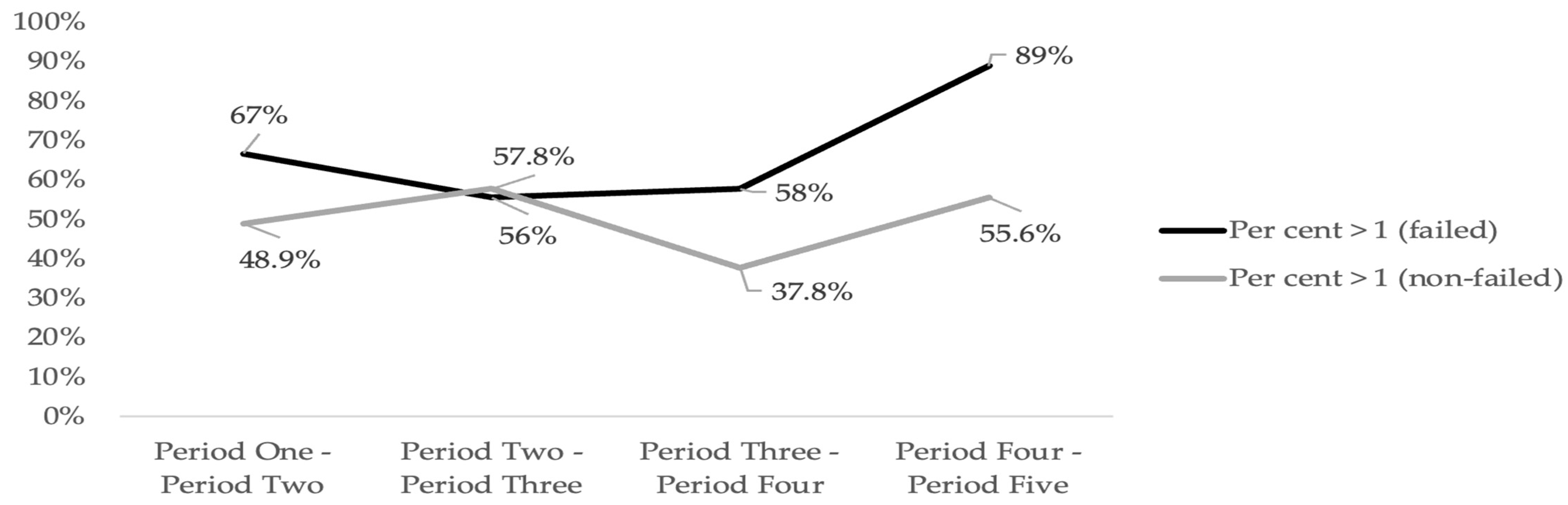
Failure Status	Index	>1 Between All Periods	>1 Between Three Periods	>1 Between Two Periods	>1 Between One Period
Yes	MPI	9%	53%	36%	2%
	PEFFCH	9%	56%	31%	4%
	TECH	2%	4%	84%	9%
No	MPI	2%	24%	44%	29%
	PEFFCH	2%	13%	71%	13%
	TECH	2%	11%	73%	13%

) was that 9% of the actually failed firms had a larger than one MPI value between all consecutive periods and 53% between three out of four consecutive periods under investigation. The respective results for the non-failed firms were 2% and 24%. Thus, the MPI can be considered a good indicator of distress status when it receives values larger than one under the “Worst Practice Frontier” approach between all or three out of four consecutive periods under investigation. MPI decomposition also offers valuable early warning signals of failure, providing insights about whether the decline stems from inefficiency or from falling behind technologically, allowing for more-targeted preventive measures, such as operational restructuring or innovation-focused investment for technology-driven gaps.

Summarizing the results, a remarkable finding is that for both failed and non-failed firms there was a deterioration in overall productivity in the majority of the period intervals. The dynamics observed can be linked to major shocks in the energy sector. The 2014–2016 drop in oil prices significantly reduced revenues, affecting all firms, and further deteriorated the financial position of the financially weaker ones, with a significant amount of debt already on their balance sheet. This revenue reduction made firms unable to invest in new technologies. The technological gap had been further widened due to the transition toward renewable energy and increasing regulatory pressure. Finally, the COVID-19 pandemic (2020) disrupted demand and supply chains, accelerating productivity decline, particularly for firms already in a distressed financial condition.

5. Concluding Remarks and New Research Avenues

This study contributes to the literature by introducing an advanced DEA version, the modified super-SBM-DEA model, to establish a corporate failure prediction model following the “Worst practice frontier” approach. A crucial part of corporate failure prediction is the appropriate selection of variables. In our research, logistic LASSO has been used as a tool for the selection of predictive variables. The findings of the empirical analysis indicated that the modified super-SBM-DEA with logistic LASSO-selected variables is superior compared to the modified super-SBM-DEA with non-LASSO-selected variables, under the “Worst Practice Frontier” approach, since it has lower Type I and Type II errors, together with higher sensitivity, specificity, and overall prediction accuracy, at a cut-off point of 0.73. The superiority of the modified super-SBM-DEA with logistic LASSO-selected variables as a corporate failure prediction model was also proven through the comparison with logistic regression. The implementation of Malmquist DEA offered insights into the dynamic process of failure before reaching the final stage of bankruptcy.

The contribution of our research is confirmed through a comparison of our results with those from previous studies. The overall prediction accuracy of the modified super-SBM-DEA model with logistic LASSO-selected variables was 85.6%, the correct prediction rate of failed firms was 91.1%, and the respective percentage for the non-failed firms was 80%. The additive super-efficiency DEA implemented by Premachandra et al. (2011) achieved 72% of bankrupt, 83.2% of non-bankrupt, and 82.6% of total correct predictions, at a cut-off point of 0.1. At a cut-off point of 0.5 (closer to the optimal cut-off point of 0.73 selected in our study), the results were 42%, 94.6%, and 92%, respectively. The failure assessment index introduced by Premachandra et al. (2011) managed to improve mostly the non-bankrupt correct predictions. Regarding the correct classification of failed firms, our model had a better correct prediction rate (91.1%) compared to the results of both models proposed by Premachandra et al. (2011). Finally, the input-oriented slacks-based measure utilized by Paradi et al. (2014) had in the distress area, regarding year one, total accuracy of 71.4%, bankrupt accuracy of 78.6%, and non-bankrupt accuracy of 62.9%.

The economic and social impact of corporate failure necessitates developing the essential warning tools to predict and avoid bankruptcy. The success of this scope is based on the best knowledge of the failure conditions and the ability to detect these factors with the appropriate financial variables. The choice of techniques to build a reliable prediction tool plays a significant role in the predictive ability of the selected variables. This conclusion is in line with the findings of the literature. Our research provides a model with these characteristics, offering a reliable predictive tool to the decision-makers.

Despite its strong predictive performance, the proposed model is not without limitations. First, the reliance on financial statement data may overlook changes in the macroeconomic environment or governance-related factors that also play a significant role. However, as pointed out also by Agarwal and Taffler (2008), the dynamic dimension of failure is reflected in the firms’ financial statements, and is usually accompanied by a long-term trend of low performance. Economic cycles with strong fluctuations can possibly affect the financial viability of firms and increase the risk of corporate failure. This risk is higher for firms that are already in a distressed financial position. Another limitation is linked to the structure of the sample. In this research, a balanced sample with one-to-one matching between failed and non-failed firms has been used. However, the number of failed firms is usually less than the number of non-failed ones. In addition, this study is based on coverage of a specific industry; extending it to a broader cross-industry sample can possibly have an impact on the predictive accuracy of the proposed model.

To address the above limitations, our research can be further enhanced by testing the results of the modified super-SBM-DEA with logistic LASSO-selected variables under the condition of an imbalanced sample, in the same direction as previous literature (Paradi & Simak, 2004; Premachandra et al., 2009). Moreover, the sample can be further enriched with firms from several economic sectors. The points above potentially constitute a topic for future research.