Impact of the COVID-19 Pandemic on the Financial Market Efficiency of Price Returns, Absolute Returns, and Volatility Increment: Evidence from Stock and Cryptocurrency Markets
Abstract
1. Introduction
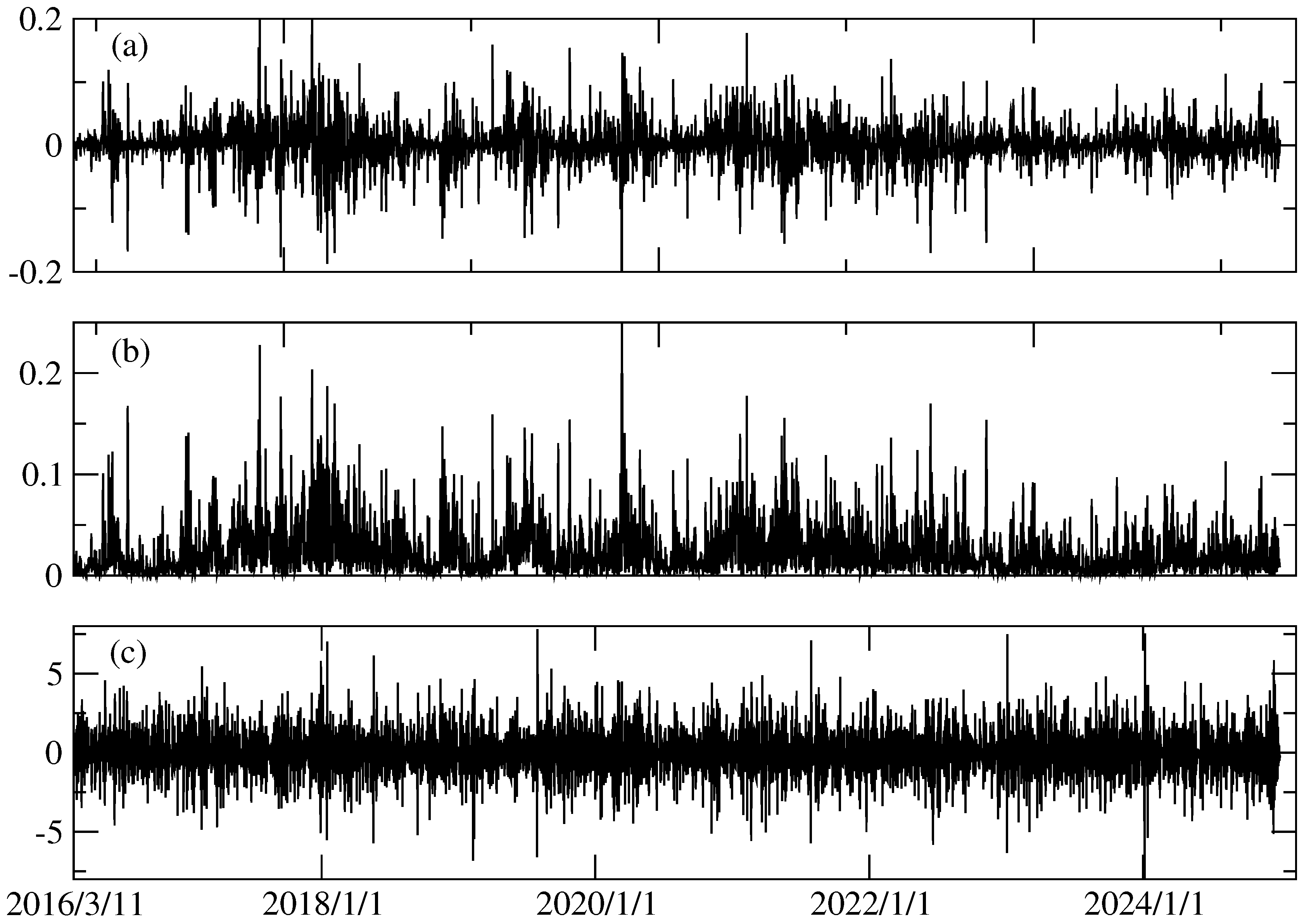
2. Data
3. Methodology
3.1. MFDFA
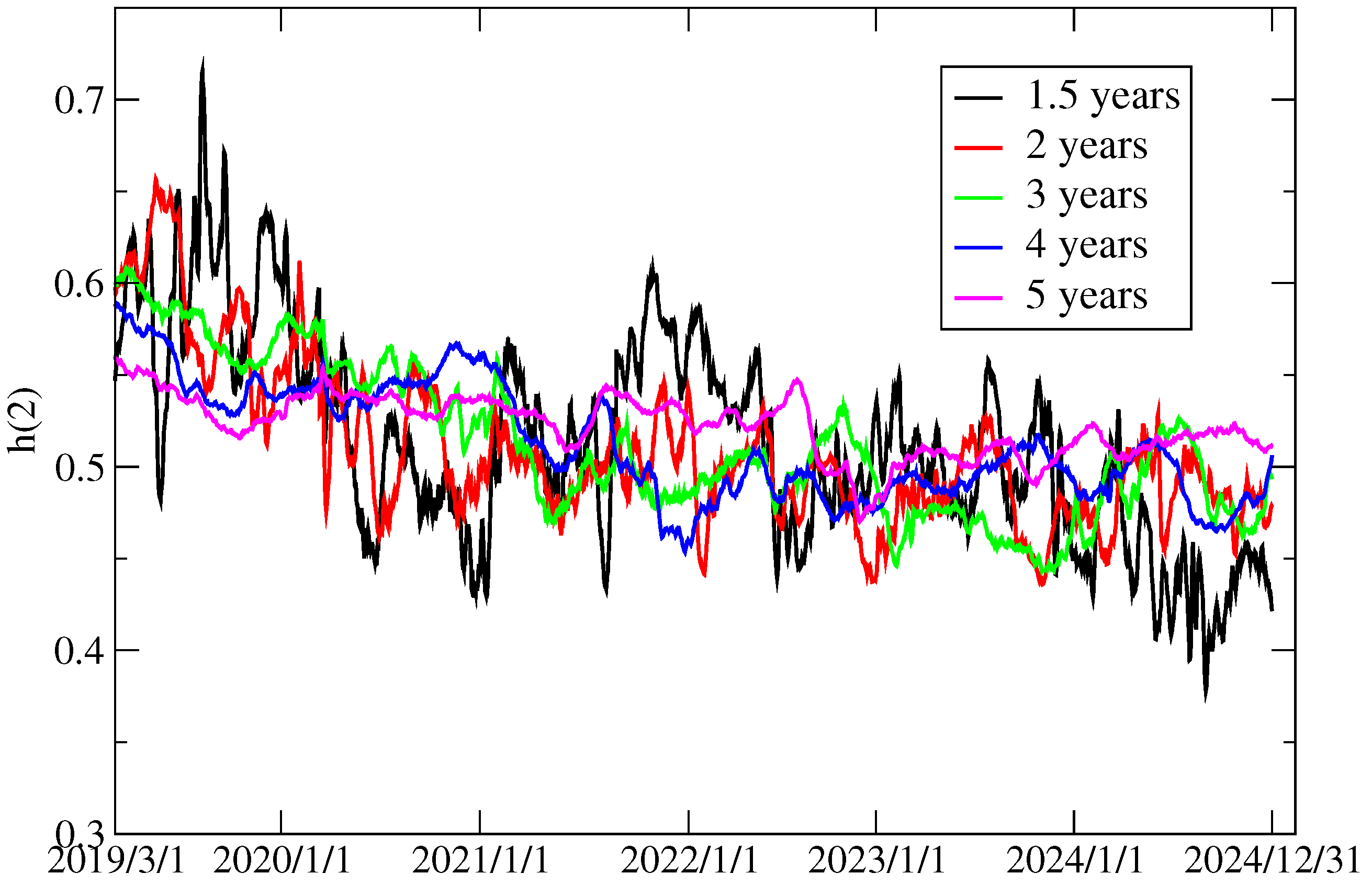
3.2. Market Efficiency Measurement by GHE
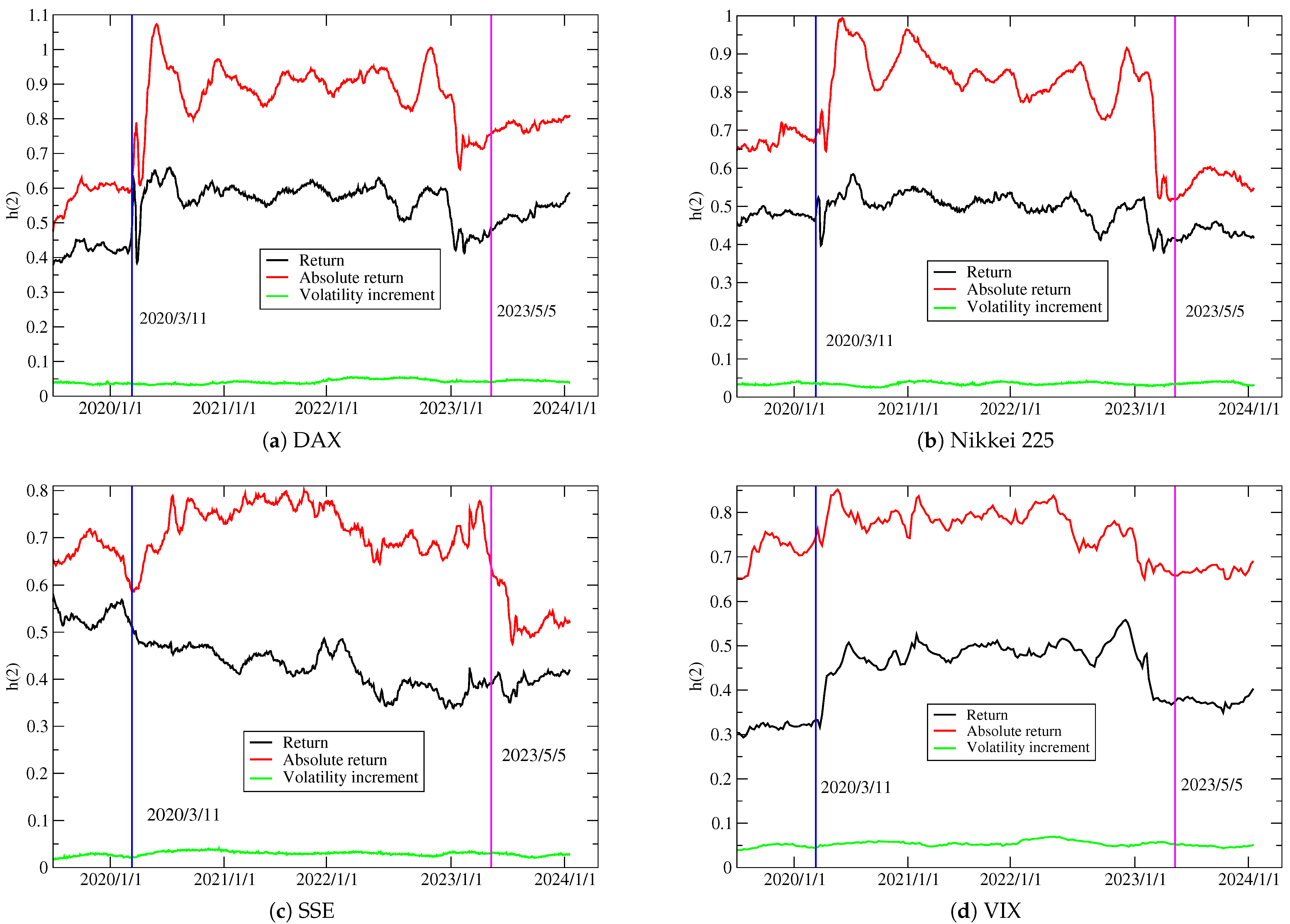
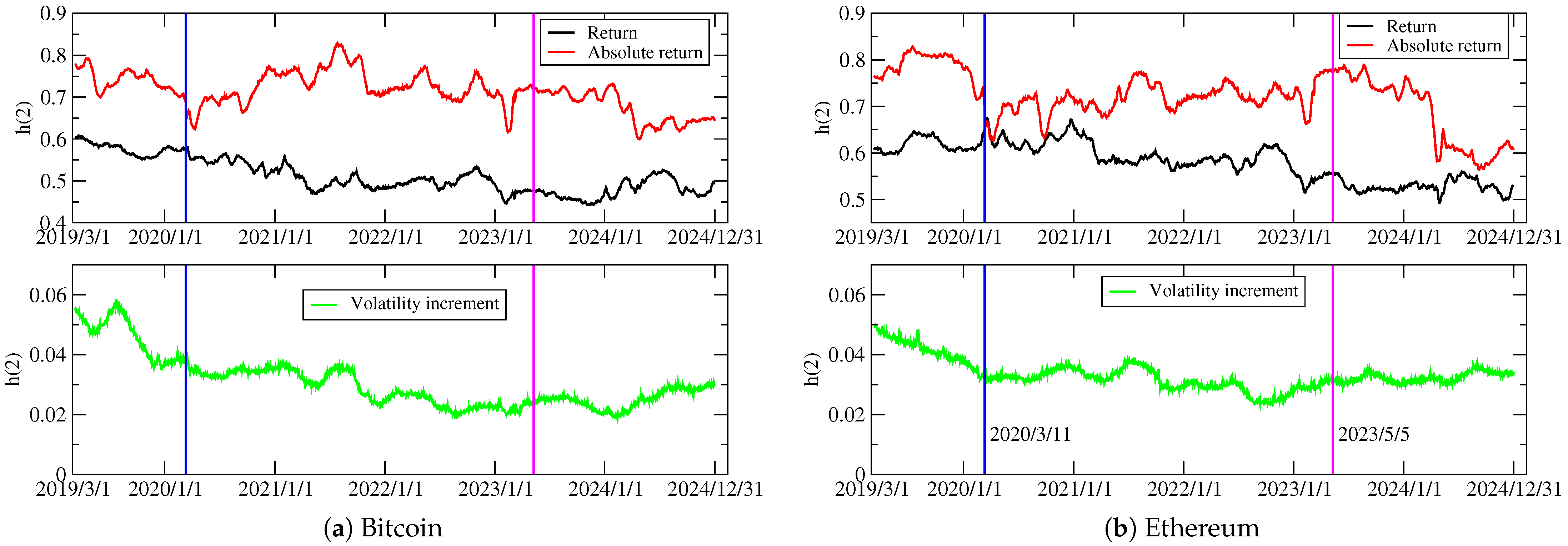
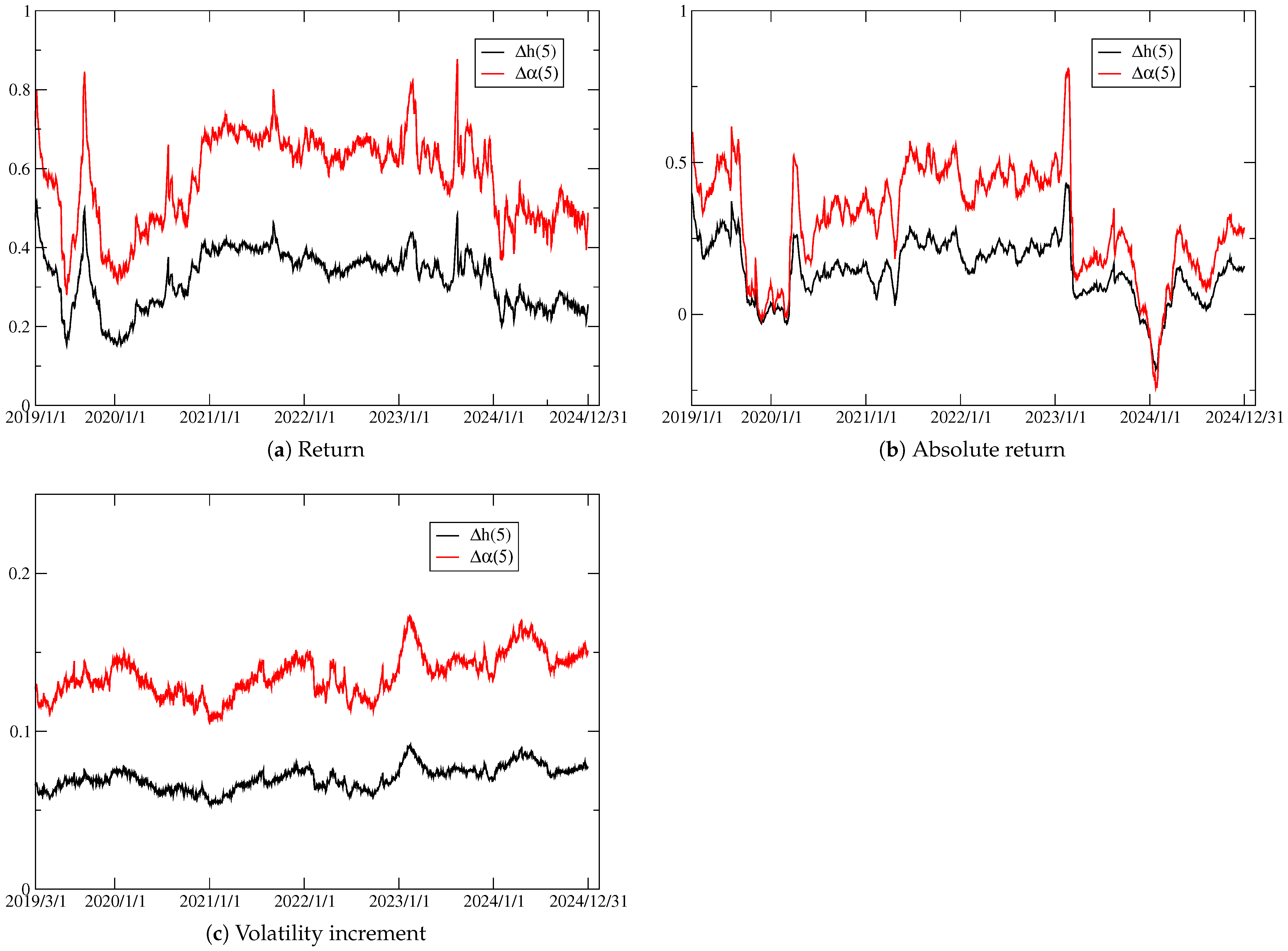
4. Empirical Results
5. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alijani, M., Banimahd, B., Nikoomaram, H., & Yaghobnezhad, A. (2021). Fractal analysis and the relationship between efficiency of capital market indices and COVID-19 in Iran. Results in Physics, 25, 104262. [Google Scholar] [CrossRef]
- Alos, E., León, J. A., & Vives, J. (2007). On the short-time behavior of the implied volatility for jump-diffusion models with stochastic volatility. Finance and Stochastics, 11(4), 571–589. [Google Scholar] [CrossRef]
- Ameer, S., Nor, S. M., Ali, S., & Zawawi, N. H. M. (2023). The impact of COVID-19 on BRICS and MSCI emerging markets efficiency: Evidence from MF-DFA. Fractal and Fractional, 7(7), 519. [Google Scholar] [CrossRef]
- Andersen, T. G., & Bollerslev, T. (1998). Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review, 39, 885–905. [Google Scholar] [CrossRef]
- Andersen, T. G., Bollerslev, T., & Dobrev, D. (2007). No-arbitrage semi-martingale restrictions for continuous-time volatility models subject to leverage effects, jumps and iid noise: Theory and testable distributional implications. Journal of Econometrics, 138(1), 125–180. [Google Scholar] [CrossRef]
- Arouxet, M. B., Bariviera, A. F., Pastor, V. E., & Vampa, V. (2022). COVID-19 impact on cryptocurrencies: Evidence from a wavelet-based Hurst exponent. Physica A: Statistical Mechanics and Its Applications, 596, 127170. [Google Scholar] [CrossRef]
- Aslam, F., Aziz, S., Nguyen, D. K., Mughal, K. S., & Khan, M. (2020a). On the efficiency of foreign exchange markets in times of the COVID-19 pandemic. Technological Forecasting and Social Change, 161, 120261. [Google Scholar] [CrossRef]
- Aslam, F., Mohti, W., & Ferreira, P. (2020b). Evidence of intraday multifractality in European stock markets during the recent coronavirus (COVID-19) outbreak. International Journal of Financial Studies, 8(2), 31. [Google Scholar] [CrossRef]
- Bariviera, A. F., Fabregat-Aibar, L., & Sorrosal-Forradellas, M.-T. (2023). Disentangling the impact of economic and health crises on financial markets. Research in International Business and Finance, 65, 101928. [Google Scholar] [CrossRef]
- Bennedsen, M., Lunde, A., & Pakkanen, M. S. (2022). Decoupling the short-and long-term behavior of stochastic volatility. Journal of Financial Econometrics, 20(5), 961–1006. [Google Scholar] [CrossRef]
- Brandi, G., & Di Matteo, T. (2022). Multiscaling and rough volatility: An empirical investigation. International Review of Financial Analysis, 84, 102324. [Google Scholar] [CrossRef]
- Choi, S.-Y. (2021). Analysis of stock market efficiency during crisis periods in the US stock market: Differences between the global financial crisis and COVID-19 pandemic. Physica A: Statistical Mechanics and Its Applications, 574, 125988. [Google Scholar] [CrossRef]
- Ding, Z., Granger, C. W., & Engle, R. F. (1993). A long memory property of stock market returns and a new model. Journal of Empirical Finance, 1(1), 83–106. [Google Scholar] [CrossRef]
- Diniz-Maganini, N., Diniz, E. H., & Rasheed, A. A. (2021). Bitcoin’s price efficiency and safe haven properties during the COVID-19 pandemic: A comparison. Research in International Business and Finance, 58, 101472. [Google Scholar] [CrossRef]
- Drożdż, S., Gȩbarowski, R., Minati, L., Oświȩcimka, P., & Wa̧torek, M. (2018). Bitcoin market route to maturity? Evidence from return fluctuations, temporal correlations and multiscaling effects. Chaos: An Interdisciplinary Journal of Nonlinear Science, 28(7), 071101. [Google Scholar] [CrossRef] [PubMed]
- Drożdż, S., Kwapień, J., Oświęcimka, P., Stanisz, T., & Wątorek, M. (2020). Complexity in economic and social systems: Cryptocurrency market at around COVID-19. Entropy, 22(9), 1043. [Google Scholar] [CrossRef] [PubMed]
- Erer, D., Erer, E., & Güngör, S. (2023). The aggregate and sectoral time-varying market efficiency during crisis periods in Turkey: A comparative analysis with COVID-19 outbreak and the global financial crisis. Financial Innovation, 9(1), 80. [Google Scholar] [CrossRef]
- Fama, E. F. (1970). Efficient capital markets: A review of theory and empirical work. The Journal of Finance, 25(2), 383–417. [Google Scholar] [CrossRef]
- Fernandes, L. H., De Araujo, F. H., Silva, J. W., Silva, I. E., & Tabak, B. M. (2022). Evaluating the efficiency of brazilian stock market indices: The case of COVID-19. Fractals, 30(1), 2250014. [Google Scholar] [CrossRef]
- Fleming, J., Kirby, C., & Ostdiek, B. (2003). The economic value of volatility timing using “realized” volatility. Journal of Financial Economics, 67(3), 473–509. [Google Scholar] [CrossRef]
- Floc’h, F. L. (2022). Roughness of the Implied Volatility. arXiv, arXiv:2207.04930. [Google Scholar]
- Fukasawa, M. (2011). Asymptotic analysis for stochastic volatility: Martingale expansion. Finance and Stochastics, 15, 635–654. [Google Scholar] [CrossRef]
- Gao, X.-L., Jiang, Z.-Q., & Zhou, W.-X. (2024). Impact of the COVID-19 pandemic on the intermittent behavior of the global spot markets of staple food crops. Journal of Management Science and Engineering, 9(4), 510–521. [Google Scholar] [CrossRef]
- Gatheral, J., Jaisson, T., & Rosenbaum, M. (2018). Volatility is rough. Quantitative Finance, 18(6), 933–949. [Google Scholar] [CrossRef]
- Hurst, H. E. (1951). Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers, 116(1), 770–799. [Google Scholar] [CrossRef]
- Jiang, Z.-Q., Xie, W.-J., Zhou, W.-X., & Sornette, D. (2019). Multifractal analysis of financial markets. Reports on Progress in Physics, 82(12), 125901. [Google Scholar] [CrossRef]
- Kantelhardt, J. W., Zschiegner, S. A., Koscielny-Bunde, E., Havlin, S., Bunde, A., & Stanley, H. E. (2002). Multifractal detrended fluctuation analysis of nonstationary time series. Physica A, 316(1), 87–114. [Google Scholar] [CrossRef]
- Lahmiri, S. (2023). The effect of the COVID-19 pandemic on multifractals of price returns and trading volume variations of cryptocurrencies. Decision Analytics Journal, 6, 100173. [Google Scholar] [CrossRef]
- Li, X., & Su, F. (2023). The dynamic effects of COVID-19 and the March 2020 crash on the multifractality of NASDAQ insurance stock markets. Fractal and Fractional, 7(1), 91. [Google Scholar] [CrossRef]
- Lim, K.-P., & Brooks, R. (2011). The evolution of stock market efficiency over time: A survey of the empirical literature. Journal of Economic Surveys, 25(1), 69–108. [Google Scholar] [CrossRef]
- Livieri, G., Mouti, S., Pallavicini, A., & Rosenbaum, M. (2018). Rough volatility: Evidence from option prices. IISE Transactions, 50(9), 767–776. [Google Scholar] [CrossRef]
- Matteo, T. D., Aste, T., & Dacorogna, M. M. (2005). Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. Journal of Banking & Finance, 29(4), 827–851. [Google Scholar]
- McAleer, M., & Medeiros, M. C. (2008). Realized volatility: A review. Econometric Reviews, 27(1–3), 10–45. [Google Scholar] [CrossRef]
- Mensi, W., Lee, Y.-J., Vo, X. V., & Yoon, S.-M. (2021). Does oil price variability affect the long memory and weak form efficiency of stock markets in top oil producers and oil Consumers? Evidence from an asymmetric MF-DFA approach. The North American Journal of Economics and Finance, 57, 101446. [Google Scholar] [CrossRef]
- Mensi, W., Sensoy, A., Vo, X. V., & Kang, S. H. (2020). Impact of COVID-19 outbreak on asymmetric multifractality of gold and oil prices. Resources Policy, 69, 101829. [Google Scholar] [CrossRef]
- Mnif, E., Jarboui, A., & Mouakhar, K. (2020). How the cryptocurrency market has performed during COVID-19? A multifractal analysis. Finance Research Letters, 36, 101647. [Google Scholar] [CrossRef]
- Naeem, M. A., Bouri, E., Peng, Z., Shahzad, S. J. H., & Vo, X. V. (2021). Asymmetric efficiency of cryptocurrencies during COVID-19. Physica A: Statistical Mechanics and Its Applications, 565, 125562. [Google Scholar] [CrossRef] [PubMed]
- Peters, R. T., & De Vilder, R. G. (2006). Testing the continuous semimartingale hypothesis for the S&P 500. Journal of Business & Economic Statistics, 24(4), 444–454. [Google Scholar]
- Raza, S. A., Shah, N., & Suleman, M. T. (2024). A multifractal detrended fluctuation analysis of Islamic and conventional financial markets efficiency during the COVID-19 pandemic. International Economics, 177, 100463. [Google Scholar] [CrossRef]
- Saâdaoui, F. (2023). Skewed multifractal scaling of stock markets during the COVID-19 pandemic. Chaos, Solitons & Fractals, 170, 113372. [Google Scholar]
- Shen, N., & Chen, J. Y. (2022). Multifractal analysis of the impact of COVID-19 on NASDAQ, CIOPI, and WTI crude oil market. Fluctuation and Noise Letters, 21(4), 2250041. [Google Scholar] [CrossRef]
- Takaishi, T. (2018). Statistical properties and multifractality of Bitcoin. Physica A, 506, 507–519. [Google Scholar] [CrossRef]
- Takaishi, T. (2020). Rough volatility of Bitcoin. Finance Research Letters, 32, 101379. [Google Scholar] [CrossRef]
- Takaishi, T. (2021). Time-varying properties of asymmetric volatility and multifractality in Bitcoin. PLoS ONE, 16(2), e0246209. [Google Scholar] [CrossRef] [PubMed]
- Takaishi, T. (2022a). Hurst exponent and Multifractal Properties in the Time Series of Bitcoin Trading Volume. International Journal of Engineering Research and Applications, 12(11), 24–29. [Google Scholar]
- Takaishi, T. (2022b). Time evolution of market efficiency and multifractality of the Japanese stock market. Journal of Risk and Financial Management, 15(1), 31. [Google Scholar] [CrossRef]
- Takaishi, T. (2025). Multifractality and sample size influence on Bitcoin volatility patterns. Finance Research Letters, 74, 106683. [Google Scholar] [CrossRef]
- Takaishi, T., & Adachi, T. (2020). Market efficiency, liquidity, and multifractality of Bitcoin: A dynamic study. Asia-Pacific Financial Markets, 27, 145–154. [Google Scholar] [CrossRef]
- Urquhart, A. (2016). The inefficiency of Bitcoin. Economics Letters, 148, 80–82. [Google Scholar] [CrossRef]
- Wang, J., Shao, W., & Kim, J. (2020). Analysis of the impact of COVID-19 on the correlations between crude oil and agricultural futures. Chaos, Solitons & Fractals, 136, 109896. [Google Scholar]
- Wang, J., & Wang, X. (2021). COVID-19 and financial market efficiency: Evidence from an entropy-based analysis. Finance Research Letters, 42, 101888. [Google Scholar] [CrossRef]
- Wang, Y., Liu, L., & Gu, R. (2009). Analysis of efficiency for Shenzhen stock market based on multifractal detrended fluctuation analysis. International Review of Financial Analysis, 18(5), 271–276. [Google Scholar] [CrossRef]
- Wei, W. C. (2018). Liquidity and market efficiency in cryptocurrencies. Economics Letters, 168, 21–24. [Google Scholar] [CrossRef]
- Zitis, P. I., Kakinaka, S., Umeno, K., Hanias, M. P., Stavrinides, S. G., & Potirakis, S. M. (2023). Investigating dynamical complexity and fractal characteristics of Bitcoin/US Dollar and Euro/US Dollar exchange rates around the COVID-19 outbreak. Entropy, 25(2), 214. [Google Scholar] [CrossRef] [PubMed]
- Zumbach, G. (2003). Volatility processes and volatility forecast with longmemory. Quantitative Finance, 4(1), 70. [Google Scholar]
- Zumbach, G. (2009). Time reversal invariance in finance. Quantitative Finance, 9(5), 505–515. [Google Scholar] [CrossRef]
- Zunino, L., Tabak, B. M., Figliola, A., Pérez, D., Garavaglia, M., & Rosso, O. (2008). A multifractal approach for stock market inefficiency. Physica A, 387(26), 6558–6566. [Google Scholar] [CrossRef]

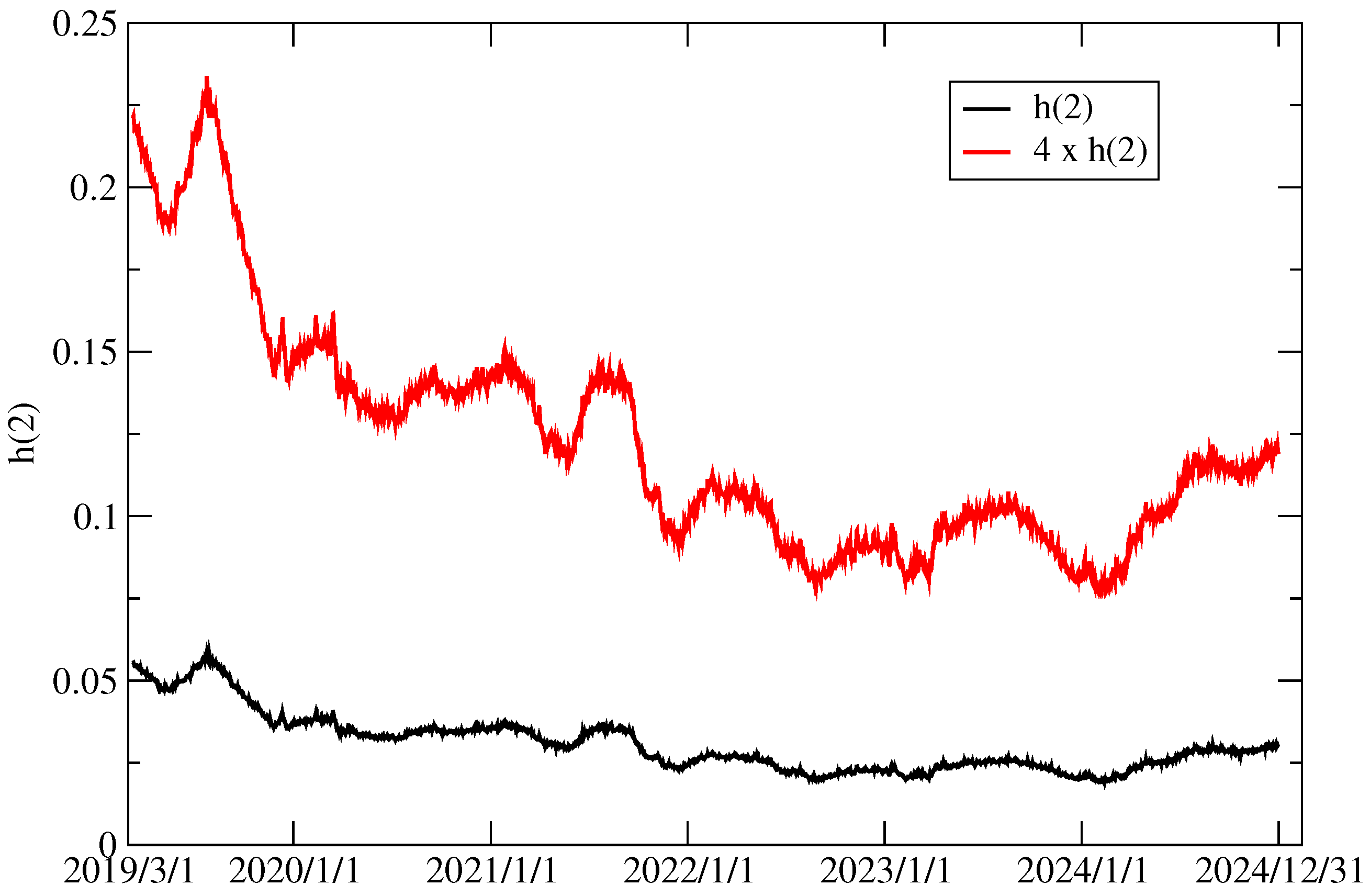
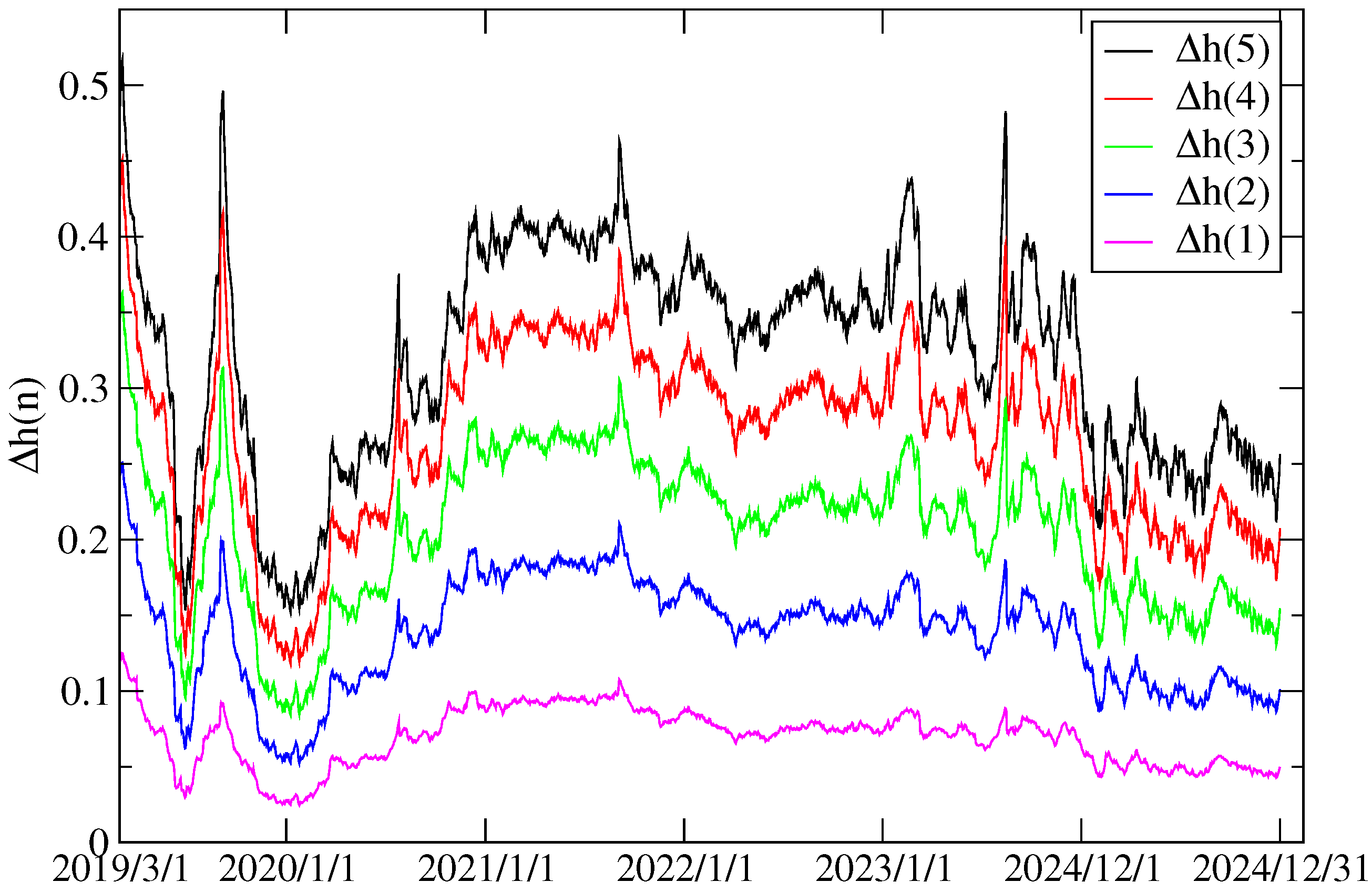
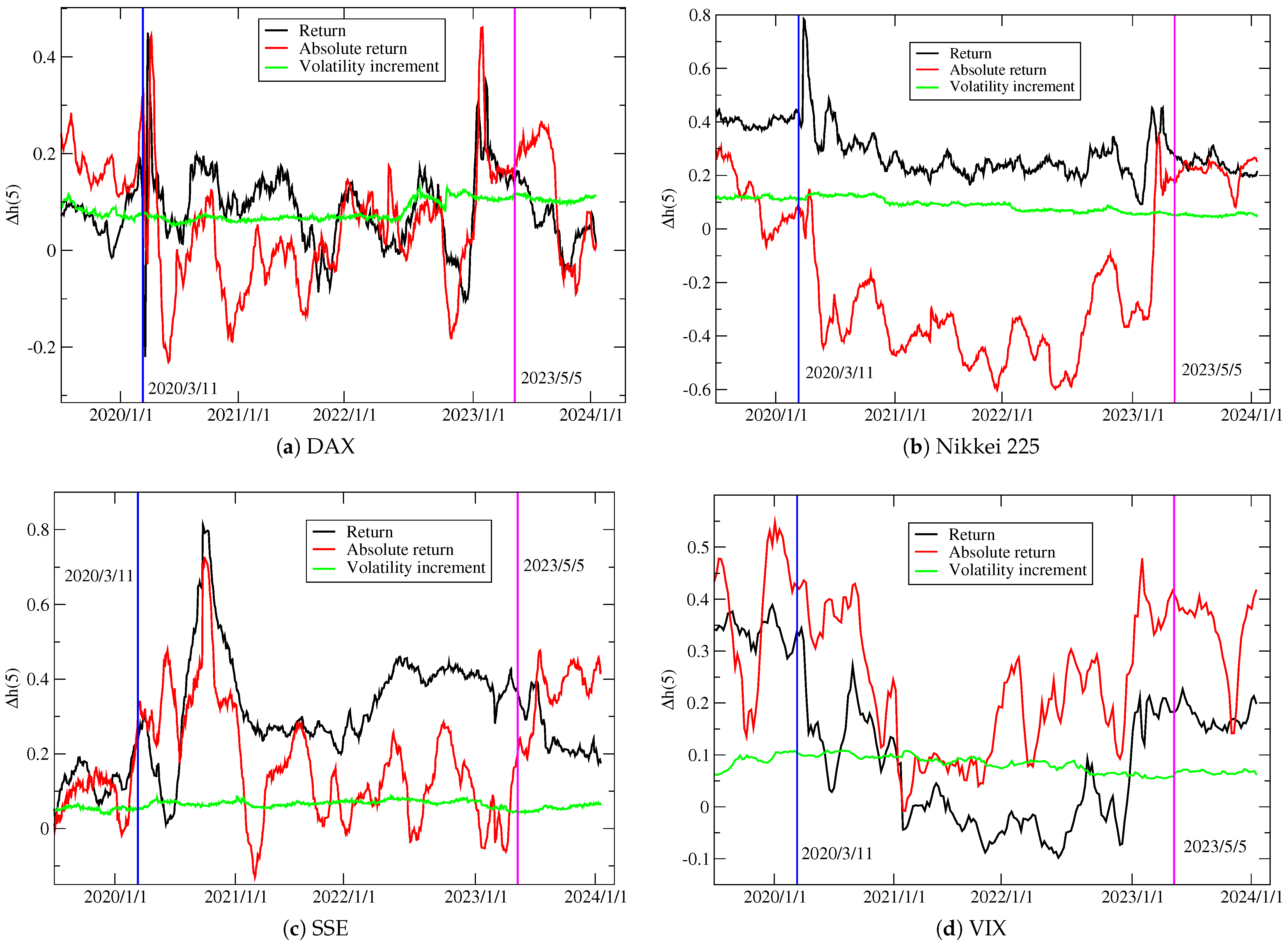
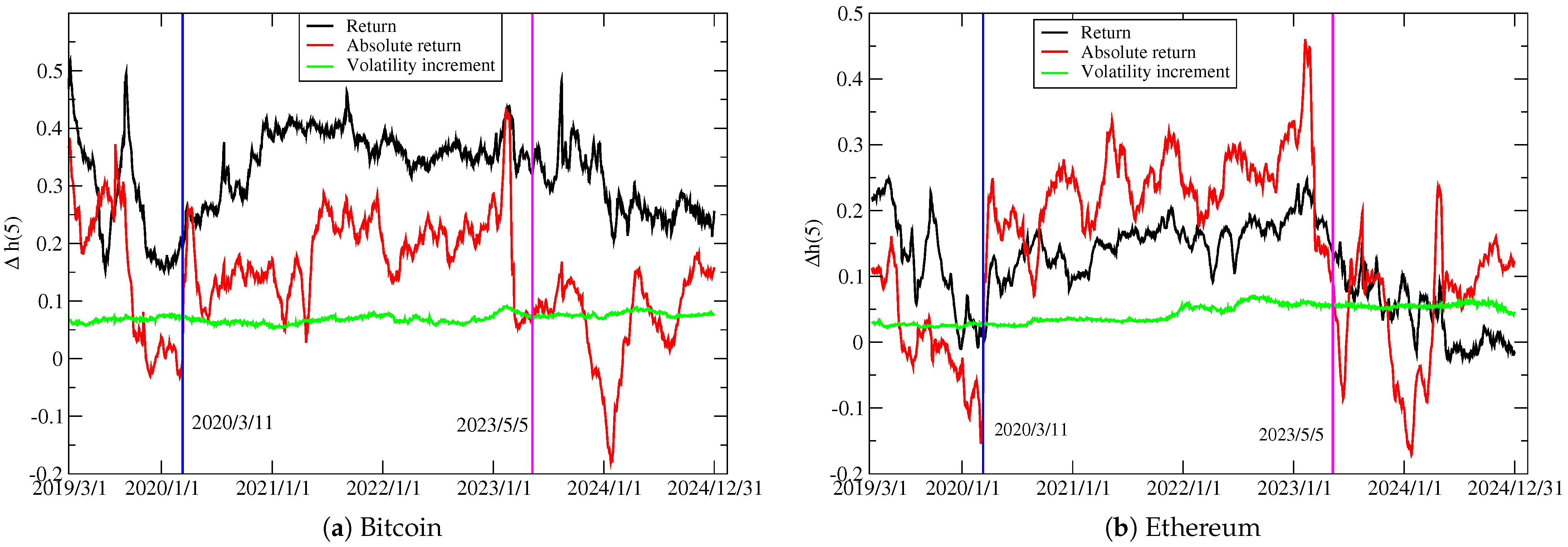
| Mean | Variance | Kurtosis | Skewness | ||
|---|---|---|---|---|---|
| (a) | DAX | 8.3(1.6) | −0.28(14) | ||
| Nikkei 225 | 8.6(2.3) | −0.3(1) | |||
| SSE | |||||
| VIX | 9(2) | 0.96(20) | |||
| Bitcoin | 16(10) | −0.80(75) | |||
| Ethereum | |||||
| (b) | DAX | 14(3) | 2.6(3) | ||
| Nikkei 225 | 17(6) | 2.7(7) | |||
| SSE | 13(1) | 2.6(1) | |||
| VIX | 20(6) | 2.8(4) | |||
| Bitcoin | 33(24) | 3.4(1.2) | |||
| Ethereum | 24(14) | ||||
| (c) | DAX | 2.6(1) | 4.36(18) | ||
| Nikkei 225 | 2.70(7) | 4.6(1) | |||
| SSE | 2.95(11) | 4.4(3) | |||
| VIX | 3.9(1) | ||||
| Bitcoin | 2.86(7) | 4.2(3) | |||
| Ethereum | 2.6(1) | 3.58(17) |
| Period | Bitcoin | Ethereum |
|---|---|---|
| 1 January 2017–31 December 2019 (before COVID-19) | 0.578 | 0.605 |
| 1 January2020–30 December 2020 (during COVID-19) | 0.493 | 0.561 |
| DAX | Nikkei 225 | SSE | VIX | Bitcoin | Ethereum | |
|---|---|---|---|---|---|---|
| Returns | negative | ◯ | × | positive | × | × |
| Returns | ◯ | ◯ | negative | positive | negative | negative |
| AR | negative | negative | negative | negative | × | × |
| AR | ◯ | negative | ∆ | positive | ∆ | negative |
| VI | × | × | × | × | × | × |
| VI | × | × | × | × | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takaishi, T. Impact of the COVID-19 Pandemic on the Financial Market Efficiency of Price Returns, Absolute Returns, and Volatility Increment: Evidence from Stock and Cryptocurrency Markets. J. Risk Financial Manag. 2025, 18, 237. https://doi.org/10.3390/jrfm18050237
Takaishi T. Impact of the COVID-19 Pandemic on the Financial Market Efficiency of Price Returns, Absolute Returns, and Volatility Increment: Evidence from Stock and Cryptocurrency Markets. Journal of Risk and Financial Management. 2025; 18(5):237. https://doi.org/10.3390/jrfm18050237
Chicago/Turabian StyleTakaishi, Tetsuya. 2025. "Impact of the COVID-19 Pandemic on the Financial Market Efficiency of Price Returns, Absolute Returns, and Volatility Increment: Evidence from Stock and Cryptocurrency Markets" Journal of Risk and Financial Management 18, no. 5: 237. https://doi.org/10.3390/jrfm18050237
APA StyleTakaishi, T. (2025). Impact of the COVID-19 Pandemic on the Financial Market Efficiency of Price Returns, Absolute Returns, and Volatility Increment: Evidence from Stock and Cryptocurrency Markets. Journal of Risk and Financial Management, 18(5), 237. https://doi.org/10.3390/jrfm18050237






