Construction of an Optimal Portfolio of Gold, Bonds, Stocks and Bitcoin: An Indonesian Case Study
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
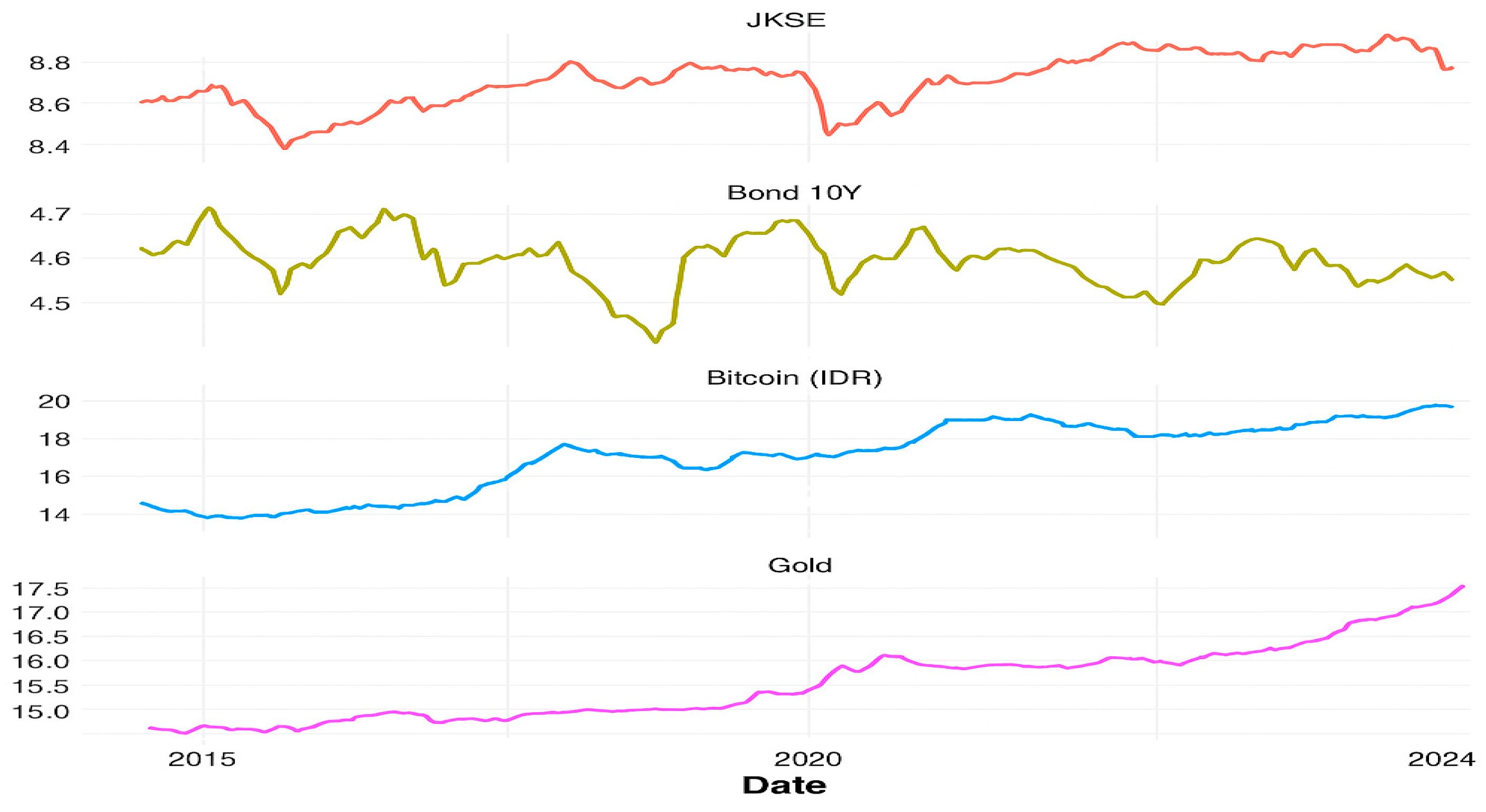
- Equity data (JKSE), gold denominated in Indonesian Rupiah (IDR), and Indonesian 10-year government bonds, retrieved from http://www.investing.com (accessed on 17 April 2023).
- Bitcoin (BTC) data, converted into IDR, obtained from https://www.coindesk.com/price/BTC/ (accessed on 17 April 2023).
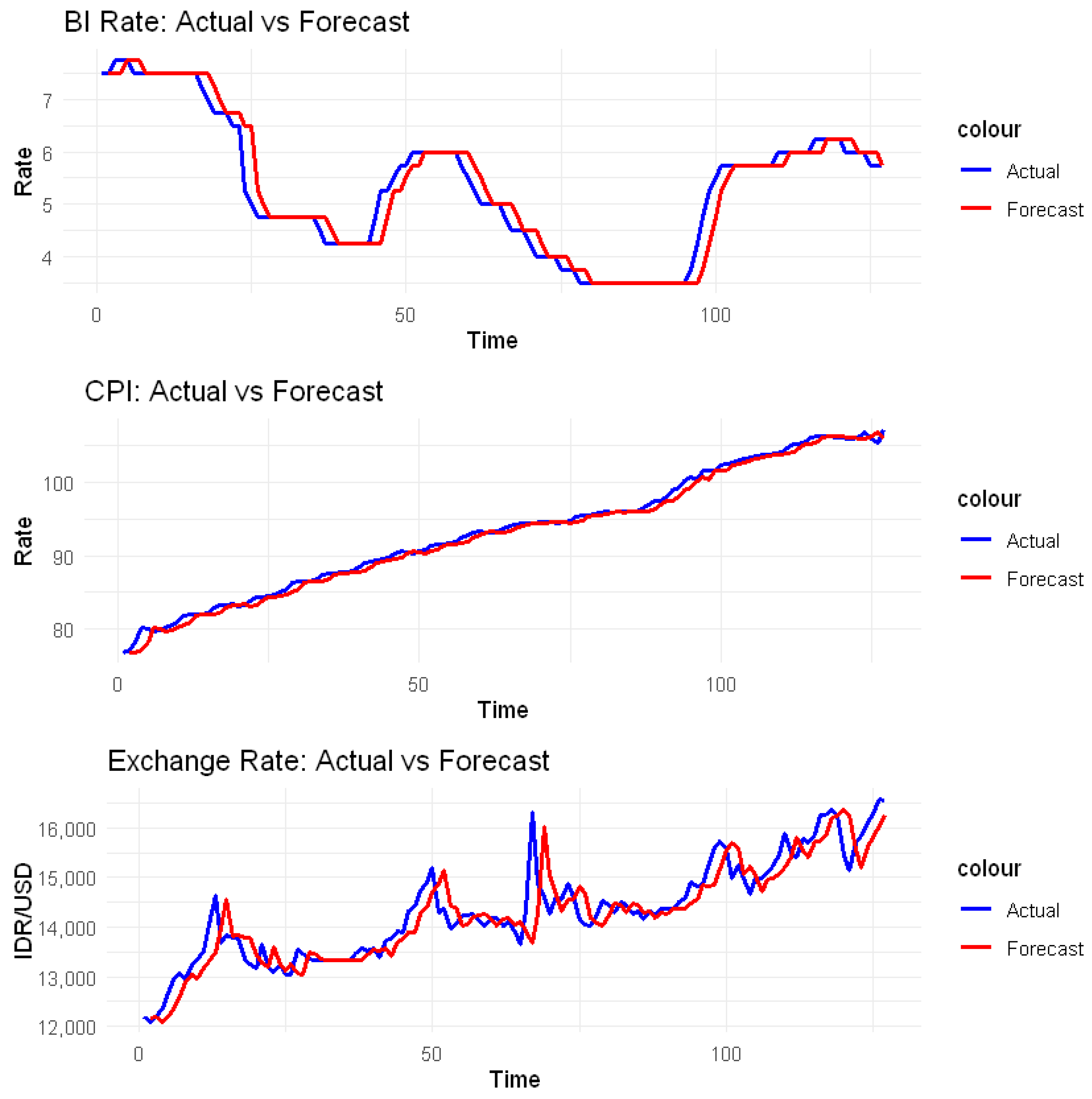
- Inflation data (Inf), collected from https://www.bps.go.id (accessed on 17 April 2023).
- Exchange rate (Exc) and Bank Indonesia interest rate (SBI) data, downloaded from the official Bank Indonesia website https://www.bi.go.id (accessed on 17 April 2023).
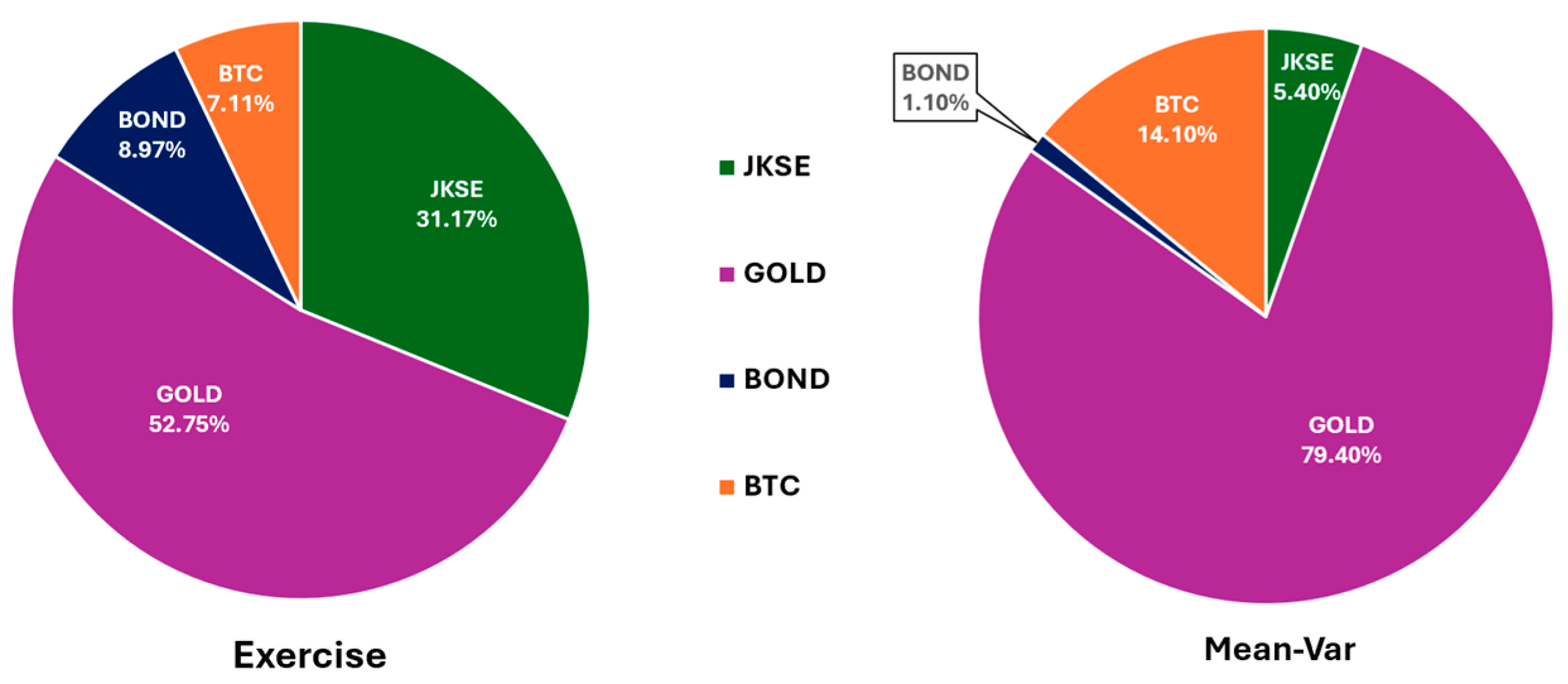
- Exercise Portfolio: The portfolio weights are determined by the expected returns and beta factors of each asset , which are derived from the mean and variance equations in the EGARCH(1,1) model. A set of assumptions has been established, first criteria is the sum of all asset weights equals 1, formulated by , where is the weight of asset. Three separate equations are constructed based on the macroeconomic beta factors of each asset. These equations are formulated under the second criterion that each asset exhibits no sensitivity to systematic risk factors, formulated by . The weights of each asset relevant to these three equations are then computed using the Gauss-Jordan elimination algorithm. A portfolio exercise is deemed valid if the expected return exceeds the threshold of one, formulated by .
- Optimal Mean–VaR Portfolio: This approach optimizes asset weights to minimize the Value-at-Risk (VaR) for a given target return level. Here, denotes the portfolio’s Value-at-Risk at the confidence level . The Mean–VaR portfolio is optimized using the Differential Evolution algorithm, which has proven highly effective in addressing non-convex optimization problems such as VaR minimization.
- The Kupiec test, also known as the Proportion of Failures (POF) test, evaluates whether the observed exception rate is statistically consistent with the expected confidence level . The test is formulated as a likelihood ratio test:where represents the number of observed VaR exceptions and denotes the total number of observations in the testing period then is the empirical exception rate. Under the null hypothesis that the true probability of exceptions equals , the test statistic follows a chi-squared distribution with one degree of freedom. The null hypothesis is rejected at the significance level (commonly 5%) if , indicating that the VaR model is misspecified. The confidence level used in this study is 95%, based on the Kupiec Test, where the number of exceedances must be less than or equal to 0.05. If the p-value exceeds 0.05, the null hypothesis H0 is accepted, indicating that the VaR model is valid; conversely, if the p-value is less than or equal to 0.05, the alternative hypothesis H1 is accepted, implying that the VaR model fails to demonstrate portfolio robustness against systematic factor fluctuations.
- The Basel Committee’s Traffic Light approach categorizes the adequacy of VaR models into three zones, based on the relationship between the observed and expected number of exceptions:
- Green Zone: The model is considered acceptable. For a 95% VaR, this corresponds to an observed exception rate not exceeding 1.2 times the expected level.
- Yellow Zone: The model is deemed questionable and subject to supervisory scrutiny. For a 95% VaR, this corresponds to an observed exception rate between 1.2 and 1.6 times the expected level.
- Red Zone: The model is rejected as inadequate. For a 95% VaR, this corresponds to an observed exception rate exceeding 1.6 times the expected level.
4. Empirical Result and Discussion
Descriptive Analysis of Data
| Asset | ER | Std Dev | Exercise | Mean Var | ||||
|---|---|---|---|---|---|---|---|---|
| Weight | ERp | Std Dev | Weight | ERp | Std Dev | |||
| JKSE | 0.002869 | 0.056300 | 0.311710 | 0.000894 | 0.017549 | 0.054000 | 0.000155 | 0.003040 |
| Gold | 0.004896 | 0.045840 | 0.527500 | 0.002583 | 0.024181 | 0.794000 | 0.003887 | 0.036397 |
| Bond | 0.000671 | 0.037560 | 0.089700 | 0.000060 | 0.003369 | 0.011000 | 0.000007 | 0.000413 |
| BTC | 0.063667 | 0.270210 | 0.071100 | 0.004527 | 0.019212 | 0.141000 | 0.008977 | 0.038100 |
| Total | 1 | 0.008063 | 0.070310 | 1 | 0.013026 | 0.077949 | ||
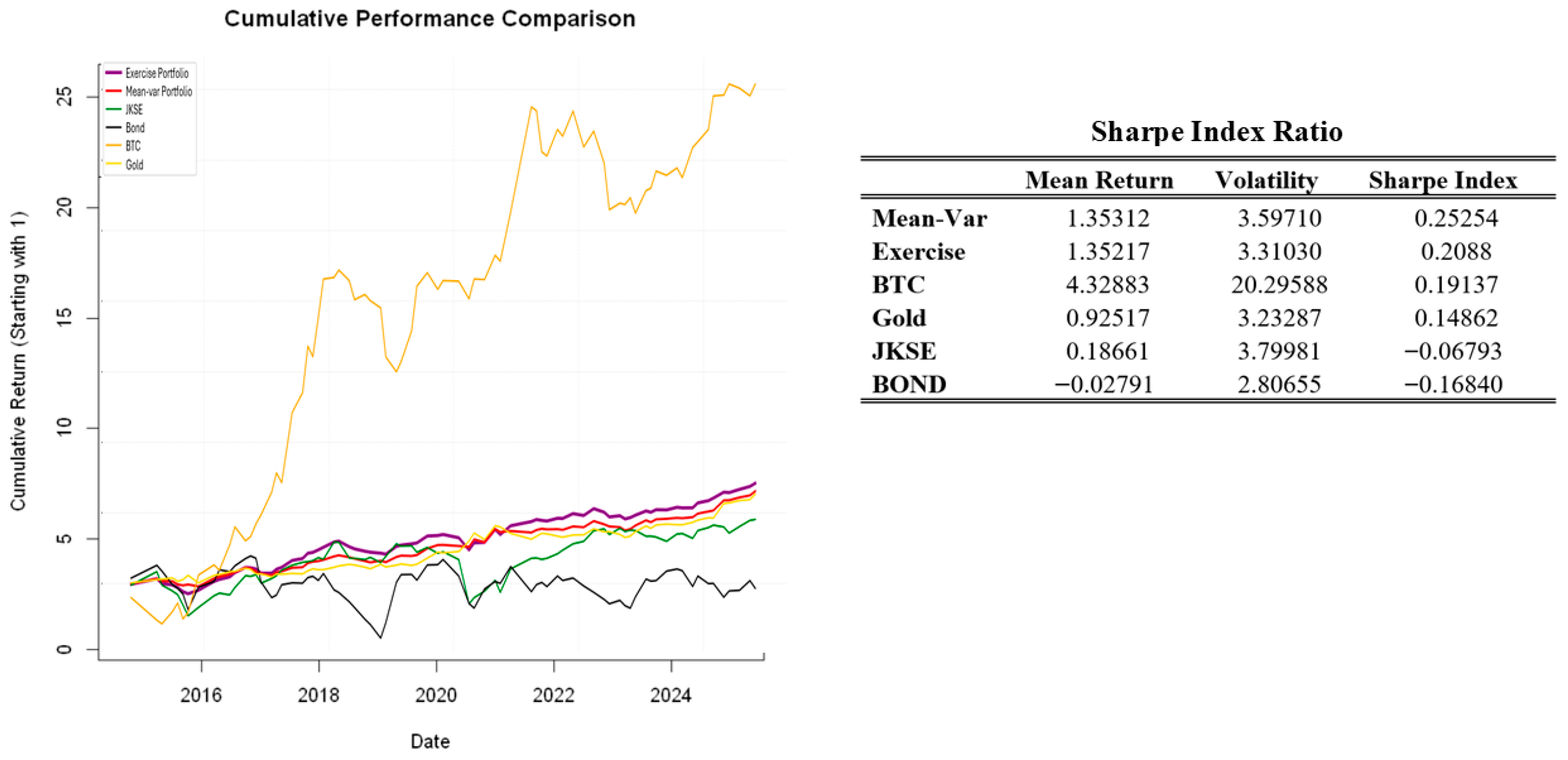
5. Conclusions and Implications
6. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Adrian, T., Crump, R. K., & Vogt, E. (2015). Nonlinearity and flight to safety in the risk-return trade-off for stocks and bonds. The Journal of The American Finance Association, 74(4), 2019. [Google Scholar]
- Aftab, M., Shah, S. Z. A., & Ismail, I. (2019). Does gold act as a hedge or a safe haven against equity and currency in Asia? Global Business Review, 20(1), 105–118. [Google Scholar] [CrossRef]
- Ampountolas, A. (2024). Enhancing forecasting accuracy in commodity and financial markets: Insights from GARCH and SVR models. International Journal of Financial Studies, 12(3), 59. [Google Scholar] [CrossRef]
- Amtiran, P. Y., Indiastuti, R., Nidar, S. R., & Masyita, D. (2017). Macroeconomic factors and stock returns in APT framework. International Journal of Economics and Management, 11(S1), 197–206. [Google Scholar]
- Arshad, S., Vu, T. H. N., Warn, T. S., & Ying, L. M. (2023). The hedging ability of gold, silver and bitcoin against inflation in asean countries. Asian Academy of Management Journal of Accounting and Finance, 19(1), 121–153. [Google Scholar] [CrossRef]
- Arshanapalli, B., d’Ouville, E., Fabozzi, F., & Switzer, L. (2006). Macroeconomic news effects on conditional volatilities in the bond and stock markets. Applied Financial Economics, 16(5), 377–384. [Google Scholar] [CrossRef]
- Baur, D. G., & Lucey, B. M. (2010). Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financial Review, 45(2), 217–229. [Google Scholar] [CrossRef]
- Baur, D. G., & McDermott, T. K. (2010). Is gold a safe haven? International evidence. Journal of Banking and Finance, 34(8), 1886–1898. [Google Scholar] [CrossRef]
- Beckmann, J., Berger, T., & Czudaj, R. (2015). Does gold act as a hedge or a safe haven for stocks? Rurh economic paper No. 502. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2561224 (accessed on 2 February 2024).
- Bulut, L., & Rizvanoghlu, I. (2020). Is gold a safe haven? The international evidence revisited. Acta Oeconomica, 70(4), 531–549. [Google Scholar] [CrossRef]
- Campbell, J. Y., Lo, A. W., & MacKinlay, A. C. (1997). The econometrics of financial markets. Macroeconomic Dynamics, 2(4), 559–562. [Google Scholar] [CrossRef]
- Capie, F., Mills, T. C., & Wood, G. (2005). Gold as a hedge against the dollar. Journal of International Financial Markets, Institutions and Money, 15(4), 343–352. [Google Scholar] [CrossRef]
- Chen, Y. F., Chiang, T. C., & Lin, F. L. (2023). Inflation, equity market volatility, and bond prices: Evidence from G7 countries. Risks, 11(11), 191. [Google Scholar] [CrossRef]
- Chinzara, Z. (2011). Macroeconomic uncertainty and conditional stock market volatility in South Africa. South African Journal of Economics, 79(1), 27–49. [Google Scholar] [CrossRef]
- Cont, R. (2001). Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance, 1(2), 223–236. [Google Scholar] [CrossRef]
- Corbet, S., Larkin, C., Lucey, B. M., Meegan, A., & Yarovaya, L. (2020). The impact of macroeconomic news on Bitcoin returns. European Journal of Finance, 26(14), 1396–1416. [Google Scholar] [CrossRef]
- Diyah Miasary, S. (2023). Penentuan Return Saham Syariah dengan Arbitrage Pricing Theory (APT) melalui Pendekatan Vector Autoregressive (VAR). Jurnal Axioma: Jurnal Matematika dan Pembelajaran, 8(2), 124–134. [Google Scholar] [CrossRef]
- Global Crypto Adoption Index. (2024). The 2024 global adoption index: Central & Southern Asia and Oceania (CSAO) region leads the world in terms of global cryptocurrency adoption. Available online: https://www.chainalysis.com/blog/2024-global-crypto-adoption-index/ (accessed on 2 February 2024).
- Heo, W., & Kim, E. (2025). Smoothing the subjective financial risk tolerance: Volatility and market implications. Mathematics, 13(4), 680. [Google Scholar] [CrossRef]
- Kaczmarek, T., Będowska-Sójka, B., Grobelny, P., & Perez, K. (2022). False safe haven assets: Evidence from the target volatility strategy based on recurrent neural network. Research in International Business and Finance, 60(c), 101610. [Google Scholar] [CrossRef]
- Köse, N., Yildirim, H., Ünal, E., & Lin, B. (2024). The Bitcoin price and Bitcoin price uncertainty: Evidence of Bitcoin price volatility. Journal of Futures Markets, 44(4), 673–695. [Google Scholar] [CrossRef]
- Maghrebi, N., Holmes, M. J., & Pentecost, E. J. (2006). Are there asymmetries in the relationship between exchange rate fluctuations and stock market volatility in pacific basin countries? Review of Pacific Basin Financial Markets and Policies, 9(2), 229–256. [Google Scholar] [CrossRef]
- Markowitz, H. (1952). Portofolio selection. The Journal of Finance, 7(1), 77–91. [Google Scholar]
- Mužić, I., & Gržeta, I. (2022). Expectations of macroeconomic news announcements: Bitcoin vs. traditional assets. Risks, 10(6), 123. [Google Scholar] [CrossRef]
- Nelson, D. B. (1991). Conditional heteroskedasticity in asset returns: A new approach. Econometrica, 59(2), 347–370. [Google Scholar] [CrossRef]
- Nieppola, O. (2009). Backtesting value-at-risk models. Journal of Financial Econometrics, 9(2), 314–343. [Google Scholar]
- Nurbarani, B. S., & Soepriyanto, G. (2022). Determinants of investment decision in cryptocurrency: Evidence from Indonesian investors. Universal Journal of Accounting and Finance, 10(1), 254–266. [Google Scholar] [CrossRef]
- Paule-Vianez, J., Prado-Román, C., & Gómez-Martínez, R. (2020). Economic policy uncertainty and Bitcoin. Is Bitcoin a safe-haven asset? European Journal of Management and Business Economics, 29(3), 347–363. [Google Scholar] [CrossRef]
- Roll, R., & Ross, S. A. (1995). The arbitrage pricing theory approach to strategic portfolio planning. Financial Analysts Journal, 51(1), 122–131. [Google Scholar] [CrossRef]
- Selmi, R., Mensi, W., Hammoudeh, S., & Bouoiyour, J. (2018). Is Bitcoin a hedge, a safe haven or a diversifier for oil price movements? A comparison with gold. Energy Economics, 74, 787–801. [Google Scholar] [CrossRef]
- Terraza, V., Boru İpek, A., & Rounaghi, M. M. (2024). The nexus between the volatility of bitcoin, gold, and american stock markets during the COVID-19 pandemic: Evidence from VAR-DCC-EGARCH and ANN models. Financial Innovation, 10(1), 22. [Google Scholar] [CrossRef]
- Zhu, Y., Taasim, S. I., & Daud, A. (2025). Volatility modeling and tail risk estimation of financial assets: Evidence from gold, oil, bitcoin, and stocks for selected markets. Risks, 13(7), 138. [Google Scholar] [CrossRef]
| Author | Asset | Economic Macro | Method | Result |
|---|---|---|---|---|
| Arshanapalli et al. (2006) and Chen et al. (2023) | Bond and stock | Interest rate, inflation, PPI | GARCH | The GARCH model is capable of capturing asymmetric effects in stock and bond markets, which are characterized by heteroskedasticity and volatility clustering. |
| Mužić and Gržeta (2022) | Gold, bond and BTC | Inflation, NFP, Initial Jobless Claims, Retail Sales and IPI | GARCH and EGARCH | Bonds are highly sensitive to shocks, in contrast to Bitcoin (BTC), which exhibits more varied responses to market disturbances. Gold, on the other hand, demonstrates greater stability and consistently displays the attributes of a safe-haven asset. |
| Köse et al. (2024) | BTC | EPU, goldprice and exchange rate | GARCH | BTC responds to shocks with heterogeneous reactions, reflected in its pronounced volatility. |
| Terraza et al. (2024) | BTC, gold and stock | Corona Virus spread | VAR-DCC-EGARCH | BTC exhibits significant volatility persistence compared to equities, whereas gold maintains relative stability with more moderate and consistent levels of volatility. |
| Arshad et al. (2023) | Gold, silver, BTC | CPI | Student-t EGARCH(1,1) and Quantile Regression | All three assets function as hedges and safe-haven assets, with their roles contingent upon prevailing return levels and inflation conditions. |
| Chinzara (2011) | Stocks | IPI, CPI, money supply, exchange rate, oil price, T-Bills and gold price | AR-GARCH, EGARCH, TARCH and VAR | Treasury Bill and exchange rate volatility are identified as the most significant drivers of stock market volatility. |
| Chen et al. (2023) | Stocks and Bonds | CPI | VAR, FAVAR and GARCH | Inflation shocks substantially increase equity volatility, while bond prices tend to decline in response to similar events, reflecting rising yield expectations. |
| Aftab et al. (2019) | Stocks and gold | Exchange rate | DCC-MGARCH | Asian equities exhibit moderate volatility, yet their respective stock markets are characterized by high overall volatility. |
| Ampountolas (2024) | Gold, stocks, commodities | Financial marketevent studies | SGARCH, EGARCH, GJR-GARCH, and FI-GARCH | Gold displays persistent and long-term volatility clustering, as indicated by SGARCH modeling. |
| Zhu et al. (2025) | Stocks, BTC, oil and gold price | Volatility of assets | EGARCH, AR, Extreme Value Theory (EVT), rolling window estimation, and distribusi skewed heavy-tail. | Among the assets analyzed, gold consistently demonstrates the lowest volatility, in stark contrast to bitcoin, which is significantly more volatile. Equities in emerging markets have medium volatility levels, but these can escalate sharply in the wake of macroeconomic shocks. |
| F | |||||||
|---|---|---|---|---|---|---|---|
| JKSE | GOLD | BOND | BTC | SBI | EXC | INF | |
| Mean | 0.0019 | 0.0091 | −0.0004 | 0.0415 | −0.0278 | 0.0047 | 0.0051 |
| Median | 0.0059 | 0.006 | −0.0021 | 0.0504 | 0.0000 | 0.0054 | 0.0043 |
| Max | 0.0902 | 0.1041 | 0.1372 | 0.5316 | 1.0000 | 0.1606 | 0.0385 |
| Min | −0.1834 | −0.0728 | −0.0829 | −0.5328 | −1.5000 | −0.0967 | −0.0125 |
| Std.Dev | 0.0393 | 0.0384 | 0.0425 | 0.2108 | 0.0290 | 0.0027 | 0.0005 |
| Skew | −1.0751 | 0.3415 | 0.3903 | 0.3541 | −0.2686 | 0.4407 | 1.4608 |
| Kurtosis | 6.7681 | 2.418 | 4.1259 | 2.7492 | 5.3659 | 4.9582 | 6.7882 |
| JB | 392.23 | 167.75 | 391.04 | 117.59 | 1226.26 | 960.71 | 4767.96 |
| C | AR(1) | ||||
|---|---|---|---|---|---|
| 0.002869 * | −0.125316 | 0.001972 * | −0.589940 * | 0.806364 * | |
| 0.004896 | 0.194009 * | −0.00631 | 0.322278 * | −0.36786 | |
| 0.000671 | −0.054078 | −0.015253 * | −0.408052 * | −0.706907 * | |
| 0.063667 * | 0.034123 * | 0.010589 * | 0.709942 * | −2.642116 * |
| Asset | Variance Equation | AIC | LL | F-LM | ||||
|---|---|---|---|---|---|---|---|---|
| + | ||||||||
| −2.078196 * | −0.013922 | 0.698329 * | 0.684407 | 0.391663 * | −3.9713 | 261.1769 | 0.8791 | |
| 0.000000 | 0.000000 | 0.999000 * | 0.999000 | - | −4.0201 | 265.2742 | 0.2750 | |
| 0.000388 | −0.014624 | 0.994674 * | 0.989161 | 0.107711 * | −4.5090 | 295.3217 | 0.4409 | |
| −0.101840 * | 0.227942 * | 0.968559 ** | 1.104781 | −0.293953 * | −0.48007 | 39.48455 | 0.8961 | |
| Equation | Exercise Portfolio | Mean-Var Portfolio | |
|---|---|---|---|
| Mean | C | 0.007848 * | 0.010851 |
| AR(1) | 0.192558 ** | 0.081365 | |
| 0.001982 | 0.081365 | ||
| −0.000070 * | 0.156908 | ||
| −0.004875 | −0.566213 | ||
| Variance | −0.325847 | 0.000001 | |
| −0.156942 | 0.000000 | ||
| 0.566165 * | 0.999000 * | ||
| + | 0.409223 | 0.999000 | |
| 0.914650 * | - |
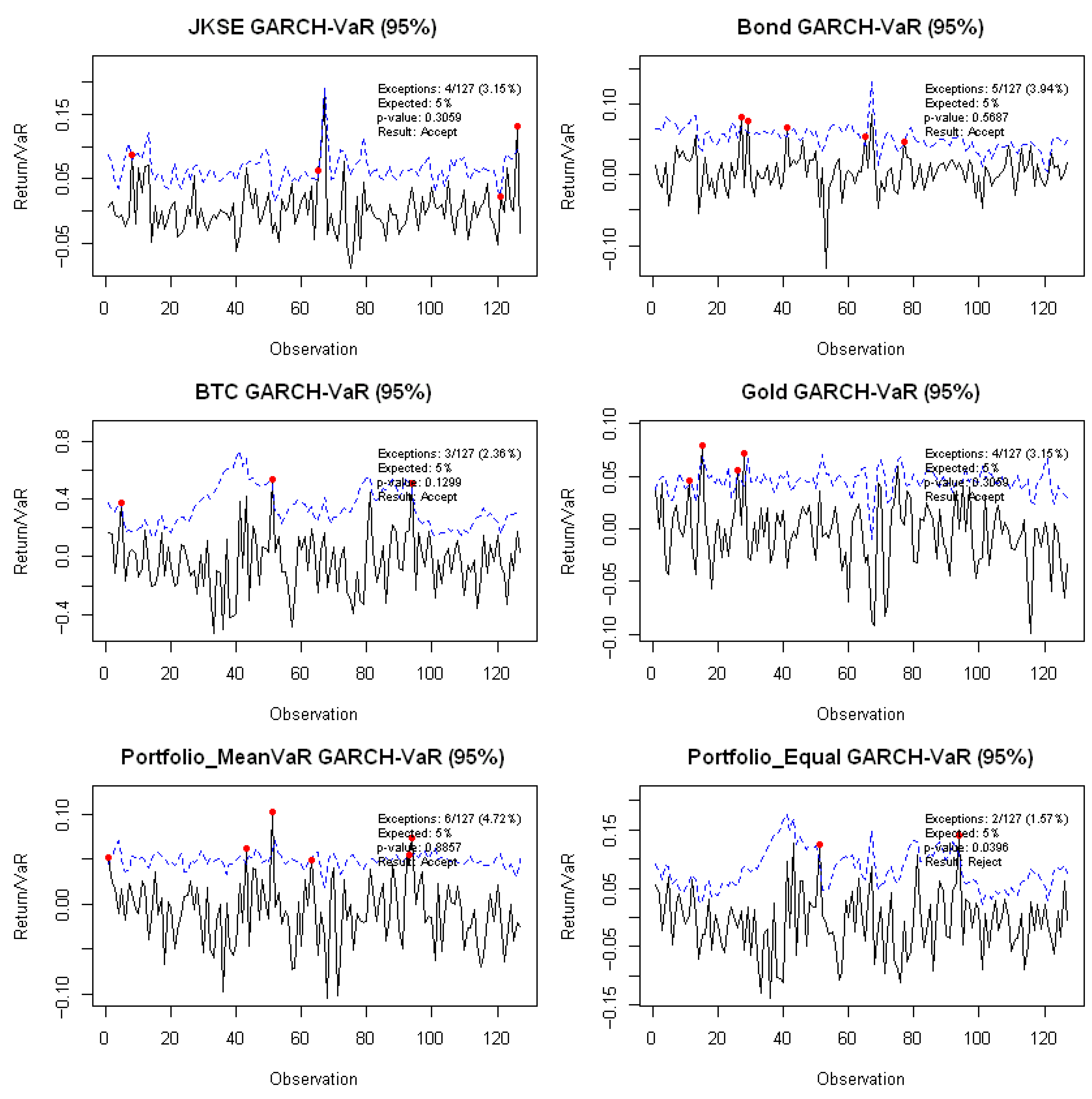
| Portfolio/Asset | Confidence Level | Number of Observation | Number of Exceptions | Test Outcome |
|---|---|---|---|---|
| JKSE | 95% | 127 | 4 | Green Zone |
| Bond | 95% | 127 | 5 | Green Zone |
| BTC | 95% | 127 | 3 | Green Zone |
| Gold | 95% | 127 | 4 | Green Zone |
| Mean-VaR Portfolio | 95% | 127 | 6 | Green Zone |
| Exercise Portfolio | 95% | 127 | 7 | Yellow Zone |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nia, V.M.; Siregar, H.; Sembel, R.; Zulbainarni, N. Construction of an Optimal Portfolio of Gold, Bonds, Stocks and Bitcoin: An Indonesian Case Study. J. Risk Financial Manag. 2025, 18, 668. https://doi.org/10.3390/jrfm18120668
Nia VM, Siregar H, Sembel R, Zulbainarni N. Construction of an Optimal Portfolio of Gold, Bonds, Stocks and Bitcoin: An Indonesian Case Study. Journal of Risk and Financial Management. 2025; 18(12):668. https://doi.org/10.3390/jrfm18120668
Chicago/Turabian StyleNia, Vera Mita, Hermanto Siregar, Roy Sembel, and Nimmi Zulbainarni. 2025. "Construction of an Optimal Portfolio of Gold, Bonds, Stocks and Bitcoin: An Indonesian Case Study" Journal of Risk and Financial Management 18, no. 12: 668. https://doi.org/10.3390/jrfm18120668
APA StyleNia, V. M., Siregar, H., Sembel, R., & Zulbainarni, N. (2025). Construction of an Optimal Portfolio of Gold, Bonds, Stocks and Bitcoin: An Indonesian Case Study. Journal of Risk and Financial Management, 18(12), 668. https://doi.org/10.3390/jrfm18120668






