Using Machine Learning to Detect Financial Statement Fraud: A Cross-Country Analysis Applied to Wirecard AG
Abstract
1. Introduction
2. Literature Review
- Foundations in FSF Research
- Foundations in ML Research
2.1. Definition of Terminology
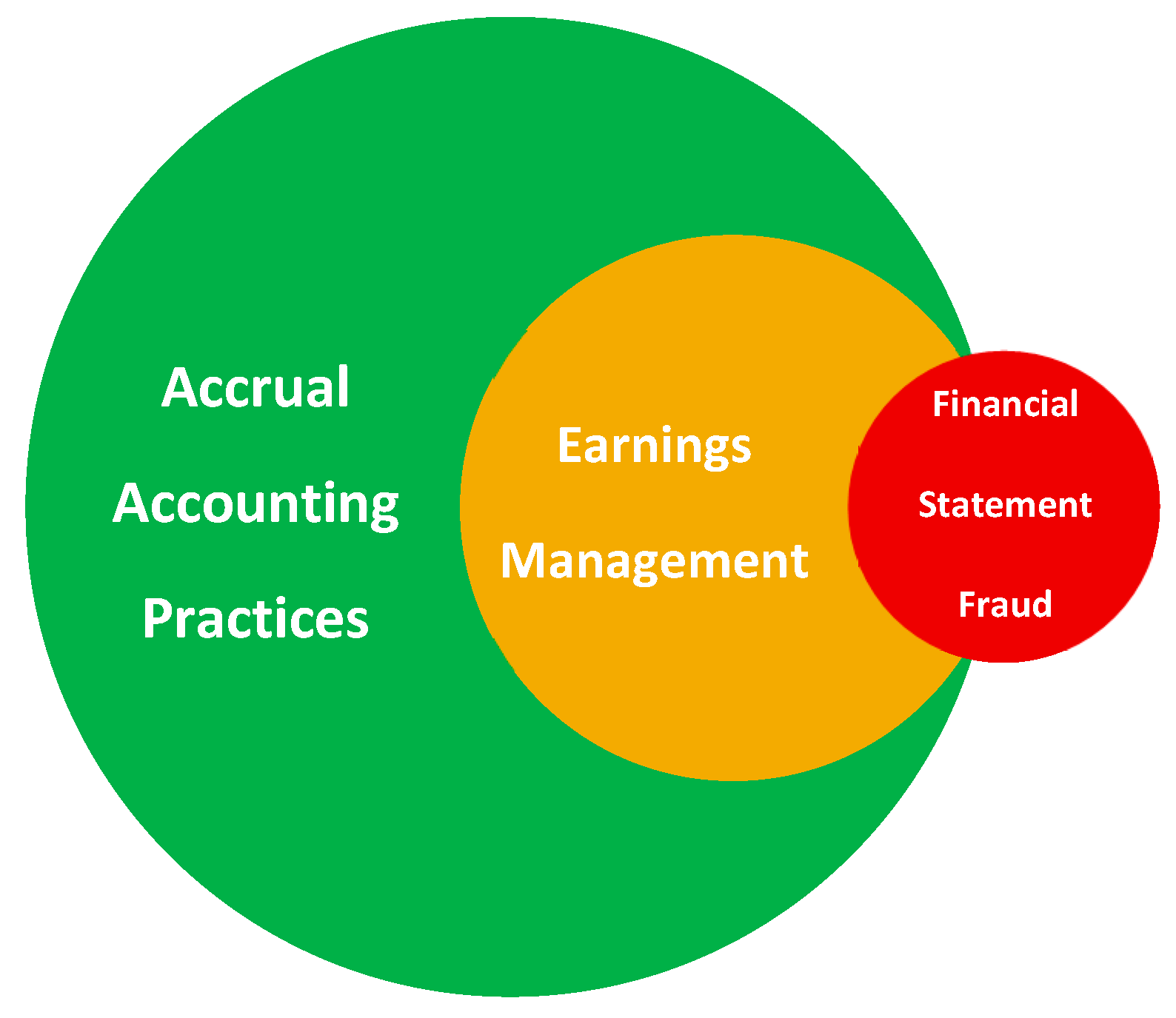
- Accrual Accounting Practices
- Earnings Management
- Financial Statement Fraud
2.2. Detecting FSF Through Financial Ratios
2.2.1. Altman Z-Score (1968)
- X1—Liquidity
- X2—Profitability
- X3—Productivity
- X4—Solvency
- X5—Efficiency
- Interpretation
- Benefits and Limitations
2.2.2. Beneish M-Score (1999)
- Days Sales in Receivables Index (DSRI)
- Gross Margin Index (GMI)
- Asset Quality Index (AQI)
- Sales Growth Index (SGI)
- Depreciation Index (DEPI)
- Sales General and Administrative Expenses Index (SGAI)
- Leverage Index (LVGI)
- Total Accruals to Total Assets (TATA)
- Interpretation
- Benefits and Limitations
2.2.3. Montier C-Score (2008)
- C1—A growing difference in net income and cash flow from operations
- C2—Days sales outstanding (DSO) is increasing
- C3—Growing days sales of inventory (DSI)
- C4—Increasing other current assets to revenues
- C5—Declines in depreciation relative to gross PPE
- C6—High total asset growth
2.2.4. Dechow F-Score (2011)
- rsstacc—RSST Accrual
- chrec—Change in Accounts Receivable
- chinv—Change in Inventory
- softassets—Percentage of Soft Assets
- chcs—Change in Cash Sales
- chroa—Change in Return on Assets
- issue—Actual Issuance
- Interpretation
- Benefits and Limitations
2.3. Detecting FSF Through Machine Learning
2.4. Hypothesis Development
3. Materials and Methods
3.1. Data
3.1.1. Financial Data
3.1.2. Fraud Data
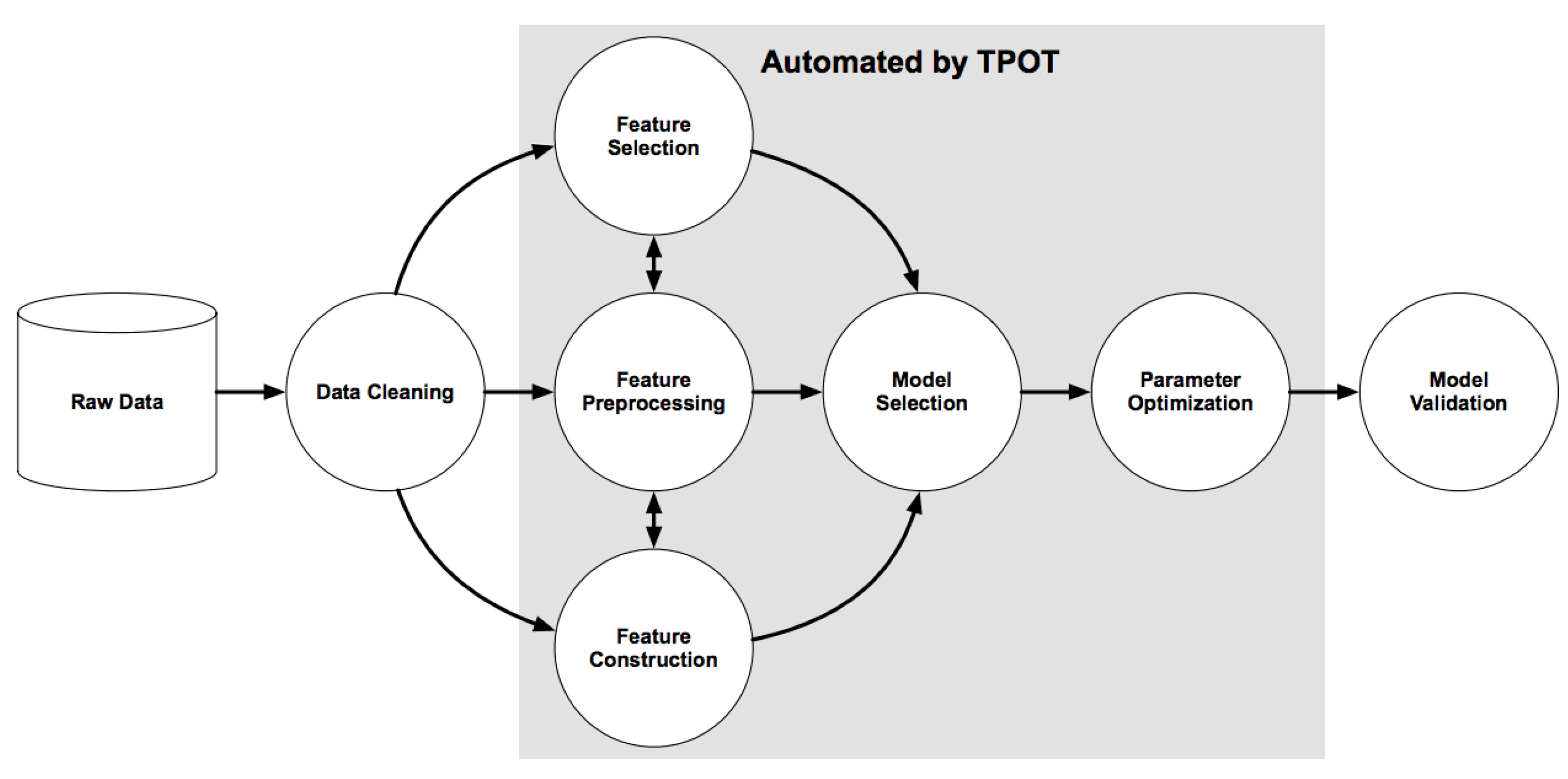
3.2. Machine Learning
3.2.1. Data Preparation
- Imbalance
- Missing Values and Outliers
3.2.2. Applying Machine-Learning Algorithms
4. Results
4.1. Model Accuracy (H1)
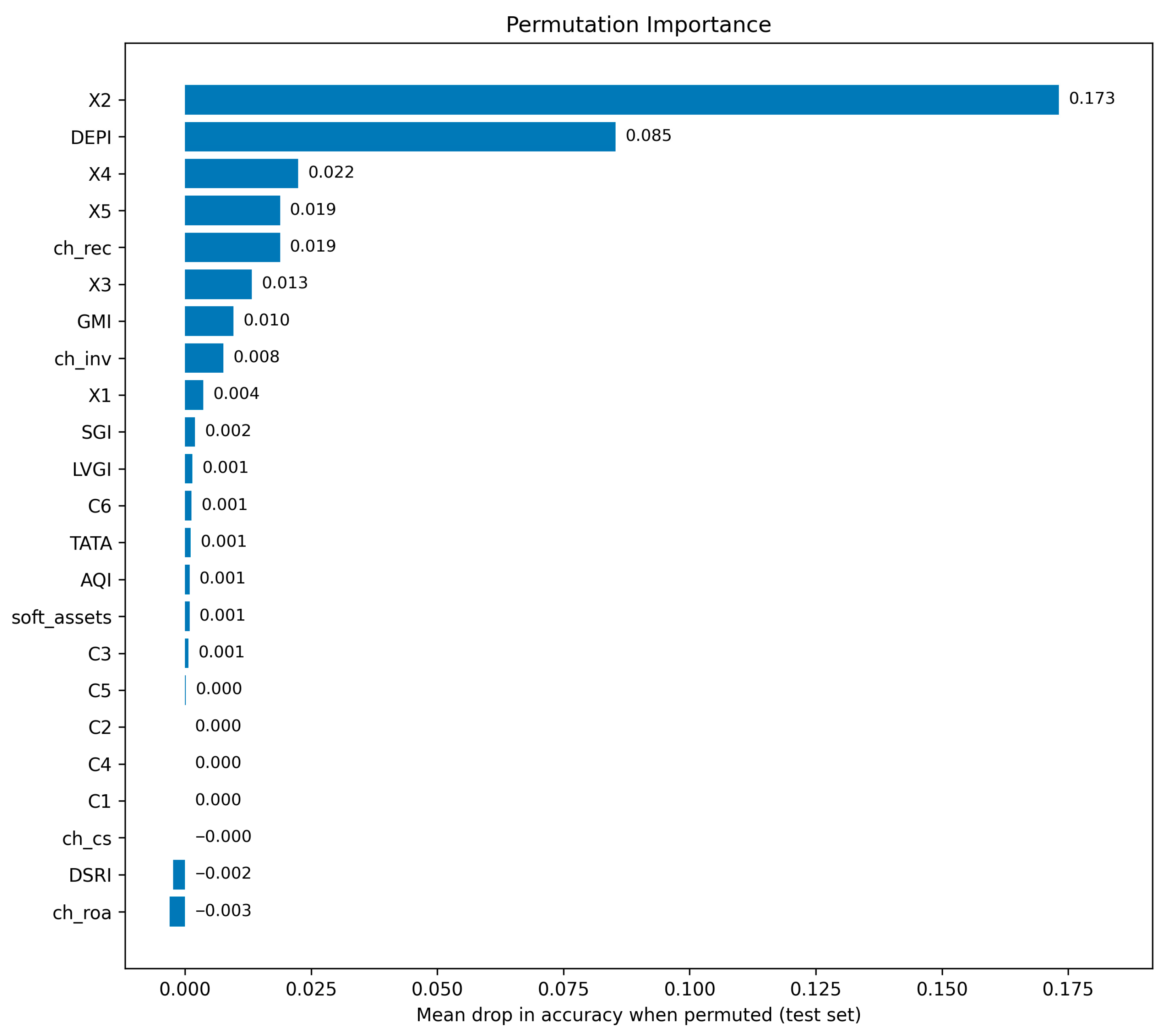
4.2. Wirecard Case Study (H2)
5. Discussion
5.1. Limitations
5.2. Future Research
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAER | Accounting and Auditing Enforcement Release |
| ANN | Artificial Neural Network |
| AUC | Area under the receiver operating characteristic curve |
| Auto-ML | Automatic Machine Learning |
| AQI | Asset Quality Index |
| BaFin | Bundesanstalt für Finanzdienstleistungsaufsicht |
| BBN | Bayesian Belief Network |
| BLR | Backward Logistic Regression |
| BLS | U.S. Bureau of Labor Statistics |
| BP-SVM | Biased-Penalty Linear Support Vector Machine |
| BQL | Bloomberg Query Language |
| CART | Classification and Regression Tree |
| CCE | Cash and cash equivalents |
| ch_cs | Change in Cash Sales |
| ch_inv | Change in Inventory |
| ch_rec | Change in Accounts Receivable |
| ch_roa | Change in Return on Assets |
| CV | Cross-validation |
| DA | Discriminant Analysis |
| DAX | Deutscher Aktienindex |
| DEPI | Depreciation Index |
| DSO | Days Sales Outstanding |
| DSI | Growing Days Sales of Inventory |
| DSRI | Days Sales in Receivables Index |
| DT | Decision Tree |
| DWD | Distance Weighted Discrimination |
| e.g., | “exempli gratia”/for example |
| EBIT | Earnings before interest and taxes |
| EC | Evolutionary Computation |
| ECB | European Central Bank |
| FED | Federal Reserve |
| FSF | Financial Statement Fraud |
| FLR | Forward Logistic Regression |
| GA | Genetic Algorithm |
| GBRT | Gradient Boosted Regression Trees |
| GLM | Generalized Linear Models |
| GMDH | Group Method Data Handling |
| GMI | Gross Margin Index |
| GP | Genetic Programming |
| IAS | International Accounting Standard |
| IASB | International Accounting Standards Board |
| ID3 | Iterative Dichotomiser 3 |
| IFRS | International Financial Reporting Standards |
| ISIN | International Securities Identification Number |
| ISYDNN | Incremental sum-of-years’-digit Weighted Average Neural Network |
| k-NN | k-Nearest Neighbors |
| LDA | Linear Discriminant Analysis |
| LMM | Large-Margin Methods |
| LR | Logistic Regression |
| LTD | Long-Term Debt |
| LVGI | Leverage Index |
| MDA | Multiple Discriminant Analysis |
| MLP | Multilayer Perceptron |
| N/A | Not available |
| PNN | Probabilistic Neural Network |
| PPE | Property, Plant and Equipment |
| PR | Probability Unit Regression |
| prob_FSF | Probability of Financial Statement Fraud |
| PSYDNN | Plain sum-of-years’-digit Weighted Average Neural Network |
| RBF | Radial Basis Function Neural Network |
| RF | Random Forest |
| rsst_acc | RSST Accrual |
| SEC | United States Securities and Exchange Commission |
| SG&A | Selling, General and Administrative Expenses |
| SGAI | Sales General and Administrative Expenses Index |
| SGI | Sales Growth Index |
| SHAP | SHapley Additive exPlanations |
| SPCNN | Simple Percentage Change Neural Network |
| SVM | Support Vector Machine |
| TATA | Total Accruals to Total Assets |
| TM | Text Mining |
| TPOT | Tree-based Pipeline Optimization Tool |
| TTF | Task-Technology Fit |
| U.S. | United States |
| USD | United States Dollar |
| US GAAP | United States Generally Accepted Accounting Principles |
| ∆FIN | Change in net financial assets |
| ∆NCO | Change in net non-current operating assets |
| ∆WC | Change in non-cash working capital |
References
- Abbasi, A., Albrecht, C., Vance, A., & Hansen, J. (2012). MetaFraud: A meta-learning framework for detecting financial fraud. MIS Quarterly, 36(4), 1293–1327. [Google Scholar] [CrossRef]
- Achmad, T., Ghozali, I., Helmina, M. R. A., Hapsari, D. I., & Pamungkas, I. D. (2023). Detecting fraudulent financial reporting using the fraud hexagon model: Evidence from the banking sector in Indonesia. Economies, 11(1), 5. [Google Scholar] [CrossRef]
- Aghghaleh, S. F., Mohamed, Z. M., & Rahmat, M. M. (2016). Detecting financial statement frauds in Malaysia: Comparing the abilities of Beneish and Dechow models. Asian Journal of Accounting and Governance, 7, 57–65. [Google Scholar] [CrossRef]
- Albizri, A., Appelbaum, D., & Rizzotto, N. (2019). Evaluation of financial statements fraud detection research: A multi-disciplinary analysis. International Journal of Disclosure and Governance, 16(4), 206–241. [Google Scholar] [CrossRef]
- Alderman, L., & Schuetze, C. F. (2020, June 26). In a German tech giant’s fall, charges of lies, spies and missing billions. The New York Times. Available online: https://web.archive.org/web/20210131232425/https://www.nytimes.com/2020/06/26/business/wirecard-collapse-markus-braun.html (accessed on 28 January 2021).
- Ali, A. A., Khedr, A. M., El-Bannany, M., & Kanakkayil, S. (2023). A powerful predicting model for financial statement fraud based on optimized XGBoost ensemble learning technique. Applied Sciences, 13(4), 2272. [Google Scholar] [CrossRef]
- Altman, E. I. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589–609. [Google Scholar] [CrossRef]
- Altman, E. I., Danovi, A., & Falini, A. (2013). Z-score models’ application to Italian companies subject to extraordinary administration. Journal of Applied Finance, 23(1), 1–10. Available online: https://ssrn.com/abstract=2275390 (accessed on 25 October 2025).
- Altman, E. I., Hartzell, J., & Peck, M. (1998). Emerging market corporate bond—A scoring system. In R. M. Levich (Ed.), Emerging market capital flows (Vol. 2, pp. 391–400). Springer. [Google Scholar] [CrossRef]
- Amiram, D., Bozanic, Z., Cox, J. D., Dupont, Q., Karpoff, J. M., & Sloan, R. (2018). Financial reporting fraud and other forms of misconduct: A multidisciplinary review of the literature. Review of Accounting Studies, 23(2), 732–783. [Google Scholar] [CrossRef]
- Anh, N., & Linh, N. (2016). Using the M-score model in detecting earnings management: Evidence from non-financial Vietnamese listed companies. VNU Journal of Science: Economics and Business, 32(2), 14–23. Available online: https://js.vnu.edu.vn/EAB/article/view/1287 (accessed on 25 October 2025).
- Anjum, S. (2012). Business bankruptcy prediction models: A significant study of the Altman’s Z-score model. Asian Journal of Management Research, 3(1), 212–219. [Google Scholar] [CrossRef]
- Appelbaum, D. (2016). Securing big data provenance for auditors: The big data provenance black box as reliable evidence. Journal of Emerging Technologies in Accounting, 13(1), 17–36. [Google Scholar] [CrossRef]
- Appelbaum, D., Kogan, A., & Vasarhelyi, M. A. (2017). Big data and analytics in the modern audit engagement: Research needs. AUDITING: A Journal of Practice & Theory, 36(4), 1–27. [Google Scholar] [CrossRef]
- Bach, F. R., Heckerman, D., & Horvitz, E. (2006). Considering cost asymmetry in learning classifiers. Journal of Machine Learning Research, 7(63), 1713–1741. Available online: https://www.jmlr.org/papers/v7/bach06a.html (accessed on 25 October 2025).
- Bai, B., Yen, J., & Yang, X. (2008). False financial statements: Characteristics of China’s listed companies and CART detecting approach. International Journal of Information Technology & Decision Making, 7(2), 339–359. [Google Scholar] [CrossRef]
- Barton, J., & Simko, P. J. (2002). The balance sheet as an earnings management constraint. The Accounting Review, 77(s-1), 1–27. [Google Scholar] [CrossRef]
- Beneish, M. D. (1999). The detection of earnings manipulation. Financial Analysts Journal, 55(5), 24–36. [Google Scholar] [CrossRef]
- Beneish, M. D., Lee, C. M. C., & Nichols, D. C. (2012). Fraud detection and expected returns. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Beneish, M. D., Lee, C. M. C., & Nichols, D. C. (2013). Earnings manipulation and expected returns. Financial Analysts Journal, 69(2), 57–82. [Google Scholar] [CrossRef]
- Bertomeu, J., Cheynel, E., Floyd, E., & Pan, W. (2018). Ghost in the machine: Using machine learning to uncover hidden misstatements. Semantic Scholar, 1–32. Available online: https://api.semanticscholar.org/CorpusID:53965228 (accessed on 25 October 2025).
- Bertomeu, J., Cheynel, E., Floyd, E., & Pan, W. (2019). Using machine learning to detect misstatements. Review of Accounting Studies. Available online: https://ssrn.com/abstract=3496297 (accessed on 25 October 2025).
- Cecchini, M., Aytug, H., Koehler, G. J., & Pathak, P. (2010a). Detecting management fraud in public companies. Management Science, 56(7), 1146–1160. [Google Scholar] [CrossRef]
- Cecchini, M., Aytug, H., Koehler, G. J., & Pathak, P. (2010b). Making words work: Using financial text as a predictor of financial events. Decision Support Systems, 50(1), 164–175. [Google Scholar] [CrossRef]
- Cheah, P. C. Y., Yang, Y., & Lee, B. G. (2023). Enhancing financial fraud detection through addressing class imbalance using hybrid SMOTE-GAN techniques. International Journal of Financial Studies, 11(3), 110. [Google Scholar] [CrossRef]
- Chen, F. H., Chi, D. J., & Zhu, J. Y. (2014). Application of random forest, rough set theory, decision tree and neural network to detect financial statement fraud—Taking corporate governance into consideration. In D.-S. Huang, V. Bevilacqua, & P. Premaratne (Eds.), International conference on intelligent computing (Vol. 8588, pp. 221–234). Springer International Publishing. [Google Scholar] [CrossRef]
- Chen, S., Goo, Y.-J. J., & Shen, Z.-D. (2014). A hybrid approach of stepwise regression, logistic regression, support vector machine, and decision tree for forecasting fraudulent financial statements. The Scientific World Journal, 2014(1), 968712. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y., & Wu, Z. (2023). Financial fraud detection of listed companies in China: A Machine Learning Approach. Sustainability, 15(1), 105. [Google Scholar] [CrossRef]
- Cheng, C.-H., Kao, Y.-F., & Lin, H.-P. (2021). A financial statement fraud model based on synthesized attribute selection and a dataset with missing values and imbalanced classes. Applied Soft Computing, 108, 107487. [Google Scholar] [CrossRef]
- Cressey, R. D. (1953). Other people’s money; A study of the social psychology of embezzlement. Free Press. [Google Scholar]
- Dechow, P. M., Ge, W., Larson, C. R., & Sloan, R. G. (2011). Predicting material accounting misstatements. Contemporary Accounting Research, 28(1), 17–82. [Google Scholar] [CrossRef]
- Dechow, P. M., Sloan, R. G., & Sweeney, A. P. (1995). Detecting earnings management. The Accounting Review, 70(2), 193–225. Available online: https://www.jstor.org/stable/248303 (accessed on 25 October 2025).
- Der Spiegel. (2020, July 22). Ex-Wirecard-Chef Braun erneut verhaftet. Available online: https://www.spiegel.de/wirtschaft/unternehmen/staatsanwaltschaft-laesst-ex-wirecard-chef-braun-erneut-verhaften-a-d361846e-b33f-4936-8945-03243a1aef2d (accessed on 24 January 2021).
- Desjardins, J. (2019, June 25). The 20 biggest bankruptcies in U.S. history. Visual Capitalist. Available online: https://www.visualcapitalist.com/the-20-biggest-bankruptcies-in-u-s-history/ (accessed on 22 December 2020).
- Dong, W., Liao, S., & Zhang, Z. (2018). Leveraging financial social media data for corporate fraud detection. Journal of Management Information Systems, 35(2), 461–487. [Google Scholar] [CrossRef]
- Dong, W., Liao, S. S., Fang, B., Cheng, X., Zhu, C., & Fan, W. (2014, July 13). The detection of fraudulent financial statements: An integrated language model. Pacific Asia Conference on Information Systems, Chengdu, China. [Google Scholar]
- Eidleman, G. J. (1995). Z scores—A guide to failure prediction. The CPA Journal, 65(2), 52–54. Available online: http://archives.cpajournal.com/old/16641866.htm (accessed on 25 October 2025).
- EpistasisLab. (2021a). Computational Genetics Laboratory (CGL). Available online: http://epistasis.org/ (accessed on 23 January 2021).
- EpistasisLab. (2021b). TPOT. Available online: http://epistasislab.github.io/tpot/ (accessed on 23 January 2021).
- Eurostat. (2017). Business survival rates in selected European countries in 2017, by length of survival. Available online: https://www.statista.com/statistics/1114070/eu-business-survival-rates-by-country-2017/ (accessed on 8 October 2020).
- Financial Accounting Standards Board (FASB). (2010). US GAAP—Receivables (Topic 310). Available online: https://storage.fasb.org/ASU%202010-XX%20Receivables%20(Topic%20310)%20Disclosures%20about%20the%20Credit%20Quality%20of%20Financing%20Receivables.pdf (accessed on 25 October 2025).
- Financial Accounting Standards Board (FASB). (2015). Inventory (Topic 330). Available online: https://storage.fasb.org/ASU%202015-11.pdf (accessed on 25 October 2025).
- Gaganis, C. (2009). Classification techniques for the identification of falsified financial statements: A comparative analysis. Intelligent Systems in Accounting, Finance & Management, 16(3), 207–229. [Google Scholar] [CrossRef]
- Glancy, F. H., & Yadav, S. B. (2011). A computational model for financial reporting fraud detection. Decision Support Systems, 50(3), 595–601. [Google Scholar] [CrossRef]
- Goel, S., Gangolly, J., Faerman, S. R., & Uzuner, O. (2010). Can linguistic predictors detect fraudulent financial filings? Journal of Emerging Technologies in Accounting, 7(1), 25–46. [Google Scholar] [CrossRef]
- Goel, S., & Uzuner, O. (2016). Do sentiments matter in fraud detection? Estimating semantic orientation of annual reports. Intelligent Systems in Accounting, Finance and Management, 23(3), 215–239. [Google Scholar] [CrossRef]
- Golec, A. (2019). Effectiveness of the Beneish model in detecting financial statement manipulations. Acta Universitatis Lodziensis. Folia Oeconomica, 2(341), 161–182. [Google Scholar] [CrossRef]
- Gomber, P., Kauffman, R. J., Parker, C., & Weber, B. (2017). On the fintech revolution: Interpreting the forces of innovation, disruption and transformation in financial services. Journal of Management Information Systems, 35(1), 220–265. Available online: https://ssrn.com/abstract=3190052 (accessed on 25 October 2025). [CrossRef]
- Goodhue, D. L., & Thompson, R. L. (1995). Task-technology fit and individual performance. Management Information Systems Quarterly, 19(2), 213–236. [Google Scholar] [CrossRef]
- Granville, K. (2020, June 19). Wirecard, a payments firm, is rocked by a report of a missing $2 billion. The New York Times. Available online: https://web.archive.org/web/20201219112713/https://www.nytimes.com/2020/06/19/business/wirecard-scandal.html/ (accessed on 20 December 2020).
- Gray, A. (2020, December 17). Luckin Coffee to pay $180m in accounting fraud settlement. Financial Times. Available online: https://www.ft.com/content/4db3b074-829f-4f1c-a256-11c7e28a31d1 (accessed on 22 December 2020).
- Green, B. P., & Choi, J. H. (1997). Assessing the risk of management fraud through neural network technology. Auditing: A Journal of Practice & Theory, 16(1), 14–28. Available online: https://www.researchgate.net/publication/245508224_Assessing_the_Risk_of_Management_Fraud_Through_Neural_Network_Technology (accessed on 25 October 2025).
- Hajek, P., & Henriques, R. (2017). Mining corporate annual reports for intelligent detection of financial statement fraud—A comparative study of machine learning methods. Knowledge-Based Systems, 128, 139–152. [Google Scholar] [CrossRef]
- Healy, P. M. (1985). The effect of bonus schemes on accounting decisions. Journal of Accounting and Economics, 7(1–3), 85–107. [Google Scholar] [CrossRef]
- Healy, P. M., & Wahlen, J. M. (1999). A review of the earnings management literature and its implications for standard setting. Accounting Horizons, 13(4), 365–383. [Google Scholar] [CrossRef]
- Hevner, A. R., March, S. T., Park, J., & Ram, S. (2004). Design science in information systems research. Management Information Systems Quarterly, 28(1), 75–106. [Google Scholar] [CrossRef]
- Hoberg, G., & Lewis, C. (2017). Do fraudulent firms produce abnormal disclosure? Journal of Corporate Finance, 43, 58–85. [Google Scholar] [CrossRef]
- Hoogs, B., Kiehl, T., Lacomb, C., & Senturk, D. (2007). A genetic algorithm approach to detecting temporal patterns indicative of financial statement fraud. Intelligent Systems in Accounting, Finance and Management, 15(1–2), 41–56. [Google Scholar] [CrossRef]
- Huang, L., Abrahams, A., & Ractham, P. (2022). Enhanced financial fraud detection using cost-sensitive cascade forest with missing value imputation. Intelligent Systems in Accounting, Finance and Management, 29(3), 133–155. [Google Scholar] [CrossRef]
- Huang, S., & Liang, X. (2013). Fraud detection model by using support vector machine techniques. International Journal of Digital Content Technology and Its Applications, 15(1), 32–37. [Google Scholar] [CrossRef]
- Humpherys, S. L., Moffitt, K. C., Burns, M. B., Burgoon, J. K., & Felix, W. F. (2011). Identification of fraudulent financial statements using linguistic credibility analysis. Decision Support Systems, 50(3), 585–594. [Google Scholar] [CrossRef]
- Hung, D. N., Ha, H. T. V., & Binh, D. T. (2017). Application of F-score in predicting fraud, errors: Experimental research in Vietnam. International Journal of Accounting and Financial Reporting, 7(2), 303–322. [Google Scholar] [CrossRef]
- Hylas, R. E., & Ashton, R. H. (1982). Audit detection of financial statement errors. The Accounting Review, 57(4), 751–765. Available online: https://www.jstor.org/stable/247410 (accessed on 25 October 2025).
- Jones, M. J. (2011). Creative accounting, fraud and international accounting scandals. John Wiley & Sons. [Google Scholar] [CrossRef]
- Kim, W., & Kim, S. (2025). Enhancing Corporate Transparency: AI-based detection of financial misstatements in Korean firms using NearMiss sampling and explainable models. Sustainability, 17(19), 8933. [Google Scholar] [CrossRef]
- Kim, Y. J., Baik, B., & Cho, S. (2016). Detecting financial misstatements with fraud intention using multi-class cost-sensitive learning. Expert Systems with Applications, 62, 32–43. [Google Scholar] [CrossRef]
- Kirkos, E., Spathis, C., & Manolopoulos, Y. (2007). Data mining techniques for the detection of fraudulent financial statements. Expert Systems with Applications, 32(4), 995–1003. [Google Scholar] [CrossRef]
- Kotsiantis, S., Koumanakos, E., Tzelepis, D., & Tampakas, V. (2006). Forecasting fraudulent financial statements using data mining. International Journal of Computational Intelligence, 3(2), 104–110. Available online: https://www.researchgate.net/publication/228084523_Forecasting_fraudulent_financial_statements_using_data_mining (accessed on 25 October 2025).
- Le, T. T., Fu, W., & Moore, J. H. (2020). Scaling tree-based automated machine learning to biomedical big data with a feature set selector. Bioinformatics, 36(1), 250–256. [Google Scholar] [CrossRef] [PubMed]
- Lev, B., & Thiagarajan, S. R. (1993). Fundamental information analysis. Journal of Accounting Research, 31(2), 190–215. [Google Scholar] [CrossRef]
- Li, B., Yu, J., Zhang, J., & Ke, B. (2016). Detecting accounting frauds in publicly traded U.S. firms: A machine learning approach. Asian Conference on Machine Learning, 45, 173–188. [Google Scholar]
- Li, X., Xu, W., & Tian, X. (2014). How to protect investors? A GA-based DWD approach for financial statement fraud detection. IEEE International Conference on Systems, Man and Cybernetics, 3548–3554. [Google Scholar] [CrossRef]
- Lin, C. C., Chiu, A. A., Huang, S. Y., & Yen, D. C. (2015). Detecting the financial statement fraud: The analysis of the differences between data mining techniques and experts’ judgments. Knowledge-Based Systems, 89, 459–470. [Google Scholar] [CrossRef]
- Liu, C., Chan, Y., Alam Kazmi, S. H., & Fu, H. (2015). Financial fraud detection model: Based on random forest. International Journal of Economics and Finance, 7(7), 178–188. [Google Scholar] [CrossRef]
- Liu, W., Wang, Z., & Zhang, X. (2025). Research on financial fraud detection by integrating latent semantic features of annual report text with accounting indicators. Journal of Accounting & Organizational Change. [Google Scholar] [CrossRef]
- Maccarthy, J. (2017). Using Altman Z-score and Beneish M-score models to detect financial fraud and corporate failure: A case study of Enron corporation. International Journal of Finance and Accounting, 6(6), 159–166. Available online: http://article.sapub.org/10.5923.j.ijfa.20170606.01.html (accessed on 25 October 2025).
- Mahama, M. (2015). Detecting corporate fraud and financial distress using the Altman and Beneish models. International Journal of Economics, Commerce and Management, 3(1), 1–18. Available online: https://ijecm.co.uk/wp-content/uploads/2015/01/3159.pdf (accessed on 25 October 2025).
- Mccain, T. (2017). Montier C Score—Who is Cooking the Books? Available online: https://web.archive.org/web/20220516114102/https://www.equitieslab.com/montier-c-score/ (accessed on 3 September 2025).
- Montier, J. (2008). Cooking the books, or, more sailing under the black flag (pp. 1–8). Société Générale Mind Matters. [Google Scholar]
- Ngai, E. W. T., Hu, Y., Wong, Y. H., Chen, Y., & Sun, X. (2011). The application of data mining techniques in financial fraud detection: A classification framework and an academic review of literature. Decision Support Systems, 50(3), 559–569. [Google Scholar] [CrossRef]
- Nugroho, D. S., & Diyanty, V. (2022). Hexagon fraud in fraudulent financial statements: The moderating role of audit committee. Jurnal Akuntansi Dan Keuangan Indonesia, 19(1), 46–67. [Google Scholar] [CrossRef]
- Olson, R. S., Bartley, N., Urbanowicz, R. J., & Moore, J. H. (2016a). Evaluation of a tree-based pipeline optimization tool for automating data science. In GECCO ‘16: Proceedings of the 2016 genetic and evolutionary computation conference (GECCO 2016) (pp. 485–492). Association for Computing Machinery. [Google Scholar] [CrossRef]
- Olson, R. S., Urbanowicz, R. J., Andrews, P. C., Lavender, N. A., Kidd, L. C., & Moore, J. H. (2016b). Automating biomedical data science through tree-based pipeline optimization. In Applications of evolutionary computation (Vol. 9597, pp. 123–137). Springer International Publishing. [Google Scholar] [CrossRef]
- Omar, N., Johari, Z. A., & Smith, M. (2017). Predicting fraudulent financial reporting using artificial neural network. Journal of Financial Crime, 24(2), 362–387. [Google Scholar] [CrossRef]
- Pai, P. F., Hsu, M. F., & Wang, M. C. (2011). A support vector machine-based model for detecting top management fraud. Knowledge-Based Systems, 24(2), 314–321. [Google Scholar] [CrossRef]
- Perols, J. L., & Lougee, B. A. (2011). The relation between earnings management and financial statement fraud. Advances in Accounting, 27(1), 39–53. [Google Scholar] [CrossRef]
- Persons, O. S. (1995). Using financial statement data to identify factors associated with fraudulent financial reporting. Journal of Applied Business Research, 11(3), 38–46. [Google Scholar] [CrossRef]
- Price, R. A., III, Sharp, N. Y., & Wood, D. A. (2011). Detecting and predicting accounting irregularities: A comparison of commercial and academic risk measures. Accounting Horizons, 25(4), 755–780. [Google Scholar] [CrossRef]
- Purda, L., & Skillicorn, D. (2015). Accounting variables, deception, and a bag of words: Assessing the tools of fraud detection. Contemporary Accounting Research, 32(3), 1193–1223. [Google Scholar] [CrossRef]
- Rahul, K., Steh, N., & Dinesh Kumar, U. (2018). Spotting earnings manipulation: Using machine learning for financial fraud detection. International Conference on Innovative Techniques and Applications of Artificial Intelligence, 11311, 343–356. [Google Scholar] [CrossRef]
- Ravisankar, P., Ravi, V., Raghava Rao, G., & Bose, I. (2011). Detection of financial statement fraud and feature selection using data mining techniques. Decision Support Systems, 50(2), 491–500. [Google Scholar] [CrossRef]
- Rezaee, Z. (2005). Causes, consequences, and deterence of financial statement fraud. Critical Perspectives on Accounting, 16(3), 277–298. [Google Scholar] [CrossRef]
- Richardson, S. A., Sloan, R. G., Soliman, M. T., & Tuna, I. (2005). Accrual reliability, earnings persistence and stock prices. Journal of Accounting and Economics, 39(3), 437–485. [Google Scholar] [CrossRef]
- Schuchter, A., & Levi, M. (2016). The fraud triangle revisited. Security Journal, 29(2), 107–121. [Google Scholar] [CrossRef]
- scikit-learn. (2021a). GradientBoostingClassifier. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html (accessed on 24 January 2021).
- scikit-learn. (2021b). KNeighborsClassifier. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html (accessed on 24 January 2021).
- Sharma, A., & Kumar Panigrahi, P. (2012). A review of financial accounting fraud detection based on data mining techniques. International Journal of Computer Applications, 39(1), 37–47. [Google Scholar] [CrossRef]
- Song, X. P., Hu, Z. H., Du, J. G., & Sheng, Z. H. (2014). Application of machine learning methods to risk assessment of financial statement fraud: Evidence from China. Journal of Forecasting, 33(8), 611–626. [Google Scholar] [CrossRef]
- Sukmadilaga, C., Winarningsih, S., Handayani, T., Herianti, E., & Ghani, E. K. (2022). Fraudulent financial reporting in ministerial and governmental institutions in indonesia: An analysis using hexagon theory. Economies, 10(4), 86. [Google Scholar] [CrossRef]
- Tagesschau. (2020, July 22). Neue haftbefehle gegen Wirecard-manager. Available online: https://web.archive.org/web/20210305135753/https://www.tagesschau.de/wirtschaft/wirecard-staatsanwaltschaft-103.html (accessed on 2 September 2025).
- Tarjo, & Herawati, N. (2015). Application of Beneish M-score models and data mining to detect financial fraud. Procedia—Social and Behavioral Sciences, 211, 924–930. [Google Scholar] [CrossRef]
- Throckmorton, C. S., Mayew, W. J., Venkatachalam, M., & Collins, L. M. (2015). Financial fraud detection using vocal, linguistic and financial cues. Decision Support Systems, 74, 78–87. [Google Scholar] [CrossRef]
- Toms, S. (2019). Financial scandals: A historical overview. Accounting and Business Research, 49(5), 477–499. [Google Scholar] [CrossRef]
- U.S. Bureau of Labor Statistics. (2020). Survival of private sector establishments by opening year. Available online: https://www.bls.gov/bdm/us_age_naics_00_table7.txt (accessed on 8 October 2020).
- USC Marshall School of Business. (2020). Accounting and auditing enforcement release (AAER) dataset. Available online: https://sites.google.com/usc.edu/aaerdataset/ (accessed on 3 September 2025).
- U.S. Securities and Exchange Commission. (n.d.). Accounting and auditing enforcement releases (AAER). Available online: https://www.sec.gov/divisions/enforce/friactions.shtml (accessed on 21 January 2021).
- Vousinas, G. L. (2019). Advancing theory of fraud: The S.C.O.R.E. model. Journal of Financial Crime, 26(1), 372–381. [Google Scholar] [CrossRef]
- Wang, G., Ma, J., & Chen, G. (2023). Attentive statement fraud detection: Distinguishing multimodal financial data with fine-grained attention. Decision Support Systems, 167, 113913. [Google Scholar] [CrossRef]
- Warshavsky, M. (2012). Analyzing earnings quality as a financial forensic tool. Financial Valuation and Litigation Expert Journal, 39, 16–20. Available online: https://www.scribd.com/document/199209631/Analyzing-Earnings-Quality-as-a-Financial-Forensics-Tool (accessed on 25 October 2025).
- West, J., & Bhattacharya, M. (2016). Intelligent financial fraud detection: A comprehensive review. Computers & Security, 57, 47–66. [Google Scholar] [CrossRef]
- Whiting, D. G., Hansen, J. V., McDonald, J. B., Albrecht, C., & Albrecht, W. S. (2012). Machine learning methods for detecting patterns of management fraud. Computational Intelligence, 28(4), 505–527. [Google Scholar] [CrossRef]
- Wirecard AG. (2019). News & publications, financial reports. Available online: https://web.archive.org/web/20201023020946/https://ir.wirecard.com/websites/wirecard/English/5000/news-_-publications.html#financialreports (accessed on 25 January 2021).
- Wolfe, D. T., & Hermanson, D. R. (2004). The fraud diamond: Considering the four elements of fraud. Available online: https://digitalcommons.kennesaw.edu/facpubs/1537/ (accessed on 25 October 2025).
- Zhang, C., Cho, S., & Vasarhelyi, M. (2022). Explainable Artificial Intelligence (XAI) in auditing. International Journal of Accounting Information Systems, 46, 100572. [Google Scholar] [CrossRef]
- Zhang, Z., Ma, Y., & Hua, Y. (2022). Financial fraud identification based on stacking ensemble learning algorithm: Introducing MD&A text information. Computational Intelligence and Neuroscience, 2022(1), 1780834. [Google Scholar] [CrossRef]
- Zhang, Z., Wang, Z., & Cai, L. (2025). Predicting financial fraud in Chinese listed companies: An enterprise portrait and machine learning approach. Pacific-Basin Finance Journal, 90, 102665. [Google Scholar] [CrossRef]
- Zhu, S., Ma, T., Wu, H., Ren, J., He, D., Li, Y., & Ge, R. (2025). Expanding and interpreting financial statement fraud detection using supply chain knowledge graphs. Journal of Theoretical and Applied Electronic Commerce Research, 20(1), 26. [Google Scholar] [CrossRef]



| Company | Assets (USD bn) | Filed | Fraud Involved | |
|---|---|---|---|---|
| 1. | Lehman Brothers, Inc. | 691.06 | 2008 | Yes |
| 2. | Washington Mutual, Inc. | 327.91 | 2008 | No |
| 3. | WorldCom, Inc. | 103.91 | 2002 | Yes |
| 4. | General Motors Corp. | 82.29 | 2009 | No |
| 5. | CIT Group, Inc. | 71.00 | 2009 | No |
| 6. | Pacific Gas and Electric | 71.00 | 2019 | No |
| 7. | Enron Corp. | 65.50 | 2001 | Yes |
| 8. | Conseco, Inc. | 61.39 | 2002 | Yes |
| 9. | MF Global, Inc. | 41.00 | 2011 | No |
| 10. | Chrysler LLC | 39.30 | 2009 | No |
| 11. | Thornburg Mortgage, Inc. | 36.52 | 2009 | No |
| 12. | Pacific Gas and Electric | 36.15 | 2001 | No |
| 13. | Texaco, Inc. | 34.94 | 1987 | No |
| 14. | Financial Corporation of America | 33.86 | 1988 | No |
| 15. | Refco, Inc. | 33.33 | 2005 | Yes |
| 16. | IndyMac Bancorp, Inc. | 32.73 | 2008 | No |
| 17. | Global Crossing Ltd. | 30.19 | 2002 | Yes |
| 18. | Bank of New England Corp. | 29.77 | 1991 | No |
| 19. | General Growth Properties, Inc. | 29.56 | 2009 | No |
| 20. | Lyondell Chemical Corp. | 27.39 | 2009 | No |
| Altman Z-Score | Interpretation |
|---|---|
| Non-distress Zone | |
| Gray Zone | |
| Distress Zone |
| Beneish M-Score | Interpretation |
|---|---|
| Manipulation likely | |
| Manipulation unlikely |
| Dechow F-Score | Interpretation |
|---|---|
| High risk | |
| Substantial risk | |
| Above normal risk | |
| Normal or low risk |
| Study | Fraudulent/Non-fraudulent Firm Years, Country | Supervised Classification Algorithms Used (Accuracy in Percent) |
|---|---|---|
| (Green & Choi, 1997) | 86/86 US | Balances Accuracies (BA) 1: PSYDNN (70.0), SPCNN (71.2), ISYDNN (50.0) |
| (Kotsiantis et al., 2006) | 41/123 Greek | Stacking (95.1), C4.5 (91.2), SVM (78.7) |
| (Kirkos et al., 2007) | 38/38 Greek | BBN (90.3), MLP (80.0), ID3 (73.6) |
| (Hoogs et al., 2007) | 51/339 US | GA (90.8) |
| (Bai et al., 2008) | 24/124 Chinese | CART (92.5), LR (89.6) |
| (Gaganis, 2009) | 199/199 Greek | PNN (90.2), SVM (88.4), MLP (88.4), LDA (87.8) |
| (Cecchini et al., 2010a) | 132/3187 US | SVM (90.3) 2 (AUC 0.878; fraud recall 80.0%, non-fraud recall 90.6%) |
| (Cecchini et al., 2010b) | 61/61 US | TM + SVM (82.0), TM (75.4) |
| (Goel et al., 2010) | 126/622 US | TM (89.5) |
| (Dechow et al., 2011) | 293/79358 US | LR (63.7) |
| (Ravisankar et al., 2011) | 101/101 Chinese | PNN (98.1), GP (94.1), GMDH (93.0), MLP (78.8), SVM (73.4) |
| (Humpherys et al., 2011) | 101/101 US | TM + C4.5 (67.3), TM + Naïve Bayes (67.3), TM + SVM (65.8) |
| (Glancy & Yadav, 2011) | 100 US | TM (83.9) |
| (Pai et al., 2011) | 25/50 Taiwanese | SVM (92.0), C4.5 (84.0), RBF (82.7), MLP (82.7) |
| (Whiting et al., 2012) | 114/114 US | RF (90.1), Rule Ensemble (88.2), Stochastic Gradient Boosting (86.3), LR (72.3), PR (68.6) |
| (S. Huang & Liang, 2013) | Taiwanese (1:4) | SVM (92.0), LR (76.0) |
| (Dong et al., 2014) | 26/26 Chinese | TM (78.1) |
| (Song et al., 2014) | 110/440 Chinese | Voting (88.9), SVM (85.5), MLP (85.1), C5.0 (78.6), LR (77.9) |
| (S. Chen et al., 2014) | 66/66 Taiwanese | C5.0 (85.7), LR (81.0), SVM (72.0) |
| (F. H. Chen et al., 2014) | 47/47 Taiwanese | C5.0 (79.0), Rough Set (78.9), MLP (67.1) |
| (X. Li et al., 2014) | 12/45 US | DWD (91.2), SVM (89.5), C4.5 (82.5), MLP (75.4) |
| (Lin et al., 2015) | 127/447 Taiwanese | MLP (92.8), CART (90.3), LR (88.5) |
| (C. Liu et al., 2015) | 138/160 Chinese | RF (88.0), SVM (80.2), CART (66.4), k-NN (60.1), LR (42.9) |
| (Purda & Skillicorn, 2015) | 1407/4708 US | TM (83.0) |
| (Throckmorton et al., 2015) | 41/1531 US | Audio + TM (81.0) |
| (Y. J. Kim et al., 2016) | 788/2156 US | LR (88.4), SVM (87.7), BBN (82.5) |
| (Goel & Uzuner, 2016) | 180/180 US | TM (81.8) |
| (Omar et al., 2017) | 75/475 Malaysian | MLP (94.9), LR (92.4) |
| (Bertomeu et al., 2018) | 1227/8471 US | Detection rates 3: GBRT (49.5), LR (46.2), BLR (46.8), FLR (46.8) |
| (Dong et al., 2018) | 64/64 US | TM + SVM (75.5), TM + ANN (63.2), TM + DT (63.1), TM + LR (54.5) |
| (Rahul et al., 2018) | 39/1200 Indian | AdaBoost (60.5), XGBoost (54.2), RF (60.4) |
| Category | Algorithm | Ø | n |
|---|---|---|---|
| ANN | Probabilistic Neural Network (PNN) | 94.2 | 2 |
| ANN | Group Method of Data Handling (GMDH) | 93.0 | 1 |
| ANN | Multilayer Perceptron (MLP) | 82.8 | 9 |
| ANN | Radial Basis Function Neural Network (RBF) | 82.7 | 1 |
| BBN | Bayesian Belief Networks (BBN) | 86.4 | 2 |
| DT | C4.5 | 85.9 | 3 |
| DT | Classification and Regression Tree (CART) | 83.1 | 3 |
| DT | C5.0 | 81.1 | 3 |
| DT | Iterative Dichotomiser 3 (ID3) | 73.6 | 1 |
| DA | Linear Discriminant Analysis (LDA) | 87.8 | 1 |
| EC | Genetic Programming (GP) | 94.1 | 1 |
| EC | Genetic Algorithm (GA) | 90.8 | 1 |
| Ensemble | Stacking | 95.1 | 1 |
| Ensemble | Voting | 88.9 | 1 |
| Ensemble | Rule Ensemble | 88.2 | 1 |
| Ensemble | Random Forest (RF) | 79.5 | 3 |
| Ensemble | Boosting | 62.6 | 4 |
| GLM | Logistic Regression (LR) | 74.4 | 11 |
| GLM | Probit Regression (PR) | 68.6 | 1 |
| GLM | Forward Logistic Regression (FLR) | 46.8 | 1 |
| GLM | Backward Logistic Regression (BLR) | 46.8 | 1 |
| k-NN | k-Nearest Neighbors (k-NN) | 60.1 | 1 |
| LMM | Distance Weighted Discrimination (DWD) | 91.2 | 1 |
| LMM | Support Vector Machine (SVM) | 84.5 | 11 |
| Other | Plain sum-of-years’-digit weighted avg. (PSYDNN) | 70.0 | 1 |
| Other | Simple Percentage Change (SPCNN) | 71.2 | 1 |
| Other | Incremental sum-of-years’-digit weighted avg. (ISYDNN) | 50.0 | 1 |
| Rough Set | Rough Set Classifier | 78.9 | 1 |
| Text | Text Mining (TM) | 74.1 | 15 |
| Category | Ø | n |
|---|---|---|
| Evolutionary Computation (EC) | 92.45 | 2 |
| Discriminant Analysis (DA) | 87.80 | 1 |
| Bayesian Belief Network (BBN) | 86.40 | 2 |
| Artificial Neural Network (ANN) | 85.32 | 13 |
| Large-Margin Methods (LMM) | 85.08 | 12 |
| Decision Tree (DT) | 82.38 | 10 |
| Rough Set | 78.90 | 1 |
| Ensemble | 74.39 | 10 |
| Text | 74.09 | 15 |
| Generalized Linear Model (GLM) | 70.08 | 14 |
| Other | 63.73 | 3 |
| k-Nearest Neighbor (k-NN) | 60.10 | 1 |
| ID | Field | Description |
|---|---|---|
| 1 | ID | Unique Identifier in the Bloomberg database |
| 2 | ISIN | International Securities Identification Number |
| 3 | Name | Name of the company |
| 4 | Period | Fiscal year of the dataset |
| 5 | QuerylistReference | A constructed field indicating total asset size |
| 6 | Timestamp | Point in time the query was executed |
| 7 | X1 | Variables used to calculate the Altman Z-Score |
| 8 | X2 | |
| 9 | X3 | |
| 10 | X4 | |
| 11 | X5 | |
| 12 | Altman Z-Score | |
| 13 | DSRI | Variables used to calculate the Beneish M-Score |
| 14 | GMI | |
| 15 | AQI | |
| 16 | SGI | |
| 17 | DEPI | |
| 18 | SGAI | |
| 19 | LVGI | |
| 20 | TATA | |
| 21 | Beneish M-Score | |
| 22 | C1 | Variables used to calculate the Montier C-Score |
| 23 | C2 | |
| 24 | C3 | |
| 25 | C4 | |
| 26 | C5 | |
| 27 | C6 | |
| 28 | Montier C-Score | |
| 29 | rsst_acc | Variables used to calculate the Dechow F-Score |
| 30 | ch_rec | |
| 31 | ch_inv | |
| 32 | soft_assets | |
| 33 | ch_cs | |
| 34 | ch_roa | |
| 35 | issue | |
| 36 | logit | |
| 37 | prob_FSF | |
| 38 | Dechow F-Score |
| Field | N/A Values Absolute (n) | N/A Values Relative (r) | Data Availability (1 − r) | Data Availability (2,014,827 − n) |
|---|---|---|---|---|
| ID | 0 | 0.00% | 100.00% | 2,014,827 |
| ISIN | 1,036,634 | 51.45% | 48.55% | 978,193 |
| Name | 2 | 0.00% | 100.00% | 2,014,825 |
| Period | 0 | 0.00% | 100.00% | 2,014,827 |
| Timestamp | 0 | 0.00% | 100.00% | 2,014,827 |
| X1 | 776,186 | 38.52% | 61.48% | 1,238,641 |
| X2 | 1,331,093 | 66.06% | 33.94% | 683,734 |
| X3 | 757,967 | 37.62% | 62.38% | 1,256,860 |
| X4 | 1,236,329 | 61.36% | 38.64% | 778,498 |
| X5 | 692,321 | 34.36% | 65.64% | 1,322,506 |
| Altman Z-Score | 1,573,337 | 78.09% | 21.91% | 441,490 |
| DSRI | 465,181 | 23.09% | 76.91% | 1,549,646 |
| GMI | 1,215,471 | 60.33% | 39.67% | 799,356 |
| AQI | 515,638 | 25.59% | 74.41% | 1,499,189 |
| SGI | 291,441 | 14.46% | 85.54% | 1,723,386 |
| DEPI | 1,358,336 | 67.42% | 32.58% | 656,491 |
| SGAI | 1,778,689 | 88.28% | 11.72% | 236,138 |
| LVGI | 942,600 | 46.78% | 53.22% | 1,072,227 |
| TATA | 1,068,151 | 53.01% | 46.99% | 946,676 |
| Beneish M-Score | 1,857,670 | 92.20% | 7.80% | 157,157 |
| C1 | 1,167,571 | 57.95% | 42.05% | 847,256 |
| C2 | 419,513 | 20.82% | 79.18% | 1,595,314 |
| C3 | 654,233 | 32.47% | 67.53% | 1,360,594 |
| C4 | 273,489 | 13.57% | 86.43% | 1,741,338 |
| C5 | 1,467,890 | 72.85% | 27.15% | 546,937 |
| C6 | 221,522 | 10.99% | 89.01% | 1,793,305 |
| Montier C-Score | 1,512,633 | 75.08% | 24.92% | 502,194 |
| rsst_acc | 1,910,865 | 94.84% | 5.16% | 103,962 |
| ch_rec | 394,346 | 19.57% | 80.43% | 1,620,481 |
| ch_inv | 654,252 | 32.47% | 67.53% | 1,360,575 |
| soft_assets | 109,570 | 5.44% | 94.56% | 1,905,257 |
| ch_cs | 616,965 | 30.62% | 69.38% | 1,397,862 |
| ch_roa | 448,078 | 22.24% | 77.76% | 1,566,749 |
| issue | 0 | 0.00% | 100.00% | 2,014,827 |
| logit | 1,918,102 | 95.20% | 4.80% | 96,725 |
| prob_FSF | 1,918,109 | 95.20% | 4.80% | 96,718 |
| Dechow F-Score | 1,918,109 | 95.20% | 4.80% | 96,718 |
| N/A Values | N/A Values Relative | Data Availability ) | ||
|---|---|---|---|---|
| 1988 | 4066 | 94,431 | 92.90% | 7.10% |
| 1989 | 4645 | 58,751 | 50.59% | 49.41% |
| 1990 | 8787 | 58,751 | 26.74% | 73.26% |
| 1991 | 10,858 | 131,524 | 48.45% | 51.55% |
| 1992 | 13,750 | 162,387 | 47.24% | 52.76% |
| 1993 | 16,435 | 187,103 | 45.54% | 54.46% |
| 1994 | 20,049 | 234,398 | 46.77% | 53.23% |
| 1995 | 22,973 | 252,817 | 44.02% | 55.98% |
| 1996 | 25,320 | 257,925 | 40.75% | 59.25% |
| 1997 | 26,766 | 241,491 | 36.09% | 63.91% |
| 1998 | 27,855 | 228,203 | 32.77% | 67.23% |
| 1999 | 28,747 | 228,956 | 31.86% | 68.14% |
| 2000 | 29,099 | 219,831 | 30.22% | 69.78% |
| 2001 | 28,565 | 201,163 | 28.17% | 71.83% |
| 2002 | 28,741 | 196,641 | 27.37% | 72.63% |
| 2003 | 28,865 | 192,725 | 26.71% | 73.29% |
| 2004 | 32,368 | 249,205 | 30.80% | 69.20% |
| 2005 | 39,395 | 367,710 | 37.34% | 62.66% |
| 2006 | 87,733 | 1,396,176 | 63.66% | 36.34% |
| 2007 | 121,002 | 1,740,341 | 57.53% | 42.47% |
| 2008 | 126,996 | 1,491,038 | 46.96% | 53.04% |
| 2009 | 123,824 | 1,328,356 | 42.91% | 57.09% |
| 2010 | 130,765 | 1,378,487 | 42.17% | 57.83% |
| 2011 | 129,095 | 1,358,542 | 42.09% | 57.91% |
| 2012 | 124,551 | 1,288,704 | 41.39% | 58.61% |
| 2013 | 123,753 | 1,257,910 | 40.66% | 59.34% |
| 2014 | 122,778 | 1,212,891 | 39.51% | 60.49% |
| 2015 | 117,618 | 1,119,914 | 38.09% | 61.91% |
| 2016 | 119,302 | 1,149,979 | 38.56% | 61.44% |
| 2017 | 111,516 | 996,002 | 35.73% | 64.27% |
| 2018 | 107,087 | 900,434 | 33.63% | 66.37% |
| 2019 | 71,523 | 508,038 | 28.41% | 71.59% |
| Total | 2,014,827 | 20,690,824 |
| Fiscal Year | Firm Years Available | Firm Years Used | Relative Usage |
|---|---|---|---|
| 1971–1987 | 273 | 0 | 0.00% |
| 1988 | 37 | 3 | 8.11% |
| 1989 | 56 | 7 | 12.50% |
| 1990 | 47 | 13 | 27.66% |
| 1991 | 58 | 15 | 25.86% |
| 1992 | 62 | 20 | 32.26% |
| 1993 | 62 | 27 | 43.55% |
| 1994 | 47 | 25 | 53.19% |
| 1995 | 52 | 26 | 50.00% |
| 1996 | 54 | 30 | 55.56% |
| 1997 | 79 | 49 | 62.03% |
| 1998 | 97 | 65 | 67.01% |
| 1999 | 126 | 81 | 64.29% |
| 2000 | 148 | 109 | 73.65% |
| 2001 | 143 | 105 | 73.43% |
| 2002 | 131 | 97 | 74.05% |
| 2003 | 109 | 81 | 74.31% |
| 2004 | 82 | 64 | 78.05% |
| 2005 | 68 | 51 | 75.00% |
| 2006 | 45 | 33 | 73.33% |
| 2007 | 45 | 32 | 71.11% |
| 2008 | 38 | 27 | 71.05% |
| 2009 | 60 | 27 | 45.00% |
| 2010 | 49 | 25 | 51.02% |
| 2011 | 42 | 20 | 47.62% |
| 2012 | 43 | 24 | 55.81% |
| 2013 | 27 | 15 | 55.56% |
| 2014 | 21 | 11 | 52.38% |
| Total | 2101 | 1082 | 51.50% |
| Fiscal Year | Firm Years Available | Firm Years Used | Relative Usage |
|---|---|---|---|
| 1879–1987 | 58 | 0 | 0.00% |
| 1988 | 4 | 0 | 0.00% |
| 1989 | 1 | 0 | 0.00% |
| 1990 | 3 | 1 | 33.33% |
| 1991 | 6 | 1 | 16.67% |
| 1992 | 4 | 1 | 25.00% |
| 1993 | 9 | 3 | 33.33% |
| 1994 | 5 | 1 | 20.00% |
| 1995 | 8 | 2 | 25.00% |
| 1996 | 7 | 3 | 42.86% |
| 1997 | 7 | 3 | 42.86% |
| 1998 | 12 | 2 | 16.67% |
| 1999 | 14 | 4 | 28.57% |
| 2000 | 15 | 6 | 40.00% |
| 2001 | 16 | 8 | 50.00% |
| 2002 | 17 | 7 | 41.18% |
| 2003 | 6 | 5 | 83.33% |
| 2004 | 10 | 6 | 60.00% |
| 2005 | 6 | 4 | 66.67% |
| 2006 | 7 | 3 | 42.86% |
| 2007 | 2 | 1 | 50.00% |
| 2008 | 4 | 1 | 25.00% |
| 2009 | 1 | 1 | 100.00% |
| Total | 222 | 63 | 28.38% |
| Country | Firm Years Used | Percentage |
|---|---|---|
| Australia | 3 | 0.26% |
| China | 2 | 0.17% |
| Germany | 7 | 0.61% |
| Greece | 2 | 0.17% |
| India | 2 | 0.17% |
| Italy | 3 | 0.26% |
| Japan | 24 | 2.10% |
| Netherlands | 11 | 0.96% |
| Spain | 1 | 0.09% |
| Sweden | 1 | 0.09% |
| United Kingdom | 1 | 0.09% |
| USA | 1088 | 95.02% |
| Total | 1145 | 100.00% |
| Data | Number |
|---|---|
| AAER Dataset (USC Marshall School of Business, 2020) | |
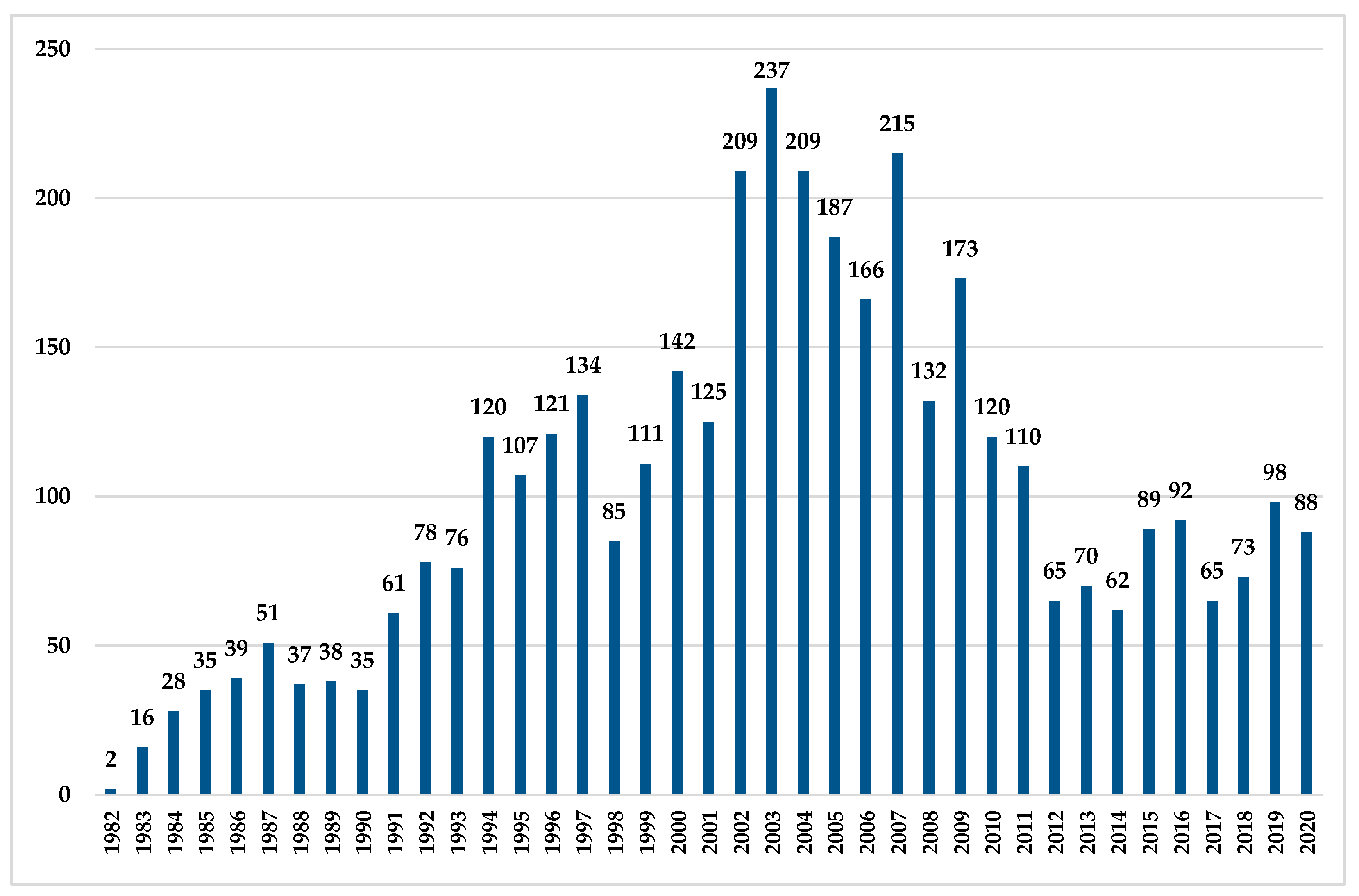
| AAERs (1982–2018) | 4012 |
| Misstatement events reported in those AAERs | 1657 |
| − Enforcements unrelated to FSF (e.g., bribes, and disclosure) or misstatements that cannot be linked to specific reporting periods | − 609 |
| = Misstatement events affecting at least one quarterly or annual financial statement | 1048 |
| Fraudulent firm years extracted from the 1048 misstatement events | 2101 |
| − Firm years before 1988 | −273 |
| − Firm years not existing in the financial data sample from Section 3.1.1 | −746 |
| = Fraudulent firm years merged with the financial data sample from Section 3.1.1 | 1082 |
| Creative Accounting Dataset (Jones, 2011, pp. 509–517) | |
| Misstatement events reported | 142 |
| Fraudulent firm years extracted from the 142 misstatement events | 222 |
| − Firm years before 1988 | 58 |
| − Firm years that also appear in the AAER dataset (duplicates) | 10 |
| − Firm years not existing in the financial data sample from Section 3.1.1 | 91 |
| = Fraudulent firm years merged with the financial data sample from Section 3.1.1 | 63 |
| Total fraudulent firm years merged with the financial data sample from Section 3.1.1 | 1145 |
| Number of N/As in 25 Fields (n) | Number of Rows Containing n N/As | Relative Amount |
|---|---|---|
| 0 | 3 | 0.26% |
| 1 | 59 | 5.15% |
| 2 | 207 | 18.08% |
| 3 | 154 | 13.45% |
| 4 | 146 | 12.75% |
| 5 | 139 | 12.14% |
| 6 | 114 | 9.96% |
| 7 | 37 | 3.23% |
| 8 | 85 | 7.42% |
| 9 | 32 | 2.79% |
| 10 | 38 | 3.32% |
| 11 | 32 | 2.79% |
| Total firm years kept (): | 1046 | 91.35% |
| 12 | 5 | 0.44% |
| 13 | 14 | 1.22% |
| 14 | 16 | 1.40% |
| 15 | 17 | 1.48% |
| 16 | 7 | 0.61% |
| 17 | 4 | 0.35% |
| 18 | 11 | 0.96% |
| 19 | 9 | 0.79% |
| 20 | 7 | 0.61% |
| 21 | 5 | 0.44% |
| 22 | 4 | 0.35% |
| 23 | 0 | 0.00% |
| 24 | 0 | 0.00% |
| 25 | 0 | 0.00% |
| Total firm years deleted (): | 99 | 8.65% |
| Total | 1145 | 100.00% |
| Data Field | Number of Rows Containing N/As (n) | Deleted? | |
|---|---|---|---|
| X1 | 277 | 26.48% | No |
| X2 | 481 | 45.98% | No |
| X3 | 225 | 21.51% | No |
| X4 | 77 | 7.36% | No |
| X5 | 225 | 21.51% | No |
| Altman Z-Score | 549 | 52.49% | Yes |
| DSRI | 28 | 2.68% | No |
| GMI | 160 | 15.30% | No |
| AQI | 59 | 5.64% | No |
| SGI | 4 | 0.38% | No |
| DEPI | 482 | 46.08% | No |
| SGAI | 929 | 88.81% | Yes |
| LVGI | 63 | 6.02% | No |
| TATA | 6 | 0.57% | No |
| Beneish M-Score | 978 | 93.50% | Yes |
| C1 | 12 | 1.15% | No |
| C2 | 3 | 0.29% | No |
| C3 | 72 | 6.88% | No |
| C4 | 0 | 0.00% | No |
| C5 | 489 | 46.75% | No |
| C6 | 0 | 0.00% | No |
| Montier C-Score | 507 | 48.47% | Yes |
| rsst_acc | 1042 | 99.62% | Yes |
| ch_rec | 3 | 0.29% | No |
| ch_inv | 72 | 6.88% | No |
| soft_assets | 18 | 1.72% | No |
| ch_cs | 68 | 6.50% | No |
| ch_roa | 62 | 5.93% | No |
| issue | 0 | 0.00% | Yes |
| logit | 1042 | 99.62% | Yes |
| prob_FSF | 1042 | 99.62% | Yes |
| Dechow F-Score | 1042 | 99.62% | Yes |
| Data Field | Average Value Replacing Missing Values in the Respective Field Actual Average (Value Used) | Number of N/As Replaced |
|---|---|---|
| X1 | 0.2642 | 277 |
| X2 | −0.2784 | 481 |
| X3 | 0.0449 | 225 |
| X4 | 7.7822 | 77 |
| X5 | 1.2802 | 225 |
| DSRI | 1.3707 | 28 |
| GMI | 0.9047 | 160 |
| AQI | 112,517.2376 (3.9461) | 59 (62) |
| SGI | 2.8458 | 4 |
| DEPI | 5.1758 | 482 |
| LVGI | 1.1594 | 63 |
| TATA | −0.0601 | 6 |
| C1 | 0.4971 (0) | 12 |
| C2 | 0.2579 (0) | 3 |
| C3 | 0.5441 (1) | 72 |
| C4 | 0.5143 (1) | 0 |
| C5 | 0.5673 (1) | 489 |
| C6 | 0.4073 (0) | 0 |
| ch_rec | 0.0366 | 3 |
| ch_inv | 0.0233 | 72 |
| soft_assets | 0.6213 | 18 |
| ch_cs | −1.5590 | 68 |
| ch_roa | −0.0003 | 62 |
| Firm Year | X1 | X2 | X3 | X4 | X5 | Z-Score |
|---|---|---|---|---|---|---|
| 2000 | NULL | NULL | NULL | 20.67 | NULL | NULL |
| 2003 | 0.14 | 0.01 | 0.01 | 5.84 | 0.48 | 4.21 |
| 2004 | 0.16 | −0.15 | 0.06 | 3.03 | 0.58 | 2.56 |
| 2005 | 0.36 | NULL | 0.14 | 5.76 | 0.73 | NULL |
| 2006 | 0.20 | 0.17 | 0.15 | 6.14 | 0.66 | 5.32 |
| 2007 | 0.06 | 0.21 | 0.14 | 3.99 | 0.54 | 3.77 |
| 2008 | 0.20 | 0.35 | 0.18 | 1.96 | 0.74 | 3.26 |
| 2009 | 0.18 | 0.35 | 0.15 | 3.32 | 0.61 | 3.80 |
| 2010 | 0.18 | 0.50 | 0.19 | 4.01 | 0.76 | 4.70 |
| 2011 | 0.34 | 0.52 | 0.17 | 3.45 | 0.74 | 4.51 |
| 2012 | 0.24 | 0.37 | 0.12 | 3.56 | 0.51 | 3.85 |
| 2013 | 0.27 | 0.37 | 0.10 | 3.92 | 0.49 | 4.00 |
| 2014 | 0.31 | 0.34 | 0.10 | 4.88 | 0.45 | 4.57 |
| 2015 | 0.25 | 0.30 | 0.09 | 3.47 | 0.40 | 3.51 |
| 2016 | 0.32 | 0.35 | 0.10 | 2.52 | 0.43 | 3.14 |
| 2017 | 0.25 | 0.34 | 0.10 | 3.98 | 0.47 | 3.96 |
| 2018 | 0.36 | 0.31 | 0.10 | 4.17 | 0.45 | 4.14 |
| Altman Z-Score | Interpretation | |||||
| Non-distress Zone | ||||||
| Gray Zone | ||||||
| Distress Zone | ||||||
| Firm Year | DSRI | GMI | AQI | SGI | DEPI | SGAI | LVGI | TATA | M-Score | M-Score 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 1.50 | 0.97 | 0.98 | 1.94 | NULL | NULL | 0.11 | −0.03 | NULL | −1.03 |
| 2003 | 6.12 | 0.78 | 7.93 | 1.54 | 0.80 | NULL | 0.26 | 0.24 | NULL | 6.72 |
| 2004 | NULL | NULL | 0.65 | 1.49 | 0.98 | NULL | 1.89 | −0.01 | NULL | −2.51 |
| 2005 | NULL | NULL | 1.22 | 7.17 | 1.50 | NULL | 0.63 | −0.04 | NULL | 3.10 |
| 2006 | NULL | NULL | 0.87 | 1.67 | 0.68 | NULL | 1.61 | −0.02 | NULL | −2.25 |
| 2007 | NULL | NULL | 0.92 | 1.64 | 1.75 | NULL | 1.23 | −0.16 | NULL | −2.70 |
| 2008 | NULL | NULL | 0.97 | 1.47 | 0.58 | NULL | 0.86 | 0.00 | NULL | −2.06 |
| 2009 | NULL | NULL | 0.88 | 1.16 | NULL | NULL | 1.07 | −0.04 | NULL | −2.59 |
| 2010 | 1.24 | NULL | 1.25 | 1.19 | NULL | 0.69 | 0.86 | 0.14 | NULL | −1.23 |
| 2011 | 1.28 | NULL | 0.98 | 1.20 | 1.53 | 0.84 | 1.06 | 0.02 | NULL | −1.88 |
| 2012 | 0.97 | NULL | 0.96 | 1.21 | 0.96 | 1.10 | 1.02 | −0.02 | NULL | −2.45 |
| 2013 | 1.06 | NULL | 1.02 | 1.22 | 0.74 | 1.12 | 1.11 | −0.03 | NULL | −2.44 |
| 2014 | 1.01 | NULL | 0.99 | 1.25 | 1.03 | 0.99 | 0.78 | −0.01 | NULL | −2.23 |
| 2015 | 0.98 | NULL | 1.07 | 1.28 | 1.18 | 1.84 | 1.21 | −0.07 | NULL | −2.75 |
| 2016 | 0.99 | NULL | 0.91 | 1.33 | 1.08 | 1.05 | 1.06 | −0.01 | NULL | −2.28 |
| 2017 | 0.83 | NULL | 0.99 | 1.45 | 0.92 | 0.89 | 1.10 | −0.06 | NULL | −2.56 |
| 2018 | 0.87 | NULL | 0.83 | 1.35 | 1.11 | 0.85 | 1.04 | −0.07 | NULL | −2.65 |
| Beneish M-Score | Interpretation | |||||||||
| Manipulation likely | ||||||||||
| Manipulation unlikely | ||||||||||
| Firm Year | C1 | C2 | C3 | C4 | C5 | C6 | C-Score | C-Score 1 |
|---|---|---|---|---|---|---|---|---|
| 2000 | 0 | 0 | NULL | 1 | NULL | 1 | NULL | 2 |
| 2003 | 0 | 1 | 0 | 1 | 1 | 1 | 4 | 4 |
| 2004 | 1 | NULL | NULL | 0 | 1 | 0 | NULL | 2 |
| 2005 | 1 | NULL | NULL | 1 | 1 | 1 | NULL | 4 |
| 2006 | 1 | NULL | 0 | 1 | 0 | 1 | NULL | 3 |
| 2007 | 0 | NULL | 1 | 1 | 1 | 1 | NULL | 4 |
| 2008 | 1 | NULL | 0 | 0 | 0 | 0 | NULL | 1 |
| 2009 | 0 | NULL | 1 | 1 | NULL | 1 | NULL | 3 |
| 2010 | 0 | 0 | 1 | 0 | NULL | 0 | NULL | 1 |
| 2011 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 |
| 2012 | 0 | 0 | 1 | 1 | 0 | 1 | 3 | 3 |
| 2013 | 0 | 0 | 1 | 1 | 0 | 1 | 3 | 3 |
| 2014 | 1 | 0 | 0 | 1 | 1 | 1 | 4 | 4 |
| 2015 | 0 | 0 | 1 | 1 | 1 | 1 | 4 | 4 |
| 2016 | 1 | 0 | 1 | 0 | 1 | 0 | 3 | 3 |
| 2017 | 0 | 0 | 1 | 0 | 0 | 1 | 2 | 2 |
| 2018 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 2 |
| Firm Year | rsstacc | chrec | chinv | softassets | chcs | chroa | Issue | probFSF | F-Score |
|---|---|---|---|---|---|---|---|---|---|
| 2000 | NULL | 0.0476 | NULL | 0.8686 | NULL | NULL | 1 | NULL | NULL |
| 2003 | NULL | 0.3198 | 0.0000 | 0.9393 | −0.3763 | 1.5374 | 1 | NULL | NULL |
| 2004 | NULL | NULL | NULL | 0.9320 | NULL | −0.2492 | 1 | NULL | NULL |
| 2005 | NULL | NULL | NULL | 0.6997 | NULL | 0.1124 | 1 | NULL | NULL |
| 2006 | NULL | NULL | −0.0070 | 0.7097 | NULL | −0.0220 | 1 | NULL | NULL |
| 2007 | NULL | NULL | 0.0047 | 0.5998 | NULL | 0.0069 | 1 | NULL | NULL |
| 2008 | NULL | NULL | −0.0035 | 0.5306 | NULL | 0.0027 | 1 | NULL | NULL |
| 2009 | NULL | NULL | 0.0006 | 0.4931 | NULL | −0.0087 | 1 | NULL | NULL |
| 2010 | 0.1920 | 0.0700 | 0.0000 | 0.6418 | NULL | 0.0043 | 1 | NULL | NULL |
| 2011 | −0.0792 | 0.1009 | 0.0007 | 0.6813 | 0.1197 | −0.0016 | 1 | 0.50% | 1.3406 |
| 2012 | −0.0386 | 0.0363 | 0.0009 | 0.5972 | 0.3820 | −0.0175 | 1 | 0.39% | 1.0588 |
| 2013 | −0.1228 | 0.0496 | 0.0024 | 0.6075 | 0.1578 | −0.0152 | 1 | 0.37% | 1.0060 |
| 2014 | 0.0140 | 0.0417 | −0.0008 | 0.5818 | 0.2662 | −0.0017 | 1 | 0.39% | 1.0463 |
| 2015 | −0.2130 | 0.0370 | 0.0001 | 0.5820 | 0.2843 | −0.0052 | 1 | 0.32% | 0.8714 |
| 2016 | −0.0599 | 0.0435 | 0.0003 | 0.5595 | 0.3066 | 0.0253 | 1 | 0.35% | 0.9331 |
| 2017 | −0.1771 | 0.0301 | 0.0022 | 0.5433 | 0.5411 | −0.0183 | 1 | 0.32% | 0.8653 |
| 2018 | −0.1109 | 0.0234 | −0.0005 | 0.4977 | 0.3835 | 0.0021 | 1 | 0.29% | 0.7802 |
| Dechow F-Score | Interpretation | ||||||||
| High risk | |||||||||
| Substantial risk | |||||||||
| Above normal risk | |||||||||
| Normal or low risk | |||||||||
| Firm Year | Predicted Class | Imputed Predictors (of 23) |
|---|---|---|
| 2000 | 1—fraudulent | 10/23 |
| 2003 | 0—non-fraudulent | 0/23 |
| 2004 | 0—non-fraudulent | 7/23 |
| 2005 | 1—fraudulent | 8/23 |
| 2006 | 1—fraudulent | 5/23 |
| 2007 | 1—fraudulent | 5/23 |
| 2008 | 0—non-fraudulent | 5/23 |
| 2009 | 0—non-fraudulent | 7/23 |
| 2010 | 0—non-fraudulent | 4/23 |
| 2011 | 0—non-fraudulent | 1/23 |
| 2012 | 0—non-fraudulent | 1/23 |
| 2013 | 0—non-fraudulent | 1/23 |
| 2014 | 1—fraudulent | 1/23 |
| 2015 | 1—fraudulent | 1/23 |
| 2016 | 1—fraudulent | 1/23 |
| 2017 | 0—non-fraudulent | 1/23 |
| 2018 | 0—non-fraudulent | 1/23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steingen, L.; Löw, E. Using Machine Learning to Detect Financial Statement Fraud: A Cross-Country Analysis Applied to Wirecard AG. J. Risk Financial Manag. 2025, 18, 605. https://doi.org/10.3390/jrfm18110605
Steingen L, Löw E. Using Machine Learning to Detect Financial Statement Fraud: A Cross-Country Analysis Applied to Wirecard AG. Journal of Risk and Financial Management. 2025; 18(11):605. https://doi.org/10.3390/jrfm18110605
Chicago/Turabian StyleSteingen, Luca, and Edgar Löw. 2025. "Using Machine Learning to Detect Financial Statement Fraud: A Cross-Country Analysis Applied to Wirecard AG" Journal of Risk and Financial Management 18, no. 11: 605. https://doi.org/10.3390/jrfm18110605
APA StyleSteingen, L., & Löw, E. (2025). Using Machine Learning to Detect Financial Statement Fraud: A Cross-Country Analysis Applied to Wirecard AG. Journal of Risk and Financial Management, 18(11), 605. https://doi.org/10.3390/jrfm18110605







