Detecting Bank-Level Liquidity Shifts: Evidence from U.S. Regulatory Data

Abstract

In the wake of the 2008–2009 Global Financial Crisis, the Federal Reserve began paying interest on reserves (IOR) on 1 October 2008—an intervention that, along with others, constituted a regime change for U.S. banks. In this study, we investigate whether banks’ liquidity adjustment was progressive and continuous or abrupt and regime-defining, and how adjustment timing differed across institutions. Using quarterly regulatory call reports from 2002:Q4 to 2015:Q4, we estimate a Gaussian hidden Markov model (HMM) to detect bank-specific regime shifts. We then use the inferred break dates in a regression framework that classifies banks’ liquidity behavior over time. We find a discrete upward shift in liquidity around 2008–2009 with pronounced cross-bank heterogeneity. The patterns persist when we stratify by asset size and remain highly concordant across geographic regions and primary regulators. To illustrate its broader relevance, we extend the framework to the COVID-19 era (2017–2023) for the four largest U.S. banks, showing that it captures comparable regime dynamics across successive phases of quantitative tightening and easing.

1. Introduction and Literature Review

An extended period of low interest rates in the early 2000s led banks to fund themselves at short-term rates close to the risk-free rate and to expand mortgage lending to a growing share of subprime borrowers, who exhibited higher default rates than traditional borrowers (Taylor, 2007). The banking system came under strain in 2007 as major mortgage lenders such as New Century Financial failed, and banks holding large quantities of mortgage-backed securities (MBS) incurred significant losses (Gorton & Metrick, 2012). As failures intensified in 2008, the Federal Reserve intervened, recognizing that banks—having held minimal reserves due to weak incentives—were ill-prepared for liquidity shocks.

To address liquidity shortfalls, the Federal Reserve introduced a range of policy tools (Cúrdia & Woodford, 2011). First, it conducted three rounds of quantitative easing (QE) in the aftermath of the 2007–2009 financial crisis, purchasing assets from banks in exchange for reserves and allowing institutions to convert illiquid assets into liquid balances (Ennis & Wolman, 2015). Second, it created new emergency lending facilities to provide term funding and improve bank liquidity. Third, it began paying interest on reserves (IOR) on 1 October 2008, offering banks a return on reserve holdings comparable to Treasury securities. These tools expanded the Federal Reserve’s balance sheet substantially. 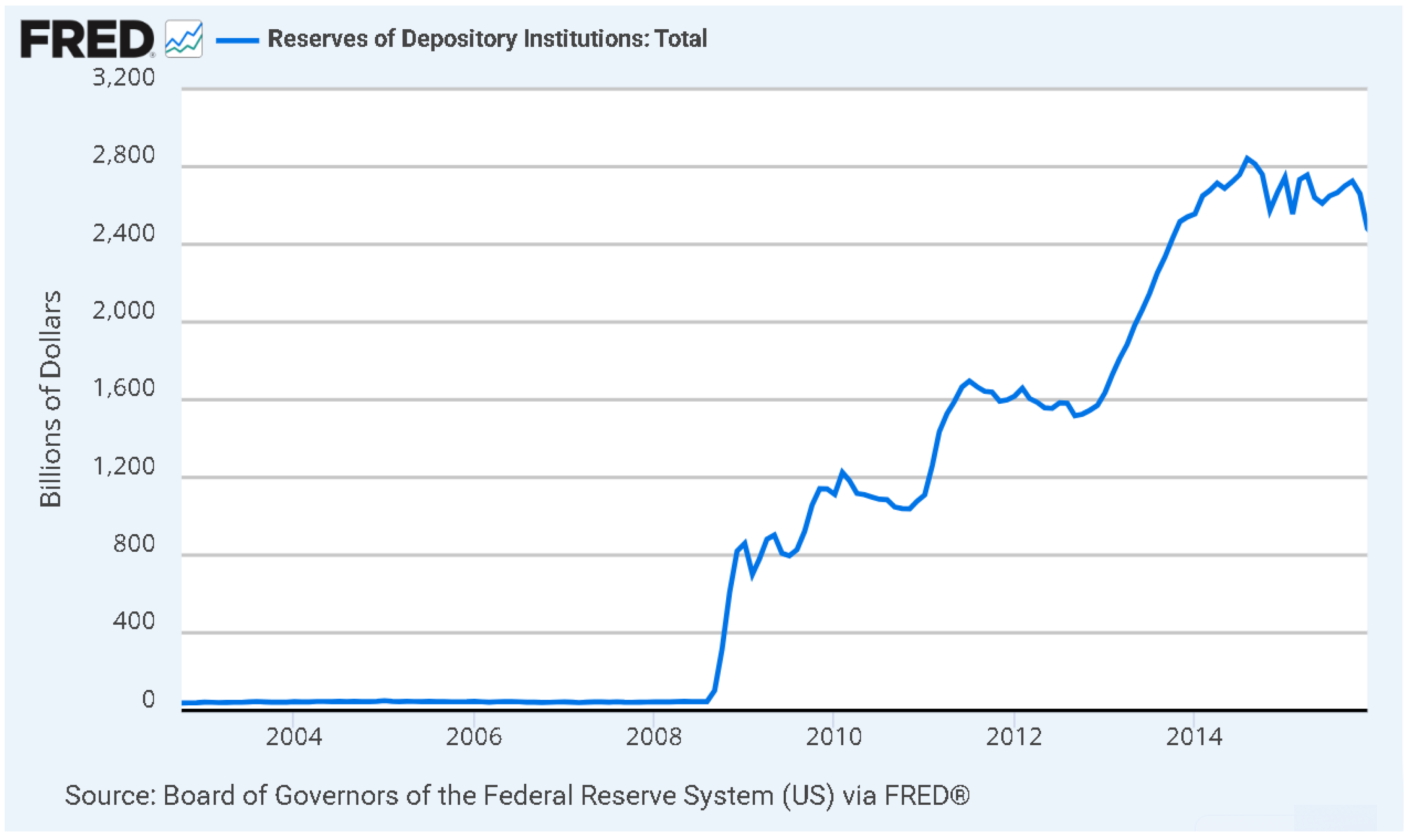As shown in Figure 1, aggregate reserves at U.S. depository institutions rose from roughly USD 50 billion in 2008:Q2 to nearly USD 3 trillion by 2014:Q1—a more than fifty-fold increase.

This study offers a micro-level analysis of the post-IOR environment, which Cochrane (2014) characterizes as a “regime shift” in bank behavior. A regime change refers to a structural shift in the behavior, policy environment, or underlying conditions governing an economic or financial system. The system operates under different rules and equilibria before and after the change (Hamilton, 1990; Kim & Nelson, 1999).

Prior to 2008, banks held minimal reserves, which were often perceived as an implicit tax on deposits (Walter & Courtois, 2009). Dutkowsky and VanHoose (2017) document that the IOR policy significantly improved the liquidity of the aggregate banking system post-IOR regime. A range of empirical work likewise finds that banks increased reserve holdings and other liquid assets in the post-crisis period, both in response to regulatory incentives and as a precaution against heightened uncertainty (Acharya & Merrouche, 2013; Berrospide, 2021; Cornett et al., 2011; Ihrig et al., 2015). Yet, not all banks adjusted simultaneously. Restructuring balance sheets with illiquid assets and making them more liquid takes time, and the effectiveness of IOR as an instrument can be constrained when interest rates approach the zero lower bound (Kashyap & Stein, 2012). Because the IOR policy coincided with other extraordinary interventions (e.g., quantitative easing and emergency lending facilities), cleanly isolating the causal effect of IOR is beyond the scope of this paper. Our goal is to map the timing and persistence of bank-specific liquidity regime shifts and assess whether adjustments were abrupt or gradual, noting their temporal alignment with policy windows while refraining from causal claims. Nevertheless, we observe that the introduction of IOR coincides a clear shift with lasting implications for monetary policy and bank liquidity management.

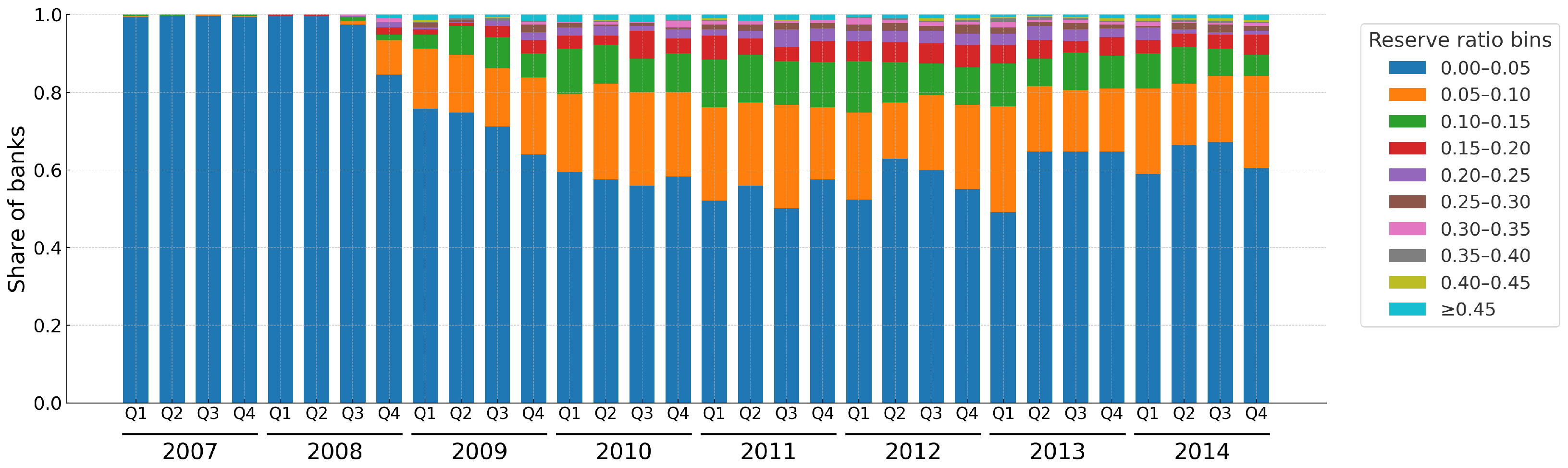
Figure 2 illustrates the distribution of reserve ratios across U.S. banks from 2007:Q1 through 2014:Q4. Prior to the crisis, reserve balances at the Federal Reserve were almost uniformly near zero, with most institutions reporting ratios below 0.05. Beginning in late 2008, the distribution broadened sharply: the share of banks with very low reserves fell, and increasing fractions appeared in higher reserve bins. By 2009, many banks held reserves equal to 5–15 percent of deposits, with some reporting even higher ratios. This new pattern persisted. Roughly half of banks continued to operate with relatively low reserves, while a large share maintained much higher ratios—including some above 30 percent. The emergence and persistence of this heterogeneity marks a fundamental change in liquidity management. The figure highlights the central motivation for our analysis: the financial crisis and the introduction of IOR coincided with a structural break in how U.S. banks managed liquidity, leading to a regime in which excess reserves became a systematic and heterogeneous feature of bank balance sheets.

With this motivation, our paper investigates bank liquidity positions by addressing these three questions:

(1)

Did bank liquidity positions improve over 2002–2015 (a period spanning the pre- and post-IOR policy environments)—particularly across banks of varying sizes and characteristics, geographic regions, and regulators?

(2)

If so, was the improvement in liquidity positions gradual and smooth or in the form of sudden and stepwise increases?

(3)

If stepwise in nature, what was the timing of these shifts? Did it occur immediately after the policy change or did the timing of adjustment vary across banks?

The first question can be addressed using standard regression techniques. However, a simple linear fit over the full sample period would likely suggest a gradual upward trend in liquidity ratios, contrary to our hypothesis (in second question) of an abrupt regime shift following the IOR policy. One remedy is to introduce a post-policy dummy variable equal to one on and after the policy change date, but this imposes a common response date and ignores the bank-level heterogeneity that motivates the third question.

To better capture this variation, we develop a regression framework incorporating bank-specific break dates. These dates are identified using a Hidden Markov Model (HMM), a statistical tool designed to detect unobserved (“hidden”) states from imperfect or noisy data. Unlike a standard Markov Model, an HMM allows regime changes to be latent, inferred from the observable data rather than assumed. In our setting, call report liquidity ratios serve as noisy indicators of underlying liquidity states, and the HMM identifies when banks transition between regimes.

This logic parallels how regulators assess bank soundness using the CAMELS framework consisting of capital adequacy (C), asset quality (A), management qality (M), earnings (E), liquidity (L), and sensitivity to market risk (S). The “L” component reflects judgments about underlying liquidity conditions, even though call report data provide only partial signals. Just as regulators infer hidden liquidity risks from observable ratios, our HMM approach treats reported balance sheet measures as stochastic emissions from unobserved liquidity states. In fact, Cole and Gunther (1998) find empirical evidence that the earlier framework known as the CAMEL ratings (without the “S” for sensitivity) provides useful private information, and yet, it decays quickly within a quarter or two. Nevertheless, these regulatory ratings are private and not publicly disclosed to avoid sparking a potential bank run.

Regulatory quarterly bank call report data offer partial visibility into bank conditions. Our methodology, thus, treats call report ratios as imperfect signals of underlying liquidity positions and uses the HMM framework to infer discrete regime shifts over time. This allows us to distinguish gradual trends from abrupt changes, and to capture heterogeneity in the timing of banks’ adjustments.

The identification of regime shifts in economic time series is a key area of study, with several prominent methodological approaches. The Markov-switching family of models, popularized by the seminal work of Hamilton (1989), posits that an observable time series is governed by a hidden, discrete-state Markov process. This framework is particularly well-suited for modeling recurrent, probabilistic shifts in dynamics, such as business cycles or periods of financial stress, where the underlying state is not directly observed. Our contribution is to deliver bank-level regime timelines with quantified uncertainty, rather than only aggregate dates or hard partitions. Using a parsimonious (left-to-right) Markov-switching specification, we can distinguish abrupt jumps from gradual drifts by reading posterior state probabilities, which is the central question of our study.

In contrast, the Threshold and Smooth Transition (TS-STAR) models (with seminal work of Tong (1990) and Teräsvirta (1994)) assume that a regime change is triggered by an observable variable crossing a specific threshold. While Threshold models capture abrupt shifts, Smooth Transition models allow for a gradual, continuous transition between regimes, making them ideal for situations where the change is not instantaneous. In comparison to TS-STAR models, our model does not require selecting an external threshold variable—which is not obvious for liquidity—while still capturing persistent, policy-driven state changes.

A third distinct strand is structural break analysis (with seminal work of Bai and Perron (1998)), which focuses on detecting permanent shifts in model parameters at a specific point in time. While this approach is effective for identifying one-time, non-recurrent events like major policy changes or financial crises, it differs from Markov-switching models that are designed to capture recurring phases in a dynamic system. Compared with structural break segmentation, our approach is more robust to transient noise, yields probabilistic rather than deterministic assignments, and scales cleanly across thousands of banks.

In summary, this paper identifies bank-specific liquidity regime shifts between 2002 and 2015 using a Hidden Markov Model. This approach improves upon traditional regression models that assume a common structural break date. The contribution of this study is two-fold. First, to our knowledge, HMM has not previously been applied to analyze bank call reports in this context, offering a novel tool for detecting institution-level policy responses. Second, understanding how banks adjust liquidity in response to IOR is critical for evaluating the transmission mechanism of monetary policy and ensuring financial stability.

Beyond analyzing the post-crisis adjustment period, we also extend the framework to a more recent policy environment to demonstrate its broader applicability. Specifically, we apply the model to the COVID-19 era (2017:Q1–2023:Q2) for the four largest U.S. banks—a period encompassing a full policy cycle of quantitative tightening (2017–2019), quantitative easing during the pandemic (2020–2021), and a return to tightening from 2022 onward. Using the same HMM specification with minor episode-specific adaptations, the model successfully captures distinct regime shifts in bank liquidity ratios that align with these macro-policy phases. This extension underscores the adaptability of the framework across different monetary environments and highlights its value for interpreting policy transmission and liquidity behavior in more recent episodes.

While prior studies (e.g., Ennis & Wolman, 2015; Judson, 2012) document increases in aggregate reserves post-IOR, they largely assume a common response date and overlook variation across institutions. Chang et al. (2014) use bank-level data similar to ours, analyzing bank call reports to understand the motives of banks for accumulation of reserves at individual banks. For this, they develop a theoretical model and conclude that the primary motives for increased levels of reserves during the 2007–2009 period was a precautionary motive due to weak balance sheets and the need to access to short term liquidity. They did not study the timing of the increase in reserves at individual banks.

Applying our HMM framework reveals that although banks generally increased reserves in response to IOR, the timing and magnitude of adjustment varied widely—differences that are obscured in conventional fixed-date regressions.

The remainder of the paper is organized as follows. Section 2 presents the methodology, model, and parameter estimation. Section 3 introduces the call report dataset and key variables. Section 4 reports the main results. Section 5 concludes with implications and directions for future research.

2. Methodology

Our empirical strategy is designed to examine whether bank liquidity ratios increased gradually or experienced discrete shifts. We employ three complementary approaches. First, the Linear Trend model estimates a simple time trend in liquidity ratios, providing a baseline view of gradual changes over the sample period. Second, a regression framework with a single structural break imposed at a specific time corresponding to the start of the IOR policy is used to capture an abrupt, uniform shift in liquidity behavior across all banks.

The third approach is a Gaussian Hidden Markov Model (HMM) incorporated into a regression model with dummy variables to endogenously identify regime change dates for each individual bank. This approach allows for heterogeneous responses to the policy change, recognizing that banks may have adjusted their liquidity positions at different times depending on institution-specific factors. By comparing the results of these three methods, we can assess whether increases in liquidity ratios in the period under study were driven by a uniform, policy-driven break, or by staggered, bank-specific regime shifts.

2.1. Linear Regression

In order to address our first question, whether a bank’s liquidity position improved during the period of study, we simply use a linear regression model. This allows us to test for gradual changes in banks’ liquidity positions over time, without imposing a structural break at the IOR policy implementation date.

We estimate the following linear trend model for each bank i:

$$L{R}_{i,t}={\beta }_{i,0}+{\beta }_{i,1}t+{ϵ}_{i,t}$$

The dependent variable $L{R}_{i,t}$ represent the liquidity ratio for bank i evaluated at quarter t. In this model, the dependent variable changes at an average constant rate ${\beta }_{i,1}$ with the passing of time t, which is the independent variable. A positive and statistically significant ${\beta }_{i,1}$ coefficient indicates that bank i’s liquidity ratio increased gradually during the period under study. This trend-based approach provides a baseline for distinguishing between a continuous increase and a potential stepwise shift.

2.2. Modeling Stepwise Increase

For the banks that had an increase in their liquidity, the above linear trend model assumes that this increase happened gradually at a constant rate. However, as explained in our second question in Section 1, we would like to investigate whether these changes are stepwise instead of being linear. As described earlier, such sudden jumps are typically referred to as regime changes and can be modeled using a set of indicator functions referred to as “dummy variable(s)”. In our context, changes in policy stances can alter the bank liquidity positions.

2.2.1. Fixed Regime Change Regression (FixRCR)

In the FixRCR model, banks are assumed to be in a low-liquidity regime until a sudden change point, after which the banks transition to a higher-liquidity regime. This regime change is modeled by applying a dummy variable named, ${\mathrm{Regime}}_{i,t}$, which takes a value of 0 prior to the regime change date $t^{★}$ (when bank i is in low-liquidity regime), and 1 on the following quarters (when the bank is in high-liquidity regime).

For each bank, we estimate the following regression model during the designated time frame:

$$L{R}_{i,t}={\beta }_{i,0}+{\delta }_i{\mathrm{Regime}}_{i,t}+{ϵ}_{i,t}$$

While this method is quick to implement, and its coefficients are easy to interpret—directly quantifying average level changes after the regime change date—it assumes that the same regime change point applies uniformly across all U.S. banks in the sample. Such a one-size-fits-all timing fails to capture the heterogeneous adjustment moment(s) observed in practice, and identifying regime change date(s) for every institution by hand is impracticable.

2.2.2. Variable Regime Change Regression (VarRCR)

As detailed above and addressed in our third question in Section 1, not only may regime changes not occur immediately after the policy change date, but they also could have happened more than once. Therefore, in the VarRCR model, we first apply a Gaussian HMM to identify bank-specific regime change dates and then use these dates to construct time dummies in the regression model.

For each bank, we estimate the following equation during the designated time frame:

$$L{R}_{i,t}={\beta }_{i,0}+\sum _{k=1}^{K-1}{\delta }_{i,k}{\mathrm{Regime}}_{i,k,t}+{ϵ}_{i,t}$$

The dependent variable $L{R}_{i,t}$ represent the quarterly liquidity ratio for bank i evaluated at time t. The independent variables, ${\mathrm{Regime}}_{i,k,t}$, are a set of dummy variables indicating which regime period the bank is in. The total number of regimes, K, varies from bank to bank and is identified through a regime change detection framework that uses Gaussian HMMs. Once the number of regime changes and the corresponding quarters where the regime change happened are identified, we designate a dummy variable for each regime except the first one, which is treated as the base period.

In the following sections, we explain how we implemented a Gaussian HMM to identify regime change points.

2.2.3. Gaussian Hidden Markov Model

Hidden Markov Models (HMMs) are probabilistic models commonly used to infer unobserved (hidden) states from observed sequential data. They were first introduced in the late 1960s (Baum & Petrie, 1966; Baum et al., 1970) and have since been widely applied across various domains. HMMs have been developed for both discrete and continuous distributions. They are very flexible and can follow either an ergodic (fully connected) or left-to-right (sequential) structure, depending on the application context (Rabiner, 1989).

Many economic and financial time series—such as bank liquidity ratios—can be influenced by underlying economic conditions or regimes including monetary policy environment or phase of the business cycle. These regimes are not directly observable, but they influence the data we can measure. HMMs allows us to model such latent (hidden) regimes and estimate how they evolve over time.

A Gaussian Hidden Markov Model is a special type of a Hidden Markov Model and it assumes that the observed data are generated by the following mechanism:

• Hidden States: There are N possible states (or regimes), denoted by $S_1,S_2,\dots ,S_N$. At each time $t=1,2,\dots ,T$, the system is in some unobserved state $q_t=S_i$ for $i=1,2,\dots ,N$. For example, $q_1=S_1,q_2=S_1,q_3=S_2,\dots ,q_T=S_N$ means the bank is in state $S_1$ at time $t=1,2$, in state $S_2$ at time $t=3$, and so on, and finally, in state $S_N$ at time $t=T$.
• Markov Property: The sequence of hidden states evolves over time as a first-order Markov chain. Subsequently, the transition probabilities are represented by an $N\times N$ transition matrix $A=\left(a_{ij}\right)$, where $a_{ij}=P(q_{t+1}=S_j|q_t=S_i)$, for $\{i,j\}\in 1,2,\dots ,N$. In other words, matrix A contains the transition probabilities for moving from state i in time t to state j in time $t+1$. Notice that the probability of transitioning to a new state depends only on the current state, not on the sequence of past states.
• Initial Probabilities: The initial probability of starting in each state i at time $t=1$ is denoted by $\pi =\left({\pi }_i\right)$, where ${\pi }_i=P(q_1=S_i)$.
• Emissions (Observations): At each time t, we observe a data point $O_t>0$, representing the bank’s liquidity ratio at that time. We denote the sequence of observations from $t=1$ to $t=T$ as $O=(O_1,O_2,\dots ,O_T)$. The observation $O_t$ depends on the current hidden state $q_t=S_i$ and is modeled as a normally distributed (hence, Gaussian) random variable. In short, we write this as $O_t|q_t=S_i\sim N({\mu }_i,{\sigma }_i^2)$, where ${\mu }_i$ is the mean and ${\sigma }_i^2$ is the variance of the emission in state $S_i$. Notice that emissions are time-homogenous as they do not depend on time even though we represent them with a time subindex as in $O_t$.

As a result, a Gaussian HMM is fully specified by the complete parameter set $\lambda =(\pi ,A,\{{\mu }_i,{\sigma }_i^2\})$. That is, the initial state probabilities $\pi$, the transition matrix A, and the normally distributed emission parameters $\{{\mu }_i,{\sigma }_i^2\}$ at each state i fully describe the Gaussian HMM.

The problem we aim to solve is to learn $\lambda =(\pi ,A,\{{\mu }_i,{\sigma }_i^2\})$ from $O=(O_1,\dots ,O_T)$ by maximizing $P(O\mid \lambda )$, which we compute via the Baum–Welch EM algorithm (Baum et al., 1970; Rabiner, 1989).

2.2.4. Implementation of a Gaussian HMM for Regime Change Identification

For each bank in our sample, we estimate a Gaussian HMM using quarterly liquidity ratios as the observed emissions, which are assumed to follow a normal distribution. As discussed earlier, the underlying liquidity state of a bank in any given quarter is unobservable and treated as a latent variable. By modeling the reported liquidity ratios as emissions from these hidden states, the Gaussian HMM provides a natural framework for detecting potential regime changes in liquidity dynamics over the sample period.

In addition, we implement a left-to-right HMM, where the state transition matrix A has the property $a_{ij}=0$ for $j<i$. We specifically adopt a left-to-right HMM structure, in which state transitions are constrained in a way that they cannot return to an already visited earlier state. This is particularly suitable for modeling regime shifts such as structural changes in financial behavior post-crisis. Throughout the period under study, the reserve ratio increases in general. Any bank with decreasing reserve ratio is treated as an outlier and removed from further analysis. The study then focuses on the timing of the regime changes for those banks. As such, the left-to-right structure is appropriate for the period under analysis covering the pre-crisis, crisis, and post-crisis periods.

To identify the hidden states, liquidity regimes, and corresponding change dates, we use the Baum–Welch algorithm, an iterative approach of “Expectation Maximization” to find a local optimal ${\lambda }^{★}$ that maximizes the likelihood of $P\left(O\right|\lambda )$.

To suppress single-quarter spikes, each liquidity ratio is replaced by a centered two-point moving average. Such short windows reduce transient noise without obscuring genuine level shifts—a strategy adopted in HMM settings such as ion-channel gating analyses (Almanjahie et al., 2015).

We choose the initial parameters as follows:

• The transition matrix A is upper triangular with main diagonal entries all set equal to 0.8 and the off-diagonal entries right above the main diagonal all set equal to 0.2. All other entries are set as 0. In symbols, we have $a_{i,i}=0.8, a_{i,i+1}=0.2$; otherwise, $a_{i,j}=0$ for $j\ne i\mathrm{or}j\ne i+1$. Consequently, the process is expected to remain in its current state with probability 0.80 and advance one state with probability 0.20; all other transitions are zero. The last state has no forward neighbor, so we treat it as absorbing with $a_{NN}=1$. Because EM can converge to a local maximum, we also ran multi-start initializations varying the stay/advance probability pairs: (0.7; 0.3), (0.75; 0.25), (0.8; 0.2), (0.85; 0.15), (0.9; 0.1). Results were stable across these starts, with the qualitative conclusions and inferred break windows unchanged.
• We initialize the state-dependent Gaussian means using quantile seeding on the smoothed liquidity ratios. For a model with N hidden states, the provisional mean for state $S_i$ is set to the ($i/N$)-th empirical quantile of the data. With three states, this places the means near the 33rd and 66th percentiles, yielding intuitive starting points corresponding to low-, medium-, and high-liquidity conditions.
• The state-dependent Gaussian variances are initialized as the global variance of the smoothed data.
• Initial state probabilities are set to be ${\pi }_1\approx 1,{\pi }_2=\cdots ={\pi }_N={10}^{-6}$ to ensure the chain begins in the first regime.

After the initialization of the parameters, they are updated at each iteration until convergence.

Selecting the number of hidden states is a key modeling decision in the HMM framework. For each bank, we estimated models with two to six states, corresponding to one to five possible regime changes. A two-state model implies a single regime shift, while a six-state model allows five shifts.

For each model, we calculated the Akaike Information Criterion (AIC) (Akaike, 1974) and Bayesian Information Criterion (BIC) (Schwarz, 1978) to evaluate model fit while penalizing unnecessary complexity. Lower values of these criteria indicate better performance. When AIC and BIC pointed to different models, we selected the model with the lower BIC. This choice reflects evidence from single-sequence HMM applications that BIC tends to be more reliable at identifying the correct number of states, whereas AIC can overestimate state counts in smaller samples (Boucheron & Gassiat, 2007).

The selected number of states and corresponding regime change dates were then used as inputs for the Variable Regime Change Regression model (VarRCR) analysis.

2.3. Model Comparison and Selection

For each bank, we compare the three models: a linear trend model to demonstrate continuous increase, a fixed regime change regression model with two states with the change occurring at a specific point, and a variable regime change regression model with optimal number of regimes and change dates identified by a Gaussian HMM. For each model, we compute the root-mean-square error (RMSE) measure using the same estimation window. We denote the RMSE values for FixRCR, VarRCR and the linear trend model with the abbreviations $RMS{E}_{\mathrm{FixRCR}}$, $RMS{E}_{\mathrm{VarRCR}}$ and $RMS{E}_{\mathrm{LinTrend}}$, respectively. Two comparisons follow:

(1)

If either stepwise model—the FixRCR or the VarRCR—achieves a lower RMSE than the linear trend model, i.e., $RMS{E}_{\mathrm{FixRCR}}<RMS{E}_{\mathrm{LinTrend}}$ or $RMS{E}_{\mathrm{VarRCR}}<RMS{E}_{\mathrm{LinTrend}}$, then discrete regime shifts explain changes in liquidity positions better than a single smooth time trend.

(2)

If the VarRCR model shows a lower RMSE than that of the FixRCR model, i.e., $RMS{E}_{\mathrm{VarRCR}}<RMS{E}_{\mathrm{FixRCR}}$, then the additional, HMM-identified dummy variables improve the model’s fit beyond a single, pre-set break date.

The model with the lowest RMSE is deemed the best explanation of the data. In addition to RMSE comparisons, we compare BIC values associated with the models in the same fashion. BIC measures model complexity and goodness of fit in a balanced way. Because BIC penalizes additional parameters, smaller values indicate a better fit–parsimony trade-off; accordingly, we prefer the model with the lowest BIC.

As a complementary procedure to our selection metrics, we quantify uncertainty around fit by constructing block-bootstrap, percentile-based 95% confidence intervals (CIs) for two bank-level contrasts by first calculating $\Delta {\mathrm{RMSE}}_{\mathrm{LinTrend}\mathrm{vs}\mathrm{Stepwise}}$, and then $\Delta {\mathrm{RMSE}}_{\mathrm{FixRCR}\mathrm{vs}\mathrm{VarRCR}}$ as follows:

$$\begin{array}{cc}\hfill \Delta {\mathrm{RMSE}}_{\mathrm{LinTrend}\mathrm{vs}\mathrm{Stepwise}}& ={\mathrm{RMSE}}_{\mathrm{LinTrend}}-min\{{\mathrm{RMSE}}_{\mathrm{FixRCR}},{\mathrm{RMSE}}_{\mathrm{VarRCR}}\},\hfill \\ \hfill \Delta {\mathrm{RMSE}}_{\mathrm{FixRCR}\mathrm{vs}\mathrm{VarRCR}}& ={\mathrm{RMSE}}_{\mathrm{FixRCR}}-{\mathrm{RMSE}}_{\mathrm{VarRCR}}.\hfill \end{array}$$

We obtain the intervals via a circular moving-block bootstrap with four-quarter blocks (2000 resamples), using in-sample residuals to compute RMSE. Intervals that exclude zero indicate a statistically meaningful difference in fit. For the first contrast, a CI entirely greater than 0 implies that the better of FixRCR/VarRCR achieves a lower RMSE than the linear trend model; for the second, a CI entirely greater than 0 implies that the VarRCR model achieves a lower RMSE than the FixRCR model.

3. Data Acquisition and Preparation

For this study, we utilize micro-level regulatory quarterly banking data provided by the Federal Financial Institutions Examination Council (FFIEC), focusing specifically on the call reports. These reports contain detailed quarterly balance sheet and income statement information, which are essential for constructing liquidity metrics that can serve as proxies for a “reserve ratio”. Micro-level call report data for U.S. depository institutions in its current form has been publicly available since 2002:Q4.

Each bank files a quarterly call report with its regulator (such as the Federal Reserve Bank) consisting of two main components: (i) the Report of Condition, which corresponds to the bank’s balance sheet, and (ii) the Report of Income, which corresponds to the bank’s income statement.

The Federal Reserve Bank publishes a data dictionary, known as the Micro Data Reference Manual (MDRM), which provides standardized descriptions for each call report item. Each item is identified by a mnemonic composed of four letters followed by four digits—for example, RCON2170, where “RCON” denotes the Report of Condition and “2170” corresponds to the total assets line item. With over 2000 data items per report for each bank, the MDRM is essential for navigating and interpreting the dataset.

A notable complication with the data is that certain item definitions change over time due to regulatory revisions. Researchers must exercise caution to ensure consistent use of data series across the study period. The Uniform Bank Performance Report (UBPR), which summarizes call report data, is particularly helpful in this regard, as it documents how key variables are constructed and how they evolve with regulatory changes. This UBPR report is also publicly accessible through FFIEC.

Given the dynamic nature of the banking sector—where institutions may merge, fail, or exit the market—we restrict our sample to banks that have complete data coverage for the full period of analysis. Any bank with missing observations is excluded from the sample.

Variable Definition and Sample Selection

With the general data background established, we now describe the construction of the key variables used in this study. Our sample spans from 2002:Q4 to 2015:Q4, capturing the period before and after the implementation of the Federal Reserve’s interest-on-reserves policy in 2008:Q4.

The primary liquidity measure we construct is the Reserves at the Fed-to-Deposits Ratio (RFDR) for the purposes of our study. It is a novel ratio which proxies for a bank’s reserve ratio and reflects its liquidity position. This ratio captures the extent to which a bank holds liquid reserves with the Fed relative to its deposit liabilities. For the numerator of this ratio, we use the call report item RCFD0090 (“Balances Due from Federal Reserve Banks”), which represents the reserves each bank holds at the Federal Reserve. These balances earn interest under the post-2008 regime and function as liquid assets that cushion against unexpected deposit outflows. For the denominator of this ratio, we use the call report item RCON2200 or RCFD2200 (“Deposits in Domestic Offices”), depending on the call report filed by the bank, representing total domestic deposits. This reflects the primary liability against which reserve liquidity is maintained.

There are more than 5000 banks in the U.S. during the period of study. We categorize banks into five groups based on asset size to facilitate our primary analysis: (i) banks with total assets exceeding USD 100 billion, (ii) banks with assets between USD 10 billion and USD 100 billion, (iii) banks with assets between USD 3 billion and USD 10 billion, (iv) banks with assets between USD 1 billion and USD 3 billion, and (v) banks with assets less than USD 1 billion.

To ensure consistency, we exclude banks with any missing data used in constructing the RFDR ratio during the sample period. As a result, our final sample composition is included in

Table 1. Bank counts by asset size group.

Group (Asset Size)	Total Number of Banks	Number of Banks with Incomplete Data	Number of Banks Analyzed
Group 1: Assets more than USD 100B	30	6	24
Group 2: Assets between USD 10–USD 100B	112	55	57
Group 3: Assets between USD 3–USD 10B	227	121	106
Group 4: Assets between USD 1–USD 3B	495	371	124
Group 5: Assets less than USD 1B	2837	2793	44

.

In addition to asset size, we further assess whether the timing and nature of liquidity regime changes vary across geographic region and chartering authority. For geographic region, we partition banks into four U.S. regions—Northeast, Midwest, South, and West. For regulation, we classify banks by their primary federal supervisor—FDIC (state nonmember), Federal Reserve (state member), and OCC (national banks)—and repeat the analysis.

Table 2. Bank counts by geographic region and regulator.

Dimension	Group	Total Number of Banks	Number of Banks with Incomplete Data	Number of Banks Analyzed
Geographic Region	West	1341	1273	68
	South	3893	3736	157
	Northeast	1140	998	142
	Midwest	4209	4052	157
Regulator	FDIC	6561	6290	271
	FED	1585	1457	128
	OCC	2477	2339	138

provides the number of banks within each group by geographical region and also by regulator.

Throughout the study, we present the results of our analysis for each group based on asset size, geographic location, and regulator. This allows us to assess whether the identified regime change patterns and shifts in liquidity ratios are consistent across institutions.

By systematically comparing results across the aforementioned groups, we are able to detect whether our findings are driven by a particular segment of the banking sector, geographic location, or regulator, or whether they hold more broadly. This approach provides multiple opportunities to discuss and interpret differences and similarities in outcomes across sub-samples, thereby fulfilling the purpose of a traditional robustness analysis.

4. Results and Discussions

In this section, we present the results of our analysis in response to the three research questions outlined in Section 1. Section 4.1 reports findings from our primary analysis of banks grouped by asset size. Section 4.2 examines results by geographic region and regulatory authority. Finally, Section 4.3 extends the VarRCR framework to compare the pre- and post-COVID-19 periods.

4.1. Results by Bank Asset Size

We report findings separately for banks within each of the five aforementioned groups. For each group, we identify banks with improving liquidity positions, compare the fit across the linear trend, FixRCR, and VarRCR models by RMSE and BIC measures, and visualize the regime change timing. We present the results for Group 1 in detail to illustrate the full workflow; the rest of the groups are reported in condensed form, highlighting similarities and differences.

The liquidity positions for Group 1 banks improved during the period (2002:Q4–2015:Q4) under study. This is observed via the positive and significant beta coefficient for the time variable t that demonstrates continuous increase in the linear trend model. Out of the 24 banks in our sample of banks in excess of USD 100 billion in assets, 23 banks have positive and significant beta coefficients.

For those 23 banks that had an increase in their liquidity, we investigate whether these changes are gradual with a constant rate or stepwise, and if they are stepwise, we further look into the timing of these increases. For this, we compare the three models described in Section 2: a continuous linear trend, a fixed regime regression (FixRCR) and a variable regime regression (VarRCR), assessing fit with RMSE and BIC.

Before discussing the results in detail, we present the visualizations in Figure 3 for the largest four U.S. banks by asset size: Bank of America, Citibank, JPMorgan Chase, and Wells Fargo. These banks make up roughly half of all the banking deposits and assets in the U.S.

The top panel for each bank includes the linear trend line. The panel in the middle includes the line associated with the FixRCR model, where we assume that the regime change occurred at a fixed point at the policy change date at 2008:Q4. Based on these graphs, we can see that manually selected breakpoints do not always align well with the actual shifts in liquidity behavior observed in the data. In many cases, the regime change dummy variable fails to capture the true turning points, leading to a poor model fit. The panel at the bottom visualizes the fitted line associated with the VarRCR model, where we identify the number of regimes and regime change dates using a Gaussian HMM.

To illustrate how one can read off and interpret from Figure 3, let us focus on subfigure (d) for Wells Fargo. The linear trend regression (top panel) captures the overall upward direction but smooths over the sharp structural break after 2008, overstating reserves in the pre-crisis period and understating the discrete jumps observed thereafter. The fixed-date dummy model (middle panel) improves on this by introducing a one-time step at 2008:Q4, but it fails to capture the continued buildup of reserves in the years following the crisis. By contrast, the variable-date dummy model using Gaussian HMMs (bottom panel) provides the closest fit, identifying multiple endogenous breakpoints that align with both the initial jump during the crisis and the subsequent upward shifts around 2012–2013. This stepwise adjustment suggests that Wells Fargo’s reserve accumulation was not a single event but an ongoing, multi-phase process of liquidity rebalancing.

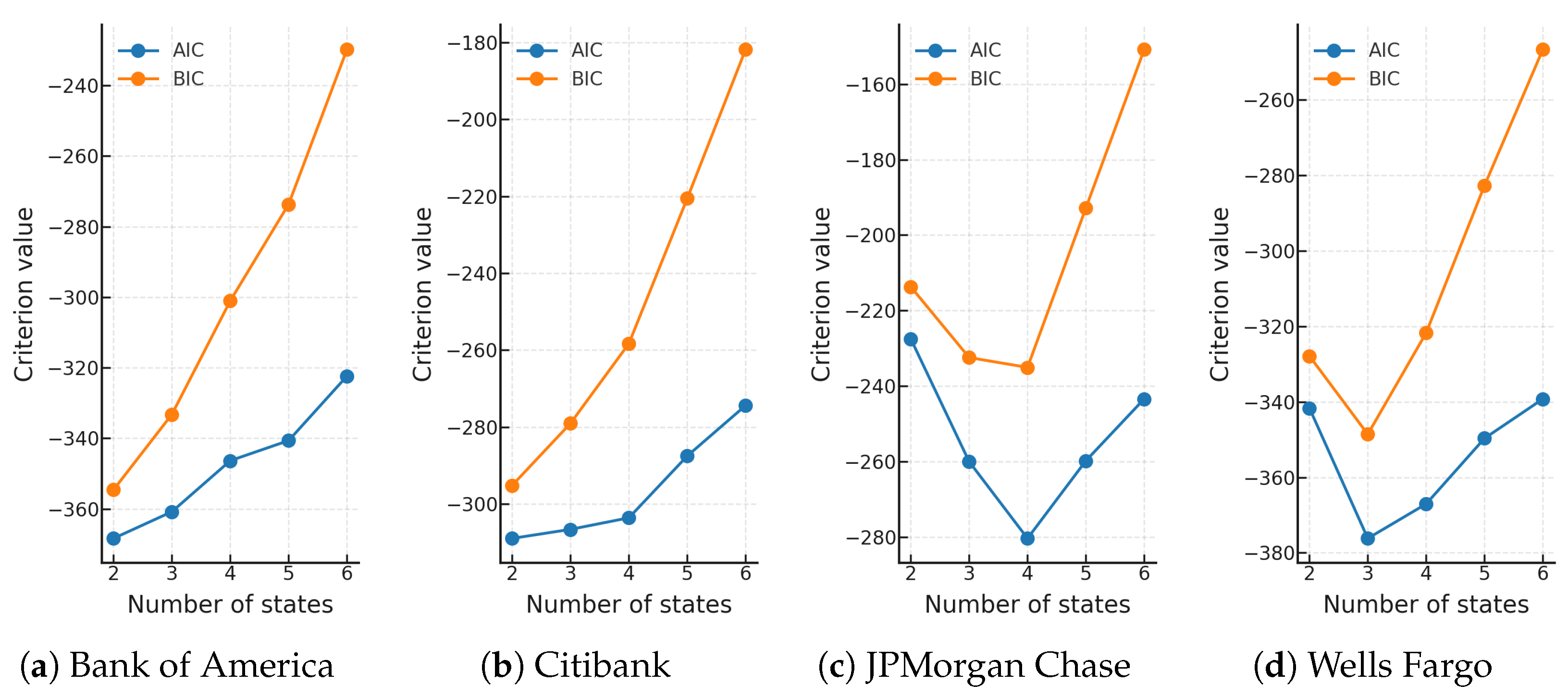
Before fitting the VarRCR models, we first determine the optimal number of states for each bank using the Gaussian HMM method introduced in Section 2. For each bank, we estimate models with two to six states and compare their Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) values to select the model with the lowest value. Figure 4 presents the AIC and BIC values for the four largest banks, illustrating how the optimal number of states are chosen. Once the number of states is determined, the corresponding regime change dates proposed by the HMM procedure are used to construct the fitted VarRCR lines shown in the bottom graph for each bank in Figure 3.

In addition to the visual inspection presented given in Figure 3,

Table 3. Model comparison by RMSE and BIC for the four largest U.S. banks. A model with a lower BIC value is preferred to a model with a higher BIC. The same is also true for RMSE.

	RMSE			BIC
Bank	LinTrend	FixRCR	VarRCR	LinTrend	FixRCR	VarRCR
Bank of America	0.0277	0.0217	0.0196	−221.84	−247.74	−258.52
Citibank	0.0396	0.0252	0.0263	−183.96	−231.68	−227.31
JPMorgan	0.0567	0.0763	0.0237	−145.91	−114.46	−230.55
Wells Fargo	0.0319	0.0449	0.0197	−206.70	−170.70	−254.20

provides a comparison of RMSE and BIC values corresponding to all three models for the largest four U.S. banks. The VarRCR model clearly outperforms both the linear trend model and FixRCR model for Bank of America, JPMorgan, and Wells Fargo. Only for Citibank, the FixRCR model yields the best RMSE and BIC, while VarRCR remains close in performance.

Based on RMSE and BIC comparisons, for 22 out of 23 banks in Group 1, stepwise regime changes (either FixRCR or VarRCR) explain changes in liquidity positions better than a linear trend model.

The next question we investigate is the timing of these regime changes. Identifying the regime change dates (as in VarRCR) instead of using a set date (as in FixRCR) worked much better for most of the banks in Group 1. Except for three banks, VarRCR either outperformed or achieved FixRCR’s RMSE and BIC values.

We performed a complementary procedure to quantify uncertainty around model fit for the banks in Group 1. Block-bootstrap 95% confidence intervals for the difference in RMSE values (ΔRMSE) indicate that stepwise models—the FixRCR or the VarRCR—are significantly better than a linear trend model in 11 of the 23 banks, with 0 of the 23 banks favoring linear trend model and 12 of the 23 banks showing no significant difference. For the VarRCR vs FixRCR comparison, confidence intervals show 4 of the 23 banks favor the VarRCR model, 0 of the 23 banks favor the FixRCR model, and 19 of the 23 banks show no significant difference. This supports our observation that stepwise regime change models, i.e., the FixRCR or VarRCR models, explain changes in banks’ liquidity positions better than a linear trend model, and the VarRCR model generally matches—or improves upon—the performance of the FixRCR model.

Table 4. Group-level model comparison based on RMSE and BIC. Note that the percentages are the share of banks meeting each criterion.

			Stepwise Models Outperform Linear Trend Model		VarRCR Model Outperforms or Achieves FixRCR Model
Group	Number of Banks Analyzed	Number of Banks with Increasing Liquidity	RMSE	BIC	RMSE	BIC
Group 2	57	49	94%	94%	96%	94%
Group 3	106	80	96%	96%	95%	91%
Group 4	124	103	97%	97%	95%	91%
Group 5	44	35	94%	94%	97%	92%

includes a similar comparison for the banks in Groups 2–5. For the banks in each group, we list the number of banks analyzed and how many of them demonstrate an increase in their liquidity positions during the period under study. Among those banks, we include the percentage of banks where a stepwise model, either FixRCR or VarRCR, better explains the increase in liquidity positions than a linear trend line based on RMSE and BIC comparisons. In the last two columns, we compare the performance of VarRCR and FixRCR, and the percentage of banks for which VarRCR outperforms or achieves FixRCR’s RMSE and BIC values. Across all groups, stepwise models overwhelmingly outperform the linear model, and VarRCR is at least as good as, and often better than, FixRCR.

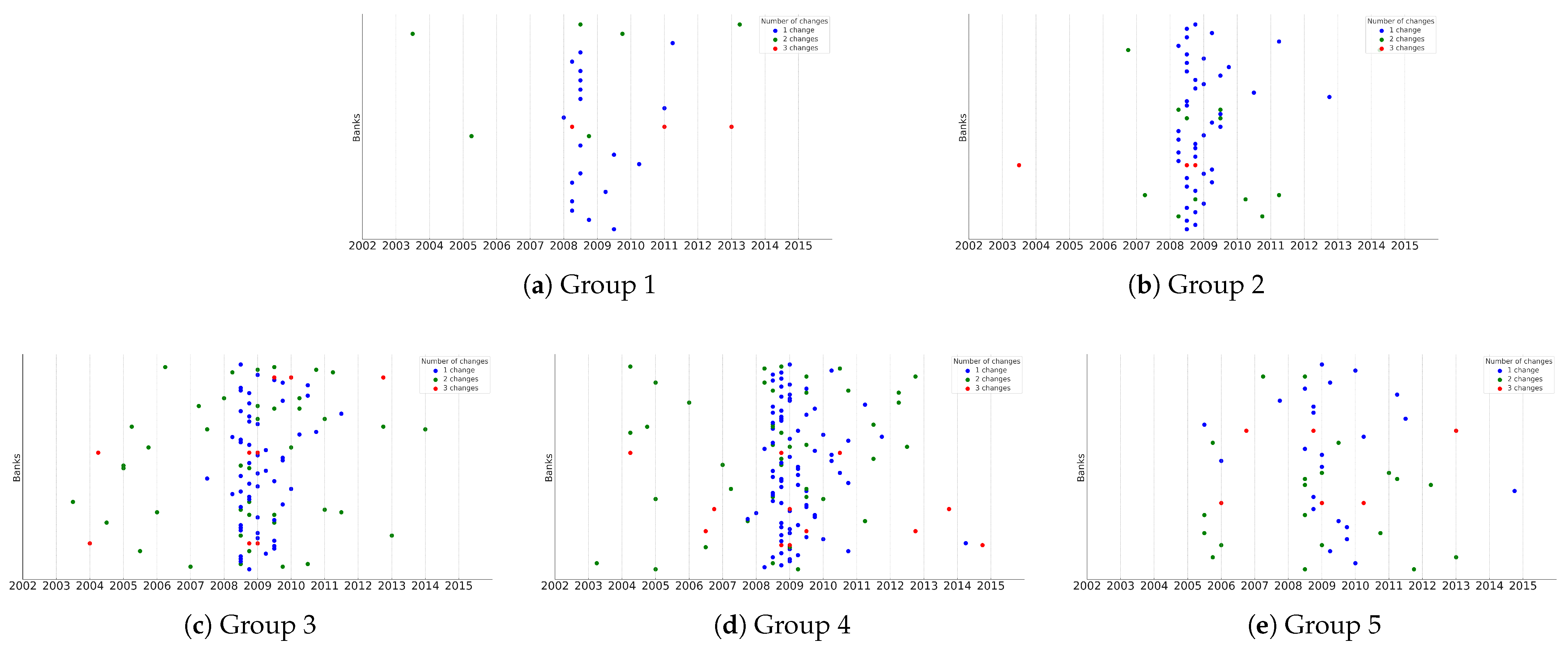
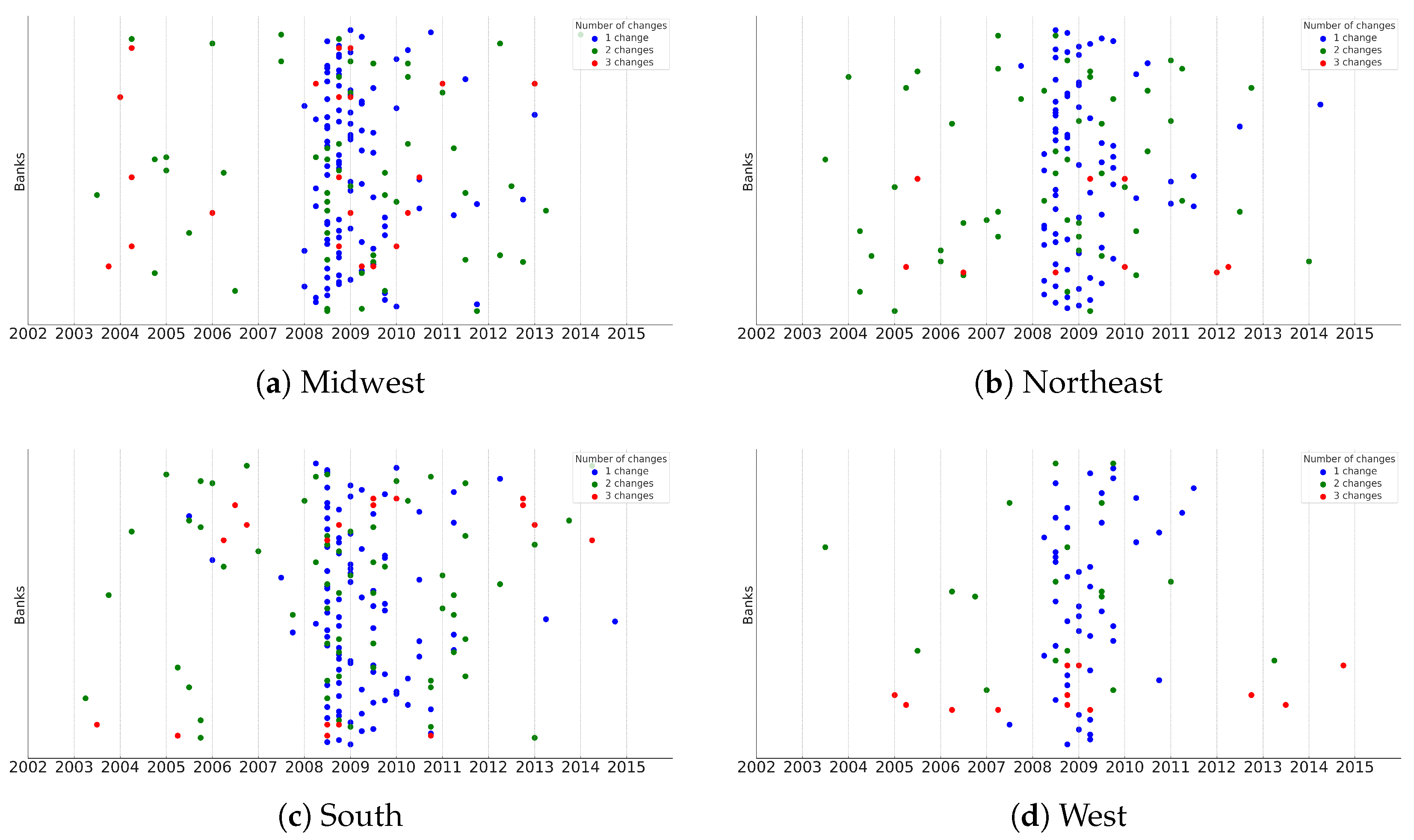
To complement the results of the model comparison, we also examine the timing of regime changes. Figure 5 presents the estimated liquidity regime change points for Groups 1–5. The horizontal axis corresponds to the year/quarter of a detected change, while the vertical axis has all banks within the corresponding group lined up from top to bottom by alphabetical order. Bank names are suppressed for clarity, with each row representing one bank. The color of each marker reflects the total number of regime changes experienced by that bank during the sample period: blue for one change, green for two changes, and red for three changes. This visualization highlights both the timing and the relative frequency of regime shifts across banks within each group.

Across all groups with the exception of banks within Group 5, a visual inspection suggests that the majority of regime changes are concentrated in periods between 2008 and 2010. The regime change dates seem to be more spread out for community banks in Group 5, while regional banks in Group 3 and Group 4 have regime change dates clustered around 2009. Additional, though smaller, concentrations appear in the early 2010s.

Banks with a single detected change tend to maintain stability after the initial transition, while those with multiple detected changes show repeated shifts, suggesting greater sensitivity to market or regulatory conditions. Later periods in the sample show relatively few regime changes, indicating a stabilization of liquidity positions following the crisis and subsequent regulatory adjustments.

4.2. Results by Geographic Region and Regulator

In this section, we report findings separately for banks grouped by geographic region and by primary regulator. For each group, we identify institutions with improving liquidity positions, compare model performance across the linear trend, FixRCR, and VarRCR frameworks using RMSE and BIC metrics, and visualize the timing of regime changes.

Table 5. Model comparison by geographic region based on RMSE and BIC.

			Stepwise Models Outperform Linear Trend Model		VarRCR Model Outperforms or Achieves FixRCR Model
Geographic Region	Number of Banks Analyzed	Number of Banks with Increasing Liquidity	RMSE	BIC	RMSE	BIC
Midwest	157	127	98%	98%	95%	91%
Northeast	142	1103	94%	93%	94%	91%
South	157	129	95%	95%	98%	95%
West	68	58	97%	97%	95%	93%

and

Table 6. Model comparison by bank regulator based on RMSE and BIC.

			Stepwise Models Outperform Linear Trend Model		VarRCR Model Outperforms or Achieves FixRCR Model
Regulator	Number of Banks Analyzed	Number of Banks with Increasing Liquidity	RMSE	BIC	RMSE	BIC
FDIC	271	216	96%	96%	96%	94%
FED	128	103	96%	96%	93%	89%
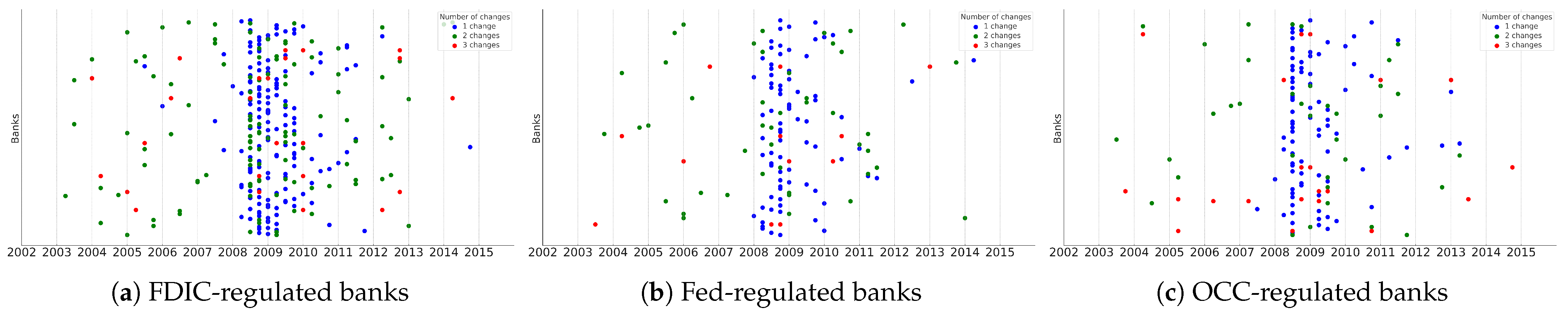
OCC	138	109	95%	95%	95%	93%

report a corresponding comparison for banks grouped by geographic location and by primary regulator, respectively.

Across both geographic and regulatory groups, stepwise models consistently outperform the linear benchmark, with VarRCR performing at least as well as, and frequently better than, FixRCR.

To complement the model comparison results, we examine the timing of regime changes. Figure 6 and Figure 7 display the estimated liquidity regime change points for banks grouped by geographic location and by primary regulator, respectively.

Across both cuts, the qualitative patterns mirror the full sample: regime changes cluster around major policy episodes (especially the one in late-2008), transitions into higher-liquidity states are persistent, and banks exhibit abrupt jumps rather than steady gradual increases. Preliminary visual inspection suggests regime change timings are closely aligned across regions and regulators, indicating limited systematic dispersion in adjustment timing.

These results suggest that while individual banks adjust at different speeds, the broad transmission of policy to bank-level liquidity is geographically and regulatorily widespread. Any differences that do appear are modest in magnitude and do not overturn our main conclusion that post-policy adjustments are discrete and often multi-phase rather than purely smooth.

4.3. Extending VarRCR to COVID-19 Era

The primary scope of our work is to understand banks’ liquidity regime changes during and after the post-IOR period, where majority of the banks experienced rising liquidity. While our analysis centers on this environment, our framework can be adapted to other settings by modestly revising the model structure or incorporating episode-specific information.

To demonstrate this, we partially extend the analysis to the COVID-19 period using the same liquidity ratio over 2017:Q1–2023:Q2 (26 quarters) for the four largest U.S. banks. The period under study centers the onset of COVID-19 (2020:Q1–Q2) and spans 12 quarters before and 12 after, consistent with our baseline design.

We estimate the same HMM specification as in the main analysis and focus on models with three breakpoints (yielding four regimes). The macro-policy backdrop features quantitative tightening (QT) in 2017–2019, quantitative easing (QE) during 2020–2021, and a return to QT from 2022 onward. Figure 8 shows the actual liquidity ratios together with the VarRCR model fit for these banks during this period, highlighting the applicability of our framework to a distinct policy and liquidity environment.

Consistent with these phases, we expected the liquidity ratio to decline during QT and rise during the pandemic/QE interval. The results align with this pattern: for each of the four banks, the HMM identifies a low-liquidity regime during 2017–2019, a shift to a higher-liquidity regime in 2020 (typically commencing in mid-2020), and evidence of moderation/partial reversion beginning in 2022 under renewed QT, with bank-specific heterogeneity in the timing and magnitude of these transitions.

5. Conclusions

This paper investigated how U.S. banks adjusted their liquidity positions during and after the 2008 financial crisis in a new policy environment. Using quarterly call report data from 2002–2015, we constructed bank-level liquidity ratios and applied Gaussian Hidden Markov Models (HMM) to detect regime shifts in liquidity behavior. These model-identified dates were then incorporated into bank-specific dummy variable regressions, allowing us to estimate structural breaks in liquidity trends without imposing a priori assumptions on timing. Lastly, we briefly explored the effects of the more recent post-COVID-19 inflationary environment, where banks faced a very different macroeconomic shock compared to the 2008 crisis.

Our findings provide several important insights. First, banks across the spectrum of asset sizes, geographic region, and regulators substantially increased their liquidity positions in the post-crisis period. Second, these adjustments were not gradual, continuous trends but instead occurred in distinct, stepwise shifts. Finally, the timing of these regime changes varied across institutions: while the general upward movement in liquidity was consistent, individual banks displayed heterogeneous adjustment dates, and in some cases, multiple structural breaks.

Taken together, these results suggest that the post-crisis transformation in bank liquidity was both profound and heterogeneous. Although aggregate data show a sharp improvement in liquidity positions after the crisis, our bank-level analysis reveals that this transformation was not instantaneous nor uniform across institutions. By demonstrating robustness across different bank size groups, geographic region, and regulators, our study provides a richer and more nuanced account of how liquidity positions evolved in the wake of the crisis and policy changes.

Our results give supervisors and bank treasurers a timed map of institution-specific liquidity regime shifts rather than only aggregate trends. Using quarterly call reports, we infer each bank’s break dates with an HMM and then classify behavior across regimes—distinguishing abrupt, stepwise adjustments from gradual drifts—so stakeholders can see who adjusted, when, and by how much (useful for targeted exams, stress-testing overlays, and evaluating reserve-remuneration policy).

While our evidence centers on the Reserves-at-Fed-to-Deposits ratio (RFDR), the regime-detection framework is agnostic to the specific liquidity metric and applies equally to alternative series. In future work, we plan to extend the analysis to cash+reserves/total assets, securities/total assets (and a High-Quality Liquid Asset-style (HQLA) proxy: cash + Treasuries + agency MBS), loans-to-deposits (inverse liquidity), wholesale-funding reliance (fed funds/repo/brokered-deposit share), and unused commitments/total assets. We will also construct a composite liquidity index (e.g., first principal component of these measures) and report concordance of break dates across proxies to assess robustness. These extensions will allow us to evaluate whether the smooth-versus-abrupt adjustment patterns documented here persist across broader facets of bank liquidity management.

Another extension of our work would be applying the regime-detection framework to broader settings. Our current analysis focuses on liquidity regime changes between 2002 and 2015. In addition, we implemented the same model for the COVID-19 era, examining the four largest banks with an exogenously specified number of regimes. The results are promising, but the model can be further refined to identify regime change dates without relying on external information. Such extensions would enhance its applicability across a wider range of financial settings.