Abstract
The growing frequency of news arrivals, partly fueled by the proliferation of data sources, has made the assumptions of the classical probability of informed trading (PIN) model outdated. In particular, the model’s assumption of a single type of information event no longer reflects the complexity of modern financial markets, making the accurate detection of information types (layers) crucial for estimating the probability of informed trading. We propose a layer detection algorithm to accurately find the number of distinct information types within a dataset. It identifies the number of information layers by clustering order imbalances and examining their homogeneity using properly constructed confidence intervals for the Skellam distribution. We show that our algorithm manages to find the number of information layers with very high accuracy both when uninformed buyer and seller intensities are equal and when they differ from each other (i.e., between 86% and 95% accuracy rates). We work with more than 500,000 simulations of quarterly datasets with various characteristics and make a large set of robustness checks.
Keywords:
multilayer probability of informed trading; MPIN; layer detection algorithm; cluster analysis; information asymmetry; private information JEL Classification:
c13; c38; G14; G17
1. Introduction
The central question addressed in this paper is “how many information layers (or types) exist in a financial dataset?”. We rely on one of the most frequently used informed trading measures in the literature, which is the probability of informed trading (PIN) of Easley et al. (1996). It is evident that any data (e.g., stock-quarter) in current financial markets is likely to include various information events that may generate information asymmetries of unequal impacts.1 This, in turn, directly challenges the main assumption in the broadly used PIN measure: that all the information events in a dataset are of a unique type, meaning they have a uniform impact on trading activity. The model has two additional assumptions: (i) at most one information event occurs per day; (ii) all the information events occur outside of trading sessions. These assumptions are also restrictive and designed so that the aggregated impact of multiple events per day or the partial impact of an information event on a day would contradict the assumption of uniformity in information events’ impacts observed daily. Thus, detecting various levels of information asymmetries in data not only spots independent information events with different magnitudes but also incorporates partial and aggregated information effects on each day. Therefore, knowing the number of information types in the data provides a better understanding of information asymmetry in financial markets.
Our paper addresses the challenge of accurately detecting the number of different information layers in financial data. We present an algorithm that analyzes financial data and categorizes information days into layers with distinct impacts on trading activity, thereby determining the number of these layers. Thus, our final output is the number of information types in data. This output is of importance for two main reasons. First, it is a useful standalone information that can be utilized by researchers and practitioners in the financial markets. Comparisons among individual assets or asset classes and through different time periods or markets can add value. For example, Ghachem and Ersan (2023a) compare the number of associated information types in small and large stocks listed in NASDAQ Stockholm. They show that on average, quarterly data for large stocks exhibit more types when compared to the one for small stocks. A larger number of information types, reflecting the existence of several distinct levels of information asymmetry, implies that the examined asset and period might be associated with a diversity of related information events. While for datasets with a single information type, researchers and practitioners can rely on the traditional PIN model and its estimates, they should be cautious in the case of multiple information types. Second, our output, i.e., the number of information layers, can also be used as a preliminary variable in estimating the probability of informed trading, for instance, via a straightforward generalization of the PIN model that retains its main features but allows for the presence of multiple information layers, i.e., information types with different impacts on trading activity (See Ersan 2016).2
Ersan (2016) devises an algorithm to estimate the number of information layers in datasets. If the rates of uninformed traders on the buy side and sell side are assumed equal to each other, this algorithm, with no adjustment to the data, has high accuracy rates, i.e., up to 96% for our simulated datasets. Theoretically, it is sensible to expect similar rates of uninformed buys and sells.3 Nevertheless, based on market conditions and overall supply and demand, these rates may differ from each other. For example, uninformed traders may place a larger number of sell orders due to the scarcity of funding through a credit crunch (Lin and Ke 2011). Slightly relaxing the assumption of equal rates on the buy and sell sides significantly reduces the estimation power of the algorithm in Ersan (2016), dropping it to as low as 24% in our tests. Ersan (2016) suggests adjusting the data in cases where the uninformed rates are assumed to be unequal. The suggested adjustment utilizes the minimum levels of buys and sells (buyer-initiated and seller-initiated trades) in a dataset as proxies for uninformed buys and sells. This relies on the assumption that the day with the minimum number of buys (sells) should be of the type of days with no positive (negative) events, thus a representative of uninformed buy (sell) rates. While implementing the layer detection algorithm with the proxy-adjustment improves the layer estimation in the case of unequal informed rates, the overall precision is not sufficient especially when the number of layers is relatively large. More specifically, our tests reveal that the estimation accuracy decreases monotonically with the simulated number of layers in a dataset, i.e., 99% for one-layer datasets while around 62% (43%) for four (eight) layer datasets.
In this paper, we provide a new algorithm with two main improvements to the algorithm of Ersan (2016), both at the level of the data adjustment and the detection of the information layers. Our algorithm not only provides very high accuracy in the detection of the information layers in the data, but also fares considerably well in the exact detection of the no-information days in the data. We identify the number of information layers correctly in more than 94% (86%) of the simulations with one (eight) layer(s) when two uninformed rates differ from each other by up to 25%-fold. Both academicians and practitioners can easily use our introduced algorithm and compare it to other algorithms that detect information layers via the use of corresponding functions and arguments in the PINstimation package of the R software.4 Researchers can also inspect the implementation of the algorithm proposed in this paper since the code is open-source and available on the GitHub and CRAN platforms.5
An accurate identification of the number of information layers might lead to significant improvements in the informed trading estimates. Ersan (2016) provides three sets of empirical evidence comparing the performances of the PIN and MPIN models. First, the study shows that only 4% of the quarterly datasets involve a single type of information event, as assumed in the PIN model, while around 75% of the datasets involve two to five layers of information with impacts of different magnitudes. This finding aligns more closely with our perception of the recent financial markets and provides supporting evidence for the validity of our main research question. Second, the estimation results using both the PIN and the MPIN model indicate that the PIN model estimates all the parameters (i.e., information event occurrence probability, bad-event probability, uninformed trading intensities, and informed trading intensity) and the probability of informed trading with marginal errors when there is a single information type (e.g., 0.1% mean absolute error for PIN estimates). However, the estimation errors become substantially high when the data contains two to eight information layers (e.g., MAE of above 4% for PIN; much larger errors for model parameters). The large estimation errors are independent of the number of layers implying that the PIN model performs well only in the case of a unique information type in the data, which is in line with the model’s main assumptions. In contrast, the MPIN model estimates the probability of informed trading as well as all the parameters with consistently high accuracy for datasets with one to eight information layers (e.g., MAEs for PIN that is 0.1% for all types of datasets). Third, using real data on 361 stocks listed on the Turkish stock exchange, the estimated probability of informed trading is significantly higher with the MPIN model, reflecting the model’s added value in capturing multiple information types in data (23.7% and 31.9% on average for the PIN and MPIN models, respectively).
The paper has the potential to contribute to two branches of literature. The first branch consists of studies proposing the extensions and modifications of the original PIN model. Due to concerns about the validity of the underlying assumptions, extended models have been suggested. Duarte and Young (2009) introduce the adjusted probability of informed trading that incorporates the probability of a liquidity shock relaxing the assumption of attributing all the excess trading to informed trading. The paper shows that the liquidity component, rather than the informed trading component, influences stock returns. Brennan et al. (2018) consider the daily conditional probabilities of information events derived from unconditional probabilities in the PIN model. Brennan et al. (2016) further differentiate between informed trading through good and bad event days. They show that PIN through bad events is priced while the other is not. Ersan (2016) proposes a multi-layer probability of informed trading that relaxes the assumptions of a single type of information event with constant impact, a single event per day, and information events occurring only outside of trading hours. Our paper proposes a new algorithm that assumes and accurately detects multiple information layers in trading data, and, thereby, aims to enhance our understanding of the nature of informed trading in modern complex trading environments.
Secondly, our paper is related to the works that focus on the challenges of the estimation of PIN models using maximum likelihood estimation. These challenges fall essentially into two categories: the floating-point exception and the convergence to a local maximum (and boundary solutions). The issue of floating-point exception is addressed mainly through the introduction of the logarithmic factorizations of the corresponding likelihood functions (e.g., Easley et al. 2010; Lin and Ke 2011). These logarithmic factorizations aim to prevent overflow problems that would arise due to the large numbers in the power terms, and it is shown that they may lead to unbiased PIN estimates. As an alternative approach, Jackson (2013) suggests rescaling the daily trade numbers. Ke et al. (2019) show that the use of factorization is more stable when compared to scaling. As for the issue of local maxima, researchers address this challenge by suggesting strategies for the determination of relevant initial parameter sets to prime the maximum likelihood estimation. Yan and Zhang (2012) suggest the use of multiple sets derived from a grid search algorithm, aiming to uniformly cover the parameter space. Gan et al. (2015) propose that a single initial parameter set derived via a clustering algorithm is sufficient in estimating the PIN model. Ersan and Alıcı (2016) suggest the use of a clustering algorithm generating a limited number of initial sets that lead to unbiased PIN estimates in a time-efficient manner. Cheng and Lai (2021) developed two strategies to derive initial parameter sets for the adjusted PIN model, namely using a grid-search algorithm and an approximation of the compound Poisson distribution using a bivariate normal distribution. The relaxation of the assumption of a single information type in trading data brings forth a new challenge to the maximum likelihood estimation of the PIN model: the beforehand determination of the number of information layers in the data.6 It follows that a correct detection of information layers in the data is essential for an accurate estimation of informed trading. Our paper provides an empirically robust algorithm to address this new challenge and accurately detect the number of layers in the datasets.
Our study may also contribute to the extensive literature on informed trading that relies on the probability of informed trading (PIN) models. These works cover diverse topics such as PIN around news arrivals (e.g., Aktas et al. 2007; Duarte et al. 2015; Dang et al. 2024) and pricing of PIN (Duarte and Young 2009; Lai et al. 2014; Brennan et al. 2016). By providing an accurate detection of information types, and thereby, more accurate estimates of informed trading, our algorithm can enhance future studies within the field. Additionally, our study relates to the broader literature that develops new measures or proxies for informed trading for examining the recent financial markets (e.g., Berkman et al. 2014; Roşu 2019; Yang et al. 2020; Boehmer et al. 2021; Lof and van Bommel 2023; Bogousslavsky et al. 2024).
The relevance of our paper is more pronounced in today’s evolved financial markets. In fact, detecting and quantifying informed trading from intraday data have become excessively challenging due to recent developments in financial markets. Markets have witnessed a significant increase in trade intensity, driven by the growing involvement of high-frequency trading (HFT) as well as advancements in financial technology (fintech). High-frequency trading, characterized by the placement of a large number of orders at extremely high speeds, has revolutionized the market dynamics. In the last 15 years, HFT has constituted more than half of the activity in developed markets (e.g., Brogaard 2010; Bazzana and Collini 2020). O’Hara (2015) points out that SEC data reflects that 98% of all orders are canceled while 23% are within 50 milliseconds. HFT activity has diverse and dynamic effects on non-HFTrs (e.g., competition, profits, and crowding out), and on the markets (e.g., liquidity, volatility, and price formation). Fintech advancements have amplified these effects by enabling easier and more widespread access to financial services through digital platforms while at the same time introducing complexity and diversity to HFT strategies (e.g., Arifovic et al. 2019; Hendershott et al. 2021; Amnas et al. 2024). Moreover, fintech developments such as blockchain and machine learning have further increased the efficiency of transactions and endowed market participants with the Internet of Things (IoT), robo-advising, and data analytics (Chen et al. 2019; El Hajj and Hammoud 2023). As a result, these recent developments led to increased financial market participation, an excessive number of orders and trades, and complexity, namely due to more convoluted interactions among the diverse types of market participants and trading strategies. In this setting, it is hard to defend the assumption of a single type of information event. The sophistication and complexity of trading activity, the high numbers of actors, and the sensitivity of markets to news events all make the existence of multiple information types very plausible. In this respect, our paper provides the underlying “infrastructure” for the accurate detection of the types of information present in the data, allowing for an accurate estimation of the probability of informed trading.
The paper is organized as follows: Section 2 reviews the layer detection concept and describes the need for data adjustment. Section 3 details our data adjustment procedure and improved layer detection algorithm. Section 4 provides empirical evidence for the accuracy rates of the algorithm and the last section concludes.
2. Layer Detection and Data Adjustment
The algorithm of Ersan (2016) for finding the number of layers in trade data relies on the distribution of absolute order imbalance. The motivation behind the choice of the absolute order imbalance is the fact that informed trade intensity is common to both buys and sells in the same layer . We will show here that clustering data based on absolute order imbalance, defined as the absolute difference between buys and sells, lacks a defined distribution when the uninformed buy and uninformed sell rates differ from each other. To address this challenge, we show theoretically that clustering on absolute order imbalance remains effective if the data are adjusted prior to the clustering step. We show that this data adjustment is performed using the uninformed buy and sell rates. Since no-information days are the days featuring only uninformed traders, the uninformed buy and sell rates are calculated using trading data relative to these days.
We begin our theoretical investigation by defining the necessary notations. Note that refers to a Poisson distribution with parameter , while refers to the Skellam distribution with the parameters and , which is the distribution of the difference of two Poisson-distributed random variables with the parameters and , respectively. Recall that the Skellam distribution is the discrete probability distribution of the difference between two independent Poisson-distributed random variables with the means and . For example, if and , then the difference follows a Skellam distribution, denoted as . In our context, as the number of buys and the number of sells are both Poisson-distributed, the order imbalance , defined as the difference between buys and sells (), is also the difference between two Poisson-distributed random variables. Therefore, is Skellam-distributed. The distribution of the different trade intensities in the unadjusted data is displayed in Table 1.

Table 1.
Distribution of trade intensities in unadjusted data.
In the case of equal uninformed rates on the buy and sell sides (), and are symmetric around zero7, then and are identically distributed, enabling the use of absolute order imbalances in the Skellam distribution tests (Figure 1). In contrast, when , and are not identically distributed, and the absolute order imbalance for the unadjusted data does not have a well-defined distribution (Figure 2).
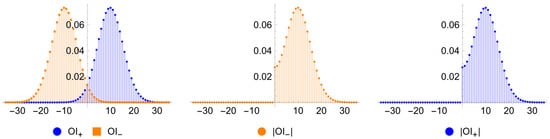
Figure 1.
Distribution of order imbalances when .
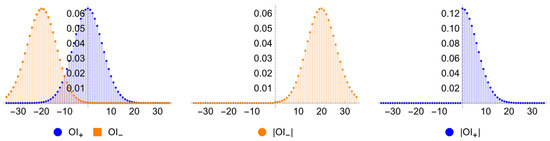
Figure 2.
Distribution of order imbalances when .
The simulations in Ersan (2016) have equal uninformed rates. Thus, the layer detection algorithm using absolute order imbalances in the unadjusted data successfully estimates the true number of layers in the simulated series. The paper proposes using the minimum daily values of buys and sells as an adjustment when relaxing the assumption of a uniform uninformed trading rate . This adjustment is applied when the levels of buys and sells on no-information days, denoted as and , are assumed to be different. Theoretically, the minimum number of buys (sells) in the data most likely belongs to a non-event day, and can, therefore, serve as proxies to uninformed buy (sell) rate. While the minimal values may proxy the uninformed rates, they are not necessarily precise estimates thereof. The main reason is that the uninformed buy (sell) rate is the average of all the intensities in all the days with no positive (negative) event. Thus, the minimal values most likely differ from the averages. Given the model assumption that buys (or sells) in any type of day follow a Poisson distribution, we do not expect large differences between the minimum and the mean values, especially when the trading intensity is high. In fact, our simulation results reveal that the accuracy rates in the use of proxy-adjustment can be as low as when the number of layers is relatively large, i.e., eight.
Our strategy of the adjustment of the data aims to derive more accurate estimates of uninformed rates as an initial step in layer detection. Let and be two Poisson-distributed random variables such that , and . We construct the adjusted buys and sells in layer as follows: and . The order imbalance for layer of the adjusted data is . We report the theoretical distributions of the trading intensities in the adjusted data in Table 2.

Table 2.
Theoretical distributions for trade intensities in adjusted data.
Since and are both Skellam-distributed with , and , then and are symmetrically distributed around . We show using the following two lemmas that and are identically distributed, which is the distribution of .
Lemma 1.
Let , with . Let with distribution function and with distribution function , then .
Proof.
See Appendix A. □
Lemma 2.
If , and , then , and are identically distributed.
Proof.
See Appendix A. □
Lemma 2 proves that the absolute order imbalance in cluster follows the distribution of , or —which are identically distributed. This was, indeed, the reason behind the data adjustment.
Clearly, is not Skellam-distributed, since the support of the Skellam distribution is while the support of is . By taking the absolute values, the negative order imbalances shift to the positive side. If the OI in layer centered on takes negative values with relatively significant probability, then taking the absolute value thickens the tail of the distribution of above , and the distribution will not behave as a Skellam distribution in the neighborhood of zero. However, if the mean of the observations is sufficiently higher than zero (the probability assigned to negative values is very low), then the distribution of observations can be approximated by a Skellam distribution.
From Table 2, we see that the cluster whose OI observations are closest to zero is the no-information cluster. In the information layer , the absolute order imbalance observations are centered on the corresponding excess trade intensity . Therefore, as long as the lowest informed trade intensity is sufficiently higher than zero , the approximation of the distribution of the observations with a Skellam distribution is justified.
In the MPIN model, and denote the means of the Poisson-distributed buys and sells on no-information days, as presented in Table 1. To estimate these means from our dataset, we first identify the no-information days, referred to as the no-information cluster. Given that the sample mean is the maximum likelihood estimator of the mean of a distribution, we use the average number of buys and sells on these no-information days as valid estimates for and . Our algorithm’s initial step is to identify the no-information days. After the identification, the averages of buys and sells are computed to provide the estimates for and , which will be utilized later for the data adjustment. In the subsequent steps, we identify the number of information layers by successively clustering the AOI* observations until all the observations within every cluster can be fitted in a confidence interval of a Skellam distribution with relevant parameters—a strategy very similar, yet not identical, to the strategy developed by Ersan (2016).
3. Precise Adjustment of Data and an Improved Detection Algorithm
The algorithm consists of three major steps, starting by finding the no-information cluster, and then adjusting the data for displacement before detecting the information layers.
3.1. Finding the No-Information Cluster
As detailed above, adding to the original random variables and two random Poisson variables and with the means and , respectively, leads to symmetric Skellam distributions for , and . We will find our estimates as the average of buys and sells from the no-information cluster.
Identifying the no-information cluster relies on its property, being the cluster with the lowest trade intensity. To differentiate between the no-information cluster and the other clusters with different distributions, we rely on the property that order imbalances within each cluster follow a Skellam distribution.
For a confidence level , we say that a cluster passes the -Skellam test if all the observations in that cluster belong to the -confidence interval of a Skellam distribution around the mean of the OI observations within that cluster. The average of the observations within each cluster is used as the center of the confidence interval, as it represents the maximum likelihood estimate of the mean for a Skellam distribution. The use of the α-Skellam test is justified as follows: if at a high confidence level α (e.g., 0.99), all the observations within a cluster fall within the confidence interval centered at the cluster average, it suggests that the observations are generated by the same distribution. If some observations fall outside this interval, it implies these observations are likely generated by a different distribution. In practical terms, this implies that significant deviations in the order imbalance (OI) indicate the presence of new information in the market. Therefore, the α-Skellam test acts as a detector for new information layers with different magnitudes. Observations within the confidence interval suggest consistent market reactions to similar information, while those outside the interval indicate responses to different types of information, suggesting a new layer of market information impacting the buys and sells.8
The steps of the algorithm are as follows:
- Sort the clusters by increasing the trade intensity, defined as the sum of average buys and sells within each cluster, and store them in a list .
- Let the no-information cluster be the cluster with the lowest trade intensity, . Initialize : .
- In each iteration,
- 4.1.
- Merge the no-information cluster with the next cluster in the list: .
- 4.2.
- Run the -Skellam test on the no-information cluster .
- 4.3.
- If passes the -Skellam test, then , and run step .
- 4.4.
- If fails the -Skellam test, the algorithm stops, and the no-information cluster is .
The theoretical values of and are approximated by the average buys and sells in the no-information cluster , and , where counts the number of elements in the cluster .
3.2. Adjusting the Data for Displacement
In the theoretical section above, we have shown that an adjustment of the data with two Poisson-distributed random variables leads to a well-defined distribution for the AOI. Here, we deviate from this ideal scenario by making two approximations:
- [1].
- First, we use the values and —estimated from the identified no-information cluster in the previous step—as the reliable estimates of the theoretical and .
- [2].
- Second, instead of generating values from the Poisson distributions centered on and , we simply add to all the observations and to all the observations . Such approximation is justified by the fact that a Poisson distribution is centered on its mean, especially when and are relatively large.
3.3. Detecting the Information Layers
This step applies a slightly modified version of the algorithm of Ersan (2016). After excluding the observations in the no-information cluster, we partition the adjusted data based on the observations. We fix a confidence level , and say that an -layer passes the -Skellam test if all the observations in that layer belong to the -confidence interval of a Skellam distribution around the average observations with that layer. The initial size of the partition .
- Cluster trading days into layers based on the adjusted absolute order imbalance .
- Run the -Skellam test on all the layers:
- 2.1.
- If the test fails for one or more layers, increase the number of layers by , and run step 1.
- 2.2.
- If all clusters pass the α-Skellam test, the algorithm stops, and the number of layers is equal to .
4. Empirical Evidence
In this section, we show the comparative results on the accuracy of alternative methods in estimating the number of layers in the simulated data series. We compare the accuracy of three methods with each other.11 These are the following:
- (1)
- nocorr (layer detection algorithm in Ersan (2016) with no correction for any difference between uninformed rates).
- (2)
- E (the same algorithm with the correction that uses minimum numbers of buys and sells in the data, as suggested in (Ersan 2016)).
- (3)
- EG (the suggested method of this paper that refers to the modified layer detection algorithm and the new correction).
We simulate the quarterly datasets of the daily numbers of buyer-initiated and seller-initiated trades (buys and sells) in line with similar studies (e.g., Lin and Ke 2011; and Ersan and Alıcı 2016), and using the function generatedata_mpin() in the PINstimation package. The function requires two-column data of the daily numbers of buys and sells. Additionally, we use two arguments of the function. First, the argument layers to set the number of layers (information types) to be included in the data, and second, the eps_ratio argument which determines the ratio of eps.s/eps.b (sell-side uninformed rate/buy-side uninformed rate) with which the data are simulated. The numbers of buys and sells are simulated based on the PIN and MPIN model assumptions such that buys (sells) follow a Poisson distribution with the mean () and sells (buys) follow a Poisson distribution with the mean () on a day with positive (negative) information layer of .12
Initially, we examine the performance of each method in estimating the number of layers when the uninformed rates are equal to each other. We simulate datasets ( sets for where is the number of layers) via the use of generatedata_mpin(series = 80,000, layers = j, eps_ratio = 1.00).
Table 3 shows the estimated number of layers with each method. The rows (columns) represent the number of simulated (estimated) layers. The table reports the shares of each number in total. While the cell in the intersection of the first row and first column stands for the share of accurately estimated cases for 1-layer simulations, the cells to its right indicate the share of cases where the estimated number is larger than the actual number. As demonstrated in Panel A, Ersan’s (2016) algorithm with no correction estimates the number of layers accurately in 86% of the datasets with a single information layer (representative of the original PIN model with a single information type).

Table 3.
Estimation accuracy for simulations with .
Moreover, the accuracy rates are slightly higher for the datasets with multiple types of information events varying between 89% and 93%. This performance is in line with Ersan (2016) and is an expected one since the simulated series have identical buy- and sell-side uninformed rates. Panel B and Panel C show the results for the use of Ersan’s (2016) correction and this paper’s suggested correction, respectively. Ersan’s (2016) correction accurately estimates the number of layers in 99% and 91% of the datasets with one and two layers, respectively. On the other hand, the estimation power diminishes dramatically with the number of layers. In 62% (43%) of the data series with four (eight) layers, the algorithm with Ersan’s (2016) correction accurately detects the number of layers. In the vast majority of the remaining cases, the estimated number of layers is one less than the actual number.
Finally, the EG correction suggested in this paper estimates the number of layers correctly in 94–95% of the sets with up to four layers. The rate is marginally lower at 86–92% for the datasets with five to eight layers. Next, we inquire about the estimation power of each method after relaxing the assumption of equal uninformed rates. We simulate 80,000 datasets with one difference. We allow eps_ratio to be in the range of (0.75, 1.25). The ratio of two uninformed trading intensities in any dataset is randomly selected from this range. While we aim at observing the results for differing rates, we do not prefer to assign too different values for uninformed rates which is in line with both PIN model assumptions and the empirical evidence provided so far in PIN studies (e.g., Brennan et al. 2018; Ersan and Alıcı 2016). Table 4 reflects the respective results.

Table 4.
Estimation accuracy for simulations with .
Panel A of Table 4 shows the poor performance of the layer detection algorithm in the absence of any correction when uninformed rates are not identical. More specifically, the share of accurate detections is 32% for one-layer datasets and as low as 24% for eight-layer sets. In the vast majority of the false estimations, the estimated number of layers is larger than the actual one. Panel B of Table 4 is qualitatively identical to Panel B of Table 3, which implies that the layer detection with the use of the correction in Ersan (2016) leads to the same results for both the equal and unequal uninformed rates cases. While obtaining consistent results and having a bias of at most one layer in vast majority of estimations favors the use of the method, the substantially low rates of exact estimates especially when there is a larger number of layers challenge its use. Panel C of Table 3 reports the estimates of our method which uses a modified version of the algorithm with the suggested/novel correction. As is the case for the E2016 correction method, the EG method estimations do not depend on whether we assume identical or different uninformed rates. Panel C of Table 3 and Table 4 have qualitatively same information. In addition to the fact that the estimation accuracy is independent of uninformed rate variation, the suggested method has substantially higher rates of the exact detection of layers in the data. In 86% of the 10,000 series with eight information types, the method accurately detects the number as eight. This is around 94% when there are one to four types of information events. In the vast majority of cases when it fails to detect the actual number accurately, the estimated number of information types is either one above or below it.
Table A1 presents the results of a more detailed analysis. We repeat the analysis reported in Table 4 with one difference. Instead of picking eps_ratio randomly from the range (0.75, 1.25), we examine the cases of certain eps_ratio values. The alternative values assigned for eps_ratio are where is an element of . For example, when , eps_ratio is either 0.999 or 1.001 with equal probabilities. We simulate 120,000 datasets: 2500 for each of the 1- to 8-layer cases, and for each of the six alternative eps_ratio values (). The table reports only the share of exact detections for the sake of brevity. The results are in line with the ones reported in Table 4. Panel A in Table A1 demonstrates that the no-correction method’s estimation power is high when the uninformed rates are identical or marginally different from each other (up to 1% difference). However, when the absolute difference between the uninformed rates increases (higher or lower eps_ratio), the estimation accuracy is substantially low. In Panels B and C, we do not observe remarkable differences with the altered eps_ratio values. Once again, the fact indicates that the use of the suggested corrections results in consistent estimation accuracy, with EG having a much higher accuracy rate.
As an additional robustness check, we repeat the analysis in Table A1 by altering the confidence level parameter used in the layer detection algorithm of Ersan (2016) and of this paper (α parameter as explained in Section 3). Throughout the paper, following Ghachem and Ersan (2023a), we use the default confidence level of 0.995 in all the layer detection methods. In order to check whether the results are special to the selected confidence level, we replicate Table A1 for two alternative confidence levels, i.e., a stricter one (0.999) and a looser one (0.99). The results are qualitatively similar in both cases. Thus, we do not report them here for the sake of brevity.
To provide further evidence on the estimation precision of the EG method, we look at the estimated number of no-event days in the data series. In case the method is good at finding the number of no-event days (thus, also the sum of event days), it is an indicator that the estimated number of layers is not arbitrary, but they match the day groups in the data and their populations. Table 5 shows the bias (in number of days) in finding the number of days in the no-event cluster. The reported results are for the simulations used in Table 4, the ones simulated with different uninformed rates. The column in the middle stands for the share of cases when the method exactly detects the number of no-event days. The exact detection rate is as high as 90% for one-layer sets. It slightly and monotonically increases to 94% for eight-layered datasets. This implies that our suggested method successfully differentiates the no-event and event days in datasets with multiple types of information. The numbers of missed days are much larger with the alternative two methods and are not reported for brevity.

Table 5.
EG corrected estimation accuracy for the number of days with no information event.
Table A2 shows the descriptive statistics for the simulated data series used in Table 4.13 The mean number of buys and sells is approximately identical (6149 and 6142, respectively). The lowest and highest values for the mean number of sells are 95 and 23,046.14 This implies a broad coverage of trading in both infrequently traded assets and actively traded assets. The mean probability of informed trading is 20%, which is in line with the empirical evidence provided in PIN studies. The mean alpha and delta parameters are around 75% and 50%. Delta, the probability of bad event occurrence, is, as expected, very close to 0.5 as we assume no a priori difference between bad and good event occurrence in simulations. Alpha, presented in the table, is the aggregate probability of observing any of the information types in the data.
Table A3 presents the descriptive statistics of the running times of the modified layer detection algorithm via the use of our suggested correction. The mean running time of the method for the simulated series used in Table 4 is substantially small. More specifically, it is 0.24 s. (0.17 s.) for one-layer (eight-layer) sets. The main reason for the longer time it takes in the case of a smaller number of layers is that the clustering procedure starts from (number of datapoints, or days) clusters and runs towards one, ending earlier for the datasets with more layers (clusters).
Above, we have discussed the overall accuracy of the EG algorithm in estimating the number of layers in the data. This accuracy, however, does depend on the accurate estimation of the uninformed trading rates, as these are used for data adjustment. We could think that the inaccurate estimates of these rates can lead to further inaccuracy in the estimation of the number of layers. Therefore, we also independently test the accuracy of the first step of our algorithm: the estimation of the uninformed trading rates. We simulate datasets and calculate the percentage deviation of the estimated uninformed trading rates from the rates empirically observed in the data. We find that the derivation of our estimates from the theoretical values of both and exceed (10%) in less than (0.1%) of the datasets. We do not report the results, but they are available upon request.
For the main analyses in the paper, we simulate a total of 280,000 datasets. The results for the first 80,000 sets are reported in Table 3; the results for the next 80,000 sets are reported in Table 4 and Table 5; and the results for the final 120,000 sets are reported in Table A1. An additional 240,000 datasets are generated for unreported robustness checks for the analyses reported in Table A1. The number of simulated datasets significantly exceeds those in the previous studies: 2500 in Lin and Ke (2011); 8000 in Yan and Zhang (2014); 1000 in Gan et al. (2015); 5000 in Ersan and Alıcı (2016); and 8000 in Ersan (2016). Our analyses proceed with various settings and data types to ensure consistent and robust results across different data characteristics and model specifications. As Table A2 presents, through the use of a significantly large number of datasets, we thoroughly cover the parameter spaces pertaining to model parameters such as total trade intensity (between around 200 and 40,000), positive and negative order imbalances (between around −12,500 and 9200), and negative and positive information event occurrence probabilities (between 0 and 1). We conduct the analyses with various settings. The initial analyses assume equal uninformed buyer and seller trading intensities, which are then varied between 0.75 and 1.25 times the other. We subsequently examine datasets of six types each with different uninformed buy and sell intensities before varying the confidence level in our algorithm for robustness checks. All these analyses are performed for eight types of datasets as we simulate datasets with one to eight layers of information each time. The high reliability achieved by a very large number of simulations and the utilization of various alternative settings in our paper is possible, partly because the layer detection stage that we focus on is computationally fast when compared to the overall estimation of the models. This enables us to simulate a large number of datasets with various settings. As Table A3 reflects, the layer detection task via our suggested algorithm ends in around 0.2 s per dataset, while this is on average 1.3 s for the estimation of the PIN model and 50 s for the estimation of the MPIN model in Ghachem and Ersan (2023a).
The overall accuracy of our algorithm is between 86% and 95% in our analyses conducted with the abovementioned diverse set of conditions. The estimation errors reported for the use of various settings and a large range of data characteristics demonstrate high stability for our algorithm’s performance. Namely, the algorithm’s accuracy rates are stable both in the case of equal and unequal rates of uninformed buyers and sellers, and robust to the altered amounts of inequalities. These remain robust for any of the data types with one to eight layers. Second, using a substantially large number of datasets (more than half a million when compared to a few thousand in similar studies) ensures that the reported results are not special to limited data with narrow representativeness but consistent through data types. Third, a striking result that reflects the stability of our algorithm is the amount of error when the algorithm fails to detect the number of layers correctly. As both Table 3 and Table 4 show, in the vast majority of cases when the algorithm fails to detect the number of information layers correctly, the error is only one layer. This is consistent in all the examined data types with one to eight layers. For example, the algorithm detects the number of layers exactly in 93.12% of the datasets with four layers. In an additional 5.59% of the datasets, the estimated number of layers is either three or five, leaving only 1.29% of the datasets with more than one (2–4) layer error. Additionally, the algorithm detects the number of days with no information event with very high accuracy and low variability. As Table 5 reports, the algorithm detects the exact number of no-event days in 90% to 94% of the datasets with one to eight layers. This provides additional support for the accurate identification of days with and without information layers.
5. Conclusions
In this paper, we propose a new algorithm that detects the number of information layers (types) in financial datasets. Our model of reference is the broadly used PIN model of Easley et al. (1996). This model, however, assumes that all the information events occurring in a dataset (e.g., affecting the trading activity in a quarter-stock pair) have a uniform impact. This does not align with the current state of financial markets where multiple sources of information asymmetries can operate each day. Ersan (2016) proposes a generalized form of the PIN model, multi-layer PIN, which estimates informed trading through extending the PIN model to a j-layer version, supplemented with an algorithm for detecting the number of layers.
We develop here a new algorithm that applies a data adjustment procedure and a priori step of estimating uninformed trading rates. We obtain substantially high rates of accuracy in information layer detection. We identify the number of layers correctly in 86% to 95% of the datasets with various settings. In almost all the remaining sets, the algorithm estimates the number of layers as one above or below the actual number of layers. In addition to the accurate estimation of the number of layers, the number of no-event days (thus the number of event days as well) is exactly identified in 90% to 94% of the simulations with one up to eight layers.
Uninformed buy and sell rates may differ from each other depending on the market conditions and the overall supply and demand. The precise identification of the number of different information layers in any data is essential in fully capturing informed trading. Therefore, through developing the necessary remedial solutions, this paper contributes to the more accurate estimation of informed trading. The main focus of this study is to handle the layer detection issue in estimating the probability of informed trading. This issue arises when we aim at capturing multiple layers of information events with different magnitudes, which is highly in line with today’s financial markets. The core outcome of our study is the proposed algorithm which detects the number of distinct information layers in a data. This not only provides useful standalone information that can be utilized by researchers and practitioners in financial markets, but also it is to be used as a preliminary variable in estimating the probability of informed trading.
Our findings carry a range of theoretical and practical implications. Theoretically, they challenge the traditional assumption of a single information type underlying the traditional models of the probability of informed trading, namely the classical PIN model or the adjusted PIN model by Duarte and Young (2009). This information would allow researchers to refine their understanding of the information landscape in modern financial markets and facilitate the development of more sophisticated extensions of the abovementioned models. Furthermore, our algorithm paves the way for a deeper exploration of information asymmetry among markets, time periods, asset classes, or assets with different characteristics. For example, Ghachem and Ersan (2023a), utilizing our algorithm, show that large stocks are associated with a larger number of information types when compared to small stocks. This distinction refines our understanding of how information asymmetry manifests across market segments. In addition to the main outcome of our algorithm (i.e., the number of information types in a financial dataset), our algorithm also partitions each trading day among different information types which allows researchers to extract further insight at the daily level. Practically, the algorithm enables investors to identify and anticipate periods of varying information asymmetry, and this is carried out by recognizing common features among information events of the same type. This ability is particularly useful for distinguishing between information types with large impacts and those with lesser effects. Investors can then leverage this insight to, among others, time their trades during periods of lower information asymmetry, thus reducing the risk of trading against more informed participants. Such benefits are even more pronounced for individual investors with limited access to information and at a comparative disadvantage. Policymakers can, through a closer inspection of the different information types and their impacts, monitor and evaluate market conditions more effectively. For instance, rare extreme-impact information events might reflect abnormal trading patterns, which might indicate the presence of insider trading or market manipulation.
Author Contributions
Conceptualization, O.E. and M.G.; methodology, O.E. and M.G.; software, O.E. and M.G.; validation, O.E. and M.G.; formal analysis, O.E. and M.G.; data curation, O.E. and M.G.; writing—original draft preparation, O.E. and M.G.; writing—review and editing, O.E. and M.G.; visualization, O.E. and M.G.; project administration, O.E.; funding acquisition, O.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific and Technological Research Council of Turkey (TUBITAK) grant number [122K637].
Data Availability Statement
The data supporting the reported results of this paper can be shared upon request.
Acknowledgments
This work was supported by the Scientific and Technological Research Council of Turkey (TUBITAK) [grant no 122K637]. We thank two anonymous referees for their contributory comments. We thank the participants at the Second Workshop on Market Microstructure and Behavioral Finance (WMMBF-II) and the seminar participants at Kadir Has University International Trade and Finance Department, for their valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Lemma A1.
Let , with . Let with distribution function and with distribution function , then .
Proof.
The distribution function of Skellam-distributed with the parameters at is given by , where is the modified Bessel function of the first kind. Analogously, the distribution function of Skellam-distributed with the parameters at is given by .
It follows that . We now make a change in variables. We define and rewrite . If , then .
The step follows from and that when z is an integer.
Now since is a distribution function, then , and we have the following:
□
Lemma A2.
If , and , then , and are identically distributed.
Proof.
Two random variables are identically distributed if they have the same cumulative distribution function. To prove that and are identically distributed, we need to prove that .
Using Lemma 1, we obtain , and .
Using these equalities in (Equation (A1)), we obtain the following:
□

Table A1.
Estimation accuracy for simulations with various eps.s/eps.b ratios.
Table A1.
Estimation accuracy for simulations with various eps.s/eps.b ratios.
| Eps Ratio-Layers | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Panel A: No correction | ||||||||
| 0 | 84.88 | 88.28 | 93.24 | 92.76 | 92.04 | 92.56 | 91.16 | 89.52 |
| 0.001 | 86.32 | 89.96 | 93.12 | 92.68 | 92.56 | 91.88 | 91 | 89.92 |
| 0.01 | 77.08 | 81.2 | 88.2 | 86.96 | 88.68 | 87.84 | 87.92 | 87.16 |
| 0.05 | 60.44 | 49.16 | 41.6 | 35.24 | 30.24 | 29.44 | 27.8 | 30.36 |
| 0.1 | 29.72 | 32.32 | 33.12 | 27.48 | 21.24 | 17.96 | 16.44 | 14.72 |
| 0.25 | 12.2 | 10.04 | 14.04 | 16 | 15.12 | 13.64 | 12.6 | 10.28 |
| Panel B: E2016 correction | ||||||||
| 0 | 98.88 | 91.48 | 78.44 | 61.2 | 53.04 | 49 | 44.44 | 42.56 |
| 0.001 | 98.84 | 91.12 | 78.2 | 61.92 | 54.28 | 47.6 | 44.8 | 40.4 |
| 0.01 | 98.64 | 91.08 | 79.88 | 60 | 53.48 | 48.16 | 44.12 | 41.76 |
| 0.05 | 98.84 | 90.28 | 79.6 | 62.56 | 54.92 | 50.08 | 44.6 | 42.72 |
| 0.1 | 98.88 | 92.2 | 78.84 | 61.84 | 50.88 | 49.88 | 43.84 | 42.64 |
| 0.25 | 98.72 | 90.36 | 79.6 | 63.12 | 54.8 | 50.08 | 45.04 | 43.12 |
| Panel C: EG correction | ||||||||
| 0 | 93.36 | 95.32 | 94.68 | 92.92 | 92.6 | 90.32 | 87.84 | 86.36 |
| 0.001 | 93.48 | 95.12 | 94.64 | 93.52 | 92.68 | 90.76 | 88.12 | 85.68 |
| 0.01 | 93.8 | 94.12 | 94.88 | 94.44 | 93.36 | 91.44 | 88.24 | 86.56 |
| 0.05 | 92.76 | 95.08 | 94.68 | 93.96 | 93.32 | 90.24 | 89.04 | 86.8 |
| 0.1 | 93.32 | 94.6 | 94.04 | 94.96 | 91.56 | 90.32 | 89.24 | 87.12 |
| 0.25 | 94.64 | 94.72 | 94.76 | 93.28 | 92.88 | 90.76 | 88.64 | 86.16 |
The table presents the distributions of the estimated number of information layers for the simulated datasets with 1 to 8 layers after relaxing the assumption of eps.b = eps.s. The sell-side uninformed trader rate is assumed to be alternating multiples (1 ± x) of the buy-side uninformed rate where x is one of the set (0, 0.001, 0.01, 0.05, 0.1, and 0.25). A total of 120,000 datasets (2500 for each of the layers 1 to 8 and for each of the six eps.s/eps.b ratios) are used. For example, for the datasets where x = 0.25, the data are generated with either 0.75 or 1.25 eps ratio, which are equally likely. The estimations are from three methods represented in Panels A to C. Panel A stands for the estimations via the layer detection algorithm suggested in Ersan (2016) with no correction applied for any differences between eps.b and eps.s. Panel B reports the statistics on the number of layers estimates via the use of the suggested correction in Ersan (2016). Panel C presents the respective results for the correction of the algorithm suggested in this paper. In each panel, the row names represent the number eps.s/eps.b ratio. In each column, the share of the correctly estimated number of datasets is reported. For example, the cell in the intersection of last row and last column in Panel A indicates that in 10.28% of the 2500 simulated datasets with 8 layers and (1 ± 0.25) of the eps.s/eps.b ratio, the method has estimated the number of layers correctly as 8.

Table A2.
Descriptive statistics of the simulated datasets.
Table A2.
Descriptive statistics of the simulated datasets.
| Mean | sd | Min | Median | Max | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Buys | 6149 | 3358 | 107 | 382 | 952 | 3349 | 6138 | 8835 | 11,476 | 13,469 | 20,793 |
| Sells | 6142 | 3467 | 95 | 369 | 931 | 3286 | 6024 | 8706 | 11,974 | 14,159 | 23,046 |
| OI | 7 | 1325 | −12,526 | −3615 | −2160 | −665 | 20 | 688 | 2136 | 3581 | 9240 |
| AOI | 2405 | 1879 | 20 | 143 | 327 | 985 | 1899 | 3349 | 6169 | 8359 | 17,037 |
| MPIN | 0.20 | 0.15 | 0.00 | 0.01 | 0.03 | 0.09 | 0.17 | 0.28 | 0.48 | 0.66 | 0.92 |
| alpha | 0.76 | 0.19 | 0.02 | 0.13 | 0.37 | 0.68 | 0.80 | 0.90 | 0.97 | 0.98 | 0.98 |
| delta | 0.50 | 0.20 | 0.00 | 0.03 | 0.17 | 0.37 | 0.50 | 0.63 | 0.83 | 0.97 | 1.00 |
| mu | 2693 | 2096 | 85 | 241 | 462 | 1046 | 2106 | 3791 | 6859 | 9317 | 19,093 |
| eps.b | 5043 | 2858 | 95 | 200 | 593 | 2571 | 5039 | 7515 | 9507 | 9901 | 10,040 |
| eps.s | 5040 | 2976 | 79 | 197 | 580 | 2516 | 4947 | 7342 | 10,088 | 11,436 | 12,476 |
The table presents the descriptive statistics of the 80,000 datasets used in the main table, Table 4. The buys and sells series are the mean number of buys and sells in each dataset. OI and AOI are the mean order imbalance and mean absolute order imbalance in each dataset. MPIN is the multi-layer probability of informed trading in each of the simulated datasets. The five intermediate parameters are the aggregated parameters calculated in each of the simulated datasets. represents the xth quantile.

Table A3.
Descriptive statistics of the running times of layer detection with EG correction.
Table A3.
Descriptive statistics of the running times of layer detection with EG correction.
| Mean | sd | Min | Median | Max | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.24 | 0.14 | 0.01 | 0.12 | 0.21 | 0.33 | 0.85 |
| 2 | 0.19 | 0.11 | 0.01 | 0.1 | 0.17 | 0.26 | 0.69 |
| 3 | 0.17 | 0.09 | 0.03 | 0.09 | 0.16 | 0.23 | 0.61 |
| 4 | 0.16 | 0.09 | 0.02 | 0.09 | 0.15 | 0.22 | 0.55 |
| 5 | 0.16 | 0.08 | 0.03 | 0.09 | 0.15 | 0.22 | 0.63 |
| 6 | 0.16 | 0.08 | 0.03 | 0.09 | 0.15 | 0.22 | 0.7 |
| 7 | 0.17 | 0.09 | 0.03 | 0.09 | 0.16 | 0.23 | 0.67 |
| 8 | 0.17 | 0.09 | 0.03 | 0.09 | 0.16 | 0.24 | 0.67 |
The table presents the descriptive statistics of the running times of layer detection with EG correction for the 80,000 datasets used in the main table, Table 4. and stand for the 25th and 75th quantiles. The running times are in seconds and from the R statistical software PINstimation (version 0.1.2) with an İ9 10900K processor.
Notes
| 1 | Firm-specific events such as CEO resignations, financial reports, mergers, and strategic alliances exert varying impacts on trading activity due to the nature and significance of the information they convey. The growing frequency of information events, along with the proliferation of data sources, has amplified their impact on market behavior, making it crucial to accurately assess their effects on trading activity (Fang and Peress 2009; Loughran and McDonald 2016). The recent literature on information overload document that stricter disclosure requirements in the last two decades have led to a substantial increase in the amount of data shared in annual reports (e.g., Guay et al. 2016; Chapman et al. 2019; Impink et al. 2022). Dyer et al. (2017) examined 10-K filing texts for more than 10,000 firms between 1996 and 2013 and found that the median text length doubled from 23,000 words in 1996 to nearly 50,000 in 2013. Boudoukh et al. (2019) employ textual analysis to identify fundamental information in public news. They find that this information accounts for 50% of the overnight idiosyncratic volatility in stock returns and most of this large share is due to the days with multiple news. They examine the impact of 18 event categories such as financials, ratings, earnings factors, forecasts, and mergers and acquisitions, composing 90 subcategories, and show the differing contributions of each event category to stock return variance. Thus, they show that stock returns and volatility vary greatly with the type of news and the magnitude of information is not the same across days. |
| 2 | The PIN model divides trading days among three types: no-information days with solely uninformed trading intensities ; good-information days with uninformed trading intensities and informed buying intensity ; and bad-information days with uninformed trading intensities and informed selling intensity . The straightforward generalization presented in Ersan (2016) assumes the existence of different levels of informed trading activities, i.e., instead of having a unique parameter , common to all information days, information days can be divided into multiple types (or layers), where each layer is associated with a distinct level of informed trading intensity . Consequently, a good-information day of type has the trading intensity rates of , while a bad-information day of type has the trading intensity rates of ; Ersan (2016) has been the only work relaxing the three assumptions in the PIN model and proposing the generalized model (MPIN). It estimates the probability of informed trading after simultaneously accounting for multiple information layers. Both models yield identical estimates when there is one type of information event in the data, whereas the traditional PIN model fails to provide accurate estimates when there are multiple layers. This is a natural consequence of the PIN model’s assumption of a single-event type. |
| 3 | The PIN model presented by Easley et al. (1996) has a single uninformed rate while Easley et al. (2002) incorporate uninformed buy and sell rates separately, reaching marginally different estimates on them. In the following literature, the mean estimates of buy-side and sell-side uninformed rates have differed from each other while the differences are relatively low (i.e., <20%). |
| 4 | PINstimation is an R software package that is developed for the estimation of various PIN models. The package includes the functions and arguments covering the computational improvements and extensions of the original PIN model, and it provides extensive data simulation and data aggregation tools. |
| 5 | Please check the R code of the function detectlayers_eg() that implements the introduced algorithm in this paper and the R code of the function detectlayers_e() for the algorithm of Ersan (2016), available at https://cran.r-project.org/web/packages/PINstimation/index.html (accessed on 1 February 2024). |
| 6 | Ghachem and Ersan (2023b) suggest using the expectation maximization (EM) algorithm to simultaneously estimate the number of layers and PIN parameters. However, this method requires the estimation of the model for all the possible numbers of information layers, which is time-consuming. |
| 7 | If , then and . These are two Skellam distributions with the same parameters but in reverse order, so they are symmetric around zero. |
| 8 | The Skellam test performed in the functions detectlayers_e and detectlayers_eg() is conducted using the function qskellam() from the R package Skellam (Lewis et al. 2016). |
| 9 | Theoretically, dividing the data into a sufficiently large number of clusters ensures that the order imbalance (OI) observations within each cluster are sufficiently similar due to the clustering algorithm’s focus on similarity. We have chosen to start with ⌊n/2⌋ initial clusters. This approach only fails in very unusual datasets, such as those containing more than ⌊n/2⌋ layers. For datasets representative of a quarter (e.g., 60 days), this would imply 30 layers, which is extremely unlikely. Ersan (2016) works with 8190 stock-quarter datasets. The largest number of layers detected in these datasets is 16. The number of layers is less than 10 in 98% of the datasets and less than 15 in 99.96% of the datasets. Change in the computation time is marginal when increasing the initial number of clusters; thus, we set the initial cluster number large enough to provide high confidence. |
| 10 | The actual step is slightly more complex than this but is equivalent to the described step in almost all the cases. It clusters trading days based on OI into clusters where , then runs the -Skellam test on all the clusters. Among all the configurations with clusters for which all the clusters pass the Skellam test, the clustering configuration that has the largest cluster with minimum trading intensity is selected as the clustering used in step 2. This modification aims to reduce the running time of the algorithm but does not alter its essence. |
| 11 | As our suggested algorithm specifically targets detecting the information layers in a dataset, the three compared methods involve the algorithm in our paper as well as the only two alternative layer detection methods that are available in the literature. Other comparisons among the overall estimation accuracy of the various PIN models are beyond the scope of our study. |
| 12 | Detailed information regarding the data simulation can be found in the PINstimation package documentation and Ghachem and Ersan (2023a). |
| 13 | |
| 14 | Buys and sells are the mean buys and sells in each dataset. Therefore, the mean statistic is the mean of these mean values. |
References
- Aktas, Nihat, Eric de Bodt, Fany Declerck, and Hervé Van Oppens. 2007. The PIN anomaly around M&A announcements. Journal of Financial Markets 10: 169–91. [Google Scholar]
- Amnas, Muhammed Basid, Murugesan Selvam, and Satyanarayana Parayitam. 2024. FinTech and Financial Inclusion: Exploring the Mediating Role of Digital Financial Literacy and the Moderating Influence of Perceived Regulatory Support. Journal of Risk and Financial Management 17: 108. [Google Scholar] [CrossRef]
- Arifovic, Jasmina, Xue-Zhong He, and Lijian Wei. 2019. High frequency trading in FinTech age: AI with speed (15 November 2019). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2771153 (accessed on 12 August 2024).
- Bazzana, Flavio, and Andrea Collini. 2020. How does HFT activity impact market volatility and the bid-ask spread after an exogenous shock? An empirical analysis on S&P 500 ETF. The North American Journal of Economics and Finance 54: 101240. [Google Scholar]
- Berkman, Henk, Paul D. Koch, and P. Joakim Westerholm. 2014. Informed trading through the accounts of children. The Journal of Finance 69: 363–404. [Google Scholar] [CrossRef]
- Boehmer, Ekkehart, Charles M. Jones, Xiaoyan Zhang, and Xinran Zhang. 2021. Tracking retail investor activity. The Journal of Finance 76: 2249–305. [Google Scholar] [CrossRef]
- Bogousslavsky, Vincent, Vyacheslav Fos, and Dmitry Muravyev. 2024. Informed trading intensity. The Journal of Finance 79: 903–48. [Google Scholar] [CrossRef]
- Boudoukh, Jacob, Ronen Feldman, Shimon Kogan, and Matthew Richardson. 2019. Information, trading, and volatility: Evidence from firm-specific news. The Review of Financial Studies 32: 992–1033. [Google Scholar]
- Brennan, Michael J., Sahn-Wook Huh, and Avanidhar Subrahmanyam. 2016. Asymmetric effects of informed trading on the cost of equity capital. Management Science 62: 2460–80. [Google Scholar] [CrossRef]
- Brennan, Michael J., Sahn-Wook Huh, and Avanidhar Subrahmanyam. 2018. High-frequency measures of informed trading and corporate announcements. The Review of Financial Studies 31: 2326–76. [Google Scholar] [CrossRef]
- Brogaard, Jonathan. 2010. High frequency Trading and Its Impact on Market Quality. Northwestern University Kellogg School of Management Working Paper. Evanston: Northwestern University Kellogg School of Management. [Google Scholar]
- Chapman, Kimball L., Nayana Reiter, Hal D. White, and Christopher D. Williams. 2019. Information overload and disclosure smoothing. Review of Accounting Studies 24: 1486–522. [Google Scholar] [CrossRef]
- Chen, Mark A., Qinxi Wu, and Baozhong Yang. 2019. How valuable is FinTech innovation? The Review of Financial Studies 32: 2062–106. [Google Scholar] [CrossRef]
- Cheng, Tsung-Chi, and Hung-Neng Lai. 2021. Improvements in estimating the probability of informed trading models. Quantitative Finance 21: 771–96. [Google Scholar] [CrossRef]
- Dang, Viet Anh, Dinh Trung Nguyen, Thu Phuong Pham, and Ralf Zurbruegg. 2024. The dynamics of informed trading around corporate bankruptcies. Finance Research Letters 63: 105385. [Google Scholar] [CrossRef]
- Duarte, Jefferson, and Lance A. Young. 2009. Why is PIN priced? Journal of Financial Economics 91: 119–38. [Google Scholar]
- Duarte, Jefferson, Edwin Hu, and Lance A. Young. 2015. What does the PIN model identify as private information. Unpublished working paper, Rice University, University of Washington. [Google Scholar]
- Dyer, Travis, Mark Lang, and Lorien Stice-Lawrence. 2017. The evolution of 10-K textual disclosure: Evidence from Latent Dirichlet Allocation. Journal of Accounting and Economics 64: 221–45. [Google Scholar] [CrossRef]
- Easley, David, Nicholas M. Kiefer, Maureen O’Hara, and Joseph B. Paperman. 1996. Liquidity, information, and infrequently traded stocks. The Journal of Finance 51: 1405. [Google Scholar]
- Easley, David, Soeren Hvidkjaer, and Maureen O’Hara. 2010. Factoring information into returns. Journal of Financial and Quantitative Analysis 45: 293–309. [Google Scholar] [CrossRef]
- Easley, David, Soeren Hvidkjaer, and Maureen O’Hara. 2002. Is information risk a determinant of asset returns? The Journal of Finance 57: 2185–221. [Google Scholar] [CrossRef]
- El Hajj, Mohammad, and Jamil Hammoud. 2023. Unveiling the influence of artificial intelligence and machine learning on financial markets: A comprehensive analysis of AI applications in trading, risk management, and financial operations. Journal of Risk and Financial Management 16: 434. [Google Scholar] [CrossRef]
- Ersan, Oguz. 2016. Multilayer Probability of Informed Trading (November 22, 2016). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2874420 (accessed on 25 March 2024).
- Ersan, Oguz, and Asli Alıcı. 2016. An unbiased computation methodology for estimating the probability of informed trading (PIN). Journal of International Financial Markets, Institutions and Money 43: 74–94. [Google Scholar] [CrossRef]
- Fang, Lily, and Joël Peress. 2009. Media coverage and the cross-section of stock returns. The Journal of Finance 64: 2023–52. [Google Scholar] [CrossRef]
- Gan, Quan, Wang Chun Wei, and David Johnstone. 2015. A faster estimation method for the probability of informed trading using hierarchical agglomerative clustering. Quantitative Finance 15: 1805–21. [Google Scholar] [CrossRef]
- Ghachem, Montasser, and Oguz Ersan. 2023a. PINstimation: An R Package for estimating probability of informed trading models. The R Journal 15: 145–68. [Google Scholar] [CrossRef]
- Ghachem, Montasser, and Oguz Ersan. 2023b. Estimation of the probability of informed trading models via an Expectation-Conditional Maximization Algorithm (12 March 2023). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4386172 (accessed on 25 March 2024).
- Guay, Wayne, Delphine Samuels, and Daniel Taylor. 2016. Guiding through the fog: Financial statement complexity and voluntary disclosure. Journal of Accounting and Economics 62: 234–69. [Google Scholar] [CrossRef]
- Hendershott, Terrence, Xiaoquan (Michael) Zhang, J. Leon Zhao, and Zhiqiang (Eric) Zheng. 2021. FinTech as a game changer: Overview of research frontiers. Information Systems Research 32: 1–17. [Google Scholar] [CrossRef]
- Impink, Joost, Mari Paananen, and Annelies Renders. 2022. Regulation-induced Disclosures: Evidence of Information Overload? Abacus 58: 432–78. [Google Scholar] [CrossRef]
- Jackson, David. 2013. Estimating PIN for firms with high levels of trading. Journal of Empirical Finance 24: 116–20. [Google Scholar] [CrossRef]
- Ke, Wen-Chyan, Hueiling Chen, and Hsiou-Wei William Lin. 2019. A note of techniques that mitigate floating-point errors in PIN estimation. Finance Research Letters 31: 458–462. [Google Scholar] [CrossRef]
- Lai, Sandy, Lillian Ng, and Bohui Zhang. 2014. Does PIN affect equity prices around the world? Journal of Financial Economics 114: 178–95. [Google Scholar] [CrossRef]
- Lewis, Jerry W., Patrick E. Brown, and Michail Tsagris. 2016. Package ‘skellam’. Available online: https://cran.r-project.org/web/packages/skellam/index.html (accessed on 1 February 2024).
- Lin, Hsiou-Wei William, and Wen-Chyan Ke. 2011. A computing bias in estimating the probability of informed trading. Journal of Financial Markets 14: 625–40. [Google Scholar] [CrossRef]
- Lof, Matthijs, and Jos van Bommel. 2023. Asymmetric information and the distribution of trading volume. Journal of Corporate Finance 82: 102464. [Google Scholar] [CrossRef]
- Loughran, Tim, and Bill McDonald. 2016. Textual analysis in accounting and finance: A survey. Journal of Accounting Research 54: 1187–230. [Google Scholar] [CrossRef]
- O’Hara, Maureen. 2015. High frequency market microstructure. Journal of Financial Economics 116: 257–70. [Google Scholar] [CrossRef]
- Roşu, Ioanid. 2019. Fast and slow informed trading. Journal of Financial Markets 43: 1–30. [Google Scholar] [CrossRef]
- Yan, Yuxing, and Shaojun Zhang. 2012. An improved estimation method and empirical properties of the probability of informed trading. Journal of Banking & Finance 36: 454–67. [Google Scholar]
- Yan, Yuxing, and Shaojun Zhang. 2014. Quality of PIN estimates and the PIN-return relationship. Journal of Banking & Finance 43: 137–49. [Google Scholar]
- Yang, Yung Chiang, Bohui Zhang, and Chu Zhang. 2020. Is information risk priced? Evidence from abnormal idiosyncratic volatility. Journal of Financial Economics 135: 528–54. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).