Abstract
Calculations about compound interest serve as the basis of most financial decisions; therefore, it is imperative to explore what mathematical knowledge people need to correctly calculate simple and compound interest. The aim of this study is to analyze the relationship between college students’ competence in calculating simple and compound interest and their understanding of the arithmetic and geometric progressions. It is also pointed out whether the results vary according to gender. Population proportion tests are carried out, and gender proportion differences are considered for inferential analysis. The dichotomous Probit model was used for correlation analysis. Results demonstrate that 59.8% of students know how to formulate a whole-number succession, and only 30.9% in the case of fractional numbers. Less than 50% of students can calculate compound interest, but 76.7% can calculate simple interest. There is no significant difference between men and women. The results show a positive relationship between male students’ competence in calculating compound interest with the possibility to correctly formulate a geometric succession. Findings can be useful for mathematics teaching strategy design and its applications in finance contexts with the purpose of training students to be better at finance decision making.
1. Introduction
During the last two decades, both developed and emerging economies have stressed the importance for children and young people of being educated in different fields so they can be better suited for making informed choices in many day-to-day settings. Financial and mathematical literacy are paramount to this end (OECD 2019a, 2019b, 2003). A certain level of mathematical literacy is required as an essential condition of financial education, inasmuch as for some financial decision making, it is imperative that people are able to perform calculations (OECD 2017, 2019c).
The Program for International Student Assessment (PISA) accentuates the importance of mathematics competence in learning processes, since students will be required to use it in certain situations, such as personal, academic, labor and social life (OECD 2003). According to the Mexican National Institute of Statistics and Geography (INEGI 2022), people’s ability to calculate financial interest is a key element of financial education. Huston (2010) points out that if somebody finds it hard to perform an operation in which arithmetic skills are needed, this will affect their financial well-being.
Studies reveal that college students struggle when they perform basic financially applied numerical and algebraic operations. In this regard, Ramos-Hernández et al. (2020) pointed out that more than half of Mexican college students fail at calculating interest rates, while 47% of students lack the necessary mathematical competence to perform a simple calculation involving the notion of financial interest to make choices about financial instruments like credit cards, investments or loans. Likewise, Moreno-García et al. (2017) identified that college students fail to calculate compound interest, and consequently, they make mistakes at interpreting financial information associated with the notion of interest rates.
The mathematical knowledge and skills students obtain from arithmetic and algebra are fundamental for their college and professional training (Martínez and Romero 2019; Liang et al. 2022). According to OECD (2019a), 44% of students in Mexico attained minimum levels of proficiency in mathematics competence in the 2018 PISA test, with different results based on gender: men scored higher than women did by 12 points. Although arithmetic and elementary algebra are indispensable for modeling situations in financial mathematics, college students have trouble understanding them (Grueso et al. 2020). Amador-Saelices and Montejo-Gámez (2016) affirm that students cannot see algebraic expressions’ usefulness to solve real situations with mathematical formulations. According to Vidaurri (2017), arithmetic and geometric progression is a key concept to deduce formulas used in financial mathematics, like simple and compound interest. As Werner and Sotskov (2006) explain, simple and compound interest calculations are an application of geometric and arithmetic progressions and the partial sums of these sequences. The thinking process that allows the student to link these concepts, geometric progression and financial interest, is called relational thinking and refers to the possibility of resorting to previous learning and using it to solve a given problem (Cavalcante et al. 2024). However, there is evidence that college students find it difficult not only to understand the progressions concept (Khaoula et al. 2020) but also its application (Grueso et al. 2020).
Considering the difficulties college students go through in understanding basic mathematical concepts to perform operations involving the financial interest concept, the following research questions are proposed: Do students understand the concept of arithmetic and geometric progression? Do they know how to apply it for calculating financial interest? Do college students know how to calculate simple and compound interest? Are there any significant differences between men and women in mathematical skills related to arithmetic and geometric progressions? Are there any significant differences between men and women concerning simple and compound interest calculation?
This study aims to analyze the relationship between the understanding college students have about arithmetic and geometric progression and their competence in calculating simple and compound interest. In this sense, it is also established whether there is a significant difference between men and women. The paper is organized as follows: The Section 2 consists of the literature review. The Section 3 describes the methodology and the research model. The Section 4 shows the analysis and results. The Section 5 presents main findings discussion, and finally there is the conclusions section.
2. Literature Review
A considerable body or research displays the learning difficulties and obstacles students have about the understanding and application of succession and series concepts (Azizah et al. 2022; Rachma and Rosjanuardi 2021; Minggi et al. 2022; Iswara et al. 2021). Results reported by Bajo et al. (2019) gave evidence that students know the numerical succession concept; however, it is established that they generally use the mathematical element the wrong way, and they determine the logical equivalence relationship between numerical succession and progression erroneously. Similarly, students are shown to be able to establish the number of terms in an arithmetic succession, but they tend to make technical errors in establishing the last term of the arithmetic succession (Minggi et al. 2022). As for Fauzia et al. (2017), they state that students encounter learning difficulties with succession and series concepts, as well as the mathematical representation of a real-life situation through arithmetic successions and progressions. Considering that the students have already taken a mathematics course in their first year of bachelor studies, the following research hypotheses are established:
H1.
College students understand successions with whole numbers.
H2.
College students understand successions with fractional numbers.
H3.
College students can formulate the general expression of succession with whole numbers.
H4.
College students can formulate the general expression of succession with fractional numbers.
H5.
College students can model a given financial situation using sequences.
There is evidence in the literature that shows that there is no difference based on gender, like Jiang (2021), who found that there were no significant differences between male students and female students in mathematical abstraction, logical reasoning and intuitive imagination. Other studies show that gender disparity in math depends on the country and context (Stoet and Geary 2012; Tsai et al. 2018), but there are numerous studies that show that students’ mathematical performance differs by gender and that male students outperform female students in mathematics (Leahey and Guo 2001; Kaiser and Zhu 2022). Based on the empirical evidence on gender differences in math student performance, the following hypotheses are proposed:
H6.
There are significant differences between men and women in their comprehension of successions with whole numbers.
H7.
There are significant differences between men and women in their comprehension of successions with fractional numbers.
H8.
There are significant differences between men and women in their ability to formulate the general expression of succession with whole numbers.
H9.
There are significant differences between men and women in their ability to formulate the general expression of succession with fractional numbers.
H10.
There are significant differences between men and women in their capability to model a given financial situation using sequences.
Some studies report low arithmetic levels regarding compound interest calculation (Hubbard et al. 2016; Fornero and Monticone 2011; Mottola 2013). Worldwide, half of the adult population understand concepts such as simple and compound interest. In Sweden, a country in the group with the highest levels of financial literacy (Klapper et al. 2015), 77.2% of the surveyed adult population answered the question of compound interest correctly (Skagerlund et al. 2018). In the International Survey of Adult Financial Literacy (INFE), less than a third part (26.3%) of the sample adults answered both questions, of simple and compound interest rate, correctly (OECD 2020). According to Lusardi (2012), 43% of the people who answered the question of compound interest wrong failed to calculate simple interest. Considering that the students have already taken a mathematics course, the following research hypotheses are established:
H11.
College students can calculate simple interest.
H12.
College students can calculate compound interest.
Likewise, some studies show that women have lower financial literacy than men do (Gudjonsson et al. 2022). According to Zissimopoulos et al. (2015), approximately 20% of college-educated women could answer a basic compound interest question, whereas around 35% of college-educated men of the same age could answer the same question. Considering the evidence regarding the gender gap, the following hypotheses are established:
H13.
There are significant differences between men and women in their ability to calculate simple interest.
H14.
There are significant differences between men and women in their ability to calculate compound interest.
The mathematical skills students have is a topic of growing concern in the scientific literature because of its relationship with decision making in different aspects of our lives (OECD 2019a; Ozkale and Erdogan 2020; Thomson et al. 2020; Liang et al. 2022). According to OECD (2019a), students need to understand financial concepts, such as interest rates, that will be relevant to them as they grow into adulthood. There is evidence showing that students who attained high scores in mathematics do also enjoy the benefits of being financially literate (OECD 2017; Muñoz-Murillo et al. 2020; Villagómez and Hidalgo 2017; Dituri et al. 2019).
According to Stewart et al. (2007), the financial formula for compound interest is a growth model called geometric succession. Arithmetic and geometric successions are topics that are studied in programs at all education levels (Cortez 2017; Bajo et al. 2019; SEP 2015; Martínez et al. 2018). Their benefit lies in the study of data patterns of different areas, including finance (Vogel 2005). High school students are expected to apply geometric succession and progression concepts to achieve a competence in the field of financial mathematics (SEP 2013). According to the evidence on the importance of arithmetic and geometric sequences for the calculation of financial interest and the gender differences found on mathematics and financial performance, the following hypotheses arise:
H15.
There is a significant gender difference in the relationship between the formulation of the general expression of a geometric sequence with whole numbers and the correct calculation of compound interest.
H16.
There is a significant gender difference in the relationship between the formulation of the general expression of a geometric sequence with fractional numbers and the correct calculation of compound interest.
3. Materials and Methods
The type of study is non-experimental, cross-sectional and descriptive, which is used to observe if there is a relationship between the comprehension college students have of the concept of arithmetic and geometric progressions and their ability to calculate financial interest.
The population was 449 undergraduate students from the business school of a private university of 2069 students in Veracruz, Mexico, enrolled in the January–June 2021 semester. The participants were all students (142) in the second semester of one of the following majors: management, accounting, economics and international markets. A semester earlier, during August–December 2020, all participants took a 48 h mathematics course that included the following topics: basic algebraic operations; linear equations; quadratic equations; logarithmic, exponential and polynomial functions; and sequences and series. In this last topic, they learned arithmetic and geometric sequences and series. Data collection was conducted by means of an online questionnaire using the Google Forms tool during the 2021 January–June semester. The questionnaire is designed to have eight single-select multiple-choice questions. Students can use paper, pencil and some technological tools at their disposal (a calculator, Excel online spreadsheets or free software).
To measure students’ understanding of arithmetic and geometric progressions, five questions proposed by Stewart et al. (2007), Bajo et al. (2019) and Minggi et al. (2022) were included. The first two allow it to be identified whether the student recognizes the numerical sequence of the progression (with whole numbers and fractional numbers). The third and fourth allow it to be identified whether students know how to express the general term of a sequence, given that several terms of the sequence are known (with whole numbers and fractional numbers). The fifth question allows it to be identified whether students know how to calculate the sum of the first consecutive terms of a progression.
To measure students’ knowledge about calculating interest, three questions from the Mexican National Financial Inclusion Survey 2021 (INEGI 2022) are used, in which the individual is required to calculate zero interest, simple interest and compound interest of a loan. The first question has the purpose of determining whether the respondent understands the concept of interest through the profits that he could receive or not when he makes a loan. The second one has the purpose of determining whether the respondent knows how to calculate the simple interest of an amount of money he invests during a year. The last question determines whether the respondent knows how to calculate the amount of money he obtains at the end of a certain period from an investment when the interest is reinvested. Lusardi and Mitchell (2008) proposed these questions. They argued that responses to these three literacy questions are positively correlated, meaning that those who answer one question correctly are also likely to get the other two right. Nevertheless, the correlation is not particularly high, which suggests that each question measures a different aspect of financial knowledge (Lusardi and Mitchell 2011).
To test hypotheses H1, H2, H3 and H4, the population proportion test
is carried out with and , where is the proportion of cases that answer the questions correctly. To test hypotheses H5 and H6, the test of differences in population proportions is carried out, with the statistic:
with . For both tests, is rejected if , with (Anderson et al. 2017). In order to determine the relationship between university students’ ability to calculate simple and compound interest with the knowledge they have about geometric progressions, the dichotomous Probit response model is used (Wooldridge 2010). The observed variable y is dichotomous (1: correct answer; 0: incorrect answer). The binary Probit response model is denoted as follows:
where G is the cumulative normal distribution function, and X denotes the questions corresponding to the expression of an arithmetic and geometric sequence. To contrast the hypotheses and estimate the Probit model, the Gretl statistical software, version 2023 (https://gretl.sourceforge.net/ accessed on 11 January 2023), is used. Table 1 presents the operationalization, coding and source of the variables under study.

Table 1.
Operationalization and coding of the research variables.
4. Results
Figure 1 presents the results obtained by the students in the sample regarding geometric progressions and compound interest knowledge.
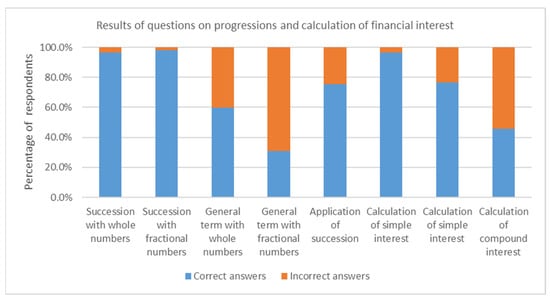
Figure 1.
Response frequency on progressions and financial interest.
From the sample, 96.4% of the students answered the question related to the sequence of whole numbers correctly, and 97.8% answered the question related to fractional numbers correctly. The above indicates that students have the mathematical ability to identify the representation that progressions can have, as well as regularities in a sequence of whole numbers and fractions. In other results, 59.8% of students answered the question about the general term of a sequence of whole numbers correctly. Almost 70% of students cannot obtain the general term of a sequence given several terms of it when the sequence involves fractional terms. To continue, 75.3% of students can lay out a problem that involves sequences and have the ability to find the sum of the terms of a sequence when the problem requires it.
Other results show that 96.4% of students correctly answered the question that required the calculation of simple interest (zero interest), 76.7% answered the simple interest question accurately and 45.7% answered the compound interest question correctly. The previous results provide evidence of the difficulty that the students in the sample had in answering questions that incorporate the concept of interest rates, especially the compound rate. Table 2 presents the results of the test of population proportion hypothesis.

Table 2.
Population proportion test on geometric progression knowledge and the calculation of financial interest.
There is statistical evidence that more than 50% of university students have knowledge of the representation of geometric progressions, in a sequence of numbers, whole numbers and fractions (p-value < 0.05). The above provides statistical support in favor of H1 and H2. More than 50% of university students know how to formulate the general expression of a sequence with whole numbers (p-value < 0.05), which supports H3, but not in the case of a sequence with fractional numbers (p-value > 0.05); therefore, H4 is rejected. More than 50% of university students have the mathematical ability to model the description of a financial situation through a sequence (p-value < 0.05), which supports H5. More than 50% of university students know how to calculate simple interest (p-value < 0.05). This result provides evidence for H11, but less than 50% know how to calculate compound interest (p-value > 0.05); therefore, H12 is rejected. Table 3 presents the difference test of population proportions on the understanding of progressions and the calculation of financial interest between men and women.

Table 3.
Test of difference in proportions on knowledge of geometric progressions and the calculation of financial interest by gender.
The greatest differences in the sample proportion between men and women occur in the question of calculating compound interest (9.70%) and in the question of the general term with fractions (5.80%), both in favor of men. In the question of the general term with whole numbers (6.50%), there is a difference in favor of women. The results of the test indicate that there is no significant difference by gender regarding their understanding of the numerical sequence of the progression (with whole and fractional numbers) (Z = 0.899, p-value > 0.05; Z = −0.704, p-value > 0.05, respectively). The above results do not support H6 and H7. There is no significant difference between men and women regarding the knowledge to express the general term of a sequence, of whole numbers and fractional numbers (Z = −0.818, p-value > 0.05; Z = 0.750, p-value > 0.05), respectively. According to these results, H8 and H9 are rejected.
There is no significant difference between men and women regarding the knowledge to calculate the sum of the first n consecutive terms of a progression (Z = 0.264, p-value > 0.05); therefore, H10 is not supported. There is no significant difference between men and women regarding the knowledge to calculate zero, simple and compound interest (Z = 0.889, p-value > 0.05; Z = 0.035, p-value > 0.05; Z = 1.037, p-value >0.05), respectively. The previous results do not provide evidence in favor of H13 and H14.
Table 4 presents the estimation results of the Probit regression model of compound interest in relation to the students’ knowledge of geometric progressions. Models 1 and 2 show the results on men and models 3 and 4 for women.

Table 4.
Probit estimation. Compound interest knowledge and inheritance by gender. Marginal effect.
From models 1 and 2, it is identified that the knowledge that students (men) have to formulate the general expression of a geometric sequence with fractional numbers has a positive and significant effect on the probability of answering the compound interest question correctly. In model 2, β = 0.8124, p-value < 0.05, respondents who answered the question on the general expression of the sequence correctly, in the case of fractional numbers, are more likely (marginal effect = 0.3104) to be able to answer the question on compound interest accurately. Model 3, in the case of women, does not identify a significant relationship between compound interest and students’ knowledge of geometric progressions. This result provides evidence to reject H15 and support H16.
5. Discussion
The competence a person must have to effectively calculate interest rates and to understand interest capitalization is essential for financial decision making (Lusardi 2019; OECD 2019c), and people with a low level in arithmetic tend to have less financial knowledge (Lusardi 2012). The empirical results of this research show the importance of arithmetic and geometric progressions for the calculation of financial interest. In our descriptive results, around 97% of university students answered the question related to the sequence of whole numbers and fractional numbers correctly. It is a high percentage, although it should be considered that the participants in the study took a mathematics course the previous semester, in which they reviewed these concepts. The result coincides with Minggi et al.’s (2022) findings but differs from the 47% reported by Khaoula et al. (2020). In our results, 59.8% of university students formulate the general expression of an arithmetic sequence correctly, and less than a third (30.9%) formulate it correctly for fractional terms. The previous results show that students know the difference between the concepts of arithmetic and geometric sequences but have difficulties expressing the general term like in Bajo et al. (2019), Minggi et al. (2022) and Rachma and Rosjanuardi (2021).
In our results, three out of four students (75.3%) answered the question on the application of succession and series in a financial situation correctly. In this regard, Rachma and Rosjanuardi (2021) argue that the errors students make in application exercises could be due to the limited use of sequences and series in contextualized situations. From the sample, 45.7% of university students answered the compound interest question correctly, consistent with other studies (Klapper et al. 2015; Ramos-Hernández et al. 2020) and differing from the 77.2% reported by Skagerlund et al. (2018).
Regarding the test of difference in population proportions on knowledge of progressions, the results indicate that there is no significant difference based on gender, which differs from Khaoula et al. (2020). The difference in proportions test on the calculation of financial interest shows that there is no significant difference by gender, which differs from what Gudjonsson et al. (2022) reported. The results of the Probit model provide evidence that the understanding that male students have of the mathematical concept of geometric sequence, with fractional numbers, has a positive and significant effect on the probability of answering the compound interest question correctly, a result that coincides with what was reported by the OECD (2017). According to Gallagher et al. (2000), male students perform better than female students when mathematical problems are difficult and complex. This could explain the gender difference observed when fractional numbers are used, but not with whole numbers. As many researchers have pointed out, this difference could be due to the lower self-confidence of women (Jouini et al. 2018; Ganley and Lubienski 2016). In their study on financial literacy and confidence, Bucher-Koenen et al. (2016) show that women are less confident in their knowledge than men. Specifically, women disproportionately answer financial knowledge questions with “do not know”, even when they know the correct answer.
6. Conclusions
Mathematics learning should enable students to develop real-life competencies to make the best choices. The results of the research provide evidence that university students have knowledge of the representation of geometric progressions. Likewise, the results show that university students know how to formulate the general expression of a sequence with whole numbers, but not for the case of a sequence with fractional numbers, an unexpected result considering that the students had a math course the previous semester that included the topic of arithmetic and geometric sequences and series. Evidence is found that university students have the mathematical ability to model the description of a financial situation through a sequence. The results also show that university students know how to calculate simple interest, but they do not know how to calculate compound interest. The population proportion difference test shows that there is no gender difference regarding the understanding of progressions and the calculation of financial interest; however, the results of the Probit model provide evidence regarding the positive relationship between the ability to calculate compound interest and the male students’ understanding of geometric progressions.
These results are important in two ways. First, it is important to teach students the application of mathematical knowledge in real-life situations, such as financial issues, so that they can be prepared to make credit, savings and investment decisions. In this way, it is necessary to emphasize in the teaching of mathematics the process of solving problems in an analytical manner. Second, it is necessary to identify the reasons for the gender gap, whether it is a lack of confidence of women or something else. Different research around the world has identified that women have lower levels of financial literacy than men and, in this sense, lower possibilities of achieving financial well-being. If mathematics education can contribute to closing this gap, it is advisable to delve deeper into its causes in order to design the teaching–learning strategy.
For future research, it is recommended to analyze how sociodemographic characteristics are related to students’ math knowledge and skills. It is also recommended to include students from all disciplinary areas and from both public and private universities.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Amador-Saelices, Ma. Victoria, and Jesús Montejo-Gámez. 2016. Una trayectoria hipotética de aprendizaje para las expresiones algebraicas basada en análisis de errores [A hypothetical learning trajectory for algebraic expressions based on error análisis]. Revista de Educación Matemática Épsilon 33: 7–30. [Google Scholar]
- Anderson, David Ray, Dennis J. Sweeney, Thomas Arthur Williams, Jeffrey D. Camm, and James J. Cochran. 2017. Statistics for Business and Economics. Boston: Cengage. [Google Scholar]
- Azizah, Nurul Izatul, Yenita Roza, and Maimunah Maimunah. 2022. Computational Thinking Process of High School Students in Solving Sequences and Series Problems. Jurnal Analisa 8: 21–35. [Google Scholar] [CrossRef]
- Bajo, José Mariano, José María Gavilán Izquierdo, and Gloria Sánchez-Matamoros García. 2019. Caracterización del esquema de sucesión numérica en estudiantes de Educación Secundaria Obligatoria [Characterization of the numerical succession scheme in Compulsory Secondary Education students]. Enseñanza de las Ciencias 37: 149–67. (In Spanish) [Google Scholar] [CrossRef]
- Bucher-Koenen, Tabea, Rob Alessie, Annamaria Lusardi, and Maarten Van Rooij. 2016. Women, Confidence, and Financial Literacy. EIB Institute. Available online: https://institute.eib.org/wp-content/uploads/2016/10/women-conf-lit.pdf (accessed on 6 March 2022).
- Cavalcante, Alexandre, Annie Savard, and Elena Polotskaia. 2024. Mathematical structures of simple and compound interest: An analysis of secondary teachers’ relational thinking. Educational Studies in Mathematics 116: 215–35. [Google Scholar] [CrossRef]
- Cortez, Romy Adriana. 2017. Un minuto para matemáticas. Una experiencia de diversión, aprendizaje y divulgación al explorar patrones numéricos [A minute for math. A fun, learning and outreach experience when exploring numerical patterns]. Educación Matemática 29: 225–43. (In Spanish) [Google Scholar] [CrossRef]
- Dituri, Philip, Andrew Davidson, and Jack Marley-Payne. 2019. Combining Financial Education with Mathematics Coursework: Findings From a Pilot Study. Journal of Financial Counseling and Planning 30: 313–22. [Google Scholar] [CrossRef]
- Fauzia, Tri Aprianti, Dadang Juandi, and Tia Purniati. 2017. Didactical design on learning arithmetic sequences and series concepts in high school level [in Bahasa]. Journal of Mathematics Education Research 1: 1–10. [Google Scholar]
- Fornero, Elsa, and Chiara Monticone. 2011. Financial literacy and pension plan participation in Italy. Journal of Pension, Economics and Finance 10: 547–64. [Google Scholar] [CrossRef]
- Gallagher, Ann M., Richard De Lisi, Patricia C. Holst, Ann V. McGillicuddy-De Lisi, Mary Morely, and Cara Cahalan. 2000. Gender differences in advanced mathematical problem solving. Journal of Experimental Child Psychology 75: 165–90. [Google Scholar] [CrossRef]
- Ganley, Colleen M., and Sarah Theule Lubienski. 2016. Mathematics confidence, interest, and performance: Examining gender patterns and reciprocal relations. Learning and Individual Differences 47: 182–93. [Google Scholar] [CrossRef]
- Grueso, Emiliano, Liliana Potosí Cruz, and Sandra Esther Suárez. 2020. Experiencia del proceso de modelación matemática como estrategia didáctica en la enseñanza de la matemática financiera [Experience of the mathematical modeling process as a didactic strategy in teaching financial mathematics]. Revista Sapientia 12: 16–26. (In Spanish) [Google Scholar] [CrossRef]
- Gudjonsson, Sigurdur, Inga Minelgaite, Kari Kristinsson, and Sigrún Pálsdóttir. 2022. Financial Literacy and Gender Differences: Women Choose People While Men Choose Things? Administrative Science 12: 179. [Google Scholar] [CrossRef]
- Hubbard, Edward, Percival Matthews, and Anya Samek. 2016. Using online compound interest tools to improve financial literacy. The Journal of Economic Education 47: 106–20. [Google Scholar] [CrossRef]
- Huston, Sandra J. 2010. Measuring Financial Literacy. Journal of Consumer Affairs 44: 296–316. [Google Scholar] [CrossRef]
- INEGI. 2022. Encuesta Nacional de Inclusión Financiera. Diseño conceptual [National Financial Inclusion Survey. Conceptual Design]. Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=889463903895 (accessed on 10 March 2023). (In Spanish).
- Iswara, Eris, Darhim, and Dadang Juandi. 2021. Students’ Critical Thinking Skills in Solving on The Topic of Sequences and Series. Plusminus: Jurnal Pendidikan Matematika 1: 385–94. [Google Scholar] [CrossRef]
- Jiang, Peijie. 2021. Gender differences in mathematics academic performance of high school students in western China. Journal of Physics: Conference Series 1978: 012038. [Google Scholar] [CrossRef]
- Jouini, Elyès, Paul Karehnke, and Clotilde Napp. 2018. Stereotypes, underconfidence and decision-making with an application to gender and math. Journal of Economic Behavior and Organization 148: 34–45. [Google Scholar] [CrossRef]
- Kaiser, Gabriele, and Yan Zhu. 2022. Gender differences in mathematics achievement: A secondary analysis of Programme for International Student Assessment data from Shanghai. Asian Journal for Mathematics Education 1: 115–30. [Google Scholar] [CrossRef]
- Khaoula, Elarif, Hassouni Taoufik, and Bouazza El Wahbi. 2020. Conceptual Evolution of the Sequences and its Transition from High School to University in Morocco. International Journal of Higher Education 9: 26–33. [Google Scholar] [CrossRef]
- Klapper, Leora, Annamaria Lusardi, and Peter Van Oudheusden. 2015. Financial Literacy around the World. Washington, DC: World Bank. Available online: https://gflec.org/wp-content/uploads/2015/11/Finlit_paper_16_F2_singles.pdf (accessed on 11 March 2023).
- Leahey, Erin, and Guang Guo. 2001. Gender Differences in Mathematical Trajectories. Social Forces 80: 713–32. [Google Scholar] [CrossRef]
- Liang, Senfeng, Ruixue Du, and Zihui Ma. 2022. Which Math Skill Matters the Most in Accounting Learning? Journal of Accounting and Finance 22: 67–78. [Google Scholar] [CrossRef]
- Lusardi, Annamaria, and Olivia S. Mitchell. 2008. Planning and Financial Literacy: How Do Women Fare? American Economic Review 98: 413–17. [Google Scholar] [CrossRef]
- Lusardi, Annamaria, and Olivia S. Mitchell. 2011. Financial Literacy and Planning: Implications for Retirement Well-Being. In Financial Literacy: Implications for Retirement Security and the Financial Marketplace. Edited by Olivia S. Mitchell and Annamaria Lusardi. Oxford and New York: Oxford University Press, pp. 17–39. [Google Scholar]
- Lusardi, Annamaria. 2012. Numeracy, Financial Literacy, and Financial Decision-Making. Numeracy 5: 2. [Google Scholar] [CrossRef]
- Lusardi, Annamaria. 2019. Financial literacy and the need for financial education: Evidence and implications. Swiss Journal of Economics and Statistics 155: 1. [Google Scholar] [CrossRef]
- Martínez, Magally, Anabelem Soberanes-Martín, and Juan Manuel Sánchez Soto. 2018. Análisis correlacional de competencias matemáticas de pruebas estandarizadas y pre-requisitos matemáticos en estudiantes de nuevo ingreso a Ingeniería en Computación [Correlational analysis of mathematical competencies of standardized tests and mathematical prerequisites in Computer Engineering freshmen]. RIDE Revista Iberoamericana para la Investigación y el Desarrollo Educativo 8: 946–74. (In Spanish) [Google Scholar] [CrossRef][Green Version]
- Martínez, María, and Tonys Romero. 2019. Transición de la aritmética al álgebra: Un estudio con estudiantes universitarios de Nicaragua [Transition from arithmetic to algebra: A study with university students in Nicaragua]. Revista Electrónica De Conocimientos, Saberes Y Prácticas 2: 29–39. (In Spanish) [Google Scholar] [CrossRef]
- Minggi, Ilham, Bernard, and Aco Fauzan. 2022. Students’ Errors Analysis in Solving Problems in the Material of Sequences and Series based on Hadar’s Criteria in terms of Students’ Mathematical Understanding. EduLine. Journal of Education and Learning Innovation 2: 54–61. [Google Scholar] [CrossRef]
- Moreno-García, Elena, Arturo García-Santillán, and Lizette Gutiérrez-Delgado. 2017. Nivel de educación financiera en escenarios de educación superior. Un estudio empírico con estudiantes del área económico-administrativa [Level of financial education in higher education. An empirical study with students of the economic-administrative area]. Revista Iberoamericana de Educación Superior 8: 163–83. [Google Scholar]
- Mottola, Gary R. 2013. In Our Best Interest: Women, Financial Literacy, and Credit Card Behavior. Numeracy 6: 4. [Google Scholar] [CrossRef]
- Muñoz-Murillo, Melisa, Pilar B. Álvarez-Franco, and Diego A. Restrepo-Tobón. 2020. The role of cognitive abilities on financial. literacy: New experimental evidence. Journal of Behavioral and Experimental Economics 84: 101482. [Google Scholar] [CrossRef]
- OECD. 2003. The PISA 2003 Assessment Framework—Mathematics, Reading, Science and Problem Solving Knowledge and Skills. Available online: https://www.oecd.org/education/school/programmeforinternationalstudentassessmentpisa/33694881.pdf (accessed on 23 March 2023).
- OECD. 2017. PISA 2015 Results (Volume IV): Students’ Financial Literacy. Paris: PISA, OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2019a. PISA 2018 Assessment and Analytical Framework. Paris: PISA, OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2019b. Policy Handbook on Financial Education for Young People in the Commonwealth of Independent States. Available online: https://www.oecd.org/financial/education/Youth-Policy-Handbook-on-Financial-Education-CIS-EN.pdf (accessed on 24 February 2023).
- OECD. 2019c. Programme for International Student Assessment (PISA) Results from PISA 2018. Available online: https://www.oecd.org/pisa/publications/PISA2018_CN_MEX.pdf (accessed on 5 February 2023).
- OECD. 2020. OECD/INFE 2020 International Survey of Adult Financial Literacy. Available online: www.oecd.org/financial/education/launchoftheoecdinfeglobalfinancialliteracysurveyreport.htm (accessed on 26 February 2023).
- Ozkale, Abdullah, and Emel Ozdemir Erdogan. 2020. A Conceptual Model for the Interaction of Mathematical and Financial Literacies. International Journal of Progressive Education 16: 288–304. [Google Scholar] [CrossRef]
- Rachma, Andina Aulia, and Rizky Rosjanuardi. 2021. Students’ Obstacles in Learning Sequence and Series Using Onto-Semiotic Approach. Jurnal Pendidikan Matematika 15: 115–32. [Google Scholar] [CrossRef]
- Ramos-Hernández, Jésica Josefina, Arturo García-Santillán, and Violetta Molchanova. 2020. Financial Literacy Level on College Students: A Comparative Descriptive Analysis between Mexico and Colombia. European Journal of Contemporary Education 9: 126–44. [Google Scholar] [CrossRef]
- Secretaría de educación Pública (SEP). 2013. Matemáticas Financieras I. Programas de Estudio [Financial Mathematics I. Study Programs]. Available online: https://dgb.sep.gob.mx/informacion-academica/programas-de-estudio/cfp_5sem/matematicas-financieras-i.pdf (accessed on 1 March 2023). (In Spanish).
- Secretaría de Educación Pública (SEP). 2015. Matemáticas I. Primer Semestre [Math I. First Semester]. México: Secretaría de Educación Pública (SEP). (In Spanish) [Google Scholar]
- Skagerlund, Kenny, Thérèse Lind, Camilla Strömbäck, Gustav Tinghög, and Daniel Västfjäll. 2018. Financial literacy and the role of numeracy–How individuals’ attitude and affinity with numbers influence financial literacy. Journal of Behavioral and Experimental Economics 74: 18–25. [Google Scholar] [CrossRef]
- Stewart, James, Rodrigo Hernández, and Constanza Sanmiguel. 2007. Introducción al Cálculo [Introduction to Calculus]. Buenos Aires: Thomson Learning. (In Spanish) [Google Scholar]
- Stoet, Gijsbert, and David C. Geary. 2012. Can stereotype threat explain the gender gap in mathematics performance and achievement? Review of General Psychology 16: 93–102. [Google Scholar] [CrossRef]
- Thomson, Sue, Lisa De Bortoli, Catherine Underwood, and Marina Schmid. 2020. PISA 2018: Financial Literacy in Australia. Australian Council for Educational Research. Available online: https://research.acer.edu.au/ozpisa/48 (accessed on 7 April 2022).
- Tsai, Shu-Ling, Michael L. Smith, and Robert M. Hauser. 2018. Gender gaps in student academic achievement and inequality. Research in the Sociology of Education 20: 181–218. [Google Scholar] [CrossRef]
- Vidaurri, Héctor Manuel. 2017. Matemáticas Financieras [Financial Math], 6th ed. México: Cengage Learning. (In Spanish) [Google Scholar]
- Villagómez, Alejandro, and José Hidalgo. 2017. Financial Literacy and Mathematics: A Study among Young Mexican High School Students. Revista Mexicana de Economía y Finanzas 12: 1–22. [Google Scholar] [CrossRef]
- Vogel, Rose. 2005. Patterns—A fundamental idea of mathematical thinking and learning. ZDM Mathematics Education 37: 445–49. [Google Scholar] [CrossRef]
- Werner, Frank, and Yuri Sotskov. 2006. Mathematics of Economics and Business. New York: Routledge. [Google Scholar]
- Wooldridge, Jeffrey M. 2010. Econometric Analysis of Cross Section and Panel Data. Cambridge and London: The MIT Press. [Google Scholar]
- Zissimopoulos, Julie M., Benjamin R. Karney, and Amy J. Rauer. 2015. Marriage and economic well being at older ages. Review of Economics of the Household 13: 1–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).