Enhancing Model Selection by Obtaining Optimal Tuning Parameters in Elastic-Net Quantile Regression, Application to Crude Oil Prices
Abstract
1. Introduction
2. Methodology
2.1. Quantile Regression
2.2. Elastic Net Regression
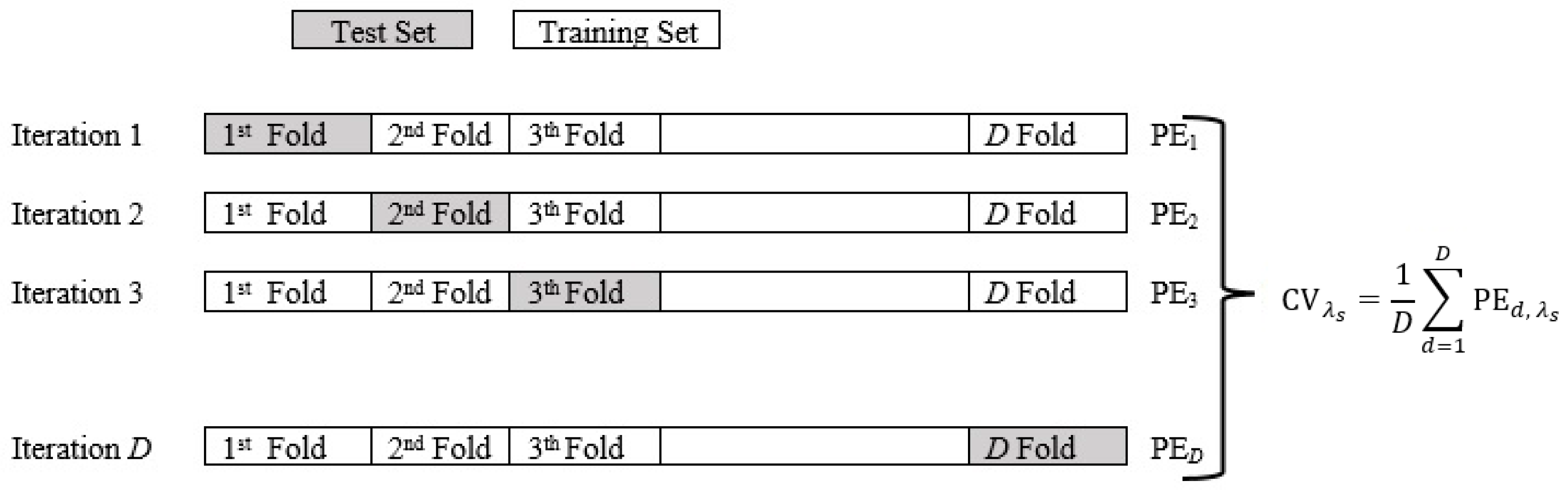
2.3. D-Fold Cross-Validation
| Algorithm 1: D-fold Cross-Validation |
|
2.4. Proposed Penalized Quantile Regression Method
- Apply the QR method at τ = (0.25, 0.50, 0.75) using all the variables:
- Using the training set only, select the optimal parameters via the D-CV method at D = 10 as follows:
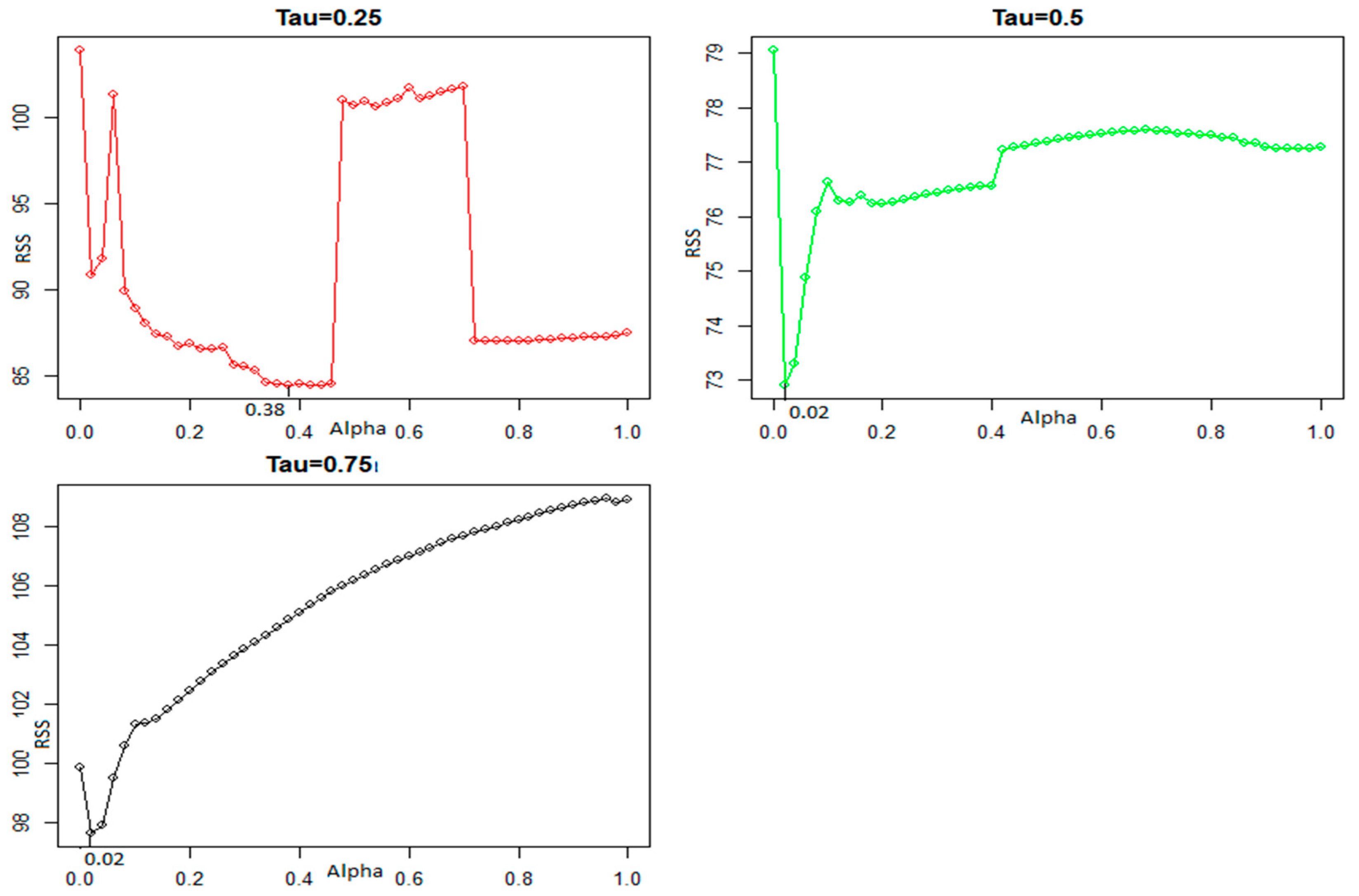
- The regularization parameter value of the sequence 0 < α < 1, where represents the relative contribution of the L1 penalty versus L2 penalty.where represents the number of values between one and zero and will be chosen. In this study, we choose .
- The tuning parameter value is at
- Based on the Equations (7) and (10) at and , the ELNET penalized regression is used as the following formula:
3. Application
3.1. Simulation Study
3.2. Application Datasets
4. Results and Discussion
4.1. Simulation Results
4.2. Application Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aastveit, Knut Are, Jamie L. Cross, and Herman K. van Dijk. 2023. Quantifying time-varying forecast uncertainty and risk for the real price of oil. Journal of Business & Economic Statistics 41: 523–37. [Google Scholar]
- Akaike, Hirotsugu, Boris Nikolaevich Petrov, and F. Csaki. 1973. Second International Symposium on Information Theory. Budapest: Akademiai Kiado, pp. 267–81. [Google Scholar]
- Al-Jawarneh, Abdullah S., and Mohd Tahir Ismail. 2024. The adaptive LASSO regression and empirical mode decomposition algorithm for enhancing modelling accuracy. Communications in Statistics-Simulation and Computation 53: 714–26. [Google Scholar] [CrossRef]
- Al-Jawarneh, Abdullah S., Mohd Tahir Ismail, Ahmad M. Awajan, and Ahmed R. M. Alsayed. 2022. Improving accuracy models using elastic net regression approach based on empirical mode decomposition. Communications in Statistics-Simulation and Computation 51: 4006–25. [Google Scholar] [CrossRef]
- Alsayed, Ahmed R. M. 2023. Turkish stock market from pandemic to Russian invasion, evidence from developed machine learning algorithm. Computational Economics 62: 1107–23. [Google Scholar] [CrossRef]
- Alsayed, Ahmed R. M., and Giancarlo Manzi. 2019. A comparison of monotonic correlation measures with outliers. WSEAS Transactions on Computers 18: 223–30. [Google Scholar]
- Alsayed, Ahmed R. M., Zaidi Isa, and Sek Siok Kun. 2018. Outliers detection methods in panel data regression: An application to environment science. International Journal of Ecological Economics & Statistics 39: 73–86. [Google Scholar]
- Alsayed, Ahmed R. M., Zaidi Isa, Sek Siok Kun, and Giancarlo Manzi. 2020. Quantile regression to tackle the heterogeneity on the relationship between economic growth, energy consumption, and CO2 emissions. Environmental Modeling & Assessment 25: 251–58. [Google Scholar]
- Amano, Robert A., and Simon Van Norden. 1998. Exchange rates and oil prices. Review of International Economics 6: 683–94. [Google Scholar] [CrossRef]
- Ambark, Ali S. A., Mohd Tahir Ismail, Abdullah S. Al-Jawarneh, and Samsul Ariffin Abdul Karim. 2023. Elastic Net Penalized Quantile Regression Model and Empirical Mode Decomposition for Improving the Accuracy of the Model Selection. IEEE Access 11: 26152–62. [Google Scholar] [CrossRef]
- Balashova, Svetlana, and Apostolos Serletis. 2021. Oil price uncertainty, globalization, and total factor productivity: Evidence from the European Union. Energies 14: 3429. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2015. Forecasting the real price of oil in a changing world: A forecast combination approach. Journal of Business & Economic Statistics 33: 338–51. [Google Scholar]
- Bloomberg. 2023. Bloomberg Terminal. Available online: https://www.bloomberg.com/professional/solution/bloomberg-terminal/ (accessed on 1 January 2023).
- Borowski, Piotr F. 2020. Zonal and Nodal Models of energy market in European Union. Energies 13: 4182. [Google Scholar] [CrossRef]
- Chand, Sohail. 2012. On tuning parameter selection of lasso-type methods—A monte carlo study. Paper presented at 2012 9th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, January 9–12; pp. 120–29. [Google Scholar]
- Davino, Cristina, Marilena Furno, and Domenico Vistocco. 2013. Quantile Regression: Theory and Applications. Hoboken: John Wiley & Sons. [Google Scholar]
- Desboulets, Loann David Denis. 2018. A review on variable selection in regression analysis. Econometrics 6: 45. [Google Scholar] [CrossRef]
- Doğrul, H. Günsel, and Ugur Soytas. 2010. Relationship between oil prices, interest rate, and unemployment: Evidence from an emerging market. Energy Economics 32: 1523–28. [Google Scholar]
- Efron, Bradley, Trevor Hastie, Iain Johnstone, and Robert Tibshirani. 2004. Least angle regression. The Annals of Statistics 32: 407–99. [Google Scholar] [CrossRef]
- Fan, Jianqing, and Runze Li. 2001. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American statistical Association 96: 1348–60. [Google Scholar] [CrossRef]
- Fan, Yingying, and Cheng Yong Tang. 2013. Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 75: 531–52. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Rob Tibshirani. 2010. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33: 1–22. [Google Scholar] [CrossRef]
- Gareth, James, Witten Daniela, Hastie Trevor, and Tibshirani Robert. 2013. An Introduction to Statistical Learning with Applications in R. New York: Springer. [Google Scholar]
- Geisser, Seymour. 1975. The predictive sample reuse method with applications. Journal of the American statistical Association 70: 320–28. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, Jerome H. Friedman, and Jerome H. Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer Science & Business Media. [Google Scholar]
- Hastie, Trevor, Robert Tibshirani, and Martin Wainwright. 2015. Statistical Learning with Sparsity: The Lasso and Generalizations. Boca Raton: CRC Press. [Google Scholar]
- Haws, David C., Irina Rish, Simon Teyssedre, Dan He, Aurelie C. Lozano, Prabhanjan Kambadur, Zivan Karaman, and Laxmi Parida. 2015. Variable-selection emerges on top in empirical comparison of whole-genome complex-trait prediction methods. PLoS ONE 10: e0138903. [Google Scholar] [CrossRef]
- He, Yanan, Ai Han, Yongmiao Hong, Yuying Sun, and Shouyang Wang. 2021. Forecasting crude oil price intervals and return volatility via autoregressive conditional interval models. Econometric Reviews 40: 584–606. [Google Scholar] [CrossRef]
- Kartal, Mustafa Tevfik. 2020. The Effect of the COVID-19 Pandemic on Oil Prices: Evidence from Turkey. Energy Research Letters. Available online: https://erl.scholasticahq.com/article/18723-the-effect-of-the-covid-19-pandemic-on-oil-prices-evidence-from-turkey (accessed on 29 May 2024).
- Kassambara, Alboukadel. 2018. Machine Learning Essentials: Practical Guide in R. Scotts Valley: CreateSpace Independent Publishing Platform. [Google Scholar]
- Kirikkaleli, Dervis, and Nezahat Doğan. 2021. Energy consumption and refugee migration in Turkey. Utilities Policy 68: 101144. [Google Scholar] [CrossRef]
- Koenker, Roger. 2004. Quantile regression for longitudinal data. Journal of Multivariate Analysis 91: 74–89. [Google Scholar] [CrossRef]
- Krozer, Yoram. 2013. Cost and benefit of renewable energy in the European Union. Renewable Energy 50: 68–73. [Google Scholar]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York: Springer. [Google Scholar]
- Lee, Young, Vy Nguyen, and Duzhe Wang. 2016. On Variable and Grouped Selections of the Elastic Net. Report CS532 961: 1–24. [Google Scholar]
- Li, Youjuan, and Ji Zhu. 2008. L 1-norm quantile regression. Journal of Computational and Graphical Statistics 17: 163–85. [Google Scholar] [CrossRef]
- Masselot, Pierre, Fateh Chebana, Diane Bélanger, André St-Hilaire, Belkacem Abdous, Pierre Gosselin, and Taha BMJ Ouarda. 2018. EMD-regression for modelling multi-scale relationships, and application to weather-related cardiovascular mortality. Science of The Total Environment 612: 1018–29. [Google Scholar] [CrossRef]
- Melkumova, L. E., and S. Ya Shatskikh. 2017. Comparing Ridge and LASSO estimators for data analysis. Procedia Engineering 201: 746–55. [Google Scholar] [CrossRef]
- Qin, Lei, Shuangge Ma, Jung-Chen Lin, and Ben-Chang Shia. 2016. Lasso Regression Based on Empirical Mode Decomposition. Communications in Statistics-Simulation and Computation 45: 1281–94. [Google Scholar] [CrossRef]
- Ray, Susmita. 2019. A quick review of machine learning algorithms. Paper presented at 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, February 14–16. [Google Scholar]
- Schwarz, Gideon. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar] [CrossRef]
- Stone, Mervyn. 1974. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society: Series B (Methodological) 36: 111–33. [Google Scholar]
- Su, Meihong, and Wenjian Wang. 2021. Elastic net penalized quantile regression model. Journal of Computational and Applied Mathematics 392: 113462. [Google Scholar] [CrossRef]
- Tibshirani, Robert. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological) 58: 267–88. [Google Scholar] [CrossRef]
- van Houwelingen, Hans C., and Willi Sauerbrei. 2013. Cross-validation, shrinkage and variable selection in linear regression revisited. Open Journal of Statistics 3: 79–102. [Google Scholar] [CrossRef]
- Xiao, Hui, and Yiguo Sun. 2019. On Tuning Parameter Selection in Model Selection and Model Averaging: A Monte Carlo Study. Journal of Risk and Financial Management 12: 109. [Google Scholar] [CrossRef]
- Yılmaz, Alper, and Hüseyin Altay. 2016. Examining the cointegration relationship and volatility spillover between imported crude oil prices and exchange rate: The Turkish case. Ege Academic Review 16: 655–71. [Google Scholar]
- Zou, Hui, and Hao Helen Zhang. 2009. On the adaptive elastic-net with a diverging number of parameters. Annals of statistics 37: 1733. [Google Scholar] [CrossRef]
- Zou, Hui, and Trevor Hastie. 2005. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67: 301–20. [Google Scholar] [CrossRef]



| Method | RSS | RMSE | MAE | MAPE | MASE | |
|---|---|---|---|---|---|---|
| τ = 0.25 | ||||||
| RR.QR | 35.5827 | 0.88624 | 0.71977 | 3.657265 | 0.794615 | |
| 39.4718 | 0.93395 | 0.76183 | 4.024955 | 0.841051 | ||
| LASSO.QR | 14.1830 | 0.56093 | 0.40053 | 1.746325 | 0.442176 | |
| 15.3082 | 0.58278 | 0.43724 | 1.999109 | 0.482706 | ||
| AdLASSO.QR (RR.W. λmin) | 14.5157 | 0.56762 | 0.41579 | 2.082011 | 0.459031 | |
| 16.0379 | 0.59633 | 0.45133 | 2.030926 | 0.498263 | ||
| AdLASSO.QR (RR.W. λ1se) | 14.7190 | 0.57034 | 0.41830 | 2.092005 | 0.461806 | |
| 16.2224 | 0.59878 | 0.45343 | 2.044566 | 0.500584 | ||
| 19.0338 | 0.64701 | 0.50269 | 2.272781 | 0.554958 | ||
| 22.9179 | 0.71031 | 0.56536 | 2.504381 | 0.624143 | ||
| 14.7433 | 0.57177 | 0.41665 | 1.89485 | 0.459972 | ||
| 17.4372 | 0.62082 | 0.47837 | 2.131715 | 0.528107 | ||
| 14.2895 | 0.56306 | 0.40377 | 1.780631 | 0.445752 | ||
| 15.7379 | 0.59067 | 0.44563 | 2.044958 | 0.491972 | ||
| 13.9615 | 0.55671 | 0.39654 | 1.776101 | 0.437778 | ||
| 15.7195 | 0.59049 | 0.44696 | 2.020386 | 0.493431 | ||
| τ = 0.5 | ||||||
| RR.QR | 30.8563 | 0.82567 | 0.69494 | 2.127862 | 0.76720 | |
| 33.5667 | 0.86207 | 0.72893 | 2.019126 | 0.80472 | ||
| LASSO.QR | 11.7178 | 0.50823 | 0.39718 | 2.592074 | 0.438483 | |
| 13.6771 | 0.54948 | 0.45072 | 2.456135 | 0.497588 | ||
| AdLASSO.QR (RR.W. λmin) | 13.385 | 0.53733 | 0.44051 | 2.604391 | 0.486318 | |
| 14.9137 | 0.56951 | 0.46914 | 2.488478 | 0.517925 | ||
| AdLASSO.QR (RR.W. λ1se) | 13.4163 | 0.53805 | 0.44168 | 2.602395 | 0.487607 | |
| 14.9282 | 0.56976 | 0.46944 | 2.48853 | 0.518257 | ||
| 16.1670 | 0.59738 | 0.48819 | 2.668777 | 0.538961 | ||
| 19.3541 | 0.65371 | 0.53790 | 2.602162 | 0.593840 | ||
| 13.1976 | 0.53957 | 0.44388 | 2.665215 | 0.490041 | ||
| 15.5554 | 0.58596 | 0.47915 | 2.659132 | 0.528980 | ||
| 12.3296 | 0.52141 | 0.42639 | 2.639871 | 0.470737 | ||
| 14.3324 | 0.56247 | 0.46268 | 2.544796 | 0.510792 | ||
| 10.3090 | 0.47689 | 0.37236 | 2.564913 | 0.411081 | ||
| 13.6800 | 0.54953 | 0.45087 | 2.515077 | 0.497758 | ||
| τ = 0.75 | ||||||
| RR.QR | 42.7458 | 0.96993 | 0.79680 | 6.288212 | 0.879659 | |
| 46.8397 | 1.01652 | 0.83617 | 6.47382 | 0.923126 | ||
| LASSO.QR | 12.9671 | 0.53623 | 0.45390 | 4.716719 | 0.501104 | |
| 14.3718 | 0.5644 | 0.46955 | 4.696969 | 0.518382 | ||
| AdLASSO.QR (RR.W. λmin) | 14.4291 | 0.55778 | 0.47079 | 4.889332 | 0.519747 | |
| 15.8043 | 0.58392 | 0.48687 | 4.910642 | 0.537499 | ||
| AdLASSO.QR (RR.W. λ1se) | 14.5222 | 0.55917 | 0.47169 | 4.892964 | 0.520746 | |
| 15.8926 | 0.58537 | 0.48803 | 4.916813 | 0.538782 | ||
| 20.6517 | 0.67191 | 0.55133 | 5.073862 | 0.608665 | ||
| 23.6645 | 0.71873 | 0.58854 | 5.305833 | 0.649741 | ||
| 13.7992 | 0.55295 | 0.46196 | 4.620298 | 0.510000 | ||
| 15.1615 | 0.57941 | 0.47896 | 4.653668 | 0.528763 | ||
| 13.0885 | 0.53868 | 0.45467 | 4.68214 | 0.501955 | ||
| 14.5195 | 0.56725 | 0.47102 | 4.675978 | 0.520007 | ||
| 12.8468 | 0.53376 | 0.45244 | 4.714046 | 0.499487 | ||
| 14.3309 | 0.56360 | 0.46864 | 4.683324 | 0.517377 | ||
| Method | RSS | Num. of V.S. | V.S. | |
|---|---|---|---|---|
| RR | 0.041839 | 109.177 | 10 | |
| 0.74835 | 77.0141 | 10 | ||
| LASSO | 0.003994 | 120.091 | 9 | |
| 0.078399 | 82.3651 | 7 | ||
| 0.013263 | 116.129 | 10 | ||
| 0.260352 | 76.9288 | 7 | ||
| 0.007987 | 117.951 | 9 | ||
| 0.142868 | 79.5524 | 7 | ||
| 0.005844 | 118.623 | 9 | ||
| 80.8656 | 7 | |||
| τ = 0.25 | ||||
| RR.QR | 103.907 | 10 | ||
| 92.046 | 10 | |||
| LASSO.QR | 87.492 | 4 | ||
| 93.659 | 3 | |||
| AdLASSO.QR (RR.W. λmin) | 100.139 | 4 | ||
| 100.797 | 3 | |||
| AdLASSO.QR (RR.W. λ1se) | 96.542 | 4 | ||
| 99.369 | 3 | |||
| 86.377 | 8 | |||
| 0.2002 | 87.614 | 5 | ||
| 100.762 | 9 | |||
| 0.1275 | 90.6738 | 4 | ||
| 87.045 | 5 | |||
| 92.967 | 4 | |||
| 84.426 | 8 | |||
| 89.458 | 5 | |||
| τ = 0.5 | ||||
| RR.QR | 79.0412 | 10 | ||
| 74.8137 | 10 | |||
| LASSO.QR | 77.2748 | 8 | ||
| 75.0064 | 5 | |||
| AdLASSO.QR (RR.W. λmin) | 79.3498 | 3 | ||
| 77.0606 | 2 | |||
| AdLASSO.QR (RR.W. λ1se) | 73.2189 | 5 | ||
| 80.3982 | 3 | |||
| 0.0390 | 76.283 | 9 | ||
| 0.1719 | 74.4287 | 8 | ||
| 0.0357 | 77.3792 | 9 | ||
| 0.1000 | 74.9740 | 6 | ||
| 0.0277 | 77.5181 | 8 | ||
| 0.0687 | 74.9286 | 6 | ||
| 72.9008 | 10 | |||
| 74.9729 | 9 | |||
| τ = 0.75 | ||||
| RR.QR | 99.8799 | 10 | ||
| 99.3733 | 10 | |||
| LASSO.QR | 108.9124 | 8 | ||
| 101.6289 | 5 | |||
| AdLASSO.QR (RR.W. λmin) | 113.2957 | 5 | ||
| 118.7315 | 4 | |||
| AdLASSO.QR (RR.W. λ1se) | 100.7581 | 5 | ||
| 105.5192 | 3 | |||
| 0.0204 | 103.2303 | 8 | ||
| 0.1334 | 102.9762 | 6 | ||
| 0.0102 | 106.1962 | 8 | ||
| 101.7987 | 5 | |||
| 0.0068 | 107.9645 | 8 | ||
| 0.0458 | 101.4287 | 5 | ||
| 97.6474 | 9 | |||
| 105.4114 | 8 | |||
| Method | RMSE | MAE | MAPE | MASE | |
|---|---|---|---|---|---|
| RR | 0.041839 | 1.1469 | 0.7806 | 1.7260 | 0.8729 |
| 0.74835 | 0.9633 | 0.7105 | 1.2235 | 0.7945 | |
| LASSO | 0.003994 | 1.2029 | 0.8069 | 1.8265 | 0.9022 |
| 0.078399 | 0.9962 | 0.7161 | 1.3324 | 0.8008 | |
| ELNET | 0.013263 | 1.1829 | 0.7974 | 1.7923 | 0.8916 |
| 0.260352 | 0.9627 | 0.7046 | 1.2343 | 0.7879 | |
| ELNET | 0.007987 | 1.1921 | 0.8018 | 1.8080 | 0.8966 |
| 0.142868 | 0.9790 | 0.7096 | 1.2885 | 0.7935 | |
| ELNET | 0.005844 | 1.1955 | 0.8035 | 1.8136 | 0.8985 |
| 0.9871 | 0.7129 | 1.3112 | 0.7972 | ||
| τ = 0.25 | |||||
| RR.QR | 1.1189 | 0.8876 | 2.537 | 0.9924 | |
| 1.0531 | 0.8610 | 2.727 | 0.9628 | ||
| LASSO.QR | 1.0267 | 0.8217 | 2.514 | 0.9187 | |
| 1.0623 | 0.8520 | 2.571 | 0.9527 | ||
| AdLASSO.QR (RR.W. λmin) | 1.0984 | 0.8644 | 2.618 | 0.9667 | |
| 1.1020 | 0.8742 | 2.639 | 0.9776 | ||
| AdLASSO.QR (RR.W. λ1se) | 1.0785 | 0.8527 | 2.704 | 0.9534 | |
| 1.0942 | 0.8661 | 2.671 | 0.9685 | ||
| 1.0201 | 0.8259 | 2.4273 | 0.9236 | ||
| 0.2002 | 1.0274 | 0.8387 | 2.5879 | 0.9378 | |
| 1.1018 | 0.8779 | 2.5650 | 0.9817 | ||
| 0.1275 | 1.0452 | 0.8432 | 2.5592 | 0.9429 | |
| 1.0241 | 0.8195 | 2.5257 | 0.9164 | ||
| 1.0583 | 0.8500 | 2.5636 | 0.9505 | ||
| 1.0086 | 0.8180 | 2.444 | 0.9146 | ||
| 1.0382 | 0.8404 | 2.565 | 0.9398 | ||
| τ = 0.5 | |||||
| RR.QR | 0.9759 | 0.7058 | 1.6486 | 0.7893 | |
| 0.9494 | 0.6876 | 1.2275 | 0.7689 | ||
| LASSO.QR | 0.9649 | 0.7037 | 1.6693 | 0.7869 | |
| 0.9506 | 0.6907 | 1.4299 | 0.7724 | ||
| AdLASSO.QR (RR.W. λmin) | 0.9778 | 0.7109 | 1.7108 | 0.7949 | |
| 0.9636 | 0.7151 | 1.6833 | 0.7996 | ||
| AdLASSO.QR (RR.W. λ1se) | 0.9392 | 0.6872 | 1.5984 | 0.7685 | |
| 0.9842 | 0.7099 | 1.3913 | 0.7938 | ||
| 0.0390 | 0.9590 | 0.6993 | 1.6403 | 0.7820 | |
| 0.1719 | 0.9470 | 0.6876 | 1.3001 | 0.7689 | |
| 0.0357 | 0.9655 | 0.7031 | 1.6494 | 0.7863 | |
| 0.1000 | 0.9504 | 0.6895 | 1.3276 | 0.7710 | |
| 0.0277 | 0.9664 | 0.7040 | 1.6612 | 0.7872 | |
| 0.0687 | 0.9501 | 0.6901 | 1.3927 | 0.7717 | |
| 0.9372 | 0.6827 | 1.3390 | 0.7634 | ||
| 0.9504 | 0.6914 | 1.1955 | 0.7731 | ||
| τ = 0.75 | |||||
| RR.QR | 1.0970 | 0.7913 | 2.9823 | 0.8848 | |
| 1.0942 | 0.7899 | 2.9192 | 0.8833 | ||
| LASSO.QR | 1.1455 | 0.8323 | 3.1377 | 0.9307 | |
| 1.1065 | 0.7785 | 2.9182 | 0.8705 | ||
| AdLASSO.QR (RR.W. λmin) | 1.1683 | 0.8644 | 3.1510 | 0.9665 | |
| 1.1960 | 0.9016 | 3.4228 | 1.0082 | ||
| AdLASSO.QR (RR.W. λ1se) | 1.1018 | 0.7837 | 2.909 | 0.8764 | |
| 1.1275 | 0.8137 | 3.1028 | 0.9099 | ||
| 0.0204 | 1.1152 | 0.8057 | 3.0121 | 0.9010 | |
| 0.1334 | 1.1139 | 0.7947 | 2.9758 | 0.8886 | |
| 0.0102 | 1.1311 | 0.8191 | 3.0654 | 0.9159 | |
| 1.1075 | 0.7847 | 2.9390 | 0.8775 | ||
| 0.0068 | 1.1405 | 0.8278 | 3.1141 | 0.9256 | |
| 0.0458 | 1.1055 | 0.7801 | 2.9212 | 0.8723 | |
| 0.02 | 1.0847 | 0.7812 | 2.8845 | 0.8736 | |
| 1.1270 | 0.8156 | 3.0404 | 0.9120 | ||
| τ 0.38 | τ 0.02 | τ 0.02 | ||||
|---|---|---|---|---|---|---|
| 0.1686 | 0.1313 | 0.1545 | 0.0904 | 0.1054 | 0.0548 | |
| 0.1225 | 0.0415 | 0.1066 | 0.0614 | 0.0306 | 0.0184 | |
| 0.3038 | 0.2110 | 0.2072 | 0.1061 | 0.1421 | 0.0703 | |
| 0.1151 | 0.0948 | 0.1360 | 0.0879 | 0.0761 | 0.0487 | |
| 0.0150 | 0 | −0.0172 | 0 | −0.0277 | 0 | |
| 0.0529 | 0 | 0.0413 | 0.0123 | 0.0648 | 0.0158 | |
| 0 | 0 | 0.0033 | 0.0026 | 0 | 0 | |
| 0.0037 | 0 | 0.0448 | 0.0128 | 0.0489 | 0.0093 | |
| 0 | 0 | 0.0133 | 0.0013 | −0.0357 | −0.0048 | |
| 0.0802 | 0.0062 | 0.0862 | 0.0531 | 0.1022 | 0.0425 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Jawarneh, A.S.; Alsayed, A.R.M.; Ayyoub, H.N.; Ismail, M.T.; Sek, S.K.; Ariç, K.H.; Manzi, G. Enhancing Model Selection by Obtaining Optimal Tuning Parameters in Elastic-Net Quantile Regression, Application to Crude Oil Prices. J. Risk Financial Manag. 2024, 17, 323. https://doi.org/10.3390/jrfm17080323
Al-Jawarneh AS, Alsayed ARM, Ayyoub HN, Ismail MT, Sek SK, Ariç KH, Manzi G. Enhancing Model Selection by Obtaining Optimal Tuning Parameters in Elastic-Net Quantile Regression, Application to Crude Oil Prices. Journal of Risk and Financial Management. 2024; 17(8):323. https://doi.org/10.3390/jrfm17080323
Chicago/Turabian StyleAl-Jawarneh, Abdullah S., Ahmed R. M. Alsayed, Heba N. Ayyoub, Mohd Tahir Ismail, Siok Kun Sek, Kivanç Halil Ariç, and Giancarlo Manzi. 2024. "Enhancing Model Selection by Obtaining Optimal Tuning Parameters in Elastic-Net Quantile Regression, Application to Crude Oil Prices" Journal of Risk and Financial Management 17, no. 8: 323. https://doi.org/10.3390/jrfm17080323
APA StyleAl-Jawarneh, A. S., Alsayed, A. R. M., Ayyoub, H. N., Ismail, M. T., Sek, S. K., Ariç, K. H., & Manzi, G. (2024). Enhancing Model Selection by Obtaining Optimal Tuning Parameters in Elastic-Net Quantile Regression, Application to Crude Oil Prices. Journal of Risk and Financial Management, 17(8), 323. https://doi.org/10.3390/jrfm17080323







