Adaptive Conformal Inference for Computing Market Risk Measures: An Analysis with Four Thousand Crypto-Assets

Abstract

This paper investigates the estimation of the value at risk (VaR) across various probability levels for the log-returns of a comprehensive dataset comprising four thousand crypto-assets. Employing four recently introduced adaptive conformal inference (ACI) algorithms, we aim to provide robust uncertainty estimates crucial for effective risk management in financial markets. We contrast the performance of these ACI algorithms with that of traditional benchmark models, including GARCH models and daily range models. Despite the substantial volatility observed in the majority of crypto-assets, our findings indicate that ACI algorithms exhibit notable efficacy. In contrast, daily range models, and to a lesser extent, GARCH models, encounter challenges related to numerical convergence issues and structural breaks. Among the ACI algorithms, Fully Adaptive Conformal Inference (FACI) and Scale-Free Online Gradient Descent (SF-OGD) stand out for their ability to provide precise VaR estimates across all quantiles examined. Conversely, Aggregated Adaptive Conformal Inference (AgACI) and Strongly Adaptive Online Conformal Prediction (SAOCP) demonstrate proficiency in estimating VaR for extreme quantiles but tend to be overly conservative for higher probability levels. These conclusions withstand robustness checks encompassing the market capitalization of crypto-assets, time-series size, and different forecasting methods for asset log-returns. This study underscores the promise of ACI algorithms in enhancing risk assessment practices in the context of volatile and dynamic crypto-asset markets.

1. Introduction

In the realm of predictive modeling and decision making, accurately quantifying uncertainty is as crucial as making accurate predictions themselves. This need for robust uncertainty estimation becomes particularly pronounced in high-stakes scenarios, where the consequences of erroneous decisions can be significant. One widely accepted approach for quantifying uncertainty is through the utilization of prediction sets, which associate each prediction with a range of potential outcomes, thereby providing a measure of the model’s confidence in its predictions.

Conformal inference, introduced by Vovk et al. (2005) and Shafer and Vovk (2008), offers a powerful framework for enhancing predictive models by constructing valid prediction sets with coverage guarantees. Unlike traditional methods that rely heavily on specific assumptions about data distributions, conformal prediction imposes minimal assumptions, primarily requiring exchangeability of the data; see Angelopoulos and Bates (2023) for a recent survey. However, in many real-world scenarios, such as time-series data or instances of distributional shift, the assumption of exchangeability may not hold, necessitating the development of adaptive techniques to handle such complexities.

Recent advancements in conformal inference have led to the emergence of adaptive conformal inference (ACI) algorithms, designed explicitly to address scenarios where data arrive sequentially, without assuming exchangeability. These algorithms dynamically adjust the width of prediction intervals in response to observed data, thereby providing adaptive and accurate uncertainty quantification. Notably, ACI algorithms have been shown to be effective in various domains, including financial forecasting, epidemiology, and image classification.

Motivated by the success of ACI algorithms in handling sequential data, we turn our attention to the task of forecasting the value at risk (VaR) using adaptive conformal inference techniques. The VaR, a measure of the maximum potential loss that an investment portfolio may face over a specified time horizon, is of paramount importance in risk management across financial institutions and investment firms. Moreover, Emmer et al. (2015) and Kratz et al. (2018) showed that the expected shortfall (ES)1 can be backtested through the approximation of several VaR estimates computed at different probability levels using a multinomial test. Accurate risk estimation is critical for ensuring financial stability and making informed investment decisions.

In this paper, we explore an innovative application of adaptive conformal inference (ACI) methods, traditionally employed for generating prediction intervals in machine learning, to the domain of financial risk management, specifically for estimating value-at-risk (VaR) measures. While ACI methods have been predominantly used to construct robust confidence intervals around mean predictions, we adapt these methods to provide precise point estimates for tail quantiles. This adaptation leverages the ability of ACI to dynamically adjust prediction intervals based on the observed data, which is particularly useful in capturing the extreme quantiles necessary for accurate VaR estimation.

The conventional use of ACI methods involves creating prediction intervals for a given mean prediction model, adjusting the interval widths based on whether recent predictions have been included or excluded within these intervals. This adaptive mechanism ensures that the prediction intervals remain reliable over time, even as the underlying data distribution shifts. In our work, we repurpose this adaptive mechanism to estimate the quantiles of the prediction errors, which are then combined with point forecasts from a simple mean prediction model. This approach allows us to accurately predict the tail quantiles, which correspond to the VaR measures. By clearly delineating this novel application of ACI methods, we provide a fresh perspective on how these techniques can be utilized beyond their traditional scope. Our main interest lies not in constructing prediction intervals around mean forecasts, but in obtaining accurate point estimates for tail quantiles directly. This focus on quantile estimation for VaR calculation is crucial for effective financial risk management, where understanding the behavior of extreme values is more relevant than the central tendency. Thus, our work bridges the gap between robust prediction interval methodologies and the specific needs of financial risk estimation, offering a valuable contribution to the field.

Specifically, we explore the application of various ACI algorithms, including Aggregated ACI by Zaffran et al. (2022), Fully Adaptive Conformal Inference by Gibbs and Candès (2022), Scale-Free Online Gradient Descent by Bhatnagar et al. (2023), and Strongly Adaptive Online Conformal Prediction by Bhatnagar et al. (2023), in the context of VaR prediction. These algorithms offer different approaches to adaptively adjusting prediction intervals, thereby catering to diverse modeling requirements and data characteristics.

The primary objectives in this study are twofold. First, we aim to conduct a comprehensive empirical evaluation to assess the performance and applicability of the proposed ACI algorithms in VaR prediction tasks, to evaluate whether these methodologies can ensure accurate and reliable estimation of uncertainty in financial risk assessment. Secondly, we perform a wide range of robustness checks to verify that the results for the baseline case also hold in different settings. Therefore, we perform a series of checks considering the market capitalization of crypto-assets, time-series size, and different forecasting methods for asset log-returns.

In the rapidly evolving landscape of cryptocurrencies, understanding risk measures is crucial for both investors and regulators. Previous empirical works have often focused on the most capitalized cryptocurrencies, such as Bitcoin and Ethereum, due to their high liquidity and significant market impact. However, the cryptocurrency market is highly diverse, encompassing assets with varying degrees of liquidity, capitalization, and investor profiles. It is for this reason that this paper aims to address this diversity by analyzing a comprehensive dataset of 4000 cryptocurrencies. This broad scope allows us to capture a wide range of market behaviors and dynamics, providing a more holistic view of risk measures across the entire cryptocurrency spectrum. By including assets with different characteristics, we can derive more robust and generalizable conclusions about the effectiveness of adaptive conformal inference (ACI) methods for computing market risk measures.

The remainder of this paper is organized as follows. In Section 2, we review the literature devoted to adaptive conformal inference algorithms, while Section 3 presents a description of the ACI algorithms under consideration, highlighting their key features and theoretical properties. Subsequently, in Section 4, we conduct extensive empirical evaluations with four thousand crypto-assets to compare the performance of these algorithms in VaR forecasting tasks, together with robustness checks. Finally, Section 5 summarizes our findings and outlines directions for future research in this domain.

2. Literature Review

Conformal inference (CI), originally proposed by Vovk et al. (1999) and Vovk et al. (2005), has emerged as a versatile framework for constructing prediction intervals around point predictions, facilitating robust uncertainty quantification across various domains (Angelopoulos and Bates 2023). It has garnered significant attention for its utility in uncertainty quantification in regression and classification tasks; see Papadopoulos (2008), Lei et al. (2013), Lei and Wasserman (2014), Vovk et al. (2018), Romano et al. (2019, 2020), Cauchois et al. (2021), and Barber et al. (2021) for several examples and detailed discussions.

However, traditional CI methods operate under the assumption of data exchangeability, wherein the joint distribution of observations remains invariant to their order. However, real-world datasets often deviate from this assumption, particularly in scenarios involving temporal dependence, such as time-series data; see Gibbs and Candès (2021, 2022), Zaffran et al. (2022), and Bhatnagar et al. (2023). In this regard, several extensions of conformal prediction techniques have addressed challenges related to distribution shift, employing methods such as reweighting and distributionally robust optimization to maintain approximately valid coverage; see Tibshirani et al. (2019), Podkopaev and Ramdas (2021), Yang et al. (2022), and Barber et al. (2023).

A recent line of research within the CI framework focuses on adaptive conformal inference (ACI) algorithms, designed to handle non-exchangeable data by dynamically adjusting prediction intervals based on observed data (Gibbs and Candès 2021). The original ACI algorithm introduces a learning rate parameter to control the rate of adaptation, with subsequent research exploring meta-algorithms to optimize this parameter. Notable ACI algorithms include the Aggregated ACI by Zaffran et al. (2022), the Fully Adaptive Conformal Inference by Gibbs and Candès (2022), the Scale-Free Online Gradient Descent by Bhatnagar et al. (2023), and the Strongly Adaptive Online Conformal Prediction by Bhatnagar et al. (2023).

Alternative lines of research have also started to explore the application of conformal prediction to time-series data by using randomization, ensembles, and other meta-algorithms to produce valid prediction sets (Chernozhukov et al. 2018; Sousa et al. 2022; Xu and Xie 2021). Other approaches include simply using vanilla conformal prediction for time series without theoretical guarantees or resorting to weaker notions of exchangeability; see Dashevskiy and Luo (2008), Wisniewski et al. (2020), Stankeviciute et al. (2021), and Kath and Ziel (2021). To keep track of the latest developments in conformal prediction, the reader may want to see the Awesome Conformal Prediction repository by Manokhin (2024).

Overall, the literature on adaptive conformal inference algorithms underscores their significance in addressing the complexities of non-exchangeable data, offering the most promising avenues for robust uncertainty quantification in diverse application domains. It is for these reasons that we will use these methodologies to compute robust market risk measures with crypto-assets.

We remark that Wisniewski et al. (2020) and Kath and Ziel (2021) are the only authors who employed (vanilla) conformal prediction to generate prediction intervals and rigorously tested their validity using unconditional and conditional coverage tests. However, their primary focus was on obtaining valid prediction intervals rather than on the tails of the distribution, which are critical for financial risk management. Wisniewski et al. (2020) evaluated their models using 19 different confidence levels, ranging from 5% to 95%, while Kath and Ziel (2021) focused on 50% and 90% prediction intervals. Despite their thorough examination, the quantiles they considered do not align with the requirements of financial risk management. Regulatory frameworks such as the Basel II agreement mandate the use of value at risk (VaR) at the 1% probability level, while Basel III suggests using expected shortfall at the 2.5% probability level. The higher quantiles examined by Wisniewski et al. (2020) and Kath and Ziel (2021) are less relevant for these purposes. Moreover, both studies revealed that although several models passed the unconditional coverage tests, almost none succeeded in the conditional coverage tests across all significance levels (see table 2 in both papers). Such results highlight the limitations of existing models in providing reliable risk measures that are crucial for serious risk management applications. In contrast to these prior works, our study pioneers the application of ACI methods specifically for estimating tail quantiles relevant to financial risk management and that are robust to distributional shifts. By focusing on quantile estimation for VaR, we address a critical gap in the literature. Our approach not only leverages the adaptive nature of ACI to dynamically adjust prediction intervals but also repurposes these intervals to provide precise point estimates for the tail quantiles. This innovative use of ACI methods extends their applicability beyond traditional prediction interval construction, offering significant benefits for the accurate estimation of risk measures. To our knowledge, this alternative use of ACI for direct quantile estimation in the context of financial risk management has not been explicitly considered in the previous literature. Thus, our work not only builds on the previous studies of Wisniewski et al. (2020) and Kath and Ziel (2021) but also introduces a novel application that enhances the toolkit available for risk managers.

3. Materials and Methods

The aim of this study is to compare the performance of four ACI algorithms with traditional volatility models for daily data, such as GARCH models and daily range models, in computing the value at risk (VaR) at various probability levels for a large set of crypto-assets. Additionally, this comparison indirectly assesses the quality of the models’ expected shortfall (ES), as proposed by Kratz et al. (2018). The ES represents the average of the worst p losses, where p is the percentile of the returns distribution. Although Gneiting (2011) demonstrated that the ES lacks a mathematical property known as elicitability and cannot be directly backtested, Emmer et al. (2015) showed that the ES becomes elicitable when conditioned on the VaR and can be backtested by approximating multiple VaR levels. This concept was further refined by Kratz et al. (2018), who introduced a multinomial test of VaR violations across multiple levels as a means of backtesting the ES.

Before presenting the outcomes of our extensive empirical evaluations, we first discuss the general structure of adaptive conformal inference, the four specific ACI algorithms used in our analysis, the benchmark volatility models for daily data, and backtesting procedures for market risk measures.

3.1. Adaptive Conformal Inference: The General Structure

We delve into an online learning scenario where we have a sequential stream of crypto-assets’ log-returns ${\left(y_t\right)}_{t\ge 1}$, one at a time; see Cesa-Bianchi and Lugosi (2006) for a detailed discussion of online learning theory. Supposing that $\alpha \in (0,1)$ is our desired empirical coverage of prediction intervals, our objective is to produce, at each time step t, a prediction interval for the upcoming log-return $y_t$. This interval is generated using an interval construction function denoted as ${\widehat{C}}_t$, that takes a parameter ${\theta }_t\in \mathbb{R}$ and produces a closed prediction interval $[l_t,u_t]$. It is essential that the interval construction function be nested, so that if ${\theta }^{\prime }>\theta$, then ${\widehat{C}}_t\left(\theta \right)$ must be a subset of ${\widehat{C}}_t\left({\theta }^{\prime }\right)$, thus indicating wider prediction intervals for larger values of $\theta$. ${\widehat{C}}_t\left(\theta \right)$ is indexed by t to highlight its potential dependence on other information available at each time point, such as a point prediction ${\widehat{\mu }}_t$. In addition, let $r_t=inf\{\theta \in \mathbb{R}:\mathbb{I}(y_t\in {\widehat{C}}_t\left(\theta \right))\}$ be the radius at time t, i.e., the smallest $\theta$ ensuring that the prediction interval covers the log-return $y_t$, and $\mathbb{I}(·)$ be the indicator function. A critical assumption used for the theoretical analysis of several ACI algorithms is the boundedness of these radii, so there exists a constant $D>0$ such that $r_t<D$ for all t.

A straightforward approach to build prediction intervals involves directly employing the parameter ${\theta }_t$ to determine the interval width. Given the point prediction ${\widehat{\mu }}_t$ at each time t, we can create a symmetric prediction interval around this point estimate as ${\widehat{C}}_t\left({\theta }_t\right)=[{\widehat{\mu }}_t-{\theta }_t,\widehat{\mu }+{\theta }_t]$. This method is known as the linear interval constructor and, in this setup, the radius is given by the absolute residual $r_t=|{\widehat{\mu }}_t-y_t|$. The original work on adaptive conformal inference (ACI) by Gibbs and Candès (2021) proposed constructing intervals based on past observed residuals. Assume we have a function S, known as a “nonconformity score”, where a common choice is given by the absolute residual $S(\mu ,y)=|\mu -y|$. Moreover, if we denote with $s_t=S({\widehat{\mu }}_t,y_t)$ the nonconformity score of the t-th log-return, then the quantile interval constructor is formulated as follows:

$${\widehat{C}}_t\left({\theta }_t\right)=[{\widehat{\mu }}_t-\mathrm{Quantile}(\theta ,\{s_1,\dots ,s_{t-1}\}),{\widehat{\mu }}_t+\mathrm{Quantile}(\theta ,\{s_1,\dots ,s_{t-1}\})],$$

where Quantile$(\theta ,M)$ is the empirical $\theta$-quantile of the elements in set M. It is easy to verify that ${\widehat{C}}_t$ is nested within ${\theta }_t$ because the quantile function is non-decreasing in $\theta$. The linear interval constructor is used with Scale-Free Online Gradient Descent by Bhatnagar et al. (2023) and Strongly Adaptive Online Conformal Prediction by Bhatnagar et al. (2023), whereas the quantile interval constructor is used with Aggregated ACI by Zaffran et al. (2022) and Fully Adaptive Conformal Inference by Gibbs and Candès (2022).

In this framework, the lower quantile $l_t$ of the interval constructor ${\widehat{C}}_t\left({\theta }_t\right)$ corresponds to the 1-day-ahead value at risk (VaR) at the probability level $p=(1-\alpha )/2$, denoted as $Va{R}_{t,p}$. Conversely, the upper quantile $u_t$ of the interval constructor ${\widehat{C}}_t\left({\theta }_t\right)$ corresponds to the 1-day-ahead value at risk (VaR) at the probability level $1-p=1-(1-\alpha )/2$, denoted as $Va{R}_{t,1-p}$.

In general, the ACI algorithms’ interactions with the data and the computations of losses follow a similar pattern, which is repeated sequentially for each time step $t=1,\dots ,T$:

• Predict ${\theta }_t$ and build the prediction interval ${\widehat{C}}_t\left({\theta }_t\right)$;
• Observe the true outcome $y_t$ and compute the radius $r_t$;
• Verify whether $y_t$ is not included in the prediction interval, $er{r}_t:=\mathbb{I}[y_t\notin {\widehat{C}}_t\left({\theta }_t\right)]$;
• Compute the so-called pinball loss $L^{\alpha }({\theta }_t,r_t)$, defined as follows:

  $$L^{\alpha }({\theta }_t,r_t)=\left\{\begin{array}{cc}\alpha ({\theta }_t-r_t),\hfill & {\theta }_t\ge r_t\hfill \\ (1-\alpha )(r_t-{\theta }_t),\hfill & {\theta }_t<r_t\hfill \end{array}\right.$$

This iterative process forms the foundation of the theoretical framework of online learning, from which theoretical results are then derived for each ACI algorithm.

The original adaptive conformal inference (ACI) algorithm proposed by Gibbs and Candès (2021) dynamically adjusts the width of prediction intervals based on observed data. Their algorithm is outlined in pseudo-code format in Appendix A. It is possible to show that the updating mechanism for the estimated radius can be derived as an online subgradient descent scheme, using the subgradient of the pinball loss function. In simple terms, if the log-return $y_t$ falls outside the prediction interval at time t ($er{r}_t=1$), the next interval widens $({\theta }_{t+1}={\theta }_t+\gamma \alpha )$. Conversely, if $y_t$ falls within the interval $(er{r}_t=0)$, the next interval narrows $({\theta }_{t+1}={\theta }_t-\gamma (1-\alpha ))$. The learning rate $\gamma$ governs the speed at which the interval width adapts to the data and is the primary tuning parameter. Theoretical considerations on coverage error bounds suggest a larger $\gamma$ to expedite coverage error decay over time. However, in practice, overly large $\gamma$ values lead to intervals exhibiting significant oscillations. Conversely, overly small $\gamma$ values result in intervals that adapt too slowly to distribution shifts. Hence, selecting an appropriate $\gamma$ value is crucial. This issue has spurred the development of ACI algorithms that are robust to the choice of this parameter. The theoretical guarantees concerning the performance of the ACI algorithm remain unaffected by the selection of the initial value ${\theta }_1$. Therefore, in practical applications any value can be chosen. Over time, the influence of the initial choice of ${\theta }_1$ diminishes proportionally to the chosen learning rate. Following Susmann et al. (2023), we set ${\theta }_1=\alpha$ when employing the quantile interval predictor, and ${\theta }_1=0$ otherwise.

Finally, we remark that in the evaluation of adaptive conformal inference (ACI) algorithms, traditional metrics such as the empirical coverage and the regret provide valuable insights into the overall performance of prediction intervals2. However, in the context of financial risk management, particularly concerning the estimation of risk measures in the tails of log-returns distributions, a more nuanced approach is required. Specifically, the focus is often directed towards assessing the quality of the estimated (tail) risk measures, such as quantiles (e.g., value at risk) or more comprehensive measures like the expected shortfall. Given the critical importance of accurately estimating tail risk, it is important to employ specialized evaluation techniques tailored to market risk measures. Consequently, backtesting procedures designed specifically for assessing the adequacy of these risk measures offer a more appropriate and rigorous means of evaluation in our case than the empirical coverage and the regret. An overview of the backtesting procedures employed in our empirical analysis is provided in Section 3.4.

3.2. ACI Algorithms: AgACI, FACI, SF-OGD, SAOCP

Aggregated ACI (AgACI) by Zaffran et al. (2022) resolves the challenge of selecting a suitable learning rate for ACI by executing multiple instances of the algorithm with varying learning rates. Subsequently, it combines the lower and upper interval bounds separately using an online aggregation-of-experts algorithm. Specifically, one aggregation algorithm aims to estimate the lower $(1-\alpha )/2$ quantile, while the other targets the upper $1-(1-\alpha )/2$ quantile. Zaffran et al. (2022) explored several online aggregation algorithms and observed similar outcomes. Therefore, we adopt their recommendation and utilize the Bernstein Online Aggregation (BOA) algorithm, implemented in the opera R package (Gaillard et al. 2023; Wintenberger 2017). BOA operates as an online algorithm, deriving predictions for the lower (or upper) prediction interval bound through a weighted average of candidate ACI prediction interval bounds, with weights determined by each candidate’s past performance concerning the quantile loss. Therefore, the prediction intervals produced by AgACI may not be symmetric around the point prediction, given the separate weights assigned to the lower and upper bounds. The primary parameter to tune in AgACI is the set of candidate learning rates $\gamma$. Susmann et al. (2023) suggest using the following learning rates: $\gamma \in \{0.001,0.002,0.004,0.008,0.016,0.032,0.064,0.128\}$. Additionally, each candidate ACI algorithm requires a starting value for ${\theta }_1$, which can be arbitrarily set to $\alpha$, as previously discussed. The AgACI algorithm is outlined in pseudo-code format in Appendix B, and it is implemented in the AdaptiveConformal R package; see Susmann et al. (2023) for more details. Finite sample bounds on the coverage error and the regret do not exist for the AgACI algorithm. Zaffran et al. (2022) performed a wide range of experiments on synthetic time series with different time dependence structures, showcasing the robustness of the AgACI algorithm and its superior performance compared to baseline methods. However, they noted at the conclusion of their paper that future research would involve a theoretical analysis of the aggregation algorithm, particularly to determine if the experimentally observed asymptotic validity holds.

Fully Adaptive Conformal Inference (FACI) by Gibbs and Candès (2022) was developed by the creators of the original ACI algorithm, in part to address the challenge of selecting the learning rate parameter $\gamma$. In this regard, FACI shares a similar objective with the AgACI algorithm, although it employs a slightly different approach. FACI also aggregates predictions from multiple instances of ACI, each executed with different learning rates. However, it differs in that it directly combines the estimated radii produced by each algorithm based on their pinball loss, employing an exponential reweighting scheme (Gradu et al. 2023). Unlike AgACI, FACI does not separately aggregate the upper and lower bounds of the intervals, and this enables the development of theoretical guarantees regarding the algorithm’s performance in a more straightforward manner. The FACI algorithm is outlined in pseudo-code format in Appendix C, and it is implemented in the AdaptiveConformal R package; see Susmann et al. (2023) for more details. The process of tuning hyperparameters involves selecting a time interval length $\left|I\right|$ to control the pinball loss, which can be arbitrarily chosen. For the hyperparameter $\sigma$, Gibbs and Candès (2022) advocate for the optimal choice $\sigma =1/\left(2\right|I\left|\right)$. Determining the third hyperparameter $\eta$ poses a greater challenge. In the absence of distribution shifts, the optimal choice for $\eta$ is

$$\eta =\sqrt{\frac{3}{\left|I\right|}}\sqrt{\frac{log(K·|I\left|\right)+2}{{\alpha }^2{(1-\alpha )}^3+{(1-\alpha )}^2{\alpha }^3}}$$

where K is the number of multiple copies of the ACI algorithm with different learning rates. We remark that this solution is optimal only for the quantile interval constructor, where ${\theta }_t$ represents a quantile of previous nonconformity scores. Alternatively, Gibbs and Candès (2022) suggest learning $\eta$ in an online manner using the following update rule:

$${\eta }_t=\sqrt{\frac{log(K·|I\left|\right)+2}{{\sum }_{s=t-\left|I\right|}^{t-1}{L}^{\alpha }({\theta }_s,r_s)}}$$

Both approaches for selecting $\eta$ yielded similar results in the empirical studies reported by Gibbs and Candès (2022). Following Susmann et al. (2023), we employed the former approach when the quantile interval construction function was selected, while we employed the latter approach for the linear interval construction function. Similar to AgACI, the grid for the learning parameter $\gamma$ consists of values from the set $\gamma \in \{0.001,0.002,0.004,0.008,$$0.016,0.032,0.064,0.128\}$. To establish a bound on the coverage error, Gibbs and Candès (2022) examined a slightly modified version of FACI in which ${\theta }_t$ is chosen randomly from the candidate ${\theta }_{t,k}$ with weights given by $p_{t,k}$, instead of taking a weighted average. They ensure that this randomized version of FACI yields results very similar to the deterministic version. The coverage error result also assumes that hyperparameters can change over time, meaning ${\eta }_t$ and ${\sigma }_t$ are specific to each time t, rather than being fixed. The authors demonstrate that the coverage error has the following specific bound, where ${\gamma }_{min}$ and ${\gamma }_{max}$ represent the smallest and largest learning rates in the grid, respectively:

$$\left|CovErr\left(T\right)\right|\le \frac{1+2{\gamma }_{max}}{T{\gamma }_{min}}+\frac{{(1+2{\gamma }_{max})}^2}{{\gamma }_{min}}exp\left({\eta }_t(1+2{\gamma }_{max})\right)\frac{1}{T}\sum _{t=1}^T{\eta }_t+2\frac{1+{\gamma }_{max}}{{\gamma }_{min}}\frac{1}{T}\sum _{t=1}^T{\sigma }_t$$

Therefore, if both ${\eta }_t$ and ${\sigma }_t$ converge to zero as $t\to \infty$, the coverage error will also converge to zero. Additionally, under mild distributional assumptions, they provide a type of short-term coverage error bound for arbitrary time spans, along with several regret bounds. For more details, we refer to Gibbs and Candès (2022).

Scale-Free Online Gradient Descent (SF-OGD) is a versatile algorithm for online learning, initially proposed by Orabona and Pál (2018). This algorithm involves updating ${\theta }_t$ through a gradient descent step, with the learning rate adapting to the scale of previously observed gradients. While SF-OGD was initially introduced within the context of adaptive conformal inference (ACI) as a sub-algorithm for SAOCP (outlined below), it has demonstrated strong performance on its own in real-world applications; see Bhatnagar et al. (2023). The SF-OGD algorithm is outlined in pseudo-code format in Appendix D, and it is implemented in the AdaptiveConformal R package; see Susmann et al. (2023) for more details. It is possible to show that the optimal selection for the learning rate is $\gamma =D/\sqrt{3}$, where D represents the maximum possible radius. In cases where D is unknown, it can be estimated by employing an initial subset of the time series as a calibration set. D can then be estimated as the maximum of the absolute residuals between the observed log-returns and the corresponding forecasts (Bhatnagar et al. 2023; Orabona and Pál 2018). Bhatnagar et al. (2023) found a bound for the coverage error of this algorithm by showing that for any learning rate $\gamma =\Theta \left(D\right)$ (where $\gamma =D/\sqrt{3}$ is optimal) and any starting value ${\theta }_1\in [0,D]$, then it holds that for any $T>1$,

$$\left|CovErr\left(T\right)\right|\le \mathcal{O}\left({(1-\alpha )}^{-2}{T}^{-1/4}logT\right)$$

We remark that the coverage bounds for SF-OGD and SAOCP below (which is a generalization of SF-OGD) are distribution-free; see Theorems 4.2 and 4.3 and their proofs in Bhatnagar et al. (2023) for the full details.

The Strongly Adaptive Online Conformal Prediction (SAOCP) algorithm by Bhatnagar et al. (2023) was introduced as an enhancement over existing ACI algorithms, offering more robust theoretical guarantees. SAOCP operates similarly to AgACI and FACI, using a set of candidate online learning algorithms to generate prediction intervals, which are subsequently aggregated using a meta-algorithm. While SF-OGD was chosen as the candidate algorithm, any algorithm with anytime regret guarantees can be employed. Unlike AgACI and FACI, where each candidate employs a distinct learning rate but contributes consistently to the final prediction intervals, SAOCP assigns identical learning rates to all candidates. However, each candidate is allocated positive weight over a specific time interval. To address rapid distribution shifts, new candidate algorithms are continuously introduced, ensuring swift adaptation and positive weighting for the most recent candidates. In essence, SAOCP functions as a meta-algorithm overseeing multiple experts, with each expert constituting an independent online learning algorithm responsible for its own active interval with a finite lifetime. At each time point t, a new expert is created, active over a finite “lifetime” that is defined as

$$L\left(t\right)=g·\underset{n\in Z}{max}\{2^n:t\equiv 0mod{2}^n\},$$

where $g\in {\mathbb{Z}}_{\ge 1}$ is a multiplier for the lifetime of each expert. Experts are weighted based on their empirical performance relative to the pinball loss function, resulting in intervals with robust regret guarantees. The SAOCP algorithm is outlined in pseudo-code format in Appendix E, and it is implemented in the AdaptiveConformal R package; see Susmann et al. (2023) for more details. The primary tuning parameter for SAOCP is the learning rate $\gamma$ of the SF-OGD sub-algorithms, with the optimal choice established as $\gamma =D/\sqrt{3}$, as discussed earlier. Bhatnagar et al. (2023) typically determine D by selecting the maximum residual from a calibration set. The second tuning parameter, which is the lifetime multiplier g, governs the duration of each expert’s lifetime. Following Bhatnagar et al. (2023), we set $g=8$. Bhatnagar et al. (2023)—theorem 4.3—showed that a bound on the coverage error of SAOCP is given by

$$\left|CovErr\left(T\right)\right|\le \mathcal{O}\left(\underset{\beta }{inf}(T^{1/2-\beta }+T^{\beta -1}{S}_{\beta }\left(T\right))\right)$$

for any $T\ge 1$, and where $S_{\beta }\left(T\right)$ is a technical measure of the smoothness of the cumulative gradients and expert weights for each of the candidate experts. For example, if there exists $\beta \in (1/2,1)$, then $S_{\beta }\left(T\right)\le \tilde{\mathcal{O}}\left(T^{\gamma }\right)$ for some $\gamma <1-\beta$, and the previous bound becomes $\left|CovErr\left(T\right)\right|\le \tilde{\mathcal{O}}\left(T^{-min\{1/2-\beta ,\beta -1+\gamma \}}\right)=o_T\left(1\right)$. Finally, we remark that the previous bound is distribution-free, and mild regularity assumptions on the distributions of the data are only required if we need to achieve approximately valid coverage on $every$ sub-interval of time. For more details, see theorem C.3 in Bhatnagar et al. (2023).

3.3. Benchmark Volatility Models for Daily Data

The GARCH(1,1) model remains a prominent benchmark model for computing market risk measures with daily data for several reasons. Firstly, it captures essential characteristics of financial time series, such as volatility clustering and time-varying volatility, which are commonly observed in real-world financial markets. Secondly, the GARCH(1,1) model is relatively parsimonious compared to other volatility models, requiring only a small number of parameters for estimation. Given its widespread use in academic research and industry practice, the GARCH(1,1) model serves as a natural reference competitor when evaluating the performance of alternative market risk models. Its inclusion as a benchmark ensures that the proposed models undergo rigorous comparison against a well-established and widely recognized standard, thus enhancing the robustness and credibility of the assessment process in risk management applications. Specifically, a simple GARCH(1,1) with constant mean $\mu$ and standardized errors $z_t$ following a symmetric Student’s t-distribution with $\nu$ degrees of freedom was used in this work to model the conditional variance ${\sigma }_t^2$ of the log-returns $y_t$:

$$\begin{array}{ccc}\hfill y_t& =& \mu +{\epsilon }_t,{\epsilon }_t=z_t\sqrt{{\sigma }_t^2},z_t\sim t_{\nu }\hfill \\ \hfill {\sigma }_t^2& =& \omega +\alpha {\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2\hfill \end{array}$$

More complex model specifications and error distributions were discarded because they resulted in much higher rates of numerical convergence failures; see Fantazzini (2022) and Fantazzini (2023) for similar evidence with crypto-assets. The complexity of estimating GARCH models and the necessity for sizable samples have been extensively documented in the literature. The seminal work by Fiorentini et al. (1996) highlighted the issues involved in GARCH model estimation, emphasizing the demand for large datasets. Furthermore, comprehensive simulation studies conducted by Hwang and Valls Pereira (2006), Fantazzini (2009), and Bianchi et al. (2011) underscored the requirement of a sample size ranging from 250 to 500 observations for obtaining reliable model estimates of basic GARCH models. For scenarios involving more complex data generating processes, even larger sample sizes were necessary to ensure robust estimation. For GARCH models with Student’s t errors, the calculation of the 1-day-ahead value at risk (VaR) at the probability level p using information up to time $t-1$ is as follows:

$$Va{R}_{t,p}={\widehat{\mu }}_t+t_{p,\widehat{\nu }}^{-1}·\sqrt{(\widehat{\nu }-2)/\widehat{\nu }}·\sqrt{{\widehat{\sigma }}_t^2}$$

Here, ${\widehat{\mu }}_t$ represents the 1-day-ahead forecast of the conditional mean, ${\widehat{\sigma }}_t^2$ denotes the 1-day-ahead forecast of the conditional variance, and $t_{p,\widehat{\nu }}^{-1}$ denotes the inverse function of the Student’s t-distribution with estimated $\widehat{\nu }$ degrees of freedom at the probability level p. The term $\sqrt{(\widehat{\nu }-2)/\widehat{\nu }}·\sqrt{{\widehat{\sigma }}_t^2}$ represents the scale parameter of the Student’s t-distribution.

The second benchmark volatility model that we consider in our analysis employs the daily range to estimate the daily conditional variance of the log-returns $y_t$. The idea of using the price range has a rich history in both the academic and professional literature, starting from the 19th century; see Nison (1994) and references therein. Notably, volatility measures derived from the daily range emerged as efficient alternatives to return-based volatility estimators, as demonstrated by several authors, beginning with Parkinson (1980). Recent research has reignited interest in range-based estimators employing the open, high, low, and close (OHLC) prices for estimating daily volatility; see Patton (2011), Molnár (2012), Chou et al. (2015), and Fiszeder et al. (2019). Intriguingly, high-frequency volatility models have shown superior performance over low-frequency models using range-based estimators for short-term forecasts, typically one day ahead (Lyócsa et al. 2021). However, for longer forecast horizons, such as up to one month, the difference in forecast accuracy diminishes, particularly for most market indices. Moreover, Fantazzini (2023) conducted a comprehensive analysis on a dataset of over 2000 crypto-assets, evaluating their credit risk by computing their probability of “death”, and found that ZPP-based models using range-based volatility estimators were a better choice for long-term forecasts up to 1 year ahead (which is the standard horizon for credit risk management). Building on Molnár (2012) and Fantazzini (2023), we will adopt the Garman–Klass volatility estimator (Garman and Klass (1980)). This estimator has been shown to produce standardized returns that are normally distributed and yields estimates comparable to those obtained from high-frequency data. The Garman–Klass estimator assumes a Brownian motion with zero drift and no opening jumps. Nonetheless, for cases involving opening jumps, as seen with illiquid assets, the jump-adjusted Garman–Klass volatility estimator described in Molnár (2012) will be employed. The formula for the jump-adjusted Garman–Klass (GK) volatility estimator for the daily conditional variance ${\sigma }_t^2$ of the log-returns $y_t$ is presented below:

$$\begin{array}{ccc}\hfill {\sigma }_{GK,t}^2& =& \left[log{\left(O_t/C_{t-1}\right)}^2+\frac{1}{2}log{\left(H_t/L_t\right)}^2-(2\times log2-1)log{\left(C_t/O_t\right)}^2\right]\hfill \end{array}$$

To forecast the dynamics of range-based daily volatilities ${\sigma }_t^2$, we employed the heterogeneous autoregressive (HAR) model proposed by Corsi (2009), which posits that the daily volatility is influenced by past volatility over different time periods:

$$\begin{array}{ccc}\hfill {\sigma }_t^2& =& {\beta }_0+{\beta }_D{\sigma }_{t-1,D}^2+{\beta }_W{\sigma }_{t-1,W}^2+{\beta }_M{\sigma }_{t-1,M}^2+{ϵ}_t,\mathrm{where}\hfill \\ & & {\sigma }_{t-1,W}^2=\frac{1}{7}\sum _{j=1}^7{\sigma }_{t-j,D}^2,{\sigma }_{t-1,M}^2=\frac{1}{30}\sum _{j=1}^{30}{\sigma }_{t-j,D}^2\hfill \end{array}$$

where ${\sigma }_D^2$, ${\sigma }_W^2$, and ${\sigma }_M^2$ denote the daily, weekly, and monthly volatility components, respectively. We adjusted the time periods for weekly and monthly volatilities to 7 and 30 days, respectively, instead of the usual 5 and 22 days, to accommodate the continuous trading in cryptocurrency exchanges. We set the conditional mean of the log-returns $y_t$ to zero when using the Garman–Klass volatility estimator. Therefore, in the case of the HAR model with daily range data, the 1-day-ahead VaR can be computed as follows:

$$Va{R}_{t,p}={\Phi }_p^{-1}·\sqrt{{\widehat{\sigma }}_t^2}$$

where ${\Phi }_p^{-1}$ denotes the inverse function of the normal distribution at the probability level p.

3.4. Backtesting Methods for Market Risk Measures

The assessment of different value-at-risk (VaR) models’ forecasting performance entails comparing the forecast VaR values against actual returns for each day. Initially, the process involves tallying the number of violations $T_1$ when the forecast VaR is lower than the actual losses, with $T=T_1+T_0$, where $T_0$ denotes the absence of VaR violations. The unconditional coverage test developed by Kupiec (1995) verifies whether the fraction of actual violations, $\widehat{\pi }=T_1/T$, is statistically significantly different from p%, so the null hypothesis is given by $H_0:\widehat{\pi }=p$. This test employs the following likelihood ratio test statistic for the null hypothesis (Kupiec 1995):

$$L{R}_{uc}=-2ln\left[{(1-p)}^{T_0}{p}^{T_1}/\left\{{(1-T_1/T)}^{T_0}{(T_1/T)}^{T_1}\right\}\right]\stackrel{H_0}{\sim }{\chi }_1^2$$

The conditional coverage test by Christoffersen (1998) tests the joint null hypothesis concerning the accuracy of the average number of VaR violations and the independence of violations. This test can identify models forecasting an excessive or insufficient number of clustered violations, but it requires at least several hundred observations for accuracy. The test statistic is presented as follows:

$$L{R}_{cc}=-2ln\left[{(1-p)}^{T_0}{p}^{T_1}\right]+2ln\left[{(1-{\pi }_{01})}^{T00}{\pi }_{01}^{T01}{(1-{\pi }_{11})}^{T10}{\pi }_{11}^{T11}\right]\stackrel{H_0}{\sim }{\chi }_2^2$$

where $T_{ij}$ is the number of observations with value i followed by j for $i,j=0,1$ and ${\pi }_{ij}=\frac{T_{ij}}{{\sum }_j{T}_{ij}}$ denotes the corresponding probabilities.

In addition to the count of VaR violations, financial regulators are concerned with their magnitude. Thus, the asymmetric quantile loss (QL) function proposed by González-Rivera et al. (2004) was computed in our analysis:

$$l(y_t,Va{R}_{p,t})=(p-d_t^p)(y_t-Va{R}_{p,t})$$

where $d_t^p=\mathbf{1}(y_t<Va{R}_{p,t})$ is the indicator function for the VaR exceedances. This function penalizes realized losses below the p-th quantile level more heavily, facilitating cost comparison among different choices.

The previous asymmetric quantile loss functions are then used by the model confidence set (MCS) by Hansen et al. (2011) to select the best VaR forecasting models at a specified confidence level. Given the differences between the QLs of models i and j at time t (expressed as $d_{ij,t}=Q{L}_{i,t}-Q{L}_{j,t}$), the MCS approach is employed to evaluate the hypothesis of equal predictive capability, denoted as $H_{0,M}:E\left(d_{ij,t}\right)=0$, for all $i,j$ in M, where M represents the set of forecasting models. The initial step involves the computation of the following t-statistics:

$$t_{i·}=\frac{{\overline{d}}_{i·}}{\widehat{var}\left({\overline{d}}_{i·}\right)}\mathrm{for}i\in M,$$

where ${\overline{d}}_{i·}=m^{-1}{\sum }_{j\in M}{\overline{d}}_{ij}$ is the simple loss of the i-th model relative to the average losses across models in the set M, ${\overline{d}}_{ij}=T^{-1}{\sum }_{t=1}^T{d}_{ij,t}$ measures the sample loss differential between models i and j, while $\widehat{var}\left({\overline{d}}_{i·}\right)$ is a bootstrapped estimate of $var\left({\overline{d}}_{i·}\right)$. Subsequently, the T-max statistic is calculated as follows: $T_{max,M}={max}_{i\in M}\left(t_{i·}\right)$. This statistic has a non-standard distribution, hence its distribution under the null hypothesis is determined via bootstrap methods involving 1000 replications. If the null hypothesis is rejected, one model is eliminated from the analysis, restarting the testing procedure anew; see Hansen et al. (2011) for more details.

Building upon an idea introduced by Emmer et al. (2015), Kratz et al. (2018) introduced a multinomial value-at-risk (VaR) test that implicitly evaluates the expected shortfall (ES) by approximating it with various VaR levels. Their approximation is defined as

$$E{S}_p\approx \frac{1}{4}[q\left(p\right)+q(0.75p+0.25)+q(0.5p+0.5)+q(0.25p+0.75)]$$

where $q\left(\gamma \right)=Va{R}_{\gamma }$. A similar but more convenient approximation for the ES at the 2.5% level, as adopted by Basel III, was proposed by Wimmerstedt (2015) and Fantazzini and Shangina (2019):

$$E{S}_{2.5\%}\approx \frac{1}{5}[Va{R}_{2.5\%}+Va{R}_{2.0\%}+Va{R}_{1.5\%}+Va{R}_{1.0\%}+Va{R}_{0.5\%}]$$

Kratz et al. (2018) suggested using several VaR probability levels $p_1,\dots ,p_N$, where $p_j=p+[(j-1)/N](1-p)$ for $j=1,\dots ,N$, starting from a given level p. If ${\mathbb{I}}_{t,j}={\mathbf{1}}_{(Y_t<Va{R}_{p_j,t})}$ represents the usual indicator function for a VaR violation at level $p_j$ and $X_t={\sum }_{j=1}^N{\mathbb{I}}_{t,j}$, then the sequence ${\left(X_t\right)}_{t=1,\dots ,T}$ counts the number of VaR violations at level $p_j$. Now, define $MN(T,({\pi }_0,\dots ,{\pi }_N))$ as a multinomial distribution with T trials, each of which may result in one of $N+1$ outcomes $\{0,1,\dots ,N\}$ with probabilities ${\pi }_0,\dots ,{\pi }_N$ that sum to one, while the observed cell counts are defined by $O_j={\sum }_{t=1}^T{I}_{(X_t=j)},j=0,1,\dots ,N$. Then, under the assumptions of unconditional coverage and independence, as in Christoffersen (1998), it can be shown that the random vector $(O_0,\dots ,O_N)$ follows the multinomial distribution $MN(T,(p_1-p_0,\dots ,p_{N+1}-p_N))$. Supposing that the estimated multinomial distribution is $MN(T,({\theta }_1-{\theta }_0,\dots ,{\theta }_{N+1}-{\theta }_N))$, where ${\theta }_j(j=1,\dots ,N)$ are the estimated distribution parameters, Kratz et al. (2018) consider the following null and alternative hypotheses:

$$\begin{array}{ccc}\hfill H_0:& & {\theta }_j=p_j,\mathrm{for}j=1,\dots ,N\hfill \\ \hfill H_1:& & {\theta }_j\ne p_j,\mathrm{for}\mathrm{at}\mathrm{least}\mathrm{one}j\in \{1,\dots ,N\}\hfill \end{array}$$

The null hypothesis can be tested using various test statistics. We refer to Cai and Krishnamoorthy (2006) for a comprehensive simulation study on the exact size and power properties of five possible tests, three of which were later employed by Kratz et al. (2018). In our empirical analysis, we utilized the exact method, the fifth test statistic reviewed by Cai and Krishnamoorthy (2006), which computes the probability of a given outcome under the null hypothesis using the multinomial probability distribution itself:

$$P(O_0,O_1,\dots ,O_N)=\frac{T!}{O_0!O_1!\dots O_N!}{(p_1-p_0)}^{O_0}{(p_2-p_1)}^{O_1}\dots {(p_{N+1}-p_N)}^{O_N}$$

Cai and Krishnamoorthy (2006) concluded that while the exact method performs well, it can be time-consuming for large numbers of cells N and sample sizes T. In such cases, simulation methods are preferable. For a comprehensive discussion on these backtesting methods and others, we refer to Fantazzini (2019), chap. 11.

3.5. Structure of the Empirical Analysis

In this study, we conduct a comprehensive empirical analysis to evaluate the performance and robustness of various methods for estimating market risk measures across a diverse set of cryptocurrencies. Our analysis consists of a baseline case that considers all assets, as well as a series of robustness checks to verify that the results for the baseline case also hold in different settings. It is structured as follows:

• Baseline case: All 4000 assets. In the baseline analysis, we included all 4000 cryptocurrencies in our dataset to provide a broad assessment of the methods under study. This diverse dataset allows us to capture a wide range of market behaviors and characteristics.
• Robustness check 1: Market capitalization of crypto-assets. We conducted a robustness check based on the market capitalization of the assets. Our dataset included daily market capitalization data for 2310 out of the 4000 assets. The remaining assets lacked these data, which may indicate transparency issues regarding their circulating supply. For a comprehensive analysis, we divided these 2310 assets into four groups of approximately equal size based on their market capitalization. The first group consists of assets with the highest market capitalization, while the fourth group includes those with the lowest capitalization.
• Robustness check 2: Time-series size. To examine the impact of time-series length on our results, we divided the assets into four groups according to the number of daily data points available. Each group contains approximately the same number of assets. The first group includes assets with the longest time series (ranging from 1613 to 4939 daily data points), and the fourth group includes assets with the shortest time series (ranging from 731 to 836 daily data points).
• Robustness check 3: Different forecasting methods. In the baseline case, we used a simple AR(1) model due to its ease of estimation and the generally weak mean dependence in crypto-assets’ log-returns. As a third robustness check, we evaluated the impact of using a more complex model specification with a robust estimation method. Specifically, we employed a single-hidden-layer neural network, utilizing seven lagged daily log-returns as inputs and three hidden units:

  $$y_t={\beta }_0+\sum _{j=1}^3{\beta }_{j}g\left({\gamma }_{0j}+\sum _{i=1}^7{\gamma }_{ij}{y}_{t-i}\right)$$
  Feed-forward neural networks with a single hidden layer are implemented in the nnet R package, and we refer to Venables and Ripley (2002), chapter 8, for the full theoretical details and the software implementation.
• Robustness check 4: Comparison with methods that predict quantiles directly. Engle and Manganelli (2004) proposed an alternative approach to quantile estimation that focuses on modeling the quantile directly rather than the entire distribution. They introduced a class of semi-parametric conditional autoregressive quantile models, known as CAViaR, which utilize quantile regression and mild distributional assumptions. These models have a structure similar to GARCH models and are formally defined as follows:

  $$\begin{array}{ccc}\hfill \mathrm{Symmetric}\mathrm{absolute}\mathrm{value}:q_t\left(p\right)& =& {\beta }_1+{\beta }_2{q}_{t-1}\left(p\right)+{\beta }_3\left|y_{t-1}\right|\hfill \\ \hfill \mathrm{Asymmetric}\mathrm{slope}:q_t\left(p\right)& =& {\beta }_1+{\beta }_2{q}_{t-1}\left(p\right)+{\beta }_3{\left(y_{t-1}\right)}^{+}+{\beta }_4{\left(y_{t-1}\right)}^{-}\hfill \\ \hfill \mathrm{Indirect}\mathrm{GARCH}(1,1):q_t\left(p\right)& =& {[{\beta }_1+{\beta }_2{q}_{t-1}^2\left(p\right)+{\beta }_3{y}_{t-1}^2]}^{1/2}\hfill \\ \hfill \mathrm{Adaptive}:q_t\left(p\right)& =& q_{t-1}\left(p\right)+{\beta }_1\left\{{[1+exp({\beta }_2·[y_{t-1}-q_{t-1}\left(p\right)])]}^{-1}-p\right\}\hfill \end{array}$$

  where $q_t\left(p\right)$ represents the p-quantile function associated with the conditional distribution of returns $y_t$, ${\left(x\right)}^{+}=max(x,0)$, and ${\left(x\right)}^{-}=-min(x,0)$ and ${\beta }_i$ are the model parameters. The asymmetric slope model is specifically designed to capture the asymmetric leverage effect, which is the tendency for volatility to be higher following a negative return than a positive return of equal magnitude. The indirect GARCH(1,1) CAViaR model is correctly specified if the underlying data are generated by a GARCH(1,1) model with an independent and identically distributed innovation process. The adaptive specification adjusts to past errors to minimize the probability of consecutively underestimating the VaR. The CAViaR parameters are estimated using the quantile regression minimization technique introduced by Koenker and Bassett (1978):

  $$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{argmin}\sum _t[p-I(y_t<q_t(\mathit{\beta },p))]·[y_t-q_t(\mathit{\beta },p)]$$

  where $\mathit{\beta }$ is the vector of parameters to be estimated, while I is the indicator function. When the quantile model is linear, this minimization can be formulated as a linear programming problem, for which the dual problem is conveniently solved. For this reason, and due to past empirical evidence, such as that provided by Abad et al. (2014) and references therein, we will use only the symmetric absolute value (SAV) model3. Moreover, given the computational burden of estimating the model for each quantile, we will limit our analysis to a selected group of crypto-assets: the two most capitalized assets (Bitcoin and Ethereum) and the two least capitalized assets (Bubble and Litecoin-Token) for which all models achieved numerical convergence.

The aim of this structure is to ensure that our empirical analysis is thorough and considers various factors that may influence the performance of the risk estimation methods.

4. Results

4.1. Data

Our study analyzed a dataset comprising 4000 crypto-assets spanning from July 2010 to January 2024. We obtained all assets, freely available from https://coinmarketcap.com/, in January 2024, ensuring that each had a time series consisting of at least 730 daily data points. We made this selection to ensure that all models used in our analysis had a minimum of one year’s worth of data for initial training and calibration. The dataset included daily open, high, low, and close prices, as well as traded volume and market capitalization. Initially, we downloaded a dataset comprising 4003 assets. However, three assets were excluded due to their close prices remaining at zero throughout the entire time span, rendering them unusable. Additionally, approximately a dozen assets exhibited unusual reported prices in the weeks preceding their delisting from coinmarketcap.com. These anomalous trading days were excluded from our analysis to maintain its integrity. The names of the 4000 crypto assets used in our analysis are listed in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 in Appendix F.

The first 365 daily observations were used to initialize the estimation of the GARCH model, with log-returns computed using the closing prices. For the HAR model, the daily range was estimated using the open, high, low, and close prices. Similarly, for the training and calibration of ACI models, log-returns were computed using the closing prices. An expanding window approach was then employed for the GARCH and HAR models, where one day of data was added incrementally to the initial sample. The models were re-estimated with the expanded dataset, and the value at risk (VaR) for the next day was computed. The ACI models were trained incrementally, one data point at a time, as detailed in the algorithms provided in Appendix B, Appendix C, Appendix D and Appendix E.

In our study, we utilize a dataset comprising 4000 cryptocurrencies, covering a wide range of market conditions and asset characteristics. This extensive dataset includes not only the most capitalized cryptocurrencies, like Bitcoin and Ethereum, but also those with lower capitalization and liquidity. The rationale behind this comprehensive approach is twofold. First, it allows us to assess the performance of ACI methods across a diverse set of assets, which is essential for understanding the general applicability and robustness of these methods. Second, by including a wide variety of cryptocurrencies, we can identify specific challenges and opportunities associated with different types of assets. This approach enables us to draw more nuanced and actionable insights that are relevant to a broader audience, including investors, portfolio managers, and regulators. Our analysis thus provides a detailed examination of market risk measures across the full spectrum of the cryptocurrency market, ensuring that our conclusions are both robust and broadly applicable.

As outlined in the previous section, we calculated the value at risk (VaR) across five probability levels ($p_1=0.5\%$, $p_2=1\%$, $p_3=1.5\%$, $p_4=2\%$, $p_5=2.5\%$) for the log-returns of each asset. This enabled us to conduct an approximate backtesting of the expected shortfall (ES) at the 2.5% level, a metric included in the Basel III agreement. While our primary focus was on the left tail of the distribution, given its significance in financial risk management, we also computed five quantiles for the right tail ($p_6=97.5\%$, $p_7=98\%$, $p_8=98.5\%$, $p_9=99\%$, $p_{10}=99.5\%$) to ensure comprehensiveness and generality.

For the ACI models, we opted to employ a simple AR(1) model to capture the dynamics of the crypto-assets’ log-returns. Although we initially attempted to utilize the Hyndman and Khandakar Hyndman and Khandakar (2008) algorithm for automatic selection of the optimal ARIMA model4, this approach encountered challenges, particularly with extremely volatile crypto-assets possessing relatively short time series (fewer than 1000 observations). Consequently, we reverted to employing a straightforward AR(1) model. In this regard, it is worth noting that the mean dependence of crypto-assets’ log-returns is generally weak. Nevertheless, as part of our robustness checks, we will examine the impact on our results when employing a more complex model specification with a robust estimation method.

4.2. Baseline Case: All 4000 Assets

In this section, we present the results of our comprehensive evaluation of value-at-risk (VaR) forecasting models applied to a dataset comprising 4000 crypto assets. Our analysis includes four adaptive conformal inference (ACI) models, one generalized autoregressive conditional heteroskedasticity (GARCH) model, and one heterogeneous autoregressive (HAR) model using daily range volatilities.

Our evaluation begins with an examination of the performance of each model using the Kupiec (1995) test, the Christoffersen (1998) test, and the multinomial VaR test by Kratz et al. (2018); see Table 1. Across all quantiles, we observed that the ACI models generally performed well, with FACI and SF-OGD emerging as the most effective models. However, AgACI and SAOCP, while providing accurate estimates for extreme quantiles ($p_1=0.5\%$ and $p_2=1\%$), were too conservative when estimating quantiles between 1% and 2.5%, with less violations than expected. In the right tail of the distribution, AgACI demonstrated better results, in line with the FACI and SF-OGD algorithms. According to the multinomial VaR test, FACI and SF-OGD were able to properly model the left and right tails of the distribution for the vast majority of crypto-assets (approximately 90% of assets), followed by AgACI (approximately 80%), while SAOCP had the worst performance among ACI algorithms, with only approximately 50% of assets where the multinomial VaR test was not rejected at the 5% probability level.

Table 1. Average number of violations in % across all assets for each quantile; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively. The results for the GARCH and HAR models only include assets for which numerical convergence was achieved.

Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_Test
AgACI	0.63	74.95	87.80	0.96	78.50	88.38	1.30	72.35	84.45	1.64	69.28	80.18	2.00	66.05	76.10	77.70
FACI	0.58	78.10	91.53	0.92	85.43	94.38	1.34	81.85	93.18	1.78	80.95	92.78	2.23	81.08	91.73	88.10
SF-OGD	0.51	96.03	95.18	0.94	96.35	96.25	1.37	95.88	95.10	1.81	94.50	93.53	2.24	94.00	92.55	86.73
SAOCP	0.64	94.03	90.00	0.96	93.83	89.08	1.31	89.58	83.73	1.56	83.03	75.25	1.86	75.18	66.80	55.15
GARCH	0.76	76.56	68.60	1.27	73.05	67.83	1.76	69.75	64.98	2.24	67.78	63.19	2.70	66.11	62.30	68.01 (*)
HAR_DR	1.08	66.50	58.24	1.33	60.24	56.03	1.53	51.18	46.05	1.71	42.51	38.73	1.88	36.40	33.21	21.36 (**)
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_Test
AgACI	97.51	70.30	88.00	97.94	71.68	88.35	98.35	71.58	87.68	98.75	75.23	86.75	99.17	68.50	80.58	79.95
FACI	97.17	76.08	92.55	97.70	77.73	92.55	98.24	78.15	92.40	98.78	82.63	93.03	99.25	74.38	87.25	88.80
SF-OGD	97.07	92.18	92.48	97.63	92.98	93.00	98.18	92.98	93.55	98.74	94.55	94.68	99.29	92.98	94.85	88.55
SAOCP	97.58	82.20	77.08	97.96	86.88	81.80	98.27	88.15	82.33	98.72	91.03	85.70	99.13	84.95	78.25	49.08
GARCH	96.82	68.55	66.83	97.35	69.57	66.68	97.89	70.41	66.68	98.45	72.52	68.31	99.05	73.31	67.88	69.62 (*)
HAR_DR	97.94	42.92	42.43	98.11	49.87	49.05	98.29	57.16	55.11	98.50	61.88	59.03	98.76	58.21	52.28	19.33 (**)

(*) The GARCH(1,1) model with standardized errors following a symmetric Student’s t-distribution did not reach numerical convergence for 96 assets (out of 4000). (**) The HAR model used for the dynamics of range-based daily volatilities did not reach numerical convergence for 104 assets (out of 4000).

Differently from the ACI algorithms, the GARCH and HAR models faced challenges in achieving numerical convergence for approximately 2.5% of assets (96 and 104 assets, respectively), particularly those with extreme variability and/or relatively small datasets ($T<1000$). Despite this, GARCH served as a reliable benchmark model, slightly underestimating VaR for the most extreme quantiles ($p_i\le 1.0\%$) while maintaining accuracy for the other quantiles. Instead, the HAR model with daily range volatilities proved to be the least effective, underestimating lower quantiles up to $p_i=1\%$, and severely overestimating higher quantiles. Similar problems emerged also for the right tail of the distribution. According to the multinomial VaR test, the GARCH model was able to model the left and right tails of the distribution for approximately 70% of assets, whereas for the HAR model this was approximately 20% of assets, thus confirming the previous problems with the tests for the single quantiles.

To identify the best VaR forecasting models, we utilized the asymmetric quantile loss (QL) function proposed by González-Rivera et al. (2004) and employed the model confidence set (MCS) method by Hansen et al. (2011); see Table 2 and Table 3. Notably, we considered only assets for which all six models reached numerical convergence. Such a choice clearly penalized ACI models, which were able to estimate quantiles for all assets, whereas this was not the case for GARCH and HAR models. Nevertheless, given that financial regulators are concerned not only with the number of VaR violations but also with their magnitude, we also compared the models using the asymmetric quantile loss and the MCS.

Table 2. Average rank of the models across all assets for each quantile based on the asymmetric quantile loss (QL) function proposed by González-Rivera et al. (2004).

Quantile	AgACI	FACI	SF-OGD	SAOCP	GARCH	HAR_DR
VaR_0.5	4.22	4.95	3.36	3.05	2.33	3.09
VaR_1.0	4.13	4.33	3.72	3.37	2.17	3.29
VaR_1.5	3.99	3.75	3.95	3.67	2.06	3.58
VaR_2.0	3.82	3.41	4.04	3.95	1.96	3.82
VaR_2.5	3.64	3.19	4.12	4.13	1.88	4.04
VaR_97.5	3.73	3.33	4.06	3.84	1.91	4.14
VaR_98.0	3.89	3.52	3.96	3.70	1.99	3.94
VaR_98.5	4.11	3.79	3.83	3.46	2.09	3.72
VaR_99.0	4.22	4.23	3.58	3.21	2.21	3.55
VaR_99.5	4.21	4.67	3.21	3.00	2.39	3.51

Table 3. Number of times (in %) when the model was included into the model confidence set (MCS) at the 10% confidence level across all assets.

Quantile	AgACI	FACI	SF-OGD	SAOCP	GARCH	HAR_DR
VaR_0.5	57.23	43.52	68.56	76.71	89.56	81.70
VaR_1.0	68.85	61.57	69.01	75.17	93.32	78.20
VaR_1.5	75.22	75.93	69.82	74.73	94.83	73.71
VaR_2.0	78.38	83.08	69.16	70.99	95.80	68.80
VaR_2.5	82.19	86.55	67.21	68.22	95.98	64.02
VaR_97.5	89.45	93.26	76.29	79.16	97.44	69.32
VaR_98.0	87.00	90.10	79.19	81.78	97.08	73.97
VaR_98.5	83.32	85.51	80.68	85.69	96.87	79.45
VaR_99.0	79.40	75.40	82.72	87.55	96.06	82.79
VaR_99.5	73.26	61.36	85.17	90.23	94.99	85.72

Our analysis reveals that the GARCH model consistently emerged as the top-ranked model for the majority of assets and was almost always included in the MCS. This underscores the enduring relevance of the GARCH(1,1) model with a Student’s t-distribution in finance when using daily data, even nearly four decades after it was originally proposed.

While ACI models demonstrated proficiency in estimating quantiles for most assets, they exhibited challenges in estimating the most extreme quantiles ($p_i\le 1\%$ and $p_i\ge 99\%$), particularly the AgACI and FACI models that showed rather large asymmetric losses and lower ranking. However, the SF-OGD and SAOCP models displayed greater precision with smaller losses. These findings have significant implications for financial risk management: while a traditional benchmark like the GARCH model remains relevant, newer approaches such as ACI models offer promising alternatives, particularly for assets with complex dynamics such as crypto-assets, albeit with some caveats in extreme quantile estimation. Given that ACI models are more precise in terms of VaR violations, while GARCH models are better in terms of asymmetric quantile losses, forecasting combinations are a possibility. We leave this interesting issue as an avenue for further research.

4.3. Robustness Check 1: Market Capitalization of Crypto-Assets

In this section, we examined the 2310 assets with daily market capitalization data and categorized them into four groups, each containing approximately the same number of assets. The first group comprises assets with the highest market capitalization in dollars, while the fourth group consists of assets with the lowest capitalization.

We computed the Kupiec (1995) test, the Christoffersen (1998) test, and the multinomial VaR test by Kratz et al. (2018) for each group, with the results presented in Table 4 and Table 5.

Table 4. Backtesting results based on market capitalization (first 2 groups): Average number of violations in % across all assets for each quantile; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Highest Market Capitalization: $259, 874,508–$1,274,831,490,851
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.50	73.31	89.95	0.81	68.11	82.84	1.12	60.83	74.00	1.48	52.34	68.28	1.86	49.74	62.91	71.75
FACI	0.50	74.87	93.41	0.90	78.86	93.07	1.34	74.87	91.85	1.80	74.18	92.03	2.28	75.56	92.03	90.12
SF-OGD	0.49	93.41	96.88	0.95	94.11	97.92	1.42	94.63	95.84	1.90	94.45	95.15	2.37	94.63	95.15	86.83
SAOCP	0.59	92.20	90.29	0.92	92.20	87.69	1.32	88.21	81.98	1.62	82.32	77.47	2.01	77.99	70.71	51.65
GARCH	0.47	83.10	76.83	0.88	76.66	70.91	1.30	70.38	68.29	1.71	69.51	67.25	2.12	69.51	65.85	72.65
HAR_DR	0.65	73.34	70.56	0.87	65.51	62.54	1.07	51.57	49.30	1.24	37.63	36.24	1.41	29.62	28.75	18.82
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.76	59.79	84.92	98.16	61.18	88.04	98.57	67.07	90.12	98.95	71.58	92.20	99.36	75.39	91.16	79.38
FACI	97.34	71.40	93.59	97.82	71.75	93.24	98.34	72.27	93.24	98.87	76.60	94.28	99.40	80.59	94.45	92.20
SF-OGD	97.28	88.39	94.97	97.79	89.95	94.63	98.31	90.12	94.45	98.84	91.16	97.05	99.36	93.93	96.01	88.21
SAOCP	97.72	80.59	76.78	98.08	86.31	81.63	98.42	89.60	84.92	98.84	92.03	87.00	99.27	89.25	84.40	50.95
GARCH	97.37	75.44	74.39	97.85	76.66	74.39	98.33	78.05	75.96	98.82	81.88	79.09	99.33	84.67	79.62	78.57
HAR_DR	98.25	43.73	47.39	98.43	54.18	56.62	98.63	63.59	66.03	98.84	69.16	68.12	99.10	59.06	57.14	17.42
	Second-Highest Market Capitalization: $56,658,794–$258,810,481
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.55	72.62	88.56	0.87	72.10	85.27	1.22	63.78	79.90	1.56	60.49	73.48	1.94	56.67	69.32	75.56
FACI	0.51	76.78	92.55	0.89	80.94	93.24	1.34	76.26	92.37	1.80	76.60	92.20	2.28	77.12	91.85	88.21
SF-OGD	0.49	95.84	96.53	0.94	95.84	95.84	1.40	95.49	95.67	1.86	92.72	93.93	2.32	95.32	94.63	88.04
SAOCP	0.59	95.49	93.59	0.93	93.76	87.69	1.28	87.52	80.24	1.55	79.38	71.75	1.86	71.58	63.43	48.18
GARCH	0.54	80.04	74.61	0.96	76.18	72.33	1.38	70.23	67.08	1.80	67.25	63.57	2.23	64.62	63.05	69.53
HAR_DR	0.72	69.79	65.72	0.93	58.66	56.01	1.11	44.52	41.52	1.28	32.51	31.10	1.44	26.68	25.97	16.96
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.63	68.28	90.64	98.05	69.84	92.20	98.44	71.92	91.51	98.84	75.56	92.37	99.28	75.74	89.77	83.36
FACI	97.24	72.27	93.07	97.75	75.04	94.11	98.28	75.04	93.41	98.82	80.94	93.24	99.34	80.94	92.89	92.03
SF-OGD	97.21	93.07	94.45	97.73	92.55	93.93	98.26	91.33	94.97	98.79	93.93	93.93	99.33	94.11	96.53	87.35
SAOCP	97.69	80.07	74.52	98.06	86.48	81.98	98.39	88.56	84.40	98.82	91.16	87.69	99.22	86.14	81.28	47.83
GARCH	97.16	73.03	71.10	97.66	75.83	74.78	98.16	77.06	73.73	98.66	78.63	75.13	99.22	78.98	75.66	74.61
HAR_DR	98.21	41.17	40.99	98.38	49.65	50.00	98.55	58.13	57.77	98.76	61.31	61.48	99.01	58.13	52.47	16.08

Table 5. Backtesting results based on market capitalization (last 2 groups): Average number of violations in % across all assets for each quantile; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Third-Highest Market capitalization: $12,235,621–$56,579,279
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.57	74.52	90.99	0.90	77.12	88.56	1.25	70.71	85.44	1.59	67.42	77.30	1.94	62.05	71.75	74.70
FACI	0.52	78.68	93.24	0.89	84.40	96.01	1.32	80.94	93.59	1.77	79.90	93.41	2.23	81.28	92.03	90.12
SF-OGD	0.48	97.23	95.32	0.93	96.71	96.01	1.36	96.01	95.67	1.83	96.71	95.84	2.28	95.32	95.49	84.23
SAOCP	0.59	94.63	91.51	0.89	93.41	88.04	1.26	86.83	83.88	1.52	81.11	72.96	1.84	71.58	64.99	51.99
GARCH	0.61	78.57	69.82	1.09	75.89	68.21	1.55	71.61	65.54	1.99	70.00	64.46	2.44	66.43	63.04	70.01
HAR_DR	1.02	64.59	61.74	1.28	61.74	56.76	1.48	50.71	46.09	1.67	41.46	39.15	1.84	35.41	31.49	20.46
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.54	70.36	89.95	97.98	73.66	90.81	98.39	72.44	89.95	98.81	74.35	89.60	99.24	71.75	85.10	82.67
FACI	97.15	73.31	93.59	97.70	75.91	92.72	98.23	78.34	93.07	98.80	81.98	93.93	99.32	77.64	90.64	92.37
SF-OGD	97.14	94.11	94.28	97.67	93.93	94.28	98.19	93.24	93.93	98.75	94.11	94.11	99.29	94.45	94.45	88.39
SAOCP	97.63	80.76	74.52	97.97	86.48	81.46	98.30	89.25	83.54	98.74	91.33	85.62	99.17	84.92	79.90	45.75
GARCH	96.87	68.75	67.86	97.40	70.36	68.04	97.95	69.46	66.61	98.51	71.25	67.50	99.12	74.64	69.82	72.14
HAR_DR	97.89	43.06	44.48	98.07	50.71	50.89	98.26	58.19	57.12	98.49	60.32	60.32	98.77	51.60	49.82	18.51
	Lowest Market Capitalization: $2589–$12,233,558
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.57	78.76	87.56	0.91	79.10	86.36	1.24	68.22	80.14	1.59	63.90	74.78	1.94	59.41	69.95	73.92
FACI	0.54	82.38	92.75	0.91	87.05	94.30	1.35	82.90	94.30	1.78	81.35	92.23	2.23	77.89	92.06	86.87
SF-OGD	0.49	96.37	93.96	0.92	95.68	95.51	1.36	96.03	94.82	1.83	94.65	93.26	2.27	93.78	93.96	86.01
SAOCP	0.61	93.26	89.98	0.93	89.98	83.42	1.27	83.07	76.34	1.53	73.92	66.67	1.80	63.56	56.13	45.08
GARCH	1.00	65.89	58.93	1.59	64.11	58.39	2.15	60.71	56.25	2.66	58.57	53.93	3.18	58.75	54.46	58.75
HAR_DR	1.26	54.51	44.96	1.54	54.34	49.38	1.75	50.62	43.72	1.94	44.42	39.29	2.11	37.70	35.93	15.22
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.62	66.15	80.83	98.05	69.26	82.38	98.47	70.98	84.63	98.86	75.82	85.49	99.26	72.54	83.77	77.37
FACI	97.22	73.40	93.78	97.75	78.93	93.96	98.30	82.73	93.09	98.84	86.01	93.44	99.32	78.76	91.02	90.33
SF-OGD	97.15	94.13	93.96	97.71	95.34	93.96	98.23	94.30	94.47	98.78	95.85	95.34	99.33	94.82	94.82	86.87
SAOCP	97.76	70.98	66.67	98.11	79.62	73.23	98.43	84.80	77.89	98.84	90.50	82.56	99.22	86.70	80.48	39.55
GARCH	96.38	57.86	56.43	96.93	58.57	54.46	97.51	58.21	53.57	98.12	60.71	55.00	98.80	58.21	52.14	56.96
HAR_DR	97.70	42.30	41.42	97.87	46.19	43.54	98.07	52.57	47.08	98.29	55.22	50.62	98.57	49.20	44.78	15.04

The empirical analysis broadly confirms the findings of the baseline case. However, it reveals that the performance of the GARCH model and, to a lesser extent, the SAOCP algorithm deteriorated significantly when focusing on assets with the lowest market capitalization. It appears that the extreme volatility of this asset class strongly impacted the numerical stability of these models. As a result, the GARCH model exhibited too many VaR violations, while the SAOCP model demonstrated too few.

It is well known that crypto-assets with lower market capitalization tend to experience higher levels of volatility. This heightened volatility can pose challenges for several modeling approaches, which may struggle to adequately capture and predict extreme movements in these assets’ prices. As such, future research could explore alternative modeling techniques specifically tailored to address the unique characteristics and dynamics of lower-capitalization crypto-assets, potentially enhancing the accuracy and robustness of risk management strategies in this segment of the market.

4.4. Robustness Check 2: Time-Series Size

As a second robustness check, we divided our assets into four groups based on the size of their time series, with each group containing approximately the same number of assets. The first group encompasses assets with the longest time series, ranging from 1613 daily data points to 4939 daily data points, while the fourth group comprises assets with the shortest time series, ranging from 731 daily data points to 836 daily data points.

We computed the Kupiec (1995) test, the Christoffersen (1998) test, and the multinomial VaR test by Kratz et al. (2018) for each group, with the results presented in Table 6 and Table 7.

Table 6. Backtesting results based on time-series size (first 2 groups): Average number of violations in % across all assets for each quantile; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Longest Time Series: 4939–1613 (Daily Data)
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.43	81.10	89.50	0.77	67.10	78.10	1.11	57.20	67.50	1.46	48.40	56.60	1.84	43.00	49.30	62.60
FACI	0.44	84.80	93.50	0.90	82.00	93.10	1.36	77.80	91.70	1.81	76.90	91.00	2.29	75.30	91.10	90.10
SF-OGD	0.47	97.50	95.90	0.93	93.80	94.90	1.40	94.50	94.70	1.89	92.90	93.90	2.37	93.80	95.40	83.30
SAOCP	0.50	96.00	91.40	0.80	86.80	77.90	1.16	76.40	67.70	1.43	62.40	53.50	1.73	49.30	41.30	31.00
GARCH	0.83	68.70	61.98	1.37	66.01	58.99	1.90	63.43	57.23	2.39	62.50	57.02	2.88	59.40	55.68	59.19
HAR_DR	1.01	56.72	50.92	1.25	51.83	47.15	1.44	43.08	38.59	1.61	34.22	32.69	1.78	29.84	27.90	3.05
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.86	52.90	80.50	98.27	57.40	83.80	98.67	62.30	86.50	99.05	68.10	92.80	99.44	80.40	93.90	76.50
FACI	97.35	62.90	94.90	97.87	68.10	94.60	98.38	72.10	94.50	98.92	76.90	94.90	99.46	85.30	96.70	93.90
SF-OGD	97.34	91.40	96.40	97.86	91.70	94.90	98.36	90.60	95.40	98.89	91.90	96.20	99.42	95.80	97.10	85.90
SAOCP	98.06	63.50	57.40	98.36	77.30	69.70	98.67	85.30	79.20	99.04	92.80	87.90	99.40	92.40	89.00	35.30
GARCH	96.70	57.95	57.02	97.24	59.61	56.30	97.80	58.26	56.40	98.38	61.67	57.23	99.00	62.60	56.71	58.26
HAR_DR	97.99	36.97	38.09	98.17	42.87	44.09	98.36	50.61	50.41	98.57	52.55	51.73	98.84	42.16	40.02	3.87
	Second-Longest Time Series: 1612–1039 (Daily Data)
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.59	74.90	88.90	0.94	78.00	90.40	1.28	69.40	87.10	1.64	65.90	82.50	2.01	62.30	79.60	80.30
FACI	0.54	78.50	93.90	0.94	85.20	94.90	1.42	79.80	95.00	1.91	78.30	95.40	2.40	78.20	94.80	91.10
SF-OGD	0.53	95.50	97.60	1.00	97.70	98.00	1.48	96.00	96.30	1.96	95.40	95.80	2.44	94.80	95.10	86.60
SAOCP	0.65	92.70	89.90	1.00	95.70	91.30	1.38	92.10	86.60	1.65	86.40	77.90	1.98	80.70	72.20	50.20
GARCH	0.73	72.91	71.30	1.22	69.69	65.56	1.69	66.06	61.63	2.15	62.84	59.52	2.61	62.64	60.62	66.06
HAR_DR	1.04	63.97	63.36	1.29	60.29	55.78	1.48	48.11	42.89	1.66	36.23	33.37	1.81	28.15	26.41	17.60
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.81	72.60	88.90	98.20	75.30	91.20	98.58	76.80	92.40	98.95	81.60	92.90	99.34	77.70	90.70	82.70
FACI	97.42	79.60	95.40	97.89	82.60	95.60	98.40	83.00	95.50	98.91	86.50	95.40	99.40	83.10	95.70	92.90
SF-OGD	97.33	94.60	96.20	97.84	94.90	96.10	98.35	94.90	96.40	98.86	96.50	96.90	99.37	95.60	97.60	86.80
SAOCP	97.89	84.80	78.90	98.21	87.70	84.00	98.50	92.00	87.20	98.89	94.10	89.40	99.26	91.40	86.70	49.20
GARCH	97.16	70.80	68.48	97.63	71.70	69.08	98.12	74.92	69.69	98.63	76.74	72.61	99.18	77.95	73.11	70.09
HAR_DR	98.11	37.15	36.13	98.27	47.08	44.42	98.43	57.83	55.78	98.62	64.48	62.54	98.87	62.13	58.96	15.35

Table 7. Backtesting results based on time-series size (last 2 groups): Average number of violations in % across all assets for each quantile; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Third-Longest Time Series: 1038–837 (Daily Data)
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.72	69.20	87.70	1.04	83.60	92.20	1.37	78.80	92.10	1.71	79.60	90.90	2.05	76.80	87.50	82.20
FACI	0.65	72.90	90.80	0.94	86.90	95.20	1.34	84.40	94.20	1.77	83.10	94.30	2.20	84.20	93.50	88.00
SF-OGD	0.51	93.90	95.40	0.92	97.30	96.30	1.32	96.80	95.80	1.74	95.40	93.90	2.16	94.90	92.90	88.90
SAOCP	0.68	92.40	92.40	1.00	96.70	93.80	1.35	95.60	91.10	1.59	91.80	84.60	1.88	86.20	78.20	65.70
GARCH	0.70	80.57	74.79	1.19	79.31	73.11	1.64	73.63	71.43	2.11	72.16	68.70	2.55	69.43	66.07	73.74
HAR_DR	1.17	69.23	61.12	1.43	62.80	58.48	1.64	52.37	48.58	1.83	43.94	41.41	2.00	38.67	34.88	27.82
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	97.41	79.10	93.60	97.85	82.40	92.40	98.28	78.90	91.60	98.69	80.60	86.30	99.12	64.90	78.70	84.20
FACI	97.11	82.80	92.70	97.66	85.10	93.80	98.23	82.00	93.20	98.77	86.70	93.90	99.24	71.00	87.60	90.10
SF-OGD	96.95	93.00	91.80	97.52	94.30	92.50	98.08	93.80	92.80	98.67	95.10	94.50	99.24	91.30	94.30	90.80
SAOCP	97.37	91.60	86.70	97.77	92.10	87.90	98.10	90.90	85.80	98.59	90.90	85.40	99.05	81.00	74.90	56.30
GARCH	96.88	75.00	74.89	97.42	77.21	74.68	97.97	77.73	73.74	98.52	77.52	72.90	99.11	78.68	75.32	77.84
HAR_DR	97.83	42.99	43.52	98.00	51.32	50.16	98.18	57.01	55.32	98.39	63.96	58.38	98.66	61.85	55.22	25.40
	Shortest Time Series: 836–731 (Daily Data)
Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_test
AgACI	0.77	74.60	85.10	1.10	85.30	92.80	1.44	84.00	91.10	1.76	83.20	90.70	2.10	82.10	88.00	86.30
FACI	0.69	76.20	87.90	0.89	87.60	94.30	1.25	85.40	91.80	1.64	85.50	90.40	2.05	86.60	87.50	83.30
SF-OGD	0.53	97.20	91.80	0.91	96.60	95.80	1.28	96.20	93.60	1.64	94.30	90.50	1.99	92.50	86.80	88.40
SAOCP	0.73	95.00	86.30	1.01	96.10	93.30	1.36	94.20	89.50	1.59	91.50	85.00	1.83	84.50	75.50	74.20
GARCH	0.78	84.06	66.40	1.31	77.30	73.66	1.82	75.88	69.73	2.30	73.66	67.61	2.77	72.96	66.80	73.56
HAR_DR	1.09	76.11	57.69	1.35	66.09	62.75	1.56	61.13	54.15	1.74	55.57	47.47	1.92	48.89	43.62	37.25
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_test
AgACI	96.97	76.60	89.00	97.43	71.60	86.00	97.86	68.30	80.20	98.30	70.60	75.00	98.78	51.00	59.00	76.40
FACI	96.80	79.00	87.20	97.36	75.10	86.20	97.95	75.50	86.40	98.52	80.40	87.90	98.90	58.10	69.00	78.50
SF-OGD	96.68	89.70	85.50	97.30	91.00	88.50	97.93	92.60	89.60	98.54	94.70	91.10	99.13	89.20	90.40	90.70
SAOCP	97.03	88.90	85.30	97.49	90.40	85.60	97.81	84.40	77.10	98.36	86.30	80.10	98.83	75.00	62.40	56.10
GARCH	96.53	70.43	67.00	97.10	69.83	66.70	97.66	70.74	66.90	98.26	74.07	70.43	98.92	73.97	66.40	72.45
HAR_DR	97.84	54.45	51.92	98.00	58.20	57.49	98.19	63.16	58.91	98.42	66.60	63.46	98.69	66.80	55.06	33.00

The empirical analysis broadly confirms the findings of the baseline case. However, it unveils some intriguing trends: AgACI, FACI, and SF-OGD exhibit consistent performances across time series of varying lengths. Instead, GARCH models seem to perform best with time series close to 1000 observations. Assets with longer time series exhibit a higher number of VaR exceedances than expected, particularly in the extreme left tail, likely attributed to significant structural breaks. Conversely, shorter time series exhibit slightly inferior performance, likely due to relatively small datasets that are insufficient for accurate parameter estimation.

SAOCP and the HAR model with daily range data perform notably better with time series containing fewer than 1000 observations compared to longer time series. It appears that these methods are more sensitive to structural breaks, which occur more frequently in assets with longer time series. This evidence indirectly corroborates the simulation studies conducted by Susmann et al. (2023), which demonstrated that SAOCP (and to some extent, SF-OGD) tend to underestimate the quantiles when faced with a distributional shift. A notable departure from the findings of Susmann et al. (2023) is that the simple SF-OGD model turned out to be pretty robust across all time samples: despite showing slightly inferior performances compared to the FACI algorithm for very long time series, these differences were mostly statistically insignificant in terms of quantile losses (not reported). Moreover, SF-OGD emerged as the top-performing model for the shortest time series.

This evidence underscores the importance of considering both the length of the time series and the model’s sensitivity to structural breaks when selecting appropriate risk forecasting methods. Future research could delve deeper into understanding the mechanisms underlying these performance disparities and explore potential refinements to enhance the accuracy and robustness of risk predictions across diverse time-series lengths.

4.5. Robustness Check 3: Different Forecasting Methods

As a third robustness check, we wanted to assess the impact on our results by employing a more complex model specification than an AR(1) model, namely, a single-hidden-layer neural network using seven lagged daily log-returns as inputs and three hidden units.

We computed the Kupiec (1995) test, the Christoffersen (1998) test, and the multinomial VaR test by Kratz et al. (2018) for the four ACI algorithms using the neural network as the forecasting model, and the results are presented in Table 8. We also computed the asymmetric QL function proposed by González-Rivera et al. (2004) and employed the MCS method by Hansen et al. (2011); see Table 9 and Table 10. Similarly to the baseline case, we considered only assets for which all six models reached numerical convergence.

Table 8. Average number of violations in % across all assets for each quantile using a neural network; % of times the Christoffersen conditional coverage (CC) test was not rejected at the 5% probability level across all assets for each quantile; % of times the Kupiec unconditional coverage (UC) test was not rejected at the 5% probability level across all assets for each quantile. The last column shows the % of times the multinomial VaR test by Kratz et al. (2018) was not rejected at the 5% probability level across all assets, for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

Model	VaR_0.5	CC_0.5	UC_0.5	VaR_1.0	CC_1.0	UC_1.0	VaR_1.5	CC_1.5	UC_1.5	VaR_2.0	CC_2.0	UC_2.0	VaR_2.5	CC_2.5	UC_2.5	ES_2.5_Test
AgACI	0.65	70.00	87.80	0.97	73.48	87.43	1.29	66.58	82.58	1.63	63.60	77.70	1.98	61.98	73.88	74.20
FACI	0.61	75.18	92.18	0.94	83.20	95.43	1.37	80.63	94.33	1.81	78.90	93.18	2.27	78.20	93.08	87.90
SF-OGD	0.52	95.38	95.98	0.96	96.58	97.35	1.40	96.30	96.23	1.86	95.60	95.15	2.31	95.18	94.28	83.03
SAOCP	0.60	93.25	89.65	0.88	88.55	83.10	1.16	78.55	72.43	1.40	71.85	63.38	1.64	62.58	55.25	46.23
Model	VaR_97.5	CC_97.5	UC_97.5	VaR_98.0	CC_98.0	UC_98.0	VaR_98.5	CC_98.5	UC_98.5	VaR_99.0	CC_99.0	UC_99.0	VaR_99.5	CC_99.5	UC_99.5	ES_97.5_Test
AgACI	97.62	63.20	83.55	98.03	64.70	84.90	98.41	64.48	85.75	98.79	69.13	86.40	99.19	63.05	79.95	76.60
FACI	97.22	73.63	93.43	97.75	75.30	93.58	98.29	75.95	94.25	98.81	80.40	94.38	99.25	70.60	87.53	88.00
SF-OGD	97.18	93.70	93.90	97.72	94.85	95.15	98.24	95.25	95.95	98.79	95.85	95.93	99.33	92.93	95.20	84.48
SAOCP	97.97	67.70	61.80	98.27	74.35	68.58	98.55	77.85	73.30	98.90	87.90	82.60	99.24	86.95	83.15	42.40

Table 9. Average rank of the models across all assets for each quantile based on the asymmetric quantile loss (QL) function proposed by González-Rivera et al. (2004). ACI algorithms use a neural network.

Quantile	AgACI	FACI	SF-OGD	SAOCP	GARCH	HAR_DR
VaR_0.5	4.45	5.26	3.68	3.39	1.84	2.37
VaR_1.0	4.25	4.67	4.03	3.84	1.71	2.51
VaR_1.5	4.12	4.16	4.24	4.17	1.62	2.69
VaR_2.0	3.97	3.83	4.35	4.47	1.53	2.85
VaR_2.5	3.84	3.62	4.43	4.64	1.48	2.98
VaR_97.5	3.89	3.75	4.39	4.49	1.44	3.05
VaR_98.0	4.06	3.91	4.31	4.30	1.51	2.91
VaR_98.5	4.26	4.22	4.14	4.04	1.57	2.76
VaR_99.0	4.34	4.65	3.93	3.75	1.68	2.66
VaR_99.5	4.46	5.12	3.62	3.38	1.80	2.62

Table 10. Number of times (in %) when the model was included into the model confidence set (MCS) at the 10% confidence level across all assets. ACI algorithms use a neural network.

Quantile	AgACI	FACI	SF-OGD	SAOCP	GARCH	HAR_DR
VaR_0.5	0.39	0.27	0.44	0.51	0.90	0.81
VaR_1.0	0.46	0.37	0.43	0.48	0.94	0.76
VaR_1.5	0.51	0.48	0.43	0.46	0.95	0.72
VaR_2.0	0.56	0.56	0.42	0.44	0.96	0.68
VaR_2.5	0.59	0.62	0.40	0.41	0.97	0.67
VaR_99.5	0.67	0.70	0.48	0.50	0.99	0.74
VaR_99.0	0.64	0.65	0.51	0.53	0.98	0.76
VaR_98.5	0.59	0.58	0.52	0.55	0.97	0.78
VaR_98.0	0.55	0.48	0.53	0.58	0.96	0.82
VaR_97.5	0.50	0.37	0.57	0.62	0.95	0.84

In terms of VaR violations, there are no notable differences among the models, except for SAOCP, where the number of instances where the Christoffersen test, the Kupiec test, and the multinomial VaR test did not reject the null hypothesis was 5–12% lower than the baseline case. This evidence suggests that the more volatile mean forecasts computed using a neural network penalized this algorithm. A similar phenomenon, albeit on a smaller scale (3–5% lower), was also observed for the AgACI algorithm.

Regarding quantile loss functions, all four ACI algorithms were strongly penalized in terms of average ranking, with SAOCP exhibiting the largest decline in ranking across all competing models. Likewise, all four ACI algorithms demonstrated a decrease in the percentage of times the models were included in the model confidence set (20–30% lower), particularly affecting the left tail of the distribution.

In general, employing a more complex forecasting model for the mean of the assets’ log-returns with ACI algorithms did not result in more precise risk estimates. This outcome can probably be attributed to the lower model bias being outweighed by the higher variance in the model estimates. These findings underscore the intricate trade-offs involved in selecting forecasting models for risk management purposes, highlighting the importance of considering both model complexity and estimation accuracy in decision-making processes.

4.6. A Comparison with Methods That Predict Quantiles Directly

As a fourth robustness check, we employed the symmetric absolute value (SAV)-CAViaR model with a selected group of crypto-assets: the two most capitalized assets (Bitcoin and Ethereum) and the two least capitalized assets (Bubble and Litecoin-Token) for which all models achieved numerical convergence. The plots of the prices of these four crypto-assets are reported in Figure 1, while the main descriptive statistics of their log-returns are shown in Table 11.

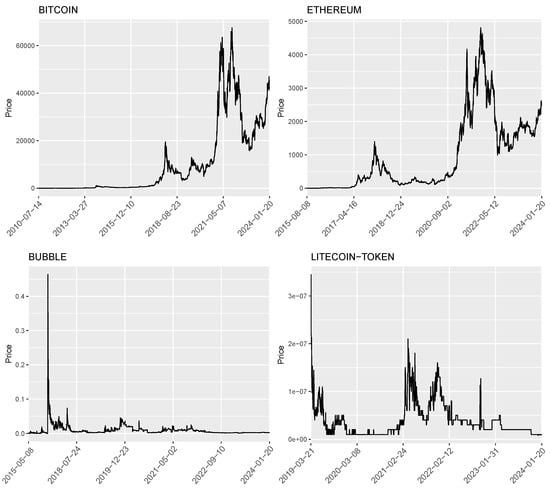
Figure 1. Plots of the prices of four crypto-assets: Bitcoin, Ethereum, Bubble, Litecoin-Token.

Table 11. Log-returns’ main descriptive statistics: Bitcoin, Ethereum, Bubble, Litecoin-Token.

Asset	Mean	SD	Min	Max	Median	Skewness	Kurtosis
Bitcoin	0.27%	0.05	−0.68	0.40	0.00	−1.02	24.03
Ethereum	0.26%	0.06	−0.55	0.41	0.00	0.01	11.75
Bubble	0.05%	0.26	−2.45	6.67	0.00	6.93	192.23
Litecoin-Token	−0.18%	0.19	−1.15	1.73	0.00	0.08	16.32

We computed the Kupiec (1995) test, the Christoffersen (1998) test, and the multinomial VaR test by Kratz et al. (2018) for the four ACI algorithms using the AR(1) as the forecasting model, for the GARCH model with Student’s t errors, for the HAR model with the daily range, and for the CAViaR-SAV model. We also computed the asymmetric QL function proposed by González-Rivera et al. (2004) and employed the MCS method by Hansen et al. (2011). The results for Bitcoin and Ethereum are presented in Table 12, while for Bubble and Litecoin-Token they are presented in Table 13.

Table 12. Number of VaR violations in % across Bitcoin and Ethereum for each quantile and model; p-values in % for the Christoffersen conditional coverage (CC) test; p-values in % for the Kupiec unconditional coverage (UC) test; asymmetric quantile loss (QL) function by González-Rivera et al. (2004); the model was included in the model confidence set (MCS): yes or no; p-values in % for the multinomial VaR test by Kratz et al. (2018), for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Bitcoin (ID = 1)
Model	VaR_0.5	CC_0.5	UC_0.5	Asymmetric QL	MCS	VaR_1.0	CC_1.0	UC_1.0	Asymmetric QL	MCS	VaR_1.5	CC_1.5	UC_1.5	Asymmetric QL	MCS	VaR_2.0	CC_2.0	UC_2.0	Asymmetric QL	MCS	VaR_2.5	CC_2.5	UC_2.5	Asymmetric QL	MCS	ES_2.5_test
AgACI	0.46	0.00	69.10	5.76	YES	0.96	0.00	79.47	8.99	YES	1.49	0.00	94.08	11.74	YES	1.95	0.02	79.25	14.00	NO	2.32	0.00	42.34	15.73	YES	84.26
FACI	0.83	0.00	0.38	5.67	YES	1.27	0.00	8.03	8.86	YES	1.75	0.00	17.70	11.18	YES	2.27	0.00	19.56	13.24	YES	2.84	0.00	14.68	15.09	YES	10.04
SF-OGD	0.66	15.12	15.39	5.18	YES	1.22	3.54	14.08	8.76	YES	1.84	0.01	7.05	11.27	YES	2.34	1.47	11.03	13.60	YES	3.06	0.73	1.89	15.70	YES	18.25
SAOCP	0.68	22.07	10.60	5.22	YES	1.20	37.81	18.23	8.27	YES	1.57	91.36	68.25	10.93	YES	2.14	37.98	49.60	13.28	YES	2.60	28.32	66.17	15.60	YES	43.33
GARCH	0.83	1.10	0.38	4.69	YES	1.64	0.04	0.01	7.91	YES	2.36	0.01	0.00	10.57	YES	3.08	0.00	0.00	12.88	YES	3.72	0.00	0.00	14.96	YES	0.01
HAR_DR	1.29	0.00	0.00	5.80	YES	1.64	0.00	0.01	9.13	YES	2.14	0.17	0.08	12.12	YES	2.43	10.21	4.60	14.88	NO	2.60	29.07	66.17	17.42	NO	0.00
CAViaR	0.33	20.20	7.83	5.13	YES	0.72	10.81	4.63	8.33	YES	1.03	1.26	0.53	10.89	YES	1.60	12.78	4.31	13.20	YES	2.10	16.28	7.40	15.15	YES	12.59
Model	VaR_97.5	CC_97.5	UC_97.5	Asymmetric QL	MCS	VaR_98.0	CC_98.0	UC_98.0	Asymmetric QL	MCS	VaR_98.5	CC_98.5	UC_98.5	Asymmetric QL	MCS	VaR_99.0	CC_99.0	UC_99.0	Asymmetric QL	MCS	VaR_99.5	CC_99.5	UC_99.5	Asymmetric QL	MCS	ES_97.5_test
AgACI	98.56	0.00	0.00	14.38	NO	98.91	0.00	0.00	12.59	NO	99.23	0.00	0.00	10.58	NO	99.54	0.00	0.00	7.99	NO	99.80	0.40	0.09	4.90	NO	0.01
FACI	97.86	2.19	11.26	13.92	NO	98.25	22.60	21.55	12.05	NO	98.73	19.34	18.49	10.01	NO	99.34	1.91	1.26	7.68	NO	99.72	0.71	2.43	4.78	NO	10.97
SF-OGD	98.05	1.42	1.25	13.59	NO	98.34	20.05	9.23	11.91	NO	98.84	5.14	4.80	9.64	NO	99.23	2.32	9.59	7.55	NO	99.67	20.20	7.83	4.29	YES	8.26
SAOCP	98.51	0.00	0.00	13.55	NO	98.62	0.26	0.14	11.82	NO	98.91	3.40	1.74	9.69	NO	99.39	1.49	0.45	7.20	NO	99.74	4.18	1.22	4.29	YES	0.00
GARCH	96.87	0.48	0.90	12.18	YES	97.46	1.23	1.29	10.40	YES	98.19	22.03	9.01	8.46	YES	98.97	60.32	85.21	6.34	YES	99.43	70.13	52.08	3.87	YES	3.73
HAR_DR	97.44	0.10	80.26	15.83	NO	97.79	0.12	32.26	13.46	NO	98.05	0.01	1.77	10.91	NO	98.36	0.00	0.01	8.11	NO	98.84	0.00	0.00	4.98	NO	0.00
CAViaR	98.25	0.26	0.06	12.59	NO	98.67	0.28	0.06	10.83	NO	98.84	5.14	4.80	8.92	NO	99.21	18.47	13.27	6.93	NO	99.58	13.36	40.33	4.22	YES	0.29
	Ethereum (ID = 1027)
Model	VaR_0.5	CC_0.5	UC_0.5	Asymmetric QL	MCS	VaR_1.0	CC_1.0	UC_1.0	Asymmetric QL	MCS	VaR_1.5	CC_1.5	UC_1.5	Asymmetric QL	MCS	VaR_2.0	CC_2.0	UC_2.0	Asymmetric QL	MCS	VaR_2.5	CC_2.5	UC_2.5	Asymmetric QL	MCS	ES_2.5_test
AgACI	0.46	0.00	69.10	3.29	YES	0.96	0.00	79.47	5.35	YES	1.49	0.00	94.08	7.31	YES	1.95	0.02	79.25	8.87	YES	2.32	0.00	42.34	10.20	YES	84.26
FACI	0.83	0.00	0.38	3.49	YES	1.27	0.00	8.03	5.45	YES	1.75	0.00	17.70	7.25	YES	2.27	0.00	19.56	8.77	YES	2.84	0.00	14.68	10.11	YES	10.04
SF-OGD	0.66	15.12	15.39	3.53	YES	1.22	3.54	14.08	5.65	YES	1.84	0.01	7.05	7.36	YES	2.34	1.47	11.03	9.08	NO	3.06	0.73	1.89	10.56	NO	18.25
SAOCP	0.68	22.07	10.60	3.44	YES	1.20	37.81	18.23	5.68	YES	1.57	91.36	68.25	7.45	YES	2.14	37.98	49.60	9.16	NO	2.60	28.32	66.17	10.74	NO	43.33
GARCH	0.55	85.93	71.12	3.22	YES	0.95	75.64	81.13	5.36	YES	1.29	40.58	34.49	7.10	YES	1.69	24.45	23.42	8.63	YES	2.09	29.67	16.21	9.98	YES	61.43
HAR_DR	1.21	0.00	0.00	3.44	YES	1.58	0.99	0.51	5.26	YES	1.95	12.83	6.68	6.84	YES	2.39	35.24	16.14	8.29	YES	2.75	57.88	40.29	9.64	YES	0.04
CAViaR	0.37	56.64	30.25	3.19	YES	0.88	66.03	52.55	5.39	YES	1.32	58.87	43.57	7.18	YES	1.91	94.41	73.44	8.64	YES	2.57	12.37	81.40	10.06	YES	71.25
Model	VaR_97.5	CC_97.5	UC_97.5	Asymmetric QL	MCS	VaR_98.0	CC_98.0	UC_98.0	Asymmetric QL	MCS	VaR_98.5	CC_98.5	UC_98.5	Asymmetric QL	MCS	VaR_99.0	CC_99.0	UC_99.0	Asymmetric QL	MCS	VaR_99.5	CC_99.5	UC_99.5	Asymmetric QL	MCS	ES_97.5_test
AgACI	98.56	0.00	0.00	9.34	YES	98.91	0.00	0.00	8.07	YES	99.23	0.00	0.00	6.57	YES	99.54	0.00	0.00	4.95	YES	99.80	0.40	0.09	3.05	YES	0.01
FACI	97.86	2.19	11.26	9.31	YES	98.25	22.60	21.55	7.90	YES	98.73	19.34	18.49	6.46	YES	99.34	1.91	1.26	4.81	YES	99.72	0.71	2.43	3.02	YES	10.97
SF-OGD	98.05	1.42	1.25	9.71	NO	98.34	20.05	9.23	8.23	NO	98.84	5.14	4.80	6.48	YES	99.23	2.32	9.59	4.80	YES	99.67	20.20	7.83	2.84	YES	8.26
SAOCP	98.51	0.00	0.00	9.83	NO	98.62	0.26	0.14	8.18	NO	98.91	3.40	1.74	6.68	NO	99.39	1.49	0.45	4.81	YES	99.74	4.18	1.22	2.81	YES	0.00
GARCH	97.91	29.67	16.21	8.87	YES	98.38	14.74	13.87	7.57	YES	98.90	14.32	7.28	6.14	YES	99.38	9.56	3.43	4.59	YES	99.63	56.64	30.25	2.81	YES	41.02
HAR_DR	96.73	2.52	1.41	9.20	YES	97.25	2.38	0.78	7.84	YES	97.80	1.58	0.47	6.40	YES	98.13	0.02	0.00	4.82	YES	98.68	0.00	0.00	2.99	YES	0.01
CAViaR	98.46	0.25	0.06	8.98	YES	98.79	0.44	0.15	7.64	YES	99.27	0.11	0.03	6.13	YES	99.52	0.89	0.23	4.51	YES	99.67	39.72	18.13	2.80	YES	0.48

Table 13. Number of VaR violations in % across Bubble and Litecoin-Token for each quantile and model; p-values in % for the Christoffersen conditional coverage (CC) test; p-values in % for the Kupiec unconditional coverage (UC) test; asymmetric quantile loss (QL) function by González-Rivera et al. (2004); the model was included in the model confidence set (MCS): yes or no; p-values in % for the multinomial VaR test by Kratz et al. (2018), for the five quantiles in the left tail (ES_2.5_test) and in the right tail (ES_97.5_test), respectively.

	Bubble (ID = 918)
Model	VaR_0.5	CC_0.5	UC_0.5	Asymmetric QL	MCS	VaR_1.0	CC_1.0	UC_1.0	Asymmetric QL	MCS	VaR_1.5	CC_1.5	UC_1.5	Asymmetric QL	MCS	VaR_2.0	CC_2.0	UC_2.0	Asymmetric QL	MCS	VaR_2.5	CC_2.5	UC_2.5	Asymmetric QL	MCS	ES_2.5_test
AgACI	0.28	30.18	12.39	9.11	YES	0.76	44.77	23.79	13.42	YES	1.18	4.17	20.98	17.09	YES	1.65	2.93	24.03	20.41	YES	2.08	8.19	20.09	23.22	YES	70.88
FACI	0.43	85.55	61.61	9.54	YES	0.99	82.57	97.03	13.25	YES	1.65	25.43	56.81	16.99	YES	1.94	2.42	83.44	20.46	YES	2.36	8.75	68.11	22.92	YES	55.15
SF-OGD	0.38	69.08	40.51	8.56	YES	0.99	82.57	97.03	13.14	YES	1.46	74.03	89.22	17.20	YES	2.17	19.42	57.52	20.40	YES	2.69	45.03	57.52	22.80	YES	72.42
SAOCP	0.43	85.55	61.61	8.97	YES	0.80	56.74	34.56	14.00	YES	1.13	27.19	14.74	17.40	YES	1.42	9.31	4.34	20.98	YES	1.94	21.67	8.41	23.91	YES	45.28
GARCH	2.69	0.00	0.00	13.74	NO	3.73	0.00	0.00	17.64	NO	4.68	0.00	0.00	20.45	NO	5.05	0.00	0.00	22.73	YES	5.90	0.00	0.00	24.66	YES	0.00
HAR_DR	0.19	7.06	2.15	9.09	YES	0.29	0.05	0.01	15.98	NO	0.33	0.00	0.00	22.13	NO	0.43	0.00	0.00	27.73	NO	0.48	0.00	0.00	32.96	NO	0.00
CAViaR	1.81	0.00	0.00	10.82	YES	2.10	0.00	0.00	14.54	YES	2.14	1.63	2.24	17.79	YES	2.76	0.47	1.80	21.17	YES	2.86	17.09	30.18	23.64	YES	0.00
Model	VaR_97.5	CC_97.5	UC_97.5	Asymmetric QL	MCS	VaR_98.0	CC_98.0	UC_98.0	Asymmetric QL	MCS	VaR_98.5	CC_98.5	UC_98.5	Asymmetric QL	MCS	VaR_99.0	CC_99.0	UC_99.0	Asymmetric QL	MCS	VaR_99.5	CC_99.5	UC_99.5	Asymmetric QL	MCS	ES_97.5_test
AgACI	98.16	0.26	4.21	27.13	YES	98.39	2.38	18.02	24.26	YES	98.72	9.55	38.29	20.53	YES	99.06	4.45	79.64	16.77	YES	99.43	85.25	66.95	11.26	YES	19.94
FACI	97.64	9.91	68.11	26.77	YES	98.16	38.78	59.93	22.99	YES	98.35	5.77	56.81	20.49	YES	98.91	7.24	69.34	16.14	YES	99.48	93.65	89.89	10.86	YES	33.70
SF-OGD	97.73	23.42	48.62	26.37	YES	98.21	8.14	49.30	23.79	YES	98.49	4.22	96.51	19.60	YES	99.01	5.55	97.03	15.58	YES	99.39	14.48	47.25	10.57	YES	60.98
SAOCP	98.16	5.65	4.21	26.29	YES	98.35	16.40	24.03	23.61	YES	98.68	12.54	49.33	19.70	YES	98.91	7.24	69.34	15.31	YES	99.39	71.29	47.25	9.99	YES	5.37
GARCH	93.72	0.00	0.00	27.10	YES	94.47	0.00	0.00	24.68	YES	95.23	0.00	0.00	21.88	YES	96.08	0.00	0.00	18.52	YES	97.50	0.00	0.00	13.96	NO	0.00
HAR_DR	99.24	0.00	0.00	34.99	NO	99.29	0.00	0.00	29.54	NO	99.48	0.01	0.00	23.71	NO	99.52	2.61	0.73	17.35	YES	99.62	70.17	42.11	10.13	YES	0.00
CAViaR	98.24	2.90	2.27	25.24	YES	98.57	2.95	4.95	22.48	YES	99.05	0.41	2.73	19.26	YES	99.29	0.57	16.68	15.05	YES	99.14	3.74	3.50	10.68	YES	0.00
	Litecoin-Token (ID = 3807)
Model	VaR_0.5	CC_0.5	UC_0.5	Asymmetric QL	MCS	VaR_1.0	CC_1.0	UC_1.0	Asymmetric QL	MCS	VaR_1.5	CC_1.5	UC_1.5	Asymmetric QL	MCS	VaR_2.0	CC_2.0	UC_2.0	Asymmetric QL	MCS	VaR_2.5	CC_2.5	UC_2.5	Asymmetric QL	MCS	ES_2.5_test
AgACI	0.21	22.85	8.65	5.56	YES	0.50	10.96	3.70	9.41	YES	1.14	2.12	24.87	12.51	YES	1.43	2.63	10.61	15.12	YES	1.78	4.13	7.02	17.67	YES	21.56
FACI	0.29	45.82	21.49	5.78	YES	0.64	33.36	14.93	8.62	YES	1.14	20.37	24.87	11.35	YES	1.43	15.40	10.61	14.42	YES	2.00	14.02	21.16	16.67	YES	57.56
SF-OGD	0.29	45.82	21.49	5.80	YES	0.71	48.74	25.54	9.21	YES	1.14	42.73	24.87	12.82	YES	1.71	53.42	42.95	15.36	YES	1.93	29.80	15.15	17.67	YES	43.39
SAOCP	0.43	90.24	69.49	5.64	YES	0.64	33.36	14.93	8.94	YES	1.07	32.08	16.27	12.49	YES	1.21	6.17	2.32	15.08	YES	1.57	4.01	1.67	17.47	YES	11.95
GARCH	4.35	0.00	0.00	16.43	NO	5.35	0.00	0.00	18.53	NO	5.92	0.00	0.00	20.03	NO	6.70	0.00	0.00	21.08	NO	6.85	0.00	0.00	21.91	YES	0.00
HAR_DR	4.49	0.00	0.00	14.24	NO	4.85	0.00	0.00	17.06	NO	4.85	0.00	0.00	19.19	NO	4.92	0.00	0.00	20.98	NO	5.06	0.00	0.00	22.57	YES	0.00
CAViaR	0.36	71.19	42.23	5.74	YES	0.50	10.96	3.70	9.49	YES	0.86	8.80	3.10	12.51	YES	1.43	20.29	10.61	15.20	YES	1.85	16.43	10.50	17.38	YES	26.40
Model	VaR_97.5	CC_97.5	UC_97.5	Asymmetric QL	MCS	VaR_98.0	CC_98.0	UC_98.0	Asymmetric QL	MCS	VaR_98.5	CC_98.5	UC_98.5	Asymmetric QL	MCS	VaR_99.0	CC_99.0	UC_99.0	Asymmetric QL	MCS	VaR_99.5	CC_99.5	UC_99.5	Asymmetric QL	MCS	ES_97.5_test
AgACI	98.00	2.47	21.16	17.82	YES	98.22	16.68	55.47	15.96	YES	98.50	1.01	99.47	13.61	YES	99.00	2.08	99.57	10.61	YES	99.22	0.01	16.33	7.10	YES	10.63
FACI	97.15	6.10	40.74	17.33	YES	97.57	1.55	27.10	15.60	YES	98.15	13.03	29.22	12.69	YES	98.93	2.69	79.48	9.97	YES	99.43	0.15	71.39	6.45	YES	80.43
SF-OGD	97.00	50.19	24.87	18.12	YES	97.79	43.48	57.87	16.02	YES	98.22	45.17	39.69	13.04	YES	98.79	60.89	43.89	9.76	YES	99.36	73.19	47.05	6.86	YES	72.73
SAOCP	98.72	0.46	0.13	17.87	YES	99.00	1.09	0.31	15.79	YES	99.00	22.71	10.02	13.53	YES	99.07	86.00	78.16	10.02	YES	99.57	90.63	69.49	6.55	YES	0.03
GARCH	92.72	0.00	0.00	21.00	YES	93.30	0.00	0.00	20.16	NO	93.72	0.00	0.00	19.18	NO	94.72	0.00	0.00	17.89	NO	95.93	0.00	0.00	15.95	NO	0.00
HAR_DR	95.08	0.00	0.00	22.68	NO	95.44	0.00	0.00	21.11	NO	95.44	0.00	0.00	19.36	NO	95.51	0.00	0.00	17.28	NO	95.86	0.00	0.00	14.57	NO	0.00
CAViaR	98.57	1.50	0.52	18.27	YES	98.86	3.69	1.25	16.66	YES	98.79	53.36	35.98	14.08	YES	99.22	64.28	39.96	10.78	YES	99.57	90.24	69.49	6.42	YES	0.75

In terms of VaR violations, all four ACI algorithms were able to properly model both the left and right tails of the return distributions, with the exception of SAOCP, which continued to show issues when modeling the right tail of the distribution. The GARCH model worked well with Ethereum but was unable to correctly estimate the quantiles for Bitcoin and the assets with the lowest capitalization. The HAR model performed the worst across all assets, while the CAViaR model passed all coverage tests for the left tail of the assets with the highest market capitalization but failed the tests for the right tail and for the assets with the lowest capitalization.

Regarding quantile loss functions, the GARCH model generally exhibited the lowest asymmetric loss functions for Bitcoin and Ethereum, followed by the CAViaR model and the ACI models. However, the GARCH model showed the worst losses (along with the HAR model) for the assets with the lowest market capitalization, whereas the ACI methods performed the best. This confirms that the extreme volatility of these types of assets strongly impacts their numerical stability. Interestingly, the CAViaR model demonstrated remarkably low losses across all assets, indicating its greater computational robustness compared to the GARCH and HAR models. It is important to note that in most instances, the differences between the models’ losses were not statistically significant, resulting in the vast majority of the considered models being included in the model confidence set.

In summary, while traditional models like GARCH and HAR exhibit strengths and weaknesses across different assets, the adaptive nature of ACI methods, particularly their robustness in highly volatile markets, highlights their potential as valuable tools in financial risk management. The CAViaR model’s consistent performance across various assets further underscores its reliability, making it an interesting alternative to more conventional approaches.

5. Discussion and Conclusions

This paper compared the performance of four adaptive conformal inference (ACI) algorithms with traditional volatility models for daily data, such as GARCH models and daily range models, in computing the value at risk (VaR) at various probability levels for 4000 crypto-assets observed between 2010 and 2024. Additionally, this comparison indirectly assessed the quality of the models’ expected shortfall (ES) by using a multinomial test of VaR violations across multiple levels as a means of backtesting the ES, as proposed by Kratz et al. (2018).

To achieve this objective, we employed four ACI algorithms, including Aggregated ACI by Zaffran et al. (2022), Fully Adaptive Conformal Inference by Gibbs and Candès (2022), Scale-Free Online Gradient Descent by Bhatnagar et al. (2023), and Strongly Adaptive Online Conformal Prediction by Bhatnagar et al. (2023). These algorithms, explicitly designed to address scenarios where data arrive sequentially, dynamically adjust the width of prediction intervals in response to observed data, thereby providing adaptive and accurate uncertainty quantification. As benchmark models for daily data, we used the GARCH(1,1) model with a symmetric Student’s t-distribution for the standardized errors and the daily range volatilities computed using the Garman–Klass estimator together with an HAR model.

In terms of VaR violations across all quantiles, FACI and SF-OGD were able to properly model the left and right tails of the distribution for the vast majority of crypto-assets, followed by AgACI, while SAOCP exhibited the poorest performance among the ACI algorithms. Conversely, the GARCH and HAR models faced challenges in achieving numerical convergence for approximately 2.5% of assets, particularly those with extreme variability and/or relatively small datasets ($T<1000$). Despite this, GARCH served as a reliable benchmark model, slightly underestimating the VaR for the most extreme quantiles ($p_i\le 1.0\%$) while maintaining accuracy for the other quantiles. In contrast, the HAR model with daily range volatilities proved to be the least effective, underestimating lower quantiles by up to $p_i=1\%$ and severely overestimating higher quantiles. Similar issues emerged for the right tail of the distribution.

Regarding asymmetric quantile loss functions, our analysis revealed that the GARCH model consistently emerged as the top-ranked model for the majority of assets and was almost always included in the model confidence set. While ACI models demonstrated proficiency in estimating quantiles for most assets, they exhibited challenges in estimating the most extreme quantiles ($p_i\le 1\%$ and $p_i\ge 99\%$), particularly the AgACI and FACI models, which showed rather large asymmetric losses and lower rankings. However, the SF-OGD and SAOCP models displayed greater precision with smaller losses.

These findings have significant implications for financial risk management: while a traditional benchmark like the GARCH model remains relevant, newer approaches such as ACI models offer promising alternatives, particularly for assets with complex dynamics such as crypto-assets, albeit with some caveats in extreme quantile estimation. Given that ACI models are more precise in terms of VaR violations, while GARCH models are better in terms of asymmetric quantile losses, forecasting combinations are a possibility, and we leave this issue as an avenue for further research.

Finally, we performed a set of robustness checks to verify that our results also held with different settings. In terms of market capitalization of crypto-assets, the results were similar to the baseline case. However, we found that the performance of the GARCH model and, to a lesser extent, the SAOCP algorithm deteriorated significantly when focusing on assets with the lowest market capitalization. It is well known that crypto-assets with lower market capitalization tend to experience higher levels of volatility. This heightened volatility can pose challenges for several modeling approaches, which may struggle to adequately capture and predict extreme movements in these assets’ prices. As such, future research could explore alternative modeling techniques specifically tailored to address the unique characteristics and dynamics of lower-capitalization crypto-assets, potentially enhancing the accuracy and robustness of risk management strategies in this segment of the market.

As a second robustness check, we divided our assets into four groups based on the size of their time series: AgACI, FACI, and SF-OGD exhibited consistent performances across time series of varying lengths. Instead, GARCH models seemed to perform best with time series close to 1000 observations. SAOCP and the HAR model with daily range data performed notably better with time series containing fewer than 1000 observations compared to longer time series. It appears that these methods are more sensitive to structural breaks, which occur more frequently in assets with longer time series. This evidence indirectly corroborates the simulation studies conducted by Susmann et al. (2023), which demonstrated that SAOCP tends to underestimate the quantiles when faced with a distributional shift. This evidence underscores the importance of considering both the length of the time series and the model’s sensitivity to structural breaks when selecting appropriate risk forecasting methods. Future research could delve deeper into understanding the mechanisms underlying these performance disparities and explore potential refinements to enhance the accuracy and robustness of risk predictions across diverse time-series lengths.

As a third robustness check, we assessed the impact on our results of employing a single-hidden-layer neural network instead of a simple AR(1) like in the baseline case. In terms of VaR violations, there are no notable differences among the models (except for SAOCP), while regarding quantile loss functions all four ACI algorithms were strongly penalized in terms of average ranking, with SAOCP exhibiting the largest decline in ranking across all competing models. In general, employing a more complex forecasting model for the mean of the assets’ log-returns with ACI algorithms did not result in more precise risk estimates. This outcome can probably be attributed to the lower model bias being outweighed by the higher variance in the model estimates. These findings underscore the intricate trade-offs involved in selecting forecasting models for risk management purposes, highlighting the importance of considering both model complexity and estimation accuracy in decision-making processes.

As a fourth robustness check, we tested the symmetric absolute value (SAV)-CAViaR model with four crypto-assets, including the most and least capitalized. The ACI algorithms effectively modeled both tails of the return distributions, except for SAOCP on the right tail. The GARCH model performed well for Ethereum but struggled with Bitcoin and low-capitalization assets. The HAR model performed the worst, while the CAViaR model passed coverage tests for the left tail of high-capitalization assets but failed for the right tail and low-capitalization assets. The GARCH model had the lowest asymmetric losses for Bitcoin and Ethereum but performed poorly for low-capitalization assets, where the ACI methods excelled. Overall, the ACI methods demonstrated robustness in highly volatile markets, and the CAViaR model showed consistent performance, making it a reliable alternative to traditional approaches.

The general recommendation for investors that emerges from our analysis is to utilize the Fully Adaptive Conformal Inference (FACI) and the Scale-Free Online Gradient Descent (SF-OGD) algorithms. These algorithms exhibit remarkable precision in providing VaR estimates across all examined quantiles, applicable to various types of crypto-assets and different market conditions. The risk estimates offered by these ACI algorithms can then be compared or even combined with those from traditional GARCH models, especially considering the latter’s proficiency in offering small asymmetric quantile losses, provided a large dataset is available. We leave this issue as an avenue for future research. We note that while GARCH(1,1) is a parsimonious and analytically appealing model, its performance is highly dependent on the size and characteristics of the data sample. Our study found that GARCH(1,1) faces computational difficulties and often fails to achieve numerical convergence for smaller datasets (fewer than 1000 observations). Furthermore, for longer datasets, the model struggles with structural breaks, leading to suboptimal performance, particularly in the extreme parts of the left tail of the distribution, as observed with Bitcoin. In contrast, the ACI algorithms offer several advantages. They are computationally more efficient and robust across a wider range of dataset sizes, from small to medium. This makes them particularly suitable for crypto-assets, which often have limited historical data or exhibit high volatility. The ACI models dynamically adjust to new data, providing more accurate and adaptive risk estimates without the computational burdens associated with GARCH models. Additionally, the simplicity and speed of ACI models enhance their tractability, making them more practical for real-time risk management and forecasting in the fast-evolving cryptocurrency market. While GARCH(1,1) remains valuable for its analytical properties and its capacity to support further financial modeling, such as deriving explicit asset valuation formulas, the ACI models fill an important gap by offering robust performance and computational efficiency across various market conditions and data constraints. Therefore, incorporating ACI models into risk management frameworks provides a complementary approach, leveraging their strengths in scenarios where traditional models like GARCH may falter.

An important limitation of this paper is the reliance on time series consisting of at least 730 daily data points, ensuring each model had a minimum of one year’s worth of data for initial training and calibration. This condition inevitably excluded a significant number of young crypto-assets, thereby restricting the depth of our analysis. One potential solution could involve utilizing high-frequency data if available, although alternative approaches should also be explored. Further research endeavors could address these limitations by incorporating additional data sources, exploring alternative model specifications, and examining the performance of forecasting models across varying time horizons and market conditions. This would enhance the robustness and applicability of risk management strategies in the dynamic landscape of crypto-assets.

As a final note, we wish to underscore that our findings align with the existing literature, highlighting the necessity of robust risk management frameworks for crypto-assets. For instance, Liu et al. (2020) emphasize the challenges and rewards of investing in cryptocurrencies, suggesting that value-at-risk (VaR) forecasting can benefit from parsimonious models. Although they discuss models under the generalized autoregressive score (GAS) framework, our study similarly finds that simpler models, such as GARCH, remain highly relevant and effective for VaR forecasting in specific scenarios. This resonates with Liu et al. (2020)’s assertion that more elaborate models do not always outperform simpler alternatives, particularly when considering the varying dynamics of crypto-assets. Trucíos and Taylor (2023) further contribute to the discourse by comparing various advanced risk forecasting methods, including long-memory processes and quantile regression-based models, and highlighting the efficacy of certain models for specific cryptocurrencies. Their exploration of the robustness of these models during turbulent periods, such as the COVID-19 pandemic, parallels our findings that no single model universally outperforms others. Additionally, their investigation into forecast combination strategies aligns with our suggestion that combining traditional models like GARCH with ACI approaches could enhance predictive performance. Müller et al. (2022) introduce the concept of range value at risk (RVaR) and demonstrate that GARCH models with various error distributions can effectively forecast RVaR for major cryptocurrencies. Our study corroborates their observation that non-normal distributions are often more suitable for VaR and expected shortfall (ES) predictions, reinforcing the notion that the choice of model and distribution significantly impacts the accuracy of risk measures and that simple volatility models, such as GARCH with a Student’s t-distribution, can produce accurate risk forecasts. Alexander and Dakos (2023) provide one of the most comprehensive reviews of the cryptocurrency risk forecasting literature, advocating for the practical application of relatively simple models over more complex alternatives. Their extensive backtesting with hourly and daily data reveals that models capturing asymmetric volatility and heavy-tailed distributions are just as effective as more sophisticated models. Our results echo this sentiment, demonstrating that models like FACI and SF-OGD can achieve reliable forecasts for crypto-assets without the need for overly computationally complex specifications, thus addressing the practical constraints faced by investors.

In conclusion, our study situates itself within the broader context of the cryptocurrency risk forecasting literature, aligning with key findings from Liu et al. (2020), Müller et al. (2022), Trucíos and Taylor (2023), and Alexander and Dakos (2023). By validating the efficacy of newer ACI models and recognizing the conditions under which they excel, our research contributes to a nuanced understanding of risk management in the cryptocurrency market. Future research should continue to explore the interplay between model complexity, data availability, and forecasting accuracy to develop robust risk management strategies that can withstand the unique challenges posed by crypto-assets.