Abstract
The expectile-based Value at Risk (EVaR) has gained popularity as it is more sensitive to the magnitude of extreme losses than the conventional quantile-based VaR (QVaR). This paper applies the expectile regression approach to evaluate the EVaR of stock market indices of Australia and Japan. We use an expectile regression model that considers lagged returns and common risk factors to calculate the EVaR for each stock market and to evaluate the interdependence of downside risk between the two markets. Our findings suggest that both Australian and Japanese stock markets are affected by their past development and the international stock markets. Additionally, ASX 200 index has significant impact on Nikkei 225 in terms of downside tail risk, while the impact of Nikkei 225 on ASX is not significant.
1. Introduction
Globalization and rapid technological advancements have led to an increasing integration of financial markets worldwide. As a result, the linkages and interdependence between national stock markets may have strengthened, which can have significant implications for corporate investment and financing strategies and international diversification. Strong interdependence would reduce the potential gains from international diversifications. Therefore, comprehending the nature and extent of return and volatility linkages across different financial markets can offer insights into diversification and hedging strategies for investors, as well as appropriate policy actions for regulatory bodies and governments. In terms of risk management, it is crucial to comprehend any linkages and transmission of risks between stock markets.
Many studies have demonstrated that increasing bilateral trade relations between countries can have a substantial impact on their stock market linkages. For example, Paramati et al. (2016) examined the impact of bilateral trade relations on the time-varying correlations of the stock markets of Australia and 10 Asian countries. Their results showed that increasing bilateral trade relations between Australia and Asian countries contributed to their stock market interdependence over time.
The economic relationship between Australia and Japan is underpinned by complementary strengths and needs. According to the Australian Bureau of Statistics, Japan was Australia’s third-largest trading partner and second-largest export destination in 2021. Australia is the single largest supplier of both industrial raw materials and energy to Japan (Australian Bureau of Statistics 2021b, Tables 14a and 14b). Meanwhile, Japan ranks second only to the United States in terms of the stock of foreign direct investment (FDI) into Australia (Australian Bureau of Statistics 2021a, Table 2).
Australia and Japan have some common and distinct features in terms of their economic structures. The Australian economy is dominated by its service sector and is rich in natural resources, while Japan is one of the largest and most developed economies in the world. Japan has a well-educated, industrious workforce, and its large, affluent population makes it one of the world’s biggest consumer markets. Manufacturing has been the most remarkable and internationally renowned feature of Japan’s economic growth.
Both Australia and Japan play critical roles in the world financial markets. Australian Securities Exchange (ASX) is one of the world’s leading financial market exchanges, offering a full suite of services, including listings, trading, clearing and settlement, across a comprehensive range of asset classes. It was created by the merger of the Australian Stock Exchange and the Sydney Futures Exchange in July 2006 and is one of the world’s top-10 listed exchange groups measured by market capitalization1.
The Tokyo Stock Exchange (TSE) is a stock exchange located in Tokyo, Japan. It is the fourth-largest stock exchange in the world by the aggregate market capitalization of its listed companies and largest in Asia. Tokyo is one of the world’s foremost centers of finance.
The economic relationship between Australia and Japan is strong, and it is essential to have a comprehensive understanding of the transmission of risk between their financial markets. This study aims to contribute to the literature by examining the influence of downside risk between the two stock markets, using the Expectile Value-at-Risk (EVaR) as the risk measure. Specifically, the paper will apply an expectile regression approach to evaluate the EVaR of the stock market indices of both countries.
The expectile regression model that includes lagged returns and some common risk factors will be used to calculate the EVaR for each stock market. The model will also be used to assess the influence between the two markets in terms of downside risk. By doing so, the study will shed light on the interdependence of the two markets and how they respond to market shocks.
Overall, this research will provide valuable insights into the dynamics of risk transmission between the financial markets of Australia and Japan, which can help investors and policymakers better understand the potential risks and opportunities in these markets.
The remainder of the paper is organized as follows. Section 2 provides a review of relevant literature and emphasizes the significance of the study. Section 3 describes the research methodology used, along with the data and sample statistics. The empirical results and analysis are presented in Section 4, and concluding remarks are provided in Section 5.
2. Related Literature
In this section, we first describe the downside risk measures, then provide a review of the literature related to risk transmission between financial markets, with a particular focus on studies that employ the EVaR approach. This section will also highlight the importance of this study in advancing our understanding of the interdependence of the Australian and Japanese financial markets.
2.1. Measures of Risk
Risk is defined as the potential for an undesirable outcome (i.e., loss of value) resulting from an action or inaction. In finance, risk is the uncertainty surrounding the future value of an asset or portfolio of financial instruments.
Measuring and managing risk is crucial in the financial industry to ensure the stability and sustainability of the financial system. A good risk measure should accurately capture the potential for losses, but not be overly conservative, as this could restrict economic growth and investment opportunities. A variety of risk measures are used in finance, including Value-at-Risk (VaR), Expected Shortfall (ES), and the Expectile Value-at-Risk (EVaR), each with its own strengths and weaknesses.
The financial disasters of the early 1990s led to significant changes in the financial landscape, with Value-at-Risk (VaR) becoming a standard risk management tool in financial and insurance institutions since the 1990s. VaR measures the potential amount a portfolio can lose for a given probability level, defined as a tail quantile of the distribution of financial returns. However, VaR has some significant drawbacks, including ignoring most of the risk’s probability distribution and not being a sub-additive risk measure (Du and Escanciano 2016; Gordy and Juneja 2010), which can result in the measure for a portfolio being less than the sum of its components’ measures.
Expected Shortfall (ES) has been proposed as a risk measure for regulatory frameworks in response to the limitations of Value at Risk (VaR) (Du and Escanciano 2016; Embrechts et al. 2014). Unlike VaR, which only considers the probability of losses exceeding a certain threshold, ES calculates the average of the VaR values below a specified level, thus including very unlikely losses with a significant impact on the portfolio value. ES is a coherent risk measure and has the property of subadditivity, thus rewarding diversification (Hult et al. 2012). In fact, Basel III2 has recommended ES as a replacement for VaR in the new regulatory framework and raised the capital ratios required for financial institutions.
In addition to their use as risk measures, VaR and ES estimation can serve as the basis for portfolio optimization (Huang et al. 2010; Lwin et al. 2017). However, it is worth noting that ES is not elicitable, meaning that there is no scoring function for which the expectation is minimized by the true ES (Gneiting 2011). Nonetheless, the benefits of ES as a coherent risk measure have led to its increased use in regulatory frameworks and portfolio optimization.
The estimation and evaluation of Expected Shortfall (ES) has been challenging in practice, as noted by Rockafellar et al. (2014). However, Fissler et al. (2016) showed that ES and VaR are jointly elicitable. They also proposed a family of scoring functions that can be used to estimate and evaluate both VaR and ES simultaneously. This has enabled researchers such as Patton et al. (2019) and Taylor (2019) to estimate dynamic models for VaR and ES based on joint scoring functions. Additionally, Meng and Taylor (2020) introduced a novel approach to estimating these two risk measures using joint scoring functions based on intraday data. These methods have advanced our ability to estimate and evaluate VaR and ES accurately, despite the challenges involved in their practical implementation.
One approach to enhancing risk measures is by identifying and accounting for structural breaks in the markets. A prevalent method involves introducing dummy variables (Anjum and Malik 2020; Patra 2021). Nevertheless, for simplicity, we employ the conventional model in this study and defer addressing this issue to future work.
2.2. Risk Transmission between Financial Markets
As global financial markets are increasingly deregulated and integrated, the risk in one financial market or asset is very likely to be transmitted to other markets or assets. Understanding risk transmission between financial markets is important for asset allocation and risk management. It also has crucial implication for policy making that aims at reducing financial contagion and the instability it causes to the economy.
Risk transmission between financial markets has been the subject of numerous studies over the past few decades. The interconnectedness of global financial markets has become increasingly apparent since the 2008 Global Financial Crisis, where the spillover effects of one market’s instability led to economic turmoil in other regions. A number of studies have sought to understand the mechanisms and channels through which risk is transmitted between financial markets.
Caporals et al. (2006) used a Vector Autoregression (VAR) model to examine the cross-market volatility spillovers between the US and European equity markets. Their results showed that spillovers were significant and that US markets were more influential in transmitting shocks to European markets than vice versa. This was corroborated by other studies, such as Forbes and Rigobon (2002) who found that US equity market volatility was a significant predictor of volatility in other major equity markets.
Later on, many studies investigate volatility spillover using multivariate GARCH models. For instance, Baele (2005) analyzed the volatility spillover effects in European equity markets. Li and Giles (2015) studied the volatility spillover effects between developed stock markets and Asian emerging stock markets. Vo and Tran (2020) investigated volatility spillovers from the US equity market to ASEAN stock markets. Zhong and Liu (2021) provided evidence on volatility spillovers between China and South-east Asian stock markets. These are just a few examples of studies that have examined the phenomenon of volatility spillovers across different equity markets.
However, in many applications, losses and gains are treated symmetrically in the measure of correlation and volatility spillover. In reality, investors have downside financial constraints and are downside risk averse, meaning they are more concerned with downside losses than upside gains. Therefore, these applications are inadequate in describing extreme bad scenarios when a significant decline in stock returns in one market generates panic and spreads to other markets, as seen in events such as the 1997 Asian financial crisis and the Global Financial Crisis in 2008.
To address these issues, some studies have distinguished extreme negative shocks from normal observations. For example, Hartmann et al. (2004) looked at extreme dependence between markets in distress periods, while Asgharian and Bengtsson (2006) and Asgharian and Nossman (2011) analyzed risk spillover with Poisson jumps. Hussain and Li (2018) considered the dependence structure between Chinese and other major stock markets based on the extreme value theory and copulas. A few studies (e.g., Adrian and Brunnermeier 2009; Bae et al. 2003; Christiansen and Ranaldo 2009) study extreme coexceedance or simultaneous extreme events of financial markets and financial institutions.
Further, a few studies have focused on risk transmission between stock markets using downside risk measures such as Expected Shortfall (ES) and Expectile Value-at-Risk (EVaR). Hong et al. (2009) provided a theoretical background for the binary response of extreme value spillover. Inspired by this concept of Granger causality in risk, Liu (2014) proposed a binary response model approach to measure and forecast extreme downside risk in Asia-Pacific markets, given information on extreme downside risks in the US and Japanese markets. In both studies, downside risk is measured by VaR. However, there is a need for more research on risk transmission between stock markets using downside risk measures such as ES and EVaR.
2.3. The Expectile Approach
The term “expectile” was first introduced by Newey and Powell (1987). One major advantage of using expectiles is that asymmetric least squares (ALS) regression is more computationally efficient than quantile regression. Computing the expectile is simpler than computing the quantile because the check-loss function is continuously differentiable. This has led to an increase in popularity in the use of expectiles in modelling risk measurement and transmission in recent years.
Expectiles provide a different approach to measuring risk as they rely on both tails of the distribution, unlike other measures such as expected shortfall and value-at-risk. Expected shortfall is sensitive to the magnitude of the lower tail returns, but only those of the lower tail. As such, it tends to be more conservative than other risk measures. VaR is not influenced by the magnitude of lower tail returns at all, increasing the chance that it underestimates the true risk involved. The expectile relies on more comprehensive information to measure risk.
The relationship between expectiles and quantiles has also encouraged the use of expectiles. Efron (1991) suggested quantiles can be estimated using the expectile. The one-to-one mapping between quantiles and expectiles has been empirically supported by Jones (1994), Abdous and Remillard (1995), and Yao and Tong (1996). Taylor (2008) estimated nonparametric value-at-risk and expected shortfall using expectiles. The emphasis has generally been placed on the computational efficiency of the expectile as compared to quantile regression, rather than on the virtues of the expectile as a risk measure. De Rossi and Harvey (2009) were the first to directly use the expectile by developing a spline-based nonparametric computation method for the time-varying expectile. Its use was still limited by the difficulty in interpreting the expectile and its asymmetry parameter. Direct use of the expectile as a risk measure has been discouraged by the expectiles’ lack of interpretation. Kuan et al. (2009) addressed the issue of interpretability by giving a more intuitive definition for the expectiles in a financial risk setting.
Additionally, Zhang and Ma (2019) examine the connections between crude oil futures markets and stock markets through expectile regressions, demonstrating the effectiveness of this approach. In a separate study, Yao et al. (2021) employ expectile regressions to assess the risk of the Chinese FinTech index, exploring associated macroeconomic risk factors.
As our objective is to examine the downside risk connection among specific markets, we utilize the a priori specified model, detailed below. Notably, Xu et al. (2016) present an intriguing application of a nonparametric approach for model specification. Furthermore, Liao et al. (2019) introduce penalized expectile regressions; however, we opt for the conventional method for simplicity.
In sum, the expectile, which is the solution to asymmetric least squares regression, resolves many of the issues of previous risk measures. In addition to addressing the shortcomings of other risk measures such as Value-at-Risk and Expected Shortfall, expectiles have unique characteristics that make them very efficient and informative for measuring risk.
3. Methodology and Data
In this section, we will detail the research methodology used in the study, including the expectile regression model, EVaR calculations, and the common risk factors used in the model. This section will also describe the data sources and sample statistics used in the study.
3.1. Traditional Downside Risk Measures
A VaR with a confidence level of , , represents the maximum potential loss for a given holding period with a probability of , see e.g., Jorion (2000). VaR is essentially the negative of the -th quantile of the return distribution and can be obtained by minimizing asymmetrically weighted mean absolute deviations. In this weighting scheme, positive deviations are assigned a weight of , while negative deviations are assigned a weight of . Bassett et al. (2004) argued that this asymmetric weighting scheme aligns with certain distorted probability assessments used in Choquet expected theory, which can describe pessimism.
To be specific, let Y denote an asset return with the distribution function . Given , the quantile based VaR (henceforth QVaR) is the negative of the -th quantile of : . It is well known that the -th quantile can be obtained by minimizing asymmetrically weighted mean absolute deviations:
where is the indicator of the event . Thus, a QVaR is a natural product of an optimization problem with an asymmetric linear loss function. The first order condition of minimizing Equation (1) is , which implies
This highlights that VaR has limitations as it depends solely on the frequency of more extreme losses without considering their magnitudes, unlike the lower partial moment. This may result in VaR being less sensitive to tail risk, meaning that two portfolios with the same VaR could have very different tail shapes. Additionally, VaR does not satisfy sub-additivity, so diversification may not decrease the risk measured by VaR, which is undesirable.
In contrast, expected shortfall (ES) considers the average of all potential losses beyond the VaR at a given confidence level, taking into account the magnitude of the loss. However, ES only accounts for the conditional downside mean, and may therefore be overly conservative.
For an asset return Y with the distribution function and given , the ES of Y at level is the mean of the -tail distribution of Y (Rockafellar and Uryasev 2002; Tasche 2002), i.e.,
where is the the -tail distribution defined as (Rockafellar and Uryasev 2002)
For a more detailed discussion, we refer to Kou and Peng (2016).
3.2. Expectile Based VaR
While the previously mentioned risk measures are still widely used, they have been criticized for their limitations. The expectile approach has emerged as a solution to many of these issues. Expectiles have unique properties that make them highly efficient and informative in measuring risk.
As opposed to quantiles, which only provide information on a specific percentile, expectiles capture information on a specific tail and are more sensitive to tail risks. Additionally, expectiles are robust to outliers and can be easily adapted to incorporate various risk factors. As such, the expectile regression model has become an increasingly popular tool in risk management and financial analysis. The EVaR of Y, an asset return with the expectile level , is the negative of -th expectile of , the distribution function, which can be obtained as the negative of that minimizes the asymmetrically weighted quadratic loss function (Newey and Powell 1987),
where is the indicator of the event . Let us denote such value of by . Then we have: with .
The first-order condition of minimizing (3) is:
which implies
Hence, is the ratio of the deviations of Y below to the overall deviations of Y from , both weighted by the distribution function. Thus, depends on both the extreme values and their probabilities (Kuan et al. 2009).
Lower values of indicate more risk aversion. Kuan et al. (2009) suggested that the EVaR can be thought of as a flexible VaR, since the tail probability associated with an expectile is not some static chosen at the outset, but changes with the underlying distribution.
Compared to the popular QVaR, EVaR is more sensitive to the extreme values of the distribution (Kuan et al. 2009; Xie et al. 2014). Furthermore, can be used to calculate ES according to the one-to-one mapping from to . Yao and Tong (1996) show that and satisfy
Hence, for any , is transformed by Equation (6), such that . ES can be obtained according to Taylor (2008) by,
3.3. Expectile Regression
Given a collection of k variables , in the information set , let denote the -th expectile of Y conditional on X. We consider the linear specification with as a parameter vector.
When the data , are available for , the linear specification can be expressed as:
where denotes the information set up to time t.
The parameter can be estimated by the value of that minimizes
whose first order condition is
We can obtain such value by the usual iteration algorithm:
- Let be an appropriate initial guess of the parameter .
- Given , the kth guess, is calculated aswhere
- Repeat Step 2, for instance, until is small enough.
Let us denote by the estimate of the parameter obtained by the algorithm above. Kuan et al. (2009) suggest that for large T the distribution of be approximated by the normal distribution with mean and variance , where
We note that Kuan et al. (2009) provide some simple numerical examples, and the proof can be attributed to Newey and Powell (1987). Furthermore, expectile regression has seen active application in recent years within financial empirical research.
3.4. Variables
To investigate if the Japanese stock market is a risk factor that influences the Australian stock market, similar to Yao et al. (2021), we use the following variables:
- ASX 200 index return;
- Nikkei 225 index return;
- S&P 500 index return; and
- CSI 300 index return.
We also use the specification
where we use the notations and .
To investigate if the Australian stock market is a risk factor that influences the Japanese stock market, we use the following variables:
- Nikkei 225 index return;
- ASX 200 index return;
- S&P 500 index return; and
- CSI 300 index return.
In both cases, the CSI 300 and S&P 500 are considered as common risk factors to both the Australian and Japanese stock markets.
3.5. Data and Sample Statistics
The two largest economies in the world are the U.S. and China, and both countries have important economic relationships with Australia and Japan. As the U.S. stock market and the Chinese stock market are major players in the global market, they are expected to have significant influence on many other stock markets, including those of Australia and Japan. Therefore, in order to examine the risk transmission between the Australian and Japanese stock markets, it is reasonable to use the CSI 300 and S&P500 as the common risk factors in the expectile regression models. By using these two factors, we can also assess the spillover effects of the U.S. and Chinese markets on the Australian and Japanese markets, and better understand the risk transmission mechanism between them.
In this paper, we use the daily closing stock index data for Australia (ASX 200), Japan (Nikkei 225), U.S. (S&P 500), and China (CSI 300) over the past 10 years, from the beginning of October 2012 to end of September 2023. The exact dates vary depending on the operating days of each market. Table 1 presents the summary statistics for the four stock index returns over the sample period.

Table 1.
Summary statistics of daily returns of the stock market indices.
Based on Table 1, it can be observed that the CSI 300 index has the highest standard deviation, while the ASX 200 index has the lowest. This suggests that the Australian stock market was comparatively less volatile than the other three stock markets during the sample period. Additionally, the negative skewness and large kurtosis of the return distributions for all four stock indices indicate that they have a fat tail in the left part, with more extreme information. This characteristic makes the expectile regression model, which is more sensitive to the left tail, a suitable tool to measure tail risk.
All Augmented Dickey–Fuller (ADF) test p-values for the return distributions of the four stock indices are greater than 0.1. This suggests that the return series are stationary and that the expectile regression model can be effectively applied.
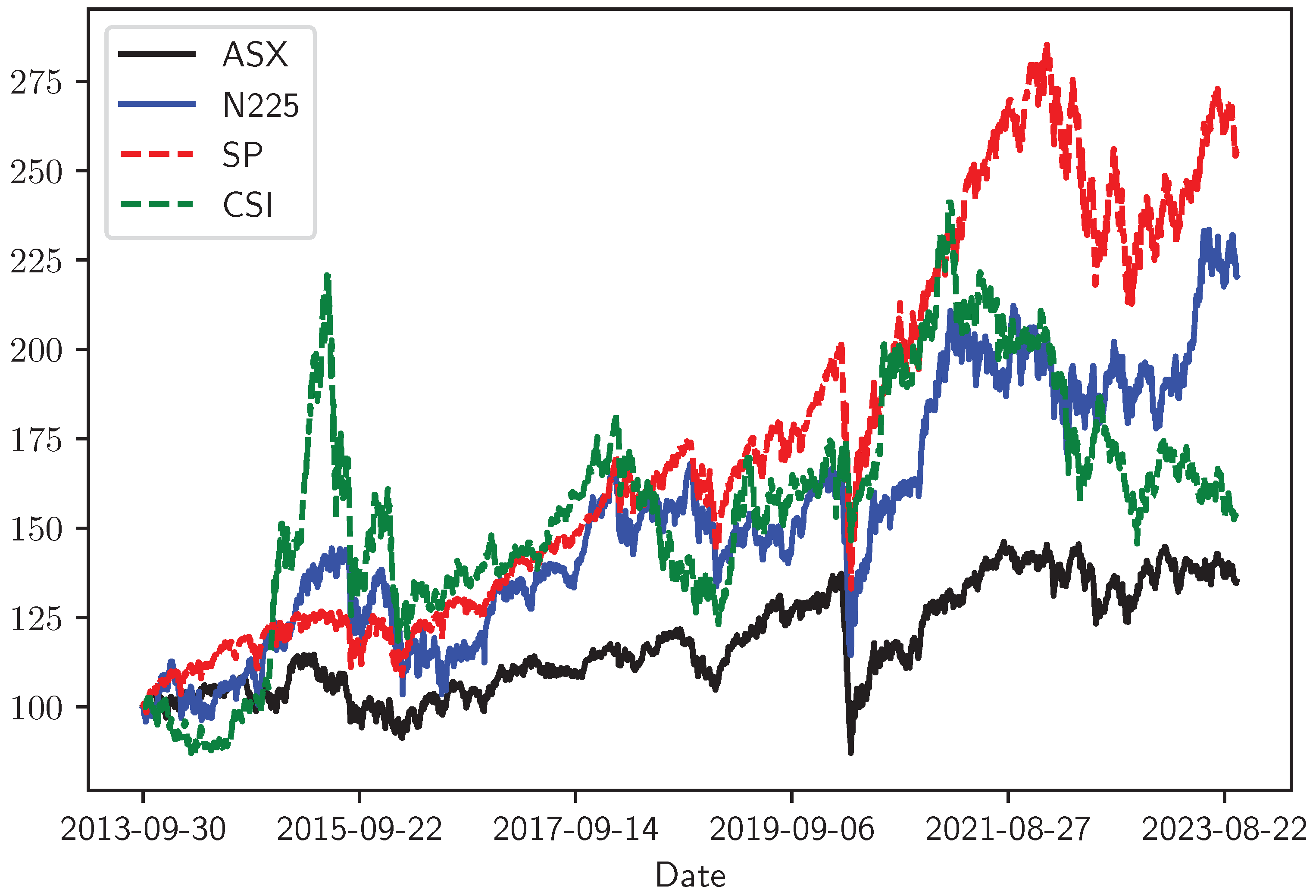
For illustrative purposes, Figure 1 displays the stock indices during the sample period from 1 October 2013, to 30 September 2023, with values normalized such that the value on 1 October 2013, is set to 100. It is evident that all indexes experienced significant fluctuations during the COVID-19 crisis.
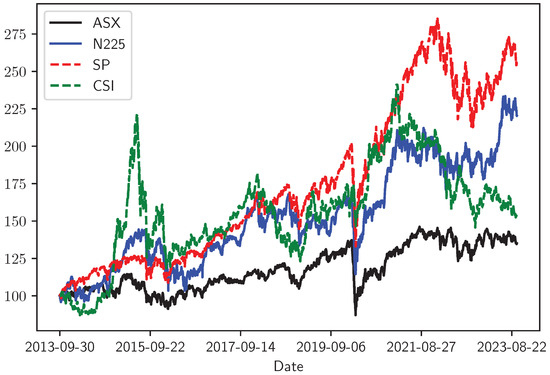
Figure 1.
The evolution of the stock indices during the sample period.
4. Empirical Results
In this section, we present the empirical results and analysis of our study. We begin by examining the Expectile based Value at Risk (EVaR) for each stock market and then move on to assessing the influence of downside risk between the Australian and Japanese markets. We also analyze the impact of lagged returns and common risk factors on the EVaR and Expected Shortfall (ES) estimates.
4.1. The Effect of Risk Factors
For the expectile regression, the corresponding is calculated according to Equation (6) for a given (1% or 5% in this paper). The final expectile regression results for the ASX 200 and Nikkei 225 indexes are reported in Table 2.

Table 2.
The expectile regression results for ASX 200 and Nikkei 225 indices. “s.e.” denotes the standard error, ***, **, * label significance at 1%, 5%, and 10% levels, respectively.
4.1.1. Results for ASX 200 Index
Regarding the expectile regression results for ASX 200, several observations can be made. First, the 0.01 expectile is significantly affected by and with coefficients of −0.7581 and 0.6885, respectively. The 0.05 expectile is also affected by and with the coefficients of −0.5408 and 0.4340, respectively. As for the tail risk , the results suggest that negative returns of the ASX 200 index two business days before tend to indicate a lower tail risk, which results in higher EVaR. Conversely, positive returns tend to suggest higher tail risk and lower EVaR. These findings imply that ASX 200 tends to correct overreactions in terms of downside tail risk.
Second, the effect of negative returns of the S&P 500 index previous day is significant on both the 0.01 and 0.05 expectile with the coefficients of 0.7614 and 0.6062, respectively, while the CSI 300 index is not.
Third, the effect of the Nikkei 225 index previous day is not significant. The results indicate that the transmission of risk from Japanese stock markets to Australian ones can be limited.
4.1.2. Results for Nikkei 225 Index
Regarding the Nikkei 225 index, Table 2 reveals a few interesting findings as well. First, both the 0.01 and 0.05 expectile is significantly affected by the lagged and .
For the tail risk , the results indicate that the negative past returns () of the Nikkei 225 index tends to suggest a lower tail risk and push the EVaR upward while the positive past returns () tends to suggest a higher tail risk and push the EVaR downward. However, the negative past returns or positive past returns of lag 1 do not have any significant effect.
Second, the effect of the negative ASX 200 index previous day is significant, at 5% level on the 0.01 expectile , and at 1% level on the 0.05 expectile . The coefficients, 0.5495 for 0.01 expectile, and 0.4419 for 0.05 expecitle, are positive. This implies that the negative return on ASX 200 previous day tends to result in reduction in EvaR. This contrasts to the findings in Section 4.1.1 and implies that the effect of ASX 200 on Nikkei 225 is stronger than the other way round in terms of downside tail risk.
Third, the negative return on the SP 500 index previous day is significant (at 1% level) on the 0.01 expectile with the coefficient of 0.6437 and the 0.05 expectile with the coefficient of 0.5785. The CSI is not significant here.
4.1.3. The Comparison
Comparing the results of the ASX 200 and Nikkei 225, it can be concluded that the effect of Australian stock market on Japanese ones can be stronger than the other way round in terms of downside tail risk, reflecting the economic integration between Australia and Japan in the form of trade linkages and foreign direct investment. This finding is in line with the existing literature, such as Shamsuddin and Kim (2003).
It can be observed that the Nikkei 225 reacts less to past positive returns compared to the ASX 200. This result confirms the existence of a difference between the two stock markets in the mechanism of downside risk transmission, even though they are highly integrated.
4.2. EVaR Estimates
In order to test the accuracy of the model, the EVaR was estimated to analyze the past risk conditions of each stock index.
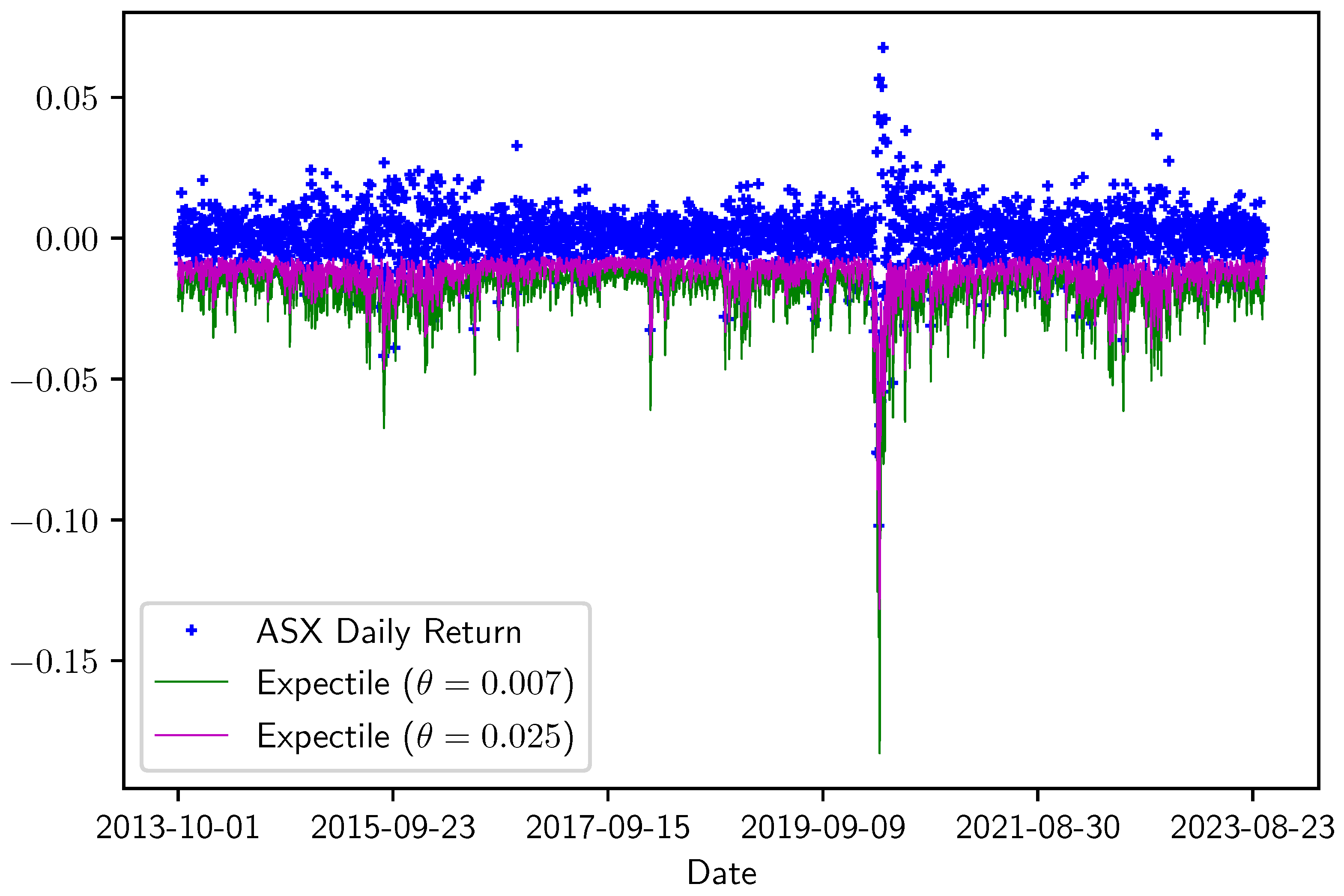
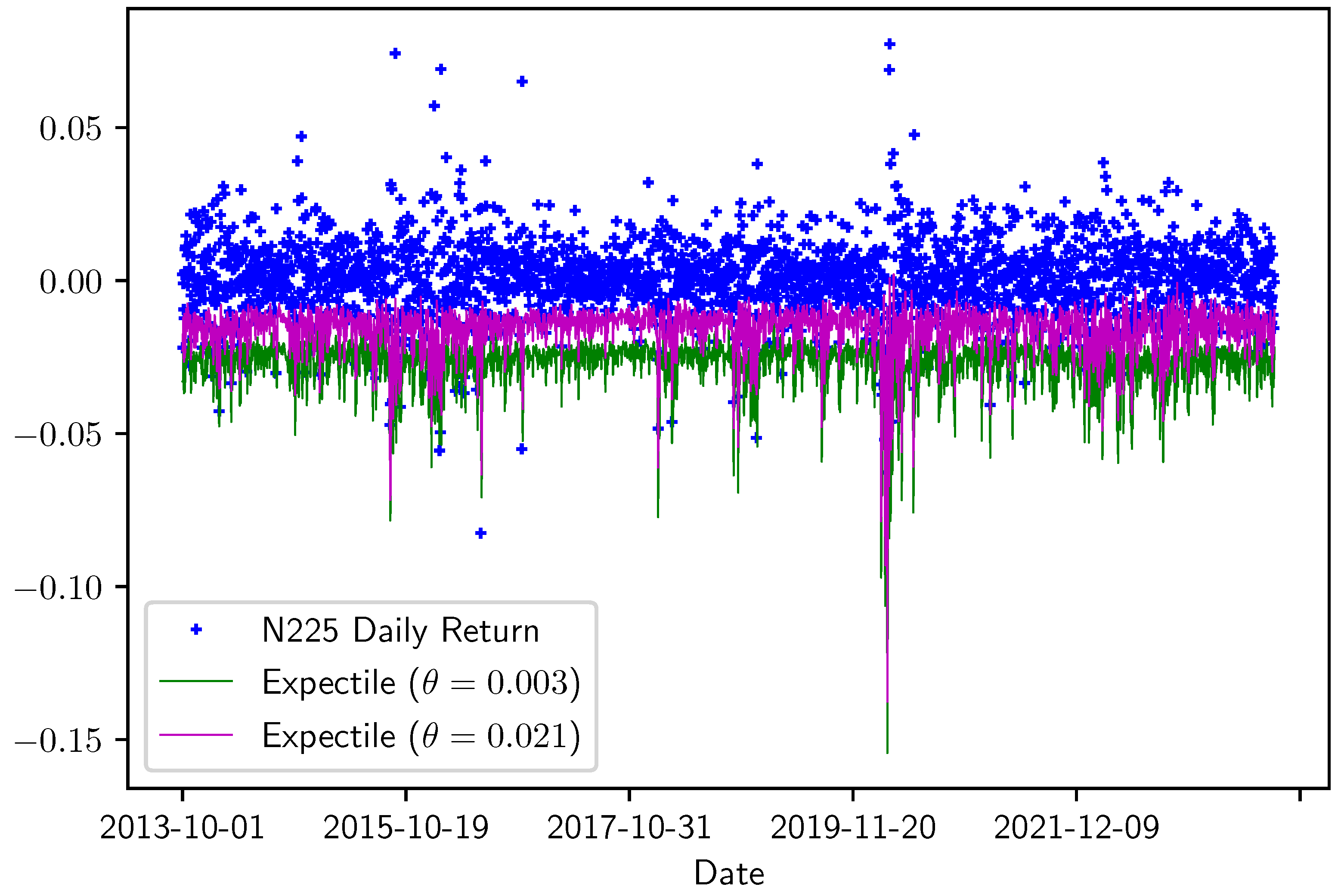
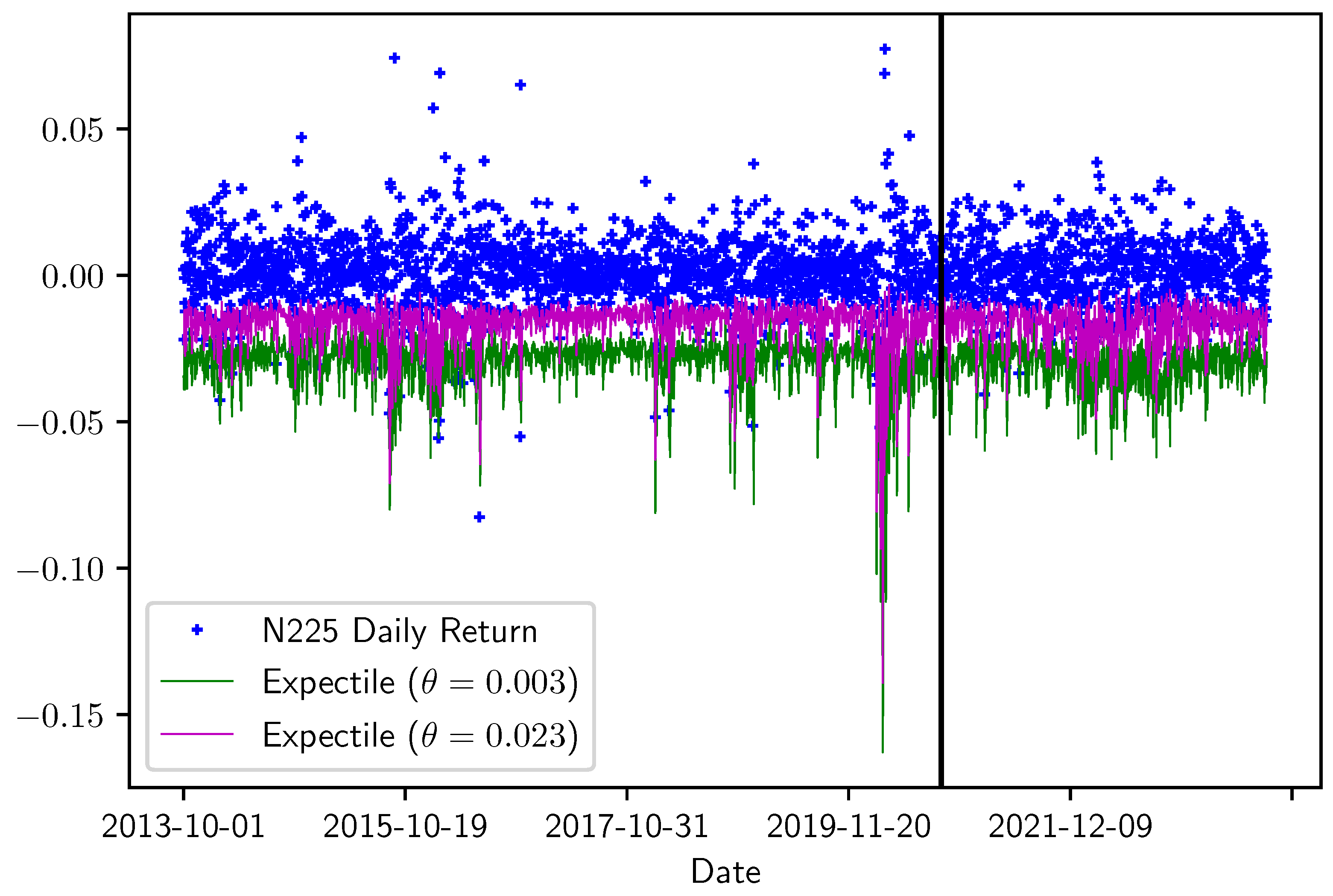
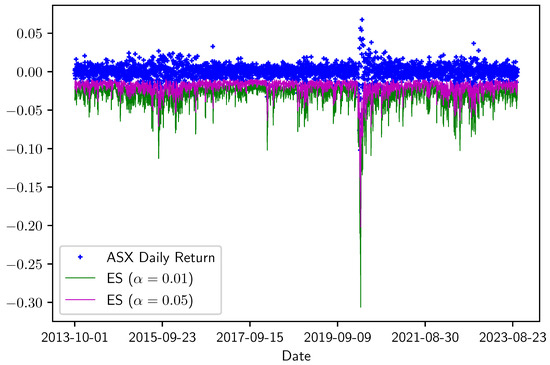
Figure 2 and Figure 3 show the in-sample for ASX 200 and Nikkei 225, respectively. Both figures display a line that covers mostly negative returns, and for both ASX 200 and Nikkei 225, the effectiveness of the model under 0.01 quantile is better than the 0.05 quantile level.
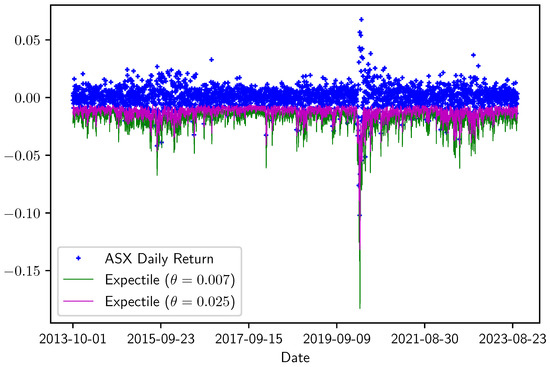
Figure 2.
In-sample of ASX 200 index for and . In-sample period: 1 October 2012 to 30 September 2023.
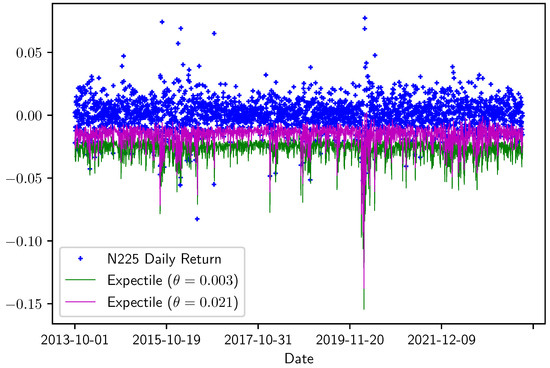
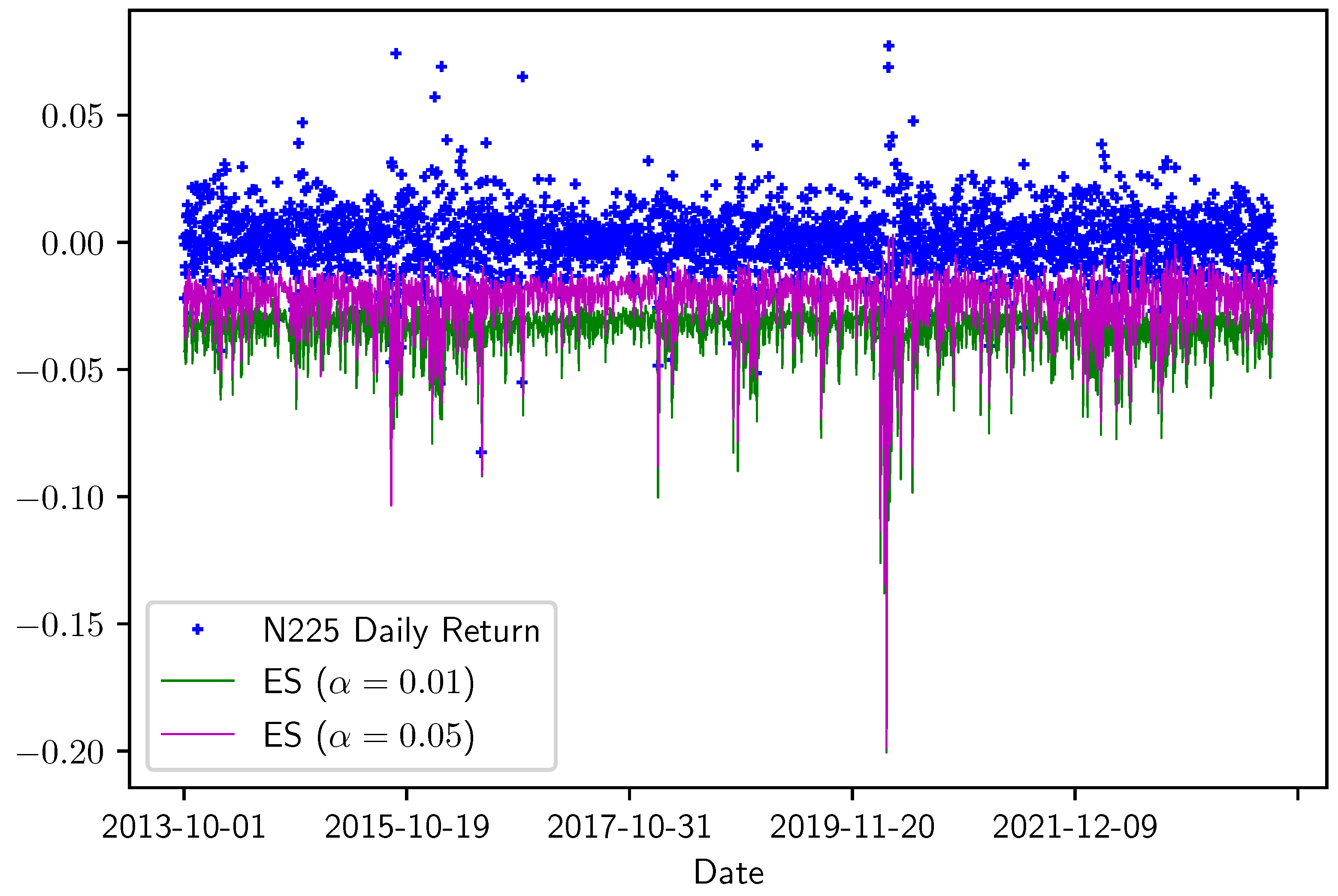
Figure 3.
In-sample of Nikkei 225 index for and . In-sample period: 1 October 2012 to 30 September 2023.
Interestingly, the EVaR of either index is larger during periods of high volatility in the return series, such as during the Chinese stock market crash in 2015 or at the beginning of the COVID-19 crisis in early 2020. However, the EVaR of Nikkei 225 is also high during a few other periods.
A few observations can be made from Table 3. The mean EVaR values of the ASX 200 index are 0.0186 and 0.0131 under 0.01 and 0.05 quantiles, respectively. These estimates suggest that the potential maximum loss of investing in the ASX 200 index one day ahead with 99% and 95% probabilities is 1.87% and 1.31%, respectively.

Table 3.
EVaR and the tail probability of ASX 200 and Nikkei 225 indices.
The mean EVaR values of the Nikkei 225 index are 0.0276 and 0.0163 under 0.01 and 0.05 quantiles, respectively. These estimates suggest that the potential maximum loss of investing in the Nikkei 225 index one day ahead with 99% and 95% probabilities is 2.76% and 1.63%, respectively.
The mean EVaR values of the ASX 200 index under two quantiles are smaller than those of the Nikkei 225 index, while the maximum EVaR values of the ASX 200 index under 0.01 expectiles is larger than that of the Nikkei 225 index.
4.3. Out-of-Sample Estimation
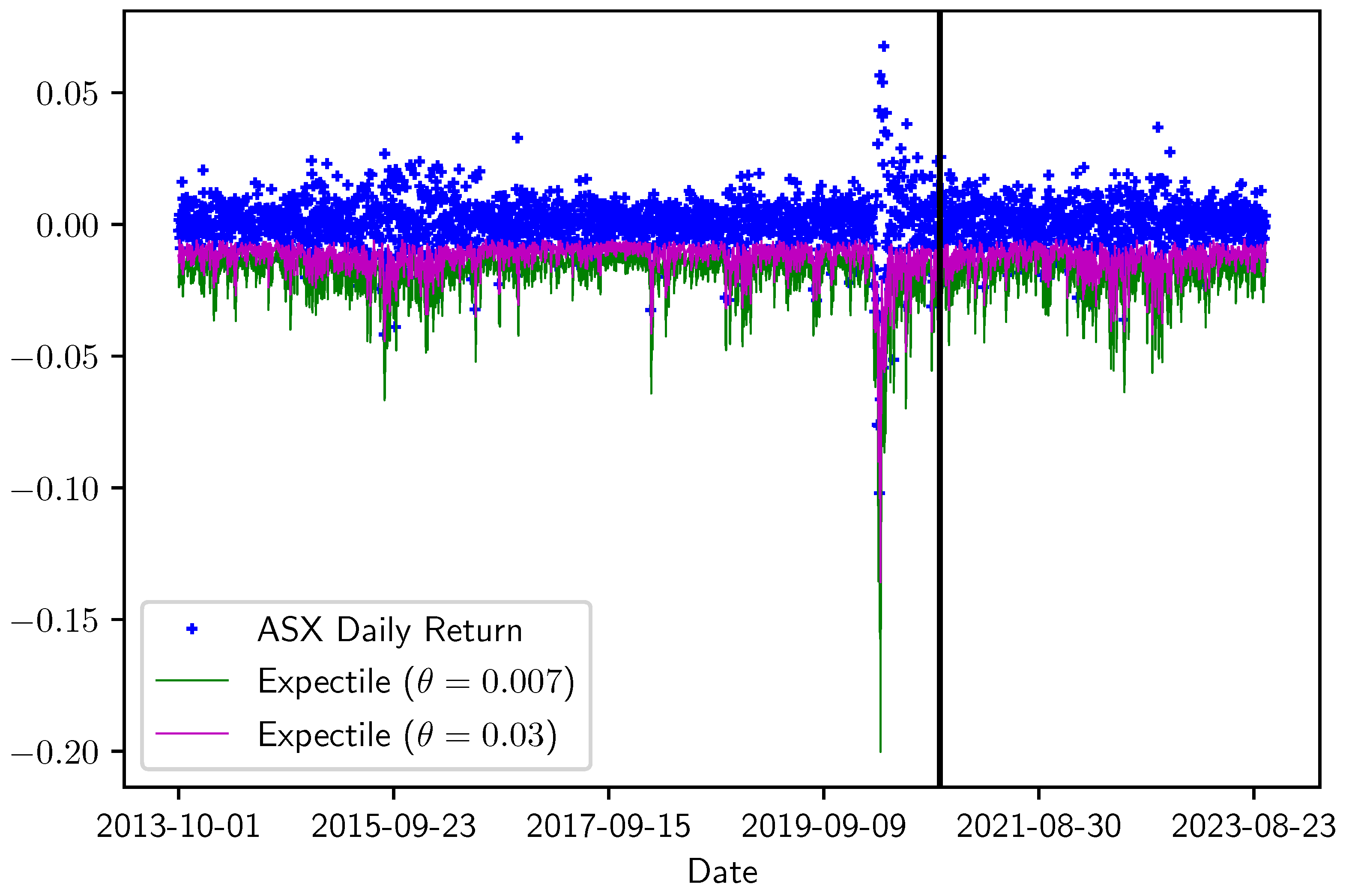
To verify the robustness of the expectile regression results, we compare the in-sample and out-of-sample estimates. We use data from a seven-year in-sample period (1 October 2013, to 30 September 2020) to estimate the parameter and obtain the expectiles for both in-sample and out-of-sample periods (1 October 2020, to 30 September 2023).
Table 4 compares the numbers of exceedances over the estimated expectile. It indicates that the ratio (or tail probability) remains largely consistent between the in-sample and out-of-sample periods, except for the Nikkei 225 with , where the out-of-sample estimate appears biased toward the conservative side.

Table 4.
Comparison of the number of exceedances over the estimated expectiles between in-sample and out-of -sample. In-sample period: 1 October 2013 to 30 September 2020. Out-of-sample period: 1 October 2020 to 30 September 2023.
Figure 4 and Figure 5 display the in-sample and out-of-sample estimates of expectiles and realized returns.
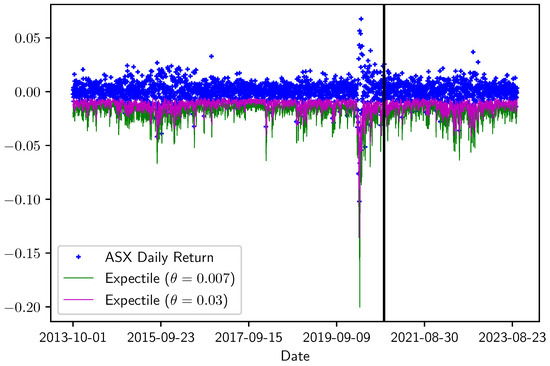
Figure 4.
In-sample period: 1 October 2013 to 30 September 2020, the (left) side of the bar, and out-of-sample period: 1 October 2020 to 30 September 2023, the (right) side of the bar.
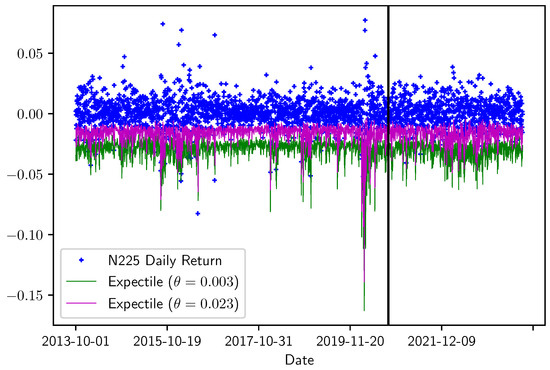
Figure 5.
In-sample period: 1 October 2013 to 30 September 2020, the (left) side of the bar, and out-of-sample period: 1 October 2020 to 30 September 2023, the (right) side of the bar.
4.4. ES Estimates
Let us now consider the popular ES measure for evaluating the expected loss when investing in ASX 200 and Nikkei 225. Table 5 reports the mean and max ES values, as well as the tail probabilities under 1% and 5% probabilities.

The in-sample ES values for the ASX 200 index suggest that the mean risk when investing in it one day ahead is 3.12% and 2.01% with 1% and 5% probabilities, respectively. In contrast, the in-sample ES values for the Nikkei 225 index indicate that the mean risk is 3.58% and 2.34% with 1% and 5% probabilities, respectively. Thus, on average, the risk of investing in Nikkei 225 is higher than that of ASX 200. These results further confirm the suitability of the expectile model.
Additionally, the lower tail probability values in Table 5 indicate that our model is highly accurate.
5. Concluding Remarks
This study investigates the downside risk in Australian and Japanese stock markets and examines whether the two markets influence each other in terms of downside risk. To accomplish this, we use a novel approach based on the expectile regression model that accounts for both lagged returns and macroeconomic risk factors to calculate the EVaR of the ASX 200 index and Nikkei 225 index and evaluate their mutual influence.
Our analysis utilizes a ten-year sample (October 2013 to September 2023) of daily returns of the ASX 200 index and Nikkei 225 index. The EVaRs for both ASX 200 index and Nikkei 225 index are significantly influenced by negative lagged returns and returns from the S&P 500 index, while those of CSI 300 index is not significant. Moreover, the EVaR and ES of the ASX 200 index are on average smaller than those of the Nikkei 225 index.
Our findings suggest that both the Australian and Japanese stock markets are affected by their past development and international stock markets. Furthermore, our analysis indicates that the ASX 200 index has a significant impact on Nikkei 225 index downside tail risk, consistent with their close economic relationship. However, the ASX 200 index responds less to past negative or positive returns than the Nikkei 225 index. Our study’s outcomes can have practical implications for investment and risk management in the two stock markets. In risk management practice, the measure of downside tail risk is often linked to the required capital level. Consequently, our findings can significantly enhance the effectiveness of the capital allocation policies.
Finally, it is worth noting that this research offers avenues for extension in several directions. First, we note that this research has a narrow focus, and it may be more meaningful to consider pairs of many other stock markets. Thus, we can broaden the scope by investigating other stock markets and commodity markets. Second, we can enhance our research methodology by, for example, identifying and accounting for structural breaks in the markets. Given the focus of this paper, we defer these aspects to future research.
Author Contributions
Conceptualization, S.L.; methodology, S.L. and K.M.; software, K.M.; validation, S.L. and K.M.; formal analysis, S.L. and K.M.; data curation, S.L. and K.M.; writing—original draft preparation, S.L. and K.M.; writing—review and editing, S.L. and K.M.; visualization, K.M.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI #20K01765.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Only publicly available market data were used in the study.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | https://www.asx.com.au/about, accessed on 10 September 2023. |
| 2 | https://www.bis.org/bcbs/basel3.htm, accessed on 10 September 2023. |
References
- Abdous, Belkacem, and Bruno Remillard. 1995. Relating quantiles and expectiles under weighted-symmetry. Annals of the Institute of Statistical Mathematics 47: 371–84. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Markus K. Brunnermeier. 2009. CoVaR. Technical Report 348. New York: Federal Reserve Bank of New York. [Google Scholar]
- Anjum, Hassan, and Farooq Malik. 2020. Forecasting risk in the us dollar exchange rate under volatility shifts. The North American Journal of Economics and Finance 54: 101257. [Google Scholar] [CrossRef]
- Asgharian, Hossein, and Christoffer Bengtsson. 2006. Jump spillover in international equity markets. Journal of Financial Econometrics 4: 167–203. [Google Scholar] [CrossRef]
- Asgharian, Hossein, and Marcus Nossman. 2011. Risk contagion among international stock markets. Journal of International Money and Finance 30: 22–38. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. 2021a. International Investment Position, Australia: Supplementary Statistics. Canberra: Australian Bureau of Statistics. [Google Scholar]
- Australian Bureau of Statistics. 2021b. International Trade in Goods and Services, Australia. Canberra: Australian Bureau of Statistics. [Google Scholar]
- Bae, Kee-Hong, G. Andrew Karolyi, and Reneé M. Stulz. 2003. A new approach to measuring financial contagion. Review of Financial Studies 16: 717–63. [Google Scholar] [CrossRef]
- Baele, Lieven. 2005. Volatility spillover effects in european equity markets. Journal of Financial and Quantitative Analysis 40: 373–401. [Google Scholar] [CrossRef]
- Bassett, Gilbert W., Jr., Roger Koenker, and Gregory Kordas. 2004. Pessimistic portfolio allocation and choquet expected utility. Journal of Financial Econometrics 2: 477–92. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, Nikitas Pittis, and Nicola Spagnolo. 2006. Volatility transmission and financial crises. Journal of Economics and Finance 30: 376–90. [Google Scholar] [CrossRef]
- Christiansen, Charlotte, and Angelo Ranaldo. 2009. Extreme coexceedances in new eu member states’ stock markets. Journal of Banking and Finance 33: 1048–57. [Google Scholar] [CrossRef]
- De Rossi, Giuliano, and Andrew Harvey. 2009. Quantiles, expectiles, and splines. Journal of Econometrics 152: 179–85. [Google Scholar] [CrossRef]
- Du, Zaichao, and Juan Carlos Escanciano. 2016. Backtesting expected shortfall: Accounting for tail risk. Management Science 63: 940–58. [Google Scholar] [CrossRef]
- Efron, Bradley. 1991. Regression percentiles using asymmetric squared error loss. Statistica Sinica 1: 93–125. [Google Scholar]
- Embrechts, Paul, Giovanni Puccetti, Ludger Rüschendorf, Ruodu Wang, and Antonela Beleraj. 2014. An academic response to basel 3.5. Risks 2: 25–48. [Google Scholar] [CrossRef]
- Fissler, Tobias, Johanna F. Ziegel, and Tilmann Gneiting. 2016. Expected shortfall is jointly elicitable with value at risk—Implications for backtesting. Risk, 58–61. [Google Scholar]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Gneiting, Tilmann. 2011. Making and evaluating point forecasts. Journal of the American Statistical Association 106: 746–62. [Google Scholar] [CrossRef]
- Gordy, Michael B., and Sandeep Juneja. 2010. Nested simulation in portfolio risk measurement. Management Science 56: 1833–48. [Google Scholar] [CrossRef]
- Hartmann, Philipp, Stefan Straetmans, and C. G. de Vries. 2004. Asset market linkages in crisis periods. The Review of Economics and Statistics 86: 313–26. [Google Scholar] [CrossRef]
- Hong, Yongmiao, Yanhui Liu, and Shouyang Wang. 2009. Granger causality in risk and detection of extreme risk spillover between financial markets. Journal of Econometrics 150: 271–87. [Google Scholar] [CrossRef]
- Huang, Dashan, Shushang Zhu, Frank J. Fabozzi, and Masao Fukushima. 2010. Portfolio selection under distributional uncertainty: A relative robust cvar approach. European Journal of Operational Research 203: 185–94. [Google Scholar] [CrossRef]
- Hult, Henrik, Filip Lindskog, Ola Hammarlid, and Carl-Johan Rehn. 2012. Risk and Portfolio Analysis: Principles and Methods. New York: Springer. [Google Scholar]
- Hussain, Saiful Izzuan, and Steven Li. 2018. The dependence structure between chinese and other major stock markets using extreme values and copulas. International Review of Economics and Finance 56: 421–37. [Google Scholar] [CrossRef]
- Jones, M. Chris. 1994. Expectiles and m-quantiles are quantiles. Statistics Letters 20: 149–53. [Google Scholar] [CrossRef]
- Jorion, Philippe. 2000. Value at Risk: The New Benchmark for Managing Financial Risk. Chicago: McGraw-Hill. [Google Scholar]
- Kou, Steven, and Xianhua Peng. 2016. On the measurement of economic tail risk. Operations Research 64: 1056–72. [Google Scholar] [CrossRef]
- Kuan, Chung-Ming, Jin-Huei Yeh, and Yu-Chin Hsu. 2009. Assessing value at risk with care, the conditional autoregressive expectile models. Journal of Econometrics 150: 261–70. [Google Scholar] [CrossRef]
- Liao, Lina, Cheolwoo Park, and Hosik Choi. 2019. Penalized expectile regression: An alternative to penalized quantile regression. Annals of the Institute of Statistical Mathematics 71: 409–38. [Google Scholar] [CrossRef]
- Liu, Lu. 2014. Extreme downside risk spillover from the united states and japan to asia-pacific stock markets. International Review of Financial Analysis 33: 39–48. [Google Scholar] [CrossRef]
- Li, Yanan, and David E. Giles. 2015. Modelling volatility spillover effects between developed stock markets and asian emerging stock markets. International Journal of Finance and Economics 20: 155–77. [Google Scholar] [CrossRef]
- Lwin, Khin T., Rong Qu, and Bart L. MacCarthy. 2017. Mean-var portfolio optimization: A nonparametric approach. European Journal of Operational Research 260: 751–66. [Google Scholar] [CrossRef]
- Meng, Xiaochun, and James W. Taylor. 2020. Estimating value-at-risk and expected shortfall using the intraday low and range data. European Journal of Operational Research 280: 191–202. [Google Scholar] [CrossRef]
- Newey, Whitney K., and James L. Powell. 1987. Asymmetric least squares estimation and testing. Econometrica 55: 819–47. [Google Scholar] [CrossRef]
- Paramati, Sudharshan Reddy, Rakesh Gupta, and Kishore Tandon. 2016. Dynamic analysis of time-varying correlations and cointegration relationship between australia and frontier equity markets. International Journal of Business and Emerging Markets 8: 121–45. [Google Scholar] [CrossRef]
- Patra, Saswat. 2021. Revisiting value-at-risk and expected shortfall in oil markets under structural breaks: The role of fat-tailed distributions. Energy Economics 101: 105452. [Google Scholar] [CrossRef]
- Patton, Andrew J., Johanna F. Ziegel, and Rui Chen. 2019. Dynamic semiparametric models for expected shortfall (and value-at-risk). Journal of Econometrics 211: 388–413. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking and Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Rockafellar, R. Terry, Johannes O. Royset, and Sofia I. Miranda. 2014. Superquantile regression with applications to buffered reliability, uncertainty quantification, and conditional value-at-risk. European Journal of Operational Research 234: 140–54. [Google Scholar] [CrossRef]
- Shamsuddin, Abul F. M., and Jae H. Kim. 2003. Integration and interdependence of stock and foreign exchange markets: An australian perspective. Journal of International Financial Markets, Institutions and Money 13: 237–54. [Google Scholar] [CrossRef]
- Tasche, Dirk. 2002. Expected shortfall and beyond. Journal of Banking and Finance 26: 1519–33. [Google Scholar] [CrossRef]
- Taylor, James W. 2008. Estimating value at risk and expected shortfall using expectiles. Journal of Financial Econometrics 6: 231–52. [Google Scholar] [CrossRef]
- Taylor, James W. 2019. Forecasting value at risk and expected shortfall using a semi-parametric approach based on the asymmetric laplace distribution. Journal of Business and Economic Statistics 37: 121–33. [Google Scholar] [CrossRef]
- Vo, Xuan Vinh, and Thi Tuan Anh Tran. 2020. Modelling volatility spillovers from the us equity market to asean stock markets. Pacific-Basin Finance Journal 59: 101246. [Google Scholar] [CrossRef]
- Xie, Shangyu, Yong Zhou, and Alan T. K. Wan. 2014. A varying coefficient expectile model for estimating value at risk. Journal of Business and Economic Statistics 32: 576–92. [Google Scholar] [CrossRef]
- Xu, Qifa, Xi Liu, Cuixia Jiang, and Keming Yu. 2016. Nonparametric conditional autoregressive expectile model via neural network with applications to estimating financial risk. Applied Stochastic Models in Business and Industry 32: 882–908. [Google Scholar] [CrossRef]
- Yao, Qiwli, and Howell Tong. 1996. Asymmetric least squares regression and estimation: A nonparametric approach. Journal of Nonparametric Statistics 6: 273–92. [Google Scholar] [CrossRef]
- Yao, Yinhong, Jianping Li, and Xiaolei Sun. 2021. Measuring the risk of chinese fintech industry: Evidence from the stock index. Finance Research Letters 39: 101564. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun, and Shu-Jiao Ma. 2019. How to effectively estimate the time-varying risk spillover between crude oil and stock markets? evidence from the expectile perspective. Energy Economics 84: 104562. [Google Scholar] [CrossRef]
- Zhong, Yi, and Jiapeng Liu. 2021. Correlations and volatility spillovers between china and southeast asian stock markets. The Quarterly Review of Economics and Finance 81: 57–69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).