Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand
Abstract
1. Introduction
2. Materials and Methods
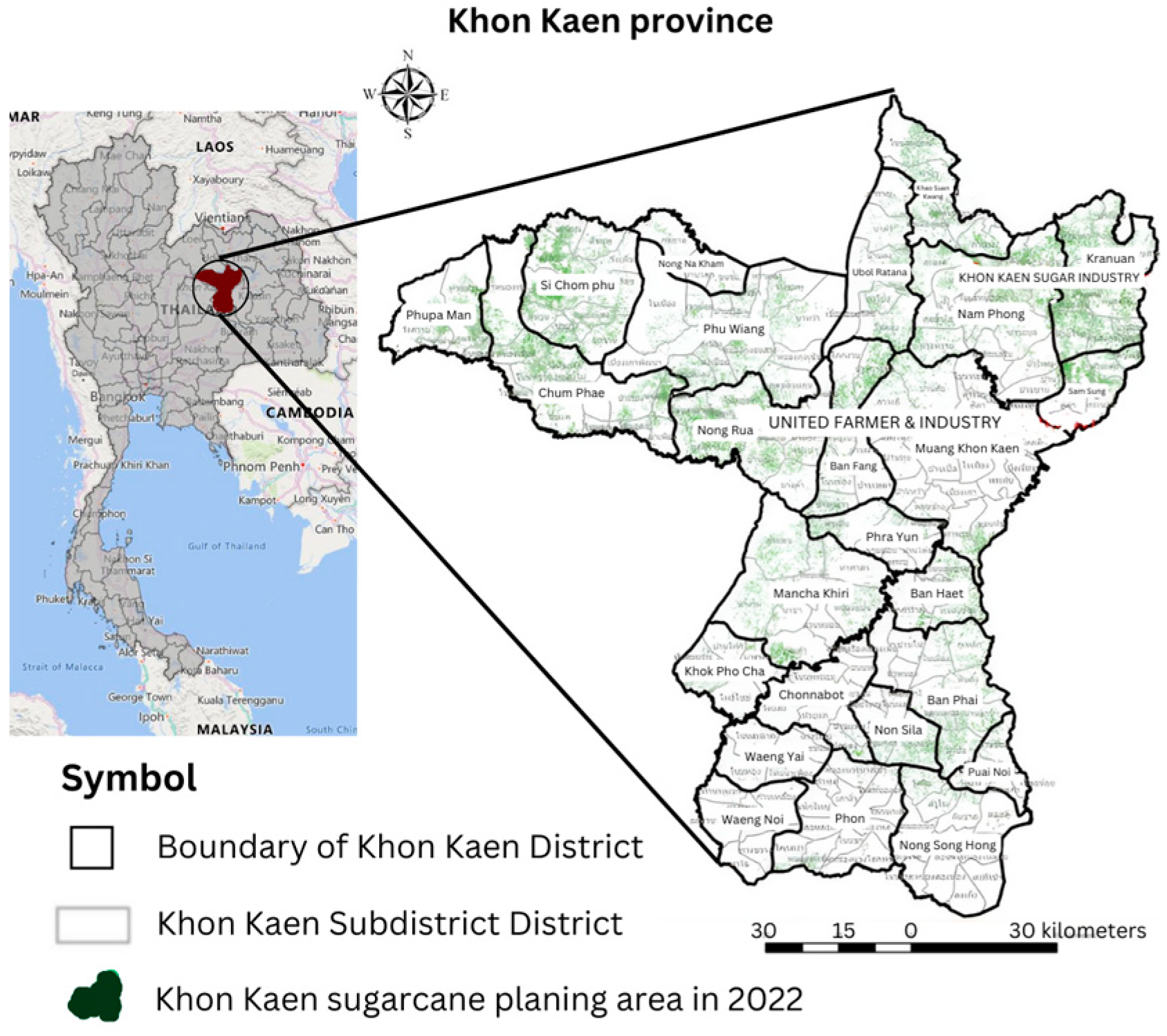
2.1. Study Area and Panel Dataset
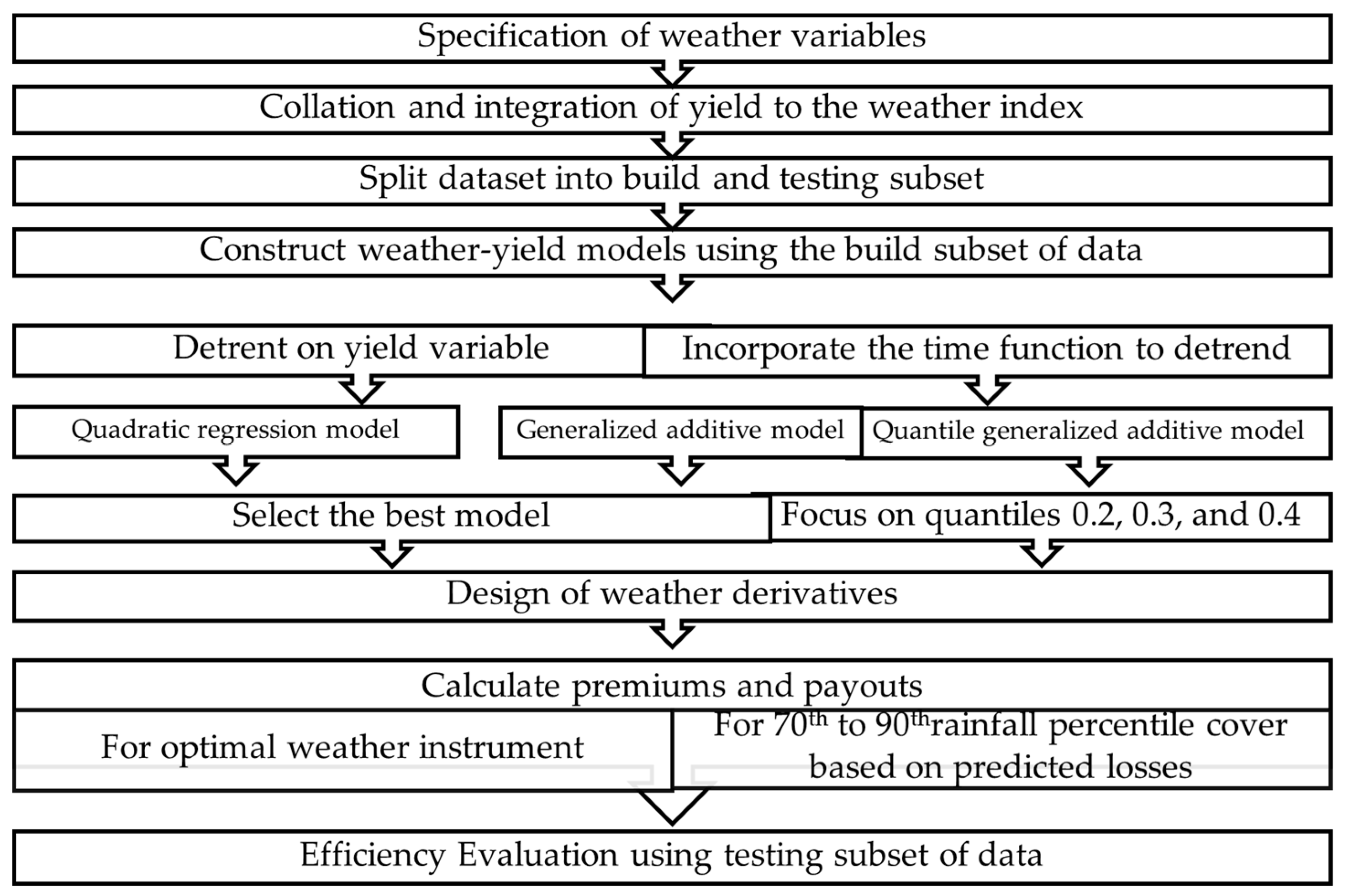
2.2. Conceptual Framework
2.2.1. Step 1: Specification of Weather Variables
2.2.2. Step 2: Integration of Data and Data Preparation
2.2.3. Steps 3–5: Regression Model Linking Yield to Climate Indices
2.2.4. Steps 6 and 7: Design of Weather Derivatives and Premium Estimation
Selection of Contract Parameters
2.2.5. Step 8: Efficiency Analysis
3. Results
3.1. Quadratic Regression Modeling Results
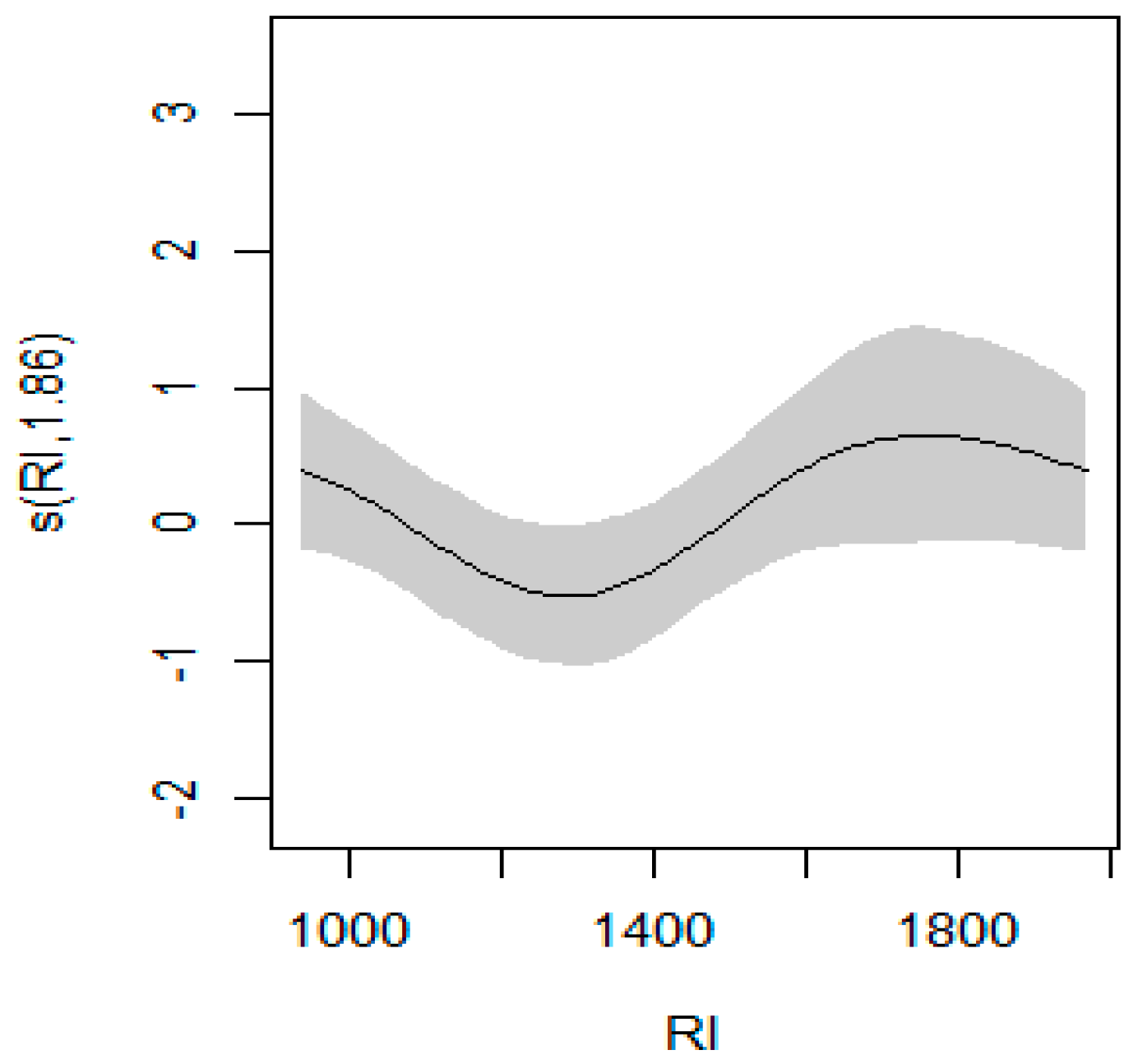
3.2. GAM Regression Modeling Results
3.3. QGAM Regression Modeling Results
3.4. Estimated Insurance Premiums and Revenues
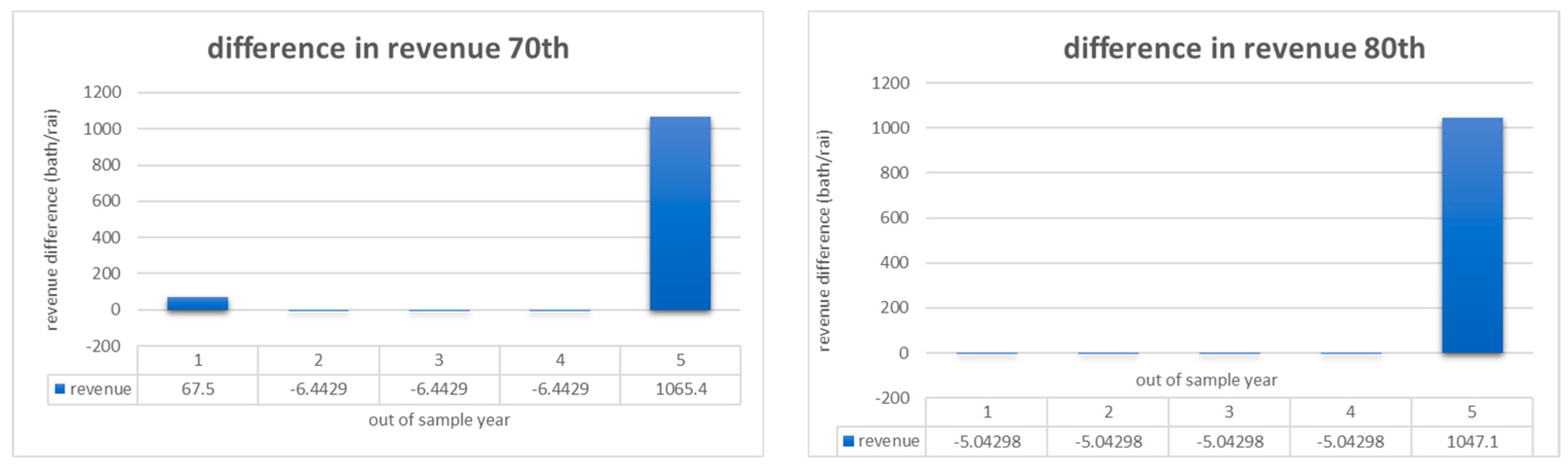
3.5. Efficiency Analysis of Weather Index
4. Discussion
4.1. Crop Yield Models and Efficiency of Weather Index Insurance for Sugarcane
4.2. Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amnuaylojaroen, Teerachai, Pavinee Chanvichit, Radshadaporn Janta, and Vanisa Surapipith. 2021. Projection of Rice and Maize Productions in Northern Thailand under Climate Change Scenario RCP8.5. Agriculture 11: 23. [Google Scholar] [CrossRef]
- Bucheli, Janic, Tobias Dalhaus, and Robert Finger. 2022. Temperature effects on crop yields in heat index insurance. Food Policy 107: 102214. [Google Scholar] [CrossRef]
- Carvalho, André Luiz de, Rômulo Simões Cezar Menezes, Ranyére Silva Nóbrega, Alexandre de Siqueira Pinto, Jean Pierre Henry Balbaud Ometto, Celso von Randow, and Angélica Giarolla. 2015. Impact of climate changes on potential sugarcane yield in Pernambuco, northeastern region of Brazil. Renewable Energy 78: 26–34. [Google Scholar] [CrossRef]
- Conradt, Sarah, Robert Finger, and Martina Spörri. 2015. Flexible weather index-based insurance design. Climate Risk Management 10: 106–17. [Google Scholar] [CrossRef]
- Fasiolo, Matteo, Simon N. Wood, Margaux Zaffran, Raphaël Nedellec, and Yannig Goude. 2020. qgam: Bayesian non-parametric quantile regression modelling in R. arXiv arXiv:2007.03303. [Google Scholar]
- Glaz, Barry, and Sarah E. Lingle. 2012. Flood duration and time of flood onset effects on recently planted sugarcane. Agronomy Journal 104: 575–83. [Google Scholar] [CrossRef]
- Gomathi, Raju, P. N. Gururaja Rao, Kookal Chandran, and A. Selvi. 2015. Adaptive responses of sugarcane to waterlogging stress: An over view. Sugar Tech 17: 325–38. [Google Scholar] [CrossRef]
- Greenland, David. 2005. Climate Variability and Sugarcane Yield in Louisiana. Journal of Applied Meteorology 44: 1655–66. [Google Scholar] [CrossRef]
- Johari, Sarah Nadirah Mohd, Nur Ainina Hanun Mat Asdi, Nur Suhaila Othman, and Sri Dania Qistina Anifruzaidi. 2022. Weather Index Based Microinsurance for Agriculture Industry. IOP Conference Series: Earth and Environmental Science 1019: 012045. [Google Scholar] [CrossRef]
- Kanchai, Thitipong, Nahatai Tepkasetkul, Tippatai Pongsart, and Watcharin Klongdee. 2023. Rainfall Data Fitting Based on An Improved Mixture Cosine Model with Markov Chain. Wseas Transactions on Information Science and Applications 20: 28–33. [Google Scholar] [CrossRef]
- Kath, Jarrod, Shahbaz Mushtaq, Ross Henry, Adewuyi Adeyinka, and Roger Stone. 2018. Index insurance benefits agricultural producers exposed to excessive rainfall risk. Weather and Climate Extremes 22: 1–9. [Google Scholar] [CrossRef]
- Kath, Jarrod, Shahbaz Mushtaq, Ross Henry, Adewuyi Ayodele Adeyinka, Roger Stone, Torben Marcussen, and Louis Kouadio. 2019. Spatial variability in regional scale drought index insurance viability across Australia’s wheat growing regions. Climate Risk Management 24: 13–29. [Google Scholar] [CrossRef]
- Kath, Jarrod, Vivekananda Mittahalli Byrareddy, Shahbaz Mushtaq, Alessandro Craparo, and Mario Porcel. 2021. Temperature and rainfall impacts on robusta coffee bean characteristics. Climate Risk Management 32: 100281. [Google Scholar] [CrossRef]
- Lobell, David B., and Christopher B. Field. 2007. Global scale climate–crop yield relationships and the impacts of recent warming. Environmental Research Letters 2: 014002. [Google Scholar] [CrossRef]
- Lobell, David B., and Marshall B. Burke. 2010. On the use of statistical models to predict crop yield responses to climate change. Agricultural and Forest Meteorology 150: 1443–52. [Google Scholar] [CrossRef]
- Mali, S. C., Prashant Kumar Shrivastava, and Harish S. Thakare. 2014. Impact of weather changes on sugarcane production. Research in Environment and Life Sciences 7: 243–46. [Google Scholar]
- Martin, Steven W., Barry J. Barnett, and Keith H. Coble. 2001. Developing and pricing precipitation insurance. Journal ofAgricultural and Resource Economics 26: 261–74. [Google Scholar]
- Office of Agricultural Economics. 2022. Available online: https://www.oae.go.th/ (accessed on 15 July 2022).
- Office of the Cane and Sugar Board. 2022. Available online: http://www.ocsb.go.th/th/home/index.php (accessed on 15 July 2022).
- Pignède, Edouard, Philippe Roudier, Arona Diedhiou, Vami Hermann N’Guessan Bi, Arsène T. Kobea, Daouda Konaté, and Crépin Bi Péné. 2021. Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data. Atmosphere 12: 1459. [Google Scholar] [CrossRef]
- Pipitpukdee, Siwabhorn, Witsanu Attavanich, and Somskaow Bejranonda. 2020. Climate Change Impacts on Sugarcane Production in Thailand. Atmosphere 11: 408. [Google Scholar] [CrossRef]
- Sattar, Abdus, S. A. Khan, and Manish Kumar. 2014. Crop Weather Relationship and Cane Yield Prediction of Sugarcane in Bihar. Journal of Agricultural Physics 14: 150–55. [Google Scholar]
- Shirsath, Paresh, Shalika Vyas, Pramod Aggarwal, and Kolli N. Rao. 2019. Designing weather index insurance of crops for the increased satisfaction of farmers, industry and the government. Climate Risk Management 25: 100189. [Google Scholar] [CrossRef]
- Singh, Harpinder, Sudhir Kumar Mishra, Kuldeep Singh, Kulvir Singh, R. K. Pal, K. K. Gill, and P. K. Kingra. 2021. Simulating the impact of climate change on sugarcane production in Punjab. Journal of Agrometeorology 23: 292–98. [Google Scholar] [CrossRef]
- Sinnarong, Nirote, Chi-Chung Chen, Bruce McCarl, and Bao-Linh Tran. 2019. Estimating the potential effects of climate change on rice production in Thailand. Paddy and Water Environment 17: 761–69. [Google Scholar] [CrossRef]
- Sinnarong, Nirote, Siwarat Kuson, Waraporn Nunthasen, Sasiwimon Puphoung, and Vannasinh Souvannasouk. 2022. The potential risks of climate change and weather index insurance scheme for Thailand’s economic crop production. Environmental Challenges 8: 100575. [Google Scholar] [CrossRef]
- Tappi, Marco, Federica Carucci, Giuseppe Gatta, Marcella Michela Giuliani, Emilia Lamonaca, and Fabio Gaetano Santeramo. 2023. Temporal and design approaches and yield-weather relationships. Climate Risk Management 40: 100522. [Google Scholar] [CrossRef]
- Thai General Insurance Association. 2022. Available online: https://www.tgia.org (accessed on 10 June 2022).
- Thai Meteorological Department. 2022. Available online: https://www.tmd.go.th (accessed on 10 June 2022).
- United States Department of Agriculture. 2022. Available online: https://www.usda.gov/ (accessed on 20 July 2022).
- Vedenov, Dmitry V., and Barry J. Barnett. 2004. Efficiency of Weather Derivatives as Primary Crop Insurance Instruments. Journal of Agricultural and Resource Economics 29: 387–403. [Google Scholar]
- Verma, Amit Kumar, Pradeep Kumar Garg, K. S. Hari Prasad, Vinay Kumar Dadhwal, Sunil Kumar Dubey, and Arvind Kumar. 2021. Sugarcane Yield Forecasting Model Based on Weather Parameters. Sugar Tech 23: 158–66. [Google Scholar] [CrossRef]
- Verma, Ram Ratan, Tapendra Kumar Srivastava, and Pushpa Singh. 2019. Climate change impacts on rainfall and temperature in sugarcane growing Upper Gangetic Plains of India. Theoretical and Applied Climatology 135: 279–92. [Google Scholar] [CrossRef]
- Verón, Santiago R., Diego de Abelleyra, and David B. Lobell. 2015. Impacts of precipitation and temperature on crop yields in the Pampas. Climatic Change 130: 235–45. [Google Scholar] [CrossRef]
- Vroege, Willemijn, Tobias Dalhaus, and Robert Finger. 2019. Index insurances for grasslands—A review for Europe and North-America. Agricultural Systems 168: 101–11. [Google Scholar] [CrossRef]
- Wang, Jin, Sai Kranthi Vanga, Rachit Saxena, Valérie Orsat, and Vijaya Raghavan. 2018. Effect of Climate Change on the Yield of Cereal Crops: A Review. Climate 6: 41. [Google Scholar] [CrossRef]
- Wang, Qingxia, Yim Soksophors, Angelica Barlis, Shahbaz Mushtaq, Khieng Phanna, Cornelis Swaans, and Danny Rodulfo. 2022. Willingness to Pay for Weather-Indexed Insurance: Evidence from Cambodian Rice Farmers. Sustainability 14: 14558. [Google Scholar] [CrossRef]
- Win, Hnin Ei. 2016. Crop Insurance in Thailand. Available online: https://ap.fftc.org.tw/article/1105 (accessed on 15 July 2022).
- Xu, Ying, Chao Gao, Xuewen Li, Taiming Yang, Xibo Sun, Congcong Wang, and De Li. 2018. The Design of a Drought Weather Index Insurance System for Summer Maize in Anhui Province, China. Journal of Risk Analysis and Crisis Response 8: 14–23. [Google Scholar] [CrossRef]


| References | RI | T | T.MIN | T.MAX | SR | Other Features |
|---|---|---|---|---|---|---|
| (Martin et al. 2001) | X | X | CO2 | |||
| (Vedenov and Barnett 2004) | X | X | ||||
| (Lobell and Field 2007) | X | X | X | X | ||
| (Lobell and Burke 2010) | X | X | ||||
| (Verón et al. 2015) | X | X | X | X | ||
| (Wang et al. 2018) | X | SH | ||||
| (Xu et al. 2018) | X | X | SH | |||
| (Shirsath et al. 2019) | X | |||||
| (Sinnarong et al. 2019) | X | X | ||||
| (Amnuaylojaroen et al. 2021) | X | X | X | |||
| (Kath et al. 2021) | X | X | ||||
| (Bucheli et al. 2022) | X | |||||
| (Tappi et al. 2023) | X | X | X | DTR | ||
| (Greenland 2005) * | X | X | X | GDDs, FH, Soil water | ||
| (Mali et al. 2014) * | X | X | X | X | RH.Max, RH.Min | |
| (Sattar et al. 2014) * | X | X | X | X | X | |
| (Carvalho et al. 2015) * | X | X | X | X | ||
| (Kath et al. 2018) * | X | |||||
| (Verma et al. 2019) * | X | X | X | RH I, RH II | ||
| (Pignède et al. 2021) * | X | X | X | X | NDVI, PE, MRH | |
| (Singh et al. 2021) * | X | X | X | X | CDC | |
| (Pipitpukdee et al. 2020) * | X | X | X | Max.rain, PD, LRP, LW, IA | ||
| (Verma et al. 2021) * | X | X | X | RH | ||
| (Sinnarong et al. 2022) * | X | X |
| Variable | Notation | Details |
|---|---|---|
| Sugarcane yield (tonne/rai) | Yt | Sugarcane yield at year t |
| Rainfall (mm) | RIt | Cumulative rainfall in the growing season (between October of year t − 1 and November of year t) |
| Maximum temperature (°C) | Tmaxt | Average maximum temperature in the growing season (between October of year t − 1 and November of year t) |
| Year of harvest | t | t stands for the year of harvest |
| Price of sugarcane yield per tonne | P | Farm gate price of the last harvest year |
| Predictor Variable | F | p-Value |
|---|---|---|
| Year | 9.319 | 0.0007 *** |
| Rainfall index | 1.625 | 0.0444 * |
| Maximum temperature | 0.284 | 0.0976 |
| Adjust R2 | 0.602 | |
| Split testing R2 | 0.691 |
| Tau | Predictor Variable | p-Value |
|---|---|---|
| 0.4 | Year | <0.0001 *** |
| Rainfall index | 0.0535 | |
| Maximum temperature | 0.0740 | |
| 0.3 | Year | <0.0001 *** |
| Rainfall index | 0.0757 | |
| Maximum temperature | 0.0657 | |
| 0.2 | Year | <0.0001 *** |
| Rainfall index | 0.0036 ** | |
| Maximum temperature | 0.0960 |
| Model | Levels of the Excessive Rainfall | Maximum Liability (baht/Rai) | Premium (baht/Rai) | Premium Rate (%) |
|---|---|---|---|---|
| GAM | 1595.42 (strike) | 1216.60 | 4.70369 | 0.38663 |
| 1492.75 (70th) | 1204.61 | 6.44293 | 0.53486 | |
| 1573 (80th) | 1213.06 | 5.04298 | 0.41572 | |
| 1789.3 (90th) | 1239.79 | 2.50249 | 0.20185 | |
| QGAM Tau = 0.4 | 1595.42 (strike) | 1704.37 | 6.58927 | 0.38661 |
| 1492.75 (70th) | 1686.47 | 9.01907 | 0.53479 | |
| 1573 (80th) | 1700.78 | 7.07056 | 0.41573 | |
| 1789.3 (90th) | 1726.82 | 3.48553 | 0.20185 | |
| QGAM Tau = 0.3 | 1595.42 (strike) | 1733.34 | 6.70155 | 0.38663 |
| 1492.75 (70th) | 1714.23 | 9.16753 | 0.53479 | |
| 1573 (80th) | 1729.55 | 7.19016 | 0.41572 | |
| 1789.3 (90th) | 1756.32 | 3.54507 | 0.20185 | |
| QGAM Tau = 0.2 | 1595.42 (strike) | 1814.64 | 7.01588 | 0.38663 |
| 1492.75 (70th) | 1795.24 | 9.60079 | 0.53479 | |
| 1573 (80th) | 1811.14 | 7.52931 | 0.41572 | |
| 1789.3 (90th) | 1838.04 | 3.71002 | 0.20185 |
| GAM | In Sample (1992–2017) | Out of Sample (2018–2022) | ||||
|---|---|---|---|---|---|---|
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6918.65 | 8.7275 | 603.900 | 10,497.44 | 9.2389 | 1410.261 |
| 80th | 6895.68 | 8.7237 | 607.180 | 10,480.12 | 9.2376 | 1409.380 |
| 90th | 6861.85 | 8.7187 | 626.675 | 10,447.41 | 9.2350 | 1407.782 |
| Strike | 6891.53 | 8.7230 | 608.646 | 10,479.13 | 9.2375 | 1409.167 |
| QGAM (0.2) | In Sample (1992–2017) | Out of Sample (2018–2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6992.90 | 8.7381 | 599.050 | 10,606.64 | 9.2475 | 1412.251 |
| 80th | 6958.33 | 8.7325 | 601.313 | 10,581.39 | 9.2455 | 1410.948 |
| 90th | 6905.63 | 8.7249 | 626.675 | 10,526.91 | 9.2413 | 1410.948 |
| Strike | 6951.80 | 8.7314 | 602.721 | 10,579.09 | 9.2454 | 1410.948 |
| QGAM (0.3) | In Sample (1992–2017) | Out of Sample (2018–2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6982.72 | 8.7367 | 599.417 | 10,591.67 | 9.2463 | 1411.978 |
| 80th | 6949.79 | 8.7313 | 601.933 | 10,567.57 | 9.2445 | 1410.734 |
| 90th | 6899.65 | 8.7241 | 626.675 | 10,515.70 | 9.2404 | 1410.734 |
| Strike | 6943.61 | 8.7303 | 603.383 | 10,565.46 | 9.2443 | 1410.734 |
| QGAM (0.4) | In Sample (1992–2017) | Out of Sample (2018–2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6979.23 | 8.736 | 599.564 | 10,586.53 | 9.2460 | 1411.885 |
| 80th | 6946.77 | 8.731 | 602.165 | 10,562.70 | 9.2441 | 1410.659 |
| 90th | 6897.49 | 8.724 | 626.675 | 10,511.66 | 9.2401 | 1410.659 |
| Strike | 6940.69 | 8.730 | 603.630 | 10,560.60 | 9.2439 | 1410.659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanchai, T.; Srisodaphol, W.; Pongsart, T.; Klongdee, W. Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand. J. Risk Financial Manag. 2024, 17, 107. https://doi.org/10.3390/jrfm17030107
Kanchai T, Srisodaphol W, Pongsart T, Klongdee W. Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand. Journal of Risk and Financial Management. 2024; 17(3):107. https://doi.org/10.3390/jrfm17030107
Chicago/Turabian StyleKanchai, Thitipong, Wuttichai Srisodaphol, Tippatai Pongsart, and Watcharin Klongdee. 2024. "Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand" Journal of Risk and Financial Management 17, no. 3: 107. https://doi.org/10.3390/jrfm17030107
APA StyleKanchai, T., Srisodaphol, W., Pongsart, T., & Klongdee, W. (2024). Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand. Journal of Risk and Financial Management, 17(3), 107. https://doi.org/10.3390/jrfm17030107






