The Use of the Partitioning Theorem to Prove Further Results Regarding the Distribution of IRRs: And an Open Question

Abstract

In 2018, Cuthbert proved that any transaction vector can be uniquely partitioned into a sequence of pure investments with strictly decreasing internal rates of return (IRRs). In a subsequent paper, Cuthbert used the partitioning theorem to derive a new sufficient condition for a transaction to have a unique IRR and proved some results regarding how the IRRs of a transaction must be distributed. This paper proves some further results on the distribution of IRRs. It also poses an open question regarding the possible relationship between the number of IRRs of a transaction and the relative sizes of the smallest and largest IRRs of the terms in the unique partition of that transaction.

1. Introduction

It will be useful to begin by setting this research in the context of earlier research on internal rates of return (IRRs) and investment appraisal. The IRR has been an important and popular tool in making investment decisions. However, multiple problems with the approach have also long been recognised; the paper by Magni (2013) provides a good review of these problems. It has also long been recognised that problems with the use of an IRR are minimal when the investment involved is a pure investment, namely, projects in which, to use the notation of Hazen (2003), there is a non-negative investment stream throughout the life of the project; for such projects, the investor is effectively never borrowing from the project, and the project also has a unique IRR. The difficult issues with the use of IRRs arise for projects in which the unrecovered investment stream becomes negative at some point during the life of the project; in a subset of such projects, there will be multiple IRRs.

For such general transactions, a number of different approaches have been suggested for making rational investment decisions. For example, Hazen (2003) demonstrated how rational decisions can be made starting from any IRR, provided that it was analysed in conjunction with its corresponding investment stream. Hartman and Schafrick (2004) presented a method for determining project acceptability based on what they denoted the relevant IRR, defined in terms of the local slope of the net present value function at the relevant cost of capital. Osborne (2010) showed how the net present value function could be described as a function of all the IRRs of the transaction, including negative and complex IRRs. Pierru (2010) provided an interpretation of how complex-valued IRRs might be simply interpreted. Magni (2010) proposed an important approach, the average internal rate of return (AIRR), which provides rational indicators of project value while avoiding the problems of multiple IRRs and is based on a pre-specified vector of capitals invested in the project.

It turns out, however, that pure investments are, in a sense, the fundamental building blocks from which any transaction can be uniquely constructed. This is an implication of the partitioning theorem proved in Cuthbert (2018), which is in itself related to earlier works by Soper (1959) and Gronchi (1986). The partitioning theorem proves that any transaction can be uniquely partitioned into a series of pure investments with strictly decreasing internal rates of return. The partitioning theorem has some direct applications to rational decision making. For example, Magni and Cuthbert (2018) showed how the invested capitals for the terms in the unique partition of a transaction are natural candidates for use as the vector of capitals invested used in defining the AIRR, hence leading to the definition of the pure investment average internal rate of return (PIAIRR). Additionally, Cuthbert (2018) showed how the unique partition of a transaction can be used to define an optimum rule for deciding when to sell a transaction.

But possibly the most interesting aspect of the partitioning theorem is not its direct application in rational decision making but in what it reveals about the structures of transactions and in the links, which are becoming clearer, between the form of the unique partition and the IRR properties of the transaction. For example, if the largest and smallest IRRs of the terms in the unique partition of a transaction are sufficiently close together (in a sense which will be made clear in Section 2 of this paper), then the transaction must have a unique IRR: this is a result proved by Cuthbert (2021). And as also shown in that paper, it is possible to derive some information about where the IRRs of a transaction must lie in the range between the smallest and largest IRRs of the terms in the unique partition; that is, it is possible to derive information about the distribution of the IRRs.

This paper is a continuation of the process of uncovering the links between the properties of a unique partition and the properties of the IRRs of the original transaction; the paper derives further results on the distribution of IRRs. However, by no means has everything been determined in this area, and this paper concludes by posing an open question, the answer to which would be of considerable interest.

The structure of the paper is as follows.

Section 2 sets out the required notation and introduces the partition theorem proved by Cuthbert (2018), together with the new sufficient condition for a transaction to have a unique IRR proved by Cuthbert (2021) and the results regarding the distribution of IRRs proved in that paper.

Section 3 provides some further preliminary notation and some required technical results, again re-stating material proved in the previous papers.

Section 4 develops new material, proving stronger results with respect to the uniqueness and distribution of IRRs in the special case in which there are two terms in the unique partition of a transaction.

Section 5 returns to the general transaction case (that is, where there may be two or more terms in a unique partition) and proves further results on the distribution of IRRs.

Section 6 poses an open question about the relationship between the gap between the smallest and largest IRRs in the terms of the unique partition and the number of IRRs of the transaction.

Section 7 finishes with some conclusions and provides possible indications for further research.

2. Notation and Background

The notation is as follows, as is used by Cuthbert (2018, 2021).

A transaction a is a vector $\left({\mathrm{a}}_0,{\mathrm{a}}_1,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)$ in which negative terms represent investments of capital and positive terms represent repayments. It is assumed that ${\mathrm{a}}_0<0$.

The standard definition of net present value is used, namely, the net present value (NPV) of the payment stream a, calculated at a discount rate u (u > −1) is

$$\mathrm{NPV}(a,\mathrm{u})={\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{j}}{(1+\mathrm{u})}^{-\mathrm{j}}}$$

Any discount rate $\sigma$ such that $\mathrm{NPV}(a,\sigma )=0$ is defined to be an IRR of a.

When a is a transaction vector and $\sigma$ is an IRR of a, the invested capital ${\mathrm{d}}_{\mathrm{k}}$ at the start of a period k is defined by the formulae

$${\mathrm{d}}_0=0,\mathrm{and}{\mathrm{d}}_{\mathrm{k}}=-{\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{k}-1}{\mathrm{a}}_{\mathrm{j}}}{(1+\sigma )}^{\mathrm{k}-\mathrm{j}-1},\mathrm{k}=1,\dots ,\mathrm{n}.$$

The following recursive relationship then holds:

$${\mathrm{d}}_1={-\mathrm{a}}_0,\mathrm{and}{\mathrm{d}}_{\mathrm{j}+1}=(1+\sigma {)\mathrm{d}}_{\mathrm{j}}{-\mathrm{a}}_{\mathrm{j}},(\mathrm{j}\ge 1).$$

It can readily be shown that ${\mathrm{d}}_{\mathrm{n}+1}=0$.

Pure investments are those in which the invested capitals ${\mathrm{d}}_{\mathrm{j}}$ are all non-negative. Formally, if a is a transaction vector with IRR $\sigma$ and if ${\mathrm{d}}_{\mathrm{j}}\ge 0$ for all j, a is defined as a pure investment. As proved originally by Soper (1959) and in a result generalised by Gronchi (1986), every pure investment has exactly one IRR.

The operation of partitioning a transaction, as defined by Cuthbert (2018), can be regarded as the process of splitting the transaction into non-overlapping segments.

Formally, if a is a vector, then for any k, the vectors (${\mathrm{a}}_0{,\mathrm{a}}_1,....{\mathrm{a}}_{\mathrm{k}}$), (${\mathrm{a}}_{\mathrm{k}+1},....{\mathrm{a}}_{\mathrm{n}}$) represent a partitioning of a. So, for example, (3,5,4) can be partitioned as (3,5) and (4).

On occasion, it will be convenient to retain the positions of the partitioning vectors in the original n + 1 length vector, so it is sometimes useful to express a partition using long-form notation, for example, (3,5,0) and (0,0,4). The long-form notation is additive: (3,5,4) = (3,5,0) + (0,0,4).

The standard definition of IRR only applies for discount rates greater than −1. Cuthbert (2018) adopted the convention that if a vector consists only of terms which are negative or zero (with at least one strictly negative term), then this corresponds to a pure investment transaction with IRR = −1.

The basic results proved by Cuthbert (2018, 2021) are as follows.

The key result proved by Cuthbert (2018) is the following:

Partitioning Theorem

Let a be a transaction vector. Then there exists a unique integer K ≥ 1 and a partition a(1), a(2), …, a(K) of a in which each of the a(1), …, a(K) are pure investments and where

IRR(a(1)) > IRR(a(2)) > … > IRR(a(K)).

Moreover, the integer K and the partition a(1), …, a(K) are unique.

The IRRs of the terms in the above partition are denoted as ${\sigma }_1$ to ${\mathsf{\sigma }}_{\mathrm{K}}$, respectively. Then, as was also shown by Cuthbert (2018), when K > 1, all the IRRs of a must lie strictly between ${\mathsf{\sigma }}_{\mathrm{K}}$ and ${\sigma }_1$.

For transactions for which ${\mathsf{\sigma }}_{\mathrm{K}}$ > −1 (that is, transactions for which the last non-zero term is positive), the quantity $\tau$ is defined as

$$\tau =\frac{(1+{\mathsf{\sigma }}_1)}{(1+{\mathsf{\sigma }}_{\mathrm{K}})}.$$

Then, the following sufficient condition for a to have a unique IRR was proved by Cuthbert (2021).

Theorem 1.

Let a be a transaction of length (n + 1), with $a_0<0$, $a_n>0$, and n ≥ 3.

Then, if $\tau \le \frac{n^2}{{(n-2)}^2}$, a has a unique IRR.

For transactions for which the condition of Theorem 1 is not satisfied (that is, transactions for which $\tau >\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$), then the quadratic equation

$$(\mathrm{n}-1){\mathrm{x}}^2-[\mathrm{n}+\tau (\mathrm{n}-2)]\mathrm{x}+\tau (\mathrm{n}-1)=0$$

(1)

has two real roots. Denote the larger and smaller of these roots as ${\mathrm{r}}^{+}$ and ${\mathrm{r}}^{-},$ respectively. Thus,

$${\mathrm{r}}^{+}=\frac{\left[\mathrm{n}+\mathsf{\tau }\left(\mathrm{n}-2\right)\right]+{[{(\mathrm{n}+\mathsf{\tau }\left(\mathrm{n}-2)\right)}^2-4\mathsf{\tau }{\left(\mathrm{n}-1\right)}^2]}^{0.5}}{2(\mathrm{n}-1)},\mathrm{and}$$

$${\mathrm{r}}^{-}=\frac{\left[\mathrm{n}+\mathsf{\tau }\left(\mathrm{n}-2\right)\right]-{[{(\mathrm{n}+\mathsf{\tau }\left(\mathrm{n}-2)\right)}^2-4\mathsf{\tau }{\left(\mathrm{n}-1\right)}^2]}^{0.5}}{2(\mathrm{n}-1)}.$$

Then the following theorem, which provides information about where the IRRs of a must be distributed in the interval ]${\mathsf{\sigma }}_{\mathrm{K}}$, ${\sigma }_1$[, was proved by Cuthbert (2021).

Theorem 2.

Let $\mathit{a}$ be a transaction of length (n + 1), with a₀ < 0, $a_n$ > 0, and n ≥ 3.

If $\tau >\frac{n^2}{{(n-2)}^2}$, then

(i)

a has at most one IRR, $\rho ,$ such that

$$(1+\rho )\ge \frac{(1+{\sigma }_1)}{r^{-}}$$

(ii)

a has at most one IRR, $\rho$, such that

$$(1+\rho )\le \frac{(1+{\sigma }_1)}{r^{+}}$$

(iii)

if a has multiple IRRs, it has at least one IRR, $\rho$, such that

$$\frac{(1+{\sigma }_1)}{r^{+}}\le \left(1+\rho \right)\le \frac{(1+{\sigma }_1)}{r^{-}}$$

Finally, the following theorem, also proved by Cuthbert (2021), provides information about the distribution of IRRs in the case in which ${\mathsf{\sigma }}_{\mathrm{K}}$ = −1. Note that in this case, a does not necessarily need to have any IRRs but when it does have at least one IRR, the following must hold.

Theorem 3.

Let $\mathit{a}$ be a transaction of length (n + 1), with a₀ < 0, a_n < 0, and $n$ ≥ 2, and suppose that $\mathit{a}$ has at least one IRR. Then,

(i)

a has at most one IRR, $\rho$, such that

$$(1+\rho )>(1-\frac{1}{n})(1+{\sigma }_1)$$

(ii)

a has at least one IRR, $\rho$, such that

$$(1+\rho )\le (1-\frac{1}{n})(1+{\sigma }_1)$$

3. Preliminaries

This section introduces some further notation and preliminary theory by summarising material originally provided by Cuthbert (2021). This material will be required in the proofs of the main results, which follow in the later sections of the paper.

Extremal Transactions

Cuthbert (2018) defined a very simple transaction as a transaction in which there are only two non-zero terms, with a negative immediately preceding a positive term.

An extremal transaction of length (n + 1) is defined here as a transaction which has a very simple transaction at positions 0 and 1, a very simple transaction at positions n − 1 and n, and has all other terms equal to zero.

The derivative of the net present value function at 0.

If a is a transaction with the IRR $\sigma$ and the invested capitals ${\mathrm{d}}_{\mathrm{j}}$, then it is a standard result, first proved by Hazen (2003), that

$$\mathrm{NPV}(\mathbf{a},\mathrm{u})=(\sigma -\mathrm{u})\mathrm{NPV}(\mathbf{d},\mathrm{u}):$$

(a proof of this was given in Cuthbert (2018)).

Differentiating this expression, it follows that

$$\begin{array}{ll}{\mathrm{NPV}}^{\prime }\left(\mathbf{a},\mathrm{u}\right)& =-\mathrm{NPV}(\mathbf{d},\mathrm{u})+(\sigma -\mathrm{u}){\mathrm{NPV}}^{\prime }\left(\mathrm{d},\mathrm{u}\right)\\ & =-{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{j}}{(1+\mathrm{u})}^{-\mathrm{j}}-(\mathsf{\sigma }-\mathrm{u}){\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{jd}}_{\mathrm{j}}{(1+\mathrm{u})}^{-\mathrm{j}-1}\end{array}$$

Setting u = 0, it follows that

$$\begin{array}{ll}{\mathrm{NPV}}^{\prime }\left(\mathbf{a},0\right)& =-{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{j}}-\mathsf{\sigma }{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{jd}}_{\mathrm{j}}\hfill \\ & =-{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{(1+\mathrm{j}\mathsf{\sigma })\mathrm{d}}_{\mathrm{j}}\end{array}$$

Note also from the above expression for NPV(a, u) that

$$\mathrm{NPV}(\mathbf{a},0)={\sum }_{\mathrm{j}=0}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{j}}=\sigma {\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{j}}$$

The operation of scaling a transaction.

It will be useful in what follows to use the concept of scaling a transaction, which is defined here as follows. Let a be a transaction. Then, for any number $\rho >-1$, the transaction a scaled by $\rho$ is a new transaction ${\mathbf{a}}^{\mathbf{S}},$ defined as

$${\mathrm{a}}_{\mathrm{j}}^{\mathrm{S}}={\mathrm{a}}_{\mathrm{j}}{(1+\mathsf{\rho })}^{-\mathrm{j}}$$

The following properties of this scaling operation will be used; proofs of these properties were provided by Cuthbert (2021).

(i)

If $\sigma$ is an IRR of a, then $\frac{\left(1+\sigma \right)}{\left(1+\rho \right)}-1$ is an IRR of ${\mathbf{a}}^{\mathbf{S}}.$

(ii)

The unique partition of ${\mathbf{a}}^{\mathbf{S}}$ into pure investments is the same as the partition of a.

(iii)

If a has a unique partition into pure investments with the IRRs ${\sigma }_1$, … ${\mathsf{\sigma }}_{\mathrm{K}}$, where ${\mathsf{\sigma }}_{\mathrm{K}}>-1$, and if the quantity $\tau$ = $\mathsf{\tau }(\mathbf{a})$ is defined as

$$\tau =\frac{(1+{\mathsf{\sigma }}_1)}{(1+{\mathsf{\sigma }}_{\mathrm{K}})},$$

then $\tau$ is invariant under the scaling of a.

(iv)

The derivative of the function NPV(${\mathbf{a}}^{\mathbf{S}}$, u) at u has the same sign (positive, negative, or zero) as the derivative of NPV(a, x) at x = (1 + $\rho$)(1 + u) − 1.

4. The K = 2 Case

This section proves new results on the distribution of IRRs in the special case where there are two terms in the unique partition of a into pure investments, that is, in the notation used above, when K = 2. What is proved here is that if such a transaction has an IRR which is sufficiently close to ${\sigma }_1$ or sufficiently close to ${\sigma }_2$, then this must in fact be the unique IRR of a. This section also proves a stronger result than this for a sub-class of the K = 2 case consisting of extremal transactions (extremal transactions were defined above, in Section 3). It is useful to begin with the extremal case first, since that provides a building block for the more general K = 2 case.

Extremal Transactions

Consider an extremal transaction of order n whose first two terms have the IRR ${\sigma }_1$ and whose last two terms have the IRR ${\sigma }_2$, where ${\sigma }_1$ > ${\sigma }_2$. (Note that if ${\sigma }_1$ < ${\sigma }_2$, then by the partition theorem, a is a pure investment and so has a unique IRR.) Then a can be written

$$\mathbf{a}=({\mathrm{a}}_0,-{\mathrm{a}}_0(1+{\sigma }_1),\dots \dots .,{\mathrm{a}}_{\mathrm{n}-1},-{\mathrm{a}}_{\mathrm{n}-1}(1+{\sigma }_2)),$$

where ${\mathrm{a}}_0$ < 0 and ${\mathrm{a}}_{\mathrm{n}-1}$ < 0.

As before, define $\tau$ as $\tau$ = $\frac{(1+{\sigma }_1)}{(1+{\sigma }_2)}$. By Theorem 1, if $\tau \le \frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$, then a has a unique IRR, so we can restrict our attention to transactions for which $\tau >\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$. For these transactions, the quadratic equation at (1) above, namely,

$$\mathrm{f}(\mathrm{x})=(\mathrm{n}-1){\mathrm{x}}^2-[\mathrm{n}+\tau (\mathrm{n}-2)]\mathrm{x}+\tau (\mathrm{n}-1)=0$$

has two real roots. As before, denote the larger and smaller of these roots as ${\mathrm{r}}^{+}$ and ${\mathrm{r}}^{-},$ respectively. In fact, it is easy to establish that f($\frac{\mathrm{n}}{(\mathrm{n}-1)}$) > 0, so both ${\mathrm{r}}^{+}$ and ${\mathrm{r}}^{-}$ are greater than $\frac{\mathrm{n}}{(\mathrm{n}-1)}$; this is a fact which will be required later.

It turns out that for extremal transactions, there is a very strong relationship between the location of an IRR and the slope of the net present value function at that IRR. This relationship is summed up in the following lemma.

Lemma 1.

Let a be an extremal transaction as defined above, and let $\rho$ be an IRR of a. Then

(i)

${\mathit{NPV}}^{\prime }\left(\mathit{a},\rho \right)$ < 0 if and only if (1 + $\rho$) < $\frac{(1+{\sigma }_1)}{r^{+}}$ or (1 + $\rho$) > $\frac{(1+{\sigma }_1)}{r^{-}}$

(ii)

${\mathit{NPV}}^{\prime }\left(\mathit{a},\rho \right)$  = 0 if and only if (1 + $\rho$) = $\frac{(1+{\sigma }_1)}{r^{+}}$ or (1 + $\rho$) = $\frac{(1+{\sigma }_1)}{r^{-}}$

(iii)

${\mathit{NPV}}^{\prime }\left(\mathit{a},\rho \right)$ > 0 if and only if $\frac{(1+{\sigma }_1)}{r^{+}}$ < (1 + $\rho$) < $\frac{(1+{\sigma }_1)}{r^{-}}$.

Proof. 

The proof is provided in Appendix A. □

Now, define the transaction b($\theta$) for 0 $\le \theta \le 1$ by

$$\mathbf{b}(\theta )=(-\theta ,\theta (1+{\sigma }_1),\dots \dots \dots ,-(1-\theta ),(1-\theta )(1+{\sigma }_2)).$$

(2)

Then it follows readily that a = K b($\theta$) when K = −(${\mathrm{a}}_0$ + ${\mathrm{a}}_{\mathrm{n}-1}$) and for the specific value of $\theta$ = $\frac{{\mathrm{a}}_0}{{\mathrm{a}}_0+{\mathrm{a}}_{\mathrm{n}-1}}$.

Since the multiplicative constant K has no effect on the number or values of IRRs, we can restrict our attention to examining the behaviour of the IRRs of the family b($\theta$) for 0 < $\theta$ < 1.

The next step is to define two specific values of $\mathsf{\theta }$, which will be denoted as $\mathsf{\theta }(\mathrm{r})$, where r can be either ${\mathrm{r}}^{+}$ or ${\mathrm{r}}^{-}$. The definition of the values $\mathsf{\theta }(\mathrm{r})$ is as follows:

$$\mathsf{\theta }(\mathrm{r})={[1+(\left(\mathrm{n}-1\right)\mathrm{r}-\mathrm{n})\frac{{(1+{\mathsf{\sigma }}_1)}^{(\mathrm{n}-1)}}{{\mathrm{r}}^{(\mathrm{n}-1)}}]}^{-1}$$

(3)

where r can be either ${\mathrm{r}}^{+}$ or ${\mathrm{r}}^{-}$.

Since, as already noted, both ${\mathrm{r}}^{+}$ and ${\mathrm{r}}^{-}$ are greater than $\frac{\mathrm{n}}{(\mathrm{n}-1)}$, the second term in the square bracket in the definition of $\mathsf{\theta }(\mathrm{r})$ is positive, so $\mathsf{\theta }(\mathrm{r})$ does indeed have a value which is less than 1.

The transaction b($\mathsf{\theta }(\mathrm{r})$) can then be written

$$\begin{array}{l}\mathbf{b}(\mathsf{\theta }(\mathrm{r}))=\mathsf{\theta }(\mathrm{r})\{-1,(1+{\sigma }_1),\dots \\ \dots \dots ,{(\mathrm{n}-\left(\mathrm{n}-1\right)\mathrm{r})\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{(\mathrm{n}-1)}}}^{(\mathrm{n}-1)},{\left(\left(\mathrm{n}-1\right)\mathrm{r}-\mathrm{n}\right)\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{\left(\mathrm{n}-1\right)}}}^{\left(\mathrm{n}-1\right)}(1+{\mathsf{\sigma }}_2)\}.\end{array}$$

As will be shown, the two transactions b($\mathsf{\theta }(\mathrm{r})$) occupy an important transitional position with respect to the properties of the IRRs of an extremal transaction. These transactions also have a number of special properties. First of all, b($\mathsf{\theta }(\mathrm{r})$) has an IRR equal to $\frac{(1+{\mathsf{\sigma }}_1)}{\mathrm{r}}$ − 1. This is proved in Appendix A. In fact, it is tedious but straightforward to verify that this value is actually a repeated IRR of b($\mathsf{\theta }(\mathrm{r})$) and that the function NPV(b($\mathsf{\theta }({\mathrm{r}}^{+})$), u) is concave up at its repeated IRR $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$ − 1, while the function NPV(b($\mathsf{\theta }({\mathrm{r}}^{-})$), u) is concave down at its repeated IRR $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}$ − 1.

The transaction b($\mathsf{\theta }({\mathrm{r}}^{+})$) can have at most three IRRs by Descartes’ law of signs. Since the function NPV(b($\mathsf{\theta }({\mathrm{r}}^{+})$), u) is concave up at its repeated IRR $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$ − 1 and negative for a large u, it must have one other IRR, and this must be greater than $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$ − 1. Since the slope of the net present value function at this IRR must be negative, Lemma 1 above implies that the third IRR of b($\mathsf{\theta }({\mathrm{r}}^{+})$) must have a value larger than $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}$ − 1. A corresponding argument shows that the third IRR of b($\mathsf{\theta }({\mathrm{r}}^{-})$) must be less than $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$ − 1.

This means that the functions NPV(b($\mathsf{\theta }({\mathrm{r}}^{+})$) and NPV(b($\mathsf{\theta }({\mathrm{r}}^{-})$) must have the form which is illustrated for one specific example in Figure 1. This example illustrates the case in which n = 12, ${\sigma }_1$ = 0.1, and ${\sigma }_2$ = −0.2666, which implies a $\tau$ value of 1.5. For these values of the parameters, it follows that ${\mathrm{r}}^{+}$ = 1.306 and ${\mathrm{r}}^{-}$ = 1.1485 so that

$$\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}=0.957735\mathrm{and}\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}=0.842265.$$

Further, $\mathsf{\theta }({\mathrm{r}}^{+})$ = 0.736745 and $\mathsf{\theta }({\mathrm{r}}^{-})$ = 0.717232.

For convenience, the x-axis in Figure 1 measures the quantity (1 + u). The upper line in the chart corresponds to NPV(b($\mathsf{\theta }({\mathrm{r}}^{+})$), u), and the lower line corresponds to NPV(b($\mathsf{\theta }({\mathrm{r}}^{-})$), u).

As implied by the above theory, NPV(b($\mathsf{\theta }({\mathrm{r}}^{+})$), u) has a repeated IRR $\rho$ such that (1 + $\rho )$ = $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$ = 0.842265, and its third IRR has a value $\phi$ such that (1 + $\phi$) is greater than $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}$ = 0.957735. In fact, (1 + $\phi$) = 1.0133, as can be computed, for example, using Excel.

The lower curve, NPV(b($\mathsf{\theta }({\mathrm{r}}^{-})$), u), has the converse properties, as anticipated.

We are now almost in a position to provide a theorem which completely describes the properties of the IRRs of extremal transactions. Before doing so, one last preliminary is required in the shape of a Lemma which describes an important property of the family b($\mathsf{\theta }$), namely, that the net present value of b($\mathsf{\theta }$) at any fixed discount rate between ${\sigma }_1$ and ${\sigma }_2$ is a strictly increasing function of $\mathsf{\theta }$. More formally:

Lemma 2.

For any value of u such that ${\sigma }_2$ < u < ${\sigma }_1$, and if ${\theta }_1$ < ${\theta }_2$, then

$$\mathit{NPV}(\mathit{b}({\theta }_1),u)<\mathit{NPV}(\mathbf{b}({\theta }_2),u).$$

Proof. 

The proof is provided in Appendix A. □

Following all these preliminaries, the properties of the IRRs of extremal transactions are described in the following theorem.

Theorem 4.

Let a be an extremal transaction of order n whose first two terms have IRR ${\sigma }_1$ and whose last two terms have IRR ${\sigma }_2$.

(i) 

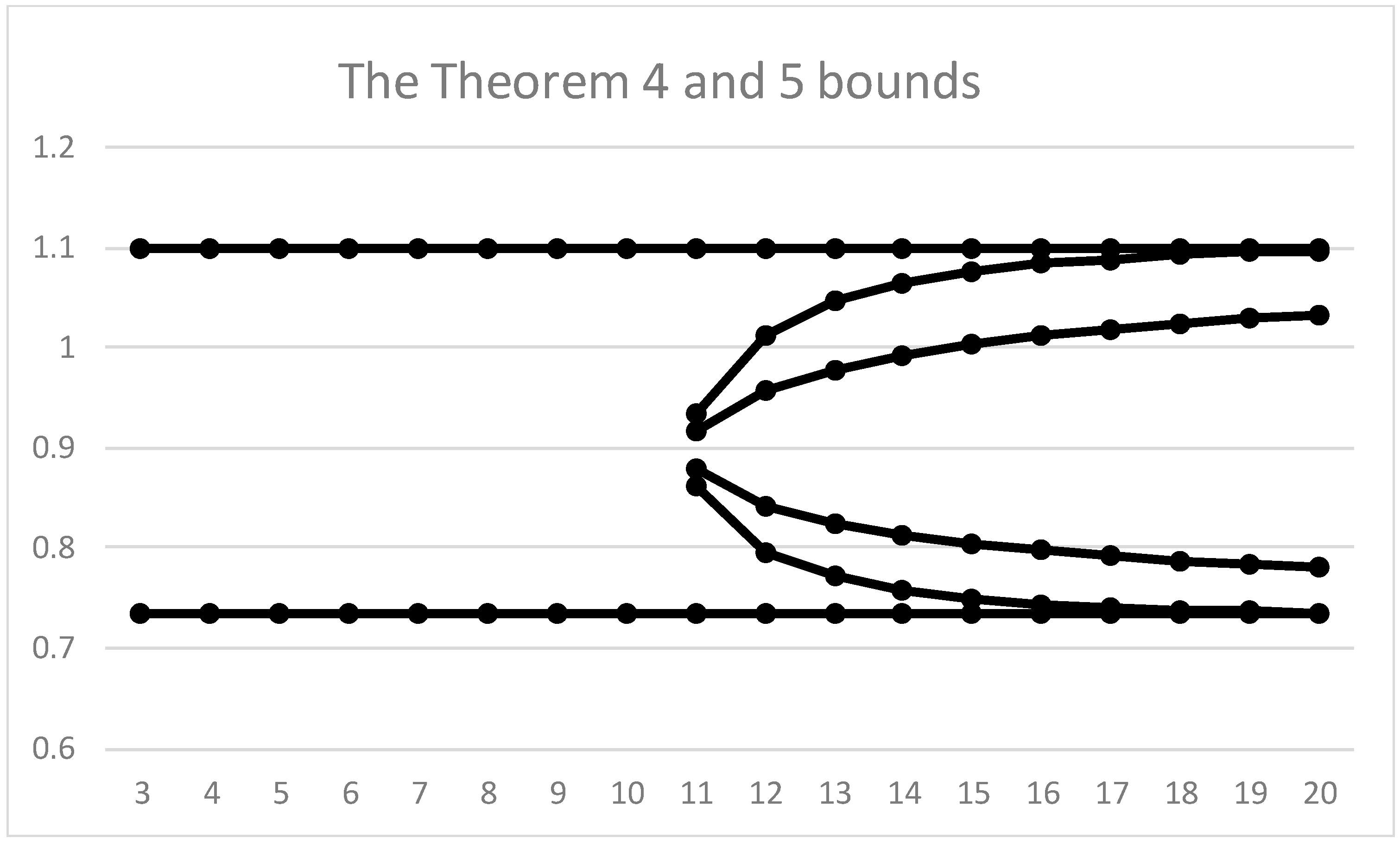
If $\frac{(1+{\sigma }_1)}{(1+{\sigma }_2)}$ $\le \frac{n^2}{{(n-2)}^2}$, then a has a unique IRR.

If $\frac{(1+{\sigma }_1)}{(1+{\sigma }_2)}$ $>\frac{n^2}{{(n-2)}^2}$, let $r^{+}$ and $r^{-}$ be the larger and smaller of roots of the quadratic in (1) above, let the quantities $\theta (r)$ be as defined as in (3) above, where r can be either $r^{+}$ or $r^{-}$, and let the transaction b($\theta$) be defined as in Equation (2) above for 0 $\le \theta \le 1$. Then,

(ii) 

If $\frac{a_0}{a_0+a_{n-1}}$ < $\theta ({\mathit{r}}^{-})$, then a has a unique IRR, and this must be less than the smallest IRR of b($\theta (r^{-}))$.

(iii) 

If $\theta (r^{-})$ < $\frac{a_0}{a_0+a_{n-1}}$ < $\theta (r^{+})$), then a must have three IRRs: one less than $\frac{(1+{\sigma }_1)}{r^{+}}$ − 1: one strictly between $\frac{(1+{\sigma }_1)}{r^{+}}$ − 1 and $\frac{(1+{\sigma }_1)}{r^{-}}$ − 1, and one strictly greater than $\frac{(1+{\sigma }_1)}{r^{-}}$ − 1. Moreover, the smallest IRR must be greater than the smallest IRR of b($\theta (r^{-}))$, and the largest IRR must be less than the largest IRR of b($\theta (r^{+}))$.

(iv) 

If $\frac{a_0}{a_0+a_{n-1}}$ > $\theta (r^{+})$, then a has a unique IRR, and this must be greater than the largest IRR of b($\theta (r^{+}))$.

Proof. 

The proof of the theorem is provided in Appendix A. □

There is an immediate corollary to Theorem 4, as follows:

Corollary 1.

With the same notation as above:

(i) 

If the extremal transaction a has an IRR which is less than the smallest IRR of b($\theta (r^{-}))$ , then a has a unique IRR.

(ii) 

If the extremal transaction a has an IRR which lies between the smallest IRR of b($\theta (r^{-}))$and the largest IRR of b($\theta (r^{+}))$, then a has three IRRs, and they all lie in this range.

(iii) 

If the extremal transaction a has an IRR which is larger than the largest IRR of b($\theta (r^{+}))$, then a has a unique IRR.

The general K = 2 case.

Theorem 4 and its corollary provide a complete description of how many IRRs an extremal transaction will have and in which regions they must be located. The results that can be proved in the general K = 2 case are less strong; however, analogous results to parts (i) and (iii) of the corollary to Theorem 4 can be proved in this case.

Let a be a transaction of order n for which K = 2, i.e., there are two terms in the unique partition of a. Let ${\sigma }_1$ and ${\sigma }_2$, as before, be the IRRs of the two terms in the unique partition of a, and assume ${\sigma }_2$ > − 1. Since a must have a unique IRR if $\tau$ = $\frac{(1+{\sigma }_1)}{(1+{\sigma }_2)}\le \frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$ it is assumed that $\tau >\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$.

Let l be the index of the last non-zero term in a(1), and let f be the index of the first non-zero term in a(2).

Let $\rho$ be any IRR of a. Then, our starting point is to define a new extremal transaction, $\widehat{\mathbf{a}}$, as follows.

$$\widehat{{\mathbf{a}}_0}=-\frac{(1+\mathsf{\rho })}{({\mathsf{\sigma }}_1-\mathsf{\rho })}{\sum }_{\mathrm{j}=0}^{\mathrm{l}}{\mathrm{a}}_{\mathrm{j}}{(1+\mathsf{\rho })}^{-\mathrm{j}}$$

$$\widehat{{\mathbf{a}}_1}=\frac{(1+\mathsf{\rho })(1+{\mathsf{\sigma }}_1)}{({\mathsf{\sigma }}_1-\mathsf{\rho })}{\sum }_{\mathrm{j}=0}^{\mathrm{l}}{\mathrm{a}}_{\mathrm{j}}{(1+\mathsf{\rho })}^{-\mathrm{j}}$$

$$\widehat{{\mathbf{a}}_{\mathrm{n}-1}}=-\frac{{(1+\mathsf{\rho })}^{\mathrm{n}}}{({\mathsf{\sigma }}_2-\mathsf{\rho })}{\sum }_{\mathrm{j}=\mathrm{f}}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{j}}{(1+\mathsf{\rho })}^{-\mathrm{j}}$$

$$\widehat{{\mathbf{a}}_{\mathrm{n}}}=\frac{{\left(1+\mathsf{\rho }\right)}^{\mathrm{n}}(1+{\mathsf{\sigma }}_2)}{({\mathsf{\sigma }}_2-\mathsf{\rho })}{\sum }_{\mathrm{j}=\mathrm{f}}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{j}}{(1+\mathsf{\rho })}^{-\mathrm{j}}$$

The following Lemma then holds.

Lemma 3.

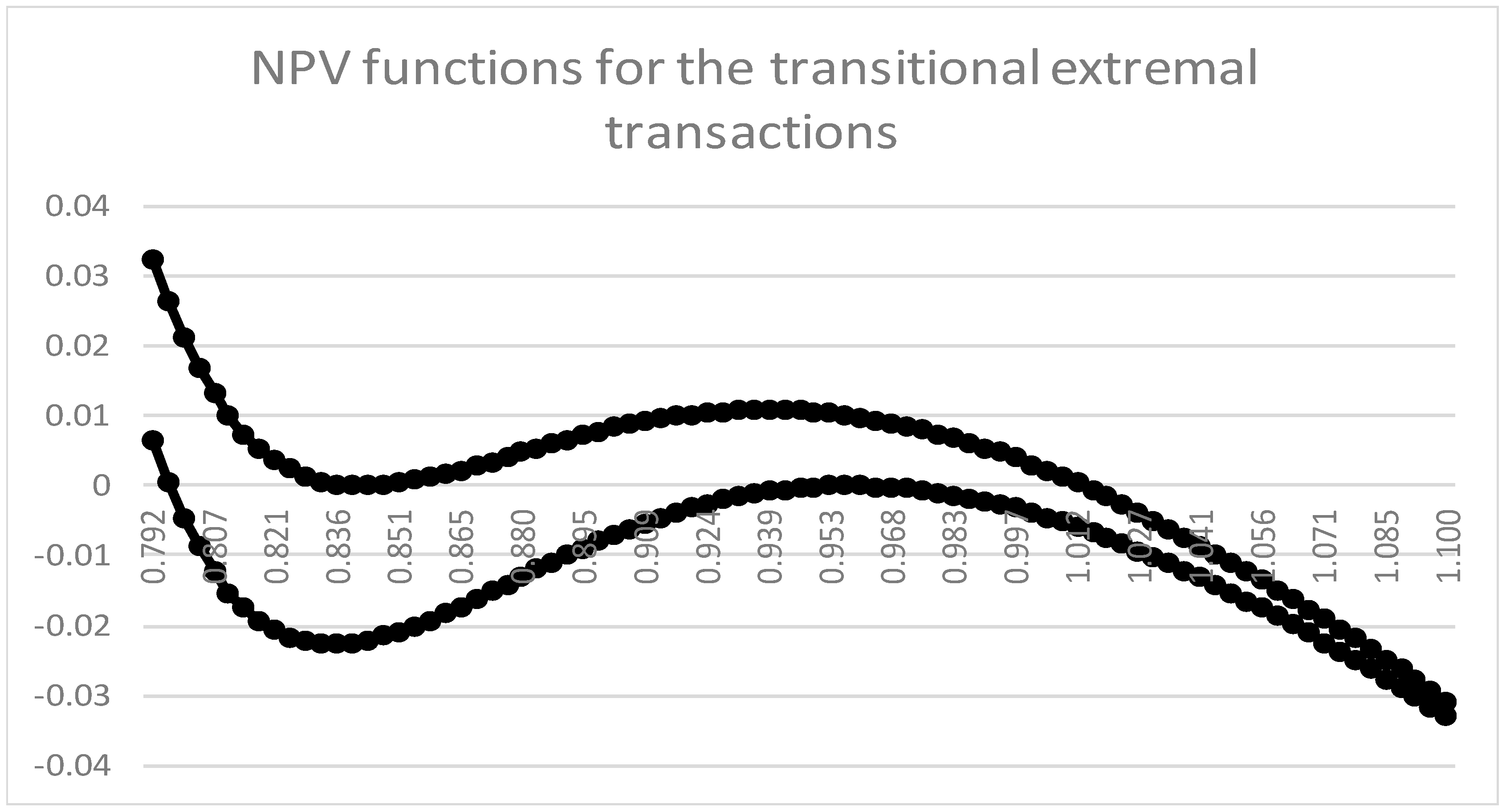
(i) 

The extremal transaction $\widehat{\mathit{a},}$ defined as above, has an IRR at $\rho$.

(ii) 

For each u satisfying ${\sigma }_2$ < u < $\rho$, it holds that

$$\mathit{NPV}(\mathit{a},u)\ge (\widehat{\mathit{a}},u);$$

(iii) 

For each u satisfying $\rho$ < u < ${\sigma }_1$, it holds that

$$\mathit{NPV}(\mathit{a},u)\le (\widehat{\mathit{a}},u).$$

Proof. 

The proof is provided in Appendix A. □

The following theorem can then be proved in the general K = 2 case.

Theorem 5.

Let a be a transaction of order n for which K = 2. Let ${\sigma }_1$ and ${\sigma }_2$ be the IRRs of the two terms in the unique partition of a, and assume ${\sigma }_2$ > −1. Further, it is assumed that $\tau$ = $\frac{(1+{\sigma }_1)}{(1+{\sigma }_2)}>\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$.

Let $r^{+}$ and $r^{-}$denote the larger and smaller roots of the quadratic equation

$$(n-1)x^2-[n+\tau (n-2)]x+\tau (n-1)=0$$

Let the transaction b($\theta$) be defined as in Equation (2) above, and let the quantities $\theta (r)$ = ${{[1+(\left(n-1\right)r-n)\frac{(1+{\sigma }_{1)}}{r^{(n-1)}}}^{(n-1)}]}^{-1},$ where r can be either $r^{+}$ or $r^{-}$.

Then,

(i) 

If a has an IRR $\rho$ such that $\rho$is less than the smallest IRR of b($\theta (r^{-}))$ , then $\rho$ is the unique IRR of a.

(ii) 

If a has an IRR $\rho$ such that $\rho$ is greater than the largest IRR of b($\theta (r^{+}))$ , then $\rho$is the unique IRR of a.

Proof. 

If either of the conditions in (i) or (ii) hold, then the corollary to Theorem 4 implies that $\rho$ must be the unique IRR of $\widehat{\mathbf{a}}$. Lemma 3 then implies that NPV(a, u) $\ge$ NPV($\widehat{\mathbf{a}}$, u) > 0 for ${\sigma }_2$ < u < $\rho$ and that NPV(a, u) $\le$ NPV($\widehat{\mathbf{a}}$, u) < 0 for $\rho$ < u < ${\sigma }_1$, hence establishing that $\rho$ is indeed the unique IRR of a and concluding the proof. □

Corollary 2.

For a transaction a as in Theorem 5, if a has an IRR $\rho$ such that $\rho$ lies between the smallest IRR of b($\mathsf{\theta }({\mathrm{r}}^{-}))$ and the largest IRR of b($\mathsf{\theta }({\mathrm{r}}^{+}))$, then all of the IRRs of a must lie in this range.

Figure 2 illustrates the various bounds which underpin Theorems 4 and 5. The figure is for the specific example in which ${\sigma }_1$ = 0.1 and ${\sigma }_2$ = −0.2666 and hence, $\tau$ = 1.5. The horizontal axis represents n. The two horizontal lines are at 1 + ${\sigma }_1$ and at 1 + ${\sigma }_2$, respectively. For n $\le$ 10, $\tau$ < $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$, so for these values of n, any transaction will have a unique IRR: this corresponds to the portion of the chart to the left of the curved lines.

For n $\ge$ 11, the inner pair of curved lines represent the quantities $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}$ and $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$, and the outer pair of curved lines represent the third IRRs of b($\mathsf{\theta }({\mathrm{r}}^{+}))$ and b($\mathsf{\theta }({\mathrm{r}}^{-}))$, respectively. So, by Theorem 5, if a transaction a for which K = 2 has an IRR such that 1 plus that IRR lies above the top curved line or below the bottom curved line, then that IRR will be the unique IRR of a.

What Figure 2 illustrates is that Theorem 5 has interesting content for values of n such that $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$ is smaller than but still relatively close to $\tau$, that is, for values of n which are just larger than $\frac{2\sqrt{\tau }}{\sqrt{\tau }-1}$.

5. Further Results Regarding the Distribution of IRRs

This section now considers general transactions (that is, with K $\ge$ 2) and proves some new results regarding the distribution of IRRs.

The implication of Theorem 2 above is that for transactions for which $\mathsf{\tau }>\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$, then a can have at most one IRR such that 1 plus that IRR lies in the interval [$\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{-}}$, (1 + ${\sigma }_1$) [: and can have at most one IRR such that 1 plus that IRR lies in the interval] (1 + ${\mathsf{\sigma }}_{\mathrm{K}}$), $\frac{(1+{\mathsf{\sigma }}_1)}{{\mathrm{r}}^{+}}$]. The purpose of this section is to prove what is essentially a type of converse result. Let a be a transaction in which the IRRs of the unique partition of a are ${\sigma }_1$, … ${\mathsf{\sigma }}_{\mathrm{K}}$, and suppose that for some k < K, ${\sigma }_{\mathrm{k}}$ and ${\sigma }_{\mathrm{k}+1}$ are sufficiently far apart, in a sense which will be established. Then, what will be proven is that there is a continuous interval within the range ] ${\sigma }_{\mathrm{k}+1}$, ${\sigma }_{\mathrm{k}}$ [ such that a can have at most one IRR such that 1 plus that IRR lies in the interval.

It is first necessary to introduce some more notation.

Let us choose some specific k which can be any value in the range 1, …, (K − 1). For this value of k, define $l$ = max{j: ${\mathit{a}}_j\left(k\right)>0$ }, that is, $l$ is the index of the last non-zero term in a(k). Similarly, define f as the index of the first non-zero term in a(k + 1).

Suppose ${\sigma }_{\mathrm{k}+1}$ > −1, and define $\mathsf{\tau }(\mathrm{k})$ as $\mathsf{\tau }(\mathrm{k})$ = $\frac{(1+{\mathsf{\sigma }}_{\mathrm{k}})}{(1+{\mathsf{\sigma }}_{\mathrm{k}+1})}$. Then, the following result holds.

Theorem 6.

Let a be a transaction with the unique partition a(1), … a(K) into pure investments. Let k be any integer such that either k < K − 1 or k = K − 1 and ${\mathsf{\sigma }}_{\mathrm{K}}$ > −1. For this value of k, define $\tau (k)$, l, and f as above. Then, if $\tau (k)$ > $\frac{{(f-l+2)}^2}{{(f-l)}^2}$, the transaction a can have at most one IRR $\rho$ such that 1 + $\rho$ lies in the interval ]$\frac{(1+{\mathsf{\sigma }}_{\mathrm{k}})}{{\mathrm{r}}^{+}}$, $\frac{(1+{\mathsf{\sigma }}_{\mathrm{k}})}{{\mathrm{r}}^{-}}$[, where $r^{+}$ and $r^{-}$ are the larger and smaller roots, respectively, of the quadratic equation

$$(f-l+1){\mathrm{x}}^2-[(f-l+2)+\tau (k)(f-l)]\mathrm{x}+\tau (k)(f-l+1)=0.$$

Proof. 

The proof is provided in Appendix B. □

The interval defined in Theorem 6 will only exist for a given k if $\mathsf{\tau }(\mathrm{k})$ > $\frac{{(f-l+2)}^2}{{(f-l)}^2}$ and will be broader the larger the left-hand side of this inequality is relative to the right-hand side. So, in a sense, Theorem 6 is only likely to provide useful information for transactions which, for some value of k, have a large step change in the value of ${\mathsf{\sigma }}_{\mathrm{k}}$ between k and (k + 1) and/or have a large gap between the index of the last non-zero term of a(k) and the first non-zero term of a(k + 1). The theorem is therefore likely to be of interest only for special transactions which satisfy these conditions.

However, the case that Theorem 6 does not cover is the case in which k = (K − 1) and ${\mathsf{\sigma }}_{\mathrm{K}}$ = −1, that is, the case in which the last non-zero term in a is negative. As we will see, a limiting argument based on Theorem 6 can be applied to study this case, and since in this limiting argument, the relevant value of $\mathsf{\tau }(\mathrm{k})$ tends to infinity, the relevant interval of uniqueness in applying Theorem 6 will become long, and a powerful result will arise. This result is as follows.

Theorem 7.

Let a be a transaction whose final non-zero term is strictly negative and suppose that a has at least one IRR. Let a(1), … a(K) be the unique partition of a into pure investments, and let l be the index of the last non-zero term in a(K − 1), and let f be the index of the first non-zero term in a(K). Then,

(i) 

a can have no more than one IRR $\rho$ such that

$$1+\rho <(1-\frac{1}{(f-l+1)})(1+{\sigma }_{(K-1)}).$$

(ii) 

a has at least one IRR $\rho$ such that

$$1+\rho \ge (1-\frac{1}{(f-l+1)})(1+{\sigma }_{(K-1)}).$$

Proof. 

The proof is provided in Appendix B. □

The following example illustrates an application of Theorem 7, and also Theorem 3.

Example 1.

Let a be the following transaction of an order n, namely,

a = (−1, a, 0, 0, …………0, −c),

where a > 0 and c > 0.

Then, in the notation of Theorem 7, (1 + ${\sigma }_1$) = a. Further, l = 1 and f = n, so (f − l + 1) = n.

So, applying Theorem 7 implies that if a has any IRRs, it has at most one IRR $\rho$ such that

1 + $\rho$ < $(1-\frac{1}{\mathrm{n}}$)(1 + a), and at least one IRR $\rho$ such that 1 + $\rho$ $\ge$ $(1-\frac{1}{\mathrm{n}}$)(1 + a).

But for this particular example, the Theorem 7 bound is the same as the Theorem 3 bound. Hence, by Theorem 3, if a has any IRRs, it has at least one IRR $\rho$ such that

1 + $\rho$ $\le$ $(1-\frac{1}{\mathrm{n}}$)(1 + a) and at most one IRR $\rho$ such that 1 + $\rho$ > $(1-\frac{1}{\mathrm{n}}$)(1 + a).

Therefore, it follows immediately that if a has a repeated IRR, it must occur at

$(1-\frac{1}{\mathrm{n}}$)(1 + a) − 1, and it is not difficult to prove that if a has an IRR at this value, then it must be a repeated IRR. It then follows from the above that if a has two separate IRRs, one must be less than $(1-\frac{1}{\mathrm{n}}$)(1 + a) − 1, and the other must be greater.

The properties of this example, which are fairly immediate consequences of Theorems 7 and 3, can be verified directly at the expense of some fairly tedious algebra.

6. An Open Question

This paper has shown how the partitioning theorem proved by Cuthbert (2018) can be used to prove further results regarding the distribution of IRRs beyond those proved by Cuthbert (2021).

Another area in which it may be possible to establish some more implications of the partitioning theorem is regarding the question of the relationship between the quantity $\tau$, as defined in this paper, and the number of IRRs of the transaction. There are intriguing indications that there is indeed some relationship between these quantities, as we will now see.

Let r denote the number of IRRs of a transaction (including repeated values). First of all, consider the case in which r = 3 (which is the smallest number of IRRs a transaction with multiple IRRs can have if its last term is positive.) Then, we know from Theorem 1 of Cuthbert (2021) that such a transaction must have $\mathsf{\tau }>\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$; however, for r = 3, $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$ = $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-\mathrm{r}+1)}^2}$.

So, for r = 3, the formula $\tau$ $\ge$ $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-\mathrm{r}+1)}^2}$ holds.

Now consider the case r = n (which, for transactions in which the last term is positive, can only occur if n is odd.) In this case, it can be proved that $\mathsf{\tau }\ge {\mathrm{n}}^2$: (this is proved in Appendix C). But again, for r = n, it holds that ${\mathrm{n}}^2$ = $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-\mathrm{r}+1)}^2}$.

So, what we have shown is that the formula

$$\tau \ge \frac{{\mathrm{n}}^2}{{(\mathrm{n}-\mathrm{r}+1)}^2}$$

holds for the cases in which r = 3 and r = n (and also trivially for r = 1).

This raises an immediate question: does the above formula hold for values of r between 5 and (n − 1)(note that since r must be odd, the case r = 4 does not arise)? Answering this question for values of r between 5 and (n − 1) looks difficult and could involve some complicated combinatorial challenges. But if it were possible to establish this relationship, it would offer a convenient way of rapidly placing an upper bound on the possible number of IRRs of any given transaction.

So, this paper ends with an open question, or rather, with two open questions. Let a be a transaction of order n (i.e., a length of (n + 1)) whose last term is positive. Let ${\sigma }_1$ be the IRR of the first term in the unique partition of a, let ${\mathsf{\sigma }}_{\mathrm{K}}$ be the IRR of the last term, and define

$\tau$ = $\frac{(1+{\mathsf{\sigma }}_1)}{(1+{\mathsf{\sigma }}_{\mathrm{K}})}$. Let r be the number of IRRs of a (including repeated values).

Then,

(i)

Is it possible to develop a lower bound for $\tau$ as a function of n and r?

And, more specifically,

(ii)

The formula $\tau$ $\ge$ $\frac{{\mathrm{n}}^2}{{(\mathrm{n}-\mathrm{r}+1)}^2}$ holds for r = 3 and r = n (and trivially for r = 1). Does this formula hold for r = 5 to (n − 1)?

7. Conclusions

This paper concerns the derivation of some further implications of the partitioning theorem proved by Cuthbert (2018). The partitioning theorem and its various consequences are of theoretical interest in their own right. But they also have important practical implications, which are worth restating here.

As shown by Cuthbert (2018), it is a simple task to derive the unique partition for any given transaction. Once that unique partition is known, then:

• The sufficient condition derived by Cuthbert (2021), namely, that a transaction has a unique IRR if $\tau \le \frac{{\mathrm{n}}^2}{{(\mathrm{n}-2)}^2}$, means that the problem of the potential existence of multiple IRRs can be immediately excluded for many transactions likely to be encountered in practice.
• As shown in the paper by Magni and Cuthbert (2018), the unique partition, in conjunction with Magni’s concept of the average internal rate of return, can be used to define a pure investment average internal rate of return (PIAIRR). The PIAIRR is a good candidate for a reliable money-weighted rate of return which may be used by practitioners in assessing investment performance.
• The results from Cuthbert (2021) and in the present paper provide useful information about where the IRRs of certain transactions are likely to be located.

But as also noted in this paper (see in particular Section 6), all of the implications of the partitioning theorem are not yet fully understood. In particular, there are indications that there may be a relationship between the quantity $\tau$ and the number of IRRs of a transaction. This is an area in which further research is required. But if it were possible to place a lower bound on $\tau$ in terms of the number of IRRs of a transaction, then this would have the useful implication that having knowledge of $\tau$ (which is readily determinable) would immediately place an upper bound on the number of possible IRRs.

In terms of future research, one priority is clearly to tackle the above open question. As has been observed, this question has been solved at the two extremes. At one extreme, where the number of IRRs of the transaction takes on the smallest possible value consistent with there being multiple IRRs, the proof essentially depends on pursuing the implications of the fact that such a transaction must have at least one IRR for which the slope of the net present value at that IRR is non-negative, that is, the approach depends on an analytical or calculus-type argument. At the other extreme, where the transaction has the maximum possible number of IRRs, the argument depends on the algebra of polynomials. Whether these two approaches can be combined to tackle the problem for the unsolved intermediate cases is unclear; it may be that some radically different approach is required.

As noted by Cuthbert (2021), it is a curiosity that almost all of the consequences of the partitioning theorem which have been derived so far depend only upon the relative magnitudes of the IRRs of the terms in the unique partition of a transaction and not on the relative sizes of the amounts of capital invested at different stages of a project’s life. It seems intuitive that stronger results should be derivable if the relative magnitudes of the different transactions in the unique partition were also brought into the argument. This could be another fruitful area for further research.

It was noted in the introduction that this paper is a contribution to the process of uncovering the links between the properties of the unique partitioning of a transaction into pure investments and the properties of the IRRs of the transaction. Attaining a better understanding of these links is important because such an understanding builds up the ability, if one is designing a transaction from scratch, to do so in a way that avoids unwelcome pathologies in the IRRs.