Deep Partial Hedging
Abstract
:1. Introduction
Basic Model Setting
- becomes maximal in the context of quantile hedging, or;
- becomes minimal in the context of efficient hedging.
2. Contribution of this Note
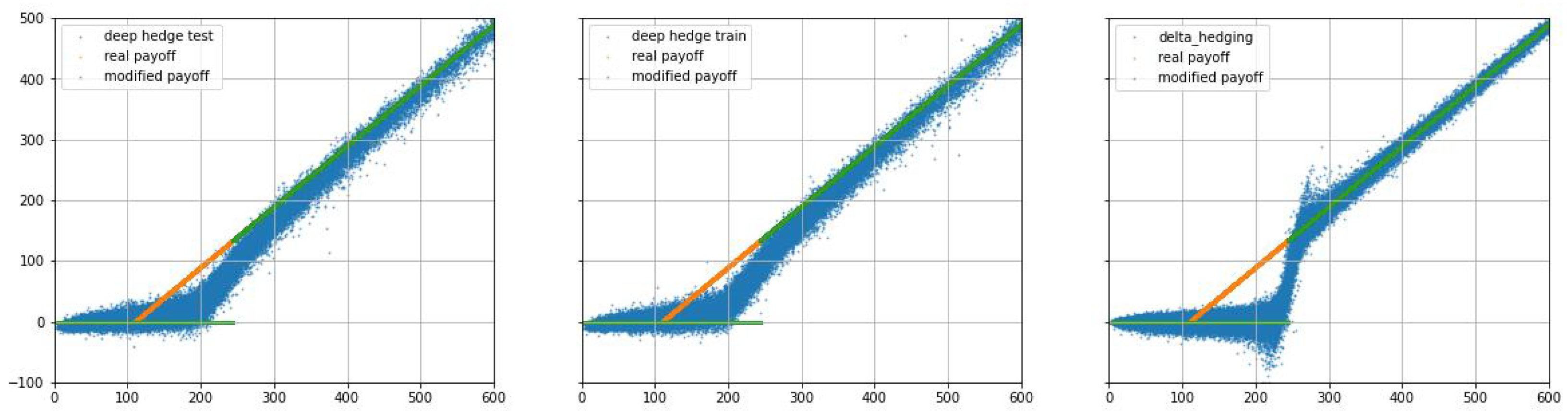
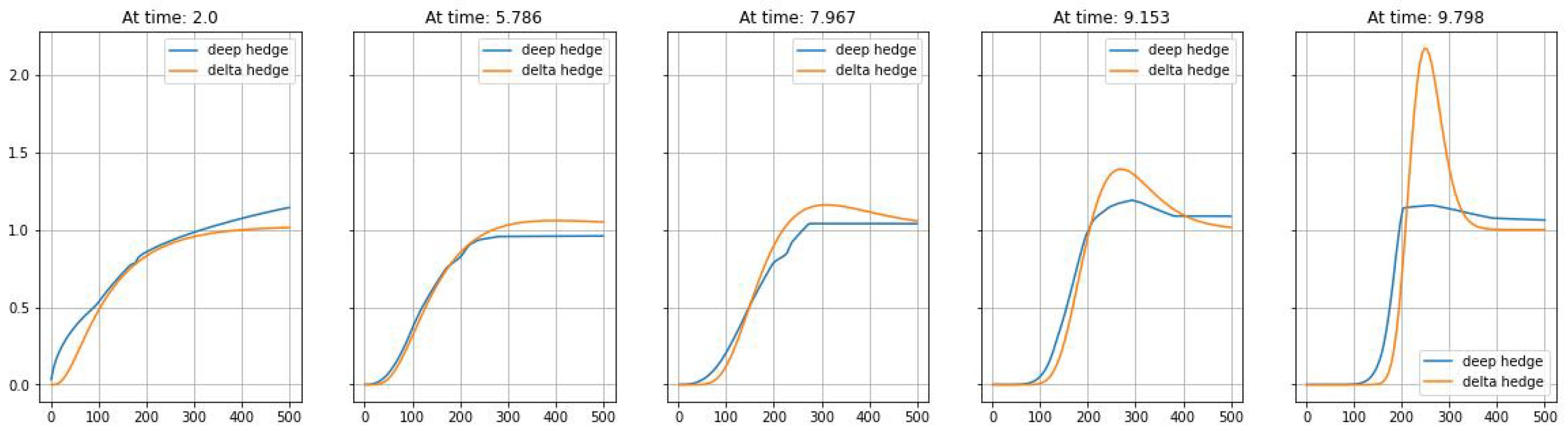
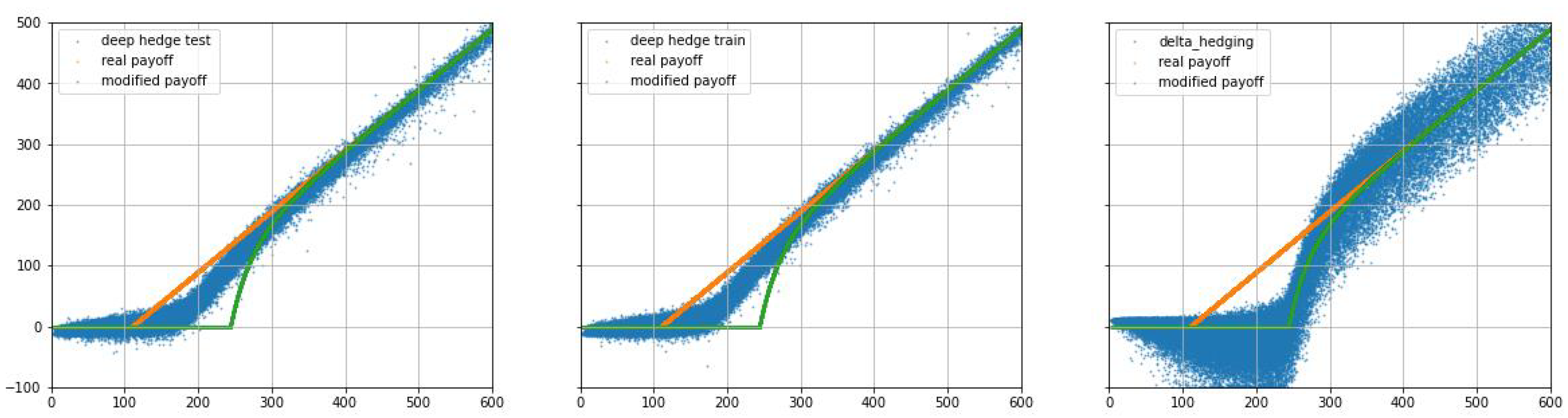
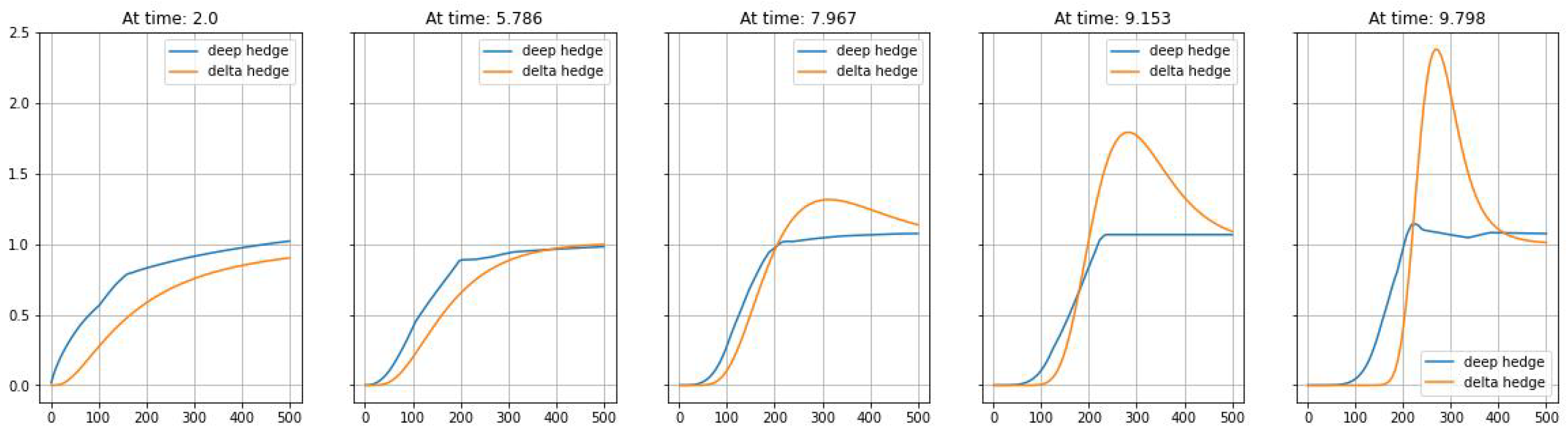
3. Numerical Results
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | In our numerical experiments, we set . |
| 2 | https://github.com/justinhou95/DeepHedging, accessed on 16 May 2022. |
References
- Buehler, Hans, Lukas Gonon, Josef Teichmann, and Ben Wood. 2019. Deep hedging. Quantitative Finance 19: 1271–91. [Google Scholar] [CrossRef]
- Föllmer, Hans, and Peter Leukert. 1999. Quantile hedging. Finance and Stochastics 3: 251–73. [Google Scholar] [CrossRef]
- Föllmer, Hans, and Peter Leukert. 2000. Efficient hedging: Cost versus shortfall risk. Finance and Stochastics 4: 117–46. [Google Scholar] [CrossRef] [Green Version]
- Föllmer, Hans, and Alexander Schied. 2016. Stochastic Finance. Berlin and Boston: de Gruyter. [Google Scholar]
- Kingma, Diederik, and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. Paper presented at the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, May 7–9. [Google Scholar]
- Leukert, Peter. 1999. Absicherungsstrategien zur Minimierung des Verlustrisikos. Ph.D. thesis, Humbold Universität zu Berlin, Berlin, Germany. [Google Scholar]
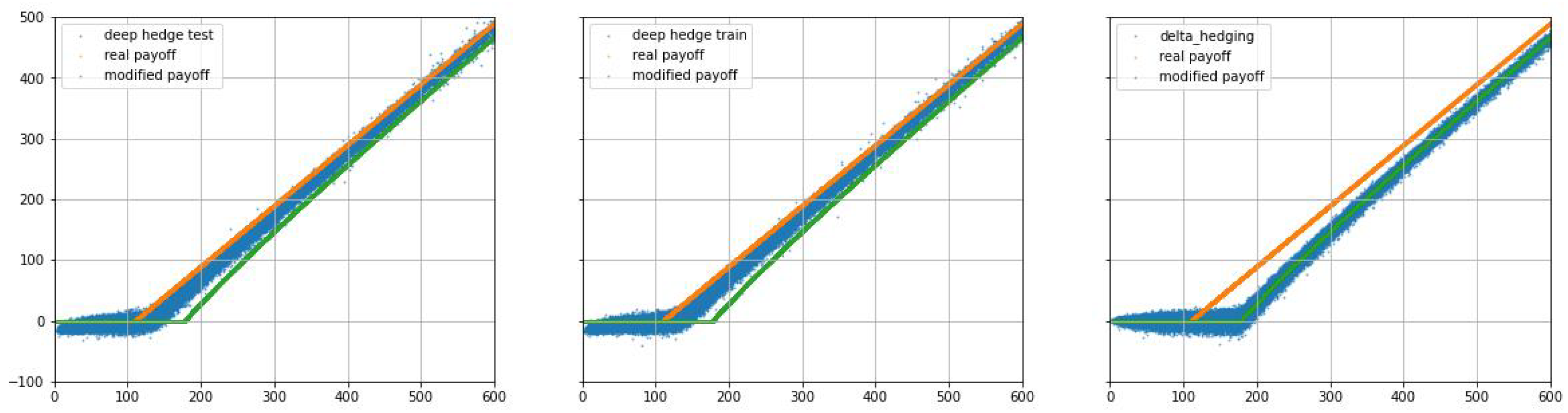
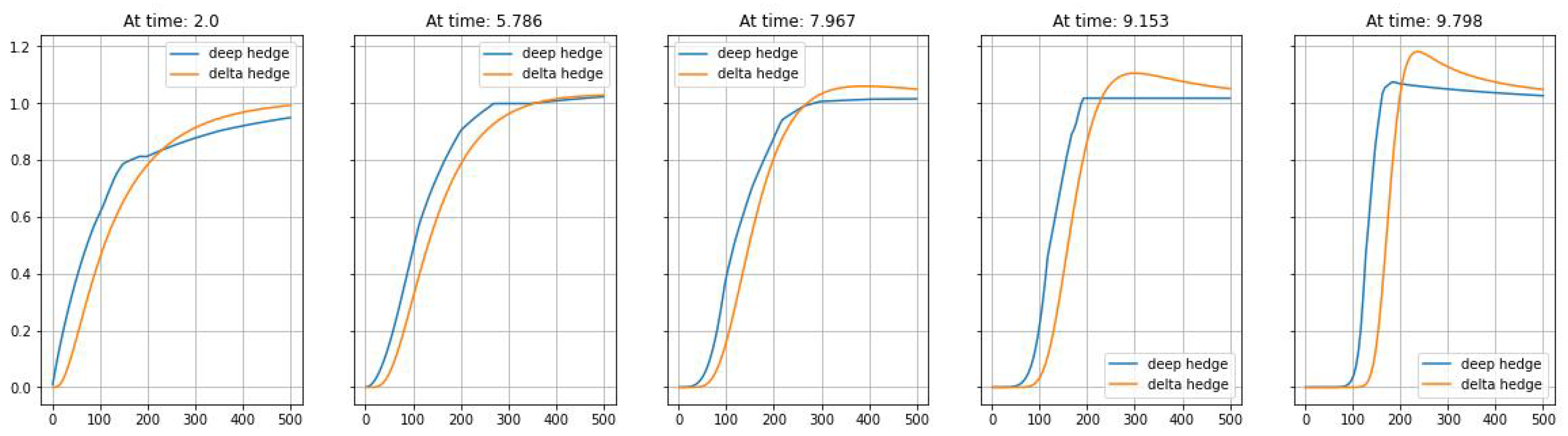
| deep hedge | 18.14 | 16.75 | 14.31 |
| delta hedge | 19.64 | 36.69 | 32.63 |
| deep hedge | 18.09 | 16.39 | 15.58 |
| delta hedge | 26.45 | 44.01 | 37.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Krabichler, T.; Wunsch, M. Deep Partial Hedging. J. Risk Financial Manag. 2022, 15, 223. https://doi.org/10.3390/jrfm15050223
Hou S, Krabichler T, Wunsch M. Deep Partial Hedging. Journal of Risk and Financial Management. 2022; 15(5):223. https://doi.org/10.3390/jrfm15050223
Chicago/Turabian StyleHou, Songyan, Thomas Krabichler, and Marcus Wunsch. 2022. "Deep Partial Hedging" Journal of Risk and Financial Management 15, no. 5: 223. https://doi.org/10.3390/jrfm15050223
APA StyleHou, S., Krabichler, T., & Wunsch, M. (2022). Deep Partial Hedging. Journal of Risk and Financial Management, 15(5), 223. https://doi.org/10.3390/jrfm15050223






