3.1. Characteristics of the Base Series
The daily cryptocurrency data sets for Bitcoin and Ethereum were taken from Yahoo finance. The data set began on 7 August 2015 and ended on 23 July 2021, producing 2170 daily observations for the cryptocurrencies. An overall sample of 5 years of daily data was chosen because this afforded a sufficient number of data points within the sub-samples for accurate analysis whilst not averaging the results over an excessively long period, particularly in the first sub-sample. The S&P500 index series was drawn from the Federal Reserve Bank of St. Louis (FRED) database,
FRED (
2021), and covered the same period. However, there were fewer trading days for the US Stock Exchange, which is more impacted by public holidays than cryptocurrencies. The three series were spliced together, missing observations were removed, and the total data set for the combined series consisted of 1504 daily observations. The data were then split into two sub-periods, pre-COVID-19, which ran from 7 August 2015 to 31 December 2019, consisting of 1107 daily observations. The post-COVID-19 data set, commenced on 2 January 2020 and terminated on 23 July 2021, consisting of 388 daily observations.
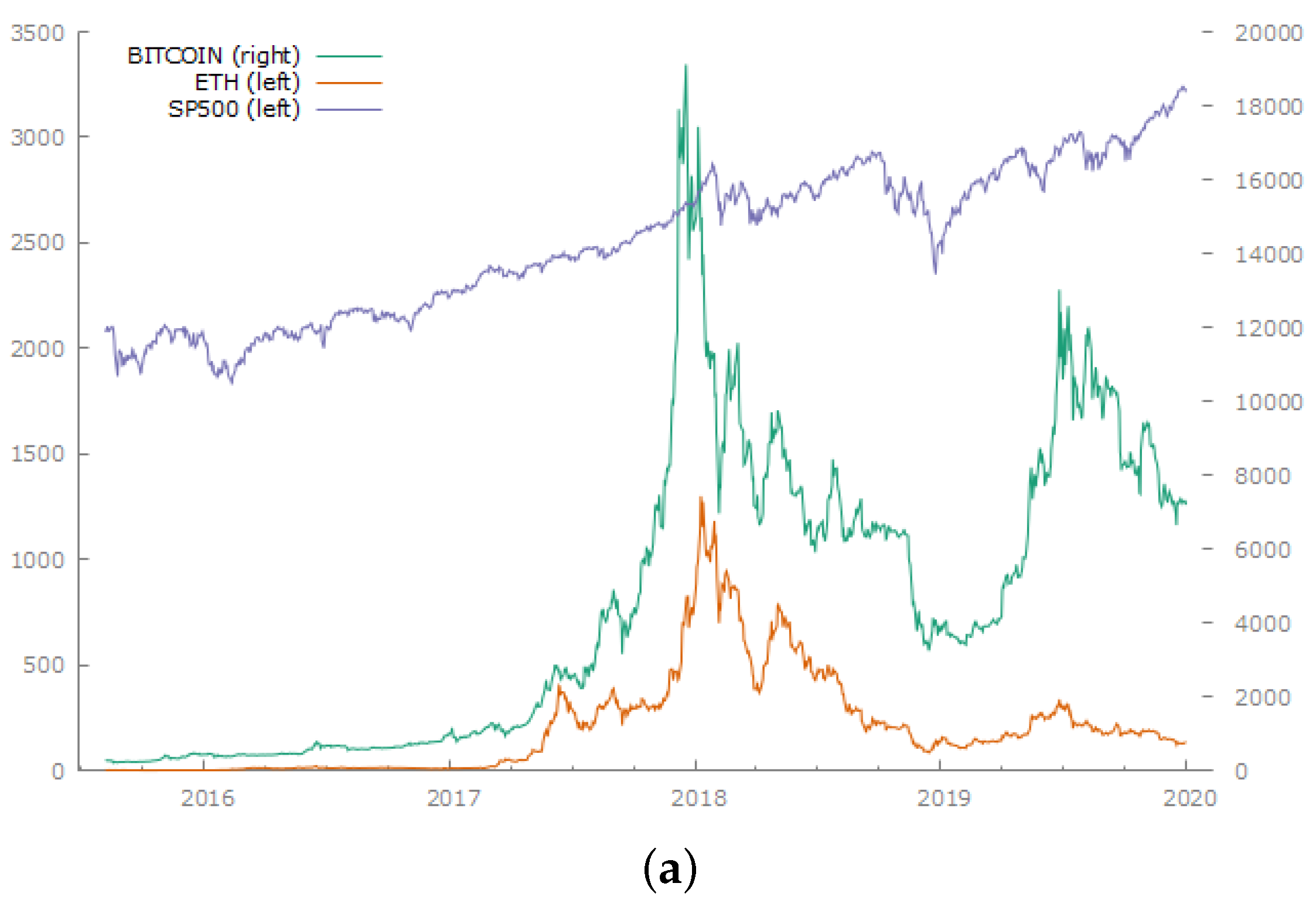
Graphs of the base price series and returns for the two sample time periods are shown in
Figure 1 and
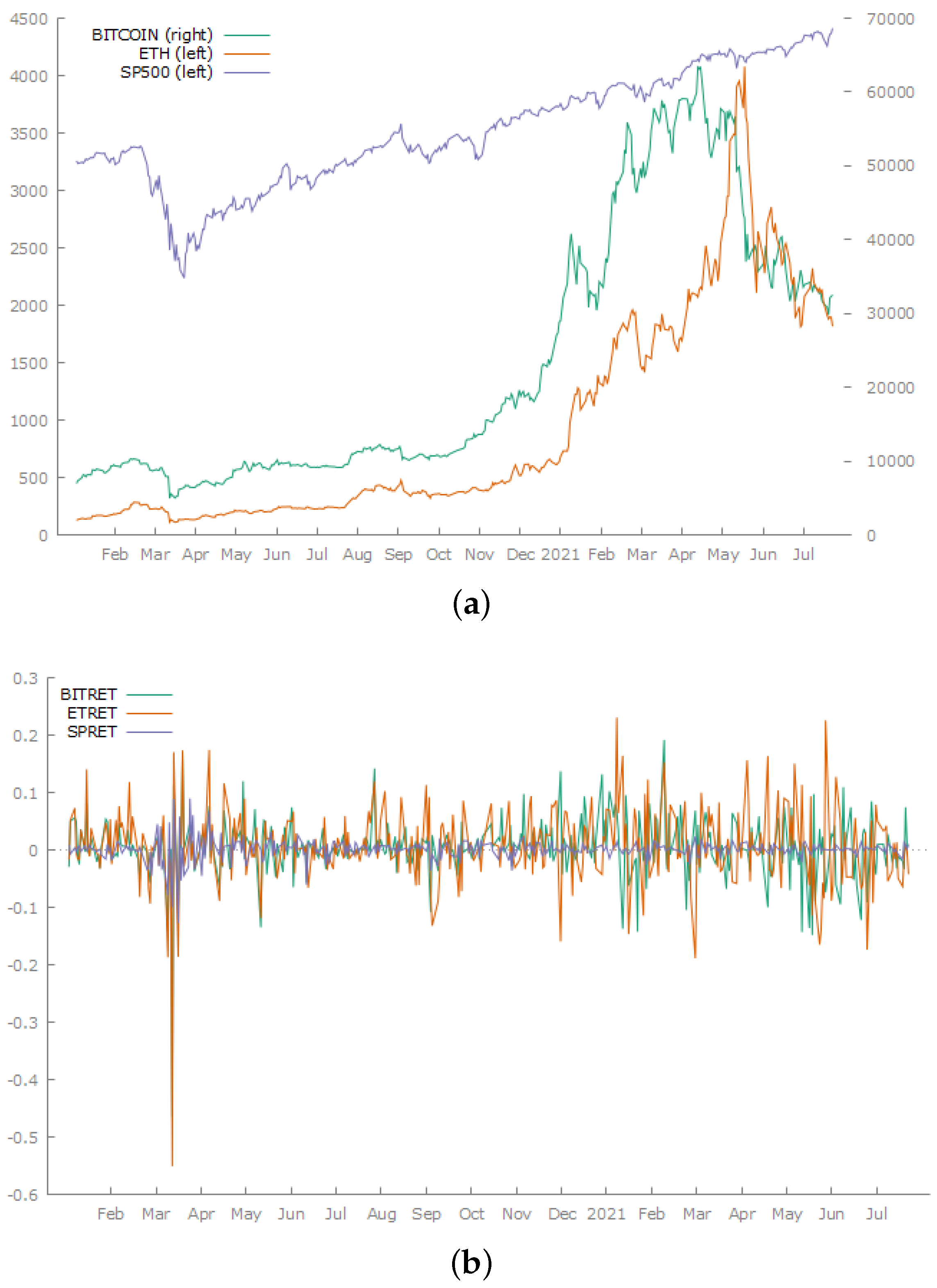
Figure 2. The three base series all show evidence of trending behaviour in both periods. Plots of the price levels and returns on the series in the post-COVID-19 period are shown in
Figure 2.
Kwiatkowski et al. (
1992) unit root tests, or more commonly termed KPSS tests, were undertaken on the levels of the series for both the pre- and post- COVID-19 samples, with the tests including a trend. The results are shown in
Table 1. These show that all three series—Bitcoin, Ethereum and the S&P500 index in levels—reject the null hypothesis of stationarity at the 1 percent level. As a result, all of the analyses were performed on the continuously compounded return series.
Descriptive statistics for these series are presented in
Table 2. It is apparent in
Table 2 that the two cryptocurrencies have higher mean returns, a greater range of returns and considerably higher standard deviations in both periods than those of the S&P500 return series. All series display negative skewness and high kurtosis relative to a normal distribution, which would have a kurtosis of 3.
The results of the four different tests of conformance to a normal distribution are reported in the bottom panels, below the descriptive statistics, in
Table 2. All four tests, namely, the Doornik–Hansen, Shapiro–Wilk, Lilliefors and Jarque–Bera tests reject the null hypothesis of a Gaussian distribution at greater than the one percent level for all three return series in both periods.
The Pearson correlation test is based on the assumption of linearity and conformance to a normal distribution. For this reason, the tests of association reported in this paper include non-parametric tests and non-linear measures of association.
3.4. Non-Linear Non-Parametric Measures of Association in Period 1
The R library package kdecopula
Nagler (
2018) was used to fit copulas to paired return series using kernel density estimates. The package contains functions that are used to estimate the copula density from data. The only mandatory input is an
matrix of copula data, in effect, data with standard uniform margins.
Bouri et al. (
2018) suggested three advantages for the use of copulas in assessing dependence. First, the copula method was designed to capture the complex and non-linear dependence structure of a multivariate distribution, enabling scrutiny of both tail dependence and the asymmetric dependence. Second, the marginal behaviour and the dependence structure are separated by the framework of copulas. This facilitates model specification and model estimation. Copulas can jointly combine different univariate models through their copula functions. Finally, copulas are invariant to increasing and continuous transformations; see
Ning (
2010).
The empirical application of copulas to financial time series of returns and the method for fitting marginal distributions was pioneered by
Patton (
2002) in his PhD thesis “Applications of Copula Theory in Financial Econometrics”, and a further description was provided in
Patton (
2006, pp. 536–37). He suggested the following models for the marginal distributions of a pair of return series:
A GARCH(1,1) model with a t-distribution was used to estimate the marginal distribution for the return series. This provided a first approximation, given that the package includes code to transform the data to uniform margins. (In the case of BITCOIN returns in period 1, an ARCH model was used, as GARCH failed to converge).
A further explanation of this approach, which features the use of a common but limited information set to model the marginal distributions, was provided by
Patton (
2013).
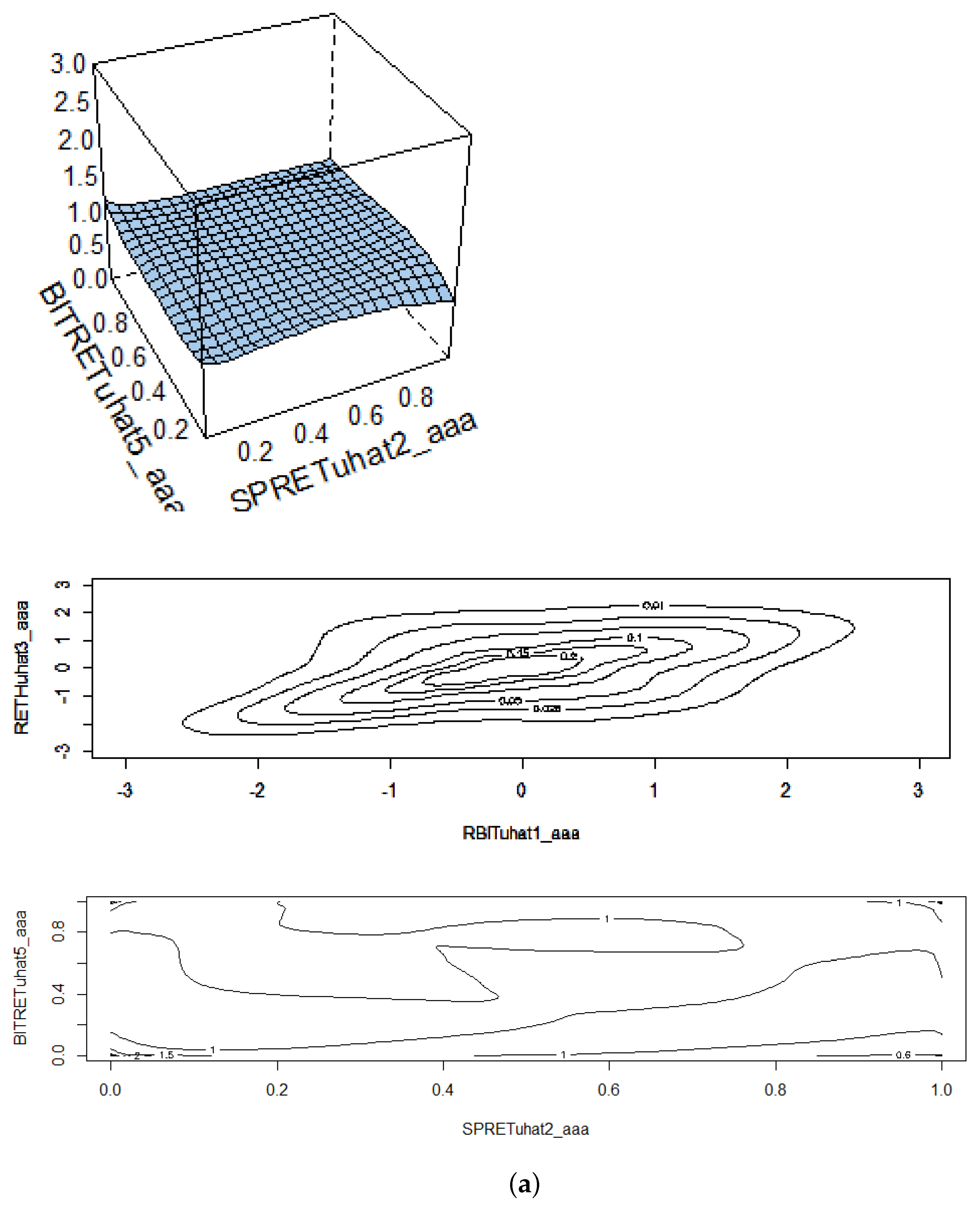
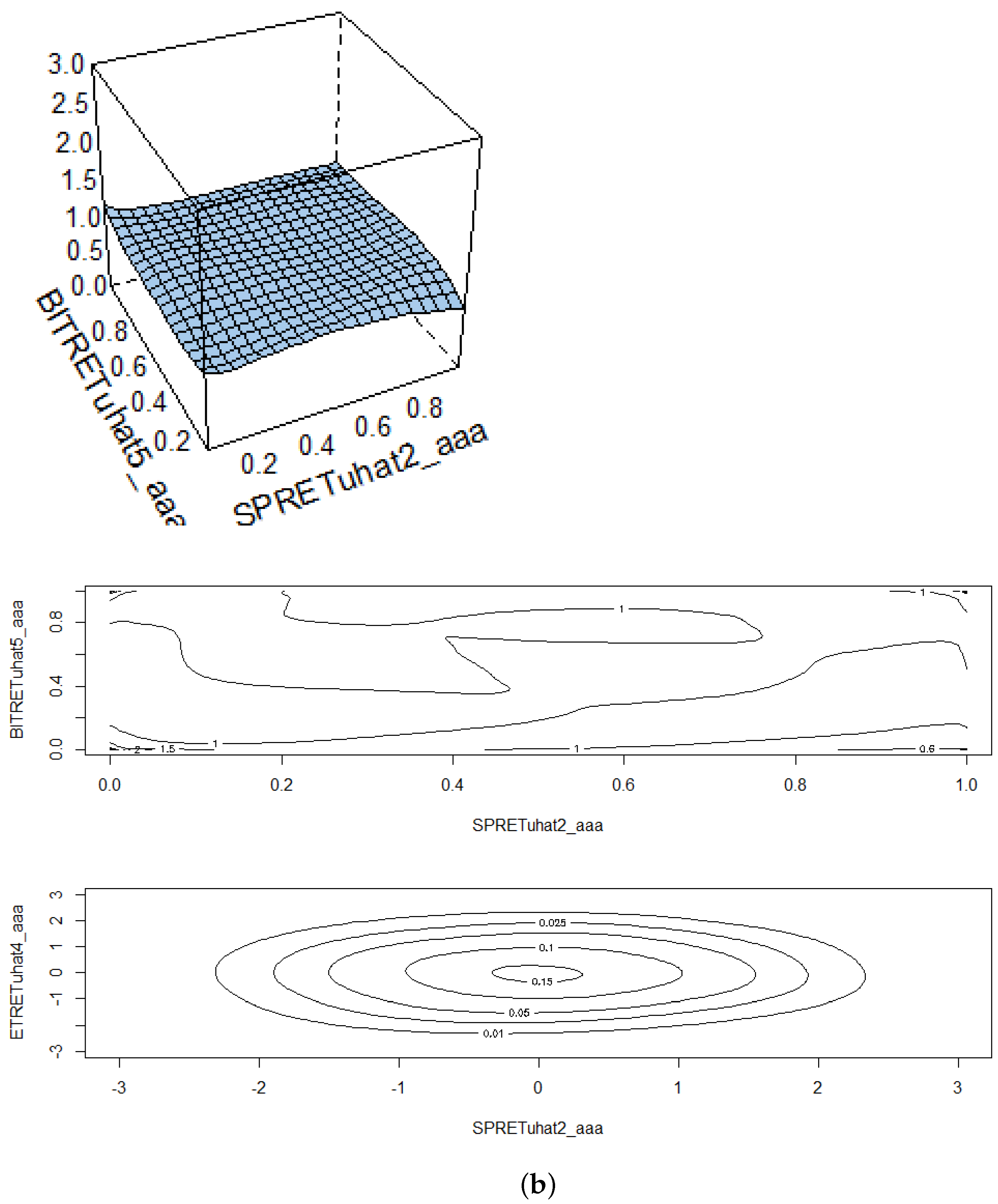
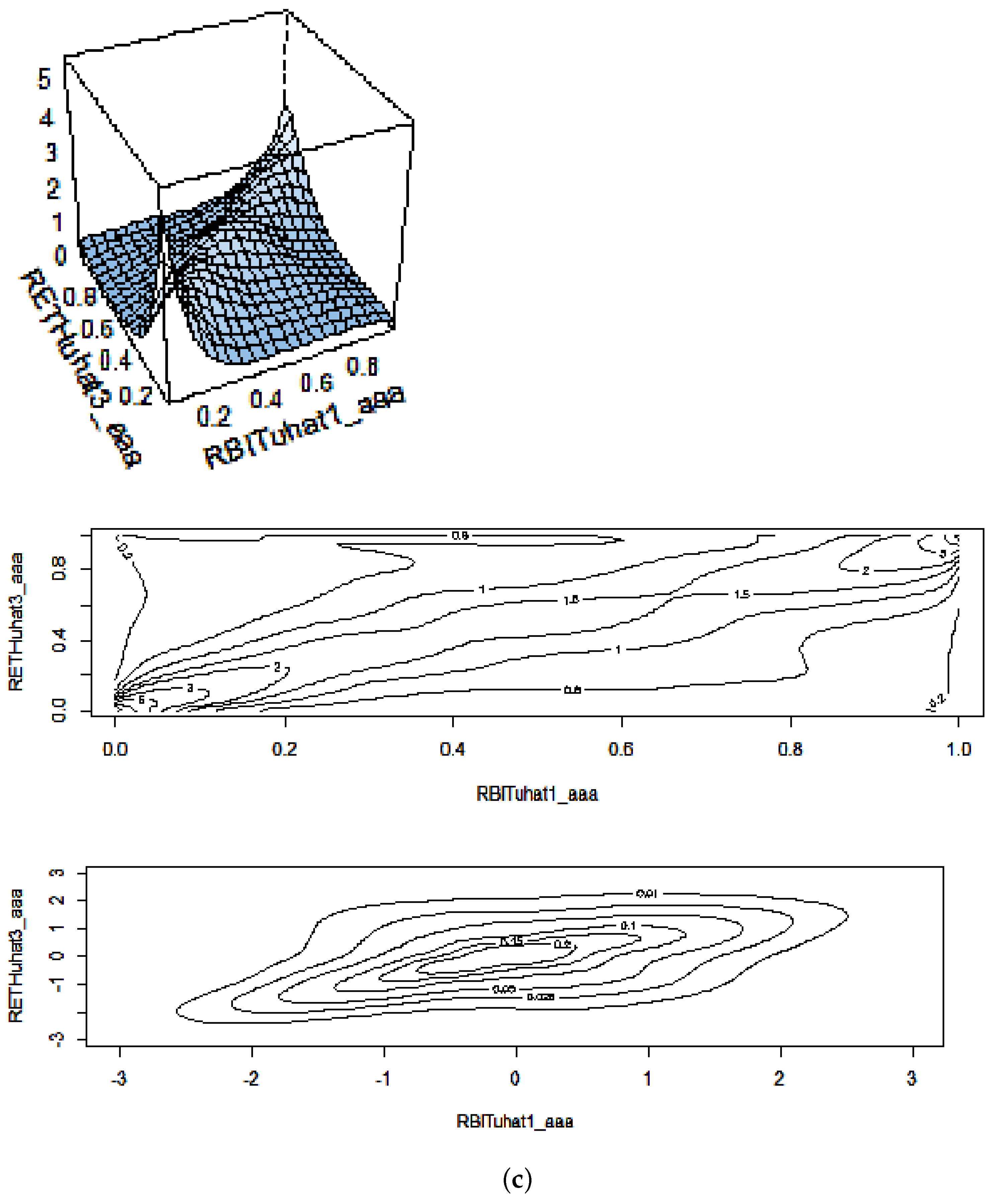
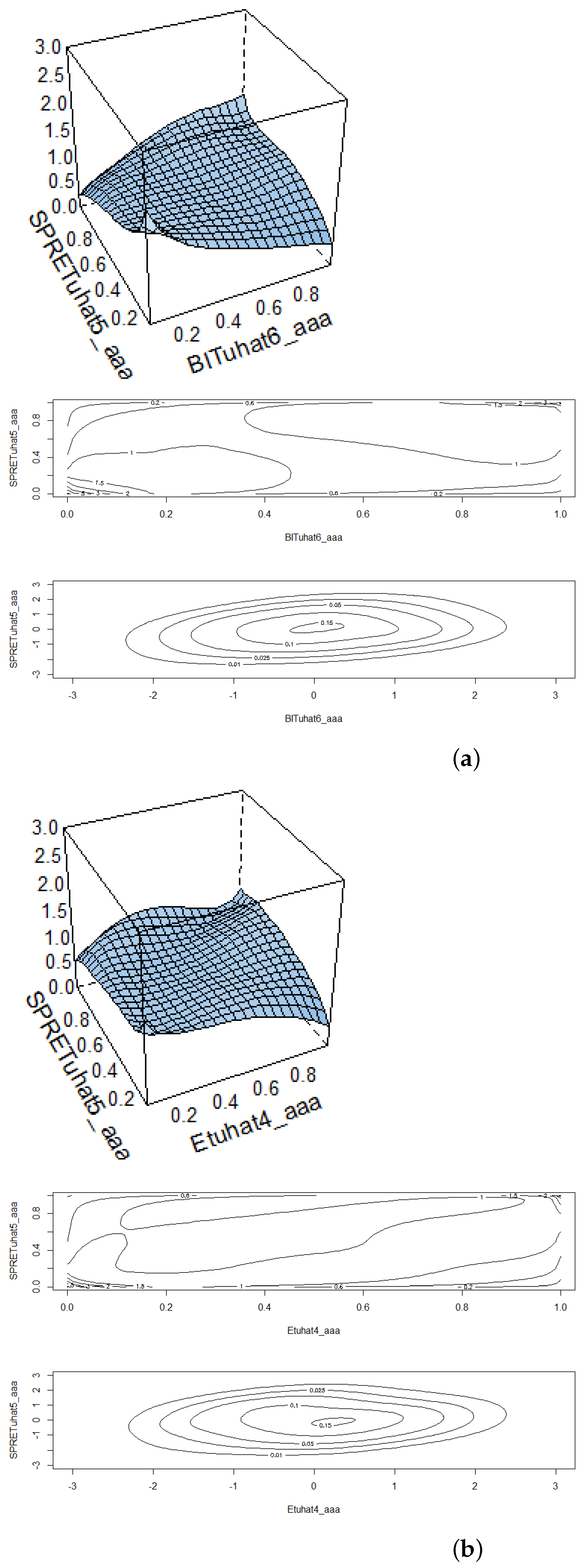
Table 8 provides a description of the results from fitting copulas to the paired series during the pre-COVID-19 period. The results are consistent with the previous estimates. There is a significant association between the returns on Bitcoin and Ethereum but a minimal association between the cryptocurrency returns and those on the S&P500 index. The diagrams in Panels A and C of
Figure 3 show that the copula surfaces are fairly flat when cryptocurrencies are paired with S&P500 returns, and the contour density plots, particularly in panel C, are almost circular, depicting low levels of association. The first contour plot in each series in the figures shows the situation with uniform marginals.
A variety of measures of association are used in
Table 8, and I shall comment briefly on the properties of some of the less frequently used ones. The
Blomquist (
1950) measure of association was developed for circumstances in which it would be valid under weak assumptions about the distribution of the data and easy to apply in practice.
Blomquist (
1950, p. 593) suggested that we consider two sample medians
and
. The cdf
is assumed to have continuous marginal cdf’s
and
in order for the probability of obtaining two equal
x-values or two equal
y-values in the sample to be zero.
Blomquist (
1950) then divided the
-plane into four regions using the lines
and
. He then suggested that some information about the correlation between
x and
y can be obtained by the number of sample points, say
belonging to the first or third quadrants, compared with the number, say
belonging to the second or fourth quadrants. After suggesting a couple of further adjustments related to the total sample size, he then suggested that a measure of correlation can be defined as follows:
Genest and Verret (
2005, p. 521) noted that “testing for independence between two continuous random variables
X and
Y is an old but important problem that has been the object of much attention in the past century. Though a great deal of literature is available on the subject, test procedures based on Pearson’s correlation continue to be the most commonly used in practice. This is in spite of the well-known fact that this coefficient is merely a measure of linear association whose effectiveness, therefore, is questionable outside the normal paradigm, including for testing purposes”. They also suggest that all modern concepts of dependence and stochastic orderings are based on copulas, including Spearman’s rho, Kendall’s tau and other nonparametric alternatives to Pearson’s correlation coefficient.
Embrechts et al. (
2002) pointed out that the dependence structure in a pair of variables
with continuous distribution
H and that margins
F and
G are best characterised by
its unique underlying copula, implicitly defined on the unit square by the following:
Modern concepts of dependence and stochastic orderings are based on copulas, which includes Spearman’s rho, Kendall’s tau and various nonparametric alternatives to Pearson’s correlation coefficient.
The copula of a random pair
is unaffected by monotone increasing transformations of the margins. Given a random sample from
H the associated pairs of ranks
are maximally invariant and can be used for a test of the hypothesis
or equivalently,
with
for all
A test based on kendall’s tau statistic can be written as
and can be used to reject the null hypothesis, for a large enough sample size
n, where
, where
stands for the cumulative distribution function of a standard normal variable.
Another option based on Spearman’s rho is as follows:
which leads to rejection of the null when the asymptotic
-value
of the two-sided test is too small.
Several other independence test statistics of the form
with specific score functions
often perform as well as or better than standard parametric tests based on Pearson’s empirical correlation
for various classes of alternatives.
Bhuchongkul (
1964) demonstrated that the van der Waerden statistic,
based on
, dominates
for alternatives of the following form:
where
and
are mutually independent random variables and
is a scalar.
Genest et al. (
2010) discussed the close relationship between
Spearman’s (
1906) footrule
Spearman (
1906), which is a nonparametric measure of association, and
Gini (
1914) coefficient. The Spearman footrule can be written as follows:
whereas the indice de cograduazione semplice, introduced by
Gini (
1914), can be written as follows:
The last two measures, reported in
Table 8 and
Table 9, are based on information criteria. Let
Xand
Y be a pair of random variables. If their joint distribution is
and the marginal distributions are
and
, the mutual information is described as follows:
where
is the Kullback–Leibler divergence. Information theory was developed by
Shannon (
1948);
Fano (
1949) developed the concept of mutual information.
Hamdan and Tsokos (
1971) discussed
Linfoot (
1957) informational measure of association between two random variables
X and
Y. The measure
is based on the information gain
in knowing that
X and
Y are mutually dependent with a given bivariate density function compared with the original knowledge that
X and
Y are statistically independent.
Linfoot (
1957) suggested that, if
X and
Y have bivariate normal distributions with correlation coefficient
, then
which led to
Linfoot (
1957) suggestion that an informational measure
of
be defined as follows:
In the case of discrete random variables
X and
Y with bivariate probabilities
and marginal probabilities
and
,
take the following form:
It is also the case that
is equivalent to
Kullback (
1959) distance-like measure between the correlated bivariate distribution and the distribution under independence.
The various measures of association for the three combinations of the paired series returns, as reported in the lower panels of each section of
Table 6, all tell a consistent story. The level of association between returns on Bitcoin and Ethereum is above 0.5, on the basis of the Spearman, Van de-Waerden and Linfoot metrics. For the definition of these measures used, see
Nelsen (
2006);
Genest and Verret (
2005);
Joe (
1989).
Genest and Verret (
2005), in their assessment based on simulations, suggested that, whilst some dependence structures are easier to detect than others, the performance of rank tests can vary substantially from one set of alternatives to another. Pearson’s test seemed to be an acceptable procedure to use when the marginal distributions are normal but not necessarily when they are not. Van der Waerden’s test is likely to perform well whenever Pearson’s test performs well. It also has the additional advantage of being marginal-free. In terms of the limits of their simulation study, van der Waerden’s test seemed to hold a slight edge over Spearman’s and Kendall’s tests, which can be viewed as being essentially equivalent.
The results in
Table 6 suggest that the degree of association between the two cryptocurrencies and the returns on the S&P500 index are virtually zero, as all of the measures bracket zero, either positively or negatively. This suggests that, in this period, investing in cryptocurrencies provides a potential diversification strategy. The concern is whether this remains the case when the market is subjected to the global shock of the pandemic? This is explored in the next sub-section.
3.6. Generalised Measure of Correlation (GMC) Analysis
Table 10 presents the results of the GMC analysis in the two periods, pre- and post-COVID-19, and the results matrix reports the cause at the top of the columns and the response along the rows. If we begin with column 2 in Period 1, SPRET, the continuously compounded return on the S&P500 Index has a negative effect on the Bitcoin return, or a GMC of −0.55 and a negative effect on the Ethereum return of −0.73. The third column indicates that the Bitcoin return BITRET has a negative effect on SPRET of −0.57 and a positive effect on ETRET of 0.83. Finally, the fourth column under ETRET shows that the Ethereum return has a negative effect on SPRET of −0.47 and a positive effect on BITRET of 0.80.
Which way does causality run in
Table 10? We can look at the coefficients above and below the diagonal in
Table 10 and see that SPRET has an effect on BITRET of −0.56, but the effect of BITRET on SPRET is −0.47. Therefore, the stronger influence is from the S&P500 to Bitcoin rather than vice-versa, but the causality runs in both directions. Similarly, the effect of SPRET on ETRET is −0.73, whilst the effect of ETRET on SPRET is −0.47. Clearly, SPRET has the larger causal impact. Finally, we can see that BITRET has an 0.83 effect on ETRET, whilst ETRET has a 0.80 effect on BITRET. Therefore, Bitcoin has the slightly stronger causal influence when it is paired with Ethereum.
In the post-COVID-19 period 2 in
Table 10, matters change dramatically. For a start, all of the GMC values have now become positive. This means that the relationship between the returns on the S&P500 Index returns, SPRET and the two cryptocurrencies, as represented by BITRET and ETRET, have increased to 0.69 and 0.68, respectively. Similarly, the influence of the cryptocurrencies on the S&P500 has become positive and greatly increased, as the last two entries in the row adjacent to SPRET are 0.68 and 0.81, respectively, which suggests that ETRET now has the largest impact on SPRET. The two cryptocurrencies have a large but slightly lower influence on one another. BITRET has a 0.77 GMC in relation to ETRET, whereas the influence of ETRET ON BITRET is now 0.72. These values are now slightly lower than the corresponding ones in the first period.
The most remarkable change is the switch in the signs of the relationships between the cryptocurrencies and the S&P500 from negative to positive, which suggests that they do not provide a strong diversification strategy in times of crisis.