Abstract
When the nominal interest rate reaches the zero lower bound (ZLB), a conventional monetary policy, namely, the adjustment of short-term interest rate, may become impractical and ineffective for central banks. Therefore, quantitative easing (QE) is one of the few available policy options of central banks for stimulating the economy and dealing with deflationary pressure. Since February 1999, the Bank of Japan (BoJ) has conducted several unconventional monetary policy programs. Considering the scarce research in this field from a structural macroeconomic model approach, a medium-scale New Keynesian DSGE model with government bonds of different maturities was developed to check the portfolio rebalancing channel of quantitative qualitative easing (QQE) conducted by the BoJ from April 2013 on the basis of the assumption of imperfect asset substitutability. The model was calibrated on the basis of the structure of the Japanese economy in April 2013. The main conclusion is that the BoJ’s asset purchase has a real effect on pushing output and inflation higher, and long-term interest rates lower. Sensitivity simulation analysis shows that, given the same size of asset purchase, the persistence of asset purchase determines the peak effect in the short run. A long-lasting asset purchase can push up inflation higher, and long-term interest rates lower for a relatively longer period, but the long-run effect on output and investment does not have much difference. The policy implication for BoJ is just to announce a long-lasting QE program and make it credible to the market.
JEL Classification:
E43; E44; E52; E58
1. Introduction
For almost 15 years, from February 1999, when the Bank of Japan (BoJ) announced the commitment to the zero interest rate policy (ZIRP), to April 2013, when it started quantitative qualitative easing (QQE), it implemented unconventional monetary policy. During the recent global financial crisis, many advanced economies had to depart from conventional ways of conducting monetary policy, as they faced the zero lower bound (ZLB) and systemic risk. The importance of an unconventional monetary policy has been realized by macroeconomists and central banks both theoretically and practically. Krugman et al. (1998), Svensson (2003), and Bernanke et al. (2004) are the early contributors in this field. Unconventional monetary policies can take many forms besides those that are generally publicly recognized. For example, during the global financial crisis, the Danish National Bank permitted the use of a negative interest rate policy (NIRP). Generally, as a main option of unconventional monetary policy, quantitative easing (QE) can be defined as the change in the composition and size of the central bank’s balance sheet. The change can be the result of the large-scale asset purchase of private assets or government bonds, and it can also occur through direct lending or capital injection from the central bank to the private sector or the financial system.
Joyce et al. (2012) comprehensively introduced the QE conducted by the Federal Reserve (Fed), the Bank of England (BoE), and the European Central Bank (ECB) with a theoretical background of unconventional monetary policy. In the United States, from December 2008 to the end of 2009, the Fed conducted the first phase of QE (QE1—officially large-scale asset purchases (LSAPs)) by expanding its portfolio assets to provide liquidity to the financial system and reduce the risk premium. Following QE1, QE2 lasted from October 2010 to June 2011 and was conducted by the Fed through the large purchase of US treasury securities. Bernanke also announced the purchase of mortgage-backed securities (MBS) in September 2012, which is known as QE3, with the objective of pushing down the long-term yield curve to support financial system reconstruction and stimulate aggregate demand. During the same period, in the UK, the BoE began a QE program by establishing the Asset Purchase Facility (APF), the operations of which are conducted by purchasing medium- and long-term UK government bonds.
Related studies on unconventional monetary policy mostly focused on empirical evidence for the policy effect of asset purchase on financial markets, especially through event study1 or time-series regression2, to check the effect on domestic yields such as the 10-year treasury yield or 30-year MBS yield3. Compared to empirical analysis focusing on the impact of asset purchase on financial markets, there are relatively few studies that investigate the impact of asset purchase on the macroeconomy. Generally, there exist three approaches in this field. The first approach does not rely on macroeconomic theory, but on statistical causality investigated by regression or nonstructural VAR methodology. Consequently, empirical results obtained from such a nonstructural approach are not stable and robust among the different choices of regressors or identification schemes. The second approach is theoretical evaluation with a dynamic stochastic general equilibrium (DSGE) macroeconomic model that has the specified transmission mechanism of unconventional monetary policy. Typical works4 using this approach are Gertler and Karadi (2011, 2013), Curdia and Woodford (2011) and Chen et al. (2012). Most only studied the transmission mechanism of unconventional monetary policy without empirically estimating the model because of the technical difficulties incurred by ZLB. The third approach, which lies somewhere between the two previous approaches, is to follow a two-step procedure. The first step is to measure the policy effect of asset purchase on the nominal interest rate; the second step is to use the interest rate as a proxy to evaluate the policy effect on macroeconomic variables with a traditional macroeconomic model5 such as the FRB/US model. It is more complicated to empirically evaluate the effect of forward guidance because forward guidance affects the future expectation of the public and the market. Unlike asset purchase, there is no consensus about the policy effect of forward guidance. The guidance may not be fully understood by market. Even if understood, the guidance may not be fully believed for the longer term given the possibility that the central banks may not be able to guarantee the consistency of future decisions beyond a shorter horizon.
Recently, as a good measure of the stance of monetary policy, shadow interest rate has been used in many works to find the empirical evidence of unconventional monetary policy. Wu and Xia (2016) and Krippner (2013) are two representative works in this field. Wang (2019a, 2019b) showed that the shadow rate can be used in the estimation of structural DSGE models. The advantage of the shadow rate is that it is a consistent measure of the stance of monetary policy, both in zero- and nonzero-interest-rate environments. When using structural macroeconomic models, the advantage of the shadow rate allows for not needing to specify the detailed transmission mechanism. The shadow rate itself contains necessary information about the stance of unconventional monetary policy. As an example, Huber and Punzi (2020) used a time-varying parameter vector autoregression (TVP-VAR) model to investigate the relationship between unconventional monetary policy and housing markets in advanced economies. Their findings suggested that the monetary policy transmission mechanism to the housing market did not change with the implementation of quantitative easing or forward guidance for most economies such as the US, the EU, and Japan.
In Japan, the first phase of QE started 15 years ago, beginning in March 2001 until March 2006. After a pause in operations from April 2006 to September 2010, the QE program, known as the comprehensive easing policy, was restarted from October 2010 and lasted until March 2013. Its purpose was to stimulate the real economy and protect the financial system from the global financial crisis by purchasing a variety of assets, including commercial papers (CP), exchange traded funds (ETF) and Japan real estate investment trusts (J-REITs). With the advent of the BoJ’s new president, Haruhiko Kuroda, the new stage of QE, known as quantitative qualitative easing (QQE), began with a more aggressive scale of balance sheet expansion and with more varieties of asset purchases than those in the past. QQE was positioned as one of Abenomics’ three arrows. At the same time, BoJ clearly declared a 2% inflation target to shape the formation of expectations. Since the start of QQE in April 2013, two and a half years passed. It is still ongoing, so a comprehensive evaluation and final conclusion about QQE may be inappropriate at this time. However, we still recognize the significance of a temporary evaluation of QQE6. Related works about BoJ’s QE generally take a nonstructural approach, including VAR analysis or event study to obtain empirical evidence about the effectiveness of QE. Especially in VAR analysis, as surveyed by Ugai (2007), different choices of variables and specifications of models lead to different results. In contrast to the nonstructural econometric approach, the DSGE framework has inherent advantages for policy evaluation. The transmission mechanism of monetary policy can be identified with a clear explanation on the basis of economic theory. In addition, to the best of our knowledge, no trials have been conducted in this area. For these reasons, we conducted an empirical project to evaluate the QQE of BoJ by the calibration and numerical simulation of the DSGE model in this study. Since September 2016, the BoJ started a new framework of monetary policy, which is known as the price stability target of 2 percent, and quantitative and qualitative monetary easing with yield curve control. In this framework, the BoJ also allows for NIRP. Fukuda (2018) investigated the impact of the BoJ’s NIRP on Asian financial markets and showed that it might have benefitted Asian economies through the positive effects on Asian stock prices. Angrick and Nemoto (2017) provided an overview of the operational implementation of NIRP in Europe and Japan.
Among existing studies, few used DSGE model methodology to study the empirical effect of the BoJ’s QE. In this paper, we develop a model and focus on the portfolio rebalancing mechanism of QE to study the effect of the QE conducted by the BoJ since April 2013. Given the fact that the model was calibrated on the basis of the structure of the Japanese economy in April 2013, there are limitations to the conclusion, which is based on that period. The main conclusion is that, through the portfolio rebalancing mechanism, the BoJ’s asset purchase had a simulative effect on the Japanese economy. However, the policy options for BoJ may be limited because, based on sensitivity analysis, if the central bank wishes to improve the effectiveness of asset purchase, a larger scale and longer period are the only two options. For the situation of the BoJ, it is better to announce a longer period of QE policy to achieve a long-lasting effect.
2. Model
Meier (2009) noted that there are different approaches to unconventional monetary policy, that can be motivated by alternative views of the transmission channels and their effect on the economy. The model developed here has the standard structure and specification of the new Keynesian DSGE model, but the bond trading market proposed by Lars and Sargent (2012, Chapter 13, Section 8) was incorporated to isolate the portfolio rebalancing mechanism of large asset purchases by the central bank. Tobin (1969) initially described this mechanism, whereby variation in the relative supplies of financial assets with different maturities and liquidities triggered by large asset purchases of the central bank can have a real effect on the yield curve due to imperfect asset substitutability.Tobin and Brainard (1963) define the imperfect substitution assumption as follows:
Assets are assumed to be imperfect substitutes for each other in wealth-owners’ portfolios. That is, an increase in the rate of return on any one asset leads to an increase in the fraction of wealth held in that asset, and to a decrease or at most no change in the fraction held in every other asset.
Relating this assumption to unconventional monetary policy, the basic idea is that the central bank’s purchase of assets held by the private sector increases the price of these assets. As asset prices increase, yields fall, stimulating aggregate demand. Even when the short-term nominal interest rate faces ZLB, asset purchases can be a practical policy instrument for the central bank. Large-scale purchases of government bonds by BoJ can be evaluated using this approach in a dynamic stochastic general equilibrium framework.
2.1. Household
There is a continuum of representative households existing continuously in where i is the indexation7. The representative household derives utility from consumption , and real money balance and disutility from labor supply . The utility function is additively separable:
where is the inverse of the elasticity of intertemporal substitution, is the degree of habit formation, is the interest rate semielasticity of money demand, and is the inverse of the Frisch elasticity of labor supply. is a preference parameter that measures the relative weight of disutility from labor supply. The household maximizes the discounted infinite stream of utility subject to intertemporal budget constraint
and the standard law of motion of capital accumulation.
is a preference shock process following
and is an i.i.d. exogenous shock.
The household allocates wealth among real money holdings , capital with rental rate and two types of government bonds8, short-term bonds , of which the maturities are equal to or shorter than 1 year with yield , and long-term bonds 9, of which the maturities are equal to or longer than 10 years with yield . The household supplies labor , receives real wages , and pays a real lump-sum tax at general aggregate price level . Investment and capital accumulation processes occur with adjustment cost and the portfolio adjustment between two kinds of bonds also accompanies cost , where is the steady state ratio of long-term bond holdings of the household to short term bond holdings ; so, at the steady state, the portfolio is adjusted to its optimal allocation and adjustment cost, which is paid in terms of the household’s income of zero.
The first-order conditions of the household’s maximization with respect to consumption , labor supply , real money , short-term bond , long-term bond , capital , and investment are given as follows.
and are two Lagrangean multipliers corresponding with budget constraints and the law of motion of capital accumulation, respectively. is the gross inflation rate at the period. For convenience, bonds and money are rewritten in real terms , and in lowercase letters.
Now we discuss the adjustment cost of the portfolio introduced above. There are necessary conditions under which the purchase of private sector assets or government securities by the central bank can be effective. As discussed by Eggertsson and Woodford (2004), if representative agents who have rational expectations with an infinite time horizon and face no credit frictions or restrictions consider assets held by the government and by the central bank to be indistinguishable from assets held by themselves, then asset purchases by the central bank change nothing. This proposition is analogous to Ricardian equivalence in fiscal theory. However, if credit or financial frictions and borrowing constraints exist, then this proposition no longer holds. In Curdia and Woodford (2011), an unconventional monetary policy, direct facility lending from the central bank to the private sector (credit easing), affected the aggregate economy. Kiyotaki and Moore (2012) described a monetary economy with the heterogeneous liquidity of financial assets. In their model, when entrepreneurs wanted to undertake new investment projects, they could only finance a limited proportion by issuing new equities. Therefore, purchases of such less-liquid equities by the central bank could change their prices, leading to real effects on investment decisions. This is the credit channel of QE. Gertler and Kiyotaki (2010), and Gertler and Karadi (2011) also contributed to this area. The framework in the above-mentioned research is highly complicated, as it includes the full sketch of financial intermediaries or the banking sector. In this study, we focus only on the portfolio-rebalancing channel of QE. This approach is more appropriate for the QE implemented by theBoJ10. Falagiarda and Marzo (2012), Zagaglia (2013), Falagiarda (2014), and Chen et al. (2012) took the same approach to evaluating the QE of the Fed and the BoE. The rationale for including portfolio-adjustment frictions was intuitional. As mentioned by Falagiarda (2014), long-term bond holdings have less liquidity. Households realize this risk and hold short-term bonds as precautionary liquidity holdings relative to their longer-term investments. Another justification for this adjustment cost comes from the theory of preferred habit. Vayanos and Vila (2009) emphasised that agents prefer different bond maturities, and any deviation from the preferred portfolio allocation is costly. More simply, the management of the portfolio itself is costly.
2.2. Firm
In the same way as in the standard new Keynesian DSGE models, final-goods firms produce homogeneous final goods by bundling differentiated intermediate goods with CES technology , so the intermediate-goods market is monopolistic. We used the type of staggered price setting of Calvo (1983) to replicate rigidity of price. As pointed out by Woodford (2003), the output of all intermediate-good firms is equal to the output of all final-goods firms, and the aggregate production function holds at the steady state when the dispersion of price is unity. is the indexation of each intermediate-goods firm and is the time-varying price mark-up that has relationship with elasticity of substitution between different intermediate goods. After log-linearizing the model, time-varying price mark-up can be represented as a cost-push mark-up shock process that follows
where is an i.i.d. shock. The cost minimization of final-goods firms leads to the intermediate-goods demand function and aggregate price index .
Under the Calvo (1983) type price setting, each period of fractions of all intermediate-goods firms can adjust price to their optimal level, and the others just index their prices to a weighted average of the inflation of the last period and steady state with weights and , respectively.
Intermediate-goods firms first minimize cost of production subject to its production technology, , where is a fixed cost keeping all intermediate-goods firms’ profits zero at the steady state. represents the TFP that follows the AR(1) process.
is an i.i.d. shock driving the TFP precess.
Aggregating the first-order condition of cost minimization over each intermediate-goods firm by and leads to the relationship of aggregate capital stock and labor supply.
Marginal cost is identical among all intermediate-goods firms.
Then, intermediate-goods firms set the optimal price to maximize the discounted profits.
The first-order condition is given by Equation (15).
where represents the optimal price set at period t. The law of motion of the general price level is given by aggregating the optimal prices set by all intermediate-goods firms in each period.
The log linearization of Equations (15) and (16) leads to the hybrid new Keynesian Phillips curve (NKPC) equation. The final aggregate output with price dispersion11 equal the aggregate of all intermediate output.
2.3. Fiscal and Monetary Authorities
The joint budget constraint of government and central bank is given by
where and are the total amount of long- and short-term government bonds, respectively. The central bank holds long-term government bonds as an asset, and supplies money as a liability, so its balance sheet variation can be represented as the change of these two parts.
Central-bank holdings of long-term governments bonds are a fraction of the total amount of long-term bonds. All households hold the remaining long-term bonds12. The asset purchase by the central bank can be described by the variation of this fraction variable that we assumed to be an AR (1) process.
Combining the joint budget constraint of government and central bank, balance sheet variation, and Equation (18) by cancelling and and rewriting the nominal terms into real terms leads to the joint budget constraint of government and central bank represented by Equation (19).
where x is the fraction of the central bank’s long-term bond holdings at the steady state. is an i.i.d shock to drive the asset purchase process. By calibrating the size of and , we can simulate the effect of asset purchase by the central bank on aggregate economic activity. needs to be carefully calibrated because it represents the exit strategy of the central bank when the central bank stops the QE and returns to the normal amount of government debt holdings.
Government spending is assumed to follow an AR (1) process with shock term . Long-term bonds supplied by the government are assumed to be an AR (1) process, as in Zagaglia (2013), where .
As proposed by Leeper (1991), to prevent inflation triggered by fiscal expansion, a passive fiscal policy rule was introduced by Falagiarda (2014) to characterize tax collection as a function of total government debt:
where and are parameters that represent the reaction to bond deviation from the steady state value. Lump-sum tax at the steady state is . Because is the real tax income of government, the bonds are also represented in real terms and . This specification shows that the deviation of government debt from a long-run steady state can be offset or compensated by the lump-sum tax collection from households.
The central bank is assumed to follow a standard Taylor (1993) rule with nominal interest-rate smoothing .
Monetary policy shock was also assumed to be an AR (1) process with disturbance term .
Lastly, we close the model by imposing aggregate resource constraint . Total output is allocated to consumption, government-investment expenditure, and two types of adjustment cost. This completes the description of the model. Steady state and log linearization are given in Appendix A and Appendix B. We have 25 endogenous variables:
and 6 exogenous variables, as follows.
Generally, the price level is not determined in the new Keynesian DSGE model. The linearization of Equations (15) and (16) leads to the NKPC equation.
2.4. Analysis of Portfolio Rebalancing Mechanism
Before proceeding to numerical simulation, we performed an analytical investigation regarding the asset market to check the transmission mechanism of QE. Log-linearizing first-order condition13 Equations (7) and (8) and combining them by cancelling , and leads to Equation (27).
where the parameters in Equations (7) and (8) can be cancelled using steady state values14 for the steady state of the model.. The above result shows that the long-term interest rate is positively related to the short-term interest rate, and the expectation of short-term interest rate and long-term bonds held by private sector, but negatively related to short-term bonds because of the imperfect substitution of two kinds of bond assets. When the central bank purchases a long-term bond from the private sector, the long-term interest rate can be reduced to stimulate the economy. Conversely, when the central bank reduces long-term bond holdings, less liquid asset holdings (long-term bonds) of the private sector increase, leading to an increase in interest-rate spread. This mechanism, the portfolio-rebalancing channel of QE, is summarized below.
Parameter represents the degree of adjustment cost in portfolio management. The existence of adjustment cost invalidates the standard arbitrage condition. When this friction disappears, , the first-order condition in the log linearization of Equations (7) and (8), is simplified to the standard Euler equation, arbitrage equation, and the term structure between long- and short-term interest rate, which are familiar in the standard DSGE models without adjustment cost of assets with different maturities.
To check QE’s transmission mechanism from the asset market to the real economy, combining the log linearization of Equations (7) and (8) by cancelling bond variables yields the Euler equation of consumption.
Following analysis of the transmission mechanism inside the asset market, the transmission mechanism from the asset market to the real economy is summarized below.
Summarizing the entire above analysis, QE in this model can be described as follows:
The above investigation describes the whole scenario. To check the accurate dynamics triggered by asset purchase by the central bank, we conducted a calibration exercise.
3. Calibration
This model was developed to simulate the effects of QQE conducted by the BoJ from April 2013. The benchmark calibration of the steady state was adjusted to match quarterly data over the most recent periods prior to April 2013. Steady state values could be calculated from the System of National Accounts (SNA) of Japan. GDP at steady state was normalized to a unit. Total government debt , short-term debt15 and long-term debt16 , long-term debt held by private sector and the central bank , were obtained from the OECD Statistical Database, Ministry of Finance in Japan17 and the BoJ, and calculated as the relative ratio to output. Steady state of model is given in Table 1.

Table 1.
Calibration for steady state.
3.1. Calibration
Structural and policy parameters are directly obtained from the DSGE literature. Parameters such as discount factor , capital share , and depreciation rate were set to their general values. Average mark-up rate in the economy was set to 0.2. Calvo type price rigidity set equal to 0.75 implies an average price duration of 4 quarters, a value consistent with much empirical evidence. Parameters in the monetary-policy rule equation take the standard values in a way that is consistent with Taylor’s original rule. To reflect a situation similar to ZLB, was set at a highly persistent value of 0.995 to prevent the short-term interest rate from responding to inflation and output change, as proposed by Falagiarda (2014) to avoid the indeterminacy of model’s solution. Other structural parameters were calibrated as the values that are generally used in the DSGE literature. Table 2 summarizes the values of all structural parameters.

Table 2.
Calibration for structural and policy parameters.
Two key parameters, and , were calibrated to replicate QE’s persistence and scale22. The BoJ announced on 4 April 2013 that the long-term bond held by BoJ would be increased from JPY 89 trillion to JPY 190 trillion from the end of 2012 to end of 2014, which meant a 113.48% increase in long-term bond holdings. Considering the inaccuracy of calibration, the was set to be 1 to simulate the effect of the long-term bond purchase by the BoJ. Other exogenous shock parameters were set to the usual values.
4. Results
Under benchmark calibration, we now report the baseline simulation results of long-term bond purchase by the BoJ. We consider a scenario in which the central bank increases its long-term bond holdings 100% and takes 6 years to gradually return to its normal level.
4.1. Baseline Simulation
Figure 1 shows the impulse response function of each variable that is represented in the percentage deviation from its steady state. Figure 1 shows that QE has a strong effect on output and investment. The effect on investment can be identified from Equation (10). From the linearized version of Equation (10),
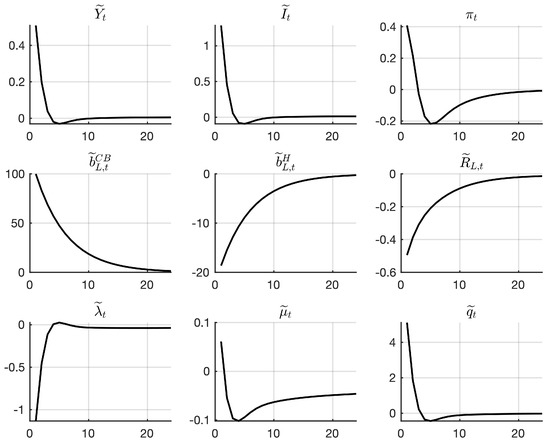
Figure 1.
Baseline simulation for BoJ’s QE.
The decrease in and increase in could lead to increasing of . This transmission mechanism is also confirmed from Figure 1. Peak impact on output and investment was almost 0.51% and 1.29%, respectively. The stimulated effect by QE lasted for almost 5 quarters. As set up in the scenario, the central bank increased its long-term bond holdings (In Figure 1, panel ) on its balance sheet by 100%, and returned to a normal level 6 years later. During the same period, long-term bonds held by the private sector (In Figure 1, panel ) decrease 18.62% and returns to a normal level 6 years later. The inflation rate increased by 0.41% from the QE stimulation. The long-term interest rate, which is critical to the investment, was decreased by 0.5%. Considering the low-interest-rate environment existing in the Japanese economy, 0.5% decreasing the yield curve is not a small number. As long as the QE has its effect, the long-term interest rate is suppressed to a low level. The baseline simulation results show that the mechanism analyzed in Section 2.4 was appropriate.
In addition, the effect stimulated by asset purchase was limited because it merely lasted for just more than 1 year. In this study, we did not explicitly introduce the balance sheet of the central bank, and BoJ operations are more complicated than what we simulated, but the positive effect of QE on the real economy could be identified with a rigorous structural explanation.
4.2. QE Sensitivity Analysis
We consider different exit strategies of the central bank’s QE and its effects. The benchmark simulation was set to be a 6-year QE policy for . As sensitivity analysis in Falagiarda (2014), we ran two more simulations for a long-lasting QE policy (8 years and ) and short-lasting QE policy (4 years and ). Figure 2 shows that the longer the duration of QE was, the stronger its effect was. Especially for long-term interest rate, the push-down effect of QE to a long-term interest rate lasted longer when the QE policy had high persistence. Table 3 shows the simulated peak impact of QE under different scenarios of QE policy.
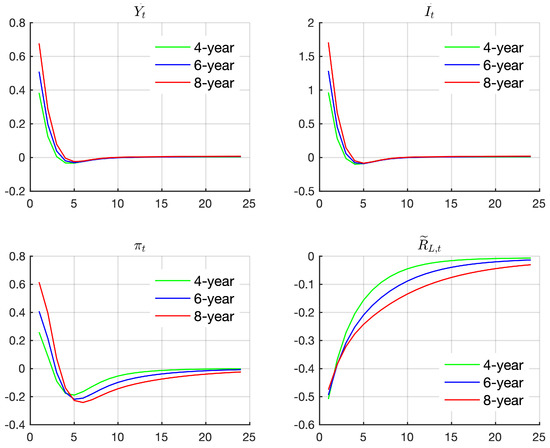
Figure 2.
Sensitivity simulation for BoJ’s QE.

Table 3.
Simulated peak impact of QE.
As mentioned in Section 3.1, is also considered to have a critical role in the effect of QE. Similar sensitivity analysis was conducted for two other cases, higher portfolio adjustment cost () and lower portfolio adjustment cost (), and they were compared with the benchmark case (). Results were similar to those in Figure 2, so we do not report the IRF here again. Sensitivity analysis shows that with a higher portfolio adjustment cost, short- and long-term bonds become less substitutable. The asset purchase conducted by the central bank thereby had macroeconomic effects. The effects were also amplified as increased. When , two kinds of bond were perfectly substitutable, and no effects could be generated by QE.
5. Concluding Remarks
In this study, a DSGE model was developed to capture the portfolio-rebalancing channel of QE, and the model was calibrated to match the Japanese economy and BoJ’s policy in April 2013.
There were two main conclusions from the simulation. First, QE policy that the BoJ introduced had an effect on the real economy, pushing up output and inflation, and pushing down long-term interest rates to stimulate investment. The peak impact on output was moderate for the benchmark case 0.51%, and the pushing-up effect lasted for merely 5 quarters, but the pushing-down effect on long-term rates was persistent, lasting for the whole period when the policy was effective. As the QE period became longer, the effect became larger. Under the same level of asset purchases, the central bank should announce a long-lasting time frame for QE policy. The second conclusion is that the key assumption in this study, the imperfect substitution of different assets and the corresponding cost of portfolio adjustment cost, is critical to the effectiveness of QE. Key parameter is not a policy-controlled parameter. So, it is not the choice for the central bank. If the central bank wishes to improve the effectiveness of QE, a larger scale and longer period are two options. Considering the huge stock of Japanese government bonds, issuing more bonds is also not a smart choice for the Japanese government. The policy implication for the BoJ is just to announce a long-lasting QE program and make it credible to the market.
Another contribution is that the developed model here can be extended to more rigorous specifications of economic agents, such as the balance sheet of the central bank and the introduction of different assets. Other important channels of QE, the credit channel and wealth channel, can be verified with the incorporation of financial intermediaries, the housing market, or financial frictions.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available dataset was used in this study. This dataset can be downloaded from the homepage of Ministry of Finance in Japan (https://www.mof.go.jp/jgbs/reference/appendix/index.htm accessed on 1 May 2021). Dynare and MATLAB codes that generates the figures and simulation results in this paper are available upon request.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. The Steady State
, , , , ,
, , ,
, , ,
, , , ,
Appendix B. The Log-Linearized Model
In our log-linearized model, we have 25 endogenous variables for 26 nonlinear equilibrium conditions. Equations (15) and (16) can be log-linearized and written as an NKPC equation, which is denoted as Equation (A15). So, we actually have 25 linear equilibrium conditions. Variables with mean the percentage deviation from its steady state, which is defined as .
For gross inflation rate , its log-linearized variable is denoted as .
Notes
| 1. | Reith (2011) provided a good a comparison of QE in Japan and the US. Gupta and Marfatia (2018), and Gupta et al. (2019) also took the event-study approach to study the impact of unconventional monetary policy on stock markets. |
| 2. | Siranova and Kotlebova (2018) used a structural vector autoregression (SVAR) model to check ECB monetary-policy effects via the banking sector in Slovenia. Caraiani et al. (2020), and Huber and Punzi (2020) discussed the wealth channel of unconventional monetary policy. Caraiani et al. (2020) used a quantile structural vector autoregressive (QSVAR) model to analyze whether the impact of monetary-policy shocks on real housing returns in the United States was contingent on the initial state of housing-market sentiment. |
| 3. | For related studies, please refer to Olmo and Sanso-Navarro (2018), Kiss and Balog (2018), Chebbi and Derbali (2019). |
| 4. | For related studies, please refer to Harrison (2011, 2012), Falagiarda (2014), Cova et al. (2015), Del Negro et al. (2017), McKay et al. (2016) and Priftis and Vogel (2016, 2017). |
| 5. | Socci et al. (2018) used the calibrated dynamic computable general equilibrium (DCGE) model of the Italian economy to check the effects of the unconventional monetary policy of ECB. |
| 6. | This paper was written in 2015, and the conclusion is based on the situation of the Japanese economy in that time. |
| 7. | Indexation of each household is omitted because they are homogenous and identical. |
| 8. | This kind of classification in also used in model calibration, the steady state ratio of two kinds of bonds with different maturities relative to the total amount of government bonds. |
| 9. | means the long-term bonds held by households. |
| 10. | BoJ also purchases risky assets such as ETFs and J-REITs from the private sector, but the quantity of these purchases is much less than the purchased quantity of Japanese government bonds is. |
| 11. | As proved in Gali (2015, Chapter 3), at the steady state, price dispersion is approximate to unity at the first order, and zero at the second order, which means that all intermediate-goods firms choose the same price, and price dispersion disappears at the steady state. |
| 12. | This is not true for a real economy because other financial institutions can hold government debt. In this model, financial intermediaries are neglected, and all private-sector households hold the remaining long-term bonds. |
| 13. | See Appendix B for log-linearization of the model. |
| 14. | See Appendix A. |
| 15. | Short-term debt includes bonds held by the central bank as the operation instrument in the interbank market plus bonds with maturity less than or equal to 1 year. |
| 16. | Long-term debt is calculated by subtracting its amount from total debt. |
| 17. | Data of Japanese government bonds can be obtained from http://www.mof.go.jp/jgbs/reference/appendix/index.htm accessed on 1 May 2021. |
| 18. | For other steady state values, see Appendix A. |
| 19. | The steady state of labor supply is calculated by assuming that the share of representative household’s time endowment spent on labor supply is equal to 0.3. |
| 20. | In similar research, this parameter was set to different values such as Chen et al. (2012) (0.015), Andres et al. (0.045), Harrison (2011, 2012) (0.1, 0.09). Following Falagiarda (2014), was set to 0.01, which means that 1% of household’s income is paid for the portfolio adjustment cost. Sensitivity analysis in the next section checks the role of this parameter in the portfolio-rebalancing channel of QE. |
| 21. | is derived from the steady state of the first-order conditions Equations (9) and (10). See Appendix A. |
| 22. | This calibration was conducted by checking the impulse response of through trial and error. Just like parameter , and were also assumed to be important in the portfolio-rebalancing channel of QE. Sensitivity analysis is given in the next section. |
References
- Andres, Javier, J. David López-Salido, and Edward Nelson. 2004. Tobin’s Imperfect Asset Substitution in Optimizing General Equilibrium. Journal of Money, Credit and Banking 36: 665–90. [Google Scholar] [CrossRef]
- Angrick, Stefan, and Naoko Nemoto. 2017. Central Banking Below Zero: The Implementation of Negative Interest Rates in Europe and Japan. Asia Europe Journal 15: 417–43. [Google Scholar] [CrossRef]
- Bernanke, Ben, Vincent Reinhart, and Brian Sack. 2004. Monetary Policy Alternatives at The Zero Bound: An Empirical Assessment. Brookings Papers on Economic Activity 2: 1–100. [Google Scholar] [CrossRef]
- Calvo, Guillermo A. 1983. Staggered Prices in A Utility-Maximizing Framework. Journal of Monetary Economics 12: 383–98. [Google Scholar] [CrossRef]
- Caraiani, Petre, Gupta Rangan, Lau Chi Keung Marco, and Hardik A. Marfatia. 2020. Effects of Conventional and Unconventional Monetary Policy Shocks on Housing Prices in the United States: The Role of Sentiment. Journal of Behavioral Finance. [Google Scholar] [CrossRef]
- Chebbi, Tarek, and Abdelkader Derbali. 2019. US Monetary Policy Surprises Transmission to European Stock Markets. International Journal of Monetary Economics and Finance 12: 3–14. [Google Scholar] [CrossRef]
- Chen, Han, Cúrdia Vasco, and Ferrero Andrea. 2012. The Macroeconomic Effects of Large-Scale Asset Purchase Programmes. The Economic Journal 122: F289–F315. [Google Scholar] [CrossRef]
- Cova, Pietro, Pagano Patrizio, and Pisani Massimiliano. 2015. Domestic and International Macroeconomic Effects of the Eurosystem Expanded Asset Purchase Programme. Economic Working Papers No. 1036. Rome: Bank of Italy, Economic Research and International Relations Area. [Google Scholar]
- Vasco, Curdia, and Woodford Michael. 2011. The Central-Bank Balance Sheet as An Instrument of Monetary Policy. Journal of Monetary Economics 58: 54–79. [Google Scholar] [CrossRef]
- Del Negro, Marco, Eggertsson Gauti, Ferrero Andrea, and Kiyotaki Nobuhiro. 2017. The Great Escape? A Quantitative Evaluation of The Fed’s Liquidity Facilities. American Economic Review 107: 824–57. [Google Scholar] [CrossRef]
- Eggertsson, Gauti B., and Woodford Michael. 2004. Optimal Monetary and Fiscal Policy in a Liquidity Trap. NBER Working Papers No. 10840. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Falagiarda, Matteo. 2014. Evaluating Quantitative Easing: A DSGE Approach. International Journal of Monetary Economics and Finance 7: 302–27. [Google Scholar] [CrossRef]
- Falagiarda, Matteo, and Massimiliano Marzo. 2012. A DSGE Model with Endogenous Term Structure. Working Papers wp830. Bologna: Universita’ di Bologna. [Google Scholar]
- Fukuda, Shin-ichi. 2018. Impacts of Japan’s Negative Interest Rate Policy on Asian Financial Markets. Pacific Economic Review 23: 67–79. [Google Scholar] [CrossRef]
- Galí, Jordi. 2015. Monetary Policy, Inflation and The Business Cycle: An Introduction to The New Keynesian Framework and Its Applications. Jersey: Princeton University Press. [Google Scholar]
- Gertler, Mark, and Peter Karadi. 2011. A Model of Unconventional Monetary Policy. Journal of Monetary Economics 58: 17–34. [Google Scholar] [CrossRef]
- Gertler, Mark, and Peter Karadi. 2013. QE 1 vs. 2 vs. 3...: A Framework for Analyzing Large-Scale Asset Purchases as A Monetary Policy Tool. International Journal of Central Banking 9: 5–53. [Google Scholar]
- Gertler, Mark, and Nobuhiro Kiyotaki. 2010. Financial Intermediation and Credit Policy in Business Cycle Analysis. In Handbook of Monetary Economics. Amsterdam: Elsevier, vol. 3, pp. 547–99. [Google Scholar]
- Gupta, Rangan, and Hardik A. Marfatia. 2018. The Impact of Unconventional Monetary Policy Shocks in The US on Emerging Market REITs. Journal of Real Estate Literature 26: 175–88. [Google Scholar] [CrossRef]
- Gupta, Rangan, Lau Chi Keng Marco, Liu Ruipeng, and Hardik A. Marfatia. 2019. Price Jumps in Developed Stock Markets: The Role of Monetary Policy Committee Meetings. Journal of Economics and Finance 43: 298–312. [Google Scholar] [CrossRef][Green Version]
- Harrison, Richard. 2011. Asset Purchase Policies and Portfolio Balance Effects: A DSGE Analysis. In Interest Rates, Prices and Liquidity: Lessons from the Financial Crisis. Cambridge: Cambridge University Press, pp. 117–43. [Google Scholar]
- Harrison, Richard. 2012. Asset Purchase Policy At The Effective Lower Bound for Interest Rates. Bank of England Working Papers 444. London: Bank of England. [Google Scholar]
- Huber, Florian, and Maria Teresa Punzi. 2020. International Housing Markets, Unconventional Monetary Policy, and The Zero Lower Bound. Macroeconomic Dynamics 24: 774–806. [Google Scholar] [CrossRef]
- Joyce, Michael, David Miles, Andrew Scott, and Dimitri Vayanos. 2012. Quantitative Easing and Unconventional Monetary Policy—An Introduction. The Economic Journal 122: F271–88. [Google Scholar] [CrossRef]
- Kiyotaki, Nobuhiro, and John Moore. 2012. Liquidity, Business Cycles, and Monetary Policy. NBER Working Papers No. 17934. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Kiss, Gábor Dávid, and Enikő Balog. 2018. Conventional and Unconventional Balance Sheet Practices and Their Impact on Currency Stability. International Journal of Monetary Economics and Finance 11: 76–94. [Google Scholar] [CrossRef]
- Krippner, Leo. 2013. Measuring The Stance of Monetary Policy in Zero Lower Bound Environments. Economics Letters 118: 135–38. [Google Scholar] [CrossRef]
- Krugman, Paul R., Kathryn M. Dominquez, and Rogoff Kenneth. 1998. It’s Baaack: Japan’s Slump and The Return of The Liquidity Trap. Brookings Papers on Economic Activity 1998: 137–205. [Google Scholar] [CrossRef]
- Lars, Ljungqvist, and Thomas J. Sargent. 2012. Recursive Macroeconomic Theory, 3rd ed. Cambridge: MIT Press. [Google Scholar]
- Leeper, Eric M. 1991. Equilibria under “Active” and “Passive” Monetary and Fiscal Policies. Journal of Monetary Economics 27: 129–47. [Google Scholar] [CrossRef]
- McKay, Alisdair, Nakamura Emi, and Steinsso Jón. 2016. The Power of Forward Guidance Revisited. American Economic Review 106: 3133–58. [Google Scholar] [CrossRef]
- Meier, Andre. 2009. Panacea, Curse, or Nonevent? Unconventional Monetary Policy in The United Kingdom. Working Paper No. 09/163. Washington: International Monetary Fund. [Google Scholar]
- Olmo, Jose, and Marcos Sanso-Navarro. 2018. Unconventional Monetary Policies and The Credit Market. International Journal of Monetary Economics and Finance 11: 480–98. [Google Scholar] [CrossRef]
- Priftis, Romanos, and Lukas Vogel. 2016. The Portfolio Balance Mechanism and QE in The Euro Area. The Manchester School 84: 84–105. [Google Scholar] [CrossRef]
- Priftis, Romanos, and Lukas Vogel. 2017. The Macroeconomic Effects of The ECB’s Evolving QE Programme: A Model-based Analysis. Open Economies Review 28: 823–45. [Google Scholar] [CrossRef]
- Reith, Matthias. 2011. Unconventional Monetary Policy in Practice: A Comparison of “Quantitative Easing” in Japan and The USA. International Journal of Monetary Economics and Finance 4: 111–34. [Google Scholar] [CrossRef]
- Siranova, Maria, and Jana Kotlebova. 2018. SVAR Description of ECB Monetary Policy Effects via Banking Sector in Individual EA Countries: Case of Slovenia. International Journal of Monetary Economics and Finance 11: 56–75. [Google Scholar] [CrossRef]
- Socci, Claudio, Severini Francesca, Pretaroli Rosita, Ahmed Irfan, and Ciaschini Clio. 2018. Unconventional Monetary Policy Expansion: The Economic Impact through A Dynamic CGE Model. International Journal of Monetary Economics and Finance 11: 140–62. [Google Scholar] [CrossRef]
- Svensson, Lars E.O. 2003. Escaping from A Liquidity Trap and Deflation: The Foolproof Way and Others. Journal of Economic Perspectives 17: 145–66. [Google Scholar] [CrossRef]
- Taylor, John B. 1993. Discretion versus Policy Rules in Practice. In Carnegie-Rochester Conference Series on Public Policy. Amsterdam: Elsevier, vol. 39, pp. 195–214. [Google Scholar]
- Tobin, James. 1969. A General Equilibrium Approach to Monetary Theory. Journal of Money, Credit and Banking 1: 15–29. [Google Scholar] [CrossRef]
- Tobin, James, and William C. Brainard. 1963. Financial Intermediaries and The Effectiveness of Monetary Controls. American Economic Review 53: 383–400. [Google Scholar]
- Ugai, Hiroshi. 2007. Effects of The Quantitative Easing Policy: A Survey of Empirical Analyses. Monetary and Economic Studies-Bank of Japan 25: 1. [Google Scholar]
- Vayanos, Dimitri, and Jean-Luc Vila. 2009. A Preferred-Habitat Model of The Term Structure of Interest Rates. NBER Working Papers No. 15487. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Wang, Rui. 2019a. Unconventional Monetary Policy in US: Empirical Evidence from Estimated Shadow Rate DSGE Model. International Journal of Monetary Economics and Finance 12: 361–89. [Google Scholar] [CrossRef]
- Wang, Rui. 2019b. Unconventional Monetary Policy in Japan: Empirical Evidence from Estimated Shadow Rate DSGE Model. Journal of International Commerce, Economics and Policy 10: 1950007. [Google Scholar] [CrossRef]
- Woodford, Michael. 2003. Interest and Prices: Foundations of A Theory of Monetary Policy. Princeton: Princeton University Press. [Google Scholar]
- Wu, Jing Cynthia, and Fan Dora Xia. 2016. Measuring The Macroeconomic Impact of Monetary Policy at The Zero Lower Bound. Journal of Money, Credit and Banking 48: 253–91. [Google Scholar] [CrossRef]
- Zagaglia, Paolo. 2013. Forecasting Long-Term Interest Rates with a General-Equilibrium Model of the Euro Area: What Role for Liquidity Services of Bonds? Asia-Pacific Financial Markets 20: 383–430. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).