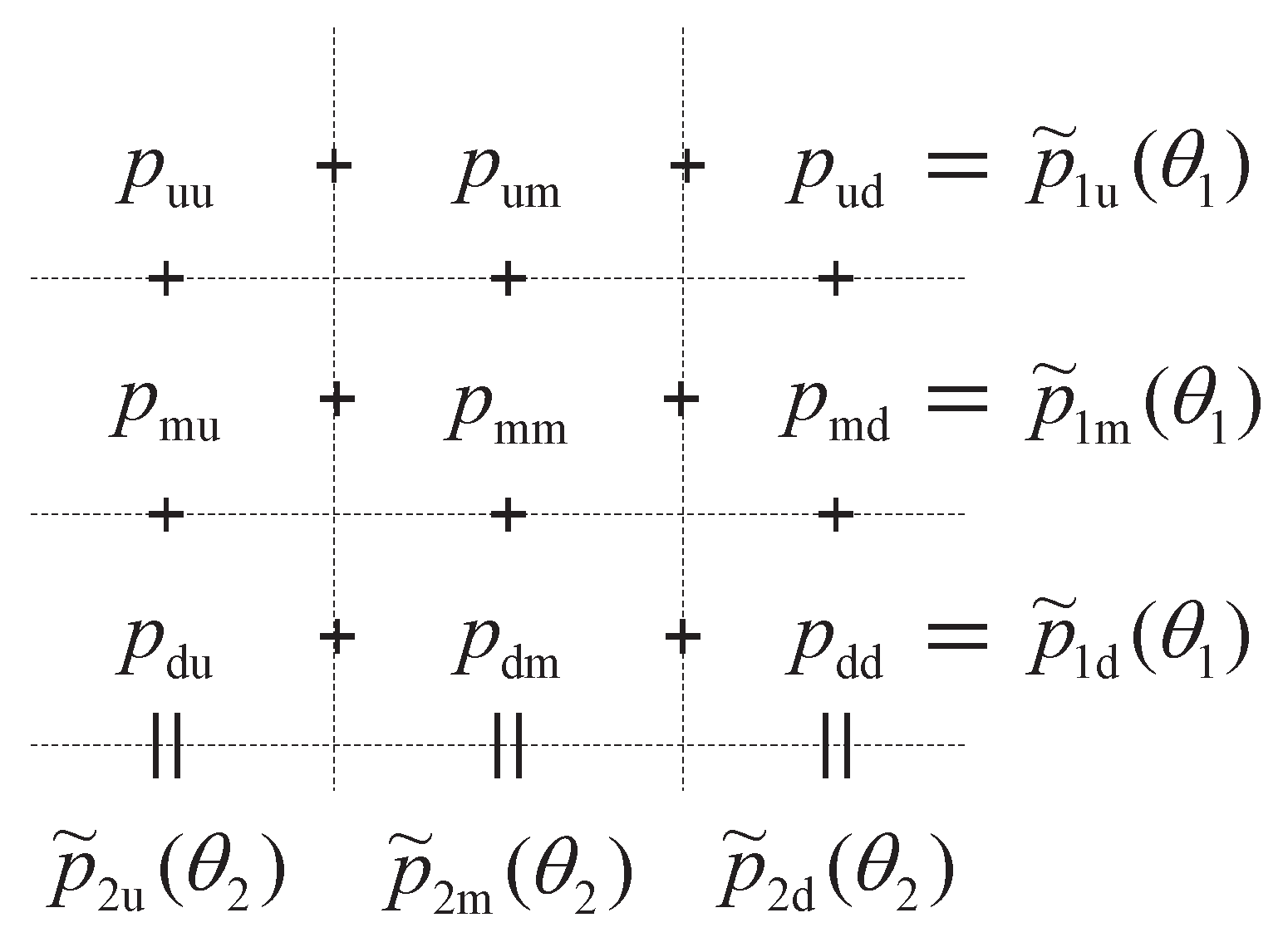In this section, we consider a more general two-factor model:
where
and
are Wiener processes with an instantaneous correlation
. Following the treatment described in (
3a)–(
3b) in
Section 2, we assume that there exist
,
such that
When both individual one-factor lattices are integrated, we shall apply the same convention to all relevant notations, such as , k, h, , and c, by adding a subscript to reflect the index of the process that each notation represents.
Our idea of using two-factor trinomial lattices to approximate (
22a)–(
22b) follows the one proposed by
Hull and White (
1994): obtain a one-factor trinomial lattice for each state variable first, then integrate both lattices to one such that nine branches (
) emanating from each lattice node. Let
,
, a definition extended directly from that in the one-factor case in
Section 2. Assume the one-factor discrete price increment, branching factor for
, and branch jump size are
,
, and
,
, respectively, as defined in
Section 2. An example is given in
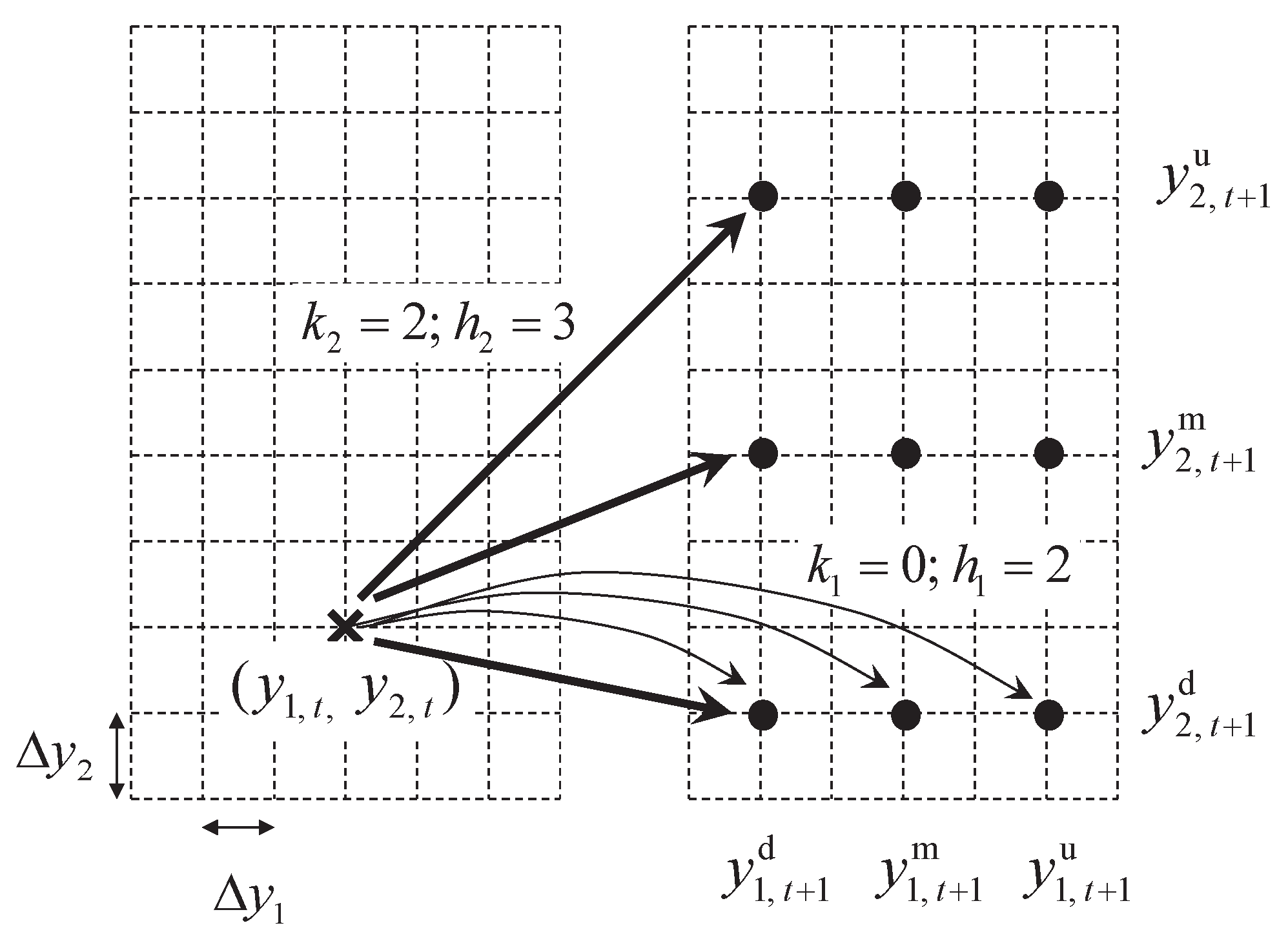
Figure 1, where a node
at time
t is shown in the left panel. The first one calculates
and
using (
5) and (
9), respectively, for each factor
l to determine the three nodes
,
, and
at time
that each factor
l will map into. The nine nodes of their combinations at
are shown in the right panel.
The main task is to solve the nine branching probabilities while matching the first two moments of each factor and their correlation. We further define
,
, and
,
. At each node, to determine the nine branching probabilities
, where
, one solves the following linear system, denoted by
:
3.1. Feasibility of the General Lattice
Consider the nine branches that emanated from a fixed node, where the one-factor branching probabilities are assumed to be
,
. These probabilities are denoted with a tilde to indicate that they are not variables. In addition, assume at this node that the corresponding error factors of the branching and the jump sizes are
and
,
. The branching probabilities can be obtained as follows (cf. (
15a)–(
15c)):
The key step is to rewrite
to the following equivalent form
, in terms of
,
, and
,
:
To maintain legibility, we denote
,
, where
In (
28),
covers all possible nodes in
,
.
is denoted with
to emphasize that it is a ‘local’ problem associated with some specific lattice node (as
and
are functions of
,
). Equations (
27a)–(
27d) intend to match the means and variances of the price deviations of the two factors, which have been met by the marginal probabilities
and
,
. Equation (
27e) is derived from (
24e) with some algebra.
Consider an initial solution
, which satisfies (
27a)–(
27f) but (
27e), unless
. To determine the range of
on the right-hand side (RHS) of (
27e) that
is feasible, consider the following two linear programs:
For a given set of
, it is clear that
is feasible, if, and only if, the RHS of (
27e) is between
and
, i.e.,
Therefore, for
,
, we have
Given the values of
and
, using (
31), the range of the correlation
between the two factors for which the lattice can guarantee feasible branching probabilities at all nodes and all stages can be identified. Next, we will show that (
31) is symmetric such that its upper bound is the negative of its lower bound.
Proposition 6. For any arbitrary , , the following equality holds: Since (
31) is symmetric, we can focus on solving
. The closed-form expression for
has been derived in
Tseng and Lin (
2007), which is duplicated in the following proposition for the sake of clarity.
Proposition 7. , wherewhere , , are from (26a)–(26c). Note that , are also functions of and . It can be seen that , , and reduce to , , and , and vice versa, respectively, by exchanging the factor indices 1 and 2.
Using the result from Proposition 6 to find the upper bound of (
31), one needs to solve
for
,
. It would be easier to solve if one could switch the two minimization operators in (
33) as follows:
It turns out that both (
33) and (
34) are equivalent, which is shown in the following proposition.
Proposition 8. Let be n continuous functions and , where is finite. Then, Next, we state the main theorem of this section.
Proposition 1. (Two-Factor Lattice Feasibility) Given a lattice configuration , is feasible for all , , if, and only if, , where Theorem 1 is general, but, unfortunately, no explicit functional expressions for are available because each of them requires solving a two-dimensional global minimum of a discontinuous function. However, given a set of lattice parameters , using numerical methods, such as exhaustive search, one can easily obtain the numerical values of .
From the perspective of minimizing computational requirements, one would prefer smaller values of
so that the grid size may not become too small. To achieve that, next, we try to maximize
over
and
for a given
pair:
Using numerical methods,
Table 1 shows the values of
for all 100 pairs of
for
. Note that, since
is symmetric,
Table 1 only displays half of the pairs with
. From
Table 1, it is clear that
is an increasing function in
and
. If one considers increasing
by 1 to be as difficult in terms of computational effort as increasing
by 1, then the diagonal elements where (
) seem to be the most efficient choices.
When
, to obtain the optimal solutions
for achieving
in (
38), it turns out that
in Theorem 1 are the smallest elements in the minimum operator in (
36), so a symmetrical optimal solution
is obtained. Using numerical methods, the values of
and the corresponding (
are summarized in
Table 2.
As an example, if
, using the optimized
from
Table 2, one can use
by using
obtained from the
Appendix A. Note that the results presented in this section are for general two-factor lattices. If the two underlying diffusion processes have some special structures, e.g., the class of square root volatility models, then
may be further increased so that the required
that guarantees lattice feasibility may be lowered. In the next section, we focus on the Heston SV model, for which explicit functional expressions for
are available.
3.2. Lattice for the Heston SV Model
Consider the Heston SV model (
Heston 1993) as follows:
where
is the logarithm of the stock price;
,
,
m, and
are positive constants.
Since both volatilities in (
39a) and (
39b) are functions of
, we focus on the MR process of
. As mentioned in
Section 2.2, if the Feller condition is satisfied,
exists for (
39b). Based on
, we can identify positive
and
. Once
is obtained, we set
Proposition 9. To implement the Heston SV model given in (39a)–(39b) using the proposed trinomial lattice and (40), if , then , , and at all nodes. Using Proposition 9, we will show that Theorem 1 has an explicit functional form for
if we set
. Since
is a constant,
is a fixed constant for all nodes. We denote it as
. Without loss of generality, we assume
. To make
, from (
5), we need to have
This can be achieved by adjusting the value of
,
, or
. Adjusting
and/or
is more straightforward than adjusting
. However, since
is a parameter for lattice configuration, we recommend adjusting the value of
slightly to eliminate the remainder of (
41) in order to make
.
With
and
, using (
31), the condition for lattice feasibility can be significantly simplified as follows:
for
,
.
Theorem 2. (Lattice feasibility for the Heston SV) Pertaining to the Heston SV model in (39a)–(39b), assume and . Given a lattice configuration , is feasible for all , , if, and only if, , wherewhere Next, we try to maximize
by adjusting the lattice configuration
while maintaining lattice feasibility. Let
Using numerical methods, the solution of (
45) is obtained as follows. When
,
is achieved at the lower bounds of
and
, where
, and
is determined by
. When
,
is achieved at
, the lower bound, and
at the point where
. That is,
where
It can be seen that
approaches 1 as
increases. The value of
for
is given in
Table 3, along with the corresponding
. Note that
is symmetric in
and
. Therefore, another solution for
is to switch
and
.
Back to the previous example, if , now it only requires with (1.1832,1.1866) or (1.1866, 1.1832) to achieve lattice feasibility, a reduction from of the optimized general model.