Abstract
This paper investigates the American option price in a two-state regime-switching model. The dynamics of underlying are driven by a Markov-modulated Geometric Wiener process. That means the interest rate, the appreciation rate, and the volatility of underlying rely on hidden states of the economy which can be interpreted in terms of Markov chains. By means of the homotopy analysis method, an explicit formula for pricing two-state regime-switching American options is presented.
1. Introduction
Pricing financial derivative is an ative field of research in mathematical finance. The pioneering work of Black and Scholes (1973) and Merton (1973) laid the foundations of field and gave rise tto a branch of the research in option pricing theory. The most options traded in the financial markets are American-style options. An American option grants its holder with the right to exercise the option before or on its expiry date. For pricing American options, one needs to determine the option price as well as its optimal exercise boundary. In the Black–Scholes framework, there is an analytical solution for pricing finite-horizon American options, which was first presented by Zhu (2006). Prior to the work of Zhu (2006), McKean (1965) and Merton (1973) pointed out that the problem of pricing American option is equivalent to a free-boundary problem. There are many methods, including analytical and numerical approximations, to solve this kind of free boundary problem. For instance, analytical approximation works include Johnson (1983); MacMillan (1986); Omberg (1987); Barone-Adesi and Whaley (1987); Barone-Adesi and Elliott (1991); Carr (1998) and Bunch and Johnson (2000). While numerical approximation work include Brennan and Schwartz (1977); Geske and Shastri (1985); Geske and Johnson (1984); Carr and Faguet (1996), and Hon and Mao (1997). An alternative approach aparting from a free boundary problem is called the decomposition method, see Jacka (1991); Kim (1990); Carr et al. (1992). Using the decomposition method, the price of an American option can be written as the sum of its European counterpart and the early exercise premium. Carr et al. (1992) proposed a variant decomposition approach, in which the price of American option can be written as its intrinsic value plus its time value. The early exercise premium is expressed in an integral form, and it implicitly relies on the early exercise boundary. The only known explicit solution for the optimal exercise boundary was found by Zhu (2006) in the form of infinite series. There are many approximation methods in the literature. In particular, the asymptotic behaviour of the optimal exercise boundary near maturity has attracted lots of attention as a promising way to derive an explicit formula, see Alobaidi and Mallier (2001); Chevalier (2005); Evans et al. (2002). However, these short-maturity asymptotic approximations of the optimal exercise boundary are not sufficiently precise under realistic model parameters, see Mallier (2002). The other numerical schemes for calculating the early exercise premium include Huang et al. (1996) and Ju (1998).
Recently, there is active research in the applications of regime switching models followed by an unobservable Markov chain to a variety of financial problems. For an overview of unobservable Markov chains and their financial applications, we refer to Elliott et al. (1994) and Elliott and Kopp (1999). Some financial applications of regime switching include Elliott and van der Hoek (1997) for asset allocation, Elliott et al. (2001) for interest rate models, Buffington and Elliott (2002a, 2002b) for pricing European and American options, Elliott et al. (2003) for volatility estimation, Guo (2001a) for option pricing, Elliott et al. (2005) for option pricing via an Esscher transformation. In addition, Guo (2001b) investigated Russian options in the regime switching model. Guo and Shepp (2001) investigated the perpetual American lookback options. Guo and Zhang (2004) priced the perpetual American options with regime switching. Jobert and Rogers (2006) priced the finite maturity American put and barrier options with regime switching using a lattice approach. Huang (2011) formulated the regime-switching American problem as an optimal control problem and used discretization methods to solve it. Lu and Putri (2020) applied Laplace transform to regime-switch the American option and obtained a semi-analytical solution. Egami and Kevkhishvili (2020) reduced an optimal stopping problem with an arbitrary value function in a two-regime environment to a pair of optimal stopping problems without regime switching. So far, there is no analytical formula for the finite-horizon regime switching American option.
Regime switching models have been used in finance practice and have recently started gaining increasing popularity. One of the key issues is how to identify the states of economy in regime switching models. In this regard, two recent publications have discussed this issue (see He and Zhu (2018) and He and Zhu (2021), in addition to using real market data in calibration, so that a practical use of regime switching models is clearly demonstrated through convincing empirical evidence. Another example that has clearly demonstrated the use of regime switching models in finance practice is the two earlier papers that were published by Elliott et al. (2003) and Elliott and Royal (2007), who used filtering methods to estimate the state of the economy from historical stock market data. In these two publications, a log-normal dynamics with Markov-switching volatility and a regime switching variance Gamma dynamics were adopted in their regime switching models, respectively.
We will extend the work of Zhu (2006) to obtain an explicit formula for pricing finite-horizon regime switching American options by means of the homotopy analysis method (HAM). HAM was first proposed by Ortega and Rheinboldt (1970) and has been successfully applied to solve a variety of heat transfer problems, see Liao (1997); Liao and Zhu (1999); and fluid-flow problems, see Liao and Zhu (1996); Liao and Campo (2002). Zhu (2006) applied HAM to derive an explicit pricing formula for American options in the Black–Scholes–Merton framework. Gounden and O’Hara (2010) extended the work of Zhu to pricing an American-style Asian option of floating strike type in the Black–Scholes–Merton model. Leung (2013) applied HAM to obtain an explicit formula for lookback options under a stochastic volatility model. Chan and Zhu (2015) used HAM to derive an explicit formula for American-style convertible bonds with regime switching.
2. The Model Formulation
Let be a complete probability space, where is an actual probability measure. Let be the time index set of the model. Let be a standard Wiener process on . We consider a continuous-time Markov chain on with a finite state space . Without a loss of generality, we can identify the state space of to be a finite set of unit vectors , where . We assume that and are independent.
Denote A for the generator . Subsequently, according to Elliott et al. (1994), the semi-martingale representation theorem is in the form of :
Here, is an -valued martingale increment process with respect to the filtration that is generated by .
The interest rate of the money market account is given by:
where with for each and denotes the inner product in .
In this case, the dynamics of underlying for the money market account are given by:
We suppose that the stock appreciation rate and the volatility of S also rely on and they are given by:
Here, and with for each .
The dynamics of underlying are then given by the following Markov-modulated geometric Wiener process:
Here, is a standard Wiener process on a complete probability space with respect to the filtration , which is the -augmentation of the natural filtration that is generated by W.
Free Boundary Problem
Let us consider an American put option with expiry T and exercise price K. In this subsection, we consider a special case with the number of regimes N, being 2 in order to simplify our discussion. We adopt the approach in Buffington and Elliott (2002b) to derive the results in this section. Given that and that , the price of the American put option at time t is given by:
where the supremum is taken over the set of stopping times taking values in .
Let . When (), the continuation region is given by:
and the stopping region is given by:
Follow the lines of Buffington and Elliott (2002b), we write for the t-section of , for each and . Let be the critical price of the American put when (); that is, when the state and the price of the underlying at time t falls below , it is rational for the holder of the American put to exercise the option at time t. Note that , for each . Subsequently, by Elliott and Kopp (1999) and Buffington and Elliott (2002b),
We shall consider the case .
Yi (2008) showed that, if then and for each in a two-state regime switching model. When , is in the common continuation region and satisfies the following pair of coupled P.D.E.s:
When ,
When ,
On the optimal curve (), it is required that satisfies a high-contact condition:
and a smooth-pasting condition:
When S is in the transition region , and satisfies the following P.D.E.:
and boundary conditions
Clearly, there are two free boundary functions, and , and two option prices, and , as listed in the above PDE systems. Which one of these is used to determine if an option should be exercised or continuously held has not been clearly stated in the literature. A flow chart could be useful for financial practitioners who wish to use our solutions to price American put options in a two-state regime switching setting.
Assumming that all of the model parameters, including and , have been extracted from market data and assumming that one knows the current status of economy, i.e., we are either in State 1 or State 2, before one decides to use a regime-switching model to price an American option. Subsequently, the actual pricing exercise needs be divided into two stages, relying on the current status of economy when a pricing task is conducted. If we are in a higher status of economy, i.e., in State 2, using the obtained in Section 3.1 would be sufficient, because, in this case, once S drops below from the above, the put option should be exercised as a result of the fact that . On the other hand, if we are in a lower status of economy, i.e., in State 1, an additional PDE system may need to be solved relying on the current underlying value. For the range of , the solution that is shown in Section 3.1 can no longer be used and one needs to use the solution shown in Section 3.2, in which has already “landed” on the payoff function. This pricing procedure can be better demonstrated with the following flow chart, see Figure 1.
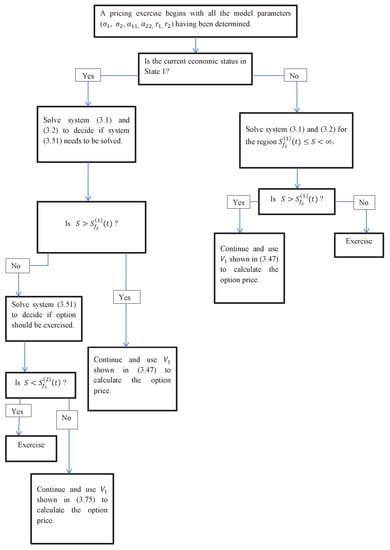
Figure 1.
An illustrative flow chart for the usage of our solutions.
Note that we use superscripts in the flow chart to denote the free boundaries that were obtained in the corresponding stage. For simplicity, they will all be removed in the next section without any ambiguity, as we have denoted each stage by a separate subsection.
3. HAM Approach
It was noted earlier that American options can be formulated as free boundary problems. Closed-form solutions of free boundary problems are notoriously difficult to derive. However, by employing the homotopy analysis method, an exact and closed-form solution can be derived, in the form of infinite series. We have defined the common continuation region and the transition region in Section 2. Each problem in these regions is solved below.
3.1. The Common Continuation Region
Firstly, let us discuss the American put value function in the common continuation region where and , satisfy the equations:
Note that and are coupled. To solve these systems effectively, we shall make all variables dimensionless by introducing dimensionless variables
With all of the primes dropped from now on, the dimensionless systems read
Here, and , which can be viewed as an interest rate relative to the volatility of the underlying asset price.
Take the Laudau transformation
to change the moving boundary to fixed boundary conditions, thus yielding:
Now, to solve (23) and (24) by the homotopy analysis method, we introduce an embedding parameter and construct unknown functions and that satisfy the following differential systems:
Here, is a differential operator that is defined as
and is a functional defined as
Equations (25) and (26) are known as the zeroth order deformation equations and they determine the continuous deformation of . To construct Equations (25) and (26), we want to find a continuous map, such that the solution we are seeking becomes the result of a continuous deformation from an initial and known function. Here, the initial state of the continuous deformation is at . With , we have, from Equations (25) and (26),
Clearly, the solutions of the differential systems (30) and (31) are in forms of
so long as the initial guess satisfies the condition
Note that, other than this condition, theoretically, there are no other requirements for the initial guess to satisfy. However, a faster convergence of the series is expected if we select a function that has already satisfied an additional condition .
With , we have
Comparing with (23) and (24), it is easy to see that the solution we seek is nothing but
In order to determine the values of and , , we can apply a Taylor’s series expansion of p to the functions and
where
To determine the coefficients in the above Taylor series expansion, we derive a set of governing equations by differentiating the zeroth-order (25) and (26), with respect to p and then set . After this process, we get
and
Additionally,
and
Here, After eliminating from the two boundary conditions at in the systems, then the systems can be written in a general form,
where
Additionally,
where
Now, let us apply the following transformation
so that (45) and (49) can be expressed in the form of a standard nonhomogeneous diffusion system:
An explicit solution of Equations (54) and (55) at each order (i.e., with each n) can now be found by splitting the linear problem into three problems, a method that is commonly used in solving linear PDEs. For further details of the solution procedure we refer to Carslaw and Jaeger (1959). The final explicit solution at each order is then:
where
Additionally,
where
and denotes the complementary error function.
For the choice of an initial guess , , any continuous functions satisfying the limiting condition can be used, we select the corresponding European option value as the initial guess with three apparent advantages given as discussed in Zhu (2006):
- the boundary condition as is automatically satisfied;
- will become 0; which we expect will foster a faster convergence of the series and it also help to simply as the first term of will vanish; and,
- also, as satisfies the condition, so and as for all , the integral containing is eliminated.
Zhu et al. (2012) provides the analytic solution of a European put option with a two-state regime switching:
for where
and
The vanishing of allows us to write the solution in a simple and closed form:
Once are found at each order by substituting Equations (61) and (62) back into Equation (53), can easily be found from the third equation of Equations (41)–(44), i.e.,
Upon finding the coefficients and from (43), (61)–(64), the final solution can be written in terms of a series of infinitely many terms, as
We also derive the exact, analytic, and closed-form formula for the optimal exercise boundaries in the form:
and
3.2. Transition Region
Let us consider the transition region between the two stopping curves:
In this region and satisfies the Black–Scholes–Merton equation
with a terminal condition
Additionally, continuity on gives:
and smoothness on gives:
To solve this system effectively, we shall make all of the variables dimensionless by introducing dimensionless variables
and also make the Laudau transformation
With all of the primes dropped from now on, the dimensionless systems with fixed boundary conditions read
We will use the homotopy analysis method to solve this nonlinear system of equations. We introduce an embedding parameter and construct unknown functions and The zeroth-order deformation is given by
Here, is a differential operator that is defined as
and is a functional defined as
With , we have
When comparing with (71), it is easy to see that the solution we seek is nothing but
If , then we have
Clearly, the solution of the differential system (77) is
so long as the initial guess satisfies the condition
The initial guess is given in Equation (60). To determine the values of and , we can apply a Taylor’s series expansion of p to the functions and
where
In order to determine the coefficients in the above Taylor series expansion, we derive a set of governing equations by differentiating the zeroth-order (72), with respect to p and then setting . After this process, we obtain
and
Here, After eliminating from the two boundary conditions at in the systems, then the systems can be written in a general form,
where
Now, we apply the following transformation
so that (84) can be written in the form of a standard nonhomogeneous diffusion system:
The final explicit solution at each order is then:
where
Once are found at each order by substituting Equations (90) back into Equation (88), can easily be found from the third equation of Equations (82) and (83), i.e.,
Upon finding the coefficients and from (88), (90), and (92), the final solution can be written in terms of a series of infinitely many terms as
4. Conclusions
By means of the homotopy analysis method, an exact analytical pricing formula for the American option under a two-state regime-switching economy is derived. It is shown that the optimal exercise boundary, which is the key difficulty in the valuation of American options, can be explicitly expressed in the form of infinite series. In addition, we provide a flow chart to show when a particular formula should be used for the easiness of using our solutions to price American put options under a two-state regime switching model.
Author Contributions
Conceptualization, L.C. and S.-P.Z.; methodology, S.-P.Z. and L.C.; Analysis, L.C.; Writing—original draft preparation, L.C.; Discussion, L.C. and S.-P.Z. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alobaidi, Ghada, and Roland Mallier. 2001. Asymptotic analysis of American call options. International Journal on Mathematics and Mathematical Sciences 27: 177–88. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, and Robert E. Whaley. 1987. Efficient analytic approximation of American option values. Journal of Finance 42: 301–20. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, and Robert J. Elliott. 1991. Approximations for the values of American options. Stochastic Analysis and Applications 9: 115–31. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–59. [Google Scholar] [CrossRef]
- Brennan, Michael, and Eduardo Schwartz. 1977. The valuation of American put options. Journal of Finance 32: 449–62. [Google Scholar] [CrossRef]
- Buffington, John, and Robert J. Elliott. 2002a. Regime switching and European options. In Stochastic Theory and Control. Edited by Lawrence Kansas. Berlin and Heidelberg: Springer, pp. 73–81. [Google Scholar]
- Buffington, John, and Robert J. Elliott. 2002b. American options with regime switching. International Journal of Theoretical and Applied Finance 5: 497–514. [Google Scholar] [CrossRef]
- Bunch, David S., and Hensher Johnson. 2000. The American put option and its critical stock price. The Journal of Finance 5: 2333–56. [Google Scholar] [CrossRef]
- Carr, Peter. 1998. Randomization and the American put. Review of Financial Studies 11: 597–626. [Google Scholar] [CrossRef]
- Carr, Peter, and Dmitri Faguet. 1996. Valuing Finite-Lived Options as Perpetual. Working paper. New York: Morgan Stanley. [Google Scholar]
- Carr, Peter, Robert Jarrow, and Ravi Myneni. 1992. Alternative characterizations of American Puts. Mathematical Finance 2: 87–106. [Google Scholar] [CrossRef]
- Carslaw, Horatio S., and John C. Jaeger. 1959. Conduction of Heat in Solids. Oxford: Clarendon Press. [Google Scholar]
- Chan, Leunglung, and Song-Ping Zhu. 2015. An analytic formula for pricing American-style convertible bonds in a regime switching model. IMA Journal of Management Mathematics 26: 403–28. [Google Scholar] [CrossRef]
- Chevalier, Etienne. 2005. Critical price near maturity for an American option on dividend-paying stock in a local volatility model. Mathematical Finance 15: 439–63. [Google Scholar] [CrossRef]
- Egami, Masahiko, and Rusudan Kevkhishvili. 2020. A direct solution method for pricing options in regime-switching models. Mathematical Finance 30: 547–76. [Google Scholar] [CrossRef]
- Elliott, Robert J., Lakhdar Aggoun, and John B. Moore. 1994. Hidden Markov Models: Estimation and Control. Berlin, Heidelberg and New York: Springer. [Google Scholar]
- Elliott, Robert J., and John van der Hoek. 1997. An application of hidden Markov models to asset allocation problems. Finance and Stochastics 3: 229–38. [Google Scholar] [CrossRef]
- Elliott, Robert J., and P. Ekkehard Kopp. 1999. Mathematics of Financial Markets. Berlin, Heidelberg and New York: Springer. [Google Scholar]
- Elliott, Robert J., William C. Hunter, and Barbara M. Jamieson. 2001. Financial signal processing. International Journal of Theoretical and Applied Finance 4: 567–84. [Google Scholar] [CrossRef]
- Elliott, Robert J., William P. Malcolm, and Allanus H. Tsoi. 2003. Robust parameter estimation for asset price models with Markov modulated volatilities. Journal of Economics Dynamics and Control 27: 1391–409. [Google Scholar] [CrossRef]
- Elliott, Robert J., Leunglung Chan, and Tak Kuen Siu. 2005. Option Pricing and Esscher Transform Under Regime Switching. Annals of Finance 1: 423–32. [Google Scholar] [CrossRef]
- Elliott, Robert J., and Andrew J. Royal. 2007. Asset prices with regime switching variance Gamma dynamics. In Hand Book on Mathematical Finance. Edited by Alain Bensoussan and Qiang Zhang. Amsterdam: Elsevier, pp. 685–711. [Google Scholar]
- Evans, Jonathan, Joseph Keller, and Rachel Kuske. 2002. American options on assets with dividends near expiry. Mathematical Finance 12: 219–37. [Google Scholar] [CrossRef]
- Geske, Robert, and Herb E. Johnson. 1984. The American put option valued analytically. Journal of Finance 39: 1511–1524. [Google Scholar] [CrossRef]
- Geske, Robert, and Kuldeep Shastri. 1985. Valuation by approximation: A comparison of alternative option valuation techniques. Journal of Financial and Quantitative Analysis 20: 45–71. [Google Scholar] [CrossRef]
- Gounden, Shashen, and John G. O’Hara. 2010. An analytic formula for the price of an American-style Asian option of floating strike type. Applied Mathematics and Computation 217: 2923–36. [Google Scholar] [CrossRef]
- Guo, Xin. 2001a. Information and option pricings. Quantitative Finance 1: 38–44. [Google Scholar] [CrossRef]
- Guo, Xin. 2001b. An explicit solution to an optimal stopping problem with regime switching. Journal of Applied Probability 38: 464–81. [Google Scholar] [CrossRef]
- Guo, Xin, and Larry Shepp. 2001. Some optimal stopping problems with non-trivial boundaries for pricing exotic options. Journal of Applied Probability 38: 647–58. [Google Scholar] [CrossRef]
- Guo, Xin, and Qing Zhang. 2004. Closed-form solutions for perpetual American put options with regime switching. SIAM Journal on Applied Mathematics 64: 2034–49. [Google Scholar]
- He, Xinjiang, and Song-Ping Zhu. 2018. On full calibration of hybrid local volatility and regime-switching models. Journal of Futures Markets 38: 586–606. [Google Scholar] [CrossRef]
- He, Xinjiang, and Song-Ping Zhu. 2021. A new algorithm for calibrating local regime-switching models. IMA Journal of Management Mathematics 32: 237–255. [Google Scholar] [CrossRef]
- Hon, Yiu-Chung, and Xian-Zhong Mao. 1997. A radial basis function method for solving options pricing model. Journal of Financial Engineering 8: 31–49. [Google Scholar]
- Huang, Jing Zhi, Marti G. Subrahmanyam, and G. George Yu. 1996. Pricing and hedging American options: A recursive integration method. Review of Financial Studies 9: 277–300. [Google Scholar] [CrossRef]
- Huang, Yiqing, Peter A. Forsyth, and George Labahn. 2011. Methods for pricing American options under regime switching. SIAM Journal on Scientific Computing 33: 2144–68. [Google Scholar] [CrossRef]
- Jacka, Saul D. 1991. Optimal stopping and the American put. Mathematical Finance 1: 1–14. [Google Scholar] [CrossRef]
- Jobert, Arnaud, and Leonard Chris G. Rogers. 2006. Option pricing with Markov-modulated dynamics. SIAM Journal on Control and Optimization 44: 2063–78. [Google Scholar] [CrossRef]
- Johnson, Herb E. 1983. An analytical approximation for the American put price. Journal of Financial and Quantitative Analysis 18: 141–148. [Google Scholar] [CrossRef]
- Ju, Nengjiu. 1998. Pricing an American option by approximating its early exercise boundary as a multipiece exponential function. Review of Financial Studies 11: 627–46. [Google Scholar] [CrossRef]
- Kim, In Joon. 1990. The analytical valuation of American options. Review of Financial Studies 3: 547–72. [Google Scholar] [CrossRef]
- Leung, Kwai Sun. 2013. An analytic pricing formula for lookback options under stochastic volatility. Applied Mathematics Letters 26: 145–49. [Google Scholar] [CrossRef][Green Version]
- Liao, Shijun. 1997. Numerically solving non-linear problems by the homotopy analysis method. Computational Mechanics 20: 530–40. [Google Scholar] [CrossRef]
- Liao, Shijun, and Antonio Campo. 2002. Analytic solutions of the temperature distribution in Blasius viscous flow problems. Journal of Fluid Mechanics 453: 411–25. [Google Scholar] [CrossRef]
- Liao, Shijun, and Ji-Mao Zhu. 1996. A short note on higher-order streamfunction-vorticity formulations of 2D steady state Navier-Stokes equations. International Journal for Numerical Methods in Fluids 22: 1–9. [Google Scholar]
- Liao, Shijun, and Song-Ping Zhu. 1999. Solving the Liouville equation with the general boundary element method approach. Boundary Element Technology 13: 407–16. [Google Scholar]
- Lu, Xiaoping, and Endah Putri. 2020. A semi-analytical valuation of American options under a two-state regime-switching economy. Physica A 538: 122968. [Google Scholar] [CrossRef]
- MacMillan, L.W. 1986. An analytical approximation for the American put prices. Advances in Futures and Options Research 1: 119–39. [Google Scholar]
- Mallier, Roland. 2002. Evaluating approximations to the optimal exercise boundary. Journal of Applied Mathematics 2: 71–92. [Google Scholar] [CrossRef]
- McKean, Henry P. 1965. A free boundary problem for the heating function arising from a problem in mathematical economics. Industrial Management Review 6: 32–39. [Google Scholar]
- Merton, Robert. 1973. Theory of rational option pricing. Bell Journal of Economics and Management Science 4: 141–83. [Google Scholar] [CrossRef]
- Omberg, Edward. 1987. The valuation of American puts with exponential exercise policies. Advances in Futures and Options Research 2: 117–42. [Google Scholar]
- Ortega, James M., and Werner C. Rheinboldt. 1970. Iterative Solution of Nonlinear Equations in Several Variables. New York: Academic Press. [Google Scholar]
- Yi, Fahuai. 2008. American put option with regime-switching volatility (finite time horizon)-Variational inequality approach. Mathematical Methods in Applied Sciences 31: 1461–77. [Google Scholar] [CrossRef]
- Zhu, Song-Ping. 2006. An exact and explicit solution for the valuation of American put options. Quantitative Finance 6: 229–42. [Google Scholar] [CrossRef]
- Zhu, Song-Ping, Alexander Badran, and Xiaoping Lu. 2012. A new exact solution for pricing European options in a two-state regime-switching economy. Computers and Mathematics with Applications 64: 2744–55. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).