A Sustainable Economic Recycle Quantity Model for Imperfect Production System with Shortages
Abstract
1. Introduction and Literature Review
- (i)
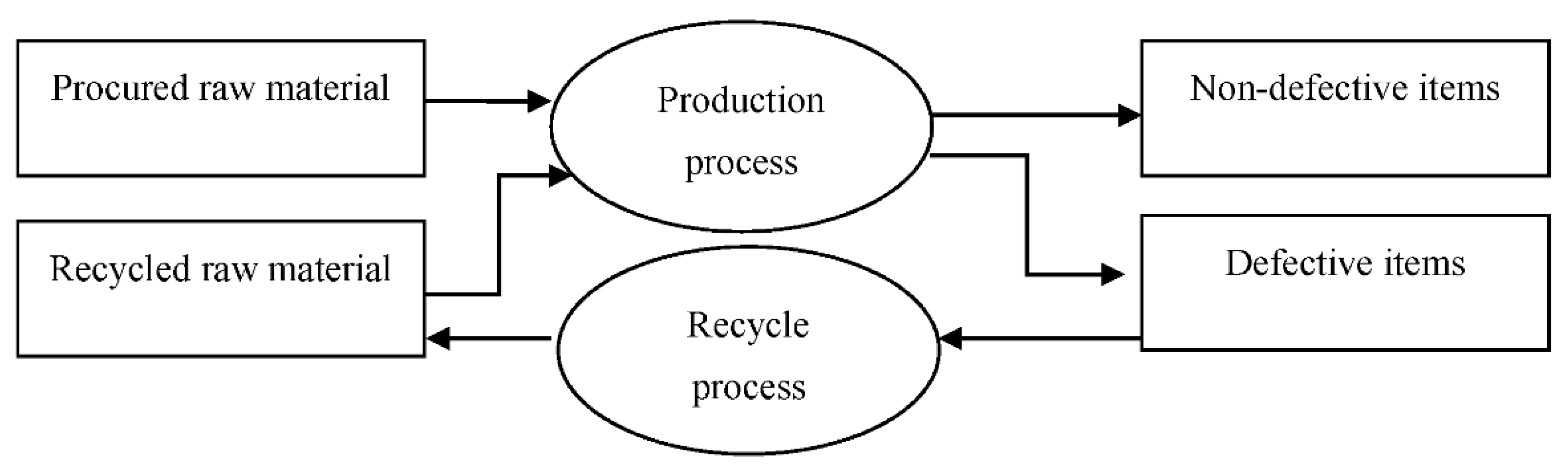
- The proposed model is developed focusing on the recycling of defective items collected from regular production after the proper screening with 100% recovery of raw materials used for production in the corresponding item category.
- (ii)
- An inventory model is developed for three-level piecewise constant demand, which varies under three different production time parts, from production run-time to production off-time with positive stock and production off-time with shortages.
2. Assumptions and Notation
2.1. Assumptions
- (i)
- The production rate is finite and fixed.
- (ii)
- The defective rate is known, and constant and defective items are produced randomly alongside the perfect product.
- (iii)
- The demand rate of the perfect product is a piecewise constant function (motivated from Bai and Varanasi (1996)):The demand during production-run and production off-times and stock-out period is as follows:
- (iv)
- The sum of the demand rate and defective rate is less than the rate of production.
- (v)
- Lead-time is negligible, and the number of shortages is acceptable while the model is considered for a single items production system.
- (vi)
- Defective items are recyclable with 100% recovery of raw material usable for the production of same product in the next cycle time, and the value of the recycled materials is higher than that of purchased materials.
- (vii)
- The holding cost per defective item is same as that of fresh items, while the recycle cost per defective item is equal irrespective of its number.
2.2. Notation
3. Model Formulation
- Case 1:
- EPQ model for defective items with three levels of piecewise constant demand under shortages
- Case 2:
- ERQ model for defective items with three levels of piecewise constant demand under shortages
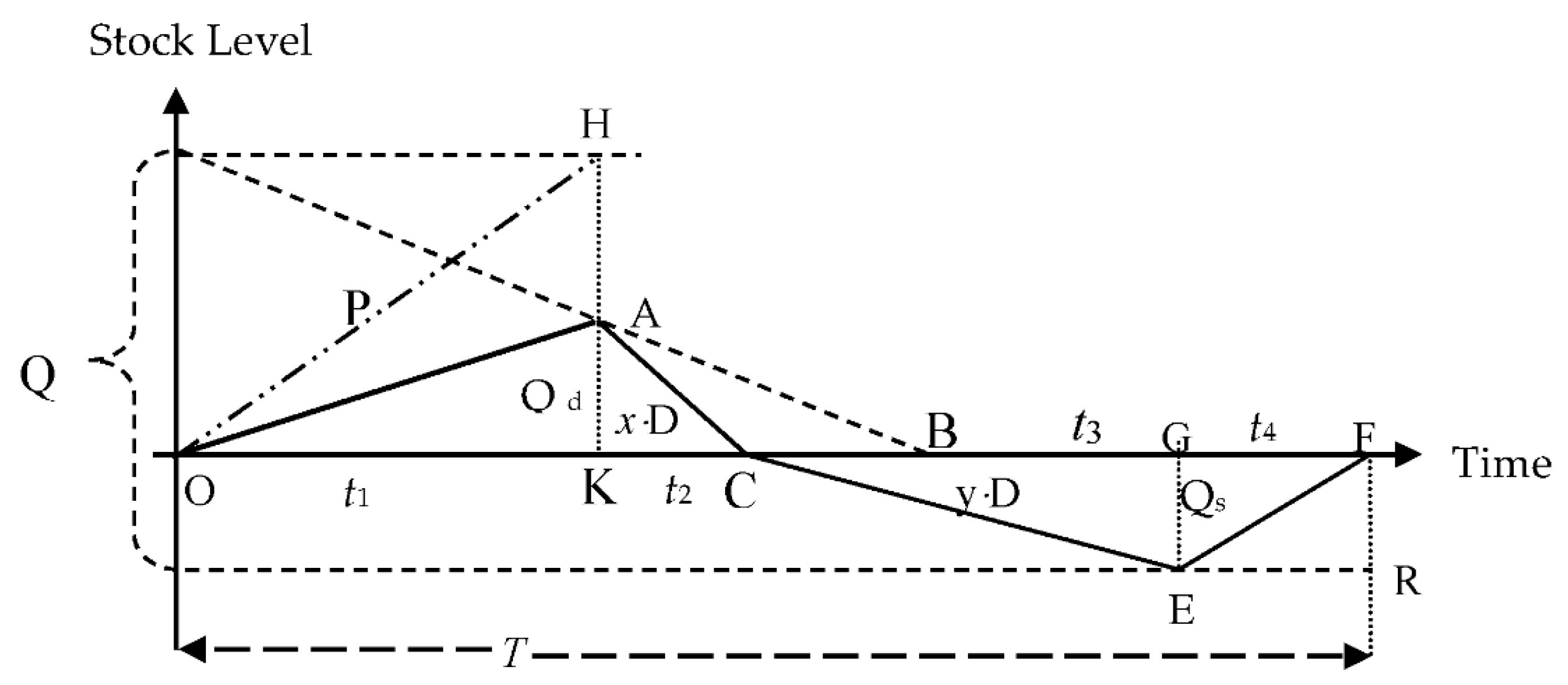
3.1. Case 1 (EPQ Model for Defective Items with Three Levels of Piecewise Constant Demand under Shortages)
- (1)
- Average setup cost or fixed cost (FC):
- (2)
- Average production cost (PC):
- (3)
- Average raw material cost (RMC):Each production lot size is a quantity for which raw materials are purchased for exact production in each time cycle. Therefore,
- (4)
- Average holding cost (HC):Defective items have no holding cost in this case. Therefore,Total inventoryAnd average inventoryTherefore,
- (5)
- Average shortage cost (SC):Hereafter, the total cost function isTCD = FC + PC + RMC + HC + SC
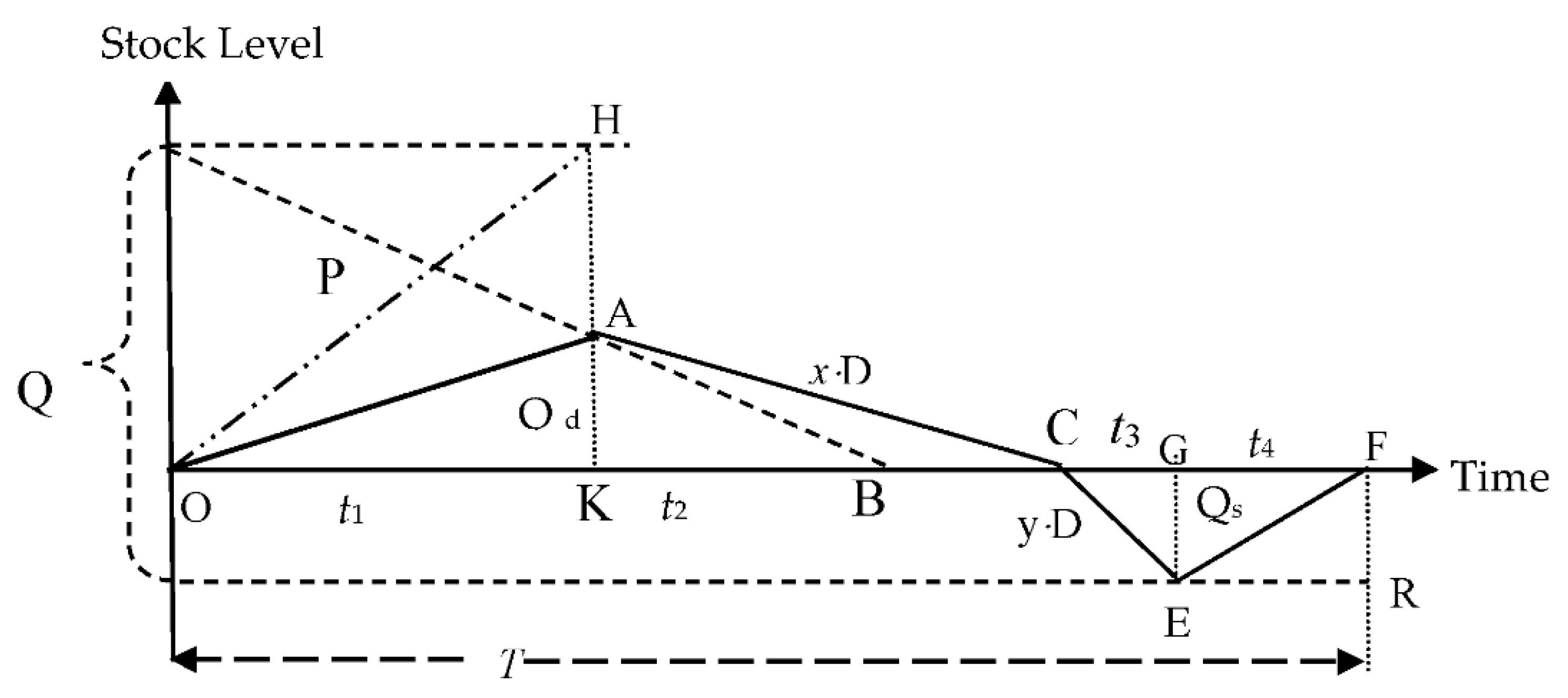
3.2. Case 2 (ERQ Model for Defective Items with Three Levels of Piecewise Constant Demand under Shortages)
- (1)
- Average production cost (PC) is:
- (2)
- Average raw material cost (RMC): Each production lot size is , but raw materials for units of items in each time cycle are purchased. Therefore,
- (3)
- Average holding cost (HC):Holding cost of defective items is included during time before the items are sent for recycling. Therefore,Total inventoryAverage inventoryHence,
- (4)
- Average shortage cost (SC):
- (5)
- Average recycle cost (RC):Hence, the total cost function isTCR = FC + PC + RMC + HC + SC + RC
4. Theoretical Derivations
4.1. Case 1 (EPQ Model for Defective Items with Three Levels of Piecewise Constant Demand under Shortages)
Special Cases
- (i)
- If d = 0, then W*=
- (ii)
- If x = y = 1 and d = 0, then we get
- (iii)
- If x = y, then,and Q* =
- (iv)
- If x = y = 1, then,And Q* =
4.2. Case 2 (ERQ Model for Defective Items with Three Levels of Piecewise Constant Demand under Shortages)
Special Cases
- (i)
- If d = 0, then W* =
- (ii)
- If x = y = 1 and d = 0, then,
- (iii)
- If x = y then,
- (iv)
- If x = y = 1, then,
4.3. Value of “m”
5. Numerical Illustrations and Case Study
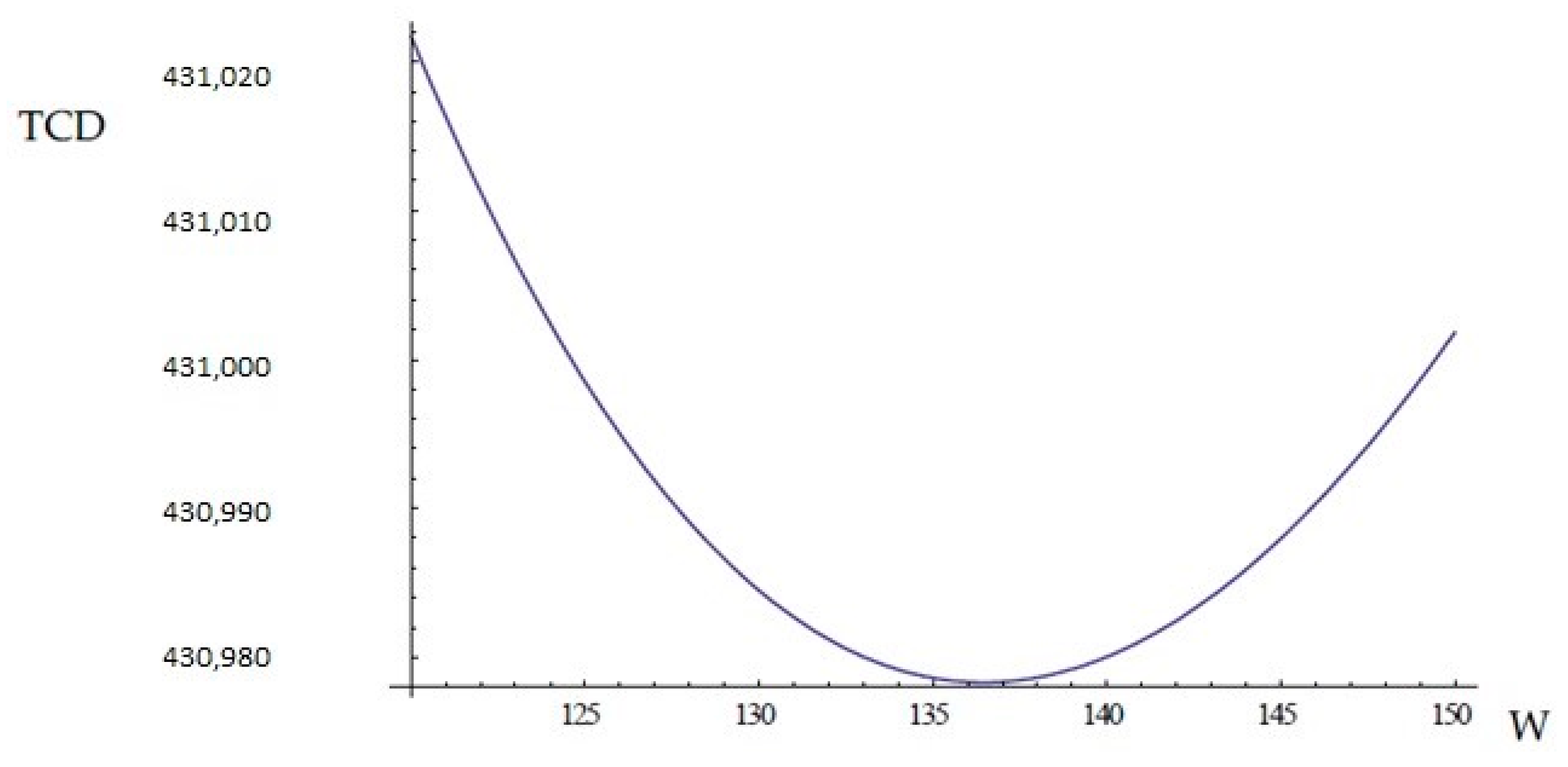
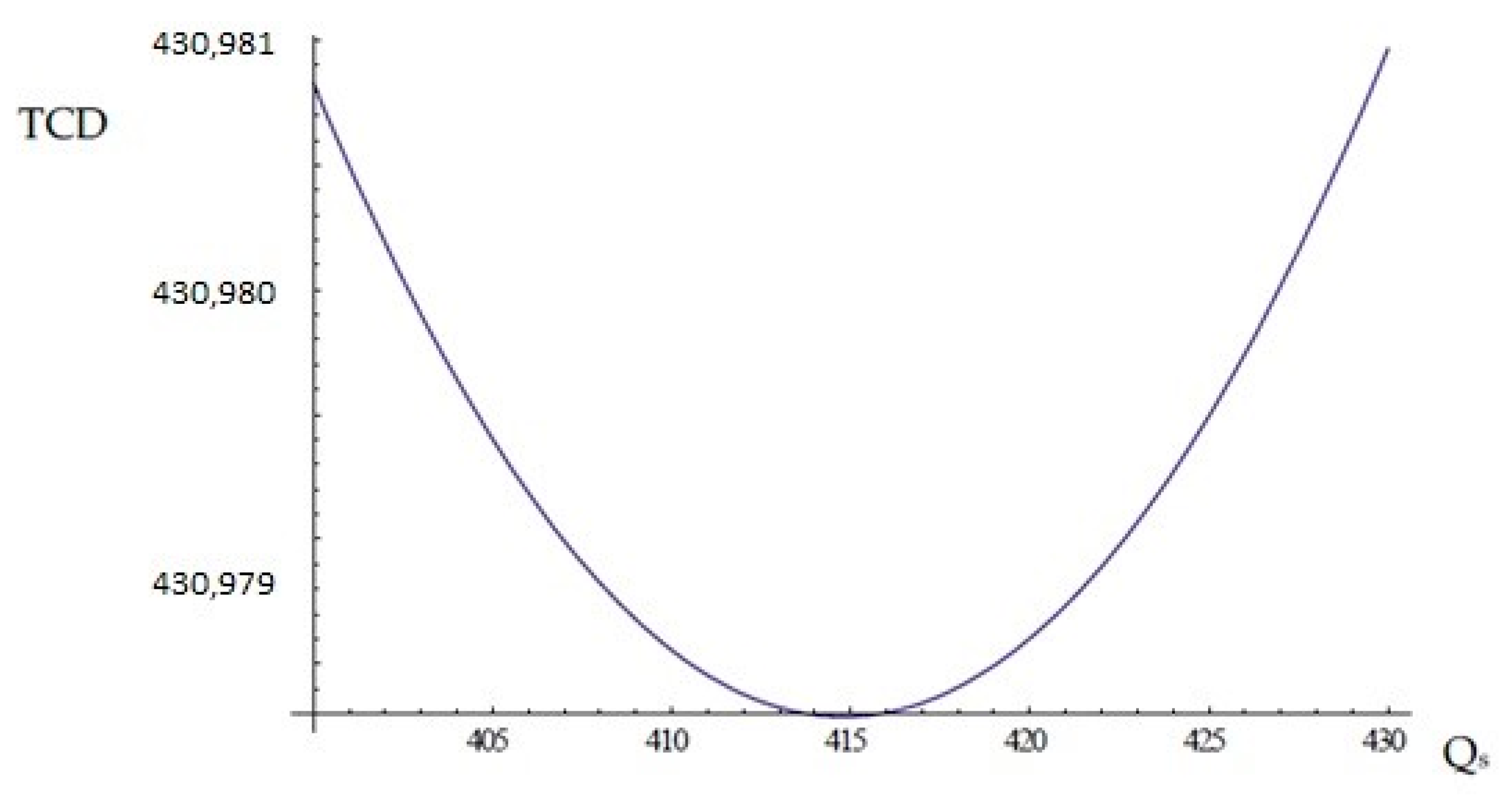
5.1. For Case 1
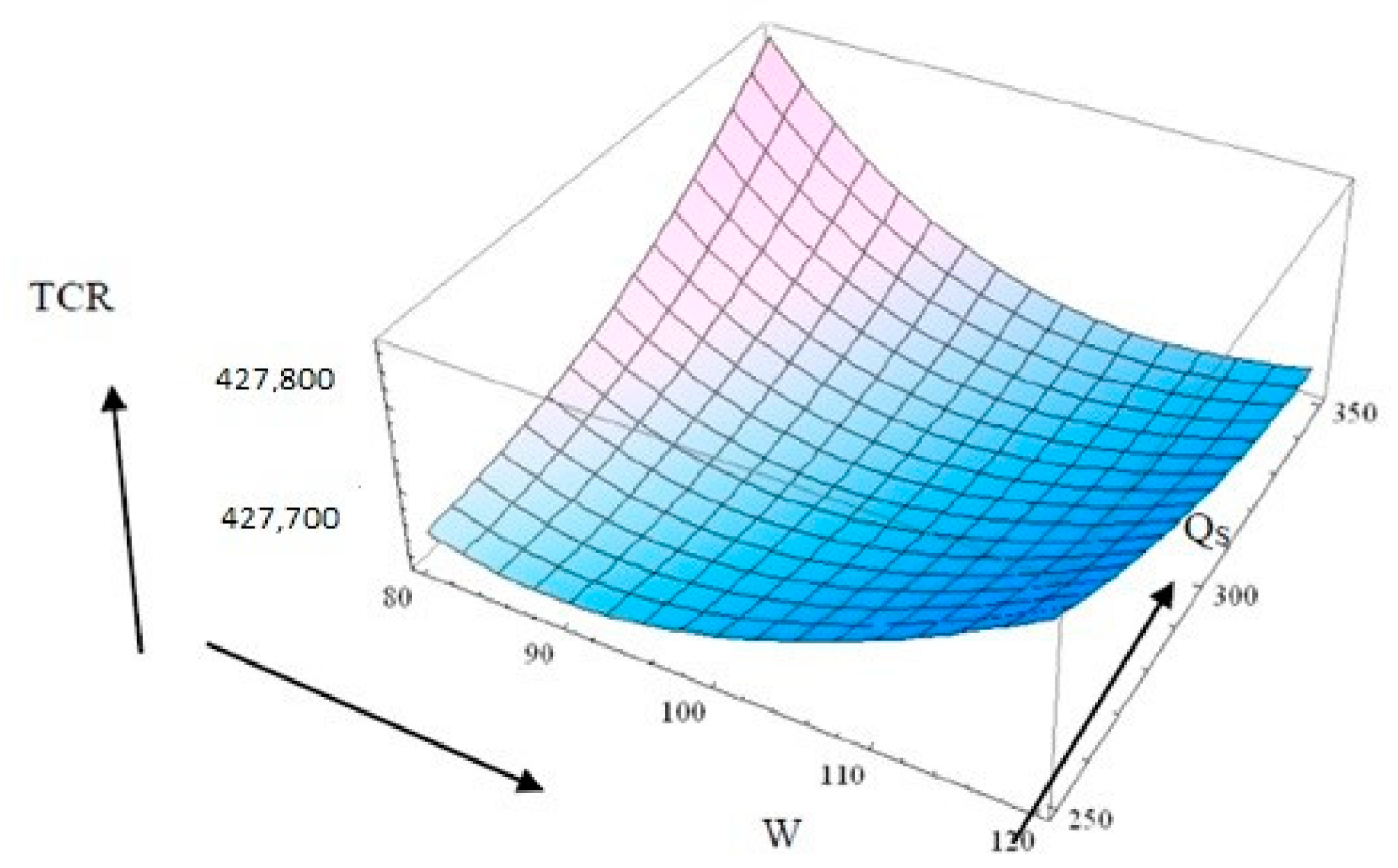
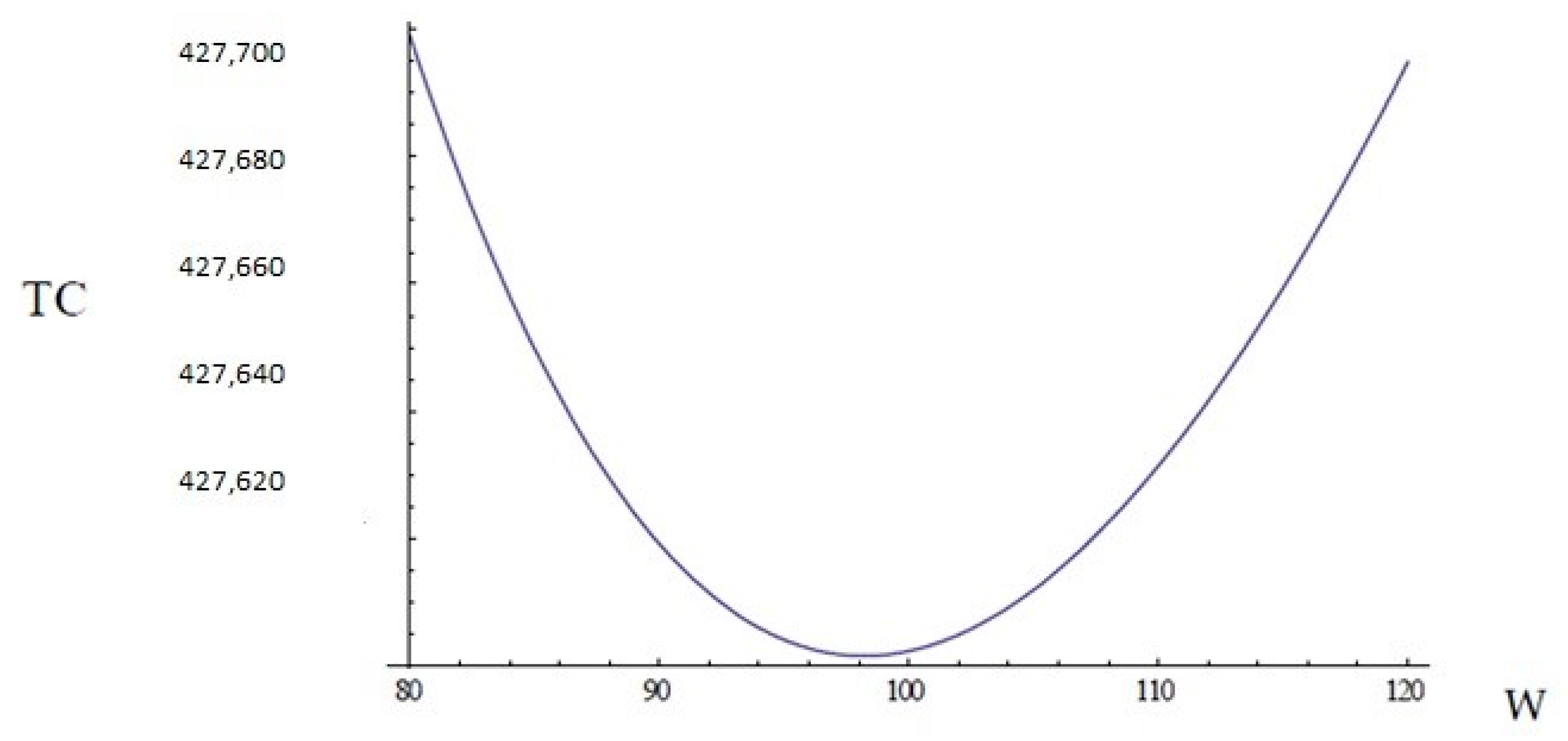
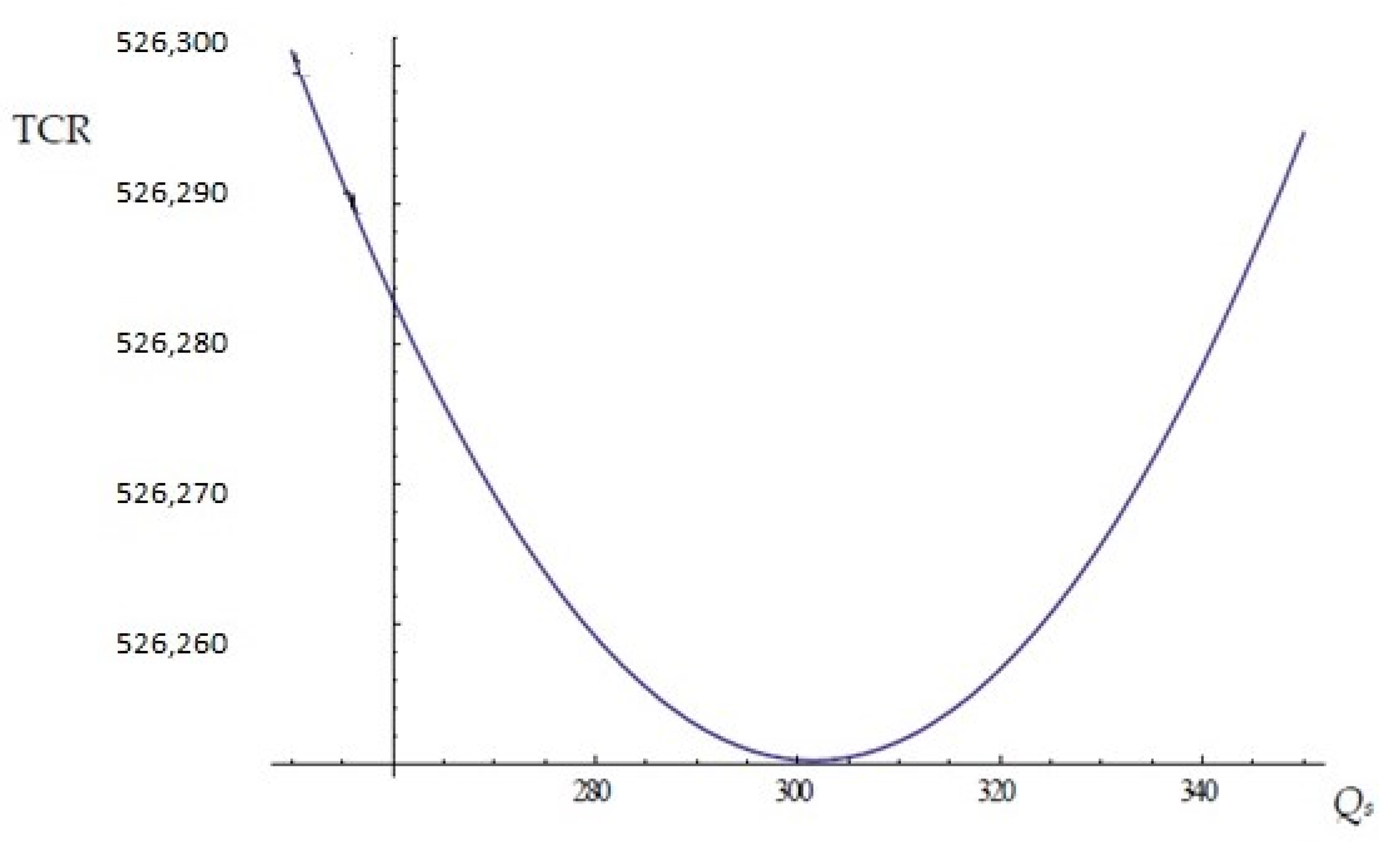
5.2. For Case 2
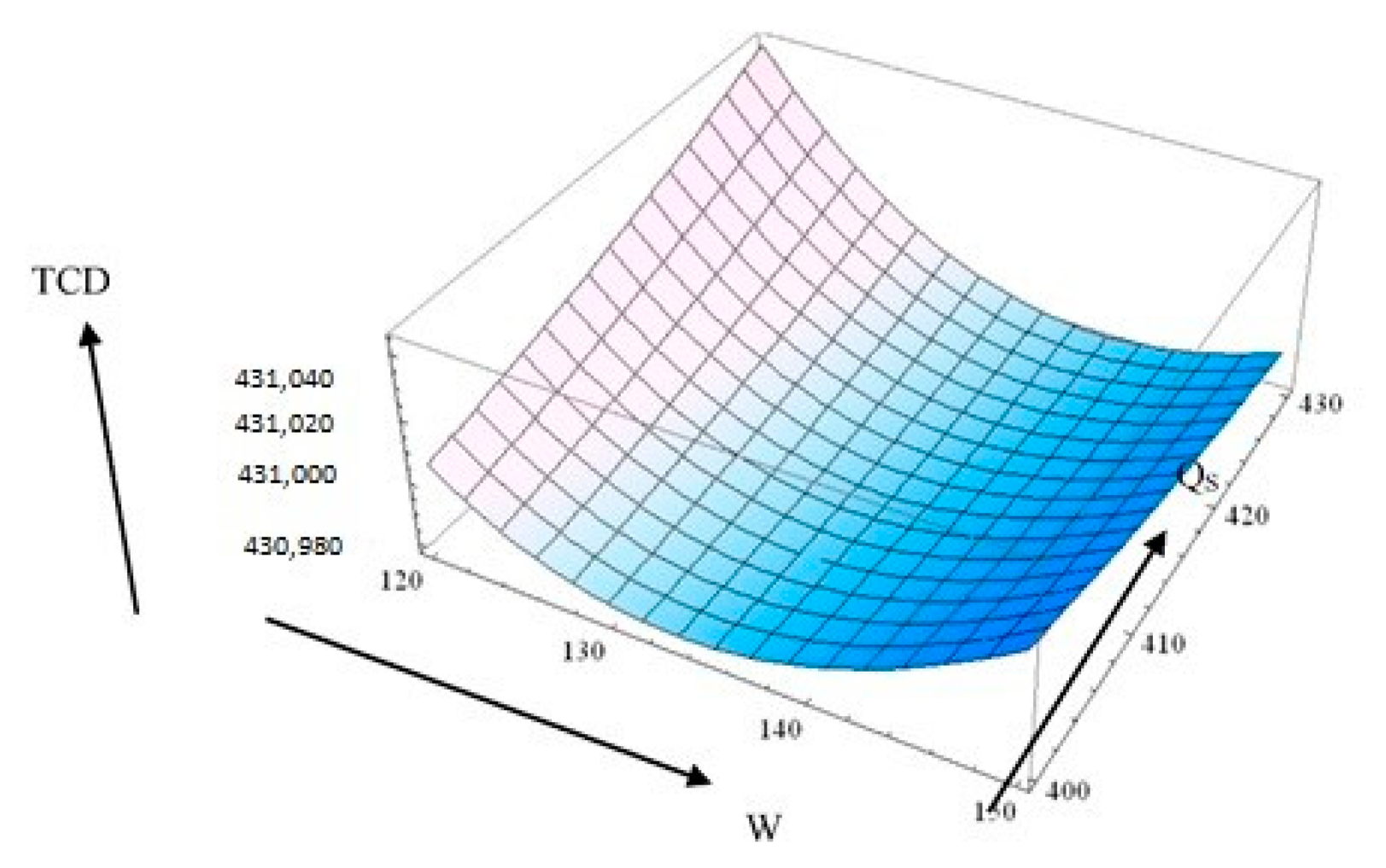
6. Sensitivity Analysis
Cost–Benefitof ERQ Model
7. Managerial Insights
- ➢
- Recycling larger or smaller quantities of defective items than the ERQ will increase the total inventory cost. Therefore, inventory managers must evaluate the ERQ of the item before recycling.
- ➢
- When the company decides to recycle, production lot sizes should be set up in favor of the ERQ, and this strategy will provide greater facility to the manager to decline the total cost.
- ➢
- If raw material costs increase significantly, recycling will benefit the company because it will diminish the load on raw-materials and use the wastage items.
- ➢
- The total cost is more sensitive to demand increases during shortage time than it is to increases during production time with positive stock.
- ➢
- If the defective rate is high, companies will receive better cost–benefit from recycling because it produces more defective items, which are usually treated as rejected, but the recycling process converts them to useable, which provides huge revenue for the managers.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alharkan, Ibrahim, Mustafa Saleh, Mageed Ghaleb, Abdulsalam Farhan, and Ahmed Badwelan. 2020. Simulation-Based Optimization of a Two-Echelon Continuous Review Inventory Model with Lot Size-Dependent Lead Time. Processes 8: 1014. [Google Scholar] [CrossRef]
- Al-Salamah, Muhammad. 2019. Economic Production Quantity in an Imperfect Manufacturing Process with Synchronous and Asynchronous Flexible Rework Rates. Operations Research Perspectives 6: 100103. [Google Scholar] [CrossRef]
- Bai, S. X., and S. Varanasi. 1996. An optimal production flow control problem with piecewise constant demand. Mathematical and Computer Modelling 24: 87–107. [Google Scholar] [CrossRef]
- Benkherouf, Lakdere, and Mohamed Omar. 2017. Optimal manufacturing batch size with rework for a finite-horizon and time-varying demand rates inventory model. RAIRO-Operations Research 51: 173–87. [Google Scholar] [CrossRef]
- Chiu, S. W., C. T. Tseng, M. F. Wu, and P. C. Sung. 2014. Multi-item EPQ model with scrap, rework and multi-delivery using common cycle policy. Journal of Applied ResearchandTechnology 12: 615–22. [Google Scholar] [CrossRef]
- Daryanto, Yosef, and Hui Ming Wee. 2019. Low carbon economic production quantity model for imperfect quality deteriorating items. Journal of Industrial Engineering and Management 1: 1–8. [Google Scholar] [CrossRef]
- Harris, Ford Whitman. 1915. What quantity to make at once. The Library of Factory Management 5: 47–52. [Google Scholar]
- Hasan, Rakibul, Abu Hashan Md Mashud, Yosef Daryanto, and Hui Ming Wee. 2020. A non-instantaneous inventory model of agricultural products considering deteriorating impacts and pricing policies. Kybernetes. ahead-of-print. [Google Scholar] [CrossRef]
- Hsu, Jia Tzer, and Lie Fern Hsu. 2014. A supplement to an EOQ model with imperfect quality items, inspection errors, shortage backordering, and sales returns. International Journal of Industrial Engineering Computation 5: 199–210. [Google Scholar] [CrossRef][Green Version]
- Hsu, Lie Fern, and Jia Tzer Hsu. 2016. Economic production quantity (EPQ) models under an imperfect production process with shortages backordered. International Journal of Systems Science 47: 852–67. [Google Scholar]
- Kang, Chang Wook, Misbah Ullah, and Biswajit Sarkar. 2018. Optimum ordering policy for an imperfect single-stage manufacturing system with safety stock and planned backorder. The International Journal of Advanced Manufacturing Technology 95: 109–20. [Google Scholar] [CrossRef]
- Liao, Jui Jung, Kuo Nan Huang, Kun Jen Chung, Shy Der Lin, Sheng Tu Chuang, and Hari Mohan Srivastava. 2020. Optimal ordering policy in an economic order quantity (EOQ) model for non-instantaneous deteriorating items with defective quality and permissible delay in payments. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A Matemáticas 114: 1–26. [Google Scholar] [CrossRef]
- Liao, Jui Jung, Kuo Nan Huang, Kun Jen Chung, Shy Der Lin, Pin Shou Ting, and Hari Mohan Srivastava. 2018. Retailer’s optimal ordering policy in the EOQ model with imperfect-quality items under limited storage capacity and permissible delay. Mathematical Methods in the Applied Sciences 41: 7624–40. [Google Scholar] [CrossRef]
- Lin, Tien Yu, and Hari Mohan Srivastava. 2015. A two-warehouse inventory model with quantity discounts and maintenance actions under imperfect production processes. Applied Mathematics and Information Sciences 9: 2493–505. [Google Scholar]
- Manna, Amalesh Kumar, Joyanta Kumar Dey, and Shyamal Kumar Mondal. 2017. Imperfect production inventory model with production rate dependent defective rate and advertisement dependent demand. Computers & Industrial Engineering 104: 9–22. [Google Scholar]
- Mashud, Abu Hashan Md, Dipa Roy, Yosef Daryanto, and Hui Ming Wee. 2021a. Joint pricing deteriorating inventory model considering the product life cycle and advance payment. RAIRO-Operations Research 55: S1069–S1088. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Dipa Roy, Yosef Daryanto, and Mohd Helmi Ali. 2020a. A Sustainable Inventory Model with Imperfect Products, Deterioration, and Controllable Emissions. Mathematics 8: 2049. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Dipa Roy, Yosef Daryanto, Ripon Kumar Chakraborty, and Ming Lang Tseng. 2021b. A controllable carbon emission and deterioration inventory model with advance payments scheme. Journal of Cleaner Production 296: 126608. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Hui Ming Wee, and Chiao Ven Huang. 2021c. Preservation technology investment, trade-credit and partial backordering model for a non-instantaneous deteriorating inventory. RAIRO-Operations Research 55: 551–77. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Hui Ming Wee, Chiao Ven Huang, and J. Z. Wu. 2020b. Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries. Mathematics 8: 1981. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Md Rakibul Hasan, Yosef Daryanto, and Hui Ming Wee. 2021d. A resilient hybrid payment supply chain inventory model for post Covid-19 recovery. Computers & Industrial Engineering, 107249. [Google Scholar] [CrossRef]
- Mishra, Umakanta, Abu Hashan Md Mashud, Ming Lang Tseng, and Jei Zang Wu. 2021. Optimizing a Sustainable Supply Chain Inventory Model for Controllable Deterioration and Emission Rates in a Greenhouse Farm. Mathematics 9: 495. [Google Scholar] [CrossRef]
- Mokhtari, Hadi. 2018. A joint internal production and external supplier order lot size optimization under defective manufacturing and rework. The International Journal of Advanced Manufacturing Technology 95: 1039–58. [Google Scholar]
- Nobil, Amir Hossein, Amir Hossein Afsar Sedigh, and Leopoldo Eduardo Cardenas Barron. 2020. Reorder point for the EOQ inventory model with imperfect quality items. Ain Shams Engineering Journal 11: 1339–43. [Google Scholar] [CrossRef]
- Oh, Yong Hui, and Hark Hwang. 2006. Deterministic inventory model for recycling system. Journal of Intelligent Manufacturing 17: 423–28. [Google Scholar] [CrossRef]
- Onwude, Daniel, Guangnan Chen, Nnanna Eke-Emezie, Abraham Kabutey, Alfadhl Yahya Khaled, and Barbara Sturm. 2020. Recent Advances in Reducing Food Losses in the Supply Chain of Fresh Agricultural Produce. Processes 8: 1431. [Google Scholar] [CrossRef]
- Palanivel, M., and Ramasamy Uthayakumar. 2016. An inventory model with imperfect items, stock dependent demand and permissible delay in payments under inflation. RAIRO-Operations Research 50: 473–89. [Google Scholar] [CrossRef]
- Popescu, Cristina Raluca Gh, and Georghe N. Popescu. 2019. An Exploratory Study Based on a Questionnaire Concerning Green and Sustainable Finance, Corporate Social Responsibility, and Performance: Evidence from the Romanian Business Environment. Journal of Risk and Financial Management 12: 162. [Google Scholar] [CrossRef]
- Rosenblatt, M. J., and H. L. Lee. 1986. Economic production cycles with imperfect production processes. IIE Transaction 18: 48–55. [Google Scholar]
- Salameh, M. K., and M. Y. Jaber. 2000. Economic production quantity model for items with imperfect quality. International Journal of Production Economics 64: 59–64. [Google Scholar] [CrossRef]
- Srivastava, Hari Mohan, Ghi Feng Yen, An Kuo Lee, Yi Xiu Wu, and Shy Der Lin. 2018. The optimal retailer’s economic production quantity (EPQ) policies with two-level trade credit under alternate due date of payment and limited storage capacity. Applied Mathematics and Information Sciences 12: 1073–89. [Google Scholar] [CrossRef]
- Srivastava, Hari Mohan, Kun Jen Chung, Jui Jung Liao, Shy Der Lin, and Shi Fang Lee. 2021. An accurate and reliable mathematical analytic solution procedure for the EOQ model with non-instantaneous receipt under supplier credits. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A Matemáticas 115: 1–22. [Google Scholar] [CrossRef]
- Tayyab, Muhammad, Biswajit Sarkar, and Bernardo Nugroho Yahya. 2019a. Imperfect Multi-Stage Lean Manufacturing System with Rework under Fuzzy Demand. Mathematics 7: 13. [Google Scholar] [CrossRef]
- Tayyab, Muhammad, Jihed Jemai, Han Lim, and Biswajit Sarkar. 2019b. A sustainable development framework for a cleaner multi-item multi-stage textile production system with a process improvement initiative. Journal of Cleaner Production 246: 119055. [Google Scholar] [CrossRef]
- Taft, E. W. 1918. The most economical production lot. The Iron Age 101: 1410–12. [Google Scholar]
- Tsai, Feng Ming, Tat Dat Bui, Ming Lang Tseng, Ming K. Lim, Kuo Jui Wu, and Abu Hashan Md Mashud. 2021. Assessing hierarchical sustainable solid waste management structure in qualitative information: Policy and regulations drive social impacts and stakeholder participation. Resources, Conservation and Recycling 168: 105285. [Google Scholar] [CrossRef]
- Viji, G., and K. Karthikeyan. 2016. An economic production quantity model for three levels of production with Weibull distribution deterioration and shortage. Ain Shams Engineering Journal 9: 1481–87. [Google Scholar] [CrossRef]
| Notation | Unit | Description |
|---|---|---|
| P | Constant | Production rate |
| D | Constant | Rate of demand of non-defective items during production run-time |
| d | Constant | Production rate defective items |
| Co | $/Cycle | Setup cost |
| Ch | $/Units | Inventory holding cost |
| Cp | $/Units | Per unit production cost |
| Cs | $/Units | Shortage cost |
| CR | $/Units | Raw material cost per unit item |
| Cr | $/Units | Recycle cost per unit item of defective items |
| TCD | $/Unit time | Total cost of inventory (for case 1) |
| TCR | $/Unit time | Total cost of inventory (for case 2) |
| t1 | Time units | Production run-time with positive stock |
| t2 | Time units | Production off-time with positive stock |
| t3 | Time units | Production off-time with negative stock |
| t4 | Time units | Production run-time with negative stock |
| x | Constant | Ratio of demand rates of production off-time with positive stock and production run-time |
| y | Constant | Ratio of demand rates of production off-time with negative stock and production run-time |
| m | Constant | Shape parameter of the accurate average demand |
| Decision variables | ||
| W | Units | Quantity of defective items produced per cycle time |
| Q | Units | Volume of lot |
| Qs | Units | Maximum shortage level |
| Qd | Units | Maximum on-hand stock of non-defective items |
| T | Time units | Production cycle time. Therefore, T = t1 + t2 + t3 + t4 |
| x | 0.5 | 0.75 | 1.75 | 5 | Observations |
|---|---|---|---|---|---|
| W* | 98 | 98 | 99 | 99 | Increase |
| Q* | 4894 | 4909 | 4929 | 4940 | Increase |
| Qs* | 301 | 299 | 295 | 293 | Decrease |
| Qd* | 90 | 94 | 99 | 102 | Increase |
| 0.225 | 0.235 | 0.248 | 0.254 | Increase | |
| 0.0410 | 0.027 | 0.012 | 0.004 | Decrease | |
| 0.133 | 0.132 | 0.131 | 0.130 | Decrease | |
| 0.752 | 0.746 | 0.737 | 0.733 | Decrease | |
| T* | 1.152 | 1.142 | 1.129 | 1.122 | Decrease |
| FC | 867 | 875 | 885 | 890 | Increase |
| RMC | 208,019 | 210,562 | 213,820 | 215,565 | Increase |
| PC | 212,264 | 214,859 | 218,184 | 219,965 | Increase |
| HC | 519 | 530 | 545 | 552 | Increase |
| SC | 347 | 344 | 340 | 338 | Increase |
| RC | 424 | 430 | 436 | 440 | Increase |
| TCR | 422,442 | 427,602 | 434,210 | 437,755 | Increase |
| y | 0.5 | 0.8 | 1.50 | 2 | 5 | Observations |
|---|---|---|---|---|---|---|
| W* | 98.36 | 99.36 | 100.4 | 100.84 | 101.2 | Increase |
| Q* | 4918 | 4968 | 5020 | 5042 | 5058 | Increase |
| Qs* | 297 | 305 | 309 | 313 | 316 | Increase |
| Qd* | 96 | 91.72 | 90.72 | 89.5 | 88 | Decrease |
| t1* | 0.24098 | 0.2293 | 0.22682 | 0.22383 | 0.22157 | Decrease |
| t2* | 0.02142 | 0.02547 | 0.02016 | 0.01989 | 0.01969 | Decrease |
| t3* | 0.13202 | 0.084992 | 0.04605 | 0.02789 | 0.01404 | Decrease |
| t4* | 0.74265 | 0.7643 | 0.77721 | 0.78455 | 0.79016 | Increase |
| T* | 1.13709 | 1.10406 | 1.07025 | 1.05619 | 1.04548 | Decrease |
| FC | 879 | 905 | 934 | 947 | 956 | Increase |
| RMC | 211,938 | 220,500 | 229,841 | 233,914 | 237,093 | Increase |
| PC | 216,263 | 225,000 | 234,532 | 238,688 | 241,931 | Increase |
| HC | 536 | 552 | 575 | 584 | 591 | Increase |
| SC | 342 | 352 | 359 | 362 | 364 | Increase |
| RC | 432 | 450 | 469 | 477 | 483 | Increase |
| TCR | 430,392 | 447,762 | 466,711 | 474,972 | 481,421 | Increase |
| d | 100 | 110 | 120 | 130 | 140 |
|---|---|---|---|---|---|
| PCB | 0.797% | 0.878% | 0.96% | 1.042% | 1.125% |
| Remarks | Cost–benefit increases with the increase in “d”. | ||||
| Cr | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|
| PCB | 0.797% | 0.697% | 0.59% | 0.497% | 0.398% |
| Remarks | Cost–benefit decreases with increase in recycle cost. | ||||
| Ch | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| PCB | 0.797% | 0.737% | 0.689% | 0.648% | 0.613% |
| Remarks | Cost–benefit decreases with increase in holding cost. | ||||
| x | 0.5 | 1 | 1.5 | 2 | 2.5 |
|---|---|---|---|---|---|
| PCB | 0.7976% | 0.7972% | 0.7970% | 0.7969% | 0.7969% |
| Remarks | “x” is not sensitive to cost–benefit. | ||||
| y | 0.5 | 1 | 1.5 | 2 | 2.5 |
|---|---|---|---|---|---|
| Percentage of cost–benefit | 0.7990% | 0.7975% | 0.7970% | 0.7968% | 0.7966% |
| Remarks | “y” is not sensitive to cost–benefit. | ||||
| 50 | 55 | 60 | 65 | 70 | |
|---|---|---|---|---|---|
| PCB | 0.797% | 0.854% | 0.906% | 0.954% | 0.997% |
| Remarks | Cost–benefit increases with the increase in raw material cost. | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlArjani, A.; Miah, M.M.; Uddin, M.S.; Mashud, A.H.M.; Wee, H.-M.; Sana, S.S.; Srivastava, H.M. A Sustainable Economic Recycle Quantity Model for Imperfect Production System with Shortages. J. Risk Financial Manag. 2021, 14, 173. https://doi.org/10.3390/jrfm14040173
AlArjani A, Miah MM, Uddin MS, Mashud AHM, Wee H-M, Sana SS, Srivastava HM. A Sustainable Economic Recycle Quantity Model for Imperfect Production System with Shortages. Journal of Risk and Financial Management. 2021; 14(4):173. https://doi.org/10.3390/jrfm14040173
Chicago/Turabian StyleAlArjani, Ali, Md. Maniruzzaman Miah, Md. Sharif Uddin, Abu Hashan Md. Mashud, Hui-Ming Wee, Shib Sankar Sana, and Hari Mohan Srivastava. 2021. "A Sustainable Economic Recycle Quantity Model for Imperfect Production System with Shortages" Journal of Risk and Financial Management 14, no. 4: 173. https://doi.org/10.3390/jrfm14040173
APA StyleAlArjani, A., Miah, M. M., Uddin, M. S., Mashud, A. H. M., Wee, H.-M., Sana, S. S., & Srivastava, H. M. (2021). A Sustainable Economic Recycle Quantity Model for Imperfect Production System with Shortages. Journal of Risk and Financial Management, 14(4), 173. https://doi.org/10.3390/jrfm14040173










