Abstract
The paper retrospectively analyses the issue of the impact of international trade on developed countries’ labour markets in the 1990s, when the majority of academic opinion denied the role of trade in the misfortunes of unskilled workers. An analytical framework is proposed in which intra-industry trade is explained in terms of countries’ factor endowments and factor intensities of goods. Unlike the traditional Heckscher–Ohlin model of inter-industry trade, the model suggested here is more consistent with stylised facts about North–South trade. The paper also proposes a method for empirically assessing factor substitution effects at the product level. Inferring the factor content of intra-industry trade from the inter-sectoral relationship between factor intensity and average unit values of exports, the paper found that the labour market effects of intra-industry trade add significantly to the estimated factor market impact of trade.
Keywords:
labour market effects of international trade; intra-industry trade; North–South trade; quality differentiation JEL Classification:
F1
1. Introduction
Over the two decades from the late 1980s to the 2008 financial crisis, the dynamics of world economy was shaped by three crucial developments that were perceived as producing significant effects on labour markets of advanced countries: (i) the opening up to market economy of China, India, and (ex-communist) Central and Eastern European countries (CEECs), which was a shift that doubled the global labour force (the “Great Doubling”, according to the words of Freeman (2007)); (ii) the spreading out of information and communication technologies that have enormously facilitated the international fragmentation of production and outsourcing of services; (iii) the growth of migration flows from developing to developed countries. All these dramatic changes in the processes of international economic integration have contributed to the increase of insecurity among workers of advanced economies, both in terms of fear of losing jobs and in terms of expected decline in remuneration.
Although these feelings of anxiety about globalisation are now supported by anecdotal evidence (look, for instance, at the populist protest!), polls, and studies based on individual-level survey data, until recent years, the majority of academic opinion did not believe that the increasing integration between advanced countries and emerging economies was producing a disruptive impact on labour markets in developed countries. Indeed, the traditional theory of international trade based on comparative advantage stands as a good parable on the benign effects of globalisation, as it states that differences in technology or factor endowments across countries are sources of mutual gain when economies trade with each other.
However, the standard model of international trade—the two-good, two-factor Heckscher–Ohlin–Samuelson (HOS) model—also makes clear that although free trade improves aggregate welfare, it leads to a redistribution of real income between factors of production. This is the reason why the HOS model was adopted as a starting point for interpreting stylised facts on trade, wages, and jobs that characterised the 1980s. In effect, in the early 1990s, the debate on the link between international trade and labour markets in advanced countries gained momentum and became increasingly popular among economists to shed light on the developments of the previous decade. Two pieces of empirical evidence triggered a renewed interest in the effects of international trade on labour markets. On the one hand, the distribution of income changed dramatically in the United States, with a widening gap between the wages of skilled and unskilled workers; although Western European countries did not show such a dramatic change in income differentials (with the exception of the UK), they did show high unemployment rates, especially among low-skilled workers. On the other hand, during the same period, a growing penetration of emerging economies’ exports into the markets of advanced economies took place (the aggressive dynamism of the so-called ‘Asian Tigers’ or ‘Asian Dragons’).
Faced with two striking empirical phenomena and a theory that links the two, there was an almost overwhelming temptation to see the empirical phenomena as confirming the theory. However, when all implications deriving from the chain of causation postulated by the HOS model were compared with empirical evidence, some crucial inconsistencies emerged. In effect, at the beginning of the 1990s, studies investigating the link between trade and the labour market carried out a simple evaluation of consistency between data and standard theory of international trade (HOS model and Stolper–Samuelson theorem). A particularly striking contribution to the debate was Lawrence and Slaughter’s comparison of the predictions of the Stolper–Samuelson analysis with the facts of industrial adjustment in the United States in the 1980s (Lawrence and Slaughter 1993). The theoretical story has three steps: (1) growing exports of unskilled–intensive products by developing countries drives down the price of these products in developed countries, thereby (2) driving down the relative wage of unskilled labour, causing substitution in production towards unskilled labour, and (3) maintaining full employment by inter-sectoral substitution of production towards more skill-intensive products. Lawrence and Slaughter (1) found no evidence of relative price changes; (2) they demonstrated (at three different levels of aggregation) that the rise in the relative wages of non-production workers was accompanied by an increase in the relative employment of non-production workers in almost all sectors, and (3) they found no evidence of an inter-sectoral shift in production. The evidence they presented was strongly suggestive of a chain of causation that runs from an exogenous increase in the demand for skilled workers in most sectors (arising from technological change) driving up the relative wage of such workers rather than the chain of causation in the Stolper–Samuelson story.
The Lawrence and Slaughter conclusion of a weak (or even inexistent) link between trade and the labour market was supported by other contributions, such as those of Krugman and Lawrence (1994), Krugman (1994), and, to a lesser degree, Sachs and Shatz (1994). Almost until the end of the 1990s, the great bulk of academic opinion was opposed to the view that there is a strong link between the growth of trade and the growth of labour market inequality. Freeman (1995), surveying the differing positions taken, noted the paradoxical fact that trade theorists are at the forefront of those denying the importance of trade in income distribution.
Incidentally, Wood (1994) and Leamer (1995) are unusual among trade economists in finding evidence of strong links between trade and labour markets. In particular, Wood—following a factor content of trade (FCT) approach modified in order to take account of North–South differences in input–output matrices—calculated the impact of North–South trade on unskilled labour demand in developed countries, and he observed that the shedding of jobs was twice the amount estimated in previous studies. The important point raised by Wood was that the previous studies did not consider that the South exports to the North are non-competing; in other words, the goods exported by developing countries are different from North products, even if they belong to the same statistical class. By using the factorial coefficients matrix of developed countries as an estimator, the previous FCT studies have underestimated the unskilled labour content of South exports to the North, and consequently, they have undervalued the displacement effect of North–South trade on unskilled labour demand in developed countries. Hence, Wood warned against the risk of understating the effects of trade on labour markets if product heterogeneity is not considered adequately.
The contributions of the 1990s that found a significant impact of trade on labour markets in advanced countries represented the minority view in the debate on trade and jobs. As mentioned above, the weight of academic opinion denied the relevance of international trade in determining the unskilled-adverse shift in labour demand in developed countries and, on the contrary, emphasised the significant role played by skill-biased technological change.
It is quite paradoxical that the idea that the labour market effects of globalisation were irrelevant was prevailing in a decade, the 1990s, in which the formation of North–South value chains represented the crucial passage from the “old paradigm” to the “new paradigm” of globalisation, according to the words of Baldwin (2006, 2011, 2013). Since the 1990s, the flourishing of North–South global value chains has profoundly changed global economic interactions and, in virtue of this transformation, the dynamics of world trade composition has been increasingly affected by flows deriving from the international fragmentation of production implying a substantial impact on labour markets. In the first decade of 2000, it was inevitable that the debate on the labour market effects of globalisation shifted from the role of trade to that of outsourcing. As early as the late 1990s, Feenstra (1998) pointed out that trade flows deriving from the vertical disintegration of production on an international scale could have the same within-industry effects as technology on the displacement of demand for unskilled workers in developed countries. Afterwards, over the first decade of the 2000s, the literature on the impact of outsourcing/offshoring on labour markets (in advanced but also in developing countries) consolidated and became copious. Among the most significant empirical contributions exploring the impact of outsourcing on labour markets, it is worth mentioning Amiti and Wei (2005, 2009); Ando and Kimura (2007); Egger and Egger (2005); Ekholm and Hakkala (2006); Helg and Tajoli (2005); Hertveldt and Michel (2012), Hsieh and Woo (2005); Geishecker (2006); Lorentowicz et al. (2005).
However, in recent years, the literature on the labour market effects of international trade has evolved by reassessing the importance of trade in influencing the level and composition of employment, and the dynamics of wage differentials. Contributions falling under the “new new” theory of international trade look at firm heterogeneity based on productivity levels (Melitz 2003) and predict that, irrespective of the countries’ relative factor endowments or sectoral comparative advantages, trade liberalisation will push only the most productive firms to export (within-sector and across all sectors); these dynamics will induce mainly the most skilled workers to work in exporting firms, either through a self-selection mechanism by employees or through a selection process by firms (exporting firms carry out a more intensive screening of workers compared to non-exporting firms). This will lead to an increase in the use of skilled labour (and skill-premium) in both countries involved in trade (Yeaple 2005; Helpman et al. 2010; Bustos 2011; Brambilla et al. 2011; Sampson 2014; Helpman 2017). Interestingly, in many of these recent contributions that look at firm-level data to capture the heterogeneity of producers and their propensity to export, international trade is not considered as an alternative to technological change to explain skill-upgrading (as was predominantly the case in the 1990s debate on trade and jobs). Rather, import competition pressures firms to introduce process and product innovations that ultimately lead to higher skilled employment. For instance, Bloom et al. (2016) analyse the introduction of so-called “defensive innovations” introduced by European countries to counter competition from Chinese products in the period 2000–2007 (actually, Adrian Wood in his 1994 book had already introduced the concept of defensive innovation, but, as mentioned above, Wood’s was a minority voice in the 1990s debate).
Recent contributions have also significantly refined the analysis of the occupational characteristics of workers by defining those tasks that are more exposed to import competition from low-wage countries and/or more likely to be relocated abroad. This more disaggregated analysis of employment characteristics renders the concept of comparative advantage based on the degree of qualification of the workforce more blurred. In other words, in the “trading tasks” literature, opened by the seminal contribution of Grossman and Rossi-Hansberg (2008), the skilled/unskilled dichotomy becomes less meaningful for understanding the effects of globalisation on labour market outcomes. For example, even jobs that require a low level of skills, such as cleaning or security work, being non-routinary, are less exposed to international competition than more skilled jobs, such as accounting or data entry, which are routinary and therefore easily outsourceable. Obviously, high-skilled jobs requiring special cognitive skills, being non-routinary (research and development, for instance) are equally less vulnerable to international competition and less transferable abroad. Therefore, based on an analytical approach that looks at a broader range of occupational characteristics, the trading tasks literature has managed to encompass the labour market polarisation phenomena that emerged in advanced countries as a result of internationalisation processes since the late 1990s: the combined growth of high-skilled and low-skilled jobs on the one hand, and the decline of medium-skilled jobs on the other hand (OECD 2017; Reijnders and de Vries 2017; Keller and Utar 2016). Finally, in recent years, numerous studies have analysed the impact of China’s spectacular export growth on the labour market of various countries. In the case of the United States, Acemoglu et al. (2016) estimate that in the period 1999–2011, the overall employment loss as a result of import competition from China ranged between 2 and 2.4 million workers. Again, in the case of the United States, Autor et al. (2013) found that the regions (Community Zones as a proxy for US local labour markets) most exposed to Chinese competition not only experienced job losses in the manufacturing sector, as a direct displacement effect associated with import growth, but they also suffered a number of indirect repercussions in the non-tradable sector, such as lower wages, higher unemployment benefits, disability benefits, etc. Dauth et al. (2014) found different results in the case of Germany. The effect of Chinese competition on German local labour markets was not very pronounced because the sectors most exposed to Chinese imports (textiles, for example) had already reduced their weight in the German production structure since the 1980s. Thus, the emergence of China as a major world exporter only led to a diversion of German imports from previous supplier countries (e.g., Southern European countries) towards China. Instead, much stronger was the displacement of German jobs generated by the growth of imports from Eastern European countries. However, this negative effect was more than offset by the growth of German exports to that area (given the strong manufacturing interdependence between Germany and Eastern Europe). Overall, Dauth et al. estimate that trade integration processes between Germany and the ‘East’ (China+Eastern Europe) have increased German employment by 420,000 jobs, contributing significantly to the resilience of the manufacturing sector. In the case of France, Malgouyres (2017) found similar results to those of Autor et al. (2013), with Chinese import competition producing substantial negative effects both on manufacturing and nonmanufacturing employment. Regarding the effects of Chinese competition on the composition of employment in the United States, Wright (2014) found that rising imports of intermediate goods from China reduced the employment of production workers but increased the number of non-production employees, with a positive impact on overall employment. Wright finds this result to be consistent with the trading tasks model. In fact, offshoring on the one hand causes direct displacement effects of workers; on the other hand, it generates cost savings (a productivity increase), which allows production to be reorganised and new hires to be undertaken. These effects mainly concern the industries that are intensive in those tasks that are offshorable (in line with the model’s predictions). According to Wright, offshoring to China caused a positive net effect, increasing US total employment by 2.6% over the period 2001–2007. Significant effects of increasing competition from China on the composition of employment were found in the case of European countries, too. Analyses conducted on firm-level data suggest in many cases a sequence in which firms respond to Chinese competition by introducing defensive innovations that shift production to high-tech segments and higher-quality products; this dynamic is ultimately reflected in a higher use of skilled labour (Mion and Zhu 2013; Bloom et al. 2016).
Vertical trade does not only include flows resulting from international production fragmentation but also the exchange of goods differentiated by quality. When quality differentiation is taken into account, then the impact of international trade on the labour market can be significant.
This paper returns retrospectively to the 1990s debate on labour market effects of international trade and offers an interpretative framework in which due attention is given to quality differentiation in trade. This approach, in parallel to the role of international product fragmentation and outsourcing, is another way to take account of the relevance of international trade for labour market outcomes in advanced economies.
In particular, the paper proposes a disaggregated treatment of the labour market effects of international trade, based on a model in which intra-industry trade is explained on Heckscher–Ohlin principles. The model is more consistent with stylised facts about North–South trade than the traditional Heckscher–Ohlin model of inter-industry trade. The model is applied to trade between Italy and “non-advanced countries” in the 1990s, a period in which the majority of academic opinion denied the link between trade and labour markets. Inferring the factor content of intra-industry trade from the inter-sectoral relationship between factor intensity and average unit values of exports, the paper finds that the labour market effects of intra-industry trade add significantly to the estimated factor market impact of trade. The paper is a factor content of trade (FCT) study in the tradition of Wood (1994), where due consideration is given to heterogeneity in trade; here, the role of quality differentiation in trade is emphasised in order to capture substantial effects of trade on labour markets.
The paper is organised in four sections. Section 2 provides a model dealing with the issue of aggregation by providing an account of intra-industry trade that is based on comparative advantage. Each sector is modelled as containing a continuum of techniques. This permits factor substitution within sectors at the level of the individual product, allowing a much richer range of substitution effects. Section 3 provides the empirical implementation of the model, which is at a level of disaggregation that is an order of magnitude different from any of the studies of the 1990s mentioned above. As already reported, the model is applied to the case of Italy’s trade with less advanced countries (LACs). The choice of this country is particularly significant because Italy’s international specialisation overlaps with that of less developed countries; therefore, in the case of Italy, the impact of international trade on the labour market is more likely to be underestimated if the heterogeneity (quality differentiation) of traded goods is not taken into due consideration. Section 4 contains some concluding remarks.
2. Product Quality, Intra-Industry Trade, and Labour Market Effects: An Analytical Framework
2.1. Introduction
Intra-industry trade (IIT) among developed countries is still the most important share of world trade, and an increasing proportion of North–South trade is assuming the form of IIT. In the debate on globalisation and labour markets, this has been one of the most striking arguments advanced by those who dispute the importance of trade in the growing pressures on less-skilled labour forces in developed economies.
The standard account of IIT sees it as the result of horizontal product differentiation in trade between similar, advanced economies. The re-allocative and distributive effects of such IIT are likely to be much less severe than those associated with inter-industry trade: exports create jobs in the same sectors in which imports destroy jobs, and the jobs created are the same kind as those destroyed.
However, the idea that adjustment to IIT is painless becomes less plausible if the product differentiation is vertical—that is to say, if products differ in quality. Differences in product quality are likely to imply differences in factor content. The growing importance of IIT in trade flows between advanced nations and developing countries should prompt a re-thinking of the usual view of IIT as two-way trade in horizontally differentiated products and encourage the modelling of vertical IIT.
2.2. The Model
This model is closely related to that used by Falvey (1981) and Falvey and Kierzkowski (1985) to model vertical product differentiation, but in the version here, product varieties enter the utility function in a symmetrical fashion: all the vertical product differentiation is on the production side. In the spirit of the Heckscher–Ohlin model, it is assumed that consumer tastes are the same in different countries. Therefore, with free trade, the same distribution of products and of product varieties enters consumption in all countries. The production side of the model is a multi-sector version of that used by Feenstra and Hanson (1996) to model the effects of capital flows. This blending of the Falvey–Kierzkowski and Feenstra–Hanson models is due to Smith (1996).
In this framework, countries’ location on the quality spectrum in each sector depends on their skill abundance, the result being intra-industry specialisation. In principle, the model could be adapted to offer a more sophisticated treatment of the skill intensity of production, but the current version has two types of labour, manual and non-manual, proxying for unskilled and skilled labour. The model explains both intra-industry trade and inter-industry trade as deriving from the factor endowment differences between countries. It implies that trade will affect inequality, and the properties of the model are consistent with the three stylised facts that Lawrence and Slaughter used in the 1990s to dismiss the Stolper–Samuelson explanation of American wage change.
2.2.1. Demand
The focus of the model is on quality differentiation in production, so the demand side is based on the simplest model of demand for differentiated products, the Dixit and Stiglitz (1977) model in which consumer preferences are represented by a two-stage utility structure.
In this version of the Dixit and Stiglitz model, it is assumed that there is a continuum of varieties of each product, and that aggregate consumption of the ith product can be represented by the sub-utility function
where ε > 1. The price index (unit cost function) representing the cost of producing a single unit of Xi is then given by
where pi(v) is the price of variety xi(v), and the demand for an individual variety is
so ε is the elasticity of demand for a variety with respect to its price relative to the price index of the product group. There is no loss of generality in assuming that the product range [0, b] is the same for every product group i, while the assumption that ε is independent of i could easily be relaxed.
The aggregate cost of all varieties of this product group is
If there are n such product groups and upper-level preferences across product groups are determined using Cobb–Douglas functions, with product group Xi having a share αi of total expenditure m, the demand function (2) for an individual variety becomes
2.2.2. Supply
The production of each variety requires both skilled and unskilled labour. Let the unit cost of production of variety v of product i in country j be
where si(v) and ui(v) are the input requirements of skilled and unskilled labour respectively and where the unit production function fi shows the substitution possibilities for producing variety i. Therefore, the chosen input coefficients will depend on relative wages and on the location of production, which can be indicated simply by writing
With Chamberlinian monopolistic competition, in which firms ignore the impact of their decisions on the aggregate price index, firms will set prices as a fixed mark-up over marginal cost, and a product variety will be supplied by the lowest cost producer, so
and the number of firms producing varieties of the product will in a free-entry equilibrium depend on the level of fixed costs.
2.2.3. Trade
If product varieties are arranged on the spectrum [0, b] in order of skill intensity, then countries will specialise in different parts of the spectrum, depending on their ratios of skilled to unskilled wages. If si(v)/ui(v) is increasing in v, and if there are two countries, with
so country 2 is the skill-abundant country; then, from (6), it follows that
Suppose now that there is some variety of product i which is produced in both countries, so that,
then Figure 1 shows that if factor-intensity reversals in the ranking of varieties are ruled out, country 2, the skill-abundant country, will produce only varieties , while country 1 will produce varieties . Clearly, ws1 > ws2 and wu1 < wu2, although it is easy to modify the model to introduce international differences in technology, and if the skill-abundant country had a technical advantage, whether neutral or skill-augmenting, that would obviously permit both wages to be higher in that country.
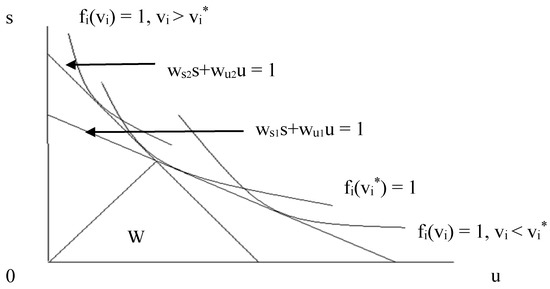
Figure 1.
Choice of technique, different varieties.
Now consider product h, which is less skill-intensive than product i, so
Now, we are ruling out factor-intensity reversals in the ranking of products and also assuming that the factor-intensity ranking of products holds across the quality spectrum. Then, Figure 2 shows that at point in the quality spectrum, the good is produced only in the less skill-abundant country.
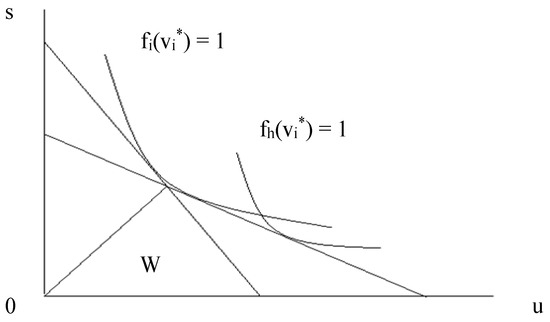
Figure 2.
Choice of technique, different products.
Both Figure 1 and Figure 2 show the application of the same economic analysis to the determination of the location of different parts of the spectrum of products and varieties. The model is in fact a version of the Heckscher–Ohlin model with two factors and many goods as presented by Deardorff (1979).
The intersection of the two iso-cost lines in both figures is at the s/u ratio given by
and all varieties produced in the skill-abundant country have s/u ratios in excess of W, while all varieties produced in the skill-scarce country have s/u ratios less than W.
For products j for which
the whole spectrum of production will be located in country 1, while for products k, for which
all production will be located in country 2.
Thus, we have the patterns of specialisation in products and varieties shown in Figure 3: products that have high skill intensity across the quality spectrum (such as product k), so that all their varieties are produced in the skill-abundant country, products with low skill intensity across the spectrum (product j), with all varieties produced in the skill-scarce country, and products such as i and h in which lower-quality varieties are produced in the skill-scarce country, but the switch-over point v* is lower for the more skill-intensive products.
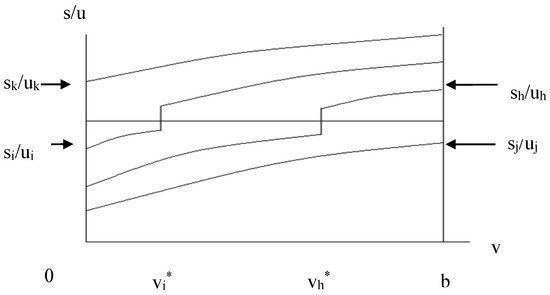
Figure 3.
Choice of location, different varieties, and products.
Since the skill-intensity of all production processes in country 1 is less than W and in country 2 is greater than W, the factor-content version of the Heckscher–Ohlin theorem in the standard two-factor model continues to hold: all the exports of country 2 are more skill-intensive than its imports, so trade will embody a net outflow of the abundant factor.
In the case of products such as i and h, varieties of which are produced in both countries, unless the distributions of varieties are strongly unbalanced towards one side of the quality spectrum, we should expect country 2 to be a net exporter of product i and a net importer of product h.
In other words, the skill-abundant country will be a net exporter of goods whose skill-intensity, averaged across the full product range, is high.
So, if we measure factor intensity at the world level, we will observe countries being net exporters of products that are intensive in their abundant factors. However, the information on the skill intensity of production is usually derived from a single country’s statistics, so the measurement of skill intensity may be affected by the fact that some varieties of some products are not produced in the country of measurement: the existence of “non-competing” imports means that the use of one country’s statistics on skill intensity will understate the true difference in skill intensity of production between countries.
Then, this is a model that is firmly in the Heckscher–Ohlin tradition in which countries have common tastes and technology, and trade arises from differences in factor endowments of countries and factor requirements of goods. The model differs from the standard textbook HOS model in that factor endowment differences explain intra-sectoral rather than inter-sectoral specialisation: it is a Heckscher–Ohlin model of intra-industry trade.
2.3. The Effects of Growth of North–South Trade
Now, consider trade in a two-country setting, in which the less skill-abundant country (‘the South’) grows. This could be interpreted as a stylised model of developments in the world economy in the 1980s, particularly the rapid growth of South East Asian economies and China entering the world market.
The growth of international trade with the South will lead to the North moving up the quality spectrum in every sector, and it will increase the demand for labour skills and push up the skill premium without there necessarily being any inter-sectoral specialisation.
In Feenstra and Hanson’s model (1996), a flow of capital from North to South raises the skill intensity of production and the skill premium in both countries. This property runs contrary to the prediction of the standard two-good two-factor HOS model, but it is in line with some evidence on what has happened to wage differentials in low-wage trading economies (Robbins 1994). Whether the skill premium rises in the South in the present model depends on the specification of the exogenous change that drives the growth of trade.
If we assume a neutral expansion of aggregate output in the South relative to the North, caused by uniform expansion of the labour supply, technical progress, or capital accumulation in the South, we should expect an increase in the relative demand for skilled labour both in the North and in the South. The Southern share of production of each good will rise. In Figure 1, the skilled/unskilled critical ratio at the value v*, dividing the spectrum of production between country 1 (South) and country 2 (North), will increase. This implies that the production of some varieties will be transferred from the North to the South. These activities will be more skilled-labour intensive than those formerly produced in the South but less skilled-labour intensive than those now produced in the North. Clearly, this dynamic of international specialisation drives up the skill intensity of production in both countries.
When the North moves “up-market” in each product, the relative demand for skilled labour rises, but the relative supply is unchanged. To restore labour market equilibrium, production will have to shift from the more skill-intensive to the less skill- intensive varieties which the North continues to produce and from the more skill-intensive to the less skill-intensive sectors, and this will require an increase in the price of the most skill-intensive varieties, which in turn will require a rise in the relative wage of skilled labour. The skill premium goes up in the North, but the South moves up-market also, and the same argument implies a rising skill premium in the South as well.
The case in which the shock is represented by a reduction of trade barriers is different. In this circumstance, a decline of transport costs, for example, will produce HO-type effects, with the relative demand for skilled labour rising in the North and falling in the South. The reason of this more conventional result is that the existence of transport costs causes the varieties in the “middle” of each continuum to be produced in both countries and therefore non-traded. When transport costs decrease, the non-traded overlapping band in the middle gets smaller and each country specialises in varieties at the respective extremes of the continuum (I owe this point to Adrian Wood).
However, if we look at the North, in all cases, the growth of international trade with the South will induce a rise in the skill premium in the North, implying a rise in the relative price of skill-intensive product varieties but uncertain effects on relative sectoral price indices (Lawrence and Slaughter observation 1), an increase in the relative employment of skilled workers in all sectors (observation 2), and no systematic inter-sectoral shifts in production (observation 3). In other words, this Heckscher–Ohlin model of intra-industry trade is consistent with all the phenomena that Lawrence and Slaughter use to cast doubt on the link between trade and the labour market. It is a model in which, clearly, trade will have factor market effects, and we now turn attention to the issue of the likely size of these effects.
3. An Empirical Application
3.1. Introduction—A Three-Digit Factor-Content Calculation
Empirical implementation of the ideas set out in the previous section is far from straightforward, because much less direct information is available about intra-sectoral trade than inter-sectoral trade. Therefore, the evidence advanced here should be interpreted as suggestive rather than conclusive.
We have chosen as the empirical case study the trade of Italy with a group of countries we label “less advanced countries” (LACs), which include all of the world except the EU, EFTA, the USA, Canada, Japan, Australia, and New Zealand. (The LACs are not quite the same as non-OECD countries: they include Turkey and the countries that joined the OECD in the 1990s.) It is a wider category of countries than “less developed countries” as usually defined, because of the inclusion of East European countries, all of Latin America, and even the most advanced of the South East Asian countries. Trade with LACs is more than half of Italy’s non-EU trade in the 1990s and thus more than 20% of all of Italy’s trade. Furthermore, this is the part of Italy’s foreign trade that might be expected to have the largest labour market impact.
The analysis focusses on manufacturing (NACE 260–495) and compares three-digit and eight-digit data (the list of sectors is included in the Appendix A). Manufacturing industries stricto sensu have been taken into account, excluding, for example, food and mining sectors. For the purpose of the work, it was not significant to include very capital-intensive industries. There are 77 three-digit NACE sectors, with a total of 6635 eight-digit CN products in the NACE-CN concordance provided with the COMEXT trade data (in 1993). NACE is a classification of sectors, CN is a classification of products, and it should be noted that no concordance, no matter how detailed, can perfectly allocate the production of each individual product to a single production sector. The year for analysis is 1993. All of the analysis of this section will use factor content calculations.
A conventional estimate of the effects of trade with the LACs on the Italian labour market may be undertaken at the three-digit NACE level at which both trade data (from the European Commission’s COMEXT database) and industrial data (from the EC industrial statistics database) are available.
The three-digit factor content calculation takes the ratios of manual and non-manual labour to the value of production in the industrial data and assumes that these ratios will apply to the production of exports and import substitutes. Such a calculation shows that trade with LACs raises the demand for manual labour in Italian non-food manufacturing by 5.02% and for non-manual labour by 6.51%. Both numbers are positive, because Italy has a trade surplus with LACs, and both numbers are non-trivial, reflecting the quantitative significance of trade with LACs. However, if one is interested in the effects of trade on the relative fortunes of skilled and unskilled labour, it is the difference between the two numbers above that is of interest, and the fact that trade with LACs raises the demand for non-manual labour by 1.5% more than the demand for manual labour is not a very impressive statistic given the scale of this trade. Furthermore, if we allow for the trade surplus and consider the impact only of a balanced change in trade, the effect on relative factor demands falls below 1%. This calculation is in line with the conventional wisdom among trade economists in the 1990s that trade with less advanced countries has a small effect on the labour markets of advanced economies.
3.2. Alternative Measures of Intra-Industry Trade
Now consider what can be learned from statistics calculated at the 8-digit CN level. There are 6635 commodities in the relevant chapters of the CN classification that correspond to the 77 NACE classes in the three-digit non-food manufacturing sectors. The difference between the two classifications is illustrated by the fact that there are 86 times more eight-digit commodities than three-digit sectors. It can also be illustrated by example: CN code 84182199 refers to “Household refrigerators, compression-type, capacity between 250 and 340 litres, excluding table models and building-in types”, and this is one of 68 commodities that correspond to NACE sector 346 “domestic electrical appliances”.
Since product descriptions are so specific at the eight-digit level, it is defensible to use unit values (the ratio of value to weight) as a meaningful indicator of product quality. We follow Abd-el-Rahman (1991), Torstensson (1991), Greenaway et al. (1995), Landesmann and Burgstaller (1998), and Fontagné et al. (1998) in using differences between the unit values of imports and exports of products in the same eight-digit class to distinguish between horizontal and vertical intra-industry trade. If the unit values of imports and exports diverge by more than 15%, this is taken as indicating that imports and exports are of different quality, so that there is vertical intra-industry trade (VIIT); while differences of less than 15% indicate horizontal intra-industry trade (HIIT).
In this paper, we take the concept of VIIT one step further by defining “VIIT+” trade as those VIIT flows where the unit values of the export flow is greater (by at least 15%) than the import unit value, while “VIIT-“ trade describes the flows where it is import unit values that are larger.
Table 1 reports total IIT, vertical IIT (VIIT+ and VIIT-), and horizontal IIT (HIIT) for Italy-LAC trade in 1993, and the statistics are illustrated in Figure 4. In Figure 4, “HO (3-digit)” refers to trade that is inter-industry at the three-digit level, “IIT (3), HO (8)” is the part of trade that appears to be intra-industry at the three-digit level but is inter-product at the eight-digit level (i.e. 22%; note that if this number is added to 57%, we get the 1’s complement of the eight-digit IIT index reported in Table 1, i.e. 79%, which is the share of inter-product trade), while the different forms of intra-industry trade at the eight-digit level are labeled in accordance with the terminology used above.

Table 1.
Indices of intra-industry trade. Italian trade with LACs. 1993.
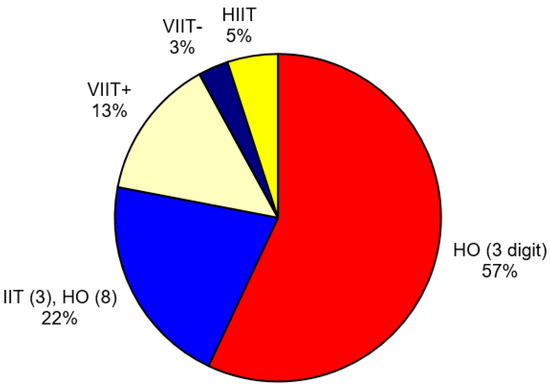
Figure 4.
Italy–LAC trade 1993.
The conventional three-digit factor-content calculations described above were based on the Heckscher–Ohlin model of inter-industry trade applied to three-digit sectors. At the three-digit level, the Grubel–Lloyd index of intra-industry trade is 43% for Italy-NAC trade in 1993. This proportion of trade is excluded from the factor-content calculation because it consists of offsetting flows of imports and exports within three-digit sectors, that is to say flows that have zero effect in the factor content calculation. However, disaggregation to the eight-digit level suggests that only 5% of trade is actually intra-industry trade in products of the same type and comparable quality. The remaining 38% consists of matching flows of imports and exports, but the matching is either of different products in the same sector (22%) or of different qualities of the same product (16%). These two kinds of matched trade are what Wood refers to as “non-competing imports”, and both have the potential to have significant labour market effects.
3.3. The Impact of Intra-Industry Trade on Labour Market
The analysis of IIT indices reported in the previous section suggests that in the case of Italian products, heterogeneity matters, and that any calculation of the factor content of trade should take this aspect into account. In particular, we expect that an eventual comparison between FCT results at the three-digit and the eight-digit level would signal substantial differences in trade impact, which is in line with the evidence above reported.
However, in the absence of industrial or labour market data at the level of disaggregation of the eight-digit CN, the task of trying to deduce how significant these labour market effects might be is a formidable one. This paper attempts to make a start on that task, but it needs to be emphasised that the calculations presented here are of a tentative nature. Confidence in the robustness of the numbers presented here would require the exercise to be repeated on data for other countries and would also be helped by a less crude treatment of the skill composition of the labour force.
The first step is to follow Greenaway and Torstensson (2000) in seeking evidence that unit value comparisons do indeed provide evidence that is consistent with the kind of model presented. Landesmann and Burgstaller (1998) have computed unit value comparisons for a number of three-digit NACE sectors for trade between the EU and a number of countries, EU and non-EU. Unit value differences between a country’s exports to the EU and all countries’ exports to the EU are computed at the eight-digit level and then averaged to the three-digit level. Cross-country regressions of income and educational data against these “price gaps” reveal significant relationships that are consistent with the model of Section 2: differences in countries’ relative endowments of human capital (measured by the percentage of the adult population with completed high school education) and of development in general (measured by GDP per worker) give rise to specialisation in different parts of the quality spectrum.
However, the key requirement is to find some indicator of skill intensity at the product level. The model implies that within an eight-digit product category, there will be a systematic relationship between the prices of product varieties and their skill intensity, and given the tight definition of an eight-digit product, we can have a degree of confidence that the main source of unit value differences is likely to be in the characteristics of the product (rather than, say, in how much raw material or intermediate product is incorporated in it). There is no such reason to suppose that there will be a systematic relationship between unit values and the skill intensity of production across eight-digit products or, a fortiori, across three-digit sectors. Therefore, a relationship between unit values and skill intensity at the three-digit level should reflect the underlying relationship within the eight-digit categories, which is overlaid by a great deal of noise. However, given that data on skill intensity are available only at the three-digit level, this is where we have to look for empirical evidence.
On the input side, the most readily available data on skill inputs are 1993 data (EC industrial statistics) for Italian inputs of manual and non-manual labour in three-digit sectors, and input coefficients were defined as ratios of non-manual labour to turnover (UNY) and manual labour to turnover (SKY). Regression of the average unit-value of Italian 1993 exports to LACs (UVX) (calculated at the eight-digit level and averaged for each sector across all eight-digit commodities) against these input coefficients across 77 three-digit sectors gave:
SKY = 1.3287 + 0.31762 ln (UVX)
(11.20) (7.19) R2 = 0.41
UNY = 4.7556 + 0.34618 ln (UVX)
(13.56) (2.65) R2 = 0.09
(t-statistics in parentheses).
(11.20) (7.19) R2 = 0.41
UNY = 4.7556 + 0.34618 ln (UVX)
(13.56) (2.65) R2 = 0.09
(t-statistics in parentheses).
At first sight, the positive coefficient in the second regression may seem surprising, but it is easily checked that the two regressions together imply that the ratio of non-manual to manual labour is increasing in the unit value of exports, which is consistent with the notion of product quality being skill-intensive. It is also acceptable that higher quality products require more of both kinds of labour.
We now take the large step of applying Equation (16) to data on the unit values of Italian exports and imports of individual eight-digit products to predict input requirements of individual products and then use the derived coefficients to conduct a factor content calculation on the full 95% of Italian–LAC trade that is not horizontal intra-industry trade. The slope coefficients in the regressions are used to adjust the input coefficients for individual products relative to the sector average, so that within each three-digit sector, the sectoral input coefficients remain at the levels given in the data and used in the three-digit factor content calculation.
We first apply this to trade that is intra-sector but inter-product, which is the first of the two ways that we interpret Wood’s “non-competing imports”. Therefore, the first calculation attempts to calculate the labour market effects of the 22% of Italian–LAC trade that is measured as intra-industry trade at the three-digit level but as inter-product trade at the eight-digit level by imputing labour input coefficients to each eight-digit commodity but the same input coefficients to exports and to import substitutes.
A further interpretation of “non-competing imports” applies to vertical intra-industry trade (vertical intra-product trade, more precisely), and in our second set of calculations, we take this into account by using the unit values of imports and the regression coefficients above to impute input coefficients to import-competing production in the factor content calculation. This second calculation goes further: by imputing separate coefficients to exports and import substitutes, it allows for factor market effects from vertical intra-industry trade at the eight-digit level.
Table 1 shows that Italy had a substantial trade surplus with the LACs in 1993, so the results are better interpreted with the effects of the trade surplus removed. This is done by considering the effect of balanced trade change: where the factor content of exports is scaled down in proportion to the excess of exports over imports.
Table A2 (reported in Appendix A) shows practically how the FCT calculation at the three-digit and the eight-digit level is implemented just looking at a single sector (NACE 365) to illustrate the method of estimation here applied.
3.4. Results
Following and generalising the procedure exemplified in Table A2 (in Appendix A) for a single sector, the FCT calculation has been undertaken at the three-digit level with reference to 77 sectors and then at the eight-digit level with reference to the 6635 products attributed to those sectors. At the three-digit level, the conventional FCT calculation estimates the labour market impact of the 57% of Italian trade with LAC that is measured as inter-industry trade (see Figure 4). At the eight-digit level, a first calculation attempts to calculate the labour market effects of the 22% of Italy-LAC trade that is measured as intra-industry trade at the three-digit level but as HO-type trade at the eight-digit level (as shown in Figure 4) by imputing labour input coefficients to each eight-digit commodity, but with the same input coefficients for exports and import substitutes. In this first calculation using the same input coefficients, the impact of the two-way trade at the eight-digit level, intra-product trade, is zero, but the labour market effects of inter-product trade are different from zero for the reason that input coefficients differ across products. In other words, this method of calculation allows us to capture the impact of HO-type trade at the eight-digit level. The second calculation goes further: by imputing separate coefficients to exports and import substitutes, it allows us to capture additional factor market effects from intra-product trade, that is to say, vertical intra-industry trade at the eight-digit level (16% of Italy-LAC trade).
Table 2 reports trade impact results. The first two columns show the factor content of trade in terms of skilled/unskilled ratio. Italian exports are more skill-intensive compared with imports from the LAC area. In addition, moving from the three-digit to the eight-digit level, the gap between exports and imports in the skilled/unskilled ratio becomes larger: 37% increase (the inclusion of VIIT in the eight-digit calculation raises the gap only marginally: 6% more). This suggests that trade impact is more pronounced if the calculation is carried out at a more disaggregated level. Columns three and four display the impact of trade in terms of labour demand for skilled and unskilled: FCT calculations at the three-digit level show that in one year, trade with LACs raises the demand for manual labour in Italian manufacturing by 5.02% and for non-manual labour by 6.51% (the percentages being expressed in relation to total manual and non-manual employment); FCT calculations at the eight-digit level reveal that the impact is slightly bigger for both types of labour: +5.12% for manual workers and +6.74% for non-manual workers (+5.16% and +6.83% in the case of the eight-digit results with VIIT). Both numbers are positive, because Italy has a trade surplus with LACs, and both numbers are non-trivial, reflecting the quantitative significance of trade with LACs.

Table 2.
The impact of Italy-LACs trade on the Italian labour market. 1993.
However, as already discussed, the results are better interpreted with the effects of the trade surplus removed. This is done by considering the effect of balanced trade change: where the factor content of exports is scaled down in proportion to the excess of exports over imports. This sort of computation is reported in columns five and six of Table 2. In the three-digit factor content calculation, balanced Italian–LAC trade implies a 0.76% increase in the demand for non-manual labour in Italy and a 0.06% reduction in the demand for manual labour. These numbers are smaller than the 6.51% and 5.02% derived from the unbalanced trade calculation, but it is the difference between the two numbers that is most meaningful: balanced trade with LACs raises the relative demand for non-manual labour in Italy by 0.82%.
The eight-digit factor content calculation using only export unit values gives a 1.20% increase in demand for non-manual labour and a 0.12% increase in demand for manual labour, so the change in the relative demand for non-manual labour rises to 1.08%. The eight-digit calculation allowing for vertical intra-industry trade implies respective changes of 1.29% and 0.16%, so a change in the relative demand for non-manual labour of 1.13%. Note that in the eight-digit calculation, the balanced trade impact raises demand for both factors. This result is not strange if we assume the existence of other production factors such as physical capital.
The analytical framework here offered provides an alternative approach to that of Wood for the calculation of the impact of what he calls “non-competing imports”, effectively intra-industry trade, on the labour market effects of trade. From FCT results above reported, three conclusions can be drawn. (1) The more disaggregated calculations produce significantly larger labour market effects of trade. (2) The scale of the difference is less than in Wood’s calculations: here, intra-industry trade has an additional impact of less than 40% (raising the relative demand effect from 0.82% to 1.08% or 1.13%). (3) Most of the labour market effect of intra-industry trade comes from allowing for inter-product specialisation within sectors rather than for intra-product trade.
4. Concluding Remarks
The paper analysed the issue of the impact of international trade on the labour market, highlighting the relevance of heterogeneity and qualitative differentiation of traded goods. A model of intra-industry trade was proposed in which countries’ factor endowments and factor intensities of goods determine international specialisation, which takes place along the quality spectrum within sectors rather than across sectors as in the traditional Heckscher–Ohlin model. The analytical framework presupposes significant trade-induced factor substitution effects (between skilled and unskilled workers), and it is compatible with the stylised facts of the 1980s−1990s that trade economists (e.g., Laurence and Slaughter) pointed to in order to deny the role of trade in the misfortunes of unskilled workers in advanced countries. The paper also proposed a method for empirically assessing factor substitution effects at the product level. Inferring the factor content of intra-industry trade from the inter-sectoral relationship between factor intensity and average unit values of exports, the paper found that the labour market effects of intra-industry trade add significantly to the estimated factor market impact of trade.
How to locate the analysis developed in this paper in relation to the debate on trade and jobs? The 1990s literature on labour market effects of international trade highlighted an apparent dichotomy between analyses aiming to estimate the trade-driven shift in labour demand via FCT calculation and the studies focussing on the link between relative wages and prices of traded goods (on this point, see the useful literature review provided by Greenaway and Nelson (2001)). Trade theorists especially have denied the existence of a strong link between trade and income distribution because empirical evidence does not support entirely the predictions of HOS model, which was assumed as the standard framework to deal with the issue. This position of trade theorists is justified mainly by the weak link emerging in the empirical analysis between factor prices and good prices and by the pervasive non-neoclassical relationship between factor ratios and relative remunerations. Even if FCT calculations provide evidence of a more robust impact of trade on labour markets (via labour demand), the majority of trade theorists do not assign great importance to this result because they consider FCT analysis theoretically ill-founded (in spite of the demonstration of Deardorff and Staiger (1988), that the FCT can be used to indicate effects of trade on relative factor prices). However, the dichotomy between the two approaches (FCT versus “prices–wages” analysis) has been emphasised excessively. As Smith (1999) has observed, the relation between the two types of method can be clarified in a context of CGE analysis: “…An advantage of the CGE approach is that it can bridge these methodological gaps by using the same model to produce results on the impact of trade both on labour demand, with factor prices unchanged, and on factor prices, when factor markets are allowed to clear” (Smith 1999, cit. p. 96).
So, the main issue is not to establish if a price-oriented approach is superior to a demand-oriented one. Whatever the methodology adopted, the point is that the standard inter-sectoral analysis fails to produce relevant labour market effects because it is not able to provide an adequate treatment of factor proportion and of intra-industry trade as trade in products that are identical in their factor proportion. The work presented here starts from identifying the inadequacy associated with the standard inter-sectoral approach and provides an FCT analysis modified to capture labour market effects acting within sectors in terms of factor substitution induced by inter-product trade and vertical intra-product trade. Once the analysis focusses on substitution effects within sectors by adopting a more disaggregated approach, the labour market effects of trade are significant. It is no coincidence that the most recent contributions that can rely on firm-level data (firm heterogeneity) and/or on a finer classification of employment characteristics (trading tasks) have rediscovered the importance of international trade for labour market outcomes.
Certainly, the methodology presented in this work to evaluate the impact of intra-industry trade on labour markets needs to be supported by further empirical investigation in terms of extension to other countries and years. For example, it would be interesting to apply the methodology here proposed to analyse the impact of the increased Chinese competition over the last two decades on the labour markets of Southern European countries, whose productions show a certain degree of overlap with China’s sectoral specialisation. In addition, a less crude approach to the modelling of the skill content of production would also be desirable
However, although the paper focusses retrospectively on facts and discussions concerning trade and jobs in the 1990s, the issues here raised are also relevant for the present. As mentioned above, from the 2000s onwards, the debate on the effects of globalisation processes on labour markets has shifted from the role of trade to that of outsourcing. However, quality product differentiation in vertical trade is as significant as international production fragmentation in interacting with labour market dynamics.
Actually, a recent strand of literature focusses on the link between income distribution, imports, and quality differentiation of traded goods. Compared to the standard theory of international trade, which looks at the impact of trade on factor markets, here, the chain of causation is reversed: from labour market conditions and income distribution to trade flows, especially with regard to imports and their quality. Empirical works going in this second direction are, among others, those of Adam et al. (2011) and Bernasconi and Wuergler (2013). Bernasconi and Wuergler (2013) find, for example, a positive relationship between per capita income and the extensive margin (or variety) of imports at various levels of sectoral disaggregation. However, the positive link between per capita income and intensive import margin emerges at the disaggregated level, while it disappears when looking at aggregate data. On the other hand, Fajgelbaum et al. (2011) and Picard and Tampieri (2016) offer theoretical support to the relationship between income distribution and the quality of internationally traded goods. In particular, their models prefigure a situation in which advanced countries are net exporters of higher quality goods and net importers of lower quality goods, while less advanced countries exhibit an opposite pattern of trade. In Fajgelbaum et al.’s (2011) model, the international specialisation pattern of a country is explained through a mechanism à la Linder based on a home-market effect: a country tends to export the goods that are most present in its domestic demand structure; therefore, rich countries tend to export higher quality goods as they are more in demand domestically. Moreover, in rich countries, international trade favours low-income groups, as it widens the spectrum of low-quality products available to them and, in this way, creates an income transfer in their favour from groups consuming a higher proportion of high-quality/price goods. Picard and Tampieri (2016) also construct an analytical framework in which income effects explain the composition of consumption, production, and the pattern of trade, but their model predicts, differently, that a country’s international specialisation in high-quality production harms, rather than favours, the segments of the population located at the lower end of the income distribution. In particular, following an increase in productivity, the country specialises in high-quality products but, from a certain point onwards, further productivity growth triggers an “immiserising growth” mechanism that reduces the welfare of less skilled domestic workers.
These recent analytical frameworks, which are attentive to the quality differentiation in trade, are useful for interpreting the interaction between domestic dynamics concerning product and factor markets and the international division of labour. Imports of low-quality goods have accompanied the labour market segmentation processes that have taken place in advanced countries. For example, in the period 2000–2009, German imports of consumer goods from China increased significantly, especially in the low-quality segment (German imports of low-quality goods from China increased from USD 2.5 billion in 2000 to USD 13 billion in 2009; see Celi et al. 2018). The availability of cheap consumer goods from China facilitated the introduction of the Hartz reforms that contributed to intensifying the segmentation of the German labour market—with the emergence of mini-jobs and the spread of the working poor—reducing the bargaining power of workers and allowing a long period of wage moderation in Germany. This change in the composition of German imports of consumer goods in favour of low-priced Chinese goods also displaced exports of medium-high quality consumer goods from southern European countries (e.g., Italy) to Germany. In truth, these countries have suffered a double displacement: the reduction of their exports of consumer goods to Germany due to the “China effect”, and the contraction of their exports of intermediate goods to Germany due to the eastward expansion of the German manufacturing platform (Celi et al. 2018). These examples, briefly provided in these concluding remarks, reveal the importance of considering the qualitative differentiation of traded goods together with international production fragmentation, when exploring the interaction between domestic socio-economic dynamics and internationalisation processes.
Funding
This research has not received any external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Appendix A.1. List of Sectors Included in the Sample

Table A1.
3-digit NACE Sectors included in the sample.
Table A1.
3-digit NACE Sectors included in the sample.
| Code | Description |
|---|---|
| 2600 | Chemical and man-made fibres (25 + 26) |
| 3110 | Foundries |
| 3120 | Forging; drop forging, closed dieforging, pressing and stamping |
| 3130 | Secondary transformation, treatment and coating of metals |
| 3140 | Manufacture of structural metal products |
| 3150 | Boilermaking, manufacture of reservoirs, tanks and other sheet-metal containers |
| 3160 | Manufacture of tools and finished metal goods, except electrical equipment |
| 3210 | Manufacture of agriculture machinery and tractors |
| 3220 | Manufacture of machine-tools for working metal, and of other tools and equipment machines |
| 3230 | Manufacture of textile machinery and accessories; manufacture of sewing machines |
| 3240 | Manufacture of machinery for the food, chemical and related industries |
| 3250 | Manufacture of plant for mines, the iron and steel industries and foundries, civil engineering |
| 3260 | Manufacture of transmission equipment for motive power |
| 3270 | Manufacture of other machinery and equipment for use in specific branches of industries |
| 3280 | Manufacture of other machinery and equipment |
| 3300 | Manufacture of office machinery and data processing machinery |
| 3410 | Manufacture of insulated wires and cables |
| 3420 | Manufacture of electrical machinery |
| 3430 | Manufacture of electrical apparatus and appliances for industrial use |
| 3440 | Manufacture of telecommunications equipment, electrical and electronic measuring and record |
| 3450 | Manufacture of radio and television receiving sets, sound reproducing and recording |
| 3460 | Manufacture of domestic type electric appliances |
| 3470 | Manufacture of electric lamps and other electric lighting equipment |
| 3510 | Manufacture and assembly of motor vehicles (including road tractors) and motor vehicle engines |
| 3520 | Manufacture of bodies for motor vehicles and of motor-drawn trailers and caravans |
| 3530 | Manufacture of parts and accessories for motor vehicles |
| 3610 | Shipbuilding |
| 3620 | Manufacture of standard and narrow-gauge railway and tramway rolling-stock |
| 3630 | Manufacture of cycles, motor-cycles and parts and accessories thereof |
| 3640 | Aerospace equipment manufacturing and repairing |
| 3650 | Manufacture of transport equipment not elsewhere specified |
| 3710 | Manufacture of measuring, checking and precision instruments and apparatus |
| 3720 | Manufacture of medical and surgical equipment and orthopaedic appliances (except footwear) |
| 3730 | Manufacture of optical instruments and photographic equipment |
| 4110 | Manufactures of vegetables and animal oils and fats |
| 4120 | Slaughtering, preparing and preserving of meat (except the butcher’s trade) |
| 4130 | Manufacture of dairy products |
| 4140 | Processing and preserving of fruit and vegetables |
| 4150 | Processing and preserving of fish and other sea foods fit for human consumption |
| 4160 | Grain milling |
| 4170 | Manufacture of spaghetti, macaroni, etc. |
| 4180 | Manufacture of starch and starch products |
| 4190 | Bread and flour confectionery |
| 4200 | Sugar manufacturing and refining |
| 4210 | Manufacture of cocoa, chocolate and sugar confectionery |
| 4220 | Manufacture of animal and poultry foods (including fish meal and flour) |
| 4230 | Manufacture of other food products |
| 4240 | Distilling of ethyl alcohol from fermented materials; spirit distilling and compounding |
| 4250 | Manufactures of wine of fresh grapes and of beverage base thereon |
| 4270 | Brewing and malting |
| 4280 | Manufactures of soft drinks, including the bottling of natural spa waters |
| 4290 | Manufacture of tobacco products |
| 4360 | Knitting industry |
| 4380 | Manufacture of carpets, linoleum and other floor coverings, including leatherclothes |
| 4390 | Miscellaneous textile industries |
| 43A+43B | Wool, Cotton, Silk, Jute, Preparation, spinning and weaving of flax, etc. |
| 4410 | Tanning and dressing of leather |
| 4420 | Manufacture of products from leather and leather substitutes |
| 4510 | Manufacture of mass-produced footwear (excluding footwear made completely of wood) |
| 4530 | Manufacture of ready-made clothing and accessories |
| 4550 | Manufacture of household textiles and other made-up textile goods (outside weaving-mills) |
| 4560 | Manufacture of furs and of fur goods |
| 4610 | Sawing and processing of wood |
| 4620 | Manufacture of semi-finished wood products |
| 4630 | Manufacture of carpentry and joinery components and of parquet flooring |
| 4640 | Manufacture of wooden containers |
| 4650 | Other wood manufactures (except furniture) |
| 4660 | Manufacture of articles of cork and articles of straw and other plainting materials |
| 4670 | Manufacture of wooden furniture |
| 4710 | Manufacture of pulp, paper and board |
| 4720 | Processing of paper and board |
| 4730 | Printing and allied industries |
| 4810 | Manufacture of rubber products |
| 4830 | Processing of plastics |
| 4930 | Photographic and cinematographic laboratories |
| 4940 | Manufacture of toys and sports goods |
| 4950 | Miscellaneous manufacturing industries |
Appendix A.2. Example of FCT Calculation for One Sector

Table A2.
Example of FCT calculation at the 3-digit and 8-digit level—NACE 365.
Table A2.
Example of FCT calculation at the 3-digit and 8-digit level—NACE 365.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sky | uny | sk cont | un cont | sk cont | un cont | |||||||
| Code | M val | M vol | X val | X vol | UVM | UVX | X | X | X | X | M | M |
| 365 | 3849 | 9144 | 1.16 | 6.55 | 10.59 | 59.85 | 4.46 | 25.19 | ||||
| 87131000 | 495 | 33 | 252 | 23 | 15 | 10.96 | 1.32 | 6.72 | 0.33 | 1.69 | 0.65 | 3.32 |
| 87139000 | 270 | 31 | 439 | 30 | 8.7097 | 14.63 | 1.41 | 6.82 | 0.62 | 2.99 | 0.38 | 1.84 |
| 87150010 | 436 | 120 | 6315 | 852 | 3.6333 | 7.41 | 1.19 | 6.58 | 7.52 | 41.56 | 0.52 | 2.87 |
| 87150090 | 2068 | 676 | 304 | 40 | 3.0592 | 7.60 | 1.20 | 6.59 | 0.36 | 2.00 | 2.48 | 13.63 |
| 87168000 | 580 | 269 | 1834 | 1188 | 2.1561 | 1.54 | 0.69 | 6.04 | 1.27 | 11.07 | 0.40 | 3.50 |
| Tot 8 digit | 10.10 | 59.32 | 4.43 | 25.16 | ||||||||
| FCT at the 3-digt level in NACE 365 SK = 10.59 − 4.46 = 6.133 UN = 59.85 − 25.19 = 34. 657 SK/UN = 0.177 | FCT at the 8-digt level in NACE 365 SK = 10.10 − 4.43 = 5.67 UN = 59.32 − 25.16 = 34.16 SK/UN = 0.166 | |||||||||||
In Table A2, in the first column all eight-digit products included in NACE 365 (manufacture of transport equipment not elsewhere specified) are shown. This sector is chosen for the illustration because it contains a small number of eight-digit products. CN code 87131000 refers to “Invalid carriages, not mechanically propelled”, CN code 87139000 refers to “Invalid carriages, motorised or otherwise mechanically propelled (excl. mechanically designed motor vehicles and bicycles), CN code 87150010 refers to “Baby carriages”, and so on. The three-digit factor content calculation takes the ratios of manual and non-manual labour to the value of production in the industrial data and assumes that these ratios will apply to the production of exports and import substitutes. The input coefficients at the three-digit level reported in column 8 and 9 (first row) are the actual ones derived from data. SKY and UNY coefficients at the eight-digit level in columns 8 and 9 are obtained by applying Equation (16) to unit values of exports (UVX) at the eight-digit level in column 7. The estimation of labour coefficients actually amounts to adjusting the observed value of the group by β (lnUVX8—lnUVXg) for each eight-digit good, where β is the slope coefficient coming from (16), UVX8 is the UVX of the eight-digit good, and UVXg is the group value (the unit value averaged across all eight-digit commodities included in the group, where the weights are export values). For example, in the case of the eight-digit code 87131000 belonging to NACE 365, input coefficients are obtained through the following calculation:
where:
SKY(87131000) = 1.16 + 0.318 (ln 10.96 − ln 6.69) = 1.32
UNY(87131000) = 6.55 + 0.346 (ln 10.96 + ln 6.69) = 6.72,
1.16 = SKY(365), observed SKY for sector 365
0.318 = β derived from (16) for SKY
10.96 = UVX (87131000), unit value of 8 digit good 87131000
6.69 = UVX (365), unit value averaged across all 8-digit goods included in 365
6.55 = UNY (365), observed UNY for sector 365
0.346 = β derived from (16) for UNY.
Then, the FCT at the three-digit and the eight-digit level is calculated by multiplying input coefficients and the value of trade flows together (products reported in columns 10–13). Table A2 shows that the FCT calculated at the three-digit level is different from the FCT at the eight-digit level: the skilled/unskilled ratio is 0.177 against 0.166. In the example reported in Table A2, the conventional procedure based on domestic input coefficients (those derived from UVX) has been pursued in order to estimate the FCT. However, a variant on the calculation in the spirit of Wood (1994) could be also undertaken: using the unit values of imports (UVM) and the regression coefficients above to impute input coefficients to import-competing production in the factor content calculation.
Appendix A.3. Sensitivity Analysis of Results
The FCT estimates at the eight-digit level are based on an inference from two statistical relationships whose robustness needs further exploration. The first step is to ask how sensitive results are to the changes of the estimated values of the intercept and slope coefficient in Equation (16). Table A3 shows the range of variation of FCT estimates at the extreme values of the 95% confidence interval for the slope coefficient.
When the FCT calculation at the eight-digit level is undertaken by assuming for both SKY and UNY equations the highest (or the lowest) value of the 95% confidence interval for the slope coefficient, results turn out to be close to those obtained with the original estimated coefficient (in Table A3, compare the second row and the fourth row with the first one. Results at the eight-digit level are reported in terms of the difference from results at the three-digit level).
When trade impact is evaluated by assuming for the SKY equation the smallest value and for UNY equation the highest value of the confidence interval, labour market effects decline and turn out to be similar to the impact gained at the three-digit level (change of 0.82% in relative demand for skilled labour; so the difference is zero). On the contrary, when the highest value of the interval is inserted in the SKY equation and the lowest value is inserted in the UNY equation, the trade impact is bigger (+0.52% or +0.62% in comparison with the calculation at the three-digit level).
In the end, confidence interval-based analysis of the results gives us an outcome consistent with what we expect when the coefficients in Equation (16) are manipulated. In particular, at the extremes of the 95% confidence interval for the slope coefficients, the range of eight-digit FCT results is from 0.82% to 1.44% for the change in relative demand for skilled labour in terms of total effects (including the three-digit inter-industry effects) or, in other words, from 0% to +0.62% in terms of the difference from results gained at the three-digit level (which are 0.82%).

Table A3.
The 8-digit impact of Italy-LACs trade on the Italian labour market. 1993. Sensitivity of results to the change of the slope coefficients in Equation (16).
Table A3.
The 8-digit impact of Italy-LACs trade on the Italian labour market. 1993. Sensitivity of results to the change of the slope coefficients in Equation (16).
| Slope Coefficients * | Increase of Balance Trade Impact on Relative Demand for Skilled Moving from the 3-digit to the 8-digit Calculation | ||
|---|---|---|---|
| Sky Equation | Uny Equation | Ho Method | VIIT Method |
| 0.31762 (original) | 0.34618 (original) | 0.26% | 0.31% |
| 0.4059 (high) | 0.6072 (high) | 0.24% | 0.29% |
| 0.2292 (low) | 0.6072 (high) | 0.00% | 0.00% |
| 0.2292 (low) | 0.08508 (low) | 0.27% | 0.33% |
| 0.4059 (high) | 0.08508 (low) | 0.52% | 0.62% |
* The term “high” and “low” refer to the values at the extremes of the 95% confidence interval for the slope coefficients in Equation (16).
I have also tested the robustness of results by using unit values of imports (UVM) instead of UVX in Equation (16). The estimated inter-sectoral relationship between input coefficients and UVMs is given by Equation (A1):
SKY = 1.3777 + 0.32355 ln (UVM)
(12.25) (7.33) R2 = 0.42
UNY = 4.9513 + 0.27024 ln (UVM)
(14.52) (2.02) R2 = 0.05
(t-statistics in parentheses)
(12.25) (7.33) R2 = 0.42
UNY = 4.9513 + 0.27024 ln (UVM)
(14.52) (2.02) R2 = 0.05
(t-statistics in parentheses)
Equation (A1) displays numbers that are very similar to those produced by Equation (16). However, the difference between the slope coefficients for SKY and UNY is slightly bigger in Equation (A1), and this predicts a significantly bigger impact of trade on labour markets.
Table A4 reports the eight-digit FCT calculation when the slope coefficients of Equation (A1) are used to estimate input requirements at the product level. As expected, the numbers in Table A4 are very close to the original estimates reported in Table 2. However, the balanced trade impact on relative demand for skilled labour is slightly bigger in the case of estimates based on Equation (A1): 1.12% against 1.08% in HO eight-digit calculations, and 1.19% against 1.13% in eight-digit calculation with VIIT. This result is quite comforting in terms of confidence in the use of UVs.

Table A4.
The impact of Italy-LACs trade on the Italian labour market. 1993. 8-digit estimates based on Equation (A1).
Table A4.
The impact of Italy-LACs trade on the Italian labour market. 1993. 8-digit estimates based on Equation (A1).
| Sk/Un Ratio in Exports | Sk/Un Ratio in Imports | Trade Impact on Skilled | Trade Impact on Unskilled | B. Trade Impact on Skilled | B. Trade Impact on Unskilled | B. Trade Impact on Relative Labor Demand | |
|---|---|---|---|---|---|---|---|
| 3 digit results | 0.427 | 0.345 | 6.51% | 5.02% | 0.76% | −0.06% | 0.82% |
| HO 8-digit results | 0.417 | 0.300 | 6.75% | 5.10% | 1.21% | 0.08% | 1.12% (1.08%) * |
| 8-digit results with VIIT | 0.417 | 0.293 | 6.84% | 5.13% | 1.30% | 0.11% | 1.19% (1.13%) * |
* Original estimates based on Equation (16) are reported in brackets.
References
- Abd-el-Rahman, Kamal. 1991. Firms’ competitive and national comparative advantages as joint determinants of trade composition. Weltwirtschaftsliches Archiv 127: 83–97. [Google Scholar] [CrossRef]
- Acemoglu, Daron, David H. Autor, David Dorn, Gordon H. Hanson, and Brendan Price. 2016. Import Competition and the Great US Employment Sag of the 2000s. Journal of Labor Economics 34: S141–98. [Google Scholar] [CrossRef]
- Adam, Antonis, Margarita Katsimi, and Thomas Moutos. 2011. Inequality and the import demand function. Oxford Economic Papers 644: 675–701. [Google Scholar] [CrossRef]
- Amiti, Mary, and Shang-Jin Wei. 2005. Fear of Service Outsourcing: Is it Justified? Economic Policy 2042: 308–47. [Google Scholar] [CrossRef]
- Amiti, Mary, and Shang-Jin Wei. 2009. Service Offshoring, Productivity and Employment: Evidence from the US. The World Economy 322: 203–20. [Google Scholar] [CrossRef]
- Ando, Mitsuyo, and Fukunari Kimura. 2007. Can Offshoring Create Domestic Jobs? Evidence from Japanese Data. Policy Insight No. 16. London: Centre for Economic Policy Research. [Google Scholar]
- Autor, David H., David Dorn, and Gordon H. Hanson. 2013. The China Syndrome: Local Labor Market Effects of Import Competition in the United States. American Economic Review 1036: 2121–68. [Google Scholar] [CrossRef]
- Baldwin, Richard E. 2006. Globalization: The Great Unbundling(s). In Globalisation Challenge for Europe, Secretariat of the Economic Council. Helsinki: Finnish Prime Minister’s Office. [Google Scholar]
- Baldwin, Richard E. 2011. Trade and Industrialisation after Globalisation’s 2nd Unbundling: How Building and Joining a Supply Chain are Different and Why It Matters. NBER Working Paper No. 17716. Available online: https://www.nber.org/system/files/working_papers/w17716/w17716.pdf (accessed on 8 June 2012).
- Baldwin, Richard E. 2013. Supply-Chain Trade: A Portrait of Global Pattern and Several Testable Hypotheses. NBER Working Paper No. 18957. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Bernasconi, Carla, and Tobias Wuergler. 2013. Per Capita Income and the Quality and Variety of Imports. Mimeo: University of Zurich. [Google Scholar]
- Bloom, Nicolas, Mirko Draka, and John Van Reenen. 2016. Trade Induced Technical Change? The Impact of Chinese Imports on Innovation, IT and Productivity. The Review of Economic Studies 831: 87–117. [Google Scholar] [CrossRef]
- Brambilla, Irene, Rafael Dix-Carneiro, Daniel Lederman, and Guido Porto. 2011. Skills, Exports, and the Wages of Seven Million Latin American Workers. The World Bank Economic Review 261: 34–60. [Google Scholar]
- Bustos, Paula. 2011. Trade Liberalization, Exports, and Technology Upgrading: Evidence on the Impact of MERCOSUR on Argentinian Firms. American Economic Review 1011: 304–40. [Google Scholar] [CrossRef]
- Celi, Giuseppe, Andrea Ginzburg, Dario Guarascio, and Annamaria Simonazzi. 2018. Crisis in the European Monetary Union: A Core-Periphery Perspective. London: Routledge. [Google Scholar]
- Dauth, Wolfgang, Sebastian Findeisen, and Jens Suedekum. 2014. The Rise of the East and the Far East: German Labor Markets and Trade Integration. Journal of the European Economic Association 126: 1643–75. [Google Scholar] [CrossRef]
- Deardorff, Alan V. 1979. Weak Links in the Chain of Comparative Advantage. Journal of International Economics 92: 197–209. [Google Scholar] [CrossRef]
- Deardorff, Alan V., and Robert W. Staiger. 1988. An interpretation of the factor content of trade. Journal of International Economics 24: 93–107. [Google Scholar] [CrossRef]
- Dixit, Avinash K., and Joseph E. Stiglitz. 1977. Monopolistic competition and optimum product diversity. American Economic Review 67: 297–308. [Google Scholar]
- Egger, Hartmut, and Peter Egger. 2005. Labor Market Effects of Outsourcing under Industrial Interdependence. International Review of Economics and Finance 143: 349–63. [Google Scholar] [CrossRef][Green Version]
- Ekholm, Karolina, and Katariina Hakkala. 2006. The Effect of Offshoring on Labour Demand: Evidence from Sweden. CEPR Discussion Paper No. 5648. London: Centre for Economic Policy Research. [Google Scholar]
- Fajgelbaum, Pablo, Gene M. Grossman, and Elhanan Helpman. 2011. Income distribution, product quality, and international trade. Journal of Political Economy 1194: 721–65. [Google Scholar] [CrossRef]
- Falvey, Rodney E. 1981. Commercial policy and intra-industry trade. Journal of International Economics 11: 459–511. [Google Scholar] [CrossRef]
- Falvey, Rodney E., and Henryk Kierzkowski. 1985. Product quality, intra-industry trade and (im)perfect competition. In Protection and Competition in International Trade. Oxford: Blackwell. [Google Scholar]
- Feenstra, Robert C. 1998. Integration of Trade and Disintegration of Production in the Global Economy. The Journal of Economic Perspectives 124: 31–50. [Google Scholar] [CrossRef]
- Feenstra, Robert, and Gordon Hanson. 1996. Foreign investment, outsourcing and relative wages. In The Political Economy of Trade Policy: Essays in Honor of Jagdish Bhagwati. Edited by Jagdish N. Bhagwati, Gene M. Grossman, Douglas A. Irwin and RobertC. Feenstra. Cambridge: MIT Press. [Google Scholar]
- Fontagné, Lionel, Michael Freudenberg, and Nicolas Péridy. 1998. Intra-Industry Trade and the Single Market: Quality Matters. Discussion Paper No. 1959. London: Centre for Economic Policy Research. [Google Scholar]
- Freeman, Richard. 1995. Are your wages set in Beijing? Journal of Economic Perspectives 9: 15–32. [Google Scholar] [CrossRef]
- Freeman, Richard B. 2007. The big Doubling: The Challenge of the New Global Labor Market. In Ending Poverty in America: How to Restore the American Dream. Edited by John Edwards, Marion Craine and Arne L. Kalleberg. New York: The New Press. [Google Scholar]
- Geishecker, Ingo. 2006. Does outsourcing to Central and Eastern Europe really threaten manual workers’ jobs in Germany? World Economy 295: 559–83. [Google Scholar] [CrossRef]
- Greenaway, David, Robert Hine, and Chris Milner. 1995. Vertical and horizontal intra-industry trade: A cross industry analysis for the United Kingdom. Economic Journal 105433: 1505–18. [Google Scholar] [CrossRef]
- Greenaway, David, and Douglas Nelson. 2001. Globalisation and Labour Markets: A Review of the Literature. In Globalisation and Labour Markets. Edited by D. Greenaway and D. Nelson. Northampton: Edward Elgar, vols. I and II. [Google Scholar]
- Greenaway, David, and Johan Torstensson. 2000. Economic geography, comparative advantage and trade within industries: Evidence from the OECD. Journal of Economic Integration 15: 260–80. [Google Scholar] [CrossRef][Green Version]
- Grossman, Gene M., and Esteban Rossi-Hansberg. 2008. Trading Tasks: A Simple Theory of Offshoring. American Economic Review 985: 1978–97. [Google Scholar] [CrossRef]
- Helg, Rodolfo, and Lucia Tajoli. 2005. Pattern of international fragmentation of production and the relative demand for labor. North American Journal of Economics and Finance 162: 233–54. [Google Scholar] [CrossRef]
- Helpman, E. 2017. Globalization and Wage Inequality. Journal of the British Academy 5: 125–62. [Google Scholar] [CrossRef]
- Helpman, Elhanan, Oleg Itskhoki, and Stephen Redding. 2010. Inequality and Unemployment in a Global Economy. Econometrica 784: 1239–83. [Google Scholar]
- Hertveldt, Bart, and Bernhard Michel. 2012. Offshoring and the Skill Structure of Labour Demand in Belgium. FPB Working Paper. pp. 7–12. Available online: https://www.plan.be/uploaded/documents/201206080832090.WP_1207_E.pdf (accessed on 23 September 2015).
- Hsieh, Chang T., and Keong T. Woo. 2005. The impact of outsourcing to China on Hong Kong’s labor market. American Economic Review 955: 1673–87. [Google Scholar] [CrossRef]
- Keller, Wolfgang, and Hale Utar. 2016. International Trade and Job Polarization: Evidence at the Worker Level. NBER Working Paper No. 22315. Available online: https://www.nber.org/system/files/working_papers/w22315/w22315.pdf (accessed on 9 August 2018).
- Krugman, Paul. 1994. Peddling Prosperity: Economic Sense and Nonsense in the Age of Diminished Expectations. New York: Norton. [Google Scholar]
- Krugman, P., and Robert Lawrence. 1994. Trade, jobs and wages. Scientific American 270: 44–49. [Google Scholar] [CrossRef]
- Landesmann, Michael, and Johann Burgstaller. 1998. Vertical product differentiation in EU markets: The relative position of East European producers. Russian & East European Finance and Trade 341: 32–78. [Google Scholar]
- Lawrence, Robert, and Matthew Slaughter. 1993. Trade and U.S. wages: Great sucking sound or small hiccup? Brookings Papers in Economic Activity, Microeconomics 2: 161–226. [Google Scholar] [CrossRef]
- Leamer, Edward E. 1995. A trade economist’s view of U.S. wages and ‘globalization’. In Imports, Exports and the American Worker. Edited by Susan Collins. Washington, DC: Brookings Institution. [Google Scholar]
- Lorentowicz, Andzelika, Dalia Marin, and Alexander Raubold. 2005. Is human Capital Losing from Outsourcing? Evidence for Austria and Poland. CEPR Discussion Paper No. 5344. Available online: https://econpapers.repec.org/paper/cprceprdp/5344.htm (accessed on 1 November 2008).
- Malgouyres, Clément. 2017. The Impact of Chinese Import Competition on the Local Structure of Employment and Wages: Evidence From France. Journal of Regional Science 573: 411–41. [Google Scholar] [CrossRef]
- Melitz, Marc J. 2003. The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity. Econometrica 716: 1695–725. [Google Scholar] [CrossRef]
- Mion, Giordano, and Linke Zhu. 2013. Import Competition From and Offshoring to China: A Curse or Blessing for Firms? Journal of International Economics 891: 202–15. [Google Scholar] [CrossRef]
- OECD. 2017. Employment Outlook 2017. Paris: OECD. [Google Scholar]
- Picard, Pierre, and Alessandro Tampieri. 2016. Income Effects and Vertical Differentiation in International Trade. University of Luxemburg. CREA Discussion Papers. Luxembourg: Center for Research in Economic Analysis, University of Luxembourg, p. 20165. [Google Scholar]
- Reijnders, Laurie S., and Gaaitzen de Vries. 2017. Job Polarization in Advanced and Emerging Countries: The Role of Task Relocation and Technological Change within Global Supply Chains. GGDC Research Memoranda No. 167. Groningen: GGDC. [Google Scholar]
- Robbins, Donald. 1994. Earnings Dispersion in Chile after Trade Liberalisation. Mimeo: Harvard University. [Google Scholar]
- Sachs, Jeffrey, and Howard Shatz. 1994. Trade and jobs in U.S. manufacturing. Brookings Papers in Economic Activity 1: 1–84. [Google Scholar] [CrossRef]
- Sampson, Thomas. 2014. Selection into Trade and Wage Inequality. American Economic Journal: Microeconomics 63: 157–202. [Google Scholar] [CrossRef]
- Smith, Alasdair. 1996. Quality Differentiation in Production and the Labour Market Effects of International Trade in Europe. European Forum: The Political Economy of an Integrated Europe. Florence: European University Institute. [Google Scholar]
- Smith, Alasdair. 1999. The labour market effects of trade: A computable general equilibrium approach. In Trade and Jobs in Europe: Much ado about Nothing? Edited by Mathias Dewatripont, André Sapir and Khalid Sekkat. Oxford: Oxford University Press. [Google Scholar]
- Torstensson, Joan. 1991. Quality differentiation and factor proportions in international trade: An empirical test of the Swedish case. Weltwirtschaftsliches Archiv 127: 183–94. [Google Scholar] [CrossRef]
- Wood, Adrian. 1994. North-South Trade, Employment and Inequality: Changing Fortunes in a Skill-Driven World. Oxford: Clarendon Press. [Google Scholar]
- Wright, Greg. 2014. Revisiting the Employment Impact of Offshoring. European Economic Review 66: 63–83. [Google Scholar] [CrossRef]
- Yeaple, Sthephen R. 2005. A Simple Model of Firm Heterogeneity, International Trade, and Wages. Journal of International Economics 651: 1–20. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).