Optimization of Inventory Holding Cost Due to Price, Weight, and Volume of Items †
Abstract
1. Introduction
2. Literature Review
3. Research Procedure
- The demand is constant over time.
- No shortages are allowed.
- All the costs, including the rate of financial cost of holding, will remain constant.
- The entire lot will be sent in a shipment
- Identify if the analysis will be done at the level of each SKU or a representative SKU from the family of items.
- Find out storage location, storage bin/pallet size, number of units in each bin/pallet, how many bins/pallets are kept on a shelf (or ground), how many bins/pallets are kept over each other on a shelf (or ground).
- Based on the current average inventory, annual sale, unit price, lead time, space cost, and cost of finance, calculate the inventory holding cost for each of the SKUs.
- The sum of all the SKUs’ inventory holding costs must be equal to the average inventory holding cost.
| I | average annual inventory of a warehouse | $ |
| h | inventory holding cost at a warehouse | % |
| hw | annual average holding cost for all items in a warehouse | $ |
| Aw | area of a warehouse | Sq. ft. |
| Cw | rent of the empty warehouse | $ |
| α | area utilization factor for storage where 0 < α < 1 | % |
| Ai | area of a rack-type i (this is the area of the pallet that is stored on the ground) | Sq. ft. |
| Si | number of shelves in the racks of type i (for storage on the ground, N = 1) | Number |
| Bj | number of bins (or pallets) type j kept on a shelf | number |
| Xk | number of stock-keeping units (SKU) in a bin (or on a pallet) where k is an SKU | Number |
| Pk | unit price of an SKU k | $/unit |
| Ik | average annual inventory of SKU k | Number |
| Cf | annual cost finance for an organization at a location | % |
| Co | cost of obsolescence | % |
| Ch | cost of handling a bin/pallet | $/unit |
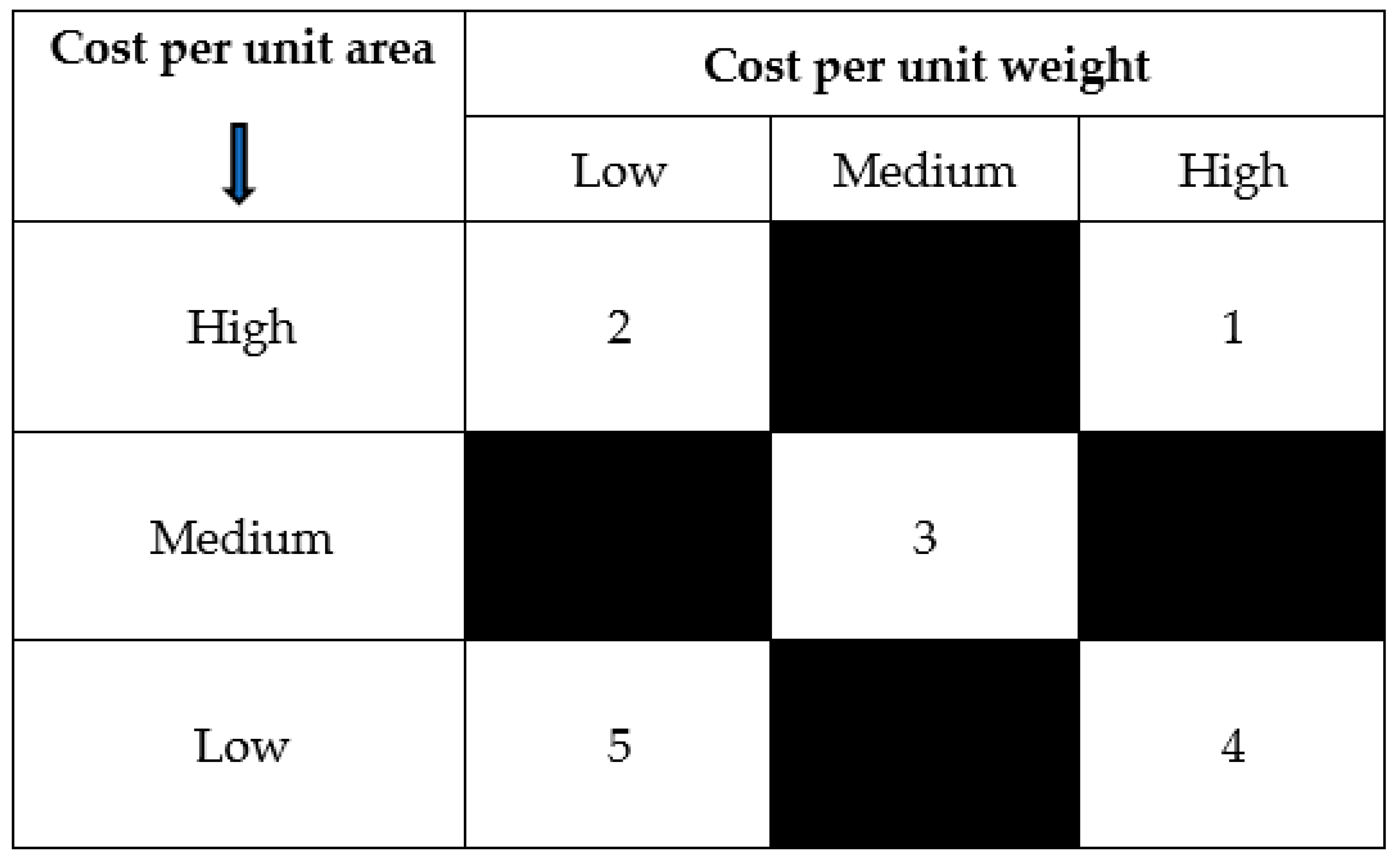
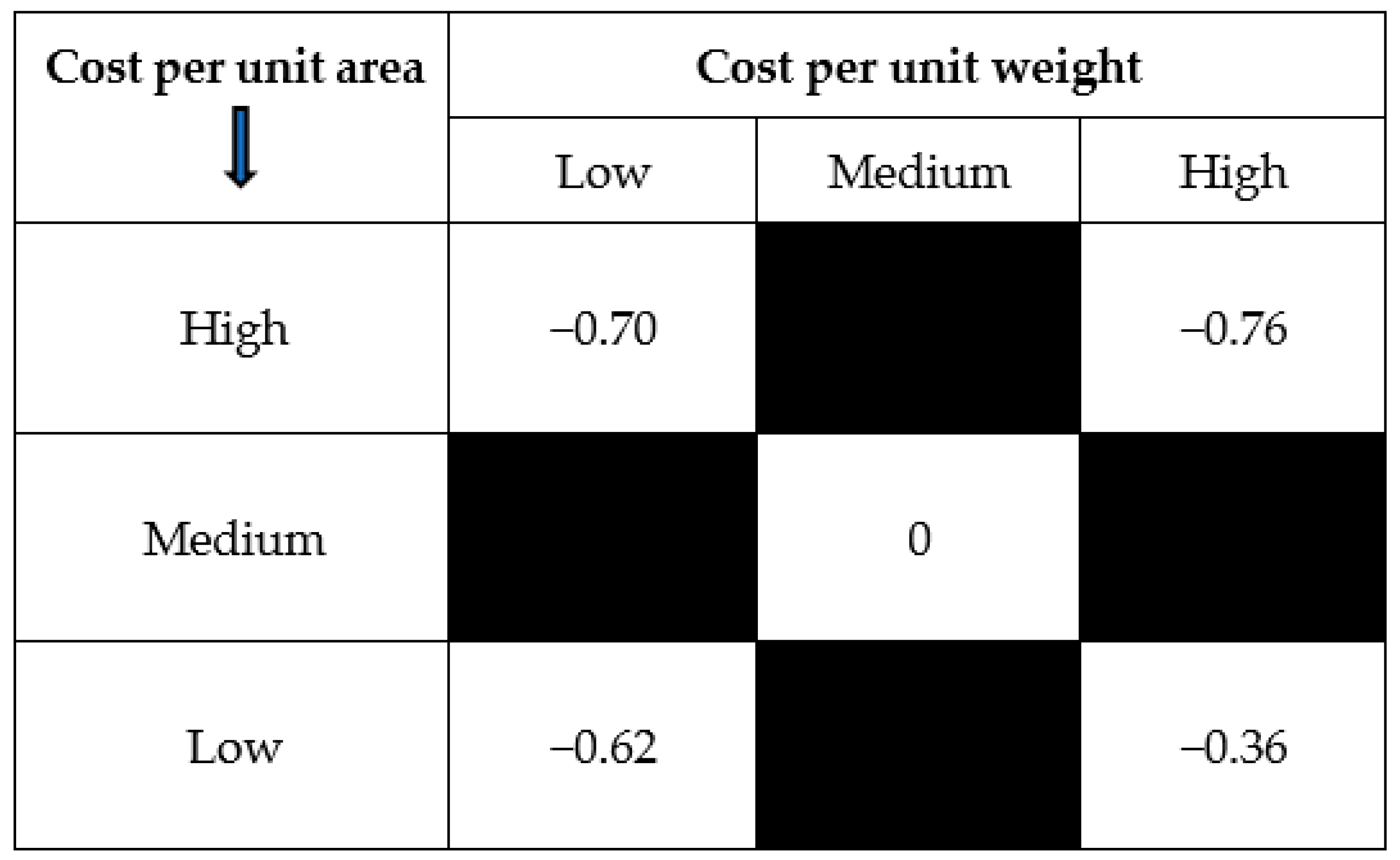
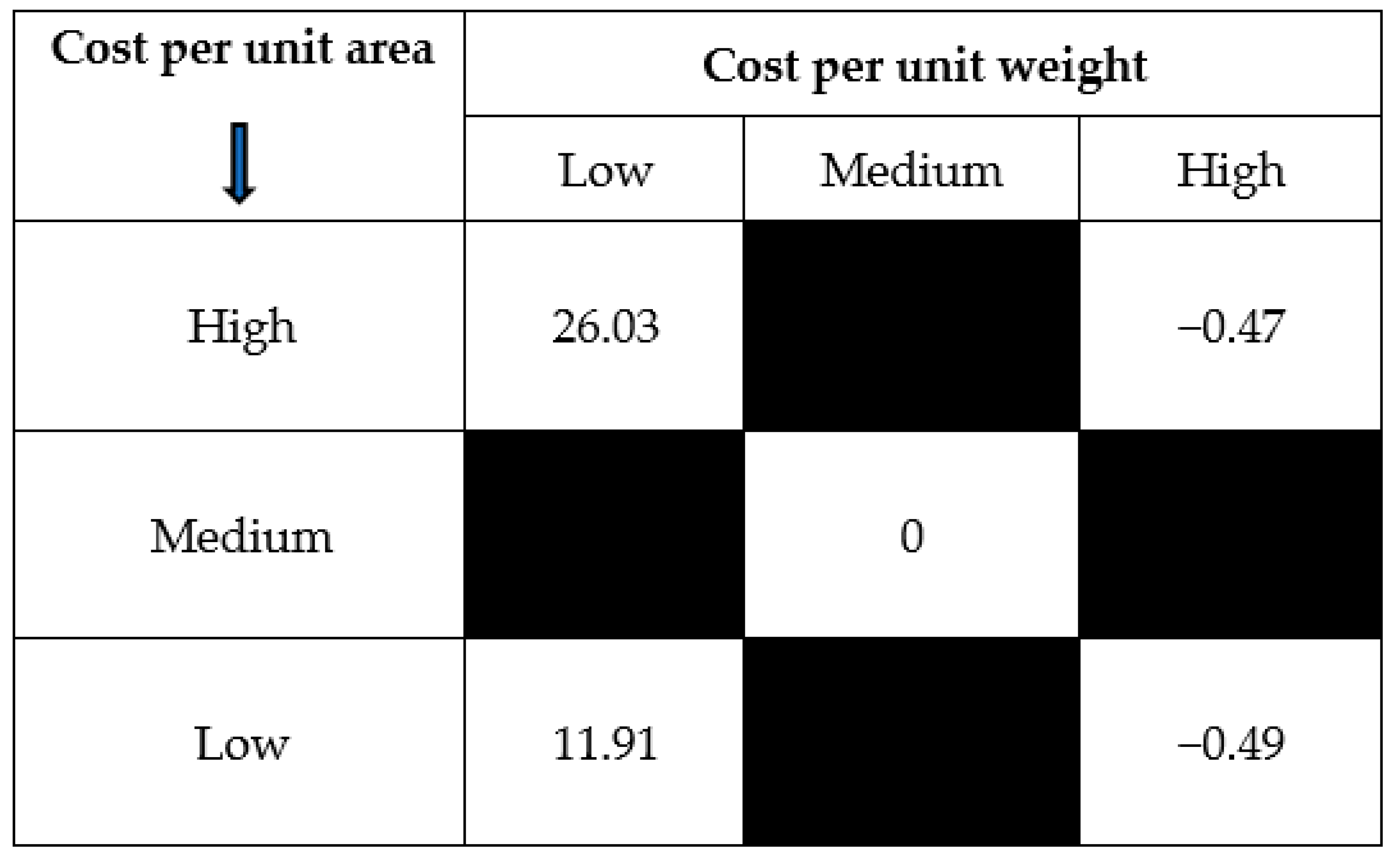
4. Analysis of Inventory in Organizations
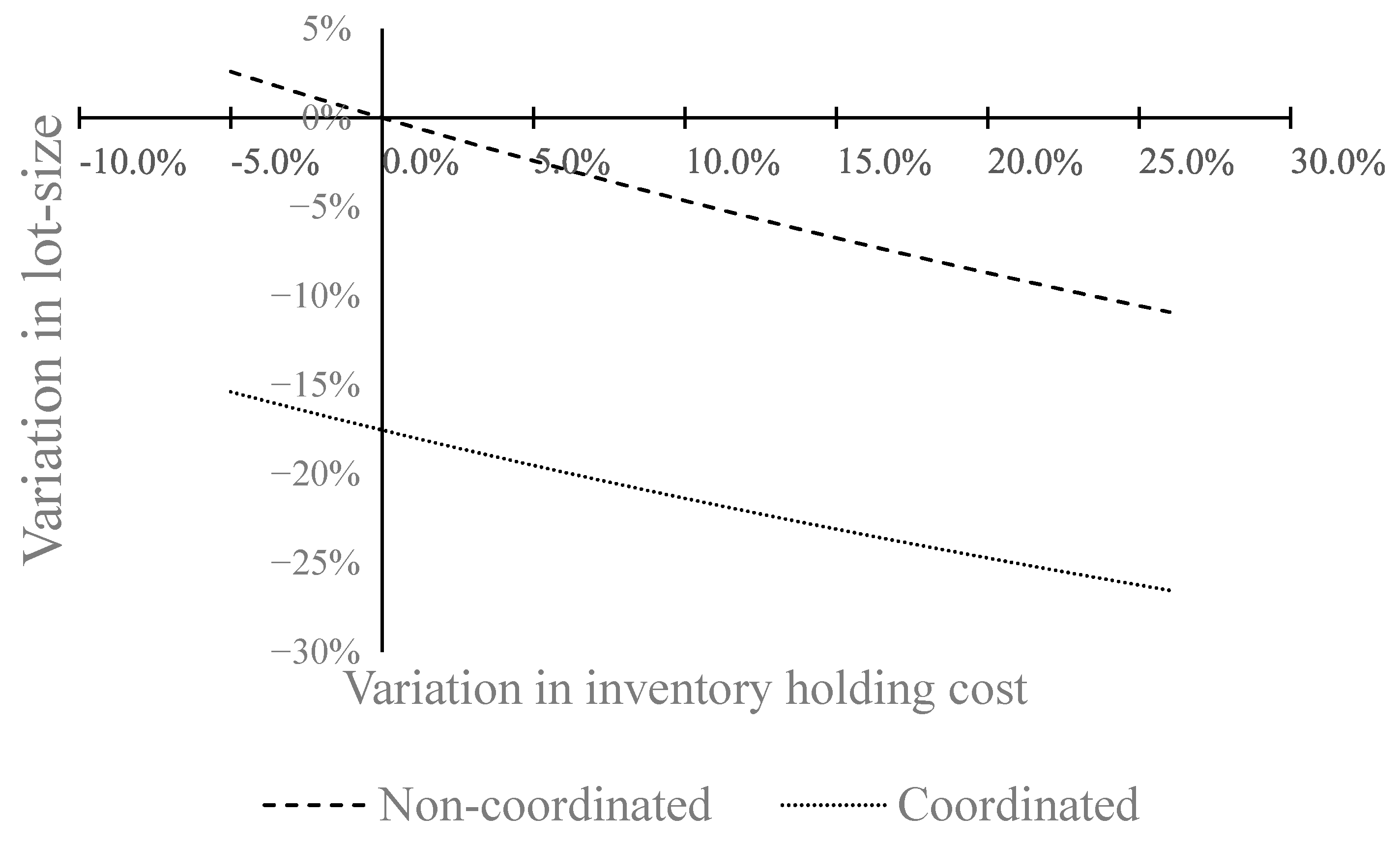
5. Numerical Example and Discussions
| Demand rate (units/year) | D | 1000 |
| Production rate (units/year) | P | 3200 |
| Buyer’s order cost ($/order) | Kb | 25 |
| Vendor’s setup cost ($/batch) | Kv | 400 |
| Mean holding cost for the vendor ($ /unit/ unit of time) | hv | 4.00 |
| Mean holding cost for the buyer ($ /unit/ unit of time) | hb | 5.00 |
| Variation in inventory holding cost (%) | +25%/−0.5% |
6. Conclusions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Aljazzar, Salem M., and Amulya Gurtu. 2019. Observations on ‘a joint economic-lot-size model for purchaser and vendor’. International Journal of Inventory Research 5: 169–87. [Google Scholar] [CrossRef]
- Aljazzar, Salem M., Amulya Gurtu, and Mohamad Y. Jaber. 2018. Delay-in-payments—A strategy to reduce carbon emissions from supply chains. Journal of Cleaner Production 170: 636–44. [Google Scholar] [CrossRef]
- Arslan, M. Can, and Metin Turkay. 2013. EOQ Revisited with Sustainability Considerations. Foundations of Computing and Decision Sciences 38: 223–49. [Google Scholar] [CrossRef]
- Bahl, Harish C. 1982. A Noniterative Multiproduct Multiperiod Production Planning Method. Operations Research Letters 1: 219–21. [Google Scholar] [CrossRef]
- Balintfy, Joseph L. 1964. On a Basic Class of Multi-Item Inventory Problems. Management Science 10: 287–97. [Google Scholar] [CrossRef]
- Banerjee, Avijit. 1986. A Joint Economic-Lot-Size Model for Purchaser and Vendor. Decision Sciences 17: 292–311. [Google Scholar] [CrossRef]
- Battini, Daria, Alessandro Persona, and Fabio Sgarbossa. 2014. A sustainable EOQ model: Theoretical formulation and applications. International Journal of Production Economics 149: 145–53. [Google Scholar] [CrossRef]
- Braglia, Marcello, and Lucio Zavanella. 2010. Modelling an industrial strategy for inventory management in supply chains: The ‘Consignment Stock’ case. International Journal of Production Research 41: 3793–808. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, Leopoldo Eduardo, Kun-Jen Chung, and Gerardo Treviño-Garza. 2014. Celebrating a century of the economic order quantity model. International Journal of Production Economics 155: 1–7. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, Leopoldo Eduardo, Ali Akbar Shaikh, Sunil Tiwari, and Gerardo Treviño-Garza. 2020. An EOQ inventory model with nonlinear stock dependent holding cost, nonlinear stock dependent demand and trade credit. Computers & Industrial Engineering 139: 105557. [Google Scholar] [CrossRef]
- Chen, Wen, Qi Feng, and Sridhar Seshadri. 2015. Inventory-Based Dynamic Pricing with Costly Price Adjustment. Production and Operations Management 24: 732–49. [Google Scholar] [CrossRef]
- Chen, Xi, Saif Benjaafar, and Adel Elomri. 2013. The carbon-constrained EOQ. Operations Research Letters 41: 172–79. [Google Scholar] [CrossRef]
- Choi, Sangjin, and S. T. Enns. 2004. Multi-product capacity-constrained lot sizing with economic objectives. International Journal of Production Economics 91: 47–62. [Google Scholar] [CrossRef]
- Container Alliance. 2020. Shipping Container Specifications. Available online: https://www.containeralliance.com/specifications.php (accessed on 27 March 2020).
- CSI Containers Services International. 2020. ISO Container Size and Type (ISO 6346)—CSI Container Services International. Available online: https://www.csiu.co/resources-and-links/iso-container-size-and-type-iso-6346 (accessed on 27 January 2021).
- Dhandapani, J., and R. Uthayakumar. 2016. Multi-item EOQ model for fresh fruits with preservation technology investment, time-varying holding cost, variable deterioration and shortages. Journal of Control and Decision 4: 1–11. [Google Scholar] [CrossRef]
- Dobson, Gregory, Edieal J. Pinker, and Ozlem Yildiz. 2017. An EOQ model for perishable goods with age-dependent demand rate. European Journal of Operational Research 257: 84–88. [Google Scholar] [CrossRef]
- Eilon, Samuel. 1959. Economic Batch-Size Determination for Multi-Product Scheduling. Journal of the Operational Research Society 10: 217–27. [Google Scholar] [CrossRef]
- Ghasemkhani, A., R. Tavakkoli-Moghaddam, S. Shahnejat-Bushehri, S. Momen, and H. Tavakkoli-Moghaddam. 2019. An integrated production inventory routing problem for multi perishable products with fuzzy demands and time windows. IFAC-PapersOnLine 52: 523–28. [Google Scholar] [CrossRef]
- Goodarzian, Fariba, Hasan Hosseini-Nasab, Jesús Muñuzuri, and Mohammad-Bagher Fakhrzad. 2020. A multi-objective pharmaceutical supply chain network based on a robust fuzzy model: A comparison of meta-heuristics. Applied Soft Computing 92: 106331. [Google Scholar] [CrossRef]
- Goyal, S. K. 1977. An Integrated Inventory Model for a Single Product System. Operational Research Quarterly 28: 539–45. [Google Scholar] [CrossRef]
- Goyal, S. K. 1988. “A Joint Economic-Lot-Size Model for Purchaser and Vendor”: A Comment. Decision Sciences 19: 236–41. [Google Scholar] [CrossRef]
- Gurtu, Amulya, Mohamad Y. Jaber, and Cory Searcy. 2015a. Impact of fuel price and emissions on inventory policies. Applied Mathematical Modelling 39: 1202–16. [Google Scholar] [CrossRef]
- Gurtu, Amulya, Cory Searcy, and Mohamad Y. Jaber. 2015b. An analysis of keywords used in the literature on green supply chain management. Management Research Review 38: 166–94. [Google Scholar] [CrossRef]
- Gurtu, Amulya, Cory Searcy, and Mohamad Y. Jaber. 2017. Emissions from international transport in global supply chains. Management Research Review 40: 53–74. [Google Scholar] [CrossRef]
- Gurtu, Amulya, Cory Searcy, and Mohamad Y. Jaber. 2019. Transportation and Sustainable Supply Chain. In Handbook on the Sustainable Supply Chain. Edited by Joseph Sarkis. Northampton: Edward Elgar, pp. 410–28. [Google Scholar]
- Harris, Ford W. 1913. How Many Parts to Make at Once. Factory, The Magazine of Management 10: 135–136, 152. [Google Scholar] [CrossRef]
- Heinen, J. Jakob, and Kai Hoberg. 2019. Assessing the potential of additive manufacturing for the provision of spare parts. Journal of Operations Management 65: 810–26. [Google Scholar] [CrossRef]
- Jaber, Mohamad Y., and Saeed Zolfaghari. 2008. Quantitative Models for Centralized Supply Chain Coordination. In Supply Chain Theory and Applications. Edited by Vedran Kordic. Rejeka: InTech, pp. 307–38. [Google Scholar]
- Jaber, Mohamad Y., Simone Zanoni, and Lucio E. Zavanella. 2013. An entropic economic order quantity (EnEOQ) for items with imperfect quality. Applied Mathematical Modelling 37: 3982–92. [Google Scholar] [CrossRef]
- Khalilpourazari, Soheyl, and Seyed Hamid Reza Pasandideh. 2016. Multi-item EOQ model with nonlinear unit holding cost and partial backordering: moth-flame optimization algorithm. Journal of Industrial and Production Engineering 34: 42–51. [Google Scholar] [CrossRef]
- Khan, Mehmood, Mohamad Y. Jaber, and Abdul-Rahim Ahmad. 2014. An integrated supply chain model with errors in quality inspection and learning in production. Omega 42: 16–24. [Google Scholar] [CrossRef]
- Nagpal, Gaurav, and Udayan Chanda. 2021. Economic order quantity model for two generation consecutive technology products under permissible delay in payments. International Journal of Procurement Management 14: 93–125. [Google Scholar] [CrossRef]
- Pasandideh, Seyed Hamid Reza, Seyed Taghi Akhavan Niaki, and Behzad Maleki Vishkaei. 2014. A multiproduct EOQ model with inflation, discount, and permissible delay in payments under shortage and limited warehouse space. Production & Manufacturing Research 2: 641–57. [Google Scholar] [CrossRef]
- Perera, Sandun, Ganesh Janakiraman, and Shun-Chen Niu. 2017. Optimality of (s, S) policies in EOQ models with general cost structures. International Journal of Production Economics 187: 216–28. [Google Scholar] [CrossRef]
- Rajput, Neelanjana, R. K. Pandey, A. P. Singh, and Anand Chauhan. 2019. An optimization of fuzzy EOQ model in healthcare industries with three different demand pattern using signed distance technique. Mathematics in Engineering, Science and Aerospace 10: 205–18. [Google Scholar]
- Rastogi, Mohit, S. Singh, Prashant Kushwah, and Shilpy Tayal. 2017. An EOQ model with variable holding cost and partial backlogging under credit limit policy and cash discount. Uncertain Supply Chain Management 5: 27–42. [Google Scholar] [CrossRef]
- Santhi, G., and K. Karthikeyan. 2018. EOQ Pharmaceutical Inventory Model for Perishable Products with Pre and Post Discounted Selling Price and Time Dependent Cubic Demand. Research Journal of Pharmacy and Technology 11. [Google Scholar] [CrossRef]
- Sundara Rajan, R., and R. Uthayakumar. 2017. Analysis and optimization of an EOQ inventory model with promotional efforts and back ordering under delay in payments. Journal of Management Analytics 4: 159–81. [Google Scholar] [CrossRef]
- Tantiwattanakul, Phattarasaya, and Aussadavut Dumrongsiri. 2019. Supply chain coordination using wholesale prices with multiple products, multiple periods, and multiple retailers: Bi-level optimization approach. Computers & Industrial Engineering 131: 391–407. [Google Scholar] [CrossRef]
- Wahab, M. I. M., S. M. H. Mamun, and P. Ongkunaruk. 2011. EOQ models for a coordinated two-level international supply chain considering imperfect items and environmental impact. International Journal of Production Economics 134: 151–8. [Google Scholar] [CrossRef]
- Waters, Donald. 2003. Inventory Control and Management, 2nd ed. West Sussex: Wiley. [Google Scholar]
- Zahran, Siraj K., Mohamad Y. Jaber, Simone Zanoni, and Lucio E. Zavanella. 2015. Payment schemes for a two-level consignment stock supply chain system. Computers & Industrial Engineering 87: 491–505. [Google Scholar] [CrossRef]
- Zhang, Jiawei. 2009. Cost Allocation for Joint Replenishment Models. Operations Research 57: 146–56. [Google Scholar] [CrossRef]
- Zissis, Dimitris, George Ioannou, and Apostolos Burnetas. 2019. Coordinating Lot Sizing Decisions Under Bilateral Information Asymmetry. Production and Operations Management 29: 371–87. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurtu, A. Optimization of Inventory Holding Cost Due to Price, Weight, and Volume of Items . J. Risk Financial Manag. 2021, 14, 65. https://doi.org/10.3390/jrfm14020065
Gurtu A. Optimization of Inventory Holding Cost Due to Price, Weight, and Volume of Items . Journal of Risk and Financial Management. 2021; 14(2):65. https://doi.org/10.3390/jrfm14020065
Chicago/Turabian StyleGurtu, Amulya. 2021. "Optimization of Inventory Holding Cost Due to Price, Weight, and Volume of Items " Journal of Risk and Financial Management 14, no. 2: 65. https://doi.org/10.3390/jrfm14020065
APA StyleGurtu, A. (2021). Optimization of Inventory Holding Cost Due to Price, Weight, and Volume of Items . Journal of Risk and Financial Management, 14(2), 65. https://doi.org/10.3390/jrfm14020065





