A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment
Abstract
1. Introduction
- More flexible selection of the risk-aversion coefficient. In Ji et al. (2019), they assume that the risk-aversion coefficient is selected from a finite and ordered set that is pre-determined by the investor. The selection of the risk-aversion coefficient is limited within this prescribed set and is only allowed to change according to its adjacent values. In this study, we modify the objective function of the mean-risk optimization model into a normalized version, so that the predicted probability of market movement from the machine learning models can be directly incorporated as an input of the risk-aversion coefficient, which alleviates the complication of specifying a prescribed set.
- More technical indicators are used to train the machine learning models.Ji et al. (2019) employ 9 different technical indicators to feed the machine learning classification models, while we will consider an extensive set of 14 technical indicators with a total of 37 features or predictors generated by the different parametric settings of those indicators.
- More comprehensive empirical tests are conducted to derive numerical insights. Using the rolling-horizon approach, Ji et al. (2019) conduct numerical tests with a horizon of 156 periods (3 years), with 104 periods in each rolling-window for in-sample training and portfolio optimization, and 52 periods (1 year) for out-of-sample performance evaluation. In this study, we carry out the empirical tests with a longer horizon of 1252 periods (24 years from 1995 to 2018), with 260 periods (5 years) in each rolling-window and 992 periods (19 years) for the out-of-sample performance evaluations.
2. Preliminaries
2.1. Gini’s Mean Difference and Mean-Gini Model
2.2. Technical Indicators
2.3. Machine Learning Classification Models
2.3.1. Logistic Regression
2.3.2. Extreme Gradient Boosting (XGBoost)
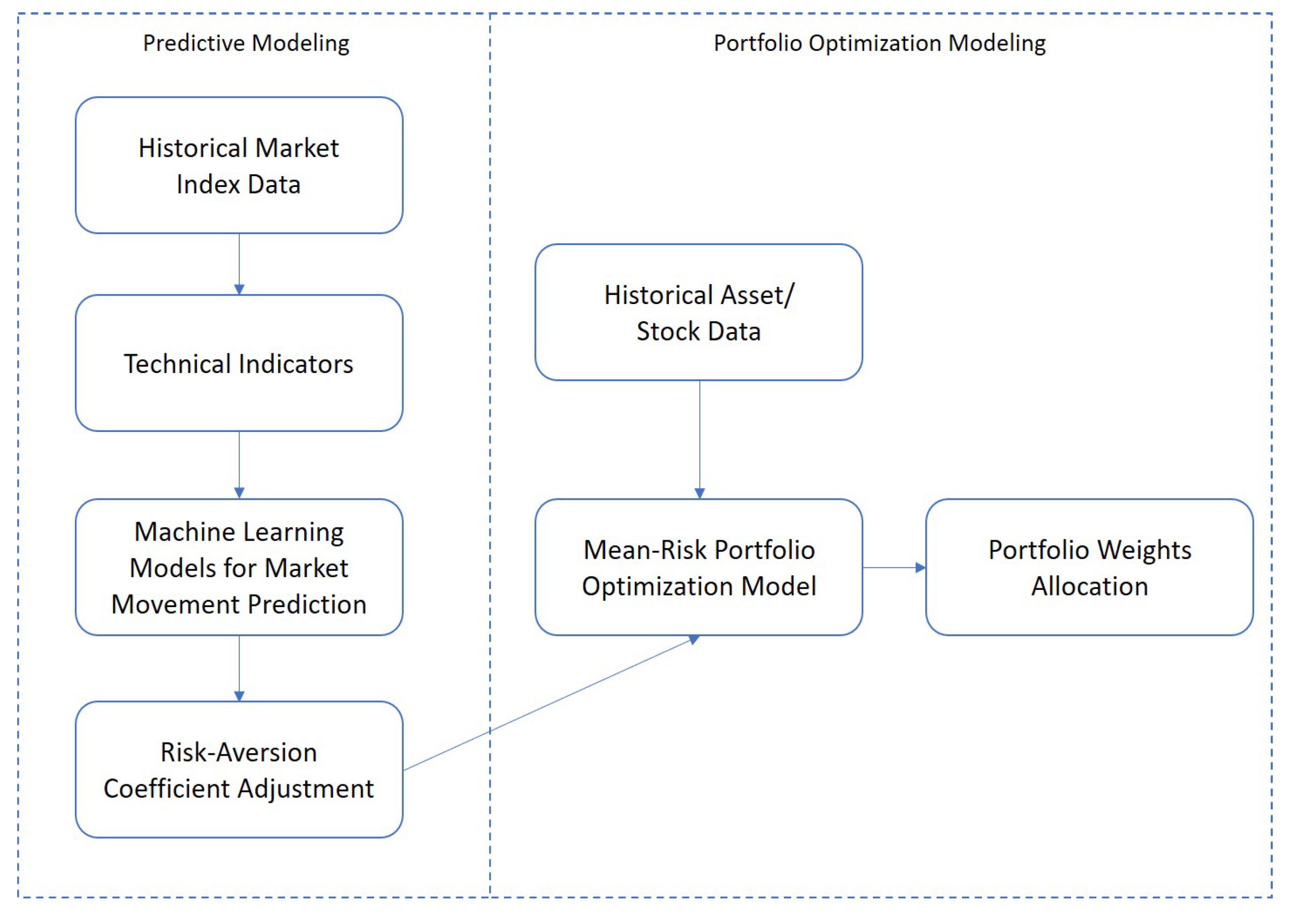
3. Machine Learning Integrated Portfolio Rebalance Framework
- A specific market is selected (e.g., S&P 500), historical information of the market index and a set of assets that belong to that market are collected. A window of periods are used as in-sample periods to build the machine learning models in a cross-validation manner and to construct the NMG portfolios. In our tests, is selected to be 260 that covers weekly returns over 5 years.
- Within the in-sample periods up to time period t, the 14 technical indicators (i.e., SMA, WMA, EMA, MACD, RSI, ADX, CCI, SMI, EMV, MFI, CMF, VWAP, BBands and SAR) are computed from the index value and are fed to the two machine learning models (i.e., LR, XGBoost) to obtain the market movement with predicted probabilities . The tuning parameters of machine learning models are selected via cross-validation. Using the new or updated risk-aversion coefficient, we solve the NMG model to obtain portfolio weights within the training window.
- We carry out the rolling horizon procedure each time by adding the data of the next week (period) in the out-of-sample periods and dropping the data of the earliest week from the in-sample periods. The technical indicators, machine learning models results, and portfolio optimization models are updated on a weekly basis.
- We repeat this procedure until the end of the selected dataset, which generates portfolios. The weight of asset i in time period t is denoted by , for . Holding the portfolio weights for one week gives the out-of-sample return at time , where denotes the return of asset i in out-of-sample period . We then evaluate the out-of-sample portfolio performance and compare them to other benchmarks.
4. Computational Tests
4.1. Data and Experimental Design
4.2. Performance Metrics
- The out-of-sample average weekly return:
- The out-of-sample standard deviation:
- The out-of-sample Gini’s Mean Difference (GMD):
- The out-of-sample Sharpe ratio:
- The out-of-sample cumulative return:
- The out-of-sample annualized return:
4.3. Computational Results and Insights
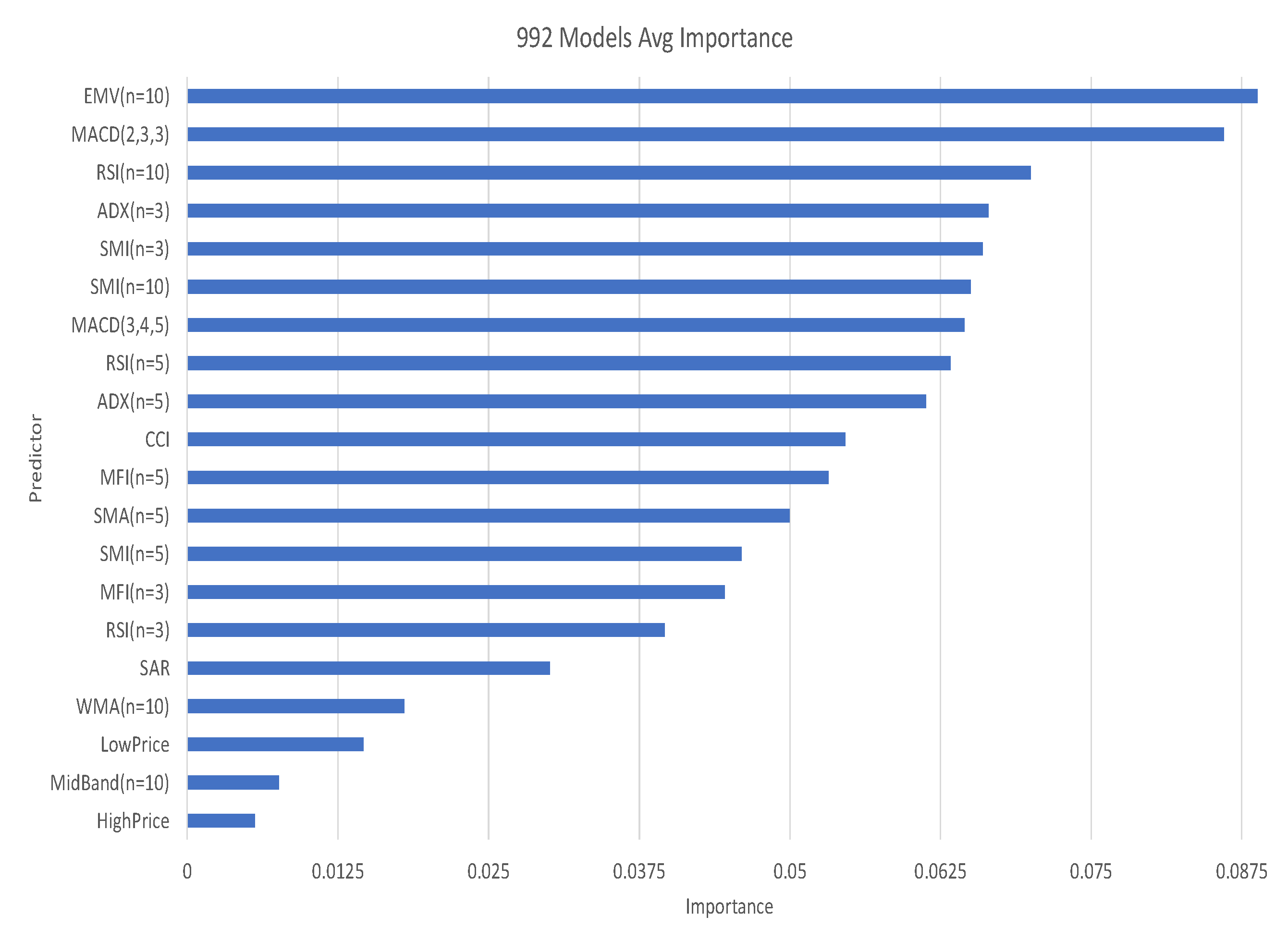
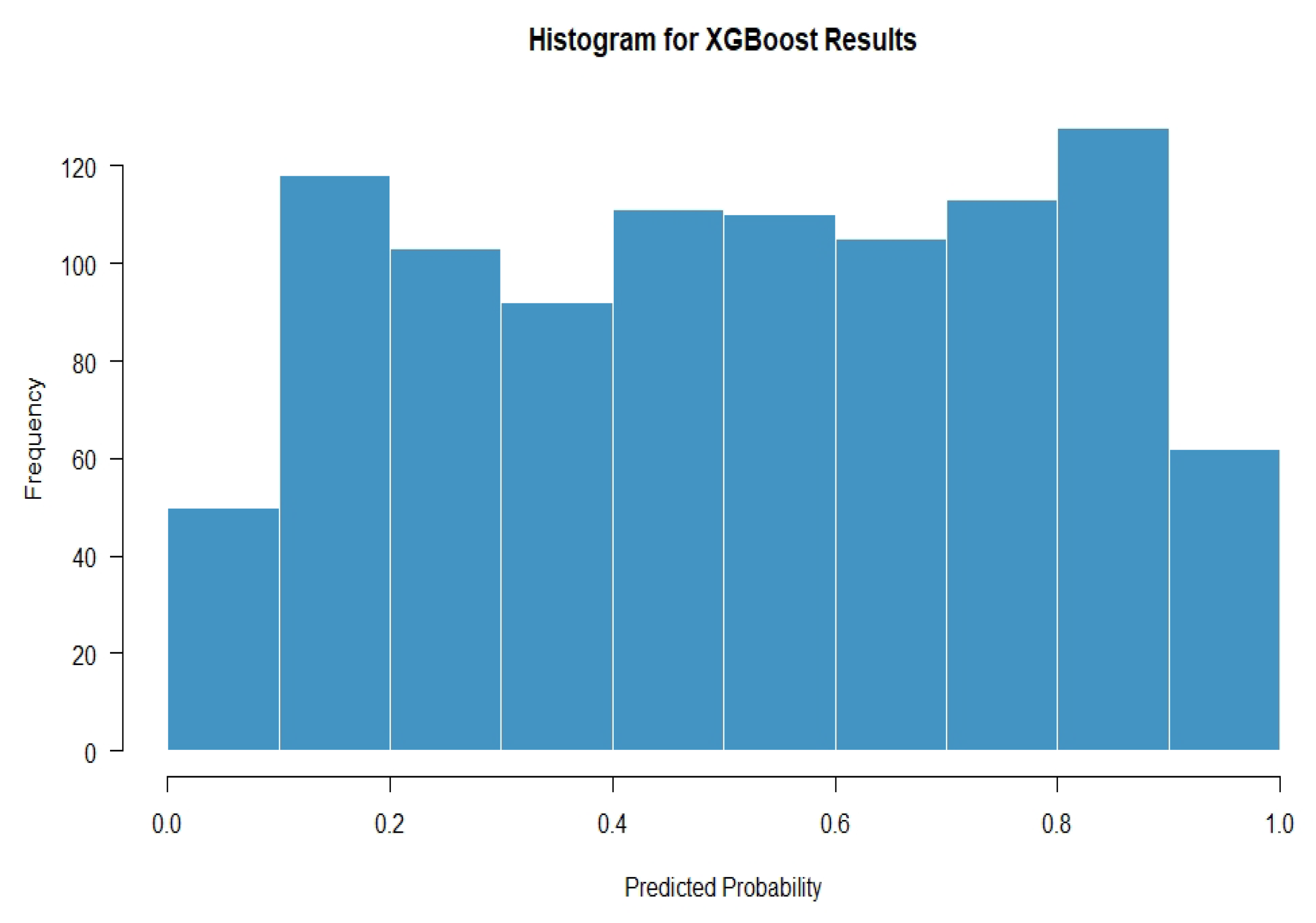
4.3.1. Results of Machine Learning Models
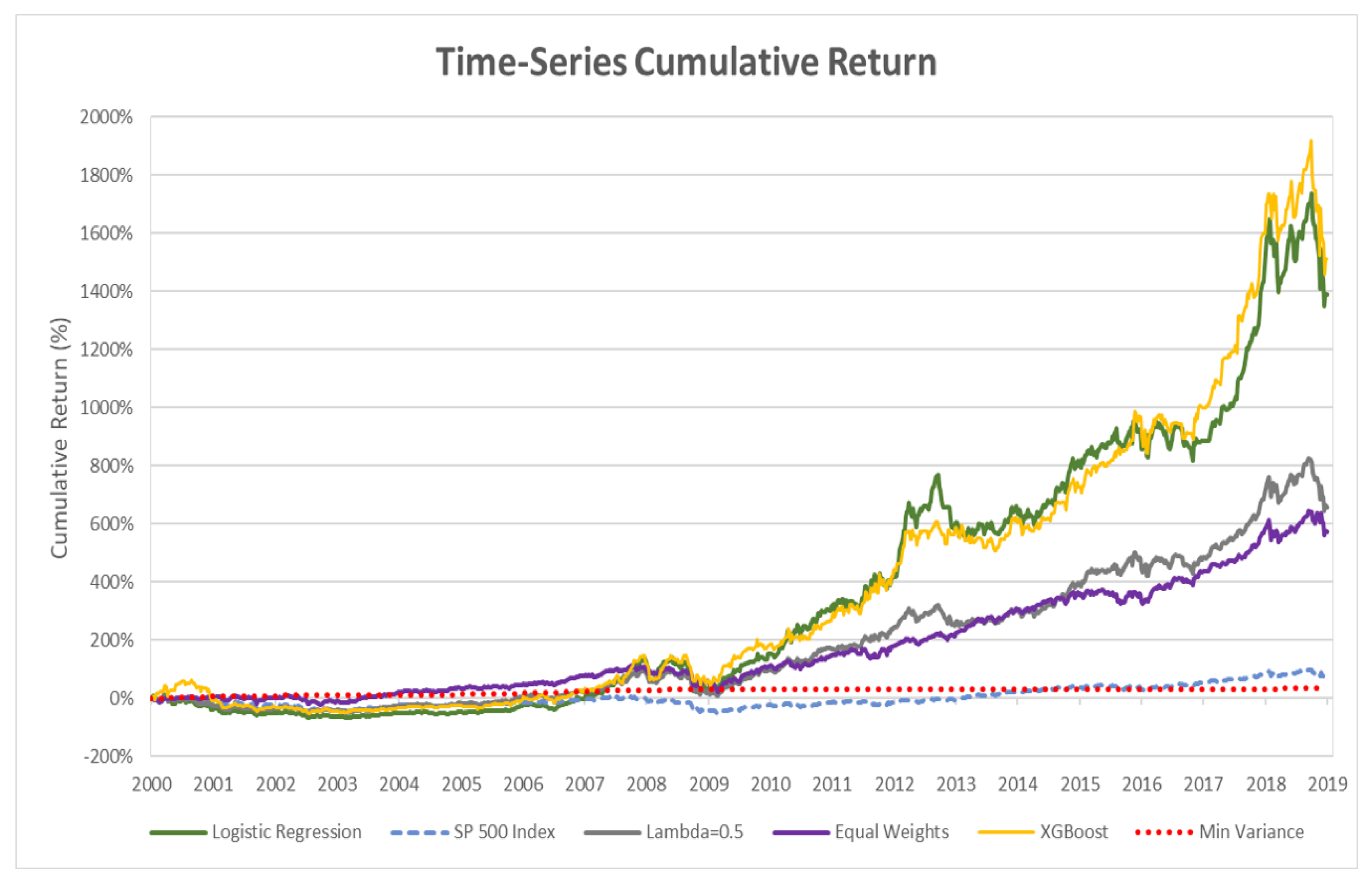
4.3.2. Evaluation of Portfolio Out-of-Sample Performance
5. Summary and Future Studies
Author Contributions
Funding
Conflicts of Interest
Appendix A. Description of Technical Indicators
- Simple Moving Average (SMA): SMA is defined as a simple linear (equally-weighted) rolling mean of the closing prices of an asset in the past n periods. We let the prices be denoted by .
- Weighted Moving Average (WMA): WMA is an adapted version of SMA, where the weight assigned to each period is not identical, but decreases in an arithmetical progression. In an n-period WMA calculation, the latest period has weight n, followed by the second latest period’s weight , until down to one.
- Exponential Moving Average (EMA): Compared to the linear decreasing of weight in WMA, EMA is computed with the weighting for each older datum decreasing exponentially in an iterative procedure.
- Moving Average Convergence/Divergence (MACD): MACD is a classical trend-following momentum indicator of the exponential moving average (EMA) of a stock or index that is used to identify short-term momentum. More specifically, MACD is calculated by subtracting the long-term EMA from the short-term EMA to obtain an intermediate trend line. An EMA is then plotted over the intermediate line to identify the buy or sell signal of the asset or the index. When the resulting MACD falls below the signal line, it is a bearish signal, which indicates that it may be time to sell. Conversely, when the MACD rises above the signal line, the indicator gives a bullish signal, which suggests that the price of the asset is likely to experience upward momentum.
- Relative Strength Index (RSI): RSI shows the strength or speed of the asset price by means of the comparison of the individual upward or downward movements of the consecutive closing prices. It is computed as the ratio of recent upward price movements to the absolute price movements. For each time period, an upward movement U (i.e., if ) or a downward movement D (i.e., if ) is characterized depending on the relative difference between the current price and the previous price .
- Average Directional Movement Index (ADX): The ADX is a combination of the positive directional indicator (denoted by ) and the negative directional indicator (denoted by ) with a smoothed moving average. The positive/negative directional movement ( and ) is calculated in a similar way as the upward/downward movement shown in RSI.
- Commodity Channel Index (CCI): CCI measures the current price level relative to an average price level over a given period of time to identify a new trend or warning of extreme conditions. The CCI is calculated as the difference between the typical price of a commodity and its simple moving average, divided by the mean absolute deviation of the typical price. The index is usually scaled by an inverse factor of 0.015 to provide more readable numbers:
- Stochastic Momentum Index (SMI): The SMI calculates where the close is relative to the midpoint of the high/low range. The values of the SMI range from +100 to −100. When the close is greater than the midpoint, the SMI is above zero, and when the close is less than the midpoint, the SMI is below zero. Extreme high/low SMI values indicate overbought/oversold conditions. A buy signal is generated when the SMI rises above −50, or when it crosses above the signal line. A sell signal is generated when the SMI falls below +50, or when it crosses below the signal line. Also look for divergence with the price to signal the end of a trend or indicate a false trend.
- Ease of Movement (EMV): The EMV describes the relationship between the price change and volume. To calculate EMV, we need to calculate midpoint move firstly. The midpoint move is computed by today’s high and low price, and yesterday’s high and low price. Then the box ratio is generated by volume, high and low price. The EMV is the ratio between the midpoint move and the box ratio. High EMV indicates when price goes up with small volume.
- Money Flow Index (MFI): The MFI measures the selling and buying pressure based on both volume and price. We can use MFI to identify the level of overbought or oversold which can present a warning of unsustainable price extremes.
- Chaikin Money Flow (CMF): The CMF quantifies the amount of Money Flow Volume during a given time period. CMF is an oscillator which is between −1 and +1. The CMF quantifies the buying and selling pressure on a given time period. When CMF moves into positive (resp. negative) territory, it indicates a buying (resp. selling) pressure. Therefore, an uptrend (resp. downtrend) is revealed by positive (resp. negative) CMF.
- Volume-weighted Average Price (VWAP): The volume-weighted average price is also known as volume weighted moving average (VWMA) which weights the price of each stocks by the volume. Therefore, when stocks are at a higher volume, they will be more weighted during the computation.
- Bollinger Bands (BBands): BBands have a Mid Band with two outer bands: Upper and Lower Band. The Mid Band is a simple moving average of the typical high, low and close price. BBands is designed to locate situations when the price goes too high or too low. If the price is higher than the Upper Band, it means the price is too high. Otherwise, when the price is lower than the Lower Band, it means the price is too low.
- Parabolic Stop-and-Reverse (SAR): The parabolic SAR indicator is used by traders to determine trend direction and potential reversals in price. The indicator uses a trailing stop and reverse method called “SAR” or stop and reverse to identify suitable exit and entry points. A dot below the price means the price is moving up, and a dot above the price bar means the price is moving down overall.
| Technical Indicators | Equation |
|---|---|
| SMA | |
| WMA | |
| EMA | , |
| MACD | |
| RSI | , U & D: upward and downward movements |
| ADX | , : positive directional movement |
| , : negative directional movement | |
| CCI | , : mean absolute deviation |
| SMI | |
| , : number of periods for initial smoothing | |
| , : number of periods for double smoothing | |
| EMV | |
| MFI | |
| CMF | |
| VWAP | |
| BBands | |
| , : standard deviation of P | |
| SAR | , : Acceleration Factor |
| , : Extreme Points |
References
- Ahmadi-Javid, Amir. 2012. Entropic value-at-risk: A new coherent risk measure. Journal of Optimization Theory and Applications 155: 1105–23. [Google Scholar] [CrossRef]
- Ahn, Dong-Hyun, Jennifer Conrad, and Robert Dittmar. 2003. Risk adjustment and trading strategies. Review of Financial Studies 16: 459–85. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. 2004. International Convergence of Capital Measurement and Capital Standards: A Revised Framework. Basel: BIS. [Google Scholar]
- Brock, William, Josef Lakonishok, and Blake LeBaron. 1992. Simple technical trading rules and the stochastic properties of stock returns. The Journal of Finance 47: 1731–64. [Google Scholar] [CrossRef]
- Cervelló-Royo, Roberto, and Francisco Guijarro. 2020. Forecasting stock market trend: A comparison of machine learning algorithms. Finance, Markets and Valuation 6: 37–49. [Google Scholar]
- Chen, Jiah-Shing, Chia-Lan Chang, Jia-Li Hou, and Yao-Tang Lin. 2008. Dynamic proportion portfolio insurance using genetic programming with principal component analysis. Expert Systems with Applications 35: 273–78. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining. New York: ACM, pp. 785–94. [Google Scholar]
- Chen, Yan, Shingo Mabu, and Kotaro Hirasawa. 2010. A model of portfolio optimization using time adapting genetic network programming. Computers & Operations Research 37: 1697–707. [Google Scholar]
- Colby, Robert W. 2002. The Encyclopedia of Technical Market Indicators. New York: McGraw-Hill. [Google Scholar]
- Conrad, Jennifer, and Gautam Kaul. 1998. An anatomy of trading strategies. Review of Financial Studies 11: 489–519. [Google Scholar] [CrossRef]
- Covel, Michael. 2004. Trend Following: How Great Traders Make Millions in Up or Down Markets. Upper Saddle River: FT Press. [Google Scholar]
- Covel, Michael. 2009. Trend Following: Learn to Make Millions in Up Or Down Markets. Upper Saddle River: FT Press. [Google Scholar]
- DeMiguel, Victor, Lorenzo Garlappi, Francisco Nogales, and Raman Uppal. 2009. A generalized approach to portfolio optimization: Improving performance by constraining portfolio norms. Management Science 55: 798–812. [Google Scholar] [CrossRef]
- Disatnik, David, and Simon Benninga. 2007. Shrinking the covariance matrix. The Journal of Portfolio Management 33: 55–63. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Jun Pan. 1997. An overview of value at risk. The Journal of Derivatives 4: 7–49. [Google Scholar] [CrossRef]
- Fabozzi, Frank, Dashan Huang, and Guofu Zhou. 2010. Robust portfolios: Contributions from operations research and finance. Annals of Operations Research 176: 191–220. [Google Scholar] [CrossRef]
- Fama, Eugene, and Marshall Blume. 1966. Filter rules and stock-market trading. Journal of Business 39: 226–41. [Google Scholar] [CrossRef]
- Freitas, Fabio, Alberto De Souza, and Ailson de Almeida. 2009. Prediction-based portfolio optimization model using neural networks. Neurocomputing 72: 2155–70. [Google Scholar] [CrossRef]
- Gaivoronski, Alexei, and Georg Pflug. 2004. Value-at-Risk in portfolio optimization: Properties and computational approach. The Journal of Risk 7: 1–31. [Google Scholar] [CrossRef]
- García, Fernando, Francisco Guijarro, and Javier Oliver. 2018a. Index tracking optimization with cardinality constraint: A performance comparison of genetic algorithms and tabu search heuristics. Neural Computing and Applications 30: 2625–41. [Google Scholar] [CrossRef]
- García, Fernando, Francisco Guijarro, Javier Oliver, and Rima Tamošiūnienė. 2018b. Hybrid fuzzy neural network to predict price direction in the German DAX-30 index. Technological and Economic Development of Economy 24: 2161–78. [Google Scholar] [CrossRef]
- Geweke, John, and Gianni Amisano. 2010. Comparing and evaluating bayesian predictive distributions of asset returns. International Journal of Forecasting 26: 216–30. [Google Scholar] [CrossRef]
- Gorgulho, António, Rui Neves, and Nuno Horta. 2011. Applying a GA kernel on optimizing technical analysis rules for stock picking and portfolio composition. Expert systems with Applications 38: 14072–85. [Google Scholar] [CrossRef]
- Guijarro, Francisco, and Prodromos Tsinaslanidis. 2019. A surrogate similarity measure for the mean-variance frontier optimisation problem under bound and cardinality constraints. Journal of the Operational Research Society, 1–16. [Google Scholar] [CrossRef]
- Hu, Hongping, Li Tang, Shuhua Zhang, and Haiyan Wang. 2018. Predicting the direction of stock markets using optimized neural networks with google trends. Neurocomputing 285: 188–95. [Google Scholar] [CrossRef]
- Ji, Ran, Miguel Lejeune, and Srinivas Prasad. 2017a. Dynamic portfolio optimization with risk-aversion adjustment utilizing technical indicators. Paper presented at the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, July 10–13; Piscataway: IEEE, pp. 1787–94. [Google Scholar]
- Ji, Ran, Miguel Lejeune, and Srinivas Prasad. 2017b. Properties, formulations, and algorithms for portfolio optimization using mean-gini criteria. Annals of Operations Research 248: 305–43. [Google Scholar] [CrossRef]
- Ji, Ran, Miguel Lejeune, and Srinivas Prasad. 2018. Interactive portfolio optimization using Mean-Gini criteria. In Financial Decision Aid Using Multiple Criteria. Berlin and Heidelberg: Springer, pp. 49–91. [Google Scholar]
- Ji, Ran, K. C. Chang, and Zhenlong Jiang. 2019. Risk-aversion adjusted portfolio optimization with predictive modeling. Paper presented at the 2019 22th International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, July 2–5; Piscataway: IEEE, pp. 1–8. [Google Scholar]
- Ko, Po-Chang, and Ping-Chen Lin. 2008. Resource allocation neural network in portfolio selection. Expert Systems with Applications 35: 330–37. [Google Scholar] [CrossRef]
- Konno, Hiroshi, and Hiroaki Yamazaki. 1991. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Management Science 37: 519–31. [Google Scholar] [CrossRef]
- Kwon, Ki-Yeol, and Richard Kish. 2002. Technical trading strategies and return predictability: NYSE. Applied Financial Economics 12: 639–53. [Google Scholar] [CrossRef]
- Lo, Andrew, Harry Mamaysky, and Jiang Wang. 2000. Foundations of technical analysis: Computational algorithms, statistical inference, and empirical implementation. The Journal of Finance 55: 1705–70. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. Journal of Finance 7: 77–91. [Google Scholar]
- Markowitz, Harry. 1959. Portfolio Selection: Efficient Diversification of Investments. New York: Wiley. [Google Scholar]
- Markowitz, Harry, Peter Todd, Ganlin Xu, and Yuji Yamane. 1993. Computation of mean-semivariance efficient sets by the critical line algorithm. Annals of Operations Research 45: 307–17. [Google Scholar] [CrossRef]
- Ni, Li-Ping, Zhi-Wei Ni, and Ya-Zhuo Gao. 2011. Stock trend prediction based on fractal feature selection and support vector machine. Expert Systems with Applications 38: 5569–76. [Google Scholar] [CrossRef]
- Ogryczak, Włodzimierz, and Andrzej Ruszczyński. 1999. From stochastic dominance to mean-risk models: Semi-deviations as risk measures. European Journal of Operational Research 116: 33–50. [Google Scholar] [CrossRef]
- Ogryczak, Włodzimierz, and Andrzej Ruszczyński. 2001. On consistency of stochastic dominance and mean-semideviations models. Mathematical Programming 89: 217–32. [Google Scholar] [CrossRef]
- Ringuest, Jeffrey, Samuel Graves, and Randy Case. 2004. Mean-Gini analysis in R&D portfolio selection. European Journal of Operational Research 154: 157–69. [Google Scholar]
- Rockafellar, Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional Value-at-Risk. Journal of Risk 2: 21–42. [Google Scholar] [CrossRef]
- Schwager, Jack. 1993. Market Wizards: Interviews with Top Traders. New York: Collins. [Google Scholar]
- Schwager, Jack. 1995. The New Market Wizards: Conversations with America’s Top Traders. New York: Wiley. [Google Scholar]
- Sehgal, Ruchika, and Aparna Mehra. 2017. Worst-case analysis of Gini mean difference safety measure. Journal of Industrial & Management Optimization, 13. [Google Scholar] [CrossRef]
- Shalit, Haim, and Doron Greenberg. 2013. Hedging with stock index options: A Mean-Extended Gini approach. Journal of Mathematical Finance 3: 119–29. [Google Scholar] [CrossRef]
- Shalit, Haim, and Shlomo Yitzhaki. 1984. Mean-Gini, portfolio theory, and the pricing of risky assets. The Journal of Finance 39: 1449–68. [Google Scholar] [CrossRef]
- Thawornwong, Suraphan, and David Enke. 2004. Forecasting stock returns with artificial neural networks. In Neural Networks in Business Forecasting. Hershey: IGI Global, pp. 47–79. [Google Scholar]
- Urbán, Andrásand Mihály Ormos. 2012. Performance analysis of equally weighted portfolios: USA and Hungary. Acta Polytechnica Hungarica 9: 155–68. [Google Scholar]
- Yitzhaki, Shlomo. 1982. Stochastic dominance, mean variance and Gini’s mean difference. American Economic Review 72: 178–85. [Google Scholar]
- Yitzhaki, Shlomo. 1983. On an extension of the Gini inequality index. International Economic Review 24: 617–28. [Google Scholar] [CrossRef]
- Zhou, Xiaocong, Jouchi Nakajima, and Mike West. 2014. Bayesian forecasting and portfolio decisions using dynamic dependent sparse factor models. International Journal of Forecasting 30: 963–80. [Google Scholar] [CrossRef]
- Zhu, Shushang, Duan Li, and Shouyang Wang. 2009. Robust portfolio selection under downside risk measures. Quantitative Finance 9: 869–85. [Google Scholar] [CrossRef]
| Indicators Name | Parameter Value |
|---|---|
| SMA[3] | Number of periods to average over: 3,5,10 |
| WMA[3] | Number of periods to average over: 3,5,10 |
| EMA[3] | Number of periods to average over: 3,5,10 |
| MACD[2] | Number of periods for fast moving average, |
| Number of periods for slow moving average, | |
| Number of periods for signal moving average, | |
| (2, 3, 3), (3, 4, 5) | |
| SMI[3] | Number of periods to use, |
| Number of periods for initial smoothing, | |
| Number of periods for double smoothing, | |
| (3, 3, 3), (5, 5, 5), (10, 10, 10) | |
| ADX[3] | Number of periods to use for DX calculation: 3, 5, 10 |
| RSI[3] | Number of periods for moving averages: 3, 5, 10 |
| CCI | Number of periods for moving average: 20 |
| EMV[3] | Number of periods for moving average: 3, 5, 10 |
| BBands[3] | Number of periods for moving average: 3, 5, 10 |
| SAR | Acceleration factor: 0.02 |
| Maximum acceleration factor: 0.2 | |
| MFI[3] | Number of periods to use: 3, 5, 10 |
| CMF[3] | Number of periods to use: 3, 5, 10 |
| VWAP[3] | Number of periods to average over: 3,5,10 |
| S&P 500 Sectors | Ticker | Company Name |
|---|---|---|
| Communication Services | DIS | The Walt Disney Company |
| VZ | Verizon Communications Inc. | |
| Consumer Discretionary | HD | The Home Depot, Inc. |
| MCD | McDonald’s Corporation | |
| NKE | NIKE, Inc. | |
| Consumer Staples | KO | The Coca-Cola Company |
| PG | The Procter Gamble Company | |
| SYY | Sysco Corporation | |
| WMT | Walmart Inc. | |
| Energy | CVX | Chevron Corporation |
| XOM | Exxon Mobil Corporation | |
| Financials | AXP | American Express Company |
| JPM | JPMorgan Chase Co. | |
| Health Care | JNJ | Johnson Johnson |
| MRK | Merck Co., Inc. | |
| PFE | Pfizer Inc. | |
| WBA | Walgreens Boots Alliance, Inc. | |
| Industrials | BA | The Boeing Company |
| CAT | Caterpillar Inc. | |
| MMM | 3M Company | |
| UTX | Raytheon Technologies Corporation | |
| Information Technology | AAPL | Apple Inc. |
| CSCO | Cisco Systems, Inc. | |
| IBM | International Business Machines Corporation | |
| INTC | Intel Corporation | |
| - | IRX | 13-Week Treasury Bill |
| LR | XGBoost | Equal Weights | S&P 500 | MinVar | ||
|---|---|---|---|---|---|---|
| Average Return | 0.33% | 0.35% | 0.24% | 0.22% | 0.08% | 0.03% |
| Standard Deviation | 3.42% | 3.68% | 2.76% | 2.29% | 2.42% | 0.04% |
| GMD | 1.77% | 1.83% | 1.48% | 1.20% | 1.26% | 0.02% |
| Sharpe Ratio | 0.0970 | 0.0948 | 0.0878 | 0.0955 | 0.0335 | 0.8820 |
| Cumulative Return | 1390.65% | 1511.73% | 655.62% | 574.16% | 66.61% | 36.07% |
| Annualized Return | 15.28% | 15.76% | 11.23% | 10.57% | 2.72% | 1.63% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Ji, R.; Chang, K.-C. A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment. J. Risk Financial Manag. 2020, 13, 155. https://doi.org/10.3390/jrfm13070155
Jiang Z, Ji R, Chang K-C. A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment. Journal of Risk and Financial Management. 2020; 13(7):155. https://doi.org/10.3390/jrfm13070155
Chicago/Turabian StyleJiang, Zhenlong, Ran Ji, and Kuo-Chu Chang. 2020. "A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment" Journal of Risk and Financial Management 13, no. 7: 155. https://doi.org/10.3390/jrfm13070155
APA StyleJiang, Z., Ji, R., & Chang, K.-C. (2020). A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment. Journal of Risk and Financial Management, 13(7), 155. https://doi.org/10.3390/jrfm13070155





