3.1. The Chilean Stock Market Data Set
As an application of the methodology presented in this paper, monthly returns of shares from the Chilean Stock Market were analyzed. The data corresponded to the period from September, 2002 to March, 2020 and five companies: BSantander (one of the biggest banks in the country), ENEL (an electrical distribution company), Falabella (a retail company), LTM (an airline), and SQMB (a company from the chemical industry). The Selective Index of Share Prices (IPSA) was used as the return for the market and the 10-Years Bonds in UFs (BCU, BTU) of the Central Bank of Chile, was used as the risk-free rate, both monthly. This risk free rate is a long-rate, the trend of which is a smoother curve than that of a short-rate.
The means, standard deviations (SDs), Sharpe ratios (Sharpe), coefficients of skewness and kurtosis, and the Jarque-Bera test (JB Test) for normality of the monthly returns are presented in
Table 1. SQMB had the highest mean return (1.19% per month), while ENEL had the lowest average return (0.13%). In addition, LTM had the highest volatility (11.21%), while BSantander had the lowest volatility (5.56%) among the five assets. Furthermore, the IPSA index had a standard deviation of 4.60%, which was less than the volatility of the five assets considered. With the exception of SQMB, a lithium-producing company, Sharpe ratios were close to zero.
Except for BSantander, which has a moderate positive asymmetry, the returns of the remaining assets had a moderately negative skew. Except for BSantander, the returns of the remaining assets had a highest kurtosis. LTM showed the highest kurtosis with an estimated coefficient of 22.7946, and BSantander showed the lowest kurtosis. These coefficients provide us initial evidence of the absence of normality in the monthly returns. In fact, with the exception of BSantander, the normality hypothesis was rejected in the other assets using the Jarque-Bera test (JB Test). In brief, the descriptive statistics summary reported in
Table 1, confirmed the presence of low levels of skewness and high levels of kurtosis.
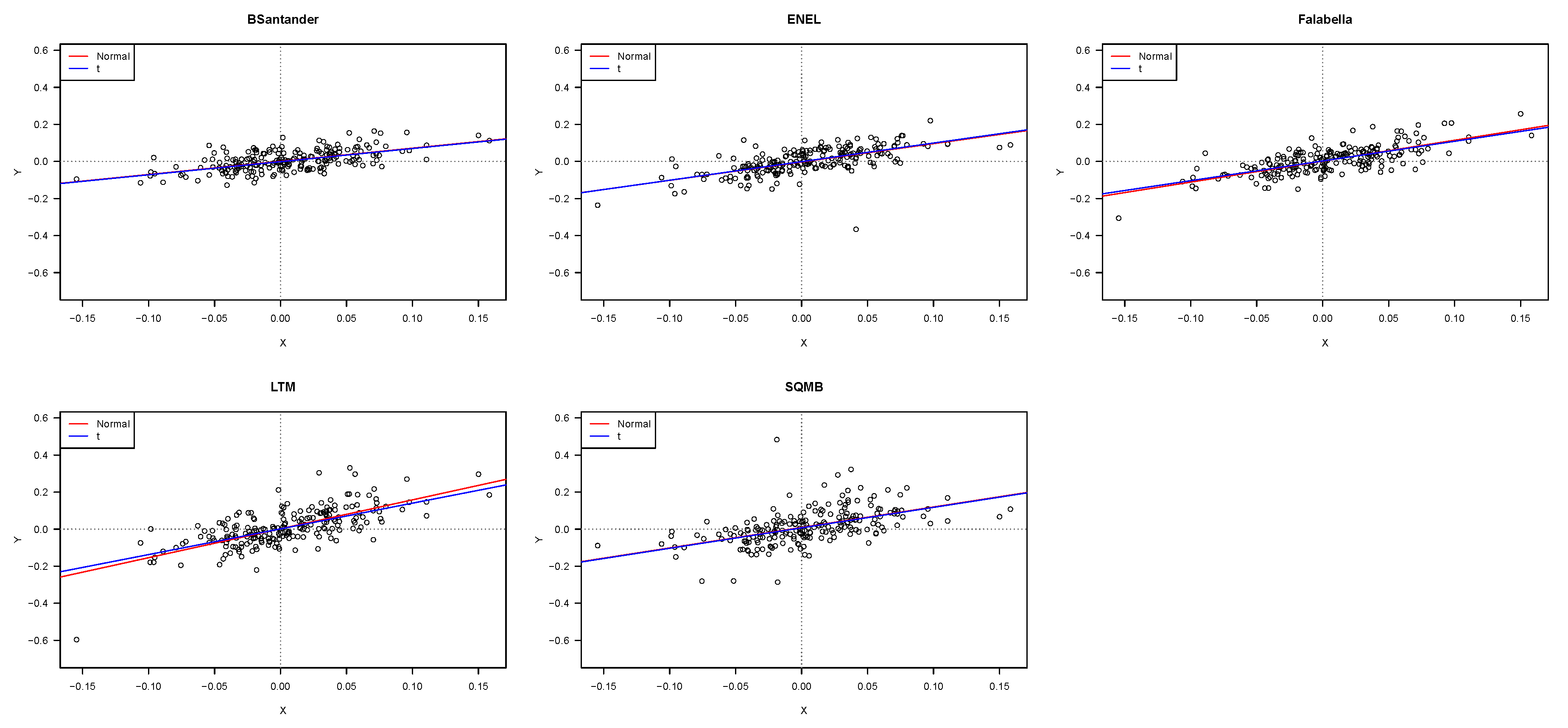
Figure 1 shows scatter plots and estimated lines for the five assets, using the normal and
t distributions. From this figure, it is possible to observe linear relationships between asset returns and IPSA returns, and potential outliers. The IPSA index returns explained between 28% and 51% of the variability of the five assets returns. The IPSA index explained 50.94% of the variability in the returns of the Falabella and 27.82% of the returns variability of SQMB.
We also performed an analysis of the heteroscedasticity and autocorrelation of the returns of the five assets. Using the White test (see
Lee 1991;
Waldman 1983;
White 1980) Falabella and LTM showed evidence of heteroscedasticity, while the Durbin-Watson test indicated evidence of first order autocorrelation only in the returns of LTM. Then, considering the significant departure from normality, high kurtosis (evidence that the returns had fat-tailed distributions), the moderate skewness, and the results of the tests for heteroscedasticity and autocorrelation of errors, it is assumed in this study that the random vectors
were iid as a multivariate
t-distribution, with zero mean and covariance matrix
and density given by (
4). For illustrative purposes, the normal distribution and tests based on weaker distributional assumptions were used, such as the GMM tests, for testing hypothesis (
3).
Table 2 presents the ML estimate for parameters of the CAPM using the normal and
t distributions. The standards errors were estimated using the expected information matrix. The results in
Table 2 show that the estimates of the coefficients
and
were very similar using both models (
NCAPM and
TCAPM), especially the systematic risk estimators (
) of the assets considered.
The following hypothesis test
was considered. In this case, it was found that
. The asymptotic distribution of the LR test for the previous hypothesis corresponded to a 50:50 mixture of chi-squares with zero and one degree of freedom, whose critical value was 2.7055 at a significance level of 5% (see, for instance
Song et al. 2007). In this case, the maximum log-likelihood for the
NCAPM was 1481.39 and for the
TCAPM, the maximum log-likelihood was 1524.06, which corresponded to a likelihood-ratio statistic of 85.34. This indicates that the
TCAPM fit the data significantly better than the
NCAPM. As suggested by a referee, for address the impact of finite samples on the
p-values and on the standard errors of the parameter estimates, we also used a nonparametric bootstrap procedure (
Chou and Zhou 2006;
Efron and Tibshirani 1993). Nevertheless, the results were very similar to those obtained using the normal and
t-distribution; therefore, they are not shown here.
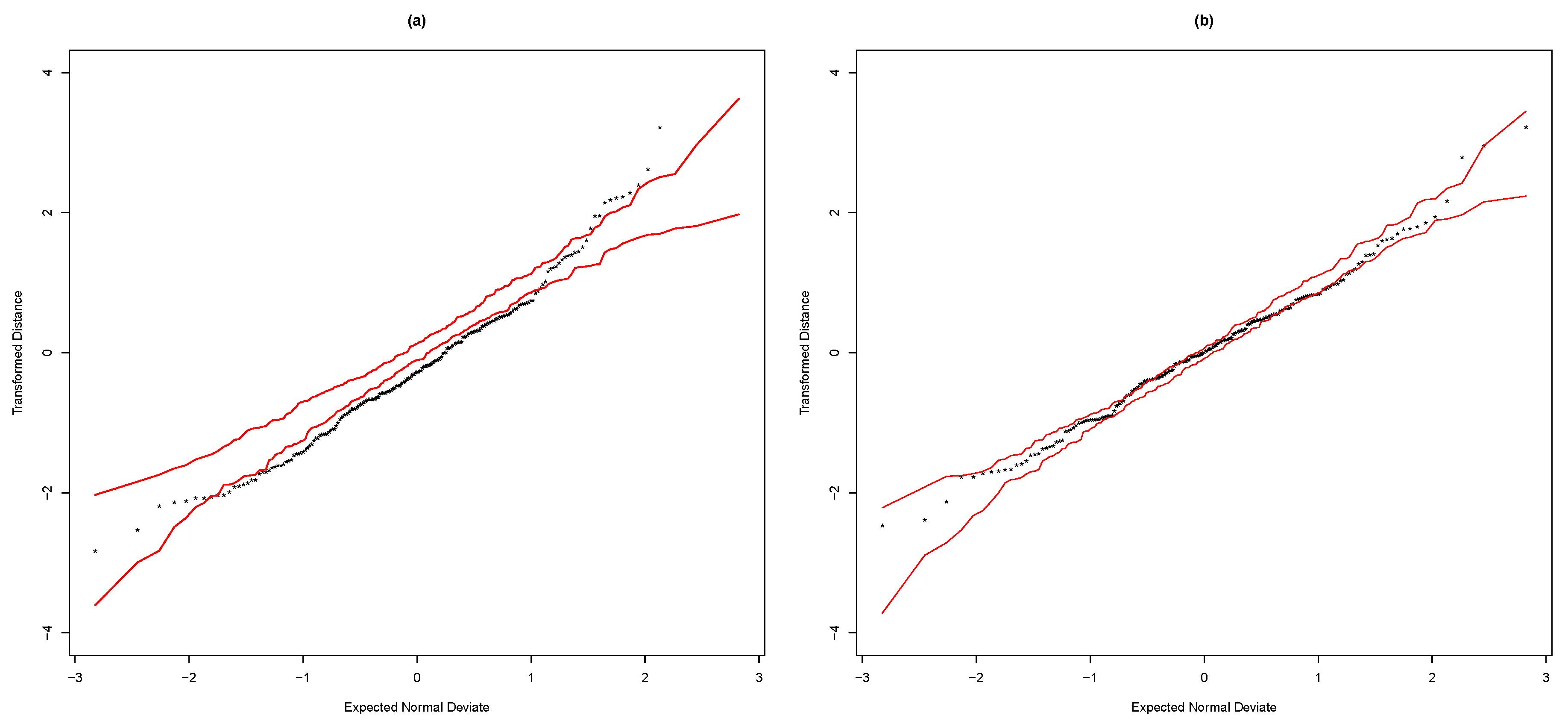
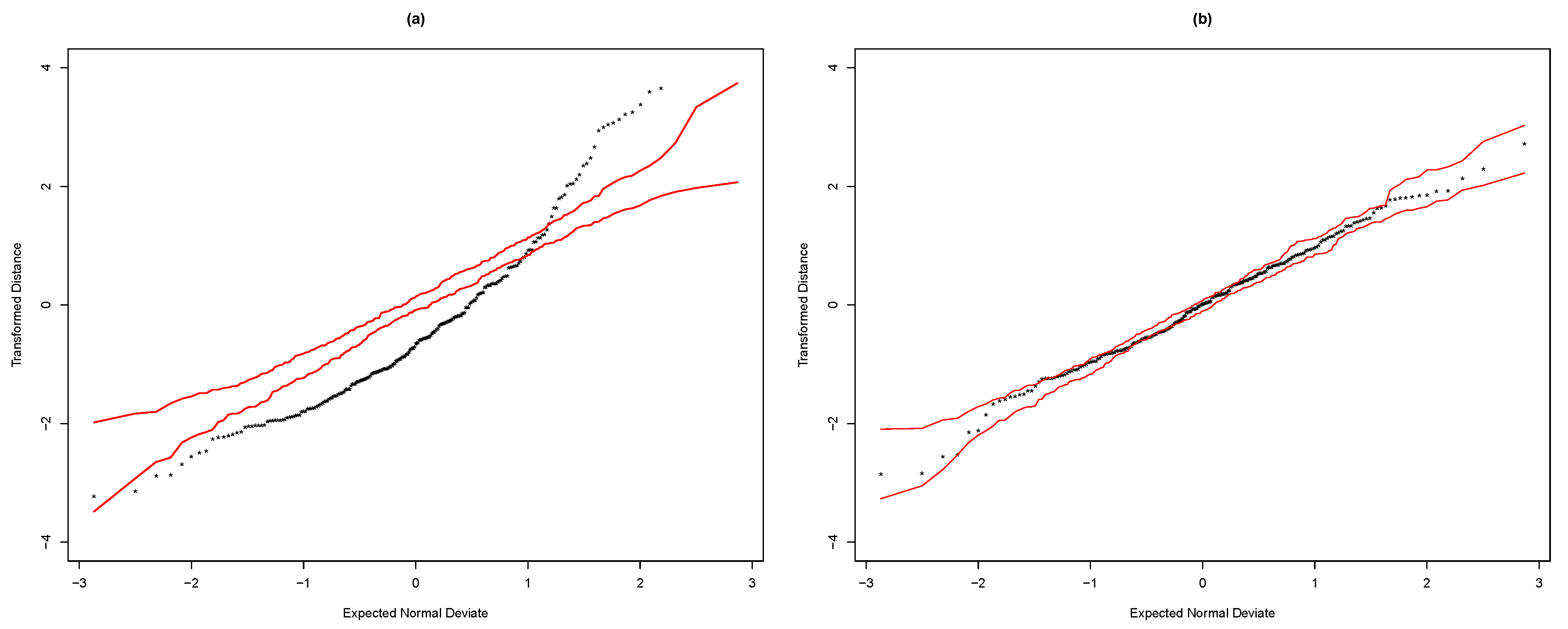
Figure 2 displays the transformed distance plots for the normal and
t distributions, see Equation (
12). These graphics confirm that the
TCAPM presented the best fit.
Table 3 presents tests results for hypothesis (
3) based on the Wald, likelihood-ratio, score, and gradient tests. The results in
Table 3 show that the mean-variance efficiency of the IPSA index is not rejected
, with any of the tests used for the three scenarios (normal,
t-distributions and the GMM).
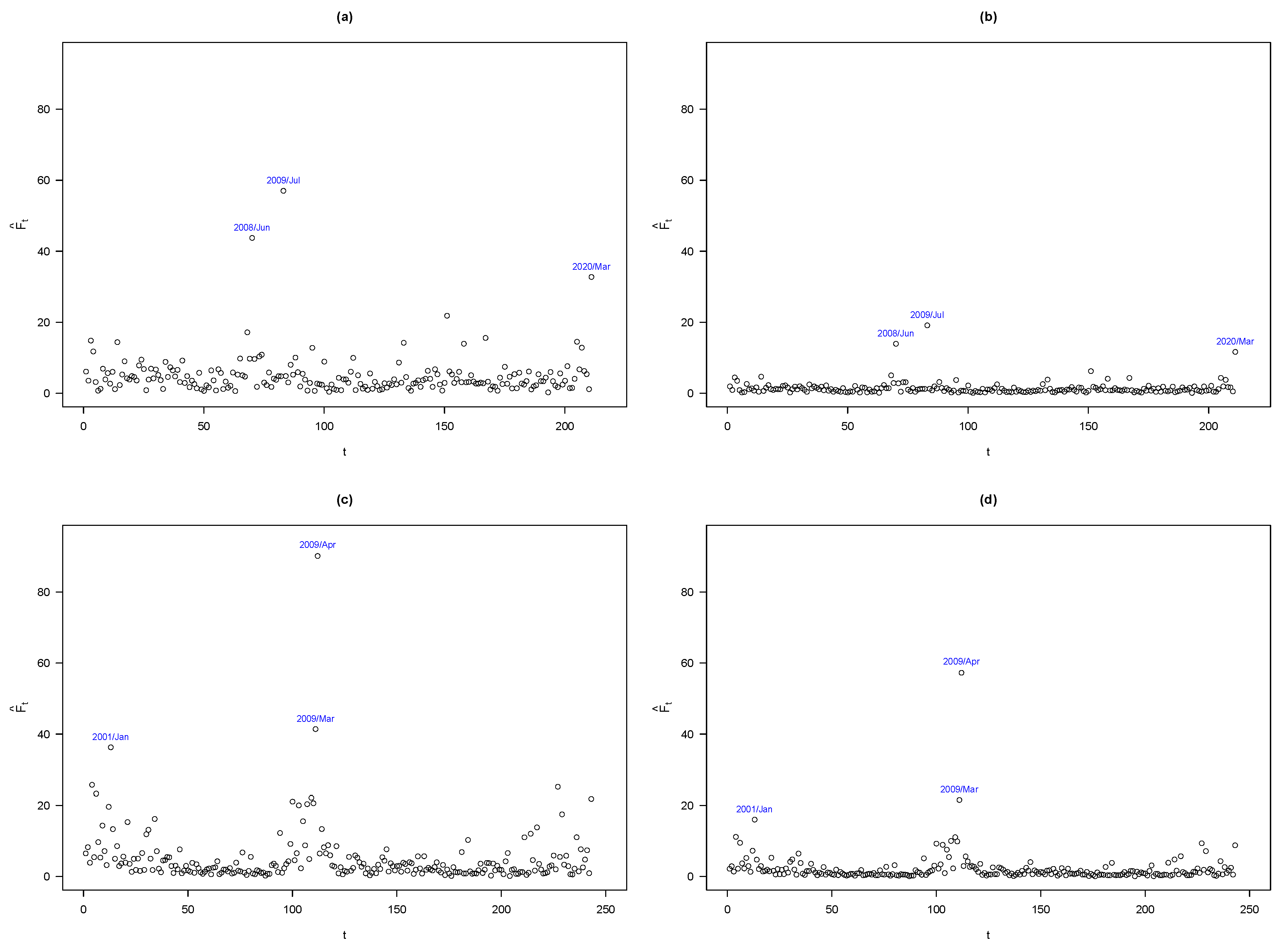
Figure 3 shows the Mahalanobis distances for the normal and
t-distribution, for both data sets; the Chilean data set and the New York Stock Exchange data set. For the Chilean data set, under normality
Figure 3a, we observe that the returns for 2008/Jun, 2009/Jul and 2020/Mar are possible outliers. For instance, in 2009/Jul, economic activity fell by 3.5%, when Chile entered a recession due to the global financial crisis, while in 2020/Mar, the fall in economic activity (initial) was due to the pandemic caused by Covid-19. Already in
Figure 3b, we see as expected, that the
TCAPM reduced the possible effect of these returns.
3.2. The New York Stock Exchange Data Set
We considered monthly returns of shares from five companies whose common stock shares trade on the New York Stock exchange, NYSE: Bank of America, Boeing, Ford Motor Company, General Electric Company and Microsoft. The S&P500 was taken as the market price. The 10-year bond yield was used as the risk-free returns; it is a long risk-free rate, similar to the one used for the Chilean data set. The excess returns were the returns minus the risk-free rate. The data corresponded to the period from January, 2000 to March, 2020.
The means, standard deviations (SD), Sharpe ratios (Sharpe), coefficients of skewness and kurtosis, and the Jarque-Bera test (JB Test) for normality of the monthly returns are presented in
Table 4. Boeing had the highest mean return (0.53% per month), while General Electric Company had the lowest average return (−0.77%). In addition, Ford had the highest volatility (13.10%), while Microsoft had the lowest volatility (8.34%) among the five assets. Furthermore, the S&P500 index had a standard deviation of 4.34%, which was less than the volatility of the five assets considered. With the exception of General Electric Company, with a negative Sharpe ratio, the other Sharpe ratios were close to zero.
The assets had a moderate (positive and negative) asymmetry. Again, the returns of the assets had a highest kurtosis. The normality hypothesis was rejected in all the assets using the Jarque-Bera test (JB Test). In brief, the descriptive statistics summary reported in
Table 4, confirmed the presence of low levels of skewness and high levels of kurtosis.
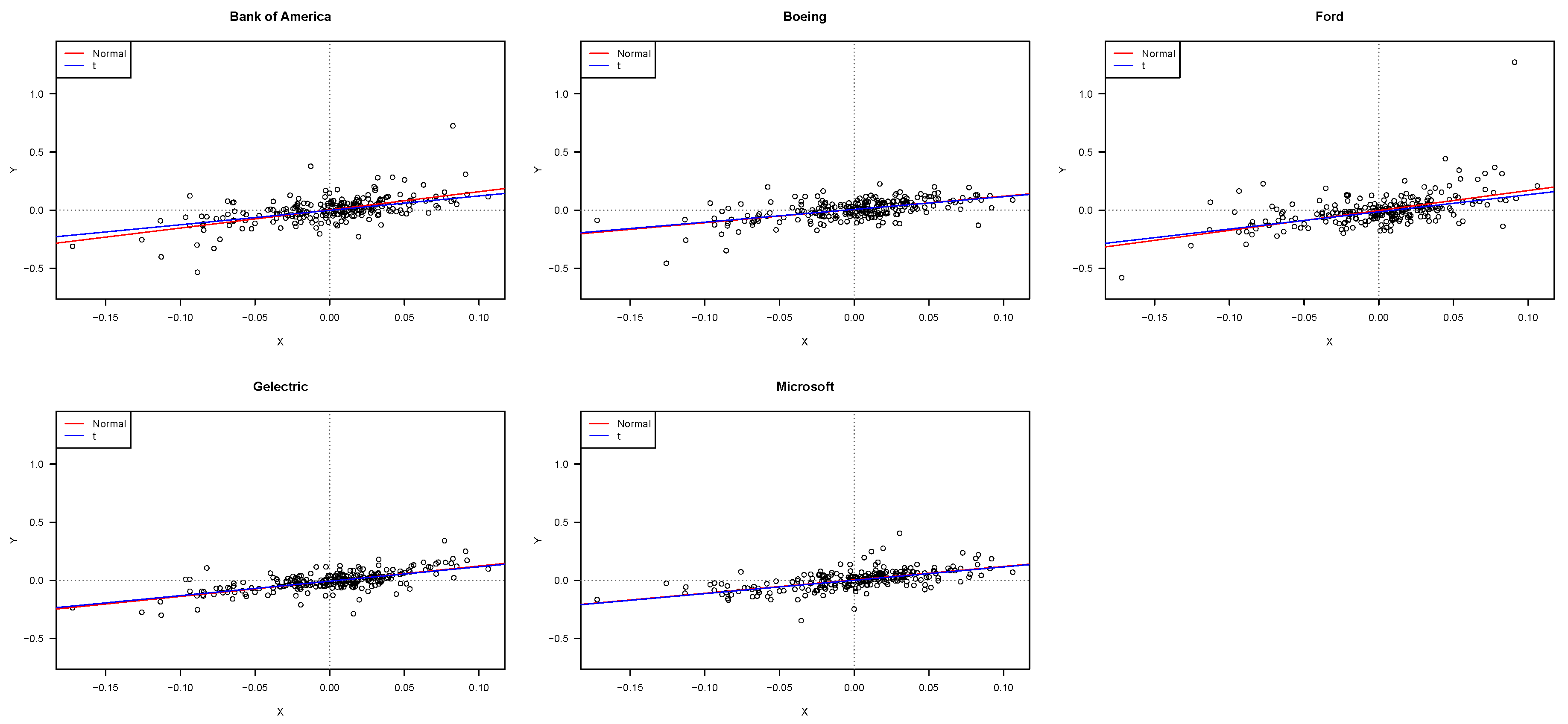
Figure 4 shows scatter plots and estimated lines of the five assets, using the normal and
t distributions. From this figure, it is possible to observe linear relationships between asset returns and S&P500 returns, and potentials outliers. In this case, the S&P500 index returns explained between 27% and 45% of the variability of the five assets returns, similar to the Chilean Data Set.
The Whites test show evidence of heteroscedasticity in Bank of America, Boeing and Ford Motor Company. The Durbin-Watson test indicates no evidence of first order autocorrelation.
Table 5 presents the ML estimate for parameters of the CAPM using the normal and
t distributions. The standards errors were estimated using the expected information matrix. Similar results to the Chilean data set were observed. For this data set, it was found that
indicating a greater departure from normality than the Chilean data set. The likelihood-ratio statistic value, for the hypothesis
was 285.8, which was highly significant. In this case, the maximum log-likelihood for the
NCAPM was 1361.2 and for the
TCAPM was 1504.1. Again, this indicates that the
TCAPM fit the data significantly better than the
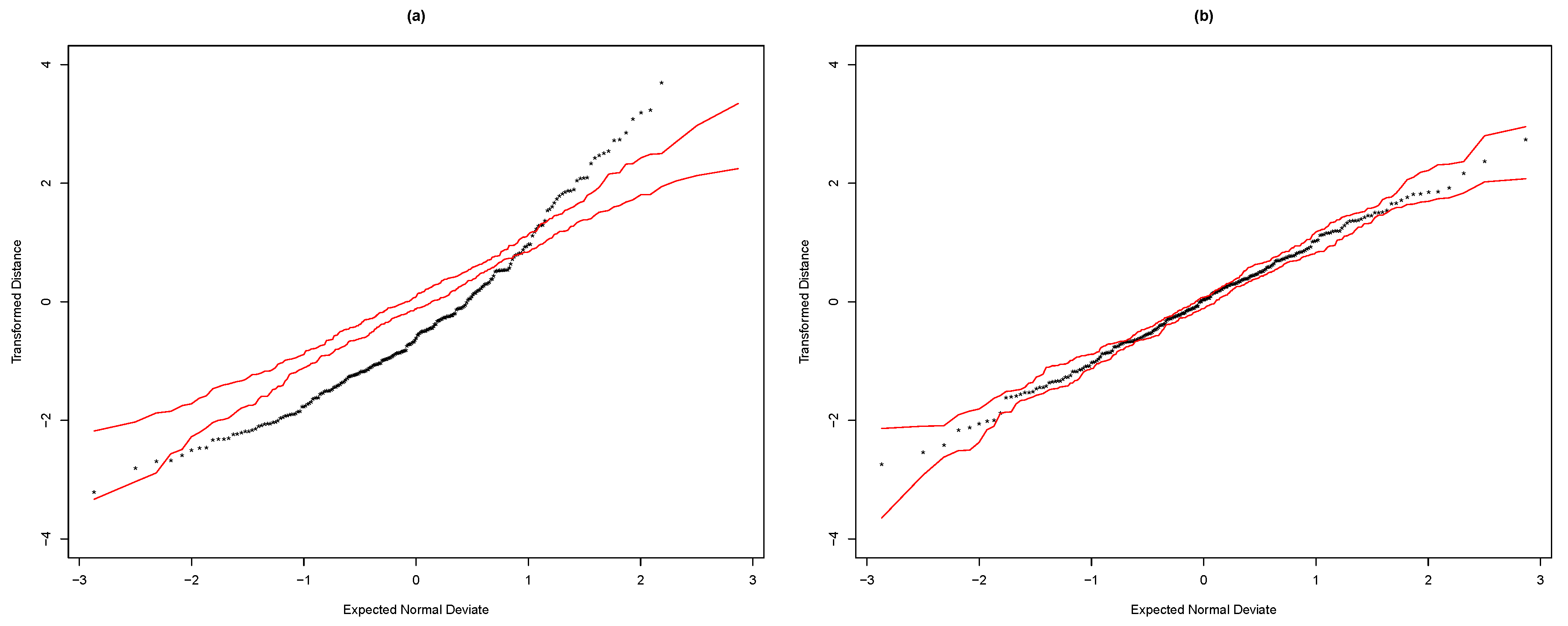
NCAPM. This was also confirmed by the transformed distance plots displayed in
Figure 5.
Table 6 presents tests results for hypothesis (
3). The results in
Table 6 show that the mean-variance efficiency of the S&P500 index could not be rejected
, with any of the tests, if we used the
NCAPM (or GMM test). However, if we used
TCAPM, the hypothesis (
3) was rejected
with any of the four tests. That is to say, there was a change in statistical inference.
As suggested by a referee, it may also be of interest to test the hypotheses
and
. The four tests were implemented to verify these hypotheses using the
t-distribution, see
Appendix C. However, with the four tests statistics, we strongly rejected the null hypotheses, and therefore they are not shown in the present study. More details about this interesting topic can be found at
Glabadanidis (
2009,
2014,
2019).
Figure 3 show the Mahalanobis distances for the
NCAPM and
TCAPM models, showing results similar to the Chilean data set, except that the return corresponding to 2009/Apr for
TCAPM (see
Figure 3d) was a possible outlier. In April 2009, the five assets had high returns, highlighting Ford Motor Company, with a 127.4%. However, when deleting these returns, there were no changes in statistical inference. Once again, this suggests that the
TCAPM provided an appropriate way for achieving robust inference.