Precious Metal Mutual Fund Performance Evaluation: A Series Two-Stage DEA Modeling Approach
Abstract
1. Introduction
2. Literature Review
2.1. Survey of DEA-Based Mutual Fund Performance Evaluation
2.2. Research Gaps in the Literature
3. Research Methods
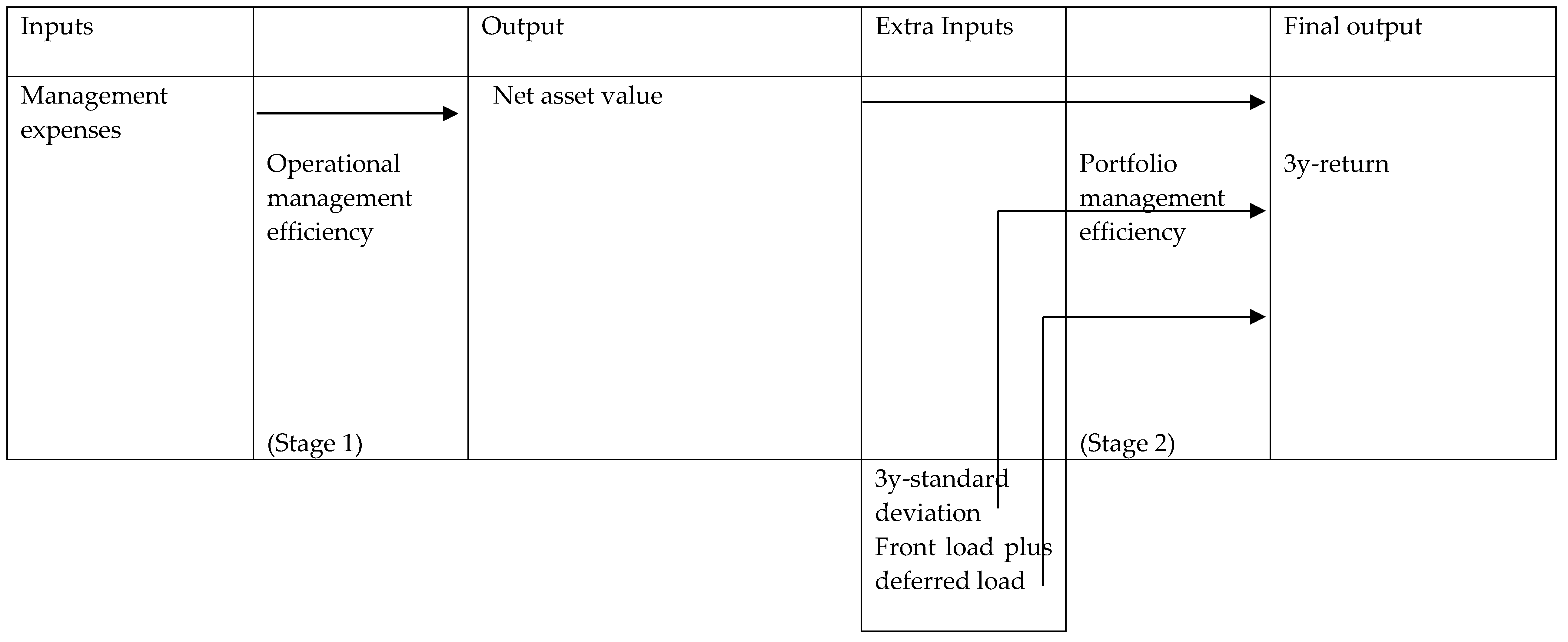
3.1. Definitions and Conceptual Framework
3.2. DEA Modeling
- ε > 0, a convenient small positive number (non-Archimedean);
- μr = output weights estimated by the model;
- vi = input weights estimated by the model.
4. Data and Identification of Input and Output Variables
4.1. Data
4.2. Input and Output Variable Specification for DEA
5. Results
5.1. First Stage Analysis—Precious Metal Mutual Fund Operational Management Performance
5.2. Second Stage Analysis—Precious Metal Mutual Fund Portfolio Management Performance
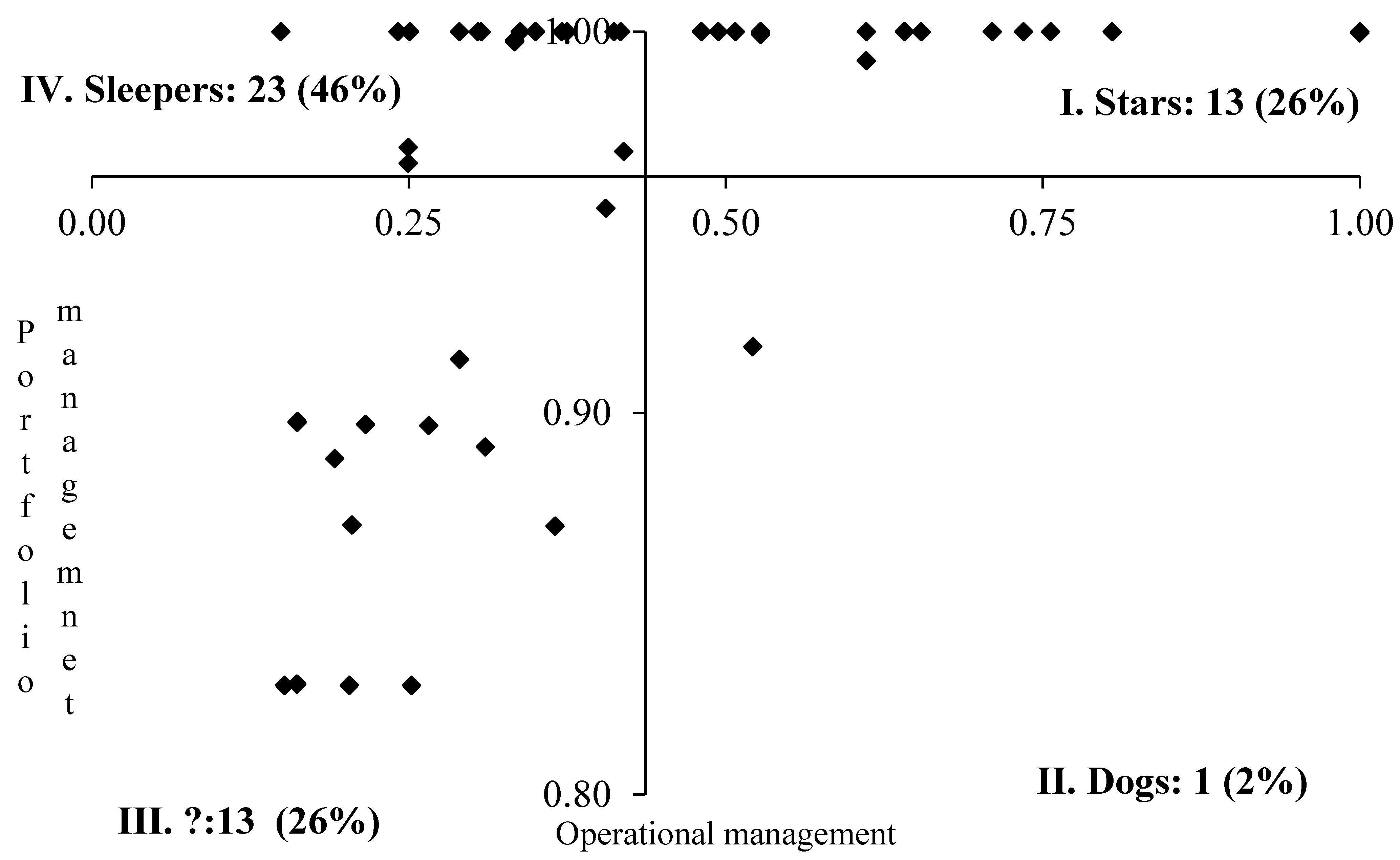
5.3. Fund Operational Management Performance vs. Portfolio Management Performance
5.4. Top Funds in Both Performance Dimensions
5.5. Two-Stage vs. One-Stage DEA Structure
6. Conclusions and Implications
6.1. Contribution of the Study
6.2. Key Conclusions
6.3. Implications
6.4. Outlook
Funding
Conflicts of Interest
References
- Andreu, Laura, Miguel Serrano, and Luis Vicente. 2019. Efficiency of mutual fund managers: A slacks-based manager efficiency index. European Journal of Operational Research 273: 1180–93. [Google Scholar] [CrossRef]
- Annaert, Jan, Julien van den Broeck, and Rudi. V. Vennet. 2003. Determinants of mutual funds underperformance: A bayesian stochastic frontier approach. European Journal of Operational Research 151: 617–32. [Google Scholar] [CrossRef]
- Baghdadabad, Mohanmmad Reza Tavakoli, Farid Habibi Tanha, and Noreha Halid. 2013. The efficiency evaluation of mutual fund managers based on DARA, CARA, IARA. Journal of Business Economics and Management 14: 677–95. [Google Scholar] [CrossRef][Green Version]
- Baker, H. Kent, Greg Filbeck, and Halil Kiymaz. 2015. Mutual Funds and Exchange-Traded Funds: Building Blocks to Wealth. New York: Oxford University Press. [Google Scholar]
- Baker, H. Kent, Greg Filbeck, and Jeffery H. Harris. 2018. Commodities: Markets, Performance, and Strategies. New York: Oxford University Press. [Google Scholar]
- Balcilar, Mehemet, and Zeynel Abidin Ozdemir. 2019. The volatility effect on precious metals price returns in a stochastic volatility in mean model with time-varying parameters. Physica A: Statistical Mechanics and Its Applications 534: 122329. [Google Scholar] [CrossRef]
- Banker, Rajiv D., Abraham Charnes, and William W. Cooper. 1984. Some models for estimating technical and scale inefficiencies in Data Envelopment Analysis. Management Science 30: 1078–92. [Google Scholar] [CrossRef]
- Banker, Rajiv, Janice Y. Chen, and Paul Klumpes. 2016. A Trade–Level DEA model to evaluate relative performance of investment fund managers. European Journal of Operational Research 255: 903–10. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2016. DEA performance assessment of mutual funds. In Data Envelopment Analysis: A Handbook of Empirical Studies and Applications. Edited by Joe Zhu. New York: Springer, pp. 229–87. [Google Scholar]
- Basso, Antonella, and Stefania Funari. 2017. The role of fund size in the performance of mutual funds assessed with DEA models. The European Journal of Finance 23: 457–73. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Cetin Ciner, and Brian M. Lucey. 2010. The macroeconomic determinants of volatility in precious metals markets. Resources Policy 35: 65–71. [Google Scholar] [CrossRef]
- Bilgin, Mehmet Huseyin, Fabian Gogolin, Marco Chi Keung Lau, and Samuel A. Vigne. 2018. Time-variation in the relationship between white precious metals and inflation: A cross-country analysis. Journal of International Financial Markets, Institutions and Money 56: 55–70. [Google Scholar] [CrossRef]
- Charnes, Abraham, William W. Cooper, and Edwardo Rhodes. 1978. Measuring the efficiency of decision making units. European Journal of Operational Research 2: 429–44. [Google Scholar] [CrossRef]
- Coelli, Timothy J., Dodla Sai Prasada Rao, Christopher J. O’Donnell, and George Edward Battese. 2005. An Introduction to Efficiency and Productivity Analysis, 2nd ed. New York: Springer. [Google Scholar]
- Galagedera, Don U. A. 2018. Modelling superannuation fund management function as a two-stage process for overall and stage-level performance appraisal. Applied Economics 50: 2439–58. [Google Scholar] [CrossRef]
- Galagedera, Don U. A. 2019. Modelling social responsibility in mutual fund performance appraisal: A two-stage data envelopment analysis model with non-discretionary first stage output. European Journal of Operational Research 273: 376–89. [Google Scholar] [CrossRef]
- Galagedera, Don U. A., and Param Silvapulle. 2002. Australian mutual fund performance appraisal using Data Envelopment Analysis. Managerial Finance 28: 60–73. [Google Scholar] [CrossRef]
- Galagedera, Don U. A., Jon Watson, Inguruwatt M. Premachandra, and Yao Chen. 2016. Modeling leakage in two-stage DEA models: An application to US mutual fund families. OMEGA International Journal of Management Science 61: 62–67. [Google Scholar] [CrossRef]
- Galagedera, Don U. A., Israfil Roshdi, Hirofumi Fukuyama, and Joe Zhu. 2018. A new network DEA model for mutual fund performance appraisal: An application to U.S. equity mutual funds. OMEGA International Journal of Management Science 77: 168–79. [Google Scholar] [CrossRef]
- Gao, Xiaohui, and Miles B. Livingston. 2008. The components of mutual fund fees. Financial Markets, Institutions & Instruments 17: 197–223. [Google Scholar]
- Glawischnig, Markus, and Margit Sommersguter-Reichmann. 2010. Assessing the performance of alternative investments using non-parametric efficiency measurement approaches: Is it convincing? Journal of Banking and Finance 34: 295–303. [Google Scholar] [CrossRef]
- Glick, Reuven, and Sylvain Leduc. 2012. Central bank announcements of asset purchases and the impact on global financial and commodity markets. Journal of International Money and Finance 31: 2078–101. [Google Scholar] [CrossRef]
- Haslem, John A. 2013. Mutual fund markets are imperfectly competitive. The Journal of Index Investing 4: 32–44. [Google Scholar] [CrossRef]
- Haslem, John A., H. Kent Baker, and David M. Smith. 2007. Identification and performance of equity mutual funds with high management fees and expense ratios. Journal of Investing 16: 32–51. [Google Scholar] [CrossRef]
- Hsieh, H. Pierre, Imen Tebourbi, Wen-Min Lu, and Nai-Yu Liu. 2020. Mutual fund performance: The decision quality and capital magnet efficiencies. Managerial and Decision Economics. [Google Scholar] [CrossRef]
- Investment Company Institute (ICI). 2015. Investment Company Fact Book, 55th ed. Washington, DC: ICI. [Google Scholar]
- Jubinski, Daniel, and Amy F. Lipton. 2013. VIX, gold, silver, and oil: How do commodities react to financial market volatility? Journal of Accounting and Finance 13: 70–88. [Google Scholar]
- Kang, Sang, Ron Mclver, and Seong-Min Yoon. 2017. Dynamic spillover effects among crude oil, precious metal, and agricultural commodity futures markets. Energy Economics 62: 19–32. [Google Scholar] [CrossRef]
- Kao, Chiang. 2014. Network data envelopment analysis: A review. European Journal of Operational Research 239: 1–16. [Google Scholar]
- Koronakos, Gregory. 2019. A taxonomy and review of the network data envelopment analysis literature. In Machine Learning Paradigms. Learning and Analytics in Intelligent Systems. Edited by George A. Tsihrintzis, Maria Virvou, Evangelos Sakkopoulos and Lakhmi C. Jain. Cham: Springer, pp. 255–311. [Google Scholar]
- Kucher, Oleg, and Suzanne McCoskey. 2017. The long-run relationship between precious metal prices and the business cycle. The Quarterly Review of Economics and Finance 65: 263–75. [Google Scholar] [CrossRef]
- Lin, Ruiyue, and Zongxin Li. 2019. Directional distance based diversification super-efficiency DEA models for mutual funds. OMEGA International Journal of Management Science. [Google Scholar] [CrossRef]
- Lucey, Brian M., and Sile Li. 2015. What precious metals act as safe havens, and when? Some US evidence, Applied Economics Letters 22: 35–45. [Google Scholar] [CrossRef]
- Luo, Guo Ying. 2002. Mutual fund fee-setting, market structure and mark-ups. Economica 69: 245–71. [Google Scholar]
- Luo, Xueming. 2003. Evaluating the profitability and marketability efficiency of large banks. An application of data envelopment analysis, Journal of Business Research 56: 627–35. [Google Scholar] [CrossRef]
- Morey, Mattew R., and Richard C. Morey. 1999. Mutual fund performance appraisals: amulti-horizon perspective with endogenous benchmarking. Omega 27: 241–58. [Google Scholar] [CrossRef]
- Murthi, B. P. S., Yoon K. Choi, and Preyas Desai. 1997. Efficiency of mutual funds and portfolio performance measurement: A non-parametric approach. European Journal of Operational Research 98: 408–18. [Google Scholar] [CrossRef]
- O’Connor, Fergal A., Brian M. Lucey, Jonathan A. Batten, and Dirk G. Baur. 2015. The financial economics of gold—A survey. International Review of Financial Analysis 41: 186–205. [Google Scholar] [CrossRef]
- Otero, Luis A., and Juan C. Reboredo. 2018. The performance of precious-metal mutual funds: Does uncertainty matter? International Review of Financial Analysis 57: 13–22. [Google Scholar] [CrossRef]
- Öztek, Mehmet F., and Nadir Öcal. 2017. Financial crises and the nature of correlation between commodity and stock markets. International Review of Economics and Finance 48: 56–68. [Google Scholar] [CrossRef]
- Pierdzioch, Christian, Marian Risse, and Sebastian Rohloff. 2016. Are precious metals a hedge against exchange-rate movements? An empirical exploration using bayesian additive regression trees. The North American Journal of Economics and Finance 38: 27–38. [Google Scholar] [CrossRef]
- Piñeiro-Chousa, Juan, M. Ángeles López-Cabarcos, Ada M. Pérez-Pico, and Belen Ribeiro-Navarrete. 2018. Does social network sentiment influence the relationship between the S&P 500 and gold returns? International Review of Financial Analysis 57: 57–64. [Google Scholar]
- Premachandra, Inguruwatt M., Joe Zhu, John Watson, and Don U.A. Galagedera. 2012. Best performing US mutual fund families from 1993 to 2008: Evidence from a novel two-stage DEA model for -efficiency decomposition. Journal of Banking Finance 36: 3302–17. [Google Scholar] [CrossRef]
- Premachandra, Inguruwatt M., Joe Zhu, John Watson, and Don U.A. Galagedera. 2016. Mutual Fund Industry Performance: A Network Data Envelopment Analysis Approach. In Data Envelopment Analysis: A Handbook of Empirical Studies and Applications. Edited by Joe Zhu. New York: Springer, pp. 165–228. [Google Scholar]
- Qadan, Mahmoud. 2019. Risk appetite and the prices of precious metals. Resources Policy 62: 136–53. [Google Scholar] [CrossRef]
- Rehman, Mobeen Ur., Syed Jawad Hussain Shahzad, Gazi Salah Uddin, and Axel Hedstrom. 2018. Precious metal returns and oil shocks: A time varying connectedness approach. Resources Policy 58: 77–89. [Google Scholar] [CrossRef]
- Salisu, Afees, Umar Ndako, and Tirimisiyu Oloko. 2019. Assessing the inflation hedging of gold and palladium in OECD countries. Resources Policy 62: 357–77. [Google Scholar] [CrossRef]
- Sánchez-González, Carlos, Jose Luis Sarto, and Luis Vicente. 2017. The efficiency of mutual fund companies: Evidence from an innovative network SBM approach. OMEGA, The International Journal of Management Science 71: 114–28. [Google Scholar] [CrossRef]
- Sekhar, G. V. Sekhar. 2017. The Management of Mutual Funds. Cham: Palgrave Macmillan. [Google Scholar]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Szmigiera, M. 2019. Mutual Funds—Statistics and Facts. Available online: https://www.statista.com/topics/1441/mutual-funds/ (accessed on 24 November 2019).
- Talbi, Marwa, Christian de Peretti, and Lotfi Belkacem. 2020. Dynamics and causality in distribution between spot and future precious metals: A copula approach. Resources Policy 66: 101645. [Google Scholar] [CrossRef]
- Tarnaud, Albane Christine, and Heleu Leleu. 2018. Portfolio analysis with DEA: Prior to choosing a model. OMEGA, The International Journal of Management Science 75: 57–76. [Google Scholar] [CrossRef]
- Thanassoulis, Emmanuel. 2001. Introduction to the Theory and Application of Data Envelopment Analysis: A Foundation Text with Integrated Software. Dordrecht: Kluwer Academic Publishers. [Google Scholar]
- Tsolas, Ioannis E. 2014. Precious metal mutual fund performance appraisal using DEA modeling. Resources Policy 39: 54–60. [Google Scholar] [CrossRef]
- Tsolas, Ioannis E. 2015. Firm credit risk evaluation: A series two-stage DEA modeling framework. Annals of Operations Research 233: 483–500. [Google Scholar] [CrossRef]
- Tuzcu, Sevgi E., and Emrah Ertugay. 2020. Is size an input in the mutual fund performance evaluation with DEA? Eurasian Economic Review. [Google Scholar] [CrossRef]
- U.S. General Accounting Office (GAO). 2000. Mutual Fund Fees: Additional Disclosure Could Encourage Price Competition. Washington, DC: GAO. [Google Scholar]
- Vigne, Samuel A., Brian M. Lucey, Fergal A. O’Connor, and Larisa Yarovaya. 2017. The financial economics of white precious metals—A survey. International Review of Financial Analysis 52: 292–308. [Google Scholar] [CrossRef]
- Zhou, Zhongbao, Qianyin Jin, Helu Xiao, Qian Wu, and Wenbin Liu. 2018. Estimation of cardinality constrained portfolio efficiency via segmented DEA. OMEGA, The International Journal of Management Science 76: 28–37. [Google Scholar] [CrossRef]
| Descriptive Statistics | Management Expenses, US$ Million | NAV, US$ Million | 3y-Standard Deviation (%) | Frond Load and Deferred Load (%) | 3y-Returns (%) |
|---|---|---|---|---|---|
| Min | 1.61 | 147.02 | 25.72 | 0.00 | −21.52% |
| Max | 28.22 | 2250.00 | 32.06 | 5.75 | −12.50% |
| Mean | 9.05 | 698.70 | 29.85 | 1.90 | −17.15% |
| Median | 6.21 | 496.46 | 29.71 | 1.00 | −17.08% |
| Standard deviation | 7.07 | 491.64 | 1.49 | 2.38 | 2.44% |
| Two-Stage DEA-Based Performance | Min | Max | Mean | Median | Standard Deviation | Efficient Funds, Number (%) |
|---|---|---|---|---|---|---|
| Operational management efficiency (%) | 14.90 | 100.00 | 43.64 | 36.80 | 23.99 | 4 (8) |
| Portfolio management efficiency (%) | 82.86 | 100.00 | 96.20 | 100.00 | 5.80 | 27 (54) |
| Single DEA-Based Performance | Min | Max | Mean | Median | Standard Deviation | Efficient Funds, Number (%) |
|---|---|---|---|---|---|---|
| Single DEA efficiency (%) | 80.25 | 100.00 | 92.82 | 94.93 | 7.60 | 25 (50) |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsolas, I.E. Precious Metal Mutual Fund Performance Evaluation: A Series Two-Stage DEA Modeling Approach. J. Risk Financial Manag. 2020, 13, 87. https://doi.org/10.3390/jrfm13050087
Tsolas IE. Precious Metal Mutual Fund Performance Evaluation: A Series Two-Stage DEA Modeling Approach. Journal of Risk and Financial Management. 2020; 13(5):87. https://doi.org/10.3390/jrfm13050087
Chicago/Turabian StyleTsolas, Ioannis E. 2020. "Precious Metal Mutual Fund Performance Evaluation: A Series Two-Stage DEA Modeling Approach" Journal of Risk and Financial Management 13, no. 5: 87. https://doi.org/10.3390/jrfm13050087
APA StyleTsolas, I. E. (2020). Precious Metal Mutual Fund Performance Evaluation: A Series Two-Stage DEA Modeling Approach. Journal of Risk and Financial Management, 13(5), 87. https://doi.org/10.3390/jrfm13050087





