Early Warning Signs of Financial Market Turmoils
Abstract
1. Introduction
2. Methodology
2.1. Market Event Detection
- The triplet series of events at times is specified as follows: if a positive return which exceeds the positive quantile occurs at day , then and if there is a negative return which is smaller than the negative quantile, then . Otherwise, no event is recorded.Thus, overall we focus on the largest of absolute returns. This threshold has been found to be well suited for detecting financial turmoil, which is thought to be accompanied by the largest absolute returns.
- For each Hawkes process, i.e., modeling positive and negative returns, we choose two independent exponential decay functions , each of which has the form
- As mark distributions we choose two independent Pareto distributions , with densitiesalong with a polynomial impact function
- The branching matrix Q has zero entries on its diagonal. We make this restriction because even without this constraint the maximum likelihood fit of this Hawkes process on the triplet series for all the stocks and models which we consider in the sequel set the diagonal parameters of the branching matrix Q to zeroish values. This implies that the intensity for the Hawkes process exhibits no self-excitation and large positive returns are triggered by negative tail returns and vice versa.
2.2. Indicators
2.2.1. Information Absorption
2.2.2. Scaling and Criticality
2.2.3. Leverage Cycle
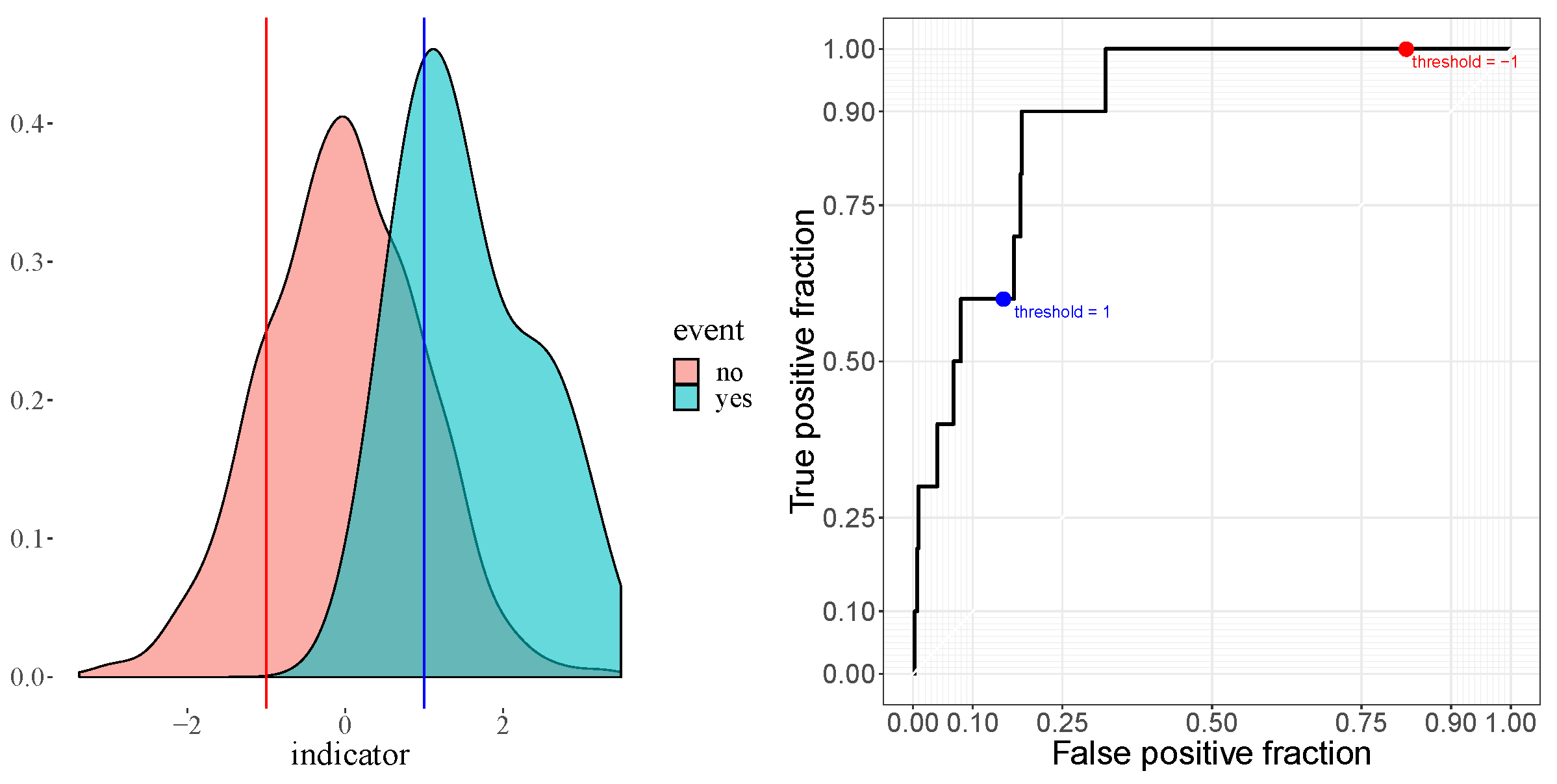
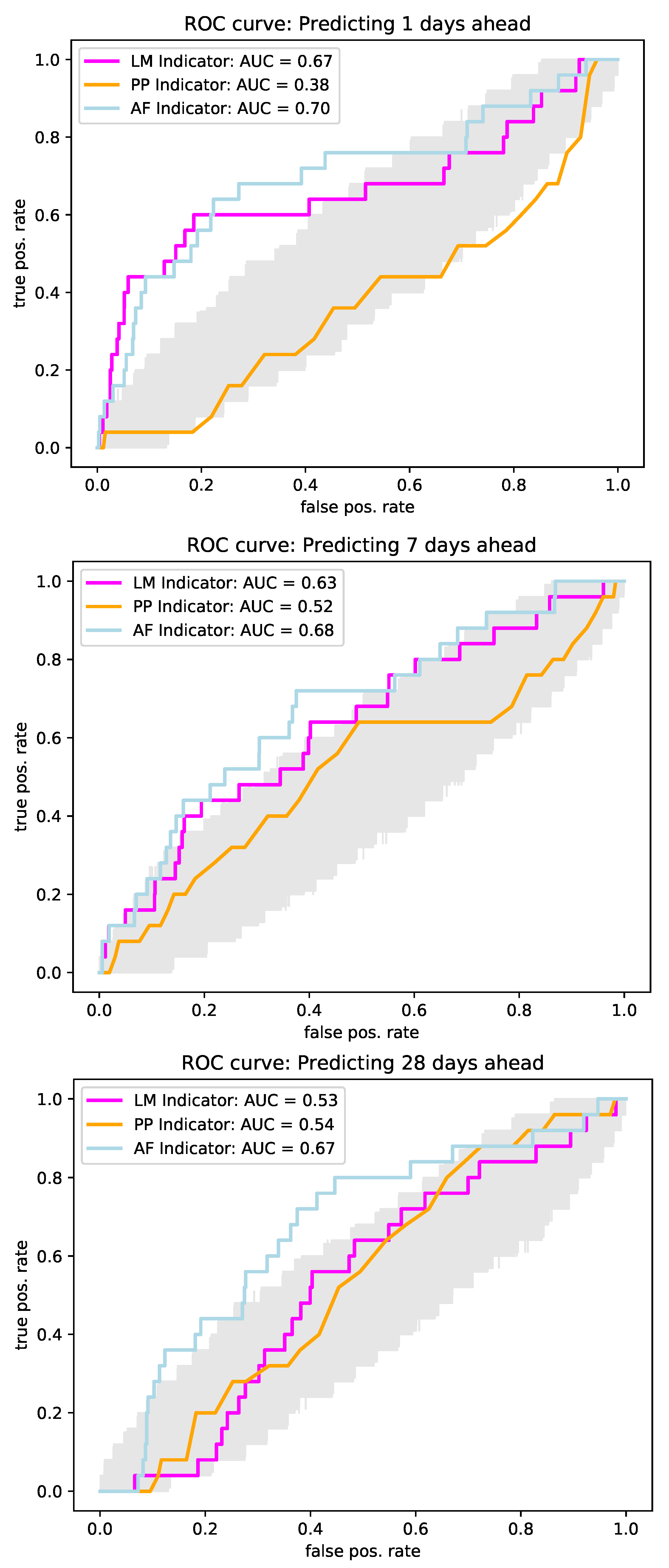
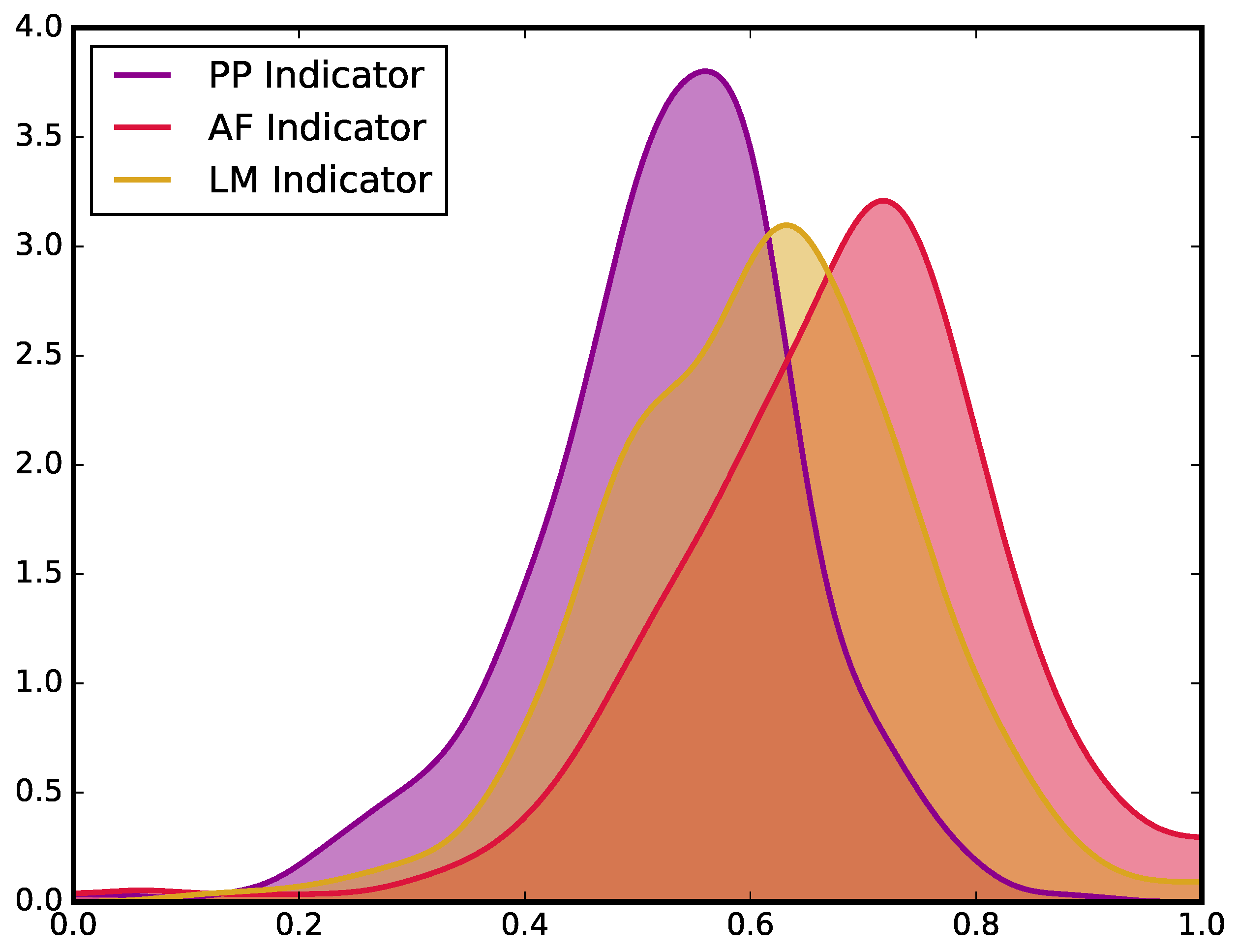
2.3. Performance Evaluation
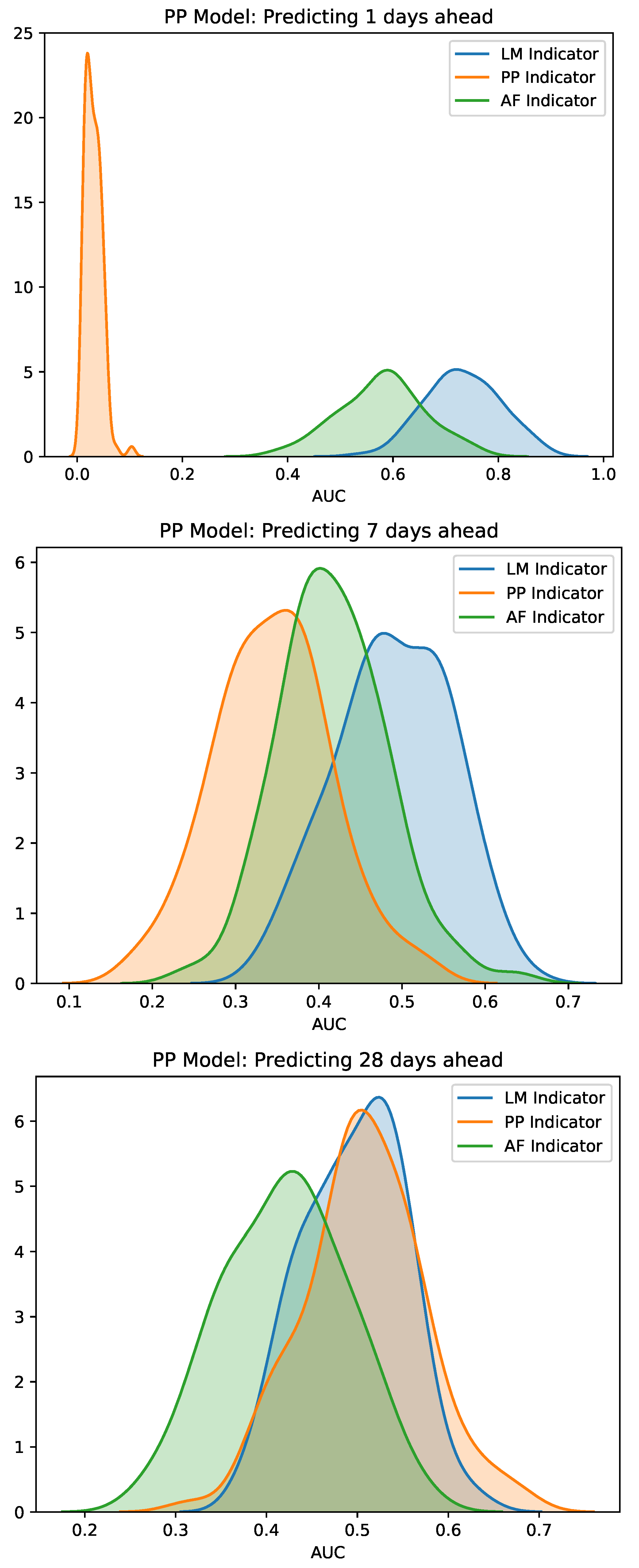
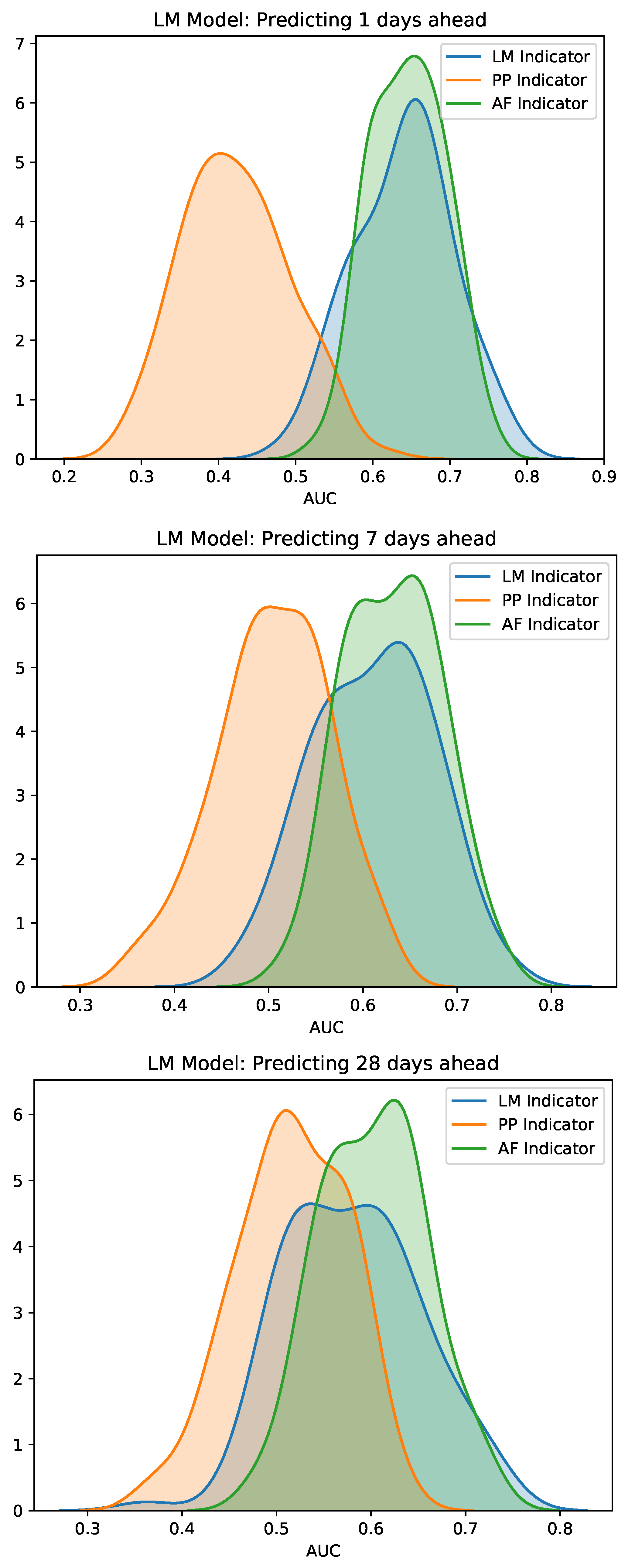
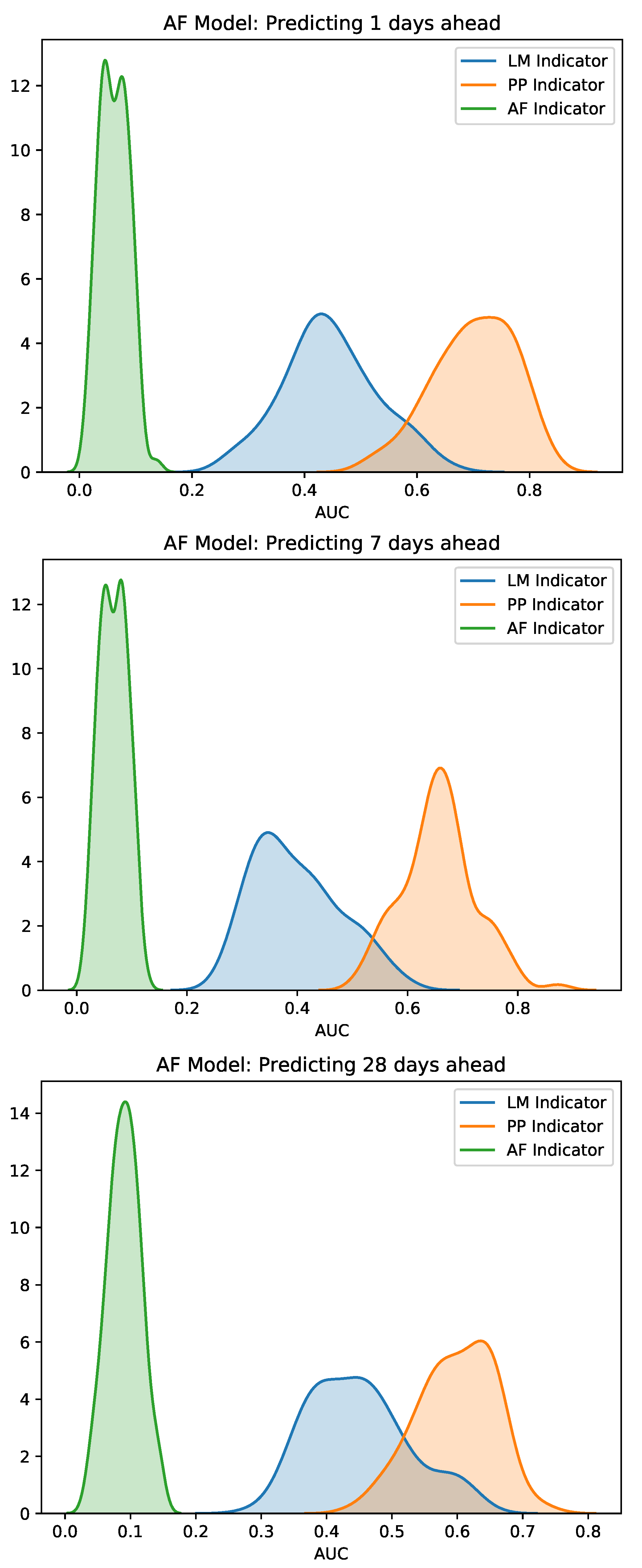
3. Results
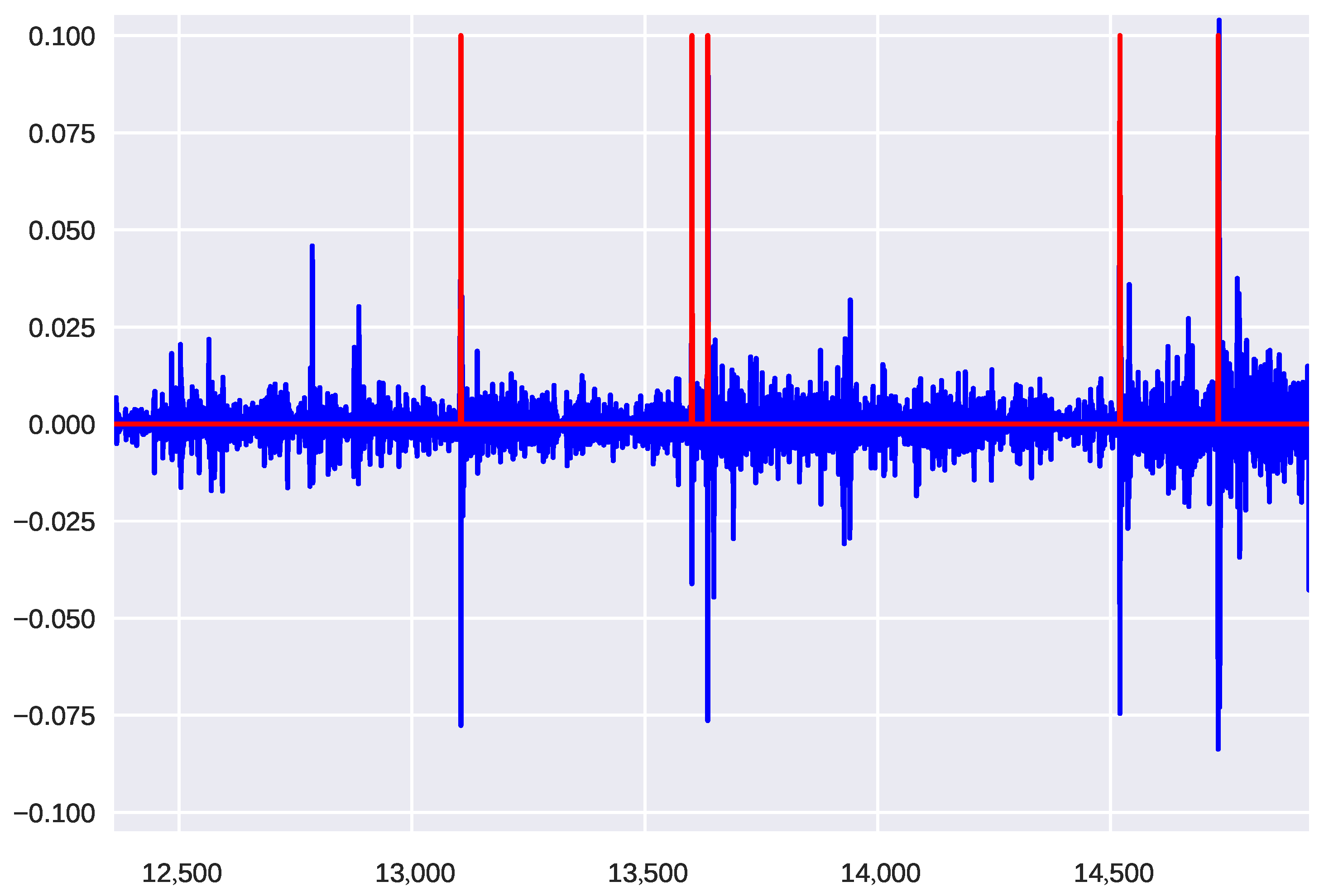
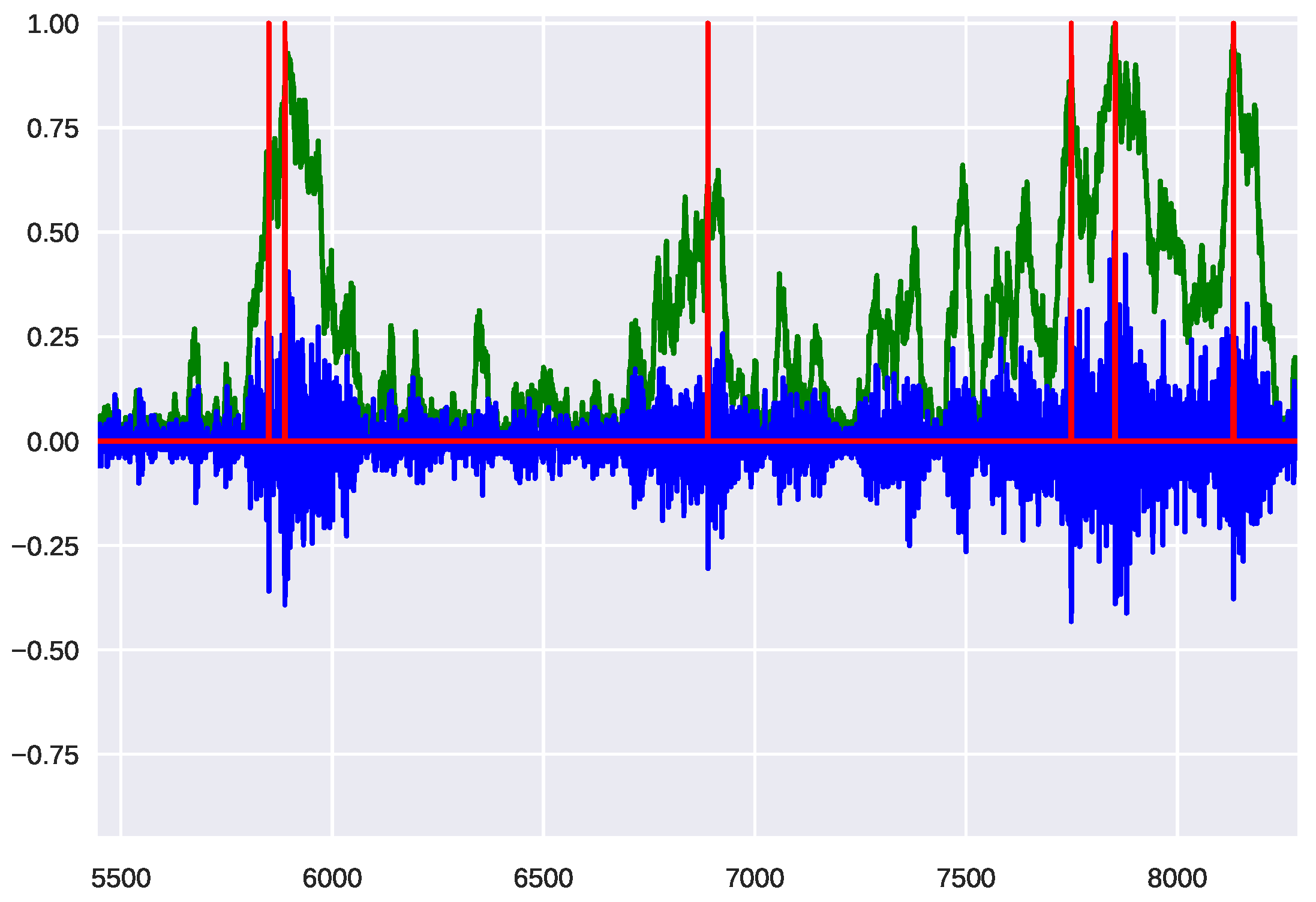
3.1. Early Warning Signals for Simulated Market Events
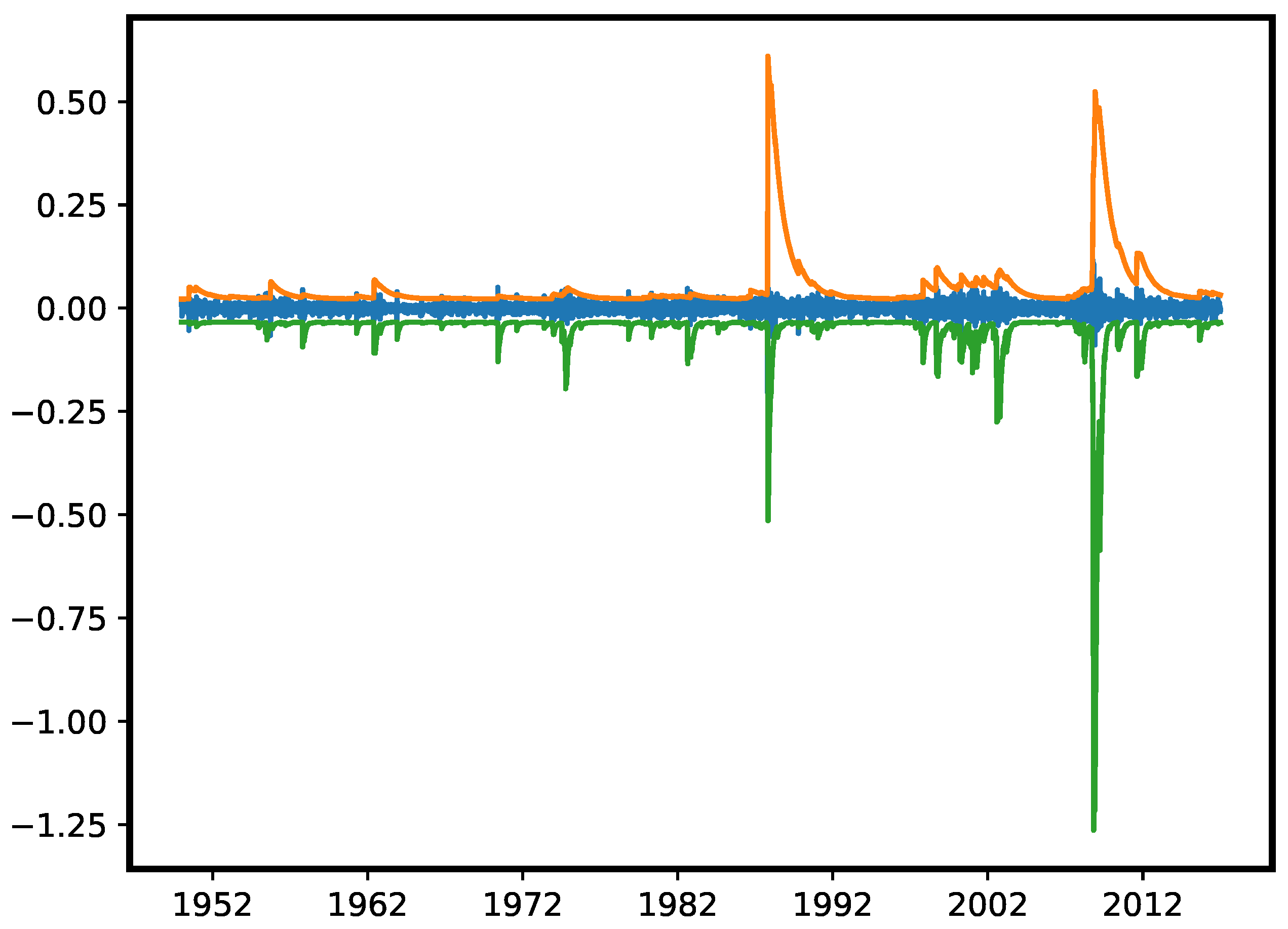
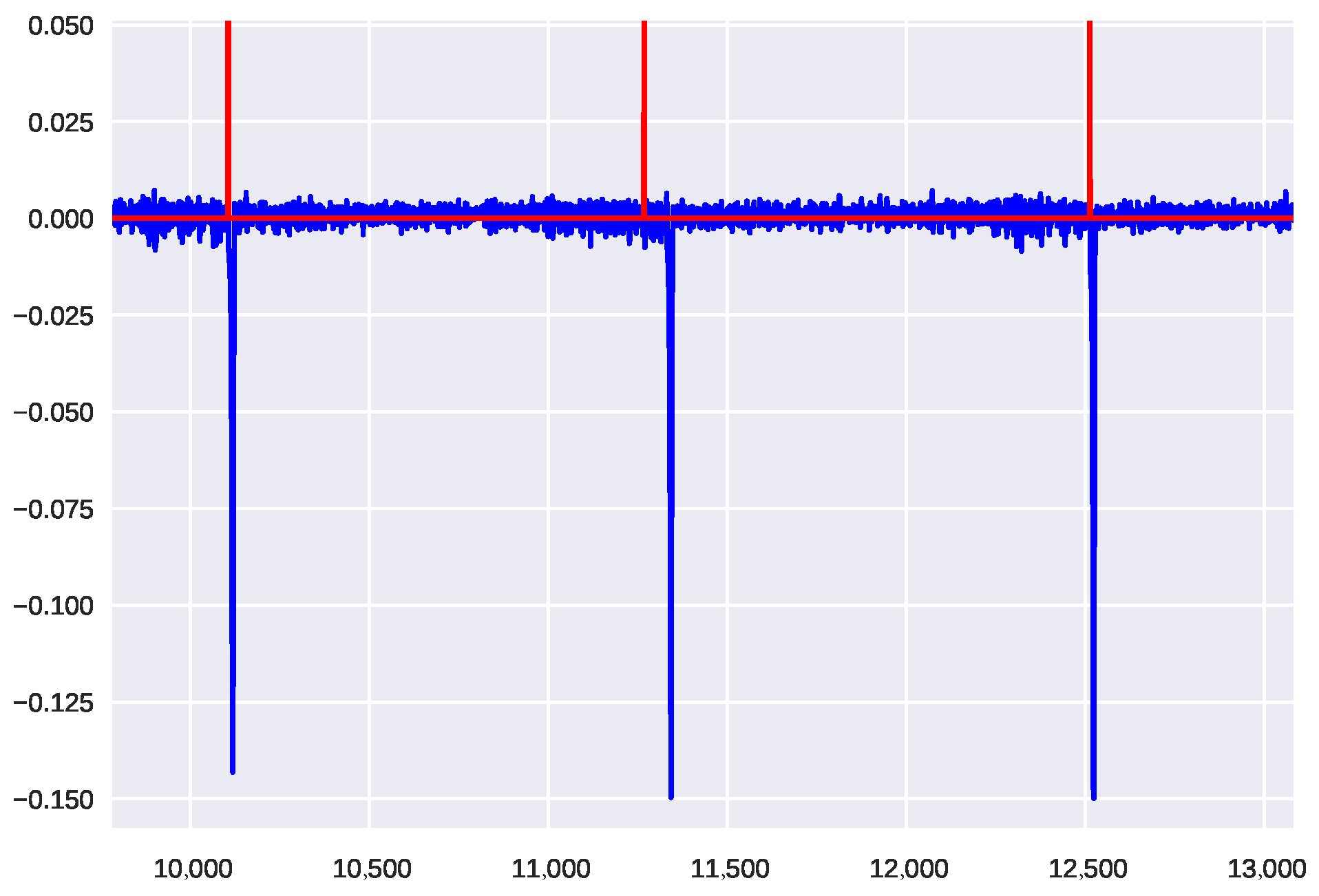
3.2. Early Warning Signals for Real Market Events
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Supporting Information
Appendix A.1. Hawkes Processes
Appendix A.2. Model Details
- Chartists switch between being optimistic or pessimistic. This decision is based on the price change —approximated as in simulations—and the opinion index capturing the prevailing population opinion, i.e.,Chartists then switch with rate from the pessimistic to the optimistic camp and in the reverse direction. Formally, the switching rates are given aswith and parameters and .
- Speculators also switch between fundamental and chartist strategies. Here, the decision is based on the excess profits gained by chartists and the difference between realized p and fundamental price . In this context, r denotes nominal dividends and R average real returns from other investments. It is assumed that these are priced at fair value, i.e., .Switching rates are now given bywith
Appendix A.3. Data Selection
| ● AA | ● BMY | ● D | ● HCA | ● MDT | ● PLD | ● TEF |
| ● AAPL | ● BNS | ● DGX | ● HD | ● MER | ● PNC | ● TEVA |
| ● ABB | ● BOX | ● DHI | ● HDI | ● MET | ● PPL | ● T |
| ● ABN | ● BP | ● DHR | ● HMC | ● MFC | ● PRU | ● TGT |
| ● ACN | ● BR | ● DIS | ● HON | ● MGM | ● PSO | ● TIA |
| ● ADBE | ● BRG | ● DO | ● HOT | ● MITSY | ● PT | ● TI |
| ● ADI | ● BRKA | ● DOW | ● HPQ | ● MMC | ● PTR | ● TJX |
| ● ADM | ● BRKB | ● DTV | ● MMM | ● PUK | ● TKA | |
| ● ADP | ● BSC | ● DUK | ● IBM | ● MO | ● PX | ● TKC |
| ● AEE | ● BSX | ● DVN | ● IBN | ● MON | ● TKG | |
| ● AEG | ● BSY | ● IGT | ● MOT | ● QCOM | ● TLD | |
| ● AEP | ● BT | ● EBAY | ● IMI | ● MRK | ● TLK | |
| ● AES | ● BTI | ● ECA | ● INFY | ● MRO | ● RAI | ● TM |
| ● AET | ● BUD | ● ED | ● ING | ● MRVL | ● RDSA | ● TMX |
| ● AFL | ● EDP | ● INTC | ● MS | ● RDSB | ● TOT | |
| ● A | ● CA | ● EFA | ● IP | ● MSFT | ● RF | ● TROW |
| ● AGN | ● CAG | ● E | ● IR | ● MTB | ● RG | ● TRP |
| ● AHC | ● CAH | ● EIX | ● ITU | ● MTU | ● RIG | ● TS |
| ● AIB | ● CAJ | ● ELE | ● ITW | ● MUR | ● RIO | ● TSM |
| ● AIG | ● CAT | ● EMR | ● IVV | ● MXIM | ● ROK | ● TVE |
| ● AKZOY | ● CB | ● ENB | ● IX | ● RTN | ● TWX | |
| ● AL | ● CBS | ● EN | ● NBR | ● RY | ● TXN | |
| ● ALL | ● CCJ | ● EOG | ● JCI | ● NCC | ● TXT | |
| ● AMAT | ● CCL | ● EON | ● JNJ | ● NE | ● SAP | ● TYC |
| ● AMD | ● CCU | ● EQR | ● JNPR | ● NEM | ● SCHW | |
| ● AMGN | ● CEG | ● ESRX | ● JPM | ● NGG | ● S | ● UBS |
| ● AMP | ● CELG | ● ETR | ● JWN | ● NHY | ● SGP | ● UL |
| ● AMT | ● CEO | ● EWJ | ● NKE | ● SHG | ● UMC | |
| ● AMX | ● CFC | ● EXC | ● KB | ● NMR | ● SHLD | ● UN |
| ● AMZN | ● C | ● KEP | ● NOC | ● SHR | ● UNH | |
| ● ANZ | ● CHK | ● FCX | ● KEY | ● NOK | ● SI | ● UPS |
| ● AOC | ● CHL | ● FDC | ● K | ● NOV | ● SKM | ● USB |
| ● APA | ● CHT | ● FDX | ● KLAC | ● NSANY | ● SLB | ● UTX |
| ● APC | ● CHU | ● FE | ● KMB | ● NSC | ● SLF | |
| ● APD | ● CI | ● F | ● KMG | ● NTT | ● SLM | ● V |
| ● ASML | ● CIT | ● FITB | ● KMI | ● NUE | ● SMP | ● VLO |
| ● AT | ● CL | ● FO | ● KNBWY | ● NVO | ● SNDK | ● VNO |
| ● AU | ● CMCSA | ● FPL | ● KPN | ● NVS | ● SNE | ● VOD |
| ● AVP | ● CME | ● FRE | ● KR | ● NWS | ● SNY | ● VZ |
| ● AXP | ● CMX | ● FRX | ● KSS | ● NXY | ● SO | |
| ● AZN | ● CN | ● FUJIY | ● KTC | ● SPG | ● WB | |
| ● | ● CNI | ● KYO | ● ODP | ● SPI | ● WBK | |
| ● BAC | ● CNQ | ● GCI | ● OMC | ● SPLS | ● WFC | |
| ● BA | ● COF | ● GD | ● L | ● ORCL | ● SPY | ● WF |
| ● BAX | ● COH | ● GDW | ● LLY | ● OTE | ● SRE | ● WFT |
| ● BBBY | ● COP | ● GE | ● LM | ● OXY | ● SSL | ● WIT |
| ● BBD | ● COST | ● GFI | ● LMT | ● STA | ● WMB | |
| ● BBL | ● CPB | ● GGP | ● LOW | ● PBRA | ● STI | ● WM |
| ● BBT | ● CSCO | ● GILD | ● LPL | ● PBR | ● STJ | ● WMT |
| ● BBV | ● CSR | ● GIS | ● LTR | ● PCAR | ● STM | ● WPPGY |
| ● BBY | ● CSX | ● GLH | ● LUV | ● PCG | ● STO | ● WY |
| ● BCE | ● CUK | ● GLW | ● LUX | ● PCU | ● STT | |
| ● BCM | ● CVS | ● GM | ● LVS | ● PCZ | ● STX | ● XL |
| ● BCS | ● CVX | ● GNW | ● LYG | ● PEG | ● SU | ● XOM |
| ● BDX | ● CX | ● GOOG | ● PEP | ● SUN | ● XRX | |
| ● BEN | ● GPS | ● MAR | ● PFE | ● SYK | ||
| ● BHI | ● DB | ● GS | ● MAS | ● PG | ● SYMC | ● YHOO |
| ● BHP | ● DCM | ● GSK | ● MBT | ● PGR | ● SYT | ● YPF |
| ● BIIB | ● DD | ● MC | ● PHG | ● SYY | ● YUM | |
| ● BK | ● DE | ● HAL | ● MCK | ● PHM | ||
| ● BMO | ● DEO | ● HBC | ● MCO | ● PKX | ● TD |
References
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. CoVaR. American Economic Review 106: 1705–41. [Google Scholar] [CrossRef]
- Aymanns, Christoph, and J. Doyne Farmer. 2015. The dynamics of the leverage cycle. Journal of Economic Dynamics & Control 50: 155–79. [Google Scholar]
- Bertschinger, Nils, and Iurii Mozzhorin. 2020. Bayesian estimation and likelihood-based comparison of agent-based volatility models. Journal of Economic Interaction and Coordination. [Google Scholar] [CrossRef]
- Boettiger, Carl, and Alan Hastings. 2012. Quantifying limits to detection of early warning for critical transitions. Journal of the Royal Society Interface 9: 2527–39. [Google Scholar] [CrossRef] [PubMed]
- Brownlees, Christian, and Robert Engle. 2017. SRISK: A conditional capital shortfall measure of systemic risk. The Review of Financial Studies 30: 48–79. [Google Scholar] [CrossRef]
- Chakraborti, Anirban, Ioane Muni Toke, Marco Patriarca, and Frédéric Abergel. 2011. Econophysics review: I. empirical facts. Quantitative Finance 11: 991–1012. [Google Scholar] [CrossRef]
- Chicago Board Options Exchange. 2019. The Cboe Volatility Index—VIX. Cboe White Papers. Available online: https://cdn.cboe.com/resources/vix/vixwhite.pdf (accessed on 20 November 2020).
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Diks, Cees, Cars Hommes, and Juanxi Wang. 2018. Critical slowing down as an early warning signal for financial crises? Empirical Economics 57: 1201–28. [Google Scholar] [CrossRef]
- Drehmann, Mathias, and Mikael Juselius. 2013. Evaluating Early Warning Indicators of Banking Crises: Satisfying Policy Requirements. Technical Report 421. Basel: Bank for International Settlements. [Google Scholar]
- Embrechts, Paul, Thomas Liniger, and Lu Lin. 2011. Multivariate hawkes processes: An application to financial data. Journal of Applied Probability 48: 367–78. [Google Scholar] [CrossRef]
- Franke, Reiner, and Frank Westerhoff. 2012. Structural stochastic volatility in asset pricing dynamics: Estimation and model contest. Journal of Economic Dynamics and Control 36: 1193–211. [Google Scholar] [CrossRef]
- Franke, Reiner, and Frank Westerhoff. 2016. Why a simple herding model may generate the stylized facts of daily returns: Explanation and estimation. Journal of Economic Interaction and Coordination 11: 1–34. [Google Scholar] [CrossRef]
- Guttal, Vishwesha, Srinivas Raghavendra, Nikunj Goel, and Quentin Hoarau. 2016. Lack of critical slowing down suggests that financial meltdowns are not critical transitions, yet rising variability could signal systemic risk. PLoS ONE 11: e0144198. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, Alan G. 1971a. Point spectra of some mutually exciting point processes. Journal of the Royal Statistical Society Series B 33: 438–43. [Google Scholar] [CrossRef]
- Hawkes, Alan G. 1971b. Spectra of some self-exciting and mutually exciting point processes. Biometrika 58: 83–90. [Google Scholar] [CrossRef]
- Liniger, Thomas. 2009. Multivariate Hawkes Processes. Ph.D. thesis, ETH Zurich, Zürich, Switzerland. [Google Scholar]
- Lux, Thomas. 2018. Estimation of agent-based models using sequential Monte Carlo methods. Journal of Economic Dynamics and Control 91: 391–408. [Google Scholar] [CrossRef]
- Lux, Thomas, and Michele Marchesi. 1999. Scaling and criticality in a stochastic multi-agent model of financial market. Letters to Nature 397: 498–500. [Google Scholar] [CrossRef]
- Lux, Thomas, and Michele Marchesi. 2000. Volatility clustering in financial markets: A microsimulation of interacting agents. International Journal of Theoretical and Applied Finance 3: 675–702. [Google Scholar] [CrossRef]
- Meisel, Christian, Andreas Klaus, Christian Kuehn, and Dietmar Plenz. 2015. Critical slowing down governs the transition to neuron spiking. PLOS Computational Biology 11: e1004097. [Google Scholar] [CrossRef]
- Ogata, Yosihiko. 1981. On Lewis’ simulation method for point processes. IEEE Transactions 27: 23–31. [Google Scholar] [CrossRef]
- Patzelt, Felix, and Klaus Pawelzik. 2013. An inherent instability of efficient markets. Scientific Reports 3: 2787. [Google Scholar] [CrossRef]
- Reinhart, Carmen M., and Kenneth S. Rogoff. 2009. This Time is Different: Eight Centuries of Financial Folly. Princeton: Princeton University Pressw. [Google Scholar]
- Samanidou, Egle, Elmar Zschischang, Dietrich Stauffer, and Thomas Lux. 2007. Agent-based models of financial markets. Reports on Progress in Physics 70: 409. [Google Scholar] [CrossRef]
- Scheffer, Marten, Jordi Bascompte, William A. Brock, Victor Brovkin, Stephen R. Carpenter, Vasilis Dakos, Hermann Held, Egbert H. van Nes, Max Rietkerk, and George Sugihara. 2009. Early-warning signals for critical transitions. Nature 461: 53–59. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, Marten, Stephen R. Carpenter, Timothy M. Lenton, Jordi Bascompte, William Brock, Vasilis Dakos, Johan van de Koppel, Ingrid A. van de Leemput, Simon A. Levin, Egbert H. van Nes, and et al. 2012. Anticipating critical transitions. Science 338: 344–48. [Google Scholar] [CrossRef] [PubMed]
- Shiller, Robert J. 2005. Irrational Exuberance. Business and Economics. Princeton: Princeton University Press. [Google Scholar]
- Stindl, Tom, and Feng Chen. 2019. Modeling extreme negative returns using marked renewal Hawkes processes. Extremes 22: 705–28. [Google Scholar] [CrossRef]
| 1. | In order to obtain volatility clustering, we had to increase ten-fold compared to the original reference. This adjustment was stable across three independent implementations of the model in Python, Haskell and C++ which all produced identical results. |
| 2. | Aymans & Farmer also discuss a policy rule for adapting . Since this does not substantially change the qualitative dynamics of the model we stick with for simplicity. |
| 3. | The bank’s equity at time t is given as . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertschinger, N.; Pfante, O. Early Warning Signs of Financial Market Turmoils. J. Risk Financial Manag. 2020, 13, 301. https://doi.org/10.3390/jrfm13120301
Bertschinger N, Pfante O. Early Warning Signs of Financial Market Turmoils. Journal of Risk and Financial Management. 2020; 13(12):301. https://doi.org/10.3390/jrfm13120301
Chicago/Turabian StyleBertschinger, Nils, and Oliver Pfante. 2020. "Early Warning Signs of Financial Market Turmoils" Journal of Risk and Financial Management 13, no. 12: 301. https://doi.org/10.3390/jrfm13120301
APA StyleBertschinger, N., & Pfante, O. (2020). Early Warning Signs of Financial Market Turmoils. Journal of Risk and Financial Management, 13(12), 301. https://doi.org/10.3390/jrfm13120301



