Abstract
In this paper, the possibility of using fundamental weighting as a tool to intentionally tilt a portfolio toward specific and unobservable risk factors in the illiquid and undeveloped Croatian stock market is explored. Thus far, fundamental-weighting has been shown to be able to outperform the cap-weighted index in such environments but no attempt regarding control for implicit factor exposure of such portfolios has been reported. Therefore, in this study principal component analysis is performed to capture the underlying risk factors of the fundamentally-weighted portfolio in order to optimize the portfolio’s performance by minimizing its volatility. Previous attempts focusing purely on portfolio risk reduction by estimating minimum variance portfolios failed both from an in-sample and out-of-sample perspective. Results in this study are based on 22 in-sample and out-of-sample tests in the period from March 2009 till March 2020. On the in-sample estimation basis, the proposed approach significantly improves the portfolio’s performance and, if restrictions to weights are imposed, it can outperform the cap-weighted benchmark. However, out-of-sample testing yielded poor results both in terms of risk and return. Such results are in contrast to findings for the developed markets but corroborate the claim that a broad investment base is needed for successful risk exposure in the long run.
1. Introduction
The Modern Portfolio Theory (MPT), based on the early work of Markowitz (1952) and Tobin (1958), introduced the concept of efficiency to asset management by maximizing the portfolio’s risk to return ratio. Further research introduced asset pricing theories such as the famous Capital Asset Pricing Model (CAPM). The CAPM represents a special case in which, among many other assumptions, there is a single factor of systematic risk. Also, the risky market portfolio is a market capitalization-weighted index enabling the model to provide the pricing framework for capital assets as presented by Sharpe (1964). However, future research had to deal with the issues of whether the market portfolio was observable, whether it necessarily had to be a cap-weighted index and whether there were more sources of systematic risk, to name a few. Regarding the last issue Arbitrage Portfolio Theory (APT) which assumes multiple factors of systematic risk was developed by Ross (1976) triggering empirical research testing and leading to a consensus that multiple factors of systematic risk exist as presented in Fama (1996). On the other hand, the research regarding the first two issues focused on the portfolio’s efficiency, seeking to optimize the reward in the form of risk premium (the return over the risk-free rate) relative to the exposure to (systematic) risk. Within this strand of research, various approaches emerged regarding efficient stock portfolio estimation ever since the market cap-weighted indices’ inefficient risk-reward ratio was exposed in equity markets by Haugen and Baker (1991) and Grinold (1992).
Over the years, the research on efficient harvesting of risk premium gradually shifted the focus from outperforming the cap-weighted benchmark toward the source of outperformance and the proper risk assessment of the newly proposed strategies (sometimes labeled the “Smart beta 2.0” approach) as discussed in Amenc et al. (2013) for instance. In this process two requirements for efficient investing, derived from the drawbacks of the cap-weighted indices and backed up by the asset pricing theory, crystallized in the research as summarized by Amenc et al. (2014): (i) efficient diversification of rewarded risk factors (efficient exposure to such factors) and (ii) efficient diversification (elimination) of unrewarded risk factors. The described process provided more efficient equity investment strategies for the developed markets (see Amenc et al. (2014) for an overview) and fostered further research in the field related to other asset classes.
This study aims to explore whether the significant progress in the field presented above can be applied to the undeveloped and illiquid stock market. Such research is scarce as researchers and practitioners alike rather focus their efforts on markets in which data availability and reliability do not present a concern. For instance, Scientific Beta Universe Construction Rules (Scientific Beta 2020) state that criteria for inclusion in the “developed market universe”, among others, include a minimum total market capitalization of 60 billion USD and a minimum turnover ratio of 10%. The reported values refer to three-year averages and the turnover ratio, as a measure of liquidity, is calculated by dividing the value of stocks traded in a year by the average market capitalization of the actual and previous year. Based on the World Bank and Zagreb Stock Exchange data, the specified indicators for the Croatian stock market are presented in Figure 1. The plotted values clearly show that both are below minimal values with the turnover ratio exhibiting a downward trend.
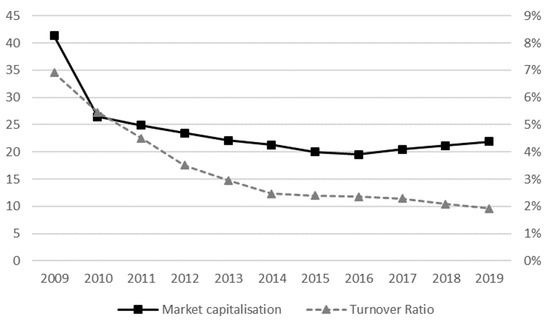
Figure 1.
Croatian stock market turnover ratio and market capitalization (three-year moving averages, market capitalization in billions of USD, the turnover ratio in %). Data from the World Bank and the Zagreb Stock Exchange.
However, in the case of the Croatian stock market, there is an additional challenge regarding the deconcentration of the Zagreb Stock Exchange’s broad-based equity market-cap-weighted index—CROBEX. In the past 11 years, the CROBEX index was composed of close to 23 constituents on average. It is free-float factor adjusted but also has a 10% maximum weight constraint leading to an average effective number of constituents of around 13 or a concentration of above 50%. This represents much higher deconcentration than in the case of cap-weighted indices in the developed markets as presented in a comprehensive overview by Amenc et al. (2006). Since developed market indices typically have many more constituents, an equivalent maximum constraint on weights to the 10% used by CROBEX would be much lower (e.g., 0.5% in the case of the S&P500 index) leading to significant deconcentration.
Amenc et al. (2006, 2011a) clearly present that poor diversification reduces efficiency and can be traced to a high concentration of market-cap-weighted benchmarks. Taking this into account helps explain why it is much more difficult to outperform the benchmark index in the Croatian stock market than in the developed markets as reported by Dolinar et al. (2017) and Zoričić et al. (2018a). It cannot be achieved by naïve diversification techniques (such as equal weighting leading to maximum deconcentration) as in the case of the developed markets. The source of outperformance in this setting, therefore, almost entirely depends on the method aimed at successful detection of the rewarded risk factors. However, it should also be paired with a proven optimization strategy regarding the reduction of exposure to unrewarded risk factors. This makes the research results based on the Croatian stock market relevant both when compared to similar research in the developed markets and in relation to other undeveloped and illiquid markets.
Based on the above, the focus of this research is testing an approach aimed at providing exposure to implicit rewarded risk factors but also taking into account the necessary control associated with it. For this purpose, this study turns to fundamental weighting following the work of Amenc et al. (2008) in order to achieve exposure to rewarded risk factors. Since in this market such factors are hardly observable and may change over time, principal component analysis (PCA) is used as suggested by Amenc et al. (2011b) for the purpose of their capturing and controlling by performing minimum variance optimization. Both in-sample and out-of-sample testing of the designed approach is performed by matching the cap-weighted benchmark’s (CROBEX index) composition for each index revision period. Altogether, 22 samples are tested in the observation period spanning from March 2009 till March 2020.
The main contribution of this paper is related to the research efforts focused on capturing the rewarded risk factors by conducting PCA in an illiquid and undeveloped market based on the fundamentally-weighted portfolio as a factor tilted investment strategy. Furthermore, the paper aims to explore whether minimum variance optimization can be applied to diversify away the unrewarded risk in such portfolios. The results of this study demonstrate that the approach used is able to notably improve the effect of applying the minimum variance optimization, albeit only on an in-sample basis and prior to the most recent decrease in liquidity. Regarding the out-of-sample estimation testing, the results, unfortunately, do not show any improvement over the previous attempts to implement efficient investing strategies in the analyzed setting, supporting the research suggesting that a broad investment base is needed for successful risk exposure in the long run.
The rest of the paper is organized as follows. A literature review is presented in the second section, while the third describes the data and methodology. The fourth section contains the findings of the empirical research followed by the discussion and concluding remarks.
2. Literature Review
The overview of strategies aimed at efficient diversification of unrewarded risk factors is best summarized by Amenc et al. (2013). For the purpose of research, in this paper, only a part of the mentioned overview is presented here in Table 1 below.

Table 1.
Overview of diversification strategies regarding unrewarded risk factors. Reproduced with permission from Amenc, Noël, Felix Goltz, and Lionel Martellini, Smart Beta 2.0., EDHEC-Risk Institute, 2013.
As presented in Table 1, the market-cap-weighted portfolio (or market index) can only be the optimal portfolio if the CAPM assumptions hold, which theoretically underpins the empirical findings regarding their inefficiency mentioned in the introduction section. Based on the MPT, the optimal portfolio regarding diversification of unrewarded risk factors is the Maximum Sharpe Ratio (MSR) portfolio. Since the Sharpe ratio measures the risk premium earned relative to a portfolio’s volatility, maximizing the MSR maximizes the investor’s risk-reward ratio. However, estimating the MSR portfolio requires the estimation of three parameters—most of all, strategies. Therefore, although this strategy does not involve any optimality risk, the parameter estimation risk is the highest. The Equally-Weighted (EW) portfolio represents the opposite extreme, while Minimum Variance Portfolios (MVP) and Risk Parity Portfolios (RPP) offer a trade-off between the two components of the risk the investors face.
Although the above-mentioned strategies aim to increase portfolio efficiency, they do so by eliminating the unrewarded (specific) risk, but they do not take into account multiple sources of systematic risk. As presented in Amenc et al. (2014) the efficient investment strategy, therefore, also needs to efficiently diversify exposure to rewarded risk factors aiming to achieve the maximum return (risk premium) per unit of systematic risk. The importance of the two-step process is emphasized due to the fact that diversification of unrewarded factors alone exposes investors to systematic risk factors, although not necessarily efficiently. As presented in Amenc et al. (2008), the outperformance of EW and Fundamentally-Weighted (FW) portfolios over the cap-weighted benchmark has been shown to be driven by exposure to rewarded risk factors other than the market factor. Based on the papers by Fama and French (1992) and Carhart (1997), these factors are typically: market, value, size, and momentum.
As pointed out, for example, by Lee and Kim (2018) the popularity of the above-mentioned strategies, often referred to as “smart beta”, has been growing since the global financial crisis filling in the role of traditional active asset management. However, in the case of emerging, let alone undeveloped and illiquid markets, comparable research is hard to find. Hamza et al. (2006) performed a somewhat comparable analysis as they addressed the benchmark issue for the emerging markets arguing in favor of the equally-weighted index. Madsstuen (2015) tested some strategies proposed as alternatives to the cap-weighted index but focused on the emerging markets’ performance potential relative to the developed markets, not on the strategies themselves. Nowak (2016) provided the only true comparable research that could be found related to testing the alternative weighting schemes on the WIG 20 index for the Polish market on the Warsaw Stock Exchange. Fundamental weighting, equal weighting, minimum variance, and maximum Sharpe ratio strategies all out-performed the benchmark but the analysis was most likely (based on the reported results) performed on an in-sample basis. Therefore, the rest of the research on the undeveloped and illiquid markets is related to the Croatian stock market. Also, as already mentioned in the introduction, outperforming the CROBEX index (market-cap-weighted equity benchmark) seems to be quite difficult to achieve.
Although it has been well documented by, for example, Amenc et al. (2006, 2011a), that cap-weighted indices in the developed markets are ill-diversified (offer limited exposure to long-term rewarded risk factors) and highly concentrated (poorly diversify away the exposure to unrewarded risk factors), in the case of CROBEX index, the deconcentration is relatively high. Therefore, unlike in the developed markets, equal weighting (naïve strategy maximizing deconcentration) does not outperform the cap-weighted benchmark index. On the contrary, it performs much worse both in terms of risk (measured by volatility) and return as reported in Dolinar et al. (2017). It can be argued, based on the empirical evidence, that in these specific market conditions additional deconcentration leads to unnecessary exposure to unrewarded risk factors. Since Dolinar et al. (2017) and Zoričić et al. (2018a) also reported that Maximum Sharpe Ratio (MSR) and Minimum Variance Portfolio (MVP) out-of-sample estimation failed to outperform the cap-weighted benchmark too, the question is raised whether a more efficient alternative to cap-weighting, as suggested by Amenc et al. (2014), can be provided. It should be mentioned, however, that while the MSR portfolio out-of-sample performance was quite similar to the equally-weighted portfolio (and only marginally better), the MVP estimation did yield a reduction in volatility. Unfortunately, the reported reduction came at the high cost of a much stronger decline in the portfolio’s return. This was also shown to be true even in the case of in-sample analysis by Škrinjarić et al. (2018). The issue regarding the stated research question therefore seems to be whether exposure to additional rewarded risk factors that could provide the source of (out) performance is possible and whether such exposure can be allocated efficiently.
Expanding the results of Kovačević et al. (2017), whose research results suggested the possibility of outperforming the CROBEX index by a fundamentally-weighted portfolio, this study aims to provide answers to the above question. The results of Kovačević et al. (2017) were further analyzed by Zoričić et al. (2018b) who used the Fama French three-factor model and an additional factor accounting for exposure to illiquid stocks. Although, research typically, as in Amenc et al. (2008, 2013), reports size and value factor tilts, Zoričić et al. (2018b) found significant exposures only to the market factor and liquidity risk (which can be associated to any strategy deviating from cap-weighting) related to the analyzed portfolio. However, due to specific market conditions, it cannot be claimed that the two detected risk factors are the only underlying rewarded sources of risk. Therefore, in this research, following Amenc et al. (2011b), the agnostic approach is taken and PCA is applied in order to try to capture the unobservable underlying rewarded risk factors of EBITDA fundamentally-weighted portfolio in Kovačević et al. (2017). Based on the PCA results, minimum variance optimization is performed in order to minimize the risk of the rewarded-risk-factor-seeking strategy. However, due to the fact that, as reported in Škrinjarić et al. (2018), the estimation of minimum variance portfolios in the illiquid and undeveloped stock market performed poorly even when in-sample estimation was analyzed, in-sample testing is conducted before carrying out out-of-sample estimation to complete the analysis.
Lastly, since the diversification effect relying on further deconcentration of the cap-weighted benchmark seems to be non-existent, the focus shifts to efficient exposure to the rewarded risk factors as the source of outperforming the CROBEX index. In this regard, it should be noted that the failure of the alternative strategies tested by Dolinar et al. (2017) and Zoričić et al. (2018a) has been blamed on fewer investment opportunities and unreliable data related to low liquidity. Unreliable data present a special challenge steering the out-of-sample estimation efforts towards strategies with lower parameter estimation risk (and lower optimality) as discussed in Amenc et al. (2013). However, the fewer investment opportunities problem seems to have even stronger implications as Amenc et al. (2016) provide empirical evidence of the importance of broad-based strategies and factor diversification as key components for successful risk exposure in the long run which emphasizes the importance of the findings in this paper.
3. Materials and Methods
Given the fact that the Croatian capital market is undeveloped and illiquid, this research is based on the CROBEX index, which is, as mentioned in the introduction, its most important benchmark. It is subject to regular revisions twice a year (in March and in September) and to extraordinary revisions. For the purpose of this analysis, only the regular revisions are taken into account.
The research covers the period from March 2009, which is the beginning of the CROBEX index’s first regular revision in 2009, till March 2020, which is the end of the second regular revision in 2019. In total, 22 regular revisions were taken into account in the analyzed period. During this time, the number of constituents of the CROBEX index varied from 15 to 25 stocks. A total number of 54 stocks were included in the index in the observed period and all of them were included in the analysis since the composition of the proposed efficient benchmark is matched for each revision to the CROBEX for the purpose of performance comparison.
As a starting point, the work of Kovačević et al. (2017) is followed since in that paper, fundamentally-weighted indices were constructed in order to test their out-of-sample performance relative to the CROBEX. The only index which succeeded to outperform the CROBEX index was a fundamentally-weighted index based on EBITDA fundamental indicators with a restriction imposed on the maximum weight of each constituent. Based on the reported results, this study solely focuses on the fundamentally-weighted EBITDA index (hereinafter “FW” refers to this particular portfolio), that is, on its composition, in order to analyze the sources of its higher returns that facilitate the outperformance of CROBEX. In Kovačević et al. (2017) weight of each stock in a fundamentally-weighted index was calculated based on fundamental indicators, in this case, EBITDA, using the following formula:
where is the fundamental weight of each index constituent i in revision t, and is the three-year average of fundamental indicators for the preceding three years. In the case of a negative value of a fundamental indicator, assigned weight to the constituent was set to zero in order to regard the fact that short selling is not allowed in the Croatian stock market. In order to achieve greater portfolio deconcentration, by following the work of Amenc et al. (2011b), restriction on the maximum weight of a constituent was introduced by setting the limit equal to /N, where N is the number of constituents in each revision and is an arbitrary parameter which was set to 5. Thus, the maximum weight of a stock in the fundamentally-weighted index was restricted from 20.0% to 33.3% depending on the number of constituents in a revision.
After obtaining fundamental weights for each revision period, in-sample and out-of-sample estimation are carried out. The in-sample estimation process is based on a “fundamentally-weighted” 26-week time-series window of returns of CROBEX constituents for each revision. The out-of-sample estimation process is based on a “fundamentally-weighted” 52-week time-series rolling-window of returns of CROBEX constituents preceding each revision. Such time-series of returns (separately for in-sample and out-of-sample analysis) are calculated using the following formula:
and are used as inputs for covariance-based PCA.
After running the PCA, factor loadings, matrix B is obtained which is used for the construction of factor returns matrix F. Based on this, a covariance matrix of factor returns denoted as Λ is calculated. Taking the pairs of factor loadings from matrix B and eigenvalues from the covariance matrix of factor returns Λ, results in PCA decomposition of the covariance matrix of stock returns denoted by , for a chosen number of components m:
In this way, this study follows Amenc et al. (2011b) in decomposing the sample covariance matrix in order to explain covariance structures by using only a few linear combinations of the original stochastic variables. In other words, such an estimated PCA-based covariance matrix is used as input for the in-sample and out-of-sample performance estimation of the proposed efficient benchmark. Hence, the estimated covariance matrix is used for in-sample and out-of-sample MVP optimization. Optimal weights of constituents of MVP are found by solving the following problem:
where w* is the vector of weights (i.e., optimal weights) that meets the above optimization problem, 1 is the vector of ones, and is the estimated covariance matrix of stock returns obtained from PCA as described above. Performance of MVP is estimated using semi-annual returns (matching CROBEX revision twice a year). Since in this paper, 22 regular revisions of the CROBEX index are covered, MVP is estimated 22 times over for 22 different data samples for in-sample and out-of-sample testing respectively. Finally, the in-sample and out-of-sample performance of MVP for the whole observed period is compared to the CROBEX index as the cap-weighted benchmark.
In addition, in order to decrease portfolio concentration in the process of optimization restriction on the minimum weight of a constituent is imposed by defining the lower limit as follows:
Higher value implies that weaker constraint is imposed leading to higher portfolio concentration. In this research, was set to different levels in order to test the portfolio’s (de)concentration on its performance. In addition, in order to ennoble this analysis, besides using a “fundamentally-weighted” time-series window of returns, for the in-sample analysis, original (untilted, i.e., not weighted) weekly returns of CROBEX constituents are also used for each revision as well. Analysis performed for such returns refers to formulas (3) to (6).
4. Results
4.1. In-Sample Analysis
The results of the performed optimization process using “fundamentally-weighted” returns as inputs for PCA on an in-sample basis are shown in Table 2 below. Average returns refer to geometric mean and are calculated based on semi-annual returns while volatility refers to their standard deviation.

Table 2.
Performance of the estimated MVP using “fundamentally-weighted” returns as inputs for PCA.
Table 2 presents in-sample testing results conducted in this study for the two halves of the observation period separately and for the whole observation period. Since 22 samples (CROBEX index revision periods) were analyzed overall, each half should contain 11 samples. However, in the second half of the period, only 10 samples are included to highlight the impact of the last CROBEX revision on the overall results.
The reported results show that based on the proposed approach, the estimated MVP benchmark is generally able to produce a higher risk to reward ratio, therefore, outperforming CROBEX in the observed period. However, results seem to point out that risk-return ratios are higher when minimum variance optimization is based on only one principal component and when constraints on portfolio weights are imposed ( = 4). Nevertheless, the source of higher risk-return ratios in the case of optimization based on one principal component are clearly higher returns accompanied by higher levels of volatility. Therefore, in this case, this study did not find any period in which the minimum variance optimization was able to produce a portfolio with volatility lower than the cap-weighted benchmark. On the other hand, minimum variance optimization based on two principal components is able to provide evidence that portfolio returns can be increased relative to the CROBEX while exhibiting portfolio risk reduction. The effect, however, is pronounced when constraints to the portfolio weights are applied, allowing the MVP portfolio to dominate over CROBEX in terms of risk for 11 consecutive CROBEX revision periods (half of the analyzed samples) in the period from March 2011 to September 2016. After this period, the specified portfolio still produced the lowest volatility of all analyzed portfolios second only to the benchmark index. This turn for the worse seems to coincide with the latest downward trend in market liquidity depicted in Figure 1 by the turnover ratio indicator. In the last analyzed sample, in which the turnover ratio fell to close to 2%, only the portfolio based on one principal component and restrictions on weights was able to outperform the benchmark. Both portfolios based on the two principal components recorded even negative returns, causing their poor overall performance. Thus, the last analyzed sample demonstrates how sensitive deviations from the cap-weighted benchmark are in the analyzed market even on an in-sample basis. It can also be noted that the same approach to data sampling and CROBEX composition matching is applied to the equally-weighted benchmark (for which no estimation is needed). Results presented in Table 2 are in line with earlier findings that the EW portfolio does not outperform the CROBEX index in any period, but they do reveal that it is more evenly matched to the tested portfolios towards the end of the observation period.
In order to validate the obtained results, further analysis is conducted by performing the same optimization process, however, based on samples of original (untilted) stock returns.
Table 3 results corroborate the domination of the fundamental-weighting method presented in Table 2 as the estimated MVP benchmark is not able to outperform CROBEX in the observed period. The PCA-based minimum variance optimization is able to decrease portfolio risk, which is the aim of a minimum variance optimization, but the portfolio return decreases even more (i.e., it is negative in all cases). This is in line with findings for minimum variance portfolios both in the out-of-sample and in-sample estimation in Zoričić et al. (2018a) and Škrinjarić et al. (2018). There are no significant differences in the results whether restrictions on the minimum weight of a constituent are imposed or not.

Table 3.
Performance of the estimated MVP using original (untilted) returns as inputs for PCA.
Since results from Table 2 favor “fundamentally-weighted” returns and since estimates based on the first two components with constraints imposed on weights outperform the benchmark but also provide evidence of risk reduction relative to CROBEX, further analysis is carried out for different levels of constraints on minimum weights in order to test them. Results are reported for the first 21 samples since the last revision period significantly distorted the overall results. Table 4 shows that for the value of parameter equal to 3, the analyzed portfolio still outperforms the benchmark. Moreover, the results show that as is set lower (e.g., equal to 2), imposing higher portfolio deconcentration ( implies equally-weighted portfolio), the portfolio performance deteriorates due to a greater decrease in return than in portfolio volatility. Most alarmingly, portfolio concentration in case of = 4 stands on average at a stunning 12.31% (corresponding to an effective number of stocks in the portfolio of only 2.83 on average). Reducing to 2 brings concentration on average to 20.53% but reduces portfolio performance. The results lead to the conclusion that outperforming a cap-weighted benchmark in the analyzed circumstances is possible but leads to extreme portfolio concentration. Portfolio performance is very sensitive to imposing restrictions on portfolio weights leading to the conclusion that results are not robust and suggesting that, due to high concentration, cannot be properly associated with diversification effects.

Table 4.
Performance of the estimated MVP (using “fundamentally-weighted” returns as inputs for PCA; two factors and different levels of on minimum).
4.2. Out-of-Sample Analysis
The results of the performed out-of-sample optimization process using “fundamentally-weighted” returns as inputs for PCA are shown in Table 5 below.

Table 5.
Out-of-sample performance of the estimated MVP using “fundamentally-weighted” returns as inputs for PCA.
While in-sample analysis provided evidence of improvement in MVP estimation when “fundamentally-weighted” returns were used the research results show that the proposed method does not meet the challenges of out-of-sample estimation. Table 4 results expose the dramatic failure of the out-of-sample performance of the estimated MVP in all analyzed cases (thus no sub-periods are reported here). Returns decrease significantly and become negative. Also, PCA-based minimum variance optimization is not able to decrease portfolio volatility regardless of the number of components used and restrictions on the weights imposed. In fact, adding additional components for the estimation, in contrast to previous conclusions, even yields poorer results. Such poor performance of out-of-sample analysis is unfortunately in line with previous research by Dolinar et al. (2017) revealing large estimation errors.
5. Discussion and Conclusions
The research addresses the challenge of implementing efficient investment strategies in the specific environment related to the illiquid and undeveloped Croatian equity market. If the effect of data reliability in this setting is ignored, the main issue is related to the successful capturing and diversification of the rewarded risk factors in a market offering fewer investment opportunities. This issue is emphasized by the relatively high deconcentration of CROBEX as the cap-weighted benchmark index which is, therefore, unlike in the developed markets, not outperformed by the equally-weighted portfolio. On the contrary, empirical evidence seems to point out that such naïve deconcentration only increases unrewarded risk factor exposure in the Croatian equity market. Therefore, it can be argued that the source of the increase in efficiency relative to the CROBEX index rests dominantly on the diversification benefits of the rewarded risk factors.
In an attempt to capture the rewarded risk factors in this study, PCA is performed on the EBITDA fundamentally-weighted portfolio, which outperformed CROBEX as reported in Kovačević et al. (2017). In order to efficiently diversify unrewarded risk factors of the factor tilted returns, minimum variance optimization is applied. Research findings show that it is possible to outperform the benchmark, albeit on an in-sample basis. The results of in-sample testing demonstrate that the tested fundamentally-weighted minimum variance portfolios outperform the cap-weighted benchmark (especially if restrictions on minimum weights of a portfolio are imposed) for most of the observed period. On the other hand, they also reveal that minimum variance optimization was not able to reduce the volatility of portfolio returns when based on only one principal component. Nevertheless, results provide evidence that, based on two principal components, portfolio volatility can be reduced while maintaining a positive portfolio return. This is contrary to results presented in Škrinjarić et al. (2018) suggesting that exposure to rewarded risk factors as advocated by Amenc et al. (2014) plays an important role even in the illiquid and undeveloped markets. However, in the case of optimization based on two principal components, the results regarding both risks and return underperform the benchmark during the most recent decline in liquidity indicating the sensitivity of deviation from the benchmark in the analyzed environment. Furthermore, results show that outperformance depends strongly on the constraints imposed on the weights in the optimization process. Also, regardless of the constraints imposed, the portfolio concentration in this study is extremely high leading to the conclusion that in order to expose to the rewarded risk factors in the analyzed market conditions, one needs to highly concentrate a portfolio. This is in contrast to the empirical findings for the developed markets. Therefore, the failure of out-of-sample testing corroborates the findings by Amenc et al. (2016), who demonstrate that a broad investment base is needed for efficient long-run rewarded factor exposure.
Nevertheless, regarding the portfolio out-of-sample estimation failure, a few limitations to the approach in this study should be considered. One is related to relying on the principal components approach for the purpose of capturing the unobservable rewarded risk factors. Although the principal components provide a set of uncorrelated factors, as thoroughly elaborated in the Meucci et al. (2015), they do involve several issues. The most relevant issues, related to the analysis conducted in this study, seem to be the statistical instability of principal components and the fact that they are not unique leading to multiple possible combinations of factors. Therefore, as suggested by Meucci et al. (2015) and other research papers following the approach, like Martellini and Milhau (2017), the minimum linear torsion method is preferred over the PCA.
Another limitation is related to the choice of a proxy for the optimal (MSR) portfolio. The minimum variance optimization method applied in this research was preferred over other methods since the research by Zoričić et al. (2018a) provided evidence of successful volatility reduction in MVP out-of-sample testing in the same market. On the other hand, from the theoretical standpoint, as presented by Amenc et al. (2013), other strategies focusing on efficient diversification of unrewarded risk involve a greater number of optimality conditions. For MVP there is only one—equal returns of portfolio constituents. An alternative method, aimed at portfolio risk reduction, which can be modified in order to be implemented in factor space is risk parity. The factor space derivative is referred to as “factor risk parity” as presented in Martellini and Milhau (2017). The method relies on the estimation of the same parameters as in the case of MVP, therefore, not increasing the parameter estimation risk of the model. Also, the method does not aim to minimize the portfolio risk but nevertheless allows for risk control by aiming to achieve equal contribution of risk factors to the portfolio risk. Moreover, another derivative, the “relaxed risk parity” method recently suggested by Gambeta and Kwon (2020) introduces even more flexibility by allowing for controlled deviations from the risk parity in a portfolio in order to increase the portfolio’s return during bullish periods in the market while reverting to risk parity in downturns.
Lastly, it should be noted that the conclusions drawn in this study are based on the analysis of only one market. Since the results provided in this study point out that in the case of out-of-sample testing, deviations from the market-cap-weighted benchmark suffer from both increase in volatility and fall in profitability, future research efforts based on the mentioned recent advances could help to significantly improve out-of-sample portfolio estimation and verify the results by analyzing different illiquid and undeveloped markets.
Author Contributions
Conceptualization, D.Z.; methodology, Z.L.G. and D.D.; validation, D.Z., D.D., and Z.L.G.; formal analysis, D.Z., D.D., and Z.L.G.; investigation, D.D. and Z.L.G.; resources, D.D. and Z.L.G.; data curation, D.D. and Z.L.G.; writing—original draft preparation, D.Z., D.D., and Z.L.G.; writing—review and editing, D.Z. and D.D.; visualization, Z.L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arnott, Robert, Jason Hsu, and Philip Moore. 2005. Fundamental Indexation. Financial Analysts Journal 61: 83–99. [Google Scholar] [CrossRef]
- Amenc, Noël, Felix Goltz, and Véronique Le Sourd. 2006. Assessing the Quality of Stock Market Indices: Requirements for Asset Allocation and Performance Measurement. An EDHEC Risk & Asset Management Research Centre Publication. Nice: EDHEC Risk and Asset Management Research Centre. [Google Scholar]
- Amenc, Noël, Felix Goltz, and Véronique Le Sourd. 2008. A Comparison of Fundamentally Weighted Indices: Overview and Performance Analysis. Nice: EDHEC Risk and Asset Management Research Centre. [Google Scholar]
- Amenc, Noël, Lionel Martellini, Felix Goltz, and Shuyang Ye. 2011a. Improved Beta? A Comparison of Index-Weighting Schemes. Nice: An EDHEC-Risk Institute Publication. [Google Scholar]
- Amenc, Noël, Felix Goltz, Lionel Martellini, and Patrice Retkowsky. 2011b. Efficient Indexation: An Alternative to Cap-Weighted Indices. The Journal of Investment Management 9: 1–23. [Google Scholar]
- Amenc, Noël, Felix Goltz, and Lionel Martellini. 2013. Smart Beta 2.0. Nice: EDHEC-Risk Institute. [Google Scholar]
- Amenc, Noël, Felix Goltz, Ashish Lodh, and Lionel Martellini. 2014. Towards Smart Equity Factor Indices: Harvesting Risk Premia without Taking Unrewarded Risks. Journal of Portfolio Management 40: 106–22. [Google Scholar] [CrossRef]
- Amenc, Noël, Frédéric Ducoulombier, Felix Goltz, Ashish Lodh, and Sivagaminathan Sivasubramanian. 2016. Diversified or Concentrated Factor Tilts? The Journal of Portfolio Management 42: 64–76. [Google Scholar] [CrossRef]
- Carhart, Mark. 1997. On Persistence in Mutual Fund Performance. Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2009. Optimal versus Naïve Diversification: How Inefficient is the 1/N Portfolio Strategy? Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef]
- Dolinar, Denis, Davor Zoričić, and Antonija Kožul. 2017. Towards the Estimation of an Efficient Benchmark Portfolio: The Case of Croatian Emerging Market. Zagreb International Review of Economics & Business 20: 13–24. [Google Scholar] [CrossRef][Green Version]
- Fama, Eugen. 1996. Multifactor Portfolio Efficiency and Multifactor Asset Pricing. Journal of Financial and Quantitative Analysis 31: 441–65. [Google Scholar] [CrossRef]
- Fama, Eugen, and Kenneth French. 1992. The Cross-Section of Expected Stock Returns. Journal of Finance 47: 427–67. [Google Scholar] [CrossRef]
- Grinold, Richard C. 1992. Are Benchmark Portfolios Efficient? The Journal of Portfolio Management 19: 34–40. [Google Scholar] [CrossRef]
- Gambeta, Vaughn, and Roy Kwon. 2020. Risk Return Trade-Off in Relaxed Risk Parity Portfolio Optimization. Journal of Risk and Financial Management 13: 237. [Google Scholar] [CrossRef]
- Hamza, Olfa, Mohamed Kortas, Jean-François L’Her, and Mathieu Roberge. 2006. International equity portfolios: Selecting the right benchmark for emerging markets. Emerging Markets Review 7: 111–28. [Google Scholar] [CrossRef]
- Haugen, Robert A., and Nardin L. Baker. 1991. The Efficient Market Inefficiency of Capitalization-Weighted Stock Portfolios. The Journal of Portfolio Management 17: 35–40. [Google Scholar] [CrossRef]
- Israelsen, Craig L. 2005. A refinement to the Sharpe ratio and information ratio. Journal of Asset Management 5: 423–27. [Google Scholar] [CrossRef]
- Kovačević, Mario, Davor Zoričić, and Zrinka Lovretin Golubić. 2017. Primjena indeksa temeljenih na fundamentalnim pokazateljima na hrvatskom tržištu kapitala. Zbornik Ekonomskog fakulteta u Zagrebu 15: 29–44. [Google Scholar] [CrossRef]
- Lee, Yongjae, and Woo Chang Kim. 2018. Why your smart beta portfolio might not work. International Journal of Financial Engineering and Risk Management 2: 351–62. [Google Scholar] [CrossRef]
- Madsstuen, Ola Simenstad. 2015. Investments in Emerging Markets: Alpha and the Benefits of Active Portfolio Management. Master’s thesis, Norwegian University of Life Sciences, Ås, Norway. [Google Scholar]
- Maillard, Sebastien, Thierry Roncally, and Jerome Teiletche. 2010. The Properties of Equally Weighted Risk Contribution Portfolios. Journal of Portfolio Management 36: 60–70. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Martellini, Lionel, and Vincent Milhau. 2017. Proverbial Baskets Are Uncorrelated Risk Factors! A Factor-Based Framework for Measuring and Managing Diversification in Multi-Asset Investment Solutions. The Journal of Portfolio Management 44: 8–22. [Google Scholar] [CrossRef]
- Meucci, Attilio, Alberto Santangelo, and Romain Deguest. 2015. Measuring Portfolio Diversification Based on Optimized Uncorrelated Factors. Risk 11: 70–75. [Google Scholar] [CrossRef]
- Nowak, Kamil. 2016. Implementation of alternative index weighting to Warsaw stock exchange. Copernican Journal of Finance & Accounting 5: 163–79. [Google Scholar]
- Ross, Stephen A. 1976. The arbitrage theory of capital asset pricing. Journal of Economic Theory 13: 341–60. [Google Scholar] [CrossRef]
- Scientific Beta. 2020. Scientific Beta Universe Construction Rules. June. Available online: https://www.scientificbeta.com/#/documentation/ground-rules/scientific-beta-universe-construction-rules (accessed on 25 November 2020).
- Sharpe, Willliam. 1964. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance 19: 425–42. [Google Scholar]
- Škrinjarić, Tihana, Davor Zoričić, and Denis Dolinar. 2018. Application of Luenberger shortage function on the Zagreb Stock Exchange: Analysis of efficient market portfolio. Croatian Operational Research Review 9: 183–97. [Google Scholar] [CrossRef]
- Tobin, James. 1958. Liquidity Preference as Behavior towards Risk. Review of Economic Studies 25: 65–85. [Google Scholar] [CrossRef]
- Zoričić, Davor, Denis Dolinar, and Zrinka Lovretin Golubić. 2018a. A test of global minimum variance portfolio in the Croatian capital market. In Book of Proceedings of 7th International Scientific Symposium Economy of Eastern Croatia-Vision and Growth. Osijek: Sveučilište Josipa Jurja Strossmayera u Osijeku, Ekonomski fakultet u Osijeku, pp. 1165–73. [Google Scholar]
- Zoričić, Davor, Denis Dolinar, and Zrinka Lovretin Golubić. 2018b. Performance Analysis of Fundamentally-Weighted Indices in the Croatian Capital Market. Zagreb International Review of Economics 21: 45–53. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).