Multifractal Analysis of Market Efficiency across Structural Breaks: Implications for the Adaptive Market Hypothesis
Abstract
1. Introduction
- To assess the impact of structural breaks on the long-memory in the price, volume, and price-volume relationship;
- To detect the possible change in the price-volume relationship among these breaks.
2. Literature Review
2.1. Multifractality and Price-Volume Relationship
2.2. MFDCCA and the Adaptive Market Hypothesis
3. Methodology
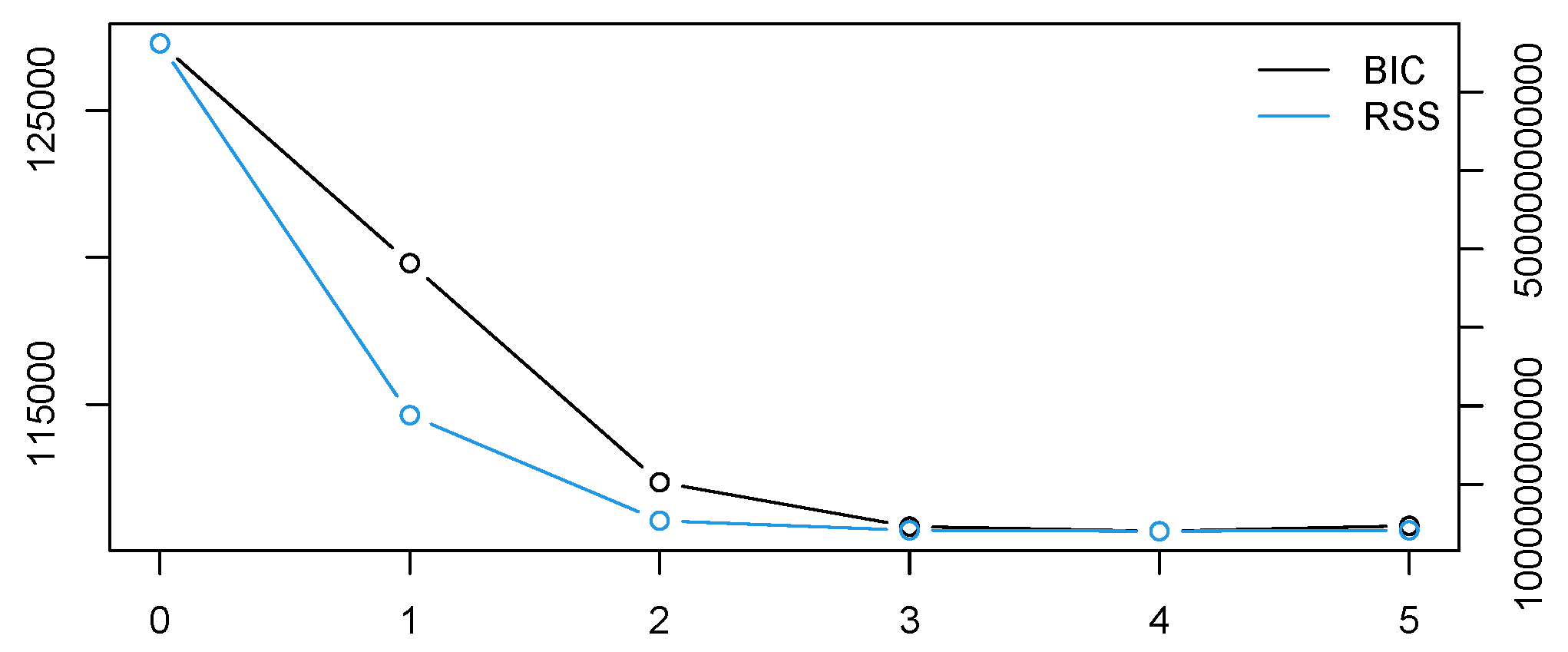
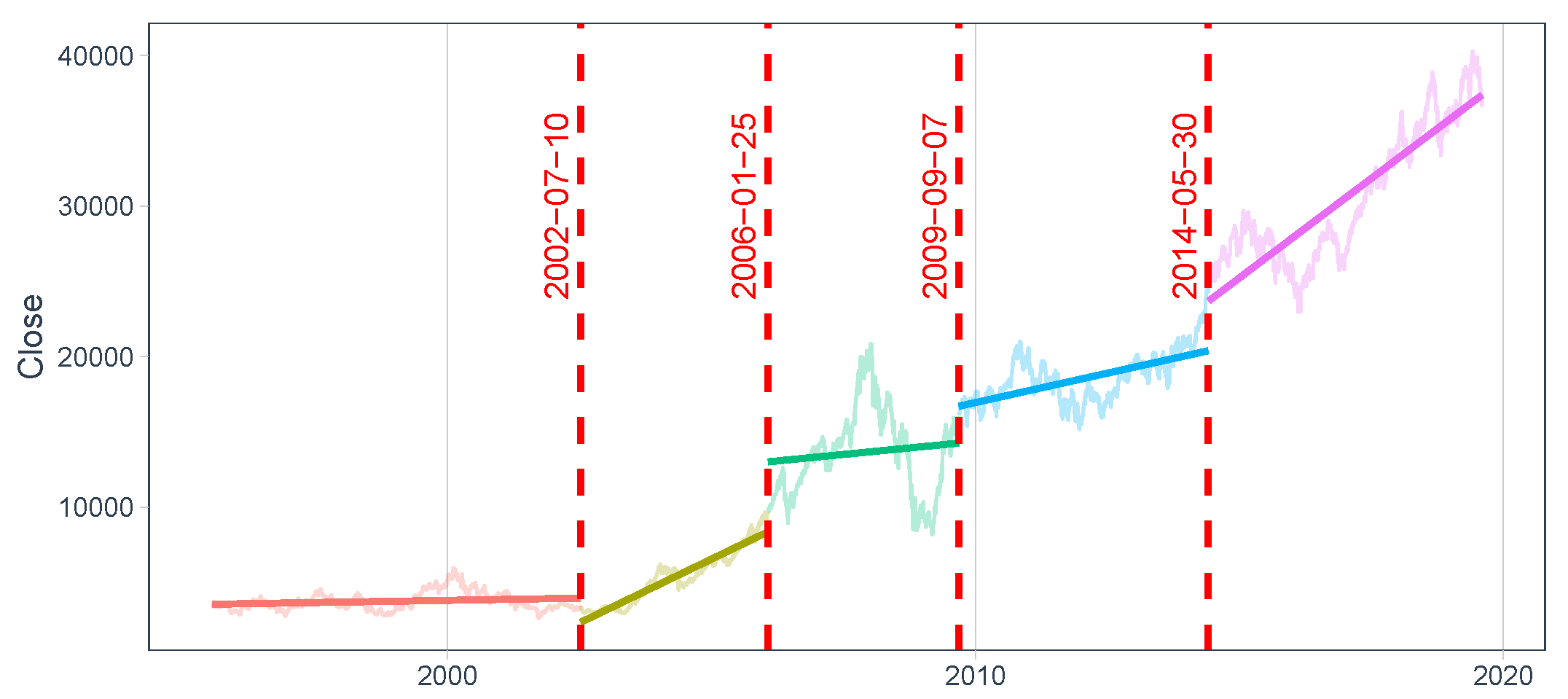
3.1. Structural Breaks
3.2. Detrended Fluctuation Analysis
3.3. MFDFA
- a
- The detrended residuals are calculated using the following equation:
- b
- The fluctuation function is calculated as the RMS of the detrended residuals:
- c
- The order of the fluctuation function is calculated for a given value of q.
- d
- The power law relation is then described by the equation:
3.4. MFDCCA
4. Data and Analysis
4.1. Data
4.2. Analysis of Structural Breaks
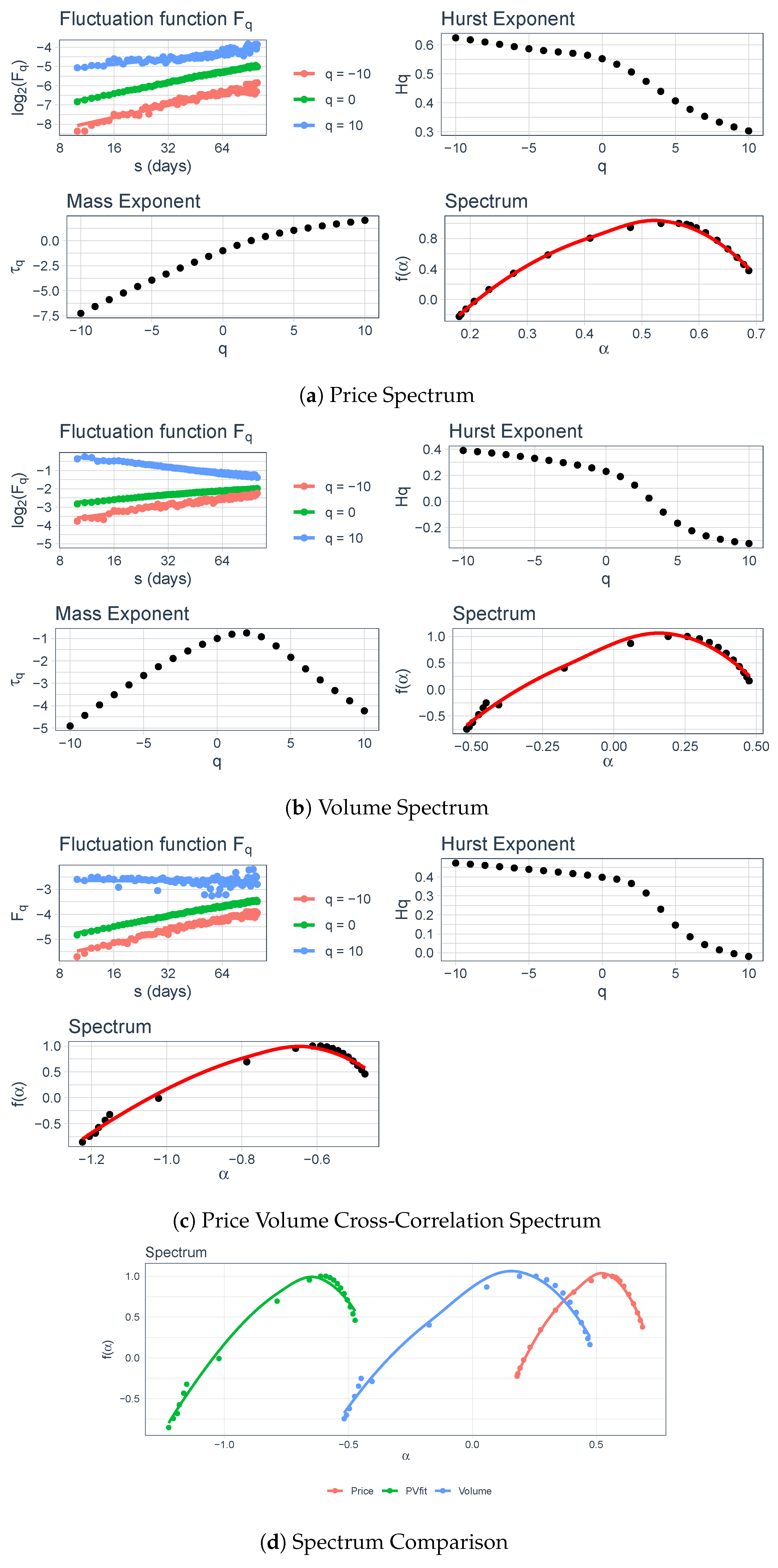
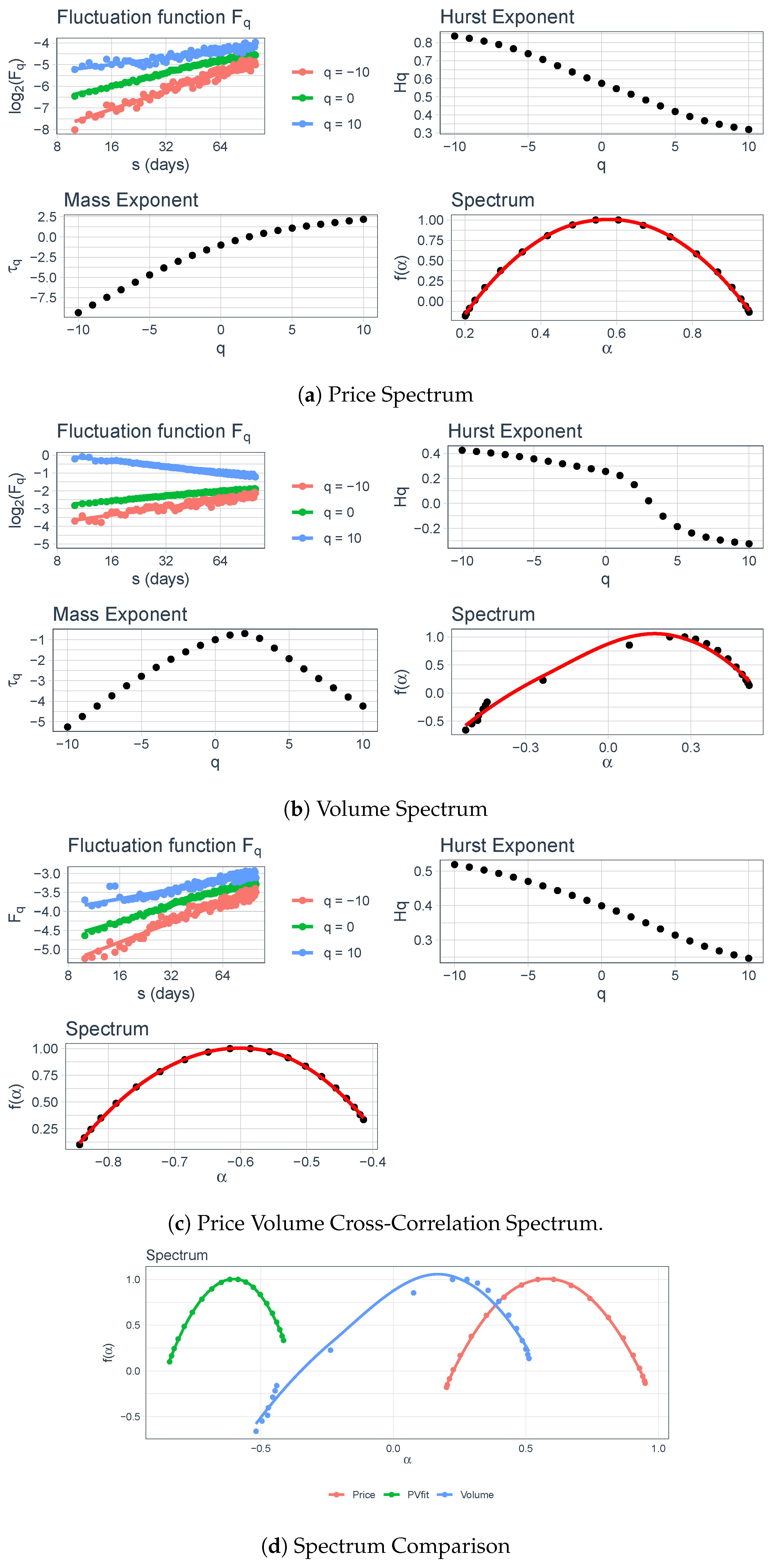
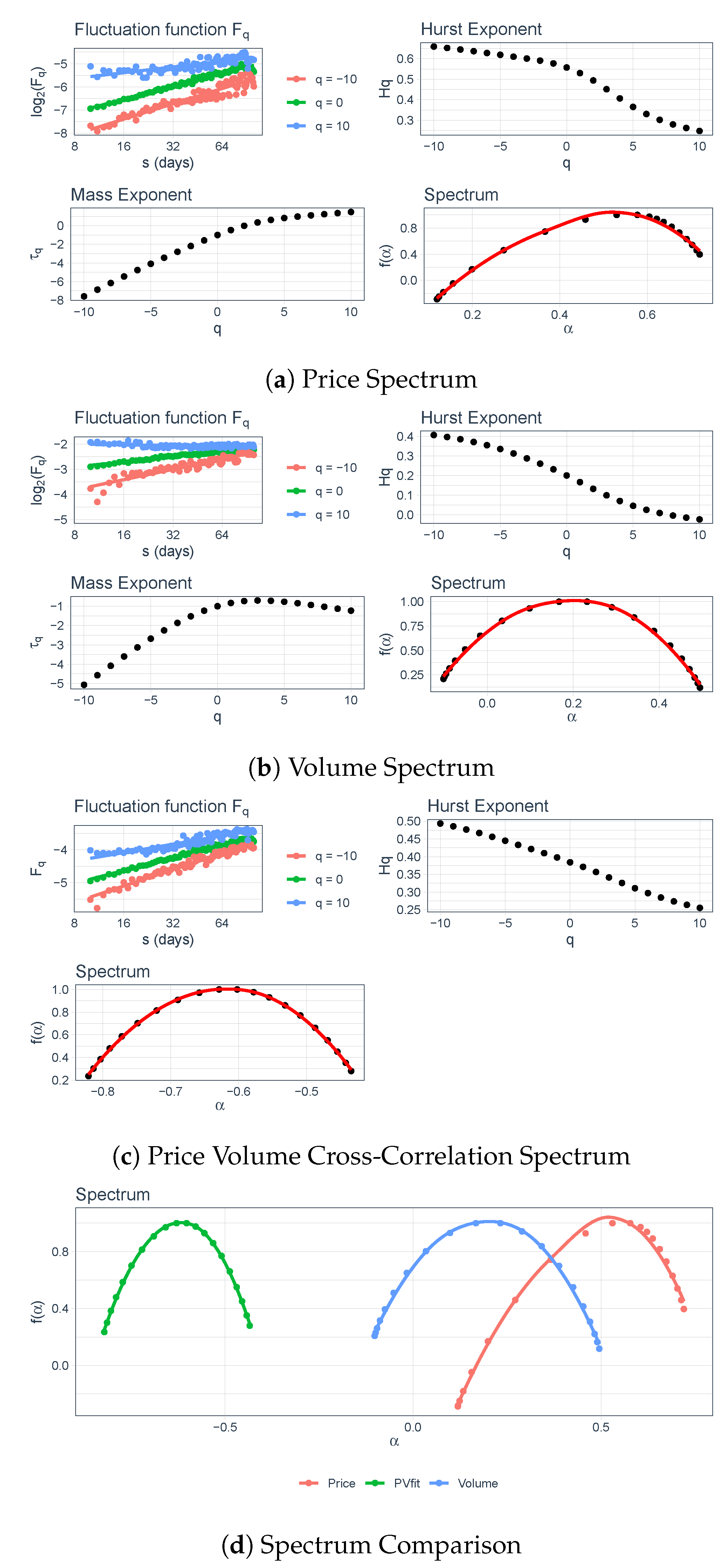
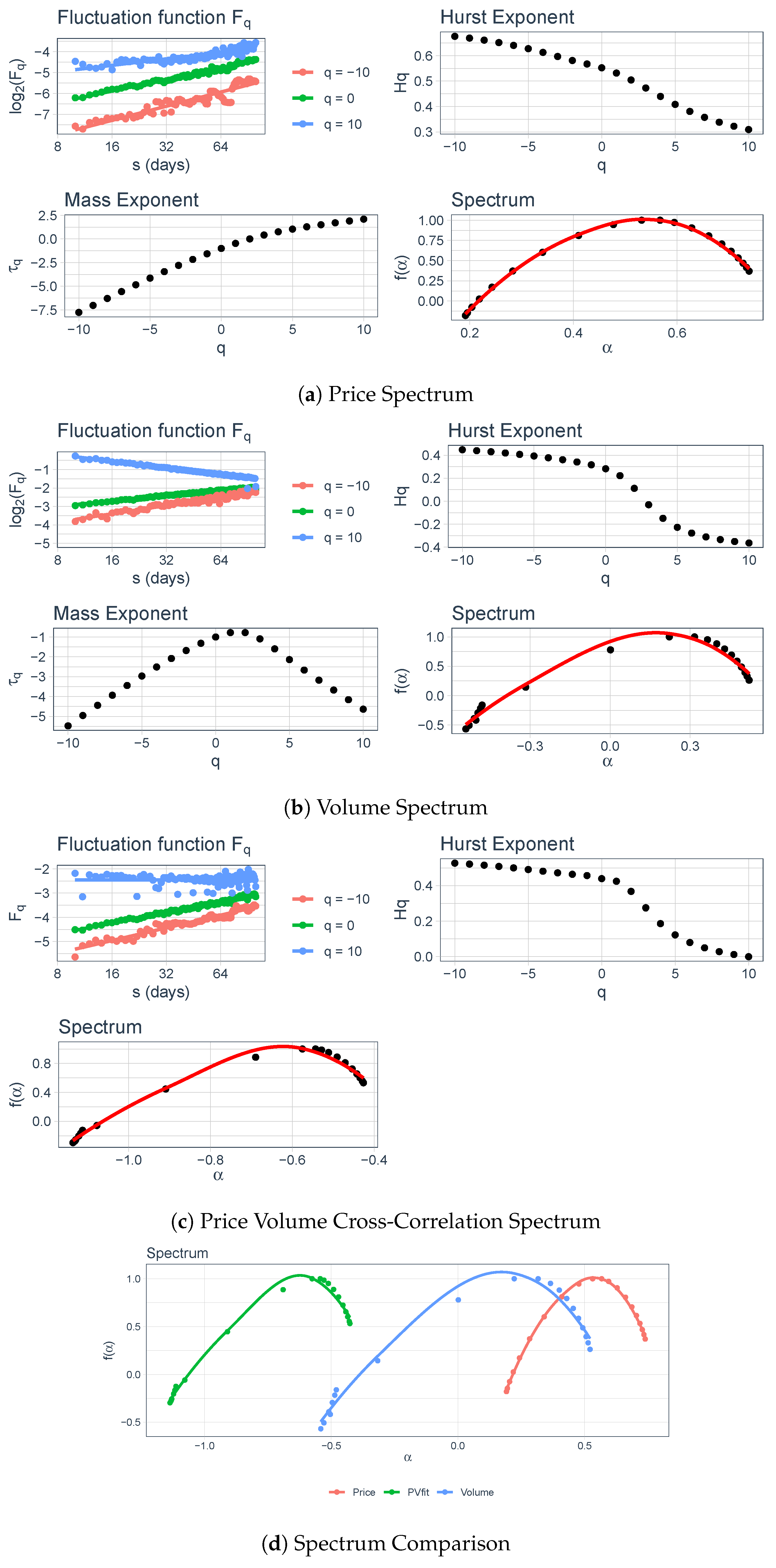
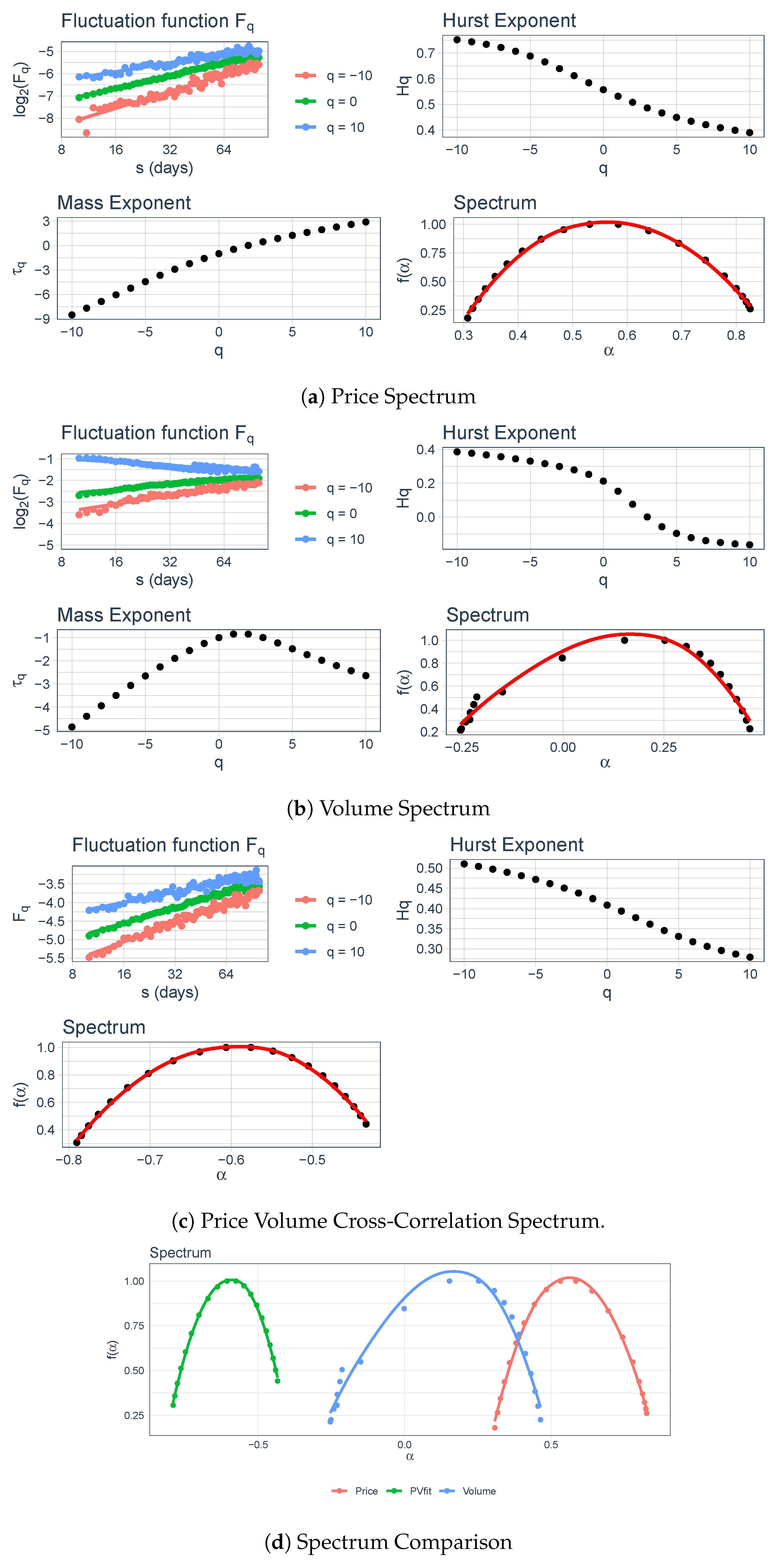
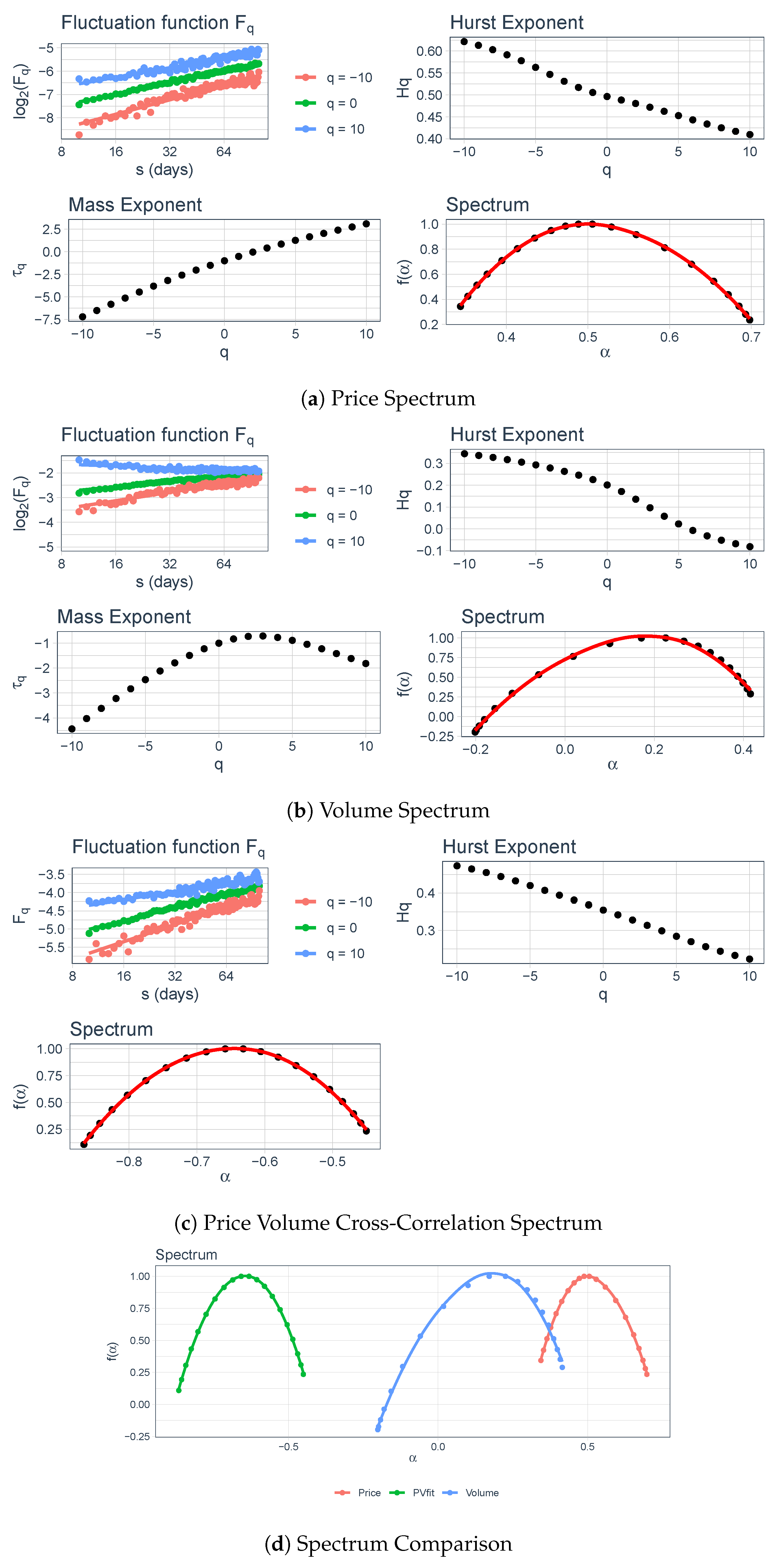
4.3. Multifractal Analysis
Interpretation of the Graphs
5. Results and Discussion
5.1. Entire Data
5.2. Segment 1–Segment 5
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMH | Adaptive Market Hypothesis |
| BIC | Bayesian Information Criteria |
| EMH | Efficient Market Hypothesis |
| MFDFA | Multifractal Detrended Fluctuation Analysis |
| MFDCCA | Multifractal Detrended Cross-Correlation Analysis |
| MDM | Mixture of Distribution Model |
| RSS | Residual Sum of Squares |
| SIF | Sequential arrival of Information Flow |
References
- Arshad, Shaista, and Syed Aun R. Rizvi. 2015. The troika of business cycle, efficiency and volatility. an east asian perspective. Physica A Statistical Mechanics and Its Applications 419: 158–70. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 1998. Estimating and testing linear models with multiple structural changes. Econometrica 66: 47–78. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 2003. Computation and analysis of multiple structural change models. Journal of Applied Econometrics 8: 1–22. [Google Scholar] [CrossRef]
- Bai, Jushan. 1994. Least squares estimation of a shift in linear processes. Journal of Time Series Analysis 15: 453–72. [Google Scholar] [CrossRef]
- Bai, Jushan. 1997. Estimation of a change point in multiple regression models. Review of Economics and Statistics 79: 551–63. [Google Scholar] [CrossRef]
- Blume, Lawrence, David Easley, and Maureen O’hara. 1994. Market statistics and technical analysis: The role of volume. The Journal of Finance 49: 153–81. [Google Scholar] [CrossRef]
- Bolgorian, Meysam, and Zahra Gharli. 2011. A multifractal detrended fluctuation analysis of gold price fluctuations. Acta Physica Polonica B 42: 159–69. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2004. The hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Physica A Statistical Mechanics and Its Applications 336: 521–37. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2005. Ranking efficiency for emerging equity markets ii. Chaos Solitons Fractals 23: 671–75. [Google Scholar] [CrossRef]
- Chen, Jie, and Arjun K. Gupta. 1997. Testing and locating variance changepoints with application to stock prices. Journal of the American Statistical association 92: 739–47. [Google Scholar] [CrossRef]
- Chen, Shiu-Sheng. 2012. Revisiting the empirical linkages between stock returns and trading volume. Journal of Banking Finance 36: 1781–88. [Google Scholar] [CrossRef]
- Clark, Peter K. 1973. A subordinated stochastic process model with finite variance for speculative prices. Econometrica 41: 135–55. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Copeland, Thomas E. 1976. A model of asset trading under the assumption of sequential information arrival. The Journal of Finance 31: 1149–68. [Google Scholar] [CrossRef]
- De Bondt, Werner F. M., and Richard Thaler. 1985. Does the stock market overreact? The Journal of Finance 40: 793–805. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Atsushi Inoue. 2001. Long memory and regime switching. Journal of Econometrics 105: 131–59. [Google Scholar] [CrossRef]
- Di Matteo, Tiziana, Tomaso Aste, and Michel M. Dacorogna. 2003. Scaling behaviors in differently developed markets. Physica A Statistical Mechanics and Its Applications 324: 183–88. [Google Scholar] [CrossRef]
- Di Matteo, Tiziana, Tomaso Aste, and Michel M. Dacorogna. 2005. Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. Journal of Banking Finance 29: 827–51. [Google Scholar] [CrossRef]
- Dutta, Srimonti, Dipak Ghosh, and Sucharita Chatterjee. 2016. Multifractal detrended cross correlation analysis of foreign exchange and sensex fluctuation in indian perspective. Physica A Statistical Mechanics and Its Applications 463: 188–201. [Google Scholar] [CrossRef]
- El Alaoui, Marwane. 2017. Price–volume multifractal analysis of the moroccan stock market. Physica A Statistical Mechanics and Its Applications 486: 473–85. [Google Scholar] [CrossRef]
- Eom, Cheoljun, Gabjin Oh, and Seunghwan Kim. 2008. Statistical investigation of connected structures of stock networks in financial time series. Journal of the Korean Physical Society 53: 3837–41. [Google Scholar] [CrossRef]
- Epps, Thomas W., and Mary Lee Epps. 1976. The stochastic dependence of security price changes and transaction volumes: Implications for the mixture-of-distributions hypothesis. Econometrica 44: 305–21. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Ferreira, Paulo, Andreia Dionísio, and SMS Movahed. 2017. Assessment of 48 stock markets using adaptive multifractal approach. Physica A Statistical Mechanics and Its Applications 486: 730–50. [Google Scholar] [CrossRef]
- Ferreira, Paulo. 2019. Assessing the relationship between dependence and volume in stock markets: A dynamic analysis. Physica A Statistical Mechanics and Its Applications 516: 90–97. [Google Scholar] [CrossRef]
- Gozbasi, Onur, Ilhan Kucukkaplan, and Saban Nazlioglu. 2014. Re-examining the turkish stock market efficiency: Evidence from nonlinear unit root tests. Economic Modelling 38: 381–84. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Namwon Hyung. 2004. Occasional structural breaks and long memory with an application to the s&p 500 absolute stock returns. Journal of Empirical Finance 11: 399–421. [Google Scholar]
- Gupta, Rakesh, and Junhao Yang. 2011. Testing weak form efficiency in the indian capital market. International Research Journal of Finance and Economics 75: 108–19. [Google Scholar]
- Hasan, Rashid, and M. Mohammed Salim. 2017. Power law cross-correlations between price change and volume change of indian stocks. Physica A Statistical Mechanics and Its Applications 473: 620–31. [Google Scholar] [CrossRef]
- Hiremath, Gourishankar S., and Jyoti Kumari. 2014. Stock returns predictability and the adaptive market hypothesis in emerging markets: Evidence from india. SpringerPlus 3: 428. [Google Scholar] [CrossRef]
- Horta, Paulo, Sérgio Lagoa, and Luis Martins. 2014. The impact of the 2008 and 2010 financial crises on the hurst exponents of international stock markets: Implications for efficiency and contagion. International Review of Financial Analysis 35: 140–53. [Google Scholar] [CrossRef]
- Inclan, Carla, and George C. Tiao. 1994. Use of cumulative sums of squares for retrospective detection of changes of variance. Journal of the American Statistical Association 89: 913–23. [Google Scholar]
- Jiang, Zhi-Qiang, Wen-Jie Xie, Wei-Xing Zhou, and Didier Sornette. 2019. Multifractal analysis of financial markets: A review. Reports on Progress in Physics 82: 125901. [Google Scholar] [CrossRef]
- Kantelhardt, Jan W., Stephan A. Zschiegner, Eva Koscielny-Bunde, Shlomo Havlin, Armin Bunde, and H. Eugene Stanley. 2002. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A Statistical Mechanics and Its Applications 316: 87–114. [Google Scholar] [CrossRef]
- Karpoff, Jonathan M. 1986. A theory of trading volume. The Journal of Finance 41: 1069–87. [Google Scholar] [CrossRef]
- Karpoff, Jonathan M. 1987. The relation between price changes and trading volume: A survey. Journal of Financial and Quantitative Analysis 22: 109–26. [Google Scholar] [CrossRef]
- Kim, Jae H. 2009. Automatic variance ratio test under conditional heteroskedasticity. Finance Research Letters 6: 179–85. [Google Scholar] [CrossRef]
- Konak, Fatih, and Yasin Şeker. 2014. The efficiency of developed markets: Empirical evidence from ftse 100. Journal of Advanced Management Science 2: 29–32. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav, and Miloslav Vosvrda. 2013. Measuring capital market efficiency: Global and local correlations structure. Physica A Statistical Mechanics and Its Applications 392: 184–93. [Google Scholar] [CrossRef]
- Laib, Mohamed, Luciano Telesca, and Mikhail Kanevski. 2019. MFDFA: MultiFractal Detrended Fluctuation Analysis. R Package Version 1.1. Available online: https://CRAN.R-project.org/package=MFDFA (accessed on 20 September 2020).
- Lamoureux, Christopher G., and William D Lastrapes. 1990. Heteroskedasticity in stock return data: Volume versus garch effects. The Journal of Finance 45: 221–29. [Google Scholar] [CrossRef]
- Lee, Charles, and Bhaskaran Swaminathan. 2000. Price momentum and trading volume. The Journal of Finance 55: 2017–69. [Google Scholar] [CrossRef]
- Lo, Andrew W. 1991. Long-term memory in stock market prices. Econometrica 59: 1279–313. [Google Scholar] [CrossRef]
- Lo, Andrew W. 2004. The adaptive markets hypothesis. Journal of Portfolio Management 30: 15–29+10. [Google Scholar] [CrossRef]
- Lo, Andrew W. 2012. Adaptive markets and the new world order (corrected may 2012). Financial Analysts Journal 68: 18–29. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B., Adlai J. Fisher, and Laurent E. Calvet. 1997. A multifractal Model of Asset Returns. Cowles Foundation Discussion Paper 1164, Sauder School of Business Working Paper. New Haven: Cowles Foundation for Research in Economics. [Google Scholar]
- Patil, Ashok Chanabasangouda, and Shailesh Rastogi. 2019. Time-varying price-volume relationship and adaptive market efficiency: A survey of the empirical literature. Journal of Risk and Financial Management 12: 105. [Google Scholar] [CrossRef]
- Peng, Chung-Kang, Shlomo Havlin, H. Eugene Stanley, and Ary L. Goldberger. 1995. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos An Interdisciplinary Journal of Nonlinear Science 5: 82–87. [Google Scholar] [CrossRef] [PubMed]
- Perron, Pierre, and Yohei Yamamoto. 2019. Pitfalls of two-step testing for changes in the error variance and coefficients of a linear regression model. Econometrics 7: 22. [Google Scholar] [CrossRef]
- Podobnik, Boris, and H Eugene Stanley. 2008. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Physical Review Letters 100: 084102. [Google Scholar] [CrossRef]
- R Core Team. 2020. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rak, Rafał, Stanisław Drożdż, Jarosław Kwapień, and Paweł Oświecimka. 2015. Detrended cross-correlations between returns, volatility, trading activity, and volume traded for the stock market companies. EPL (Europhysics Letters) 112: 48001. [Google Scholar] [CrossRef]
- Razdan, Ashok. 2002. Scaling in the bombay stock exchange index. Pramana 58: 537–44. [Google Scholar] [CrossRef]
- Rizvi, Syed Aun R., and Shaista Arshad. 2017. Analysis of the efficiency–integration nexus of japanese stock market. Physica A Statistical Mechanics and Its Applications 470: 296–308. [Google Scholar] [CrossRef]
- Ruan, Qingsong, Wei Jiang, and Guofeng Ma. 2016. Cross-correlations between price and volume in chinese gold markets. Physica A Statistical Mechanics and Its Applications 451: 10–22. [Google Scholar] [CrossRef]
- Shah, Ajay. 1999. Institutional change in india’s capital markets. Economic and Political Weekly XXXIV: 183–94. [Google Scholar]
- Stošić, Dusan, Darko Stošić, Tatijana Stošić, and H. Eugene Stanley. 2015. Multifractal properties of price change and volume change of stock market indices. Physica A Statistical Mechanics and Its Applications 428: 46–51. [Google Scholar] [CrossRef]
- Sukpitak, Jessada, and Varagorn Hengpunya. 2016. The influence of trading volume on market efficiency: The dcca approach. Physica A Statistical Mechanics and its Applications 458: 259–65. [Google Scholar] [CrossRef]
- Suominen, Matti. 2001. Trading volume and information revelation in stock market. Journal of Financial and Quantitative Analysis 36: 545–65. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Goodness C Aye, and Rangan Gupta. 2019. Stock market efficiency analysis using long spans of data: A multifractal detrended fluctuation approach. Finance Research Letters 28: 398–411. [Google Scholar] [CrossRef]
- Wied, Dominik, Matthias Arnold, Nicolai Bissantz, and Daniel Ziggel. 2012. A new fluctuation test for constant variances with applications to finance. Metrika 75: 1111–27. [Google Scholar] [CrossRef]
- Zeileis, Achim, Christian Kleiber, Walter Krämer, and Kurt Hornik. 2003. Testing and dating of structural changes in practice. Computational Statistics Data Analysis 44: 109–23. [Google Scholar] [CrossRef]
- Zeileis, Achim, Friedrich Leisch, Kurt Hornik, and Christian Kleiber. 2002. Strucchange: An r package for testing for structural change in linear regression models. Journal of Statistical Software 7: 1–38. [Google Scholar] [CrossRef]
- Zhang, Xike, Gui Zhang, Luo Qiu, Bo Zhang, Yurong Sun, Zifan Gui, and Qiuwen Zhang. 2019. A modified multifractal detrended fluctuation analysis (mfdfa) approach for multifractal analysis of precipitation in dongting lake basin, china. Water 11: 891. [Google Scholar] [CrossRef]
- Zhou, Wei-Xing. 2008. Multifractal detrended cross-correlation analysis for two nonstationary signals. Physical Review E 77: 066211. [Google Scholar] [CrossRef] [PubMed]
- Zunino, Luciano, Benjamin Miranda, Tabak A. Figliola, Darío G. Pérez, M. Garavaglia, and Osvaldo A. Rosso. 2008. A multifractal approach for stock market inefficiency. Physica A Statistical Mechanics and Its Applications 387: 6558–66. [Google Scholar] [CrossRef]
- Zunino, Luciano, Massimiliano Zanin, Benjamin M. Tabak, Darío G Pérez, and Osvaldo A Rosso. 2009. Forbidden patterns, permutation entropy and stock market inefficiency. Physica A Statistical Mechanics and Its Applications 388: 2854–64. [Google Scholar] [CrossRef]
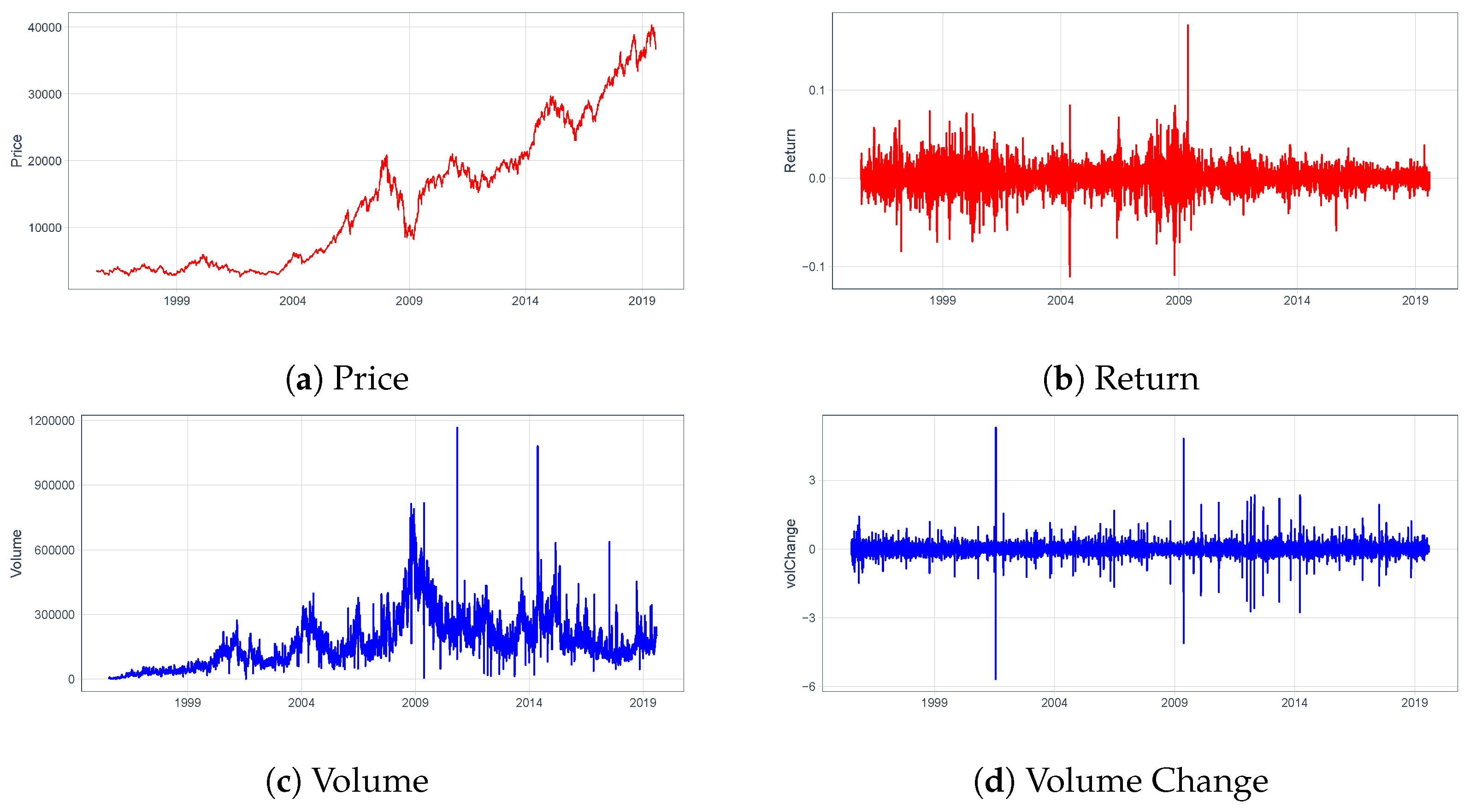
| Price | Volume | Return | volChange | |
|---|---|---|---|---|
| Number of observations | 5957 | 5957 | 5957 | 5957 |
| Minimum | 2600.12 | 423 | −0.11 | −5.68 |
| Maximum | 40,267.6 | 1,166,709 | 0.17 | 5.29 |
| Median | 13,156.7 | 148,410 | 0 | 0 |
| Mean | 14,153.1 | 167,683 | 0 | 0 |
| SE of mean | 136.58 | 1513.21 | 0 | 0 |
| CI of mean 0.95 | 267.74 | 2966.44 | 0 | 0.01 |
| Standard deviation | 10,541.3 | 116,792 | 0.01 | 0.29 |
| Price Segments | [1995-07-17, 2002-07-10] | [2002-07-10, 2006-01-25] | [2006-01-25, 2009-09-07] | [2009-09-07, 2014-05-30] | [2014-05-30, 2019-08-06] |
|---|---|---|---|---|---|
| Number of observations | 1710 | 893 | 895 | 1178 | 1280 |
| Minimum | 2600.12 | 2834.41 | 8160.4 | 15,175.1 | 22,951.83 |
| Maximum | 5933.56 | 9648.08 | 20,873.3 | 24,716.9 | 40,267.62 |
| Median | 3575.04 | 5358.35 | 13,799.5 | 18,342 | 28,798.47 |
| Mean | 3742.69 | 5341.6 | 13,614.1 | 18,536.4 | 30,533.3 |
| SE of mean | 15.11 | 60.62 | 98.07 | 49.89 | 124.99 |
| CI of mean 0.95 | 29.64 | 118.97 | 192.47 | 97.89 | 245.22 |
| Standard deviation | 624.87 | 1811.44 | 2933.86 | 1712.46 | 4471.93 |
| Segment | Fluctuation Type | Price Is Persistent | Volume Is Persistent | Price-Volume |
|---|---|---|---|---|
| Cross-Correlation | ||||
| Is Persistent | ||||
| Entire Data | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No | |
| 1 | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No | |
| 2 | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No | |
| 3 | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No | |
| 4 | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No | |
| 5 | Large fluctuations | No | No | No |
| Small fluctuations | Yes | No | No |
| Segment | Multifractal Strength | Intensity and Complexity | ||||
|---|---|---|---|---|---|---|
| Price | Volume | Price-Volume Correlation | Price | Volume | Price-Volume Correlation | |
| All Data | 0.322 | 0.714 | 0.493 | 0.506 | 0.991 | 0.752 |
| 1 | 0.518 | 0.749 | 0.273 | 0.749 | 1.030 | 0.430 |
| 2 | 0.412 | 0.430 | 0.238 | 0.601 | 0.597 | 0.387 |
| 3 | 0.367 | 0.811 | 0.527 | 0.548 | 1.063 | 0.710 |
| 4 | 0.363 | 0.550 | 0.231 | 0.518 | 0.717 | 0.356 |
| 5 | 0.212 | 0.426 | 0.251 | 0.354 | 0.617 | 0.416 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patil, A.C.; Rastogi, S. Multifractal Analysis of Market Efficiency across Structural Breaks: Implications for the Adaptive Market Hypothesis. J. Risk Financial Manag. 2020, 13, 248. https://doi.org/10.3390/jrfm13100248
Patil AC, Rastogi S. Multifractal Analysis of Market Efficiency across Structural Breaks: Implications for the Adaptive Market Hypothesis. Journal of Risk and Financial Management. 2020; 13(10):248. https://doi.org/10.3390/jrfm13100248
Chicago/Turabian StylePatil, Ashok Chanabasangouda, and Shailesh Rastogi. 2020. "Multifractal Analysis of Market Efficiency across Structural Breaks: Implications for the Adaptive Market Hypothesis" Journal of Risk and Financial Management 13, no. 10: 248. https://doi.org/10.3390/jrfm13100248
APA StylePatil, A. C., & Rastogi, S. (2020). Multifractal Analysis of Market Efficiency across Structural Breaks: Implications for the Adaptive Market Hypothesis. Journal of Risk and Financial Management, 13(10), 248. https://doi.org/10.3390/jrfm13100248





