Are CDS Spreads Sensitive to the Term Structure of the Yield Curve? A Sector-Wise Analysis under Various Market Conditions
Abstract
:1. Introduction
2. Literature Review
3. Methodology
4. Data and Results
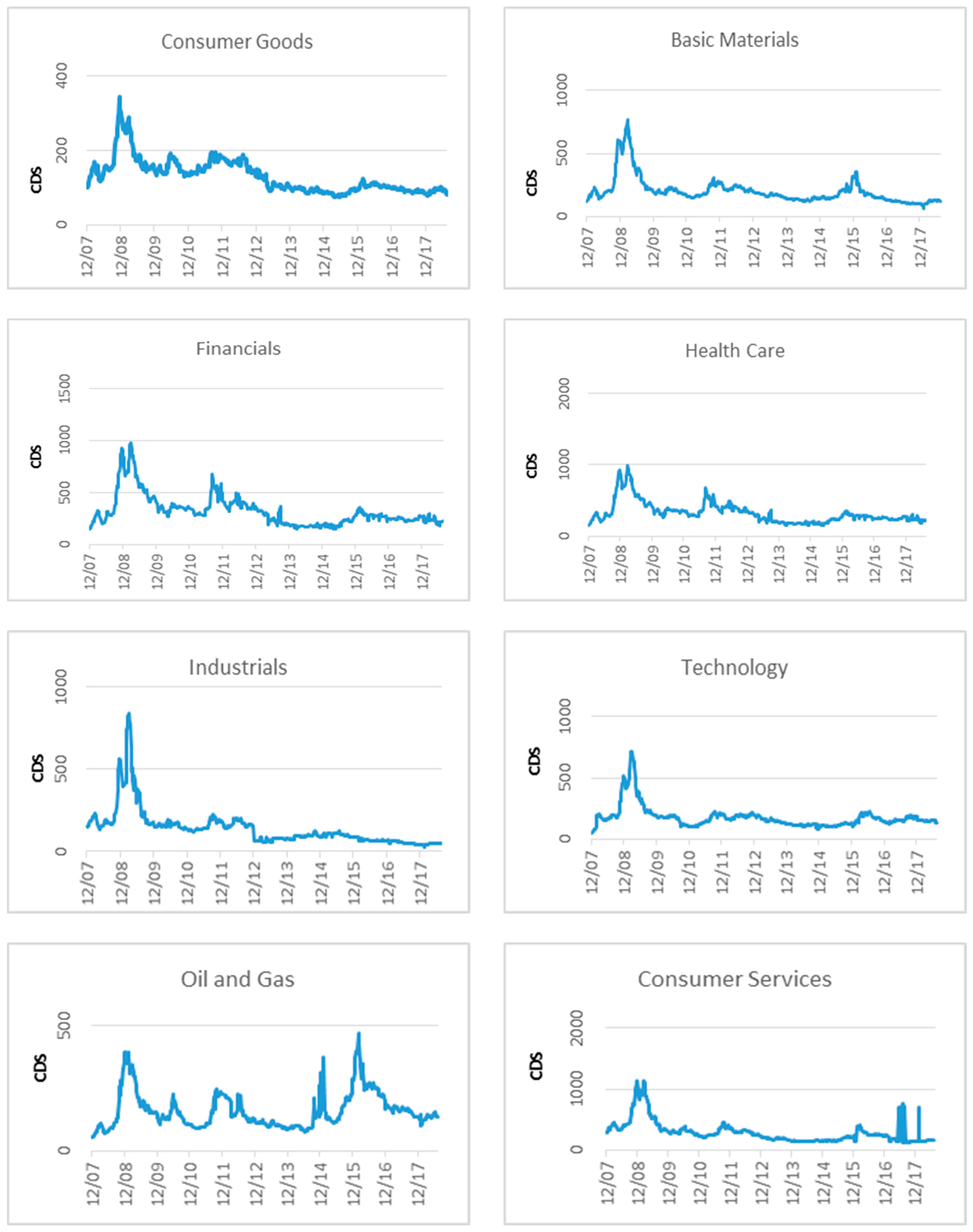
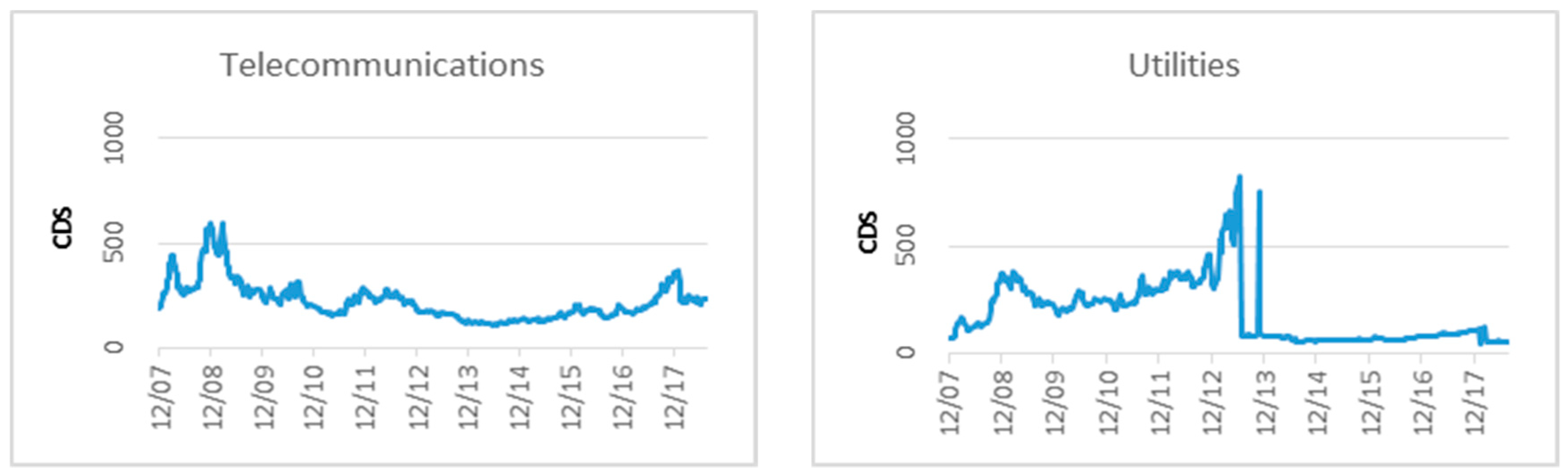
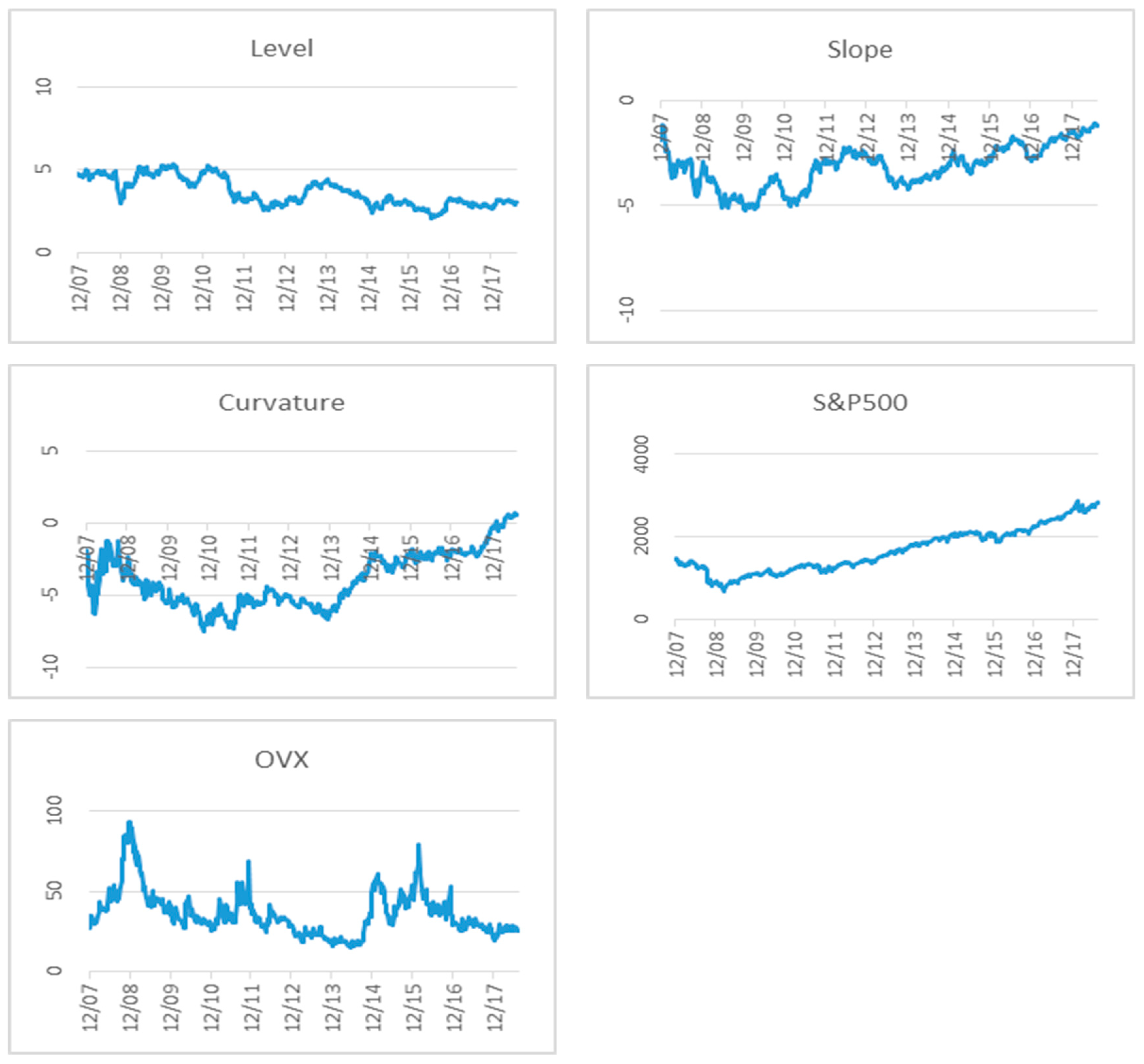
4.1. Data Overview
4.2. Empirical Results
5. Conclusions
Funding
Conflicts of Interest
References
- Alexander, Carol, and Andreas Kaeck. 2007. Regime dependent determinants of credit default swap spread. Journal of Banking and Finance 32: 1008–21. [Google Scholar] [CrossRef]
- Aver, Boštjan. 2008. An empirical analysis of credit risk factors of the Slovenian banking system. Managing Global Transitions 6: 317–34. [Google Scholar]
- Baum, Christopher F., and Chi Wan. 2010. Macroeconomic uncertainty and credit default swap spreads. Applied Financial Economics 20: 1163–71. [Google Scholar] [CrossRef]
- Bielecki, Tomasz R., and Marek Rutkowski. 2013. Valuation and Hedging of OTC Contracts with Funding Costs, Collateralization and Counterparty Credit Risk. Working Paper. Chicago, IL, USA: Illinois Institute of Technology. [Google Scholar]
- Blanco, Roberto, Simon Brennan, and Ian W. Marsh. 2005. An Empirical Analysis of the Dynamic Relation between Investment-Grade Bonds and Credit Default Swaps. Journal of Finance 60: 2255–81. [Google Scholar] [CrossRef]
- Buchinsky, Moshe. 1995. Estimating the Asymptotic Covariance Matrix for Quantile Regression Models a Monte Carlo Study. Journal of Econometrics 68: 303–38. [Google Scholar] [CrossRef]
- Chen, K. C., and Daniel Tzang. 1988. Interest-rate sensitivity of real estate investment trusts. Journal of Real Estate Research 3: 13–22. [Google Scholar]
- Chen, Ren-Raw, Xiaolin Cheng, and Liuren Wu. 2013. Dynamic Interactions between Interest-Rate and Credit Risk: Theory and Evidence on the Credit Default Swap Term Structure. Review of Finance 1: 403–41. [Google Scholar] [CrossRef]
- Cúrdia, Vasco, and Michael Woodford. 2015. Credit Frictions and Optimal Monetary Policy (No. w21820). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Devaney, Michael. 2001. Time-varying risk-premia for real estate investment trusts: A GARCH-M model. Quarterly Review of Economics and Finance 41: 335–46. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Driessen, Joost. 2005. Is default event risk priced in corporate bonds? Review of Financial Studies 18: 165–95. [Google Scholar] [CrossRef]
- Duffee, Gregory R. 1998. The relation between Treasury yields and corporate bond yield spreads. Journal of Finance 53: 2225–41. [Google Scholar] [CrossRef]
- Dufresne, Pierre Collin, Robert S. Goldstein, and J. Spencer Martin. 2001. The Determinants of Credit Spread Changes. Journal of Finance 56: 2177–207. [Google Scholar] [CrossRef]
- Düllmann, Klaus, and Agnieszka Sosinska. 2007. Credit default swap prices as risk indicators of listed German banks. Financial Markets and Portfolio Management 21: 269–92. [Google Scholar] [CrossRef]
- Ericsson, Jan, Kris Jacobs, and Rodolfo Oviedo. 2009. The determinants of credit default swap premia. Journal of Financial and Quantitative Analysis 44: 109–32. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Gikas A. Hardouvelis. 1991. The term structure as a predictor of real economic activity. Journal of Finance 46: 555–76. [Google Scholar] [CrossRef]
- Fabozzi, Frank J., Lionel Martellini, and Philippe Priaulet. 2005. Predictability in the shape of the term structure of interest rates. Journal of Fixed Income 15: 40–53. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1984. The information in the term structure. Journal of Financial Economics 13: 509–28. [Google Scholar] [CrossRef]
- Fama, Eugene, and Robert R. Bliss. 1987. The information in long-maturity forward rates. American Economic Review 77: 680–92. [Google Scholar]
- Feldhütter, Peter, and David Lando. 2008. Decomposing swap spreads. Journal of Financial Economics 88: 375–405. [Google Scholar] [CrossRef]
- Ferrer, Román, Vicente J. Bolós, and Rafael Benítez. 2016. Interest Rate Changes and Stock Returns: A European Multi-Country Study with Wavelets. International Review of Economics and Finance 44: 1–12. [Google Scholar] [CrossRef]
- Flannery, Mark J., and Christopher M. James. 1984. The Effect of Interest Rate Changes on the Common Stock Returns of Financial Institutions. Journal of Finance 39: 1141–53. [Google Scholar] [CrossRef]
- Fofack, Hippolyte L. 2005. Nonperforming Loans in Sub-Saharan Africa: Causal Analysis and Macroeconomic Implications. Working Paper Series 3769; Washington, DC: World Bank. [Google Scholar]
- Frühwirth, Manfred, Paul Schneider, and Leopold Sögner. 2010. The risk microstructure of corporate bonds: A case study from the German corporate bond market. European Financial Management 16: 658–85. [Google Scholar] [CrossRef]
- Galil, Koresh, Offer Moshe Shapir, Dan Amiram, and Uri Ben-Zion. 2014. The determinants of CDS spread. Journal of Banking & Finance 41: 271–82. [Google Scholar]
- Hirtle, Beverly J. 1997. Derivatives, Portfolio Composition, and Bank Holding Company Interest Rate Risk Exposure. Journal of Financial Services Research 12: 243–66. [Google Scholar] [CrossRef]
- ICE. 2010. Global Credit Derivatives Markets Overview: Evolution, Standardization and Clearing. Atlanta: Intercontinental Exchange, Inc. [Google Scholar]
- Kiff, John, Jennifer Elliott, Elias Kazarian, Jodi Scarlata, and Carolyne Spackman. 2009. Credit Derivatives: Systemic Risk and Policy Options. IMF Working Paper, WP/09/254. Washington, DC, USA: International Monetary Fund, November. [Google Scholar]
- Koenker, Roger, and Gilbert Bassett. 1982. Tests of Linear Hypotheses and L1 Estimation. Econometrica 50: 1577–83. [Google Scholar] [CrossRef]
- Louzis, Dimitrios P., Angelos T. Vouldis, and Vasilios L. Metaxas. 2012. Macroeconomic and bank-specific determinants of non-performing loans in Greece: A comparative study of mortgage, business and consumer loan portfolios. Journal of Banking & Finance 36: 1012–27. [Google Scholar]
- Malhotra, Jatin, and Angelo Corelli. 2018. The Determinants of CDS Spreads in Multiple Industry Sectors: A Comparison between the US and Europe. Risks 6: 89. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance 29: 449–70. [Google Scholar]
- Nelson, Charles R., and Andrew F. Siegel. 1987. Parsimonious modeling of yield curves. Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Nkusu, Mwanza. 2011. Nonperforming Loans and Macro Financial Vulnerabilities in Advanced Economies. IMF Working Papers. Washington, DC, USA: International Monetary Fund, pp. 1–27. [Google Scholar]
- Raunig, B. 2015. Firm Credit Risk in Normal Times and during the Crisis: Are Banks less risky? Applied Economics 47: 2455–469. [Google Scholar] [CrossRef]
- Shahzad, Syed Jawad Hussain, Safwan Mohd Nor, Roman Ferrer, and Shawkat Hammoudeh. 2017. Asymmetric determinants of CDS spread: U.S. industry-level evidence through the NARDL approach. Economic Modelling 60: 211–30. [Google Scholar] [CrossRef]
- Shi, Shuping, and Peter C. B. Phillips. 2017. Detecting Financial Collapse and Ballooning Sovereign Risk. Oxford Bulletin of Economics and Statistics. [Google Scholar] [CrossRef]
- Stevenson, Simon, Patrick J. Wilson, and Ralf Zurbruegg. 2007. Assessing the time-varying interest rate sensitivity of real estate securities. European Journal of Finance 13: 705–15. [Google Scholar] [CrossRef]
- Swanson, Zane, John Theis, and K. Michael Casey. 2002. REIT risk premium sensitivity and interest rates. Journal of Real Estate Finance and Economics 24: 319–30. [Google Scholar] [CrossRef]
- Tang, Dragon Yongjun, and Hong Yan. 2010. Market conditions, default risk and credit spreads. Journal of Banking & Finance 34: 743–53. [Google Scholar]
- Umar, Zaghum, Syed Jawad Hussain Shahzad, Román Ferrer, and Francisco Jareño. 2018. Does Shariah compliance make interest rate sensitivity of Islamic equities lower? An industry level analysis under different market states. Applied Economics 50: 4500–21. [Google Scholar] [CrossRef]
- Wegener, Christoph, Tobias Basse, Frederik Kunze, and Hans-Jörg von Mettenheim. 2017. Oil prices and sovereign credit risk of oil producing countries: An empirical investigation. Quantitative Finance 16: 1961–68. [Google Scholar] [CrossRef]
- Wu, Liuren, and Frank Xiaoling Zhang. 2008. A no-arbitrage analysis of economic determinants of the credit spread term structure. Management Science 54: 1160–75. [Google Scholar] [CrossRef]
- Zhu, Haibin. 2006. An empirical comparison of credit spreads between the bond market and the Credit default swap market. Journal of Financial Service Research 29: 211–35. [Google Scholar] [CrossRef]
| 1 | See Shi and Phillips (2017). Detecting Financial Collapse and Ballooning Sovereign Risk, Oxford Bulletin of Economics and Statistics. |
| 2 | LIBOR, the London Interbank Offered Rate, is used as a basis for defining the lending rates in the international interbank market for the short-term loans. |
| 3 | Nelson and Siegel (1987) used an exponential components model based on three factors to capture the changes in the yield curve. Diebold and Li (2006) and Fabozzi et al. (2005) supported this model, as it is a good fit for the yield curve. |
| 4 | Chicago Board Options Exchange (CBOE) has created the implied volatility OVX that tracks the prices for the U.S. Oil Fund Exchange-traded fund while the volatility Index, VIX represents the market’s expectation of 30-day forward-looking volatility. |
| 5 | The dataset can be downloaded from https://www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/TextView.aspx?data=yield. |
| 6 | Ferrer et al. (2016), Flannery and James (1984) and Hirtle (1997) suggested the use of midweek data series to deal with the seasonality factor. |
| Study | Sample Period | Variable for Credit Risk | Interest Rate Considered | Methods Used | Main Findings Regarding Impact of Interest Rate on Credit Risk |
|---|---|---|---|---|---|
| Fama (1984) | 1952–1988 | CDS spread | Forward rates | OLS regression | one-month forward rate is a significant determinant of spot rate |
| Fama and Bliss (1987) | 1952–1988 | CDS spread | Future spot rates, inflation and real returns | OLS regression | one-year returns on two- to five-year bonds have significant impact on yield rates |
| Estrella and Hardouvelis (1991) | 1955–1988 | CDS spread | 10-year and 2-year interest rates | OLS regression | slope of the yield curve can be used to forecast collective adjustments in next four years of real output with a positive slope indicative of economic growth |
| Dufresne et al. (2001) | 1988–1997 | CDS spread | Treasury rate | OLS regression | corporate bond CDS spreads are receptive to overall market factors rather than firm-specific factors such as changes in aggregate demand and supply |
| Düllmann and Sosinska (2007) | 2001–2005 | CDS spread | Risk-free rate | OLS regression | rising risk-free rate results in rise of CDS spreads for German banks with an increasing risk-free interest rate |
| Alexander and Kaeck (2007) | 2004–2007 | CDS spread | Risk-free rate | OLS regression | rising interest rates may be linked to stability in CDS rates |
| Ericsson et al. (2009) | 1999–2002 | CDS spread | Risk-free rate | OLS regression | risk-free rate, leverage have strong explanatory power for CDS spread determination |
| Baum and Wan (2010) | 2001–2006 | CDS spread | Risk-free rate | GARCH, fixed effects regression | macroeconomic factors serve as major determinant of CDS rates compared to treasury rates and term structure |
| Galil et al. (2014) | 2002–2013 | CDS spread | 5-year treasury rate | Time series analysis, cross-sectional analysis | ratings have significant predictive power for CDS spread changes |
| Raunig (2015) | 2004–2010 | CDS spread | Risk-free rate, 5-year treasury constant maturity rate (TCMR) | Random effects model | rise in the risk-free interest rate leads to risk-neutral drift, lowering the default probability; the differences in the responsiveness of the financial and nonfinancial sector CDS rates diminish during times of crisis |
| S.J.H. Shahzad et al. (2017) | 2007–2015 | CDS spread | Spot interest rate | NARDL approach | treasury rate, sector-wise equity prices, the VIX and the crude oil price are strong determinants of CDS spreads |
| Malhotra and Corelli (2018) | 2007–2014 | CDS spread | Euro marginal lending, U.S. federal funds effective rate | Granger causality test, regression | lending rate and CDS rates exhibit positive bidirectional causality |
| Industrial Sectors and Risk Factors | Mean | Median | Maximum | Minimum | Standard Deviation | Skewness | Kurtosis | Jarque–Bera Stat. |
|---|---|---|---|---|---|---|---|---|
| Consumer Goods | −0.05601 | −0.05 | 55.32 | −32.86 | 7.35 | 1.23 *** | 10.53 *** | 2634.2 *** |
| Basic Materials | −0.06248 | −0.61 | 141.07 | −111.05 | 17.17 | 0.92 *** | 19.77 *** | 8877.7 *** |
| Financials | 0.06002 | −0.11 | 157.02 | −162.12 | 30.33 | 0.14 *** | 6.22 *** | 870.4 *** |
| Healthcare | 0.90660 | −0.24 | 352.32 | −483.10 | 36.54 | −2.09 *** | 73.52 *** | 122,221.8 *** |
| Industrials | −0.23856 | −0.11 | 319.70 | −148.23 | 22.46 | 4.30 *** | 84.61 *** | 163,040.6 *** |
| Technology | 0.11670 | −0.27 | 113.44 | −90.24 | 14.78 | 1.22 *** | 17.83 *** | 7291.5 *** |
| Oil and Gas | 0.13079 | −0.30 | 189.86 | −199.63 | 22.37 | 0.49 *** | 32.39 *** | 23,659.7 *** |
| Consumer Services | −0.33999 | −0.58 | 588.37 | −640.23 | 71.43 | −1.23 *** | 52.58 *** | 62,433.8 *** |
| Telecommunications | −0.00506 | −0.16 | 104.46 | −95.76 | 16.11 | 0.31 *** | 9.68 *** | 2117.7 *** |
| Utilities | −0.03405 | 0.16 | 667.59 | −680.17 | 52.77 | −3.84 *** | 142.13 *** | 45,6711.7 *** |
| ΔLevel | 0.00040 | 0.00 | 0.42 | −0.55 | 0.13 | −0.01 *** | 1.17 *** | 30.4 *** |
| ΔSlope | 4.45 × 10−18 | 0.00 | 0.62 | −0.78 | 0.09 | −1.23 *** | 21.16 *** | 10,219.0 *** |
| ΔCurvature | 2.72 × 10−17 | 0.00 | 1.97 | −1.41 | 0.27 | 0.93 *** | 9.91 *** | 2290.0 *** |
| S&P 500 | −2.45 × 10−16 | 0.19 | 13.73 | −21.13 | 2.31 | −1.17 *** | 15.06 *** | 5233.6 *** |
| OVX | −0.01181 | −0.23 | 26.18 | −29.32 | 4.07 | 0.15 *** | 9.43 *** | 2001.7 *** |
| Industrial Sectors and Risk Variables | ADF Stat. | PP Stat. | KPSS Stat. |
|---|---|---|---|
| Consumer Goods | −8.502 *** | −626.501 *** | 0.0727 |
| Basic Materials | −7.856 *** | −727.026 *** | 0.0596 |
| Financials | −8.843 *** | −631.264 *** | 0.0693 |
| Healthcare | −7.858 *** | −700.496 *** | 0.1003 |
| Industrials | −9.325 *** | −487.883 *** | 0.0233 |
| Technology | −9.127 *** | −413.084 *** | 0.0626 |
| Oil and Gas | −7.342 *** | −671.233 *** | 0.0554 |
| Consumer Services | −9.251 *** | −640.066 *** | 0.0254 |
| Telecommunications | −8.847 *** | −485.997 *** | 0.0457 |
| Utilities | −9.587 *** | −614.644 *** | 0.0455 |
| ΔLevel | −7.994 *** | −545.091 *** | 0.1842 |
| ΔSlope | −9.382 *** | −528.213 *** | 1.1091 |
| ΔCurvature | −6.875 *** | −558.855 *** | 0.8472 |
| S&P 500 | −9.120 *** | −560.806 *** | 0.2921 |
| OVX | −6.847 *** | −652.779 *** | 0.0390 |
| Yield Rate Coefficient Estimates | Quantiles | |||||
|---|---|---|---|---|---|---|
| OLS | 0.05 | 0.25 | 0.5 | 0.75 | 0.95 | |
| ΔLevel | ||||||
| Consumer Goods | −7.834 *** | −6.526 | −6.548 * | −3.647 | −6.143 ** | −17.92 * |
| Basic Materials | −25.69 *** | −30.06 ** | −13.09 *** | −12.57 *** | −19.92 *** | −39.30 *** |
| Financials | −42.91 *** | −20.18 | −31.92 ** | −31.22 *** | −38.17 *** | −91.45 *** |
| Healthcare | −23.51 * | −21.87 | −26.24 ** | −23.87 *** | −31.04 ** | 4.112 |
| Industrials | −32.70 *** | −32.15 | −9.944 * | −5.272 * | −7.098 * | −36.78 ** |
| Technology | −15.23 ** | −34.26 | −15.40 *** | −10.48 *** | −11.54 ** | −27.21 * |
| Oil and Gas | −8.358 | 17.58 | −11.22 ** | −10.23 *** | −11.12 * | −38.66 *** |
| Consumer Services | −39.84 | −18.25 | −28.99 *** | −22.86 *** | −26.15 ** | −67.61 |
| Telecommunications | −23.80 *** | −19.10 | −15.49 *** | −14.34 *** | −20.67 *** | −23.36 |
| Utilities | 2.507 | −53.29 ** | −8.309 * | −8.406 ** | −9.934 * | −24.29 ** |
| ΔSlope | ||||||
| Consumer Goods | −5.848 | −3.868 | −5.108 | −7.075 | −11.75 ** | −24.31 * |
| Basic Materials | −9.721 | 4.538 | 5.812 | −1.674 | −5.480 | −6.159 |
| Financials | −50.53 *** | −56.94 *** | −3.289 | −20.35 | −50.73 ** | −76.02 ** |
| Healthcare | −34.19 * | −13.04 | −2.619 | −14.02 | −21.37 | −54.22 |
| Industrials | −7.787 | 5.048 | −0.721 | −6.848 | −16.19 *** | −19.18 |
| Technology | −10.47 | 15.02 | 3.966 | 2.825 | −6.828 | −13.68 |
| Oil and Gas | −13.91 | −34.60 * | −1.996 | −4.652 | −7.489 * | −31.49 * |
| Consumer Services | −6.435 | 13.49 | 0.113 | −5.748 | −10.19 | −4.645 |
| Telecommunications | −14.29 * | −14.11 | −6.797 | −10.06 | −12.43 | −36.47 |
| Utilities | −17.96 | −13.91 | −6.773 | −4.313 | −13.54 | 0.514 |
| ΔCurvature | ||||||
| Consumer Goods | −2.697 * | −2.121 | −1.100 | −2.109 | −3.353 ** | −3.432 |
| Basic Materials | −8.190 ** | −14.72 | −3.502 ** | −3.467 * | −5.302 ** | −11.98 *** |
| Financials | −0.505 | −10.99 | −5.150 | −3.262 | −3.435 | 1.636 |
| Healthcare | −10.10 | −3.619 | −8.110 * | −4.346 | −11.64 | −23.39 ** |
| Industrials | −8.342 * | −5.885 | −2.231 | −1.175 | −4.666 *** | −8.926 ** |
| Technology | −4.817 * | 4.140 | −0.634 | −0.692 | −2.012 ** | −13.64 *** |
| Oil and Gas | −6.139 | −17.90 *** | −3.919 ** | −2.618 | −3.420 * | −8.723 *** |
| Consumer Services | 2.901 | −0.117 | −3.256 | −0.434 | −2.317 | −16.34 |
| Telecommunications | −5.684 * | −4.080 | −6.504 ** | −5.568 * | −4.727 * | −13.20 * |
| Utilities | −5.168 | −12.61 *** | −3.399 | −2.503 * | −5.682 ** | −17.42 *** |
| Coefficient Estimates | Quantiles | |||||
|---|---|---|---|---|---|---|
| OLS | 0.05 | 0.25 | 0.5 | 0.75 | 0.95 | |
| ΔS&P 500 | ||||||
| Consumer Goods | −0.701 *** | −0.917 *** | −0.650 *** | −0.637 *** | −0.751 *** | −1.285 |
| Basic Materials | −2.333 *** | −2.285 | −2.052 *** | −2.123 *** | −2.276 *** | −3.869 *** |
| Financials | −4.206 *** | −5.579 *** | −3.621 *** | −3.051 *** | −3.872 *** | −3.744 *** |
| Healthcare | −4.283 *** | −4.843 ** | −3.487 *** | −2.746 *** | −3.046 *** | −4.740 *** |
| Industrials | −2.006 *** | −2.731 ** | −0.836 * | −0.539 * | −0.846 ** | −1.959 * |
| Technology | −1.295 *** | −1.995 | −1.016 *** | −0.897 *** | −0.879 *** | −1.855 ** |
| Oil and Gas | −0.612 | 0.000921 | −1.102 *** | −0.943 *** | −0.862 *** | −1.108 ** |
| Consumer Services | −2.987 * | −5.268 | −2.828 *** | −2.869 *** | −3.103 *** | −3.624 ** |
| Telecommunications | −1.966 *** | −1.231 | −1.848 *** | −1.751 *** | −1.980 *** | −3.056 |
| Utilities | −2.997 ** | −2.184 * | −0.938 *** | −0.847 *** | −1.083 * | −2.346 *** |
| ΔOVX | ||||||
| Consumer Goods | 0.113 | 0.354 | 0.120 * | 0.0416 | −0.00280 | −0.0973 |
| Basic Materials | −0.0842 | 0.225 | 0.132 | 0.0952 | −0.0640 | −0.630 |
| Financials | 0.0767 | 0.404 | 0.381 | 0.0783 | −0.378 | −1.004 *** |
| Healthcare | 0.241 | −0.250 | 0.230 | 0.245 | 0.706 | 1.014 |
| Industrials | 0.206 | −0.122 | 0.0230 | 0.0353 | 0.0805 | −0.746 ** |
| Technology | 0.0190 | −0.255 | 0.136 | 0.176 * | 0.168 | −0.785 |
| Oil and Gas | 0.683 ** | 1.457 | 0.312 *** | 0.197 | 0.321 | 0.140 |
| Consumer Services | 0.170 | −0.574 | −0.00940 | −0.0851 | 0.0259 | −0.239 |
| Telecommunications | 0.215 | 0.981 | 0.291 | 0.221 * | 0.153 | −0.0789 |
| Utilities | −0.210 | −0.796 | 0.0155 | 0.0432 | 0.0413 | −0.847 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aman, A. Are CDS Spreads Sensitive to the Term Structure of the Yield Curve? A Sector-Wise Analysis under Various Market Conditions. J. Risk Financial Manag. 2019, 12, 158. https://doi.org/10.3390/jrfm12040158
Aman A. Are CDS Spreads Sensitive to the Term Structure of the Yield Curve? A Sector-Wise Analysis under Various Market Conditions. Journal of Risk and Financial Management. 2019; 12(4):158. https://doi.org/10.3390/jrfm12040158
Chicago/Turabian StyleAman, Asia. 2019. "Are CDS Spreads Sensitive to the Term Structure of the Yield Curve? A Sector-Wise Analysis under Various Market Conditions" Journal of Risk and Financial Management 12, no. 4: 158. https://doi.org/10.3390/jrfm12040158
APA StyleAman, A. (2019). Are CDS Spreads Sensitive to the Term Structure of the Yield Curve? A Sector-Wise Analysis under Various Market Conditions. Journal of Risk and Financial Management, 12(4), 158. https://doi.org/10.3390/jrfm12040158




