Dealing with Low Interest Rates in Life Insurance: An Analysis of Additional Reserves in the German Life Insurance Industry
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods to Derive the ZZR Due to Low Interest Rates
2.1.1. Old Method of Calculating the ZZR in Germany (Valid from 2011–2018)
2.1.2. New Corridor Method to Calculate the ZZR in Germany (Valid from 2018)
2.2. Model Framework
2.2.1. Overview
2.2.2. Asset and Liability Dynamics
3. Results
3.1. Input Parameters and Interest Rate Scenarios
3.1.1. Input Parameters
3.1.2. Interest Rate Scenarios
3.2. The Impact of the ZZR Method on the Life Insurer under Various Interest Rate Scenarios
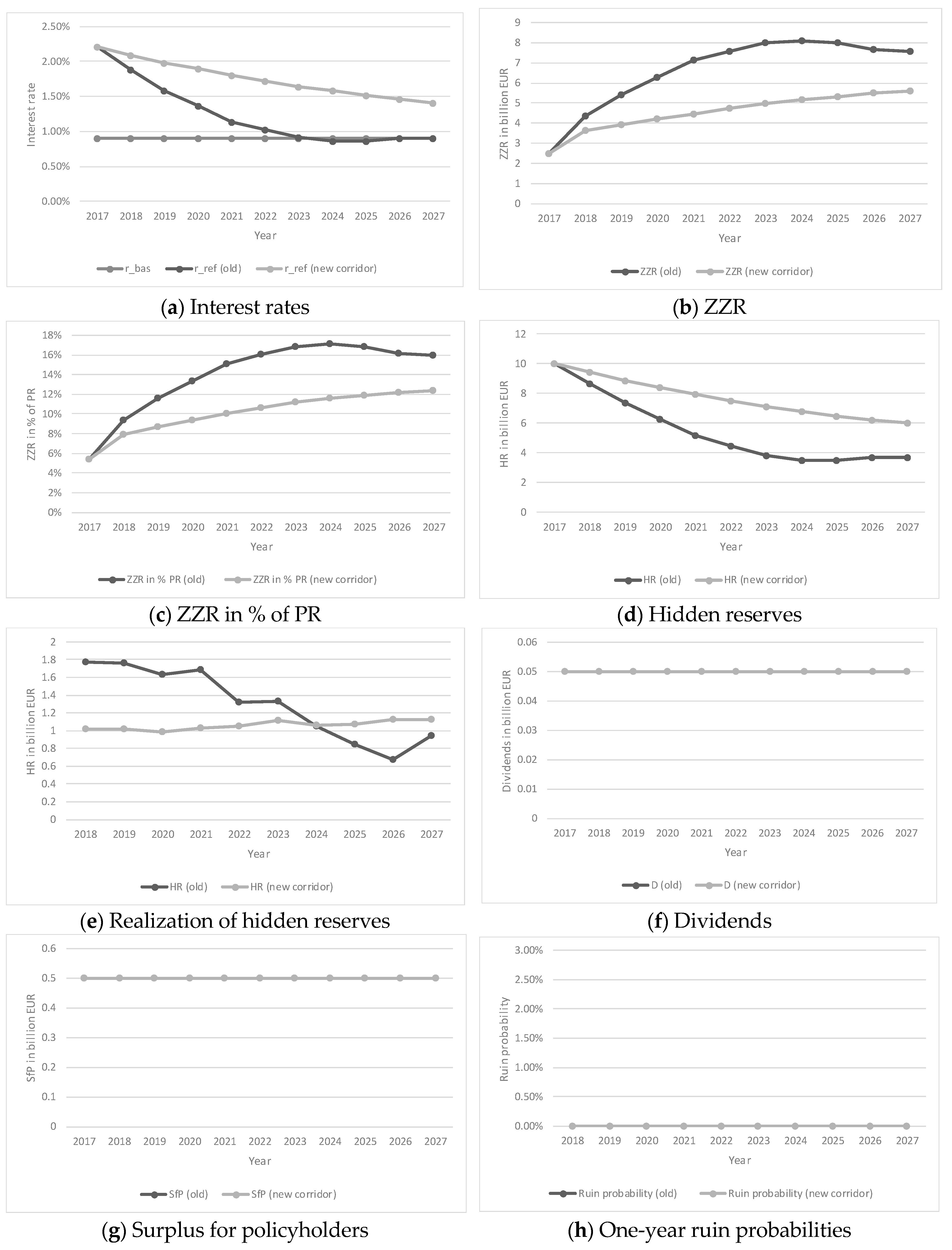
3.2.1. Interest Rate Scenario 1
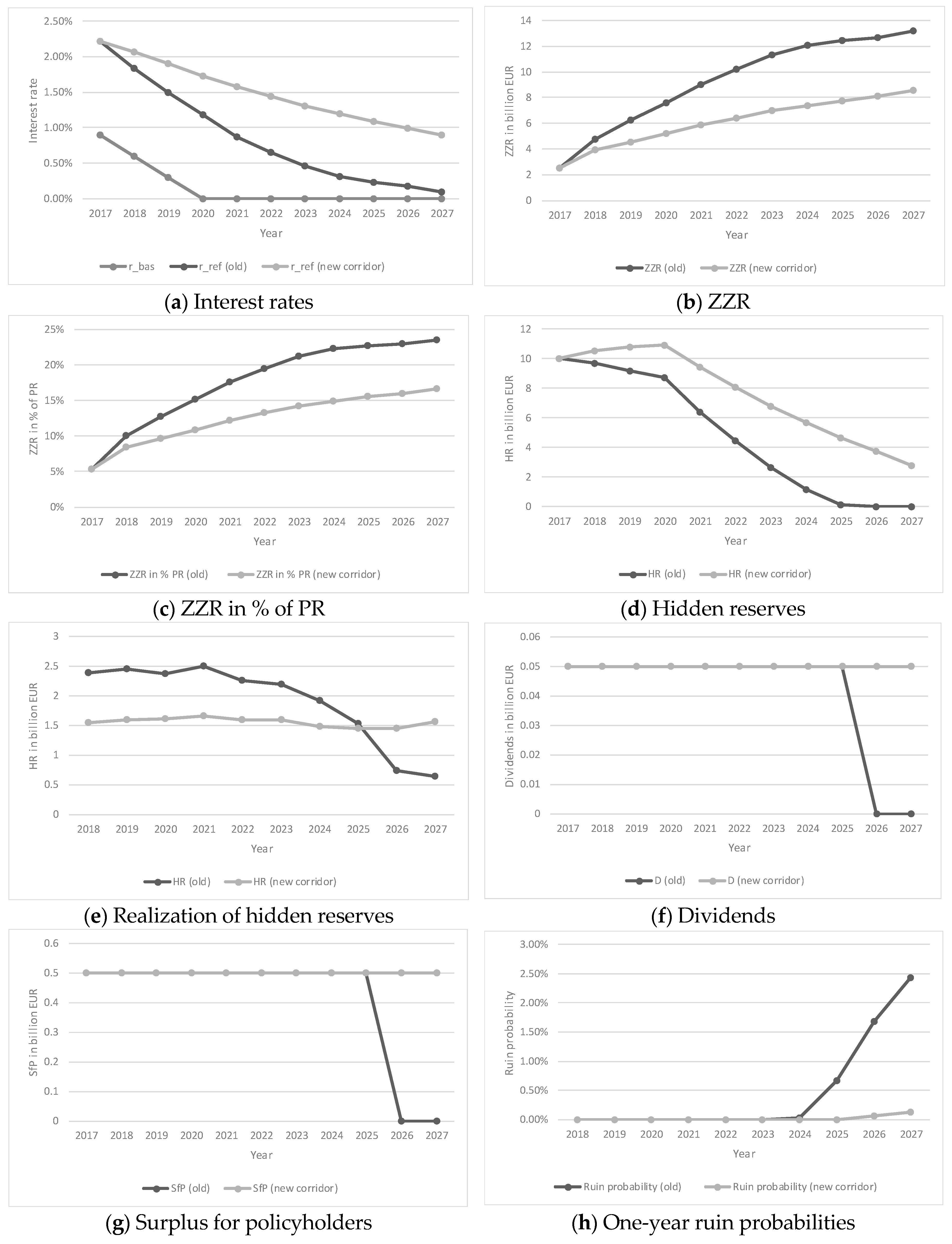
3.2.2. Interest Rate Scenario 2
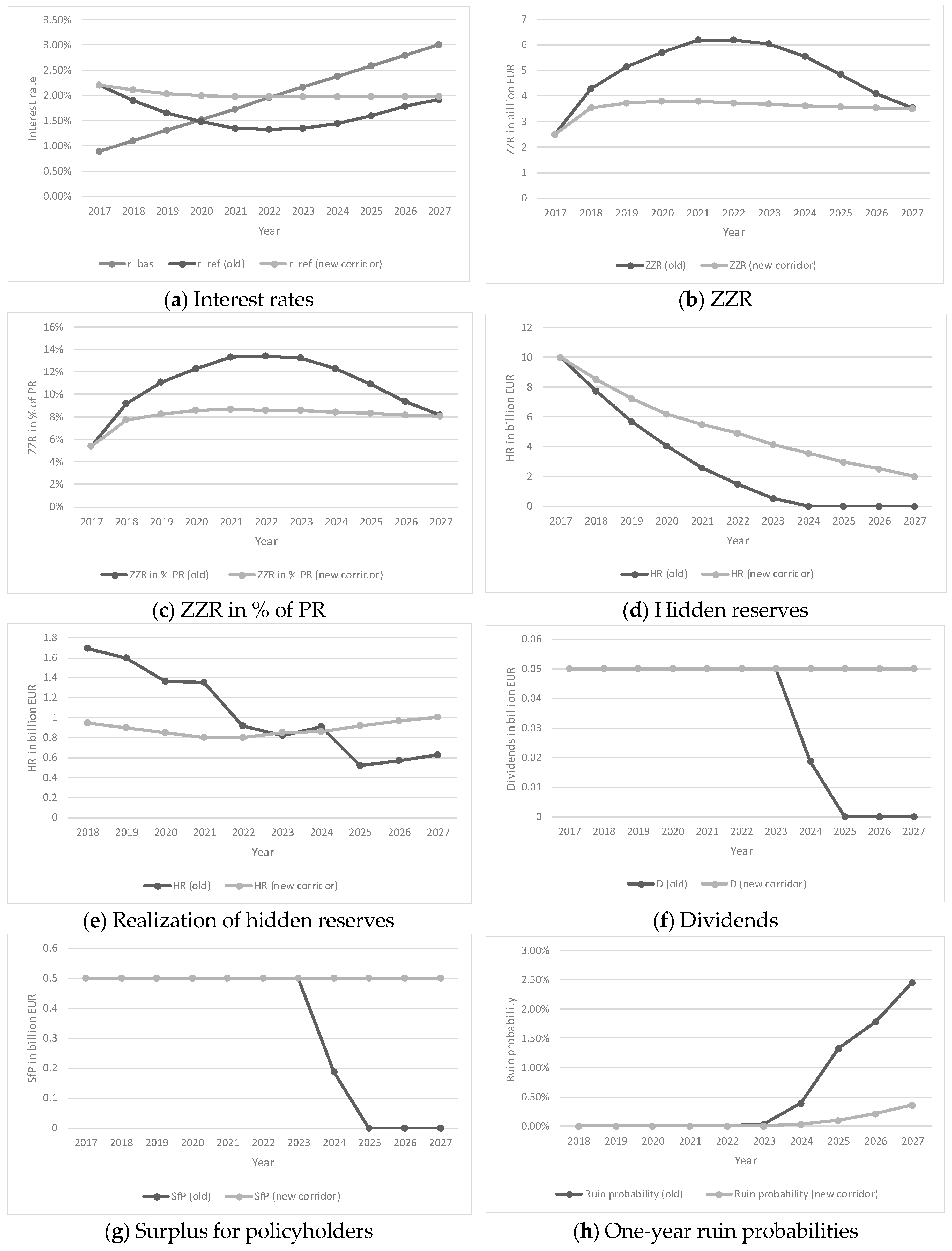
3.2.3. Interest Rate Scenario 3
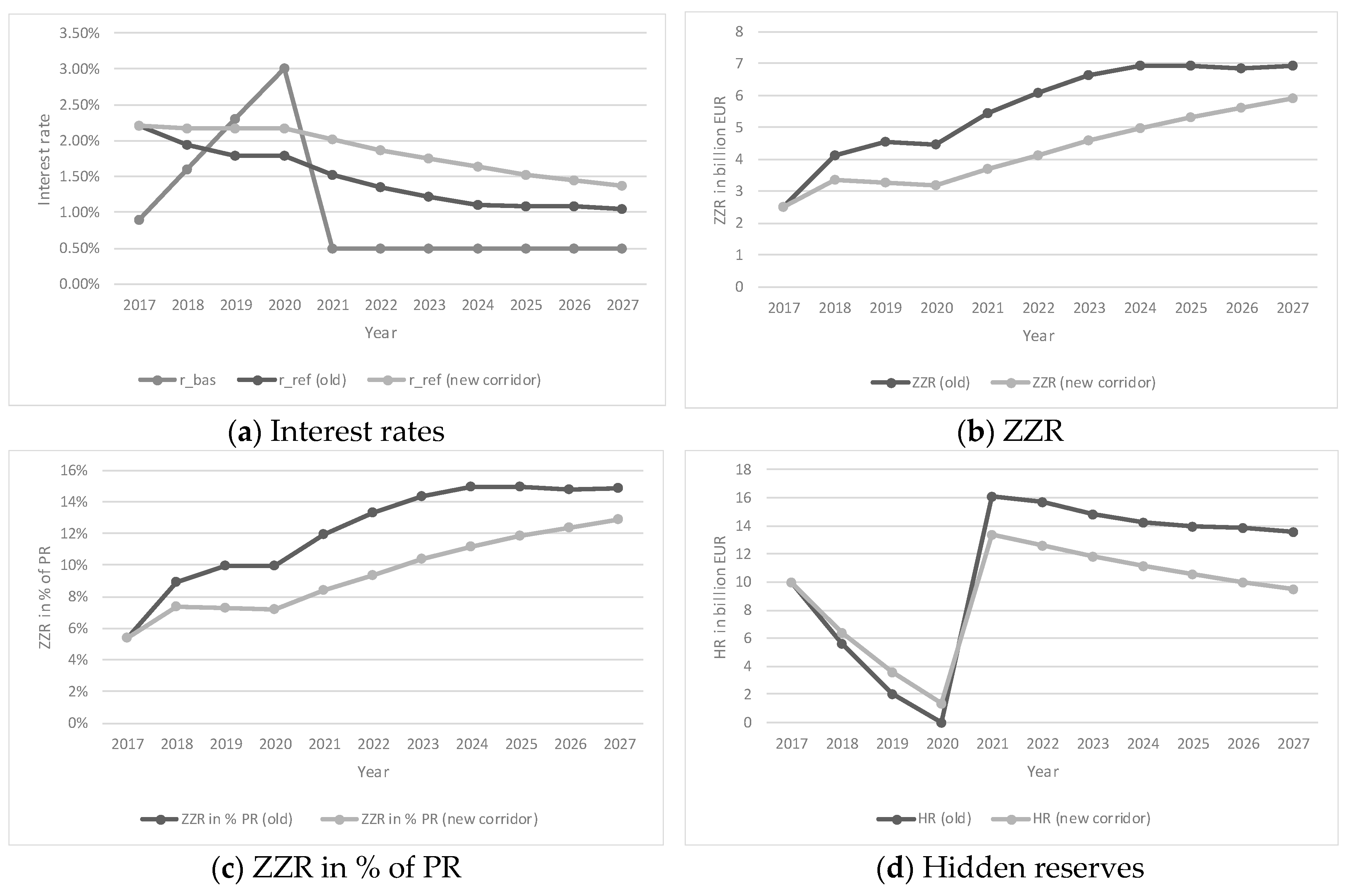
3.2.4. Interest Rate Scenario 4
4. Discussion
Funding
Conflicts of Interest
References
- Albrecht, Peter. 2015a. Versagt die Bundesregierung beim Erklären der Zinszusatzreserve? Zeitschrift für Versicherungswesen: ZfV 66: 243–44. [Google Scholar]
- Albrecht, P. 2015b. Zinszusatzreserve: Felix Austria? Zeitschrift für Versicherungswesen: ZfV 66: 346–48. [Google Scholar]
- Albrecht, Peter, and Hermann Weinmann. 2015. Zur Diskussion um die Zinszusatzreserve in der Lebensversicherung: Legaler Betrug oder mangelndes Produktverständnis? Zeitschrift für Versicherungswesen: ZfV 66: 137–39. [Google Scholar]
- Alexandrova, Maria, Alexander Bohnert, Nadine Gatzert, and Jochen Ruß. 2017. Equity-Linked Life Insurance Based on Traditional Products: The Case of Select Products. European Actuarial Journal 7: 379–404. [Google Scholar] [CrossRef]
- Assekurata. 2016. Assekurata-Marktausblick zur Lebensversicherung 2016/2017. Cologne: Assekurata. Available online: https://www.assekurata.de/fileadmin/mediendatenbank/Dokumente/Publikationen/Marktausblick/2016/Leben/Assekurata_Marktausblick_Lebensversicherung_2016_2017.pdf (accessed on 9 September 2018).
- Assekurata. 2017. Marktstudie zu Überschussbeteiligungen und Garantien 2017. Cologne: Assekurata. Available online: https://www.assekurata.de/fileadmin/mediendatenbank/Dokumente/Publikationen/Studieninfo/2017/Ueb/Praesentation_Studie_Ueberschussbeteiligungen_Garantien_2017_Homepage.pdf (accessed on 9 September 2018).
- Assekurata. 2018. Assekurata-Marktausblick zur Lebensversicherung 2018. Cologne: Assekurata. Available online: https://www.assekurata.de/fileadmin/mediendatenbank/Dokumente/Presse/Pressemitteilungen/2018/Marktausblick_Leben/Assekurata_PM_17_07_2018_Marktausblick_Lebensversicherung.pdf (accessed on 9 September 2018).
- Berdin, Elia, and Helmut Gründl. 2015. The Effects of a Low Interest Rate Environment on Life Insurers. The Geneva Papers on Risk and Insurance- Issues and Practice 40: 385–415. [Google Scholar] [CrossRef]
- BMF. 2018. Referentenentwurf des Bundesministeriums der Finanzen—Dritte Verordnung zur Änderung von Verordnungen nach dem Versicherungsaufsichtsgesetz. Available online: https://www.bundesfinanzministerium.de/Content/DE/Gesetzestexte/Gesetze_Gesetzesvorhaben/Abteilungen/Abteilung_VII/19_Legislaturperiode/2018-Dritte-Verordnung-aenderung-von-Verordnungen-nach-Versicherungsaufsichtsgesetz/1-Referentenentwurf.pdf?__blob=publicationFile&v=2 (accessed on 19 September 2018).
- Bohnert, Alexander, and Nadine Gatzert. 2014. Fair Valuation and Risk Assessment of Dynamic Hybrid Products in Life Insurance: A Portfolio Consideration. The Geneva Papers on Risk and Insurance Issues and Practice 39: 148–72. [Google Scholar] [CrossRef][Green Version]
- Bohnert, Alexander, Patricia Born, and Nadine Gatzert. 2013. Dynamic Hybrid Products in Life Insurance: Assessing the Policyholders’ Viewpoint. Insurance: Mathematics and Economics 59: 87–99. [Google Scholar] [CrossRef]
- Bohnert, Alexander, Nadine Gatzert, and Peter Løchte Jørgensen. 2015. On the Management of Life Insurance Company Risk by Strategic Choice of Product Mix, Investment Strategy and Surplus Appropriation Schemes. Insurance: Mathematics and Economics 60: 83–97. [Google Scholar] [CrossRef]
- Bohnert, Alexander, Johanna Eckert, and Nadine Gatzert. 2018. The Impact of Risk Classification in Life Insurance: An Analysis of Underwriting Risk, Underwriting Costs, and Classification Systems. Working Paper. Nuremberg: Friedrich-Alexander University Erlangen-Nürnberg (FAU). [Google Scholar]
- Consiglio, Andrea, Flavio Cocco, and Stavros Zenios. 2001. The Value of Integrative Risk Management for Insurance Products with Guarantees. Journal of Risk Finance 2: 6–16. [Google Scholar] [CrossRef]
- Dalmis, Özcan, Holger Hebben, and Matthias Matzke. 2013. Die Zinszusatzreserve im Aktiv-Passiv-Kontext. Zeitschrift für Versicherungswesen 64: 3–85. [Google Scholar]
- DAV. 2016. ZZR—Zeit Zu Renovieren?! Cologne: DAV. Available online: http://www.qx-club.de/2016_03_01_ZZR_qx_Club_final.pdf (accessed on 9 September 2018).
- DAV. 2017. Im Interesse der Kunden: Zinszusatzreserve muss neu kalibriert warden. Cologne: DAV. Available online: https://aktuar.de/fachartikelaktuaraktuell/AA39_Zinszusatzreserve.pdf (accessed on 9 September 2018).
- Eckert, Johanna, Nadine Gatzert, and Michael Martin. 2016. Valuation and Risk Assessment of Participating Life Insurance in the Presence of Credit Risk. Insurance: Mathematics and Economics 71: 382–93. [Google Scholar] [CrossRef]
- Eling, Martin, and Stefan Holder. 2013. The Value of Interest Rate Guarantees in Participating Life Insurance Contracts: Status Quo and Alternative Product Design. Insurance: Mathematics and Economics 53: 491–503. [Google Scholar] [CrossRef][Green Version]
- GDV. 2018. Die Deutsche Lebensversicherung in Zahlen 2018. Berlin: GDV. Available online: https://www.gdv.de/resource/blob/34084/953b4048365cf01fb254ba9175b0d948/lebensversicherung-in-zahlen-2018-data.pdf (accessed on 9 September 2018).
- Hieber, Peter, Ralf Korn, and Matthias Scherer. 2015. Analyzing the Effect of Low Interest Rates on the Surplus Participation of Life Insurance Policies with Different Annual Interest Rate Guarantees. European Actuarial Journal 5: 11–28. [Google Scholar] [CrossRef]
- Hieber, Peter, Jan Natolski, and Ralf Werner. 2019. Fair Valuation of Cliquet-style Return Guarantees in (Homogeneous and) Heterogeneous Life Insurance Portfolios. Scandinavian Actuarial Journal 2019: 478–507. [Google Scholar] [CrossRef]
- Holsboer, Jan. 2000. The Impact of Low Interest Rates on Insurers. The Geneva Papers on Risk and Insurance Issues and Practice 25: 33–58. Available online: www.jstor.org/stable/41952510 (accessed on 16 July 2019).
- Kling, Alexander, Andreas Richter, and Jochen Ruß. 2007a. The Interaction of Guarantees, Surplus Distribution, and Asset Allocation in With-Profit Life Insurance Policies. Insurance: Mathematics and Economics 40: 164–78. [Google Scholar] [CrossRef]
- Kling, Alexander, Andreas Richter, and Jochen Ruß. 2007b. The Impact of Surplus Distribution on the Risk Exposure of With Profit Life Insurance Policies Including Interest Rate Guarantees. Journal of Risk and Insurance 74: 571–89. [Google Scholar] [CrossRef]
- Reuß, Andreas, Jochen Ruß, and Jochen Wieland. 2016. Participating Life Insurance Products with Alternative Guarantees: Reconciling Policyholders’ and Insurers’ Interests. Risks 4: 11. [Google Scholar] [CrossRef]
- Schmeiser, Hato, and Joël Wagner. 2014. A Proposal on How the Regulator Should Set Minimum Interest Rate Guarantees in Participating Life Insurance Contracts. Journal of Risk and Insurance 82: 659–86. [Google Scholar] [CrossRef]
- Wieland, Jochen. 2017. Runoff or Redesign? Alternative Guarantees and New Business Strategies for Participating Life Insurance. European Actuarial Journal 7: 29–50. [Google Scholar] [CrossRef]
| 1 | By “old high-yield securities”, we mean securities the life insurer has had in their books for a long time. Book value and market value for these securities differ particularly strongly from each other, implying high hidden assets. |
| 2 | We assume that the life insurer pays the annuities to the policyholders at the beginning of the year. Moreover, we assume that the life insurer pays the lump sum payments on maturity to endowment holders at the beginning of the year. However, lump sum payments on death are paid at the end of the year. |
| 3 | If , the life insurer must invest the money, which is why this increases the market value and the book value of assets exactly in that amount. However, if , the life insurer must pay the negative amount. The market value is therefore reduced exactly by that amount. However, the book value differs, possibly due to hidden reserves from the market value, and therefore must be reduced by an amount that has to be adjusted by the difference between the book and market values of assets. The philosophy behind this asymmetric treatment is the careful accounting principles of local GAAP in Germany. |
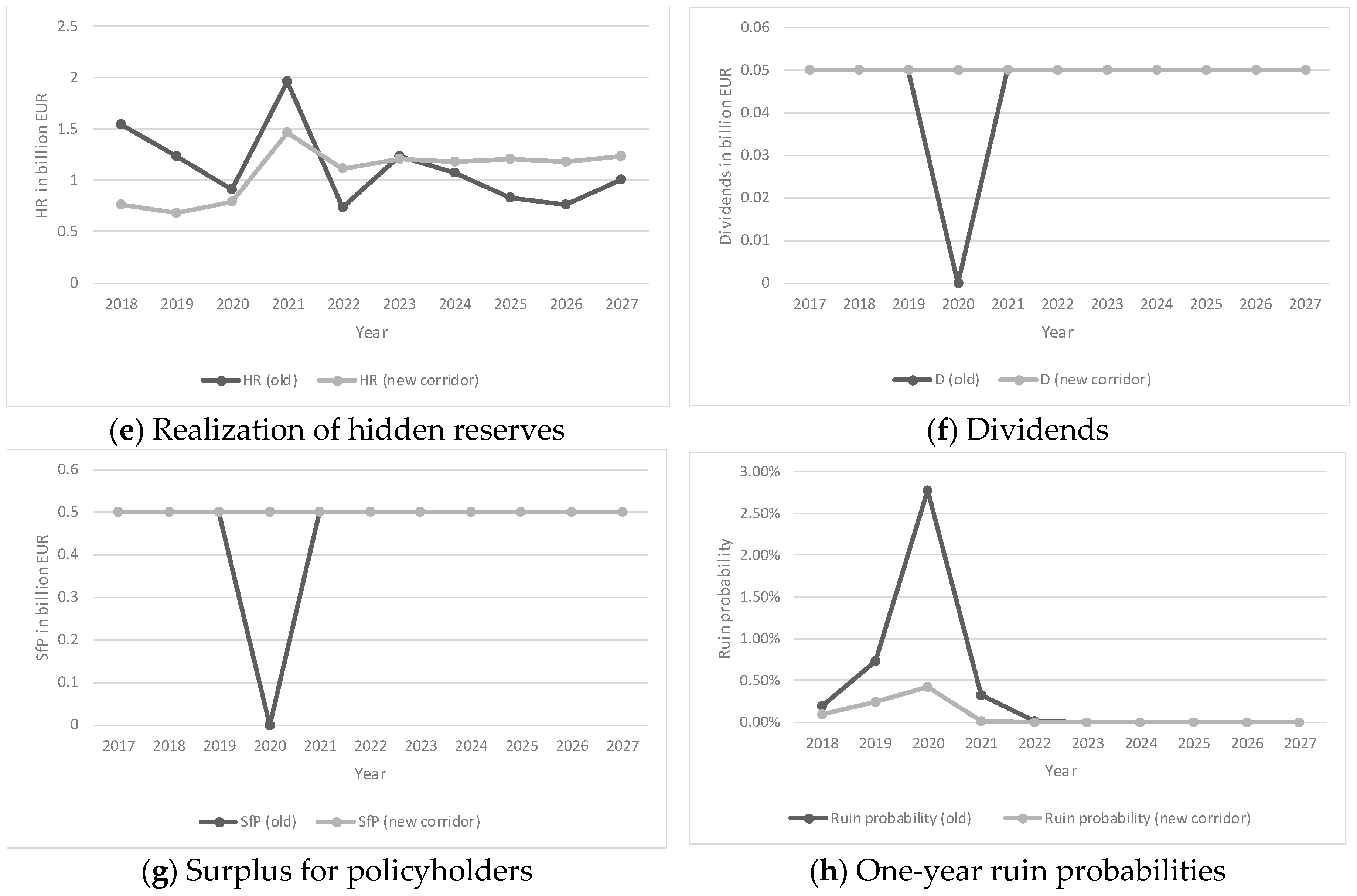
| 4 | Note that we neglected transaction costs. Taking transaction costs into account would have worsened the effect of realizing hidden reserves. |
| 5 | Note that the results using the new corridor method were based on (see BMF 2018). Sensitivity analyses for the new corridor method showed more similar results compared to the old setting using a higher x and less similar results using a lower x. This was also the case for the other interest rate scenarios. |
| 6 | Note that this also shows a problem regarding a fair distribution of hidden reserves among policyholders. Terminating policies obtain a share of hidden reserves. If hidden reserves are realized before terminating, this increases the surplus, in which policyholders also participate. However, since realized hidden reserves are used to finance the ZZR, policyholders do not participate in them. Only when the ZZR decreases does this allow the policyholders to participate. Therefore, in the case of the old method, the share of hidden reserves for policyholders with terminating policies, e.g., in 2022 was too low, while other policyholders (especially new policyholders) benefited, implying an unfair distribution among policyholders in the portfolio. |
| Assets | Liabilities |
|---|---|
| Assets | Liabilities |
|---|---|
| Start Date (01/01) | Actuarial Interest Rate in % | Annual Annuity Payment in Million EUR | Actuarial Reserve (Excl. ZZR) at t = 0 in Million EUR | ZZR at in Million EUR |
|---|---|---|---|---|
| 1986 | 3.00 | 143.36 | 834.75 | 25.89 |
| 1994 | 3.50 | 599.41 | 4348.65 | 262.12 |
| 2000 | 4.00 | 600.85 | 5514.65 | 525.99 |
| 2003 | 3.25 | 302.39 | 3185.30 | 200.51 |
| 2006 | 2.75 | 322.05 | 3884.90 | 142.49 |
| 2011 | 2.25 | 289.13 | 4282.40 | 136.64 |
| 2014 | 1.75 | 151.67 | 2615.55 | 0 |
| 2016 | 1.25 | 62.54 | 1219.00 | 0 |
| 2017 | 0.90 | 29.26 | 614.80 | 0 |
| Start Date (01/01) | Actuarial Interest Rate in % | Lump sum Payment in Million EUR | Actuarial Reserve (Excl. ZZR) at t = 0 in Million EUR | ZZR at in Million EUR |
|---|---|---|---|---|
| 1986 | 3.00 | 819.56 | 630.00 | 55.32 |
| 1994 | 3.50 | 5321.17 | 3282.00 | 532.64 |
| 2000 | 4.00 | 8526.75 | 4162.00 | 918.83 |
| 2003 | 3.25 | 5012.82 | 2404.00 | 329.22 |
| 2006 | 2.75 | 6211.13 | 2932.00 | 218.16 |
| 2011 | 2.25 | 7064.13 | 3232.00 | 18.65 |
| 2014 | 1.75 | 3842.03 | 1974.00 | 0 |
| 2016 | 1.25 | 1519.91 | 920.00 | 0 |
| 2017 | 0.90 | 672.66 | 464.00 | 0 |
| Scenario | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% | 0.90% |
| 2 | 0.60% | 0.30% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| 3 | 1.11% | 1.32% | 1.53% | 1.74% | 1.95% | 2.16% | 2.37% | 2.58% | 2.79% | 3.00% |
| 4 | 1.60% | 2.30% | 3.00% | 0.50% | 0.50% | 0.50% | 0.50% | 0.50% | 0.50% | 0.50% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eckert, C. Dealing with Low Interest Rates in Life Insurance: An Analysis of Additional Reserves in the German Life Insurance Industry. J. Risk Financial Manag. 2019, 12, 119. https://doi.org/10.3390/jrfm12030119
Eckert C. Dealing with Low Interest Rates in Life Insurance: An Analysis of Additional Reserves in the German Life Insurance Industry. Journal of Risk and Financial Management. 2019; 12(3):119. https://doi.org/10.3390/jrfm12030119
Chicago/Turabian StyleEckert, Christian. 2019. "Dealing with Low Interest Rates in Life Insurance: An Analysis of Additional Reserves in the German Life Insurance Industry" Journal of Risk and Financial Management 12, no. 3: 119. https://doi.org/10.3390/jrfm12030119
APA StyleEckert, C. (2019). Dealing with Low Interest Rates in Life Insurance: An Analysis of Additional Reserves in the German Life Insurance Industry. Journal of Risk and Financial Management, 12(3), 119. https://doi.org/10.3390/jrfm12030119





