Analysis of a Global Futures Trend-Following Strategy
Abstract
:1. Introduction
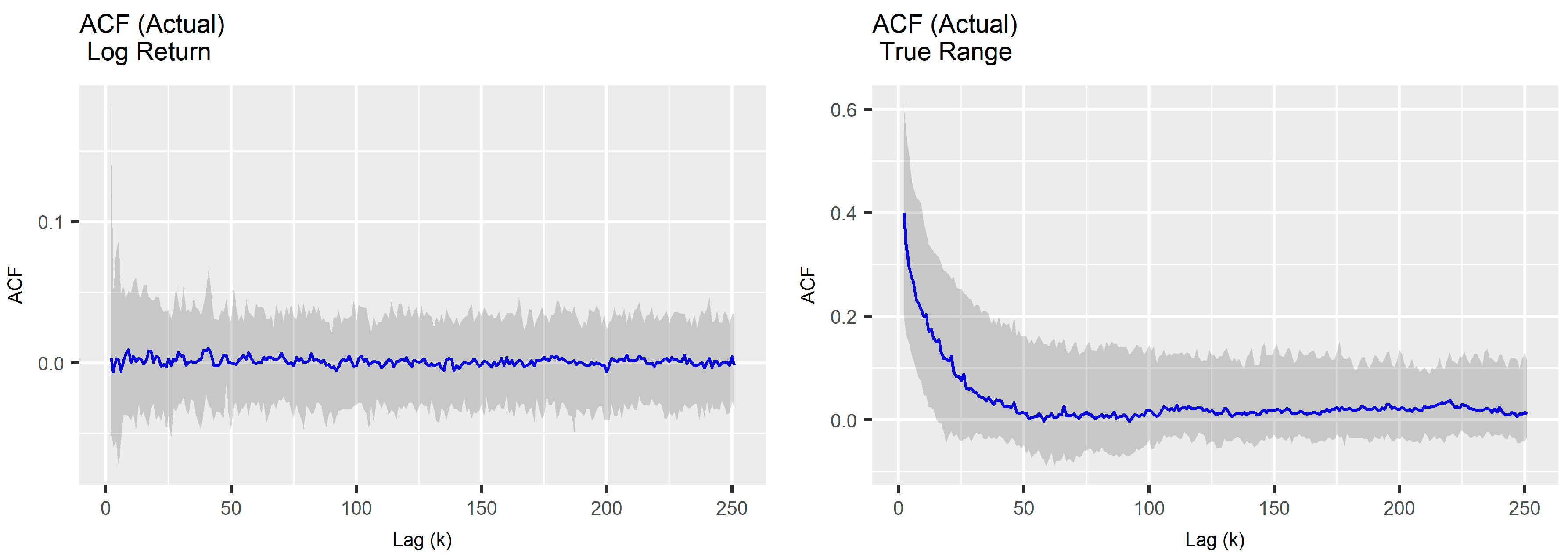
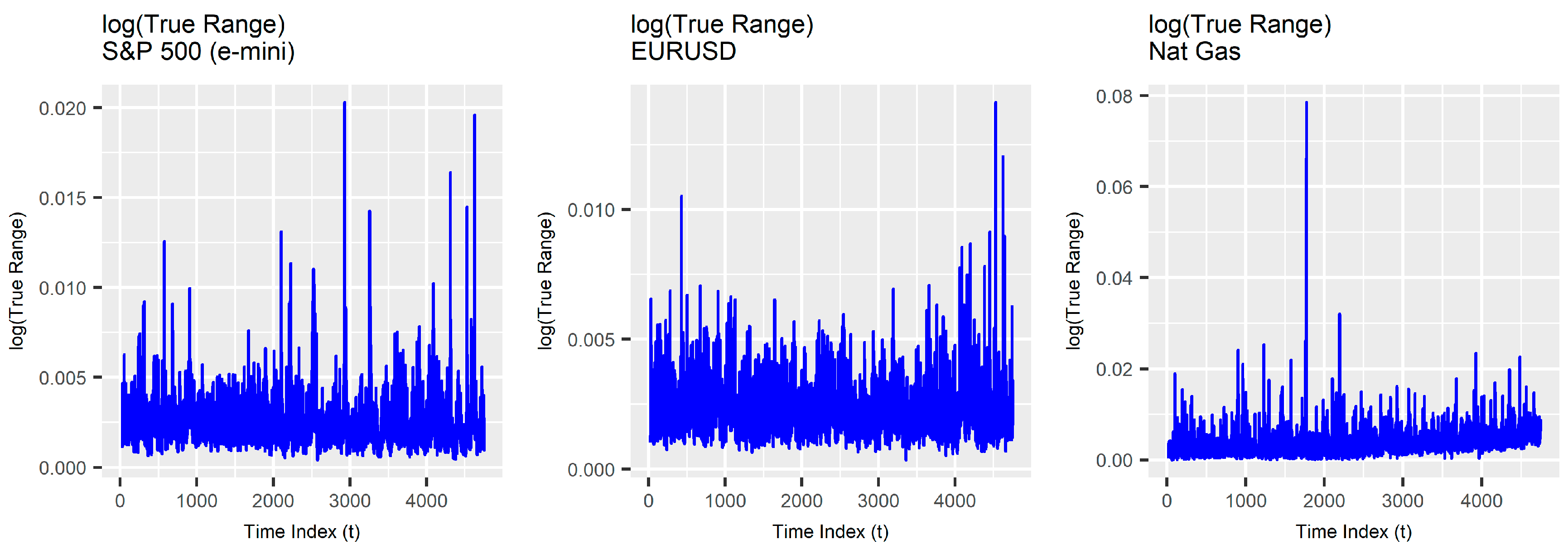
Stylized Facts
2. Materials and Methods
2.1. Data Acquisition and Transformation
2.2. Software
- buildGlobalFuturesDataset.R: Extracts data from a MySQL database and builds the R data set.
- establishStylizedFacts.R: Used to explore the stylized facts.
- calibrateMarketModelLRD_log.R: Calibrates the market model.
- selectTradingModelParameters.R: Used to explore the trading model parameters via brute force search.
- simulateMarketModelLRD_rerun_2.R: Simulates the market model and computes the sensitivities.
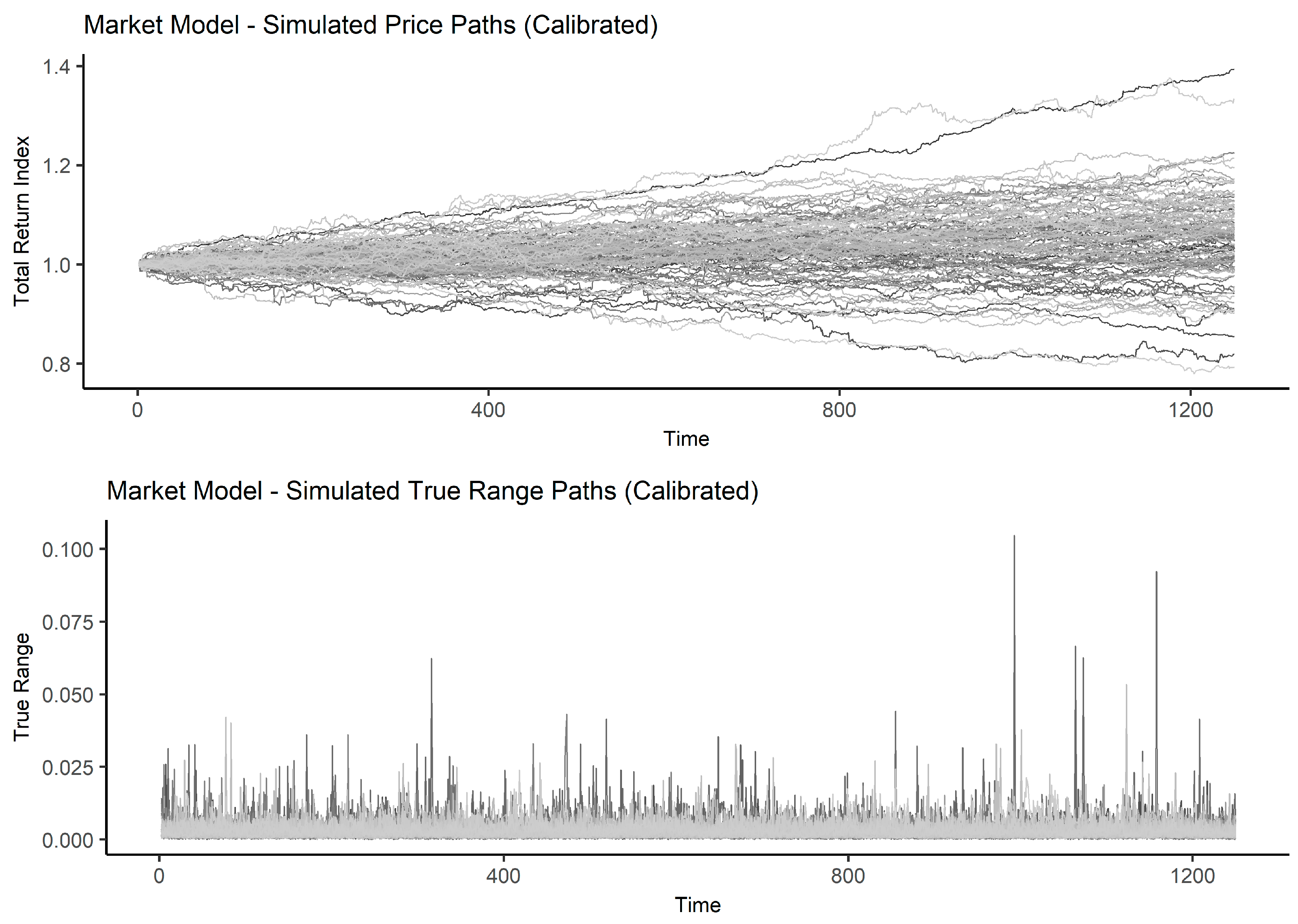
2.3. Market Model Specifications
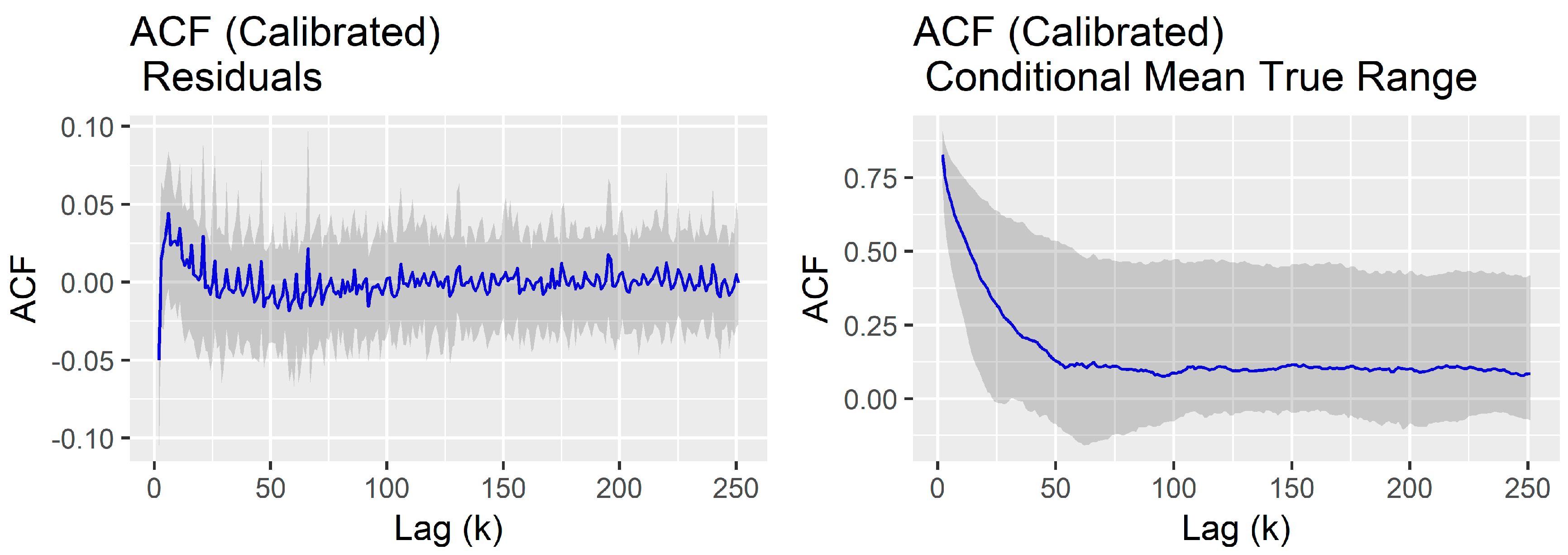
2.4. Market Model Calibration
2.5. Trading Model Specifications
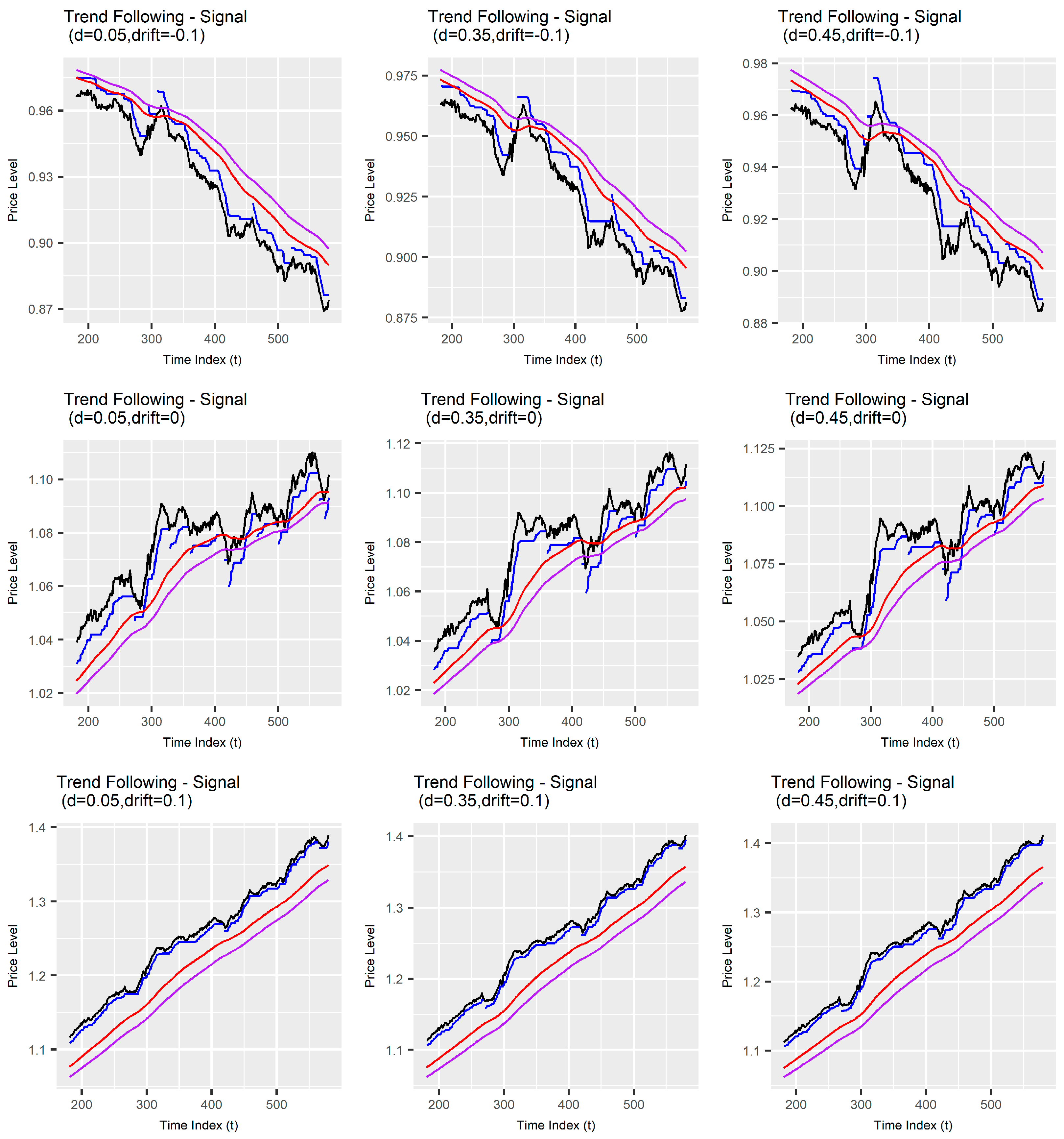
2.5.1. Long Position
2.5.2. Short Position
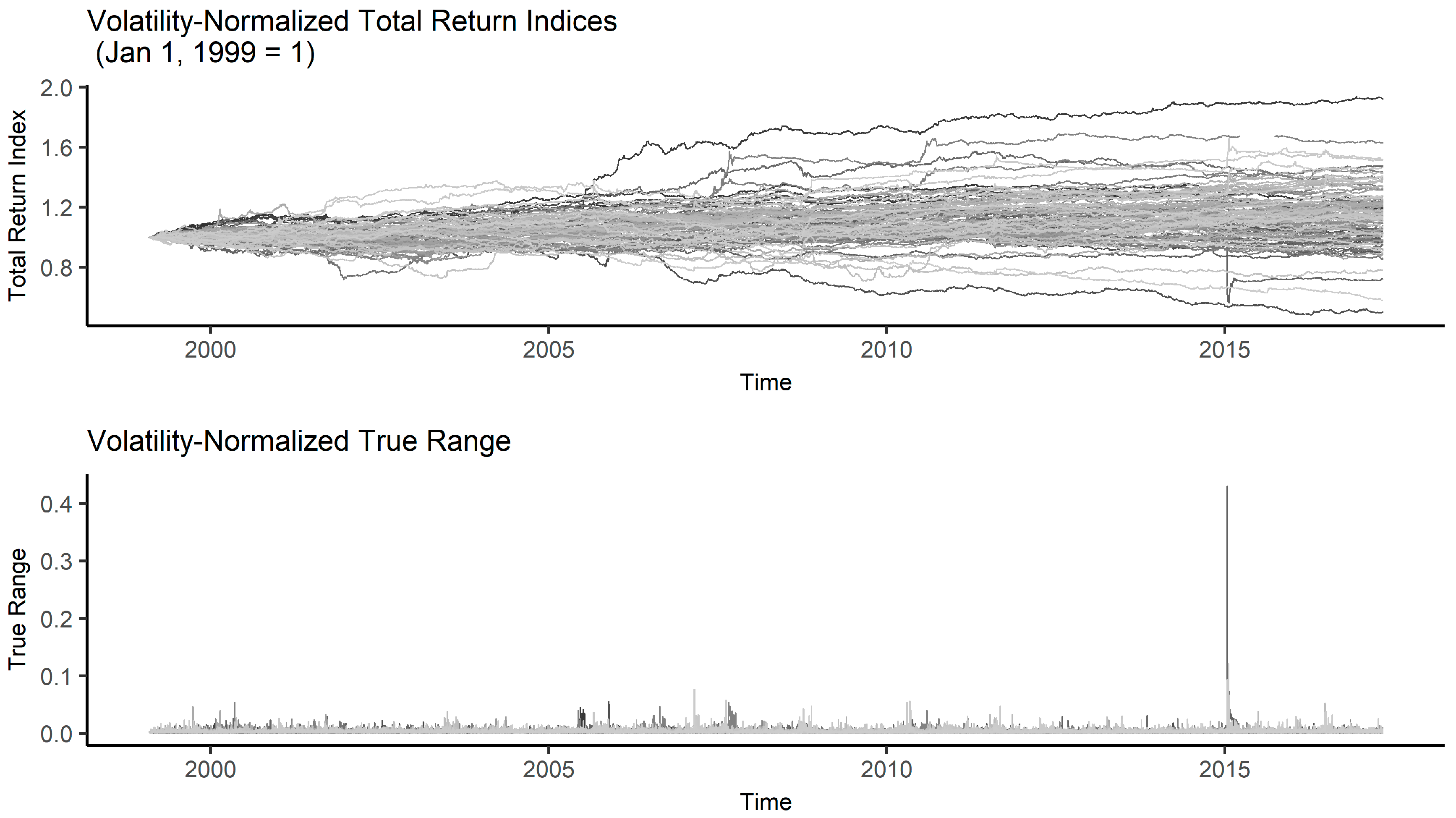
3. Results
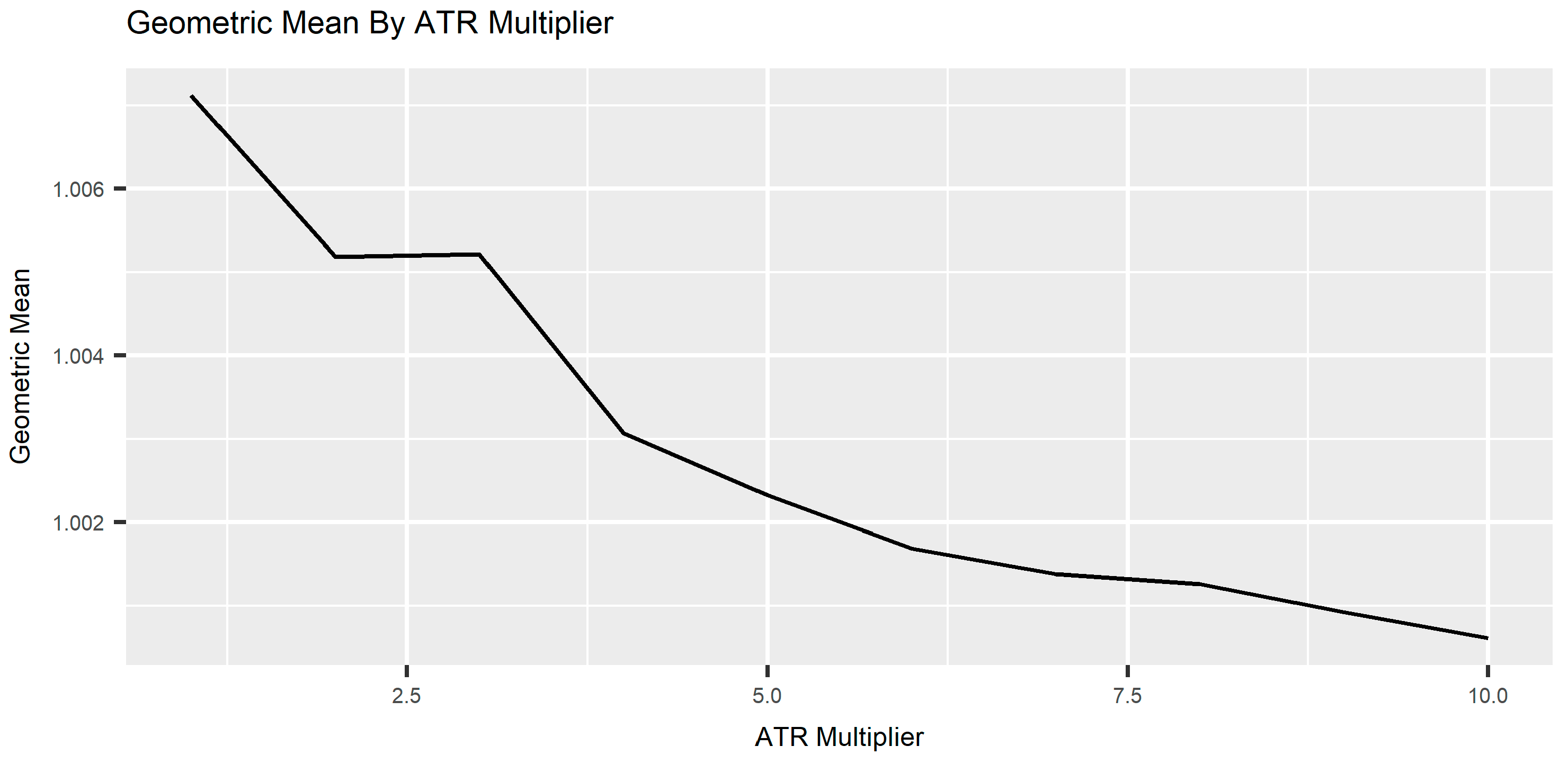
3.1. Parameter Selection
3.2. Sensitivity Analysis
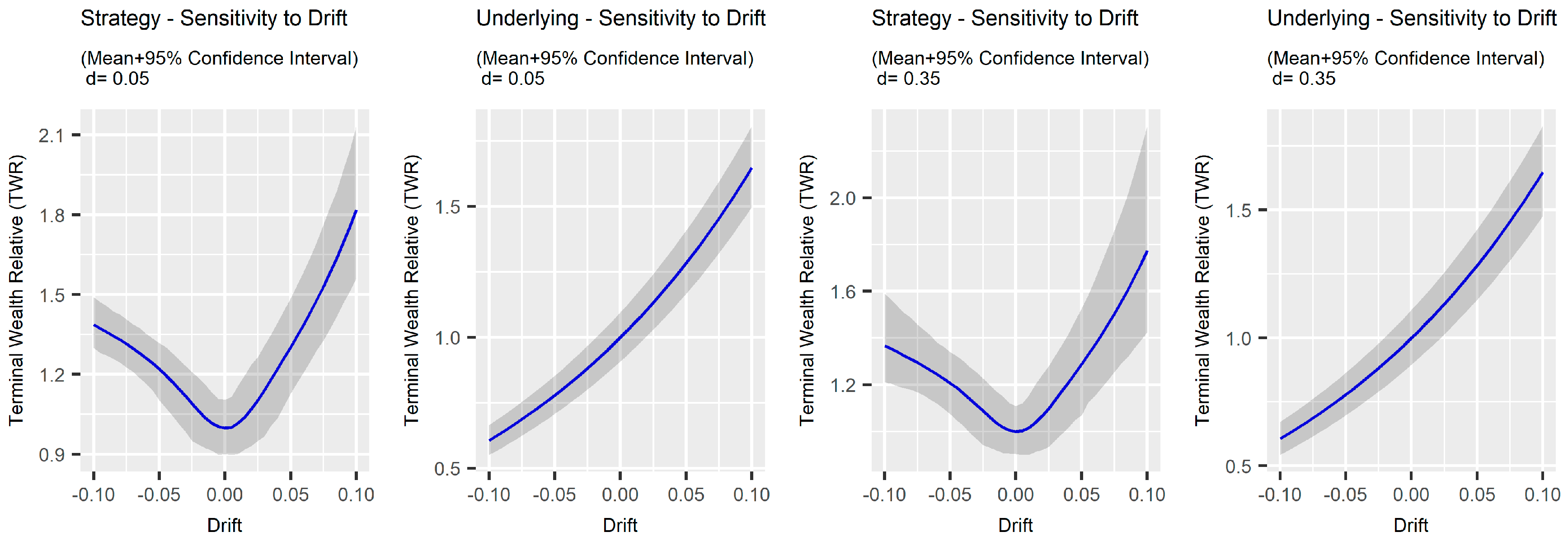
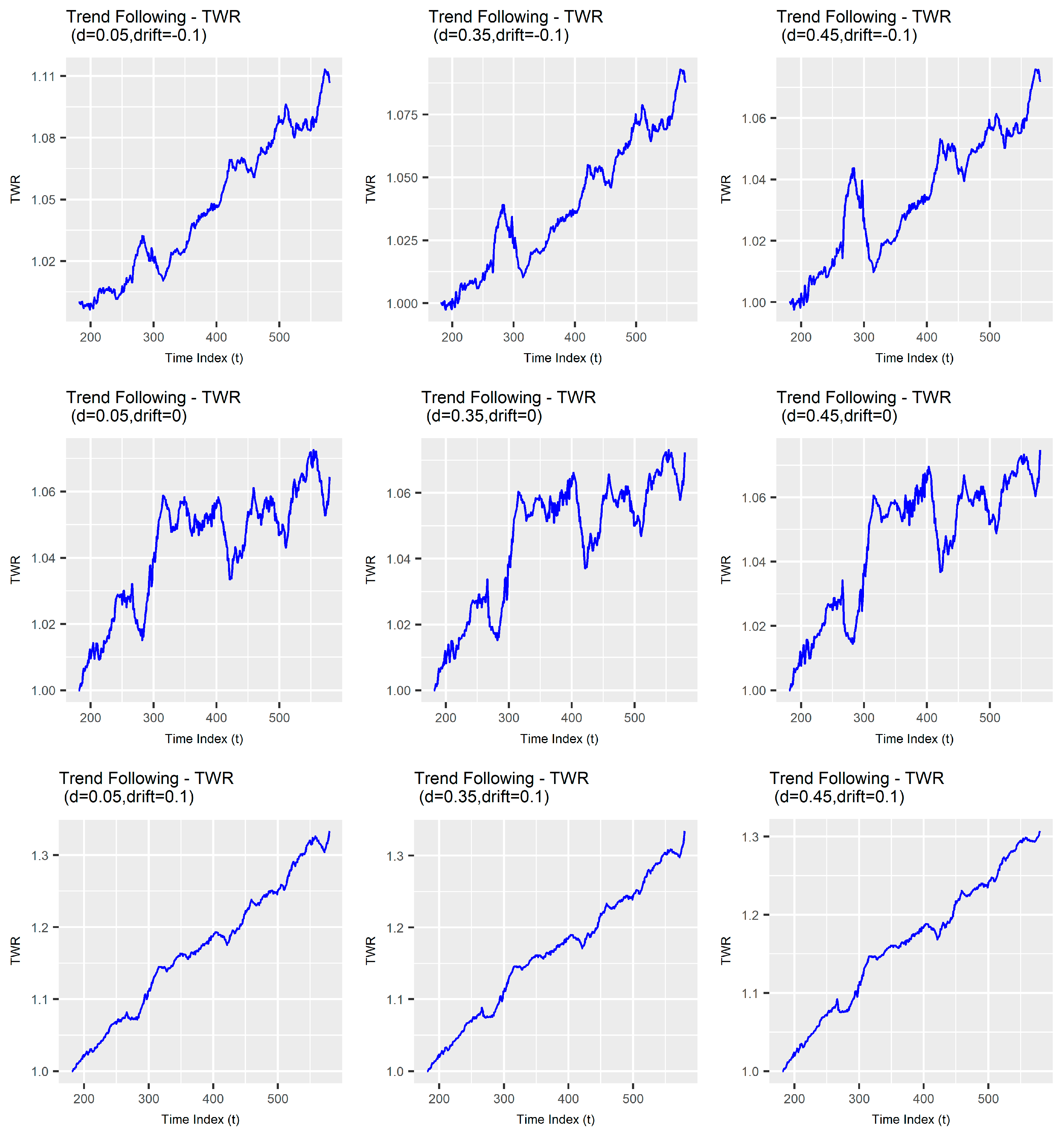
3.2.1. Trend Sensitivity
3.2.2. Serial Dependence in True Range Sensitivity
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Item # | Instrument Name | d | log(V) | var(e) | mu |
| 1 | Brent Crude Oil | 0.2355 | −6.2819 | 0.1489 | 0.0092 |
| 2 | Crude Oil | 0.2209 | −6.3405 | 0.17 | 0.0122 |
| 3 | Ethanol | 0.2809 | −6.7159 | 0.4139 | 0.0571 |
| 4 | Gas Oil | 0.2198 | −6.3044 | 0.1542 | 0.0096 |
| 5 | Gas-RBOB | 0.2011 | −6.1794 | 0.1672 | 0.0022 |
| 6 | Heating Oil | 0.2449 | −6.2499 | 0.1439 | 0.0099 |
| 7 | Nat Gas | 0.2886 | −6.14 | 0.1594 | −0.0022 |
| 8 | WTI Crude Oil | 0.2177 | −6.2201 | 0.3278 | −0.0024 |
| 9 | ECX EUA Emissions | 0.3822 | −5.7152 | 0.1031 | −0.0142 |
| 10 | Nat Gas | 0.372 | −5.8487 | 0.4072 | −0.0386 |
| 11 | AUDUSD | 0.2638 | −6.185 | 0.14 | 0.0067 |
| 12 | CADUSD | 0.2694 | −6.1393 | 0.1334 | 0.002 |
| 13 | CHFUSD | 0.2222 | −6.1448 | 0.1587 | 0.0034 |
| 14 | EURUSD | 0.2132 | −6.1638 | 0.1455 | 0.0014 |
| 15 | GBPUSD | 0.2373 | −6.1258 | 0.1397 | 0.0004 |
| 16 | JPYUSD | 0.2847 | −6.0951 | 0.1754 | −0.0058 |
| 17 | NZDUSD | 0.183 | −6.2719 | 0.3233 | 0.0123 |
| 18 | US Dollar Index | 0.183 | −6.0317 | 0.1807 | −0.0018 |
| 19 | EURCHF | 0.3317 | −6.1226 | 0.5683 | −0.0181 |
| 20 | EURGBP | 0.203 | −5.9885 | 0.4755 | −0.0013 |
| 21 | EURJPY | 0.2507 | −6.35 | 0.4758 | 0.0084 |
| 22 | BRLUSD | 0.2252 | −6.5292 | 0.7088 | 0.0223 |
| 23 | CZKUSD | 0.0844 | −6.5137 | 1.1831 | −0.0043 |
| 24 | HUFUSD | 0.0897 | −6.4835 | 1.1712 | −0.0073 |
| 25 | MXNUSD | 0.3382 | −6.1907 | 0.1611 | 0.005 |
| 26 | PLNUSD | 0.1315 | −6.5222 | 1.1359 | 0.0062 |
| 27 | RUBUSD | 0.2953 | −6.163 | 0.3264 | 0.0046 |
| 28 | ZARUSD | 0.1748 | −6.2179 | 0.6859 | −0.0049 |
| 29 | USDKRW | 0.273 | −6.0789 | 0.2116 | −0.0022 |
| 30 | Corn | 0.3198 | −6.0545 | 0.172 | −0.0009 |
| 31 | Oats | 0.3307 | −6.2312 | 0.2129 | 0.0118 |
| 32 | Rough Rice | 0.286 | −6.0389 | 0.208 | −0.0084 |
| 33 | Soybean Meal | 0.3132 | −6.322 | 0.1647 | 0.0203 |
| 34 | Soybean Oil | 0.244 | −6.1338 | 0.1459 | 0.0053 |
| 35 | Soybeans | 0.2783 | −6.2305 | 0.1561 | 0.0164 |
| 36 | Wheat | 0.2748 | −6.0158 | 0.1416 | −0.0066 |
| 37 | Corn | 0.286 | −6.5743 | 0.6159 | 0.0274 |
| 38 | Milling Wheat | 0.3447 | −6.5546 | 0.6575 | 0.0339 |
| 39 | Rapeseed | 0.2804 | −6.5859 | 0.5275 | 0.0166 |
| 40 | Wheat | 0.3195 | −6.2202 | 0.4898 | 0.0065 |
| 41 | Dow Jones Industrial (mini) | 0.3304 | −6.1172 | 0.1621 | 0.0105 |
| 42 | MSCI EAFE (mini) | 0.3136 | −6.1508 | 0.2195 | 0.01 |
| 43 | Nasdaq 100 (e-mini) | 0.3325 | −6.1532 | 0.1491 | 0.0136 |
| 44 | Russell 2000 (mini) | 0.3029 | −6.1539 | 0.1477 | 0.0125 |
| 45 | SP 500 (e-mini) | 0.3359 | −6.1039 | 0.1596 | 0.0089 |
| 46 | Belgian 20 | 0.239 | −6.0888 | 0.2724 | 0.0123 |
| 47 | CAC 40 | 0.293 | −6.1944 | 0.1899 | 0.007 |
| 48 | DAX | 0.2998 | −6.2708 | 0.2117 | 0.0081 |
| 49 | DJ Euro STOXX 50 | 0.309 | −6.0845 | 0.1636 | 0.0058 |
| 50 | EOE (Amsterdam) | 0.2994 | −5.9945 | 0.1449 | 0.0028 |
| 51 | FTSE 100 | 0.3368 | −5.9297 | 0.1181 | 0.004 |
| 52 | IBEX 35 | 0.2771 | −6.2074 | 0.1749 | 0.0072 |
| 53 | MIB FTSE | 0.3057 | −6.2135 | 0.1974 | 0.0011 |
| 54 | Nikkei 225 | 0.2941 | −6.3303 | 0.3148 | 0.0055 |
| 55 | OMX | 0.386 | −6.9382 | 0.165 | 0.0124 |
| 56 | SPTSE 60 | 0.2485 | −6.0678 | 0.1485 | 0.0113 |
| 57 | SMI | 0.3235 | −5.9756 | 0.1364 | 0.008 |
| 58 | SPI 200 | 0.2745 | −6.3048 | 0.2375 | 0.0099 |
| 59 | TOPIX | 0.2845 | −6.2746 | 0.2545 | 0.0074 |
| 60 | MSCI EM (mini) | 0.2801 | −6.0982 | 0.1943 | −0.0027 |
| 61 | MSCI Taiwan | 0.2195 | −6.1515 | 0.1817 | 0.0092 |
| 62 | SP CNX Nifty | 0.1867 | −6.3298 | 0.4275 | 0.0175 |
| 63 | Hang Seng | 0.1864 | −6.2192 | 0.1769 | 0.0128 |
| 64 | Hang Seng (mini) | 0.1814 | −6.1844 | 0.1782 | 0.0128 |
| 65 | Hang Seng China Enterprises | 0.2633 | −6.2258 | 0.153 | 0.0158 |
| 66 | IPC | 0.3258 | −5.8855 | 0.1262 | 0.0064 |
| 67 | KOSPI 200 | 0.2357 | −6.5445 | 0.4424 | 0.0126 |
| 68 | Feeder Cattle | 0.2522 | −6.1331 | 0.1549 | 0.0109 |
| 69 | Lean Hogs | 0.2451 | −5.9264 | 0.1445 | −0.0064 |
| 70 | Live Cattle | 0.2083 | −6.1276 | 0.1491 | 0.0088 |
| 71 | Copper | 0.2635 | −6.1975 | 0.1522 | 0.0091 |
| 72 | Gold | 0.3005 | −6.18 | 0.1894 | 0.0108 |
| 73 | Palladium | 0.3813 | −6.2387 | 0.2212 | 0.0111 |
| 74 | Platinum | 0.3442 | −6.2491 | 0.1652 | 0.011 |
| 75 | Silver | 0.3047 | −6.1876 | 0.1795 | 0.0066 |
| 76 | USD Deliverable Swap 10 year | 0.299 | −6.0867 | 0.208 | 0.0123 |
| 77 | USD Deliverable Swap 5 year | 0.2849 | −6.0717 | 0.2412 | 0.007 |
| 78 | USD Govt 10yr | 0.2797 | −6.2127 | 0.1532 | 0.0173 |
| 79 | USD Govt 15–30yr | 0.2606 | −6.1806 | 0.1457 | 0.0141 |
| 80 | USD Govt 2yr | 0.2951 | −6.2539 | 0.1923 | 0.0209 |
| 81 | USD Govt 30yr | 0.3198 | −6.1727 | 0.1455 | 0.0156 |
| 82 | USD Govt 5yr | 0.2751 | −6.2401 | 0.1649 | 0.0176 |
| 83 | AUD Govt 10yr | 0.1748 | −6.3502 | 0.3921 | 0.0076 |
| 84 | AUD Govt 3yr | 0.1689 | −6.3336 | 0.4123 | 0.0084 |
| 85 | CAD Govt 10yr | 0.2198 | −6.1027 | 0.2192 | 0.0182 |
| 86 | CHF Govt 10yr | 0.2652 | −6.3925 | 0.3511 | 0.02 |
| 87 | DEM Govt 10yr | 0.2364 | −6.4194 | 0.2785 | 0.0172 |
| 88 | DEM Govt 2yr | 0.2896 | −6.3881 | 0.3155 | 0.0179 |
| 89 | DEM Govt 5yr | 0.2472 | −6.4036 | 0.2799 | 0.0186 |
| 90 | FRF Govt 10yr | 0.3146 | −6.098 | 0.1477 | 0.0307 |
| 91 | GBP Govt 10yr | 0.2338 | −6.0316 | 0.1308 | 0.0132 |
| 92 | ITL Govt 10yr | 0.4065 | −5.9488 | 0.1303 | 0.0201 |
| 93 | ITL Govt 2yr | 0.4559 | −6.019 | 0.2678 | 0.0294 |
| 94 | JPY Govt 10yr (mini) | 0.3342 | −6.3402 | 0.2904 | 0.0182 |
| 95 | KRW Govt 10yr | 0.295 | −6.3422 | 0.2746 | 0.0275 |
| 96 | Butter | 0.2603 | −6.0707 | 0.8538 | 0.0164 |
| 97 | Cocoa | 0.2437 | −6.11 | 0.1751 | 0.0011 |
| 98 | Coffee | 0.2895 | −6.0532 | 0.1854 | −0.0044 |
| 99 | Cotton 2 | 0.3031 | −6.1075 | 0.181 | −0.0023 |
| 100 | Lumber | 0.2773 | −5.9161 | 0.1449 | −0.0138 |
| 101 | Milk-Class III Fluid | 0.3337 | −6.1052 | 0.3525 | 0.0072 |
| 102 | Orange Juice | 0.2462 | −6.1736 | 0.2549 | 0.0069 |
| 103 | Robusta Coffee | 0.3565 | −6.0909 | 0.2177 | 0.0004 |
| 104 | Sugar 11 | 0.3112 | −6.2256 | 0.1673 | 0.0063 |
| 105 | Sugar 5 | 0.2975 | −6.2787 | 0.2071 | 0.0126 |
| 106 | TSR20 Rubber | 0.3321 | −6.1874 | 0.3907 | 0.0106 |
| 107 | Cocoa | 0.3086 | −5.9108 | 0.1417 | 0.0039 |
| 108 | USD STIR | 0.4512 | −6.1231 | 0.2431 | 0.0303 |
| 109 | AUD STIR | 0.2282 | −6.0767 | 0.3378 | 0.0081 |
| 110 | CAD STIR | 0.3843 | −5.9982 | 0.2806 | 0.0265 |
| 111 | CHF STIR | 0.4136 | −6.0595 | 0.2454 | 0.0332 |
| 112 | EUR STIR | 0.4227 | −5.7489 | 0.2022 | 0.0162 |
| 113 | GBP STIR | 0.33 | −5.9621 | 0.2374 | 0.0244 |
| 114 | VIX | 0.4345 | −5.9535 | 0.237 | −0.0443 |
| 115 | VSTOXX (mini) | 0.4162 | −5.9015 | 0.1454 | −0.0248 |
Appendix B
Evaluation Measures
- If AHPRT is less than or equal to 1, then regardless of the other two variables, SDHPRT and T, our result can be no greater than 1 (i.e., our total return will be less than or equal to zero).
- If AHPRT is less than 1, then as T approaches infinity, TWRT approaches zero. This means that if AHPRT is less than 1, we will eventually go broke.
- If AHPRT is greater than 1, increasing T increases our TWRT.
- If we reduce our SDHPRT more than we reduce our AHPRT our TWRT will rise.
References
- Beran, Jan. 1995. Maximum likelihood estimation of the differencing parameter for invertible short and long memory autoregressive integrated moving average models. Journal of the Royal Statistical Society: Series B Methodological 57: 659–72. [Google Scholar] [CrossRef]
- Beran, Jan, Yuanhua Feng, and Sucharita Ghosh. 2015. On EFARIMA and ESEMIFAR models. In Empirical Economic and Financial Research. Edited by Jan Beran, Yuanhua Feng and Hartmut Hebbel. Advanced Studies in Theoretical and Applied Econometrics. Cham: Springer International Publishing, pp. 239–53. [Google Scholar]
- Bollerslev, Tim, Ray Y. Chou, and Kenneth F. Kroner. 1992. ARCH modeling in finance: A review of the theory and empirical evidence. Journal of Econometrics 52: 5–59. [Google Scholar] [CrossRef]
- Brock, William A., and Pedro J. F. de Lima. 1996. Nonlinear time series, complexity theory, and finance. Handbook of Statistics 14: 317–361. [Google Scholar]
- Brunetti, Celso, and Peter M. Lildholdt. 2007. Time series modeling of daily Log-Price ranges for CHF/USD and USD/GBP. The Journal of Derivatives 15: 39–59. [Google Scholar] [CrossRef]
- Chou, Ray Yeutien. 2005. Forecasting financial volatilities with extreme values: The conditional autoregressive range (CARR) model. Journal of Money, Credit and Banking 37: 561–82. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitive Finance 1: 223–36. [Google Scholar] [CrossRef]
- Curtis, Faith. 2007. Way of the Turtle: The Secret Methods that Turned Ordinary People into Legendary Traders: The Secret Methods That Turned Ordinary People into Legendary Traders. New York: McGraw Hill Professional. [Google Scholar]
- De Prado, Marcos Lopez. 2018. Advances in Financial Machine Learning. Hoboken: Wiley. [Google Scholar]
- Farmer, J. Doyne, and John Geanakoplos. 2009. The virtues and vices of equilibrium and the future of financial economics. Complexity 14: 11–38. [Google Scholar] [CrossRef]
- Fox, Robert, and Murad S. Taqqu. 1986. Large-Sample properties of parameter estimates for strongly dependent stationary gaussian time series. The Annals of Statistics 14: 517–32. [Google Scholar] [CrossRef]
- Giraitis, Liusdas, and Donatas Surgailis. 1990. A central limit theorem for quadratic forms in strongly dependent linear variables and its application to asymptotical normality of whittle’s estimate. Probability Theory and Related Fields 86: 87–104. [Google Scholar] [CrossRef]
- Gourieroux, Christian, and Joann Jasiak. 2001. Financial Econometrics: Problems, Models, and Methods. Princeton: Princeton University Press, vol. 1. [Google Scholar]
- Haslett, John, and Adrian E. Raftery. 1989. Space-Time modelling with Long-Memory dependence: Assessing ireland’s wind power resource. Journal of the Royal Statistical Society: Series C Applied Statistics 38: 1–21. [Google Scholar] [CrossRef]
- Hurst, Brian, Yao Hua Ooi, and Lasse Heje Pedersen. 2017. A Century of Evidence on Trend-Following Investing. SSRN. Available online: https://ssrn.com/abstract=2993026 (accessed on 26 June 2019).
- McLeod, A. Ian, Hao Yu, and Zinovi L. Krougly. 2007. Algorithms for linear time series analysis: With R package. Journal of Statistical Software 23: 1–26. [Google Scholar] [CrossRef]
- Mills, Terence C. 1999. The Econometric Modelling of Financial Time Series, 2nd ed.Cambridge: Cambridge University Press. [Google Scholar]
- Pagan, Adrian. 1996. The econometrics of financial markets. Journal of Empirical Finance 3: 15–102. [Google Scholar] [CrossRef]
- Rao, C. R., and G. S. Maddala, eds. 1996. Handbook of Statistics: Statistical Methods in Finance. New York: Elsevier, vol. 14. [Google Scholar]
- Shephard, Neil. 1996. Statistical aspects of ARCH and stochastic volatility. In Time Series Models. Edited by D. R. Cox, D. V. Hinkley and O. E. Barndorff-Nielsen. Boston: Springer, pp. 1–67. [Google Scholar]
- Veenstra, J. Q., and A. McLeod. 2015. arfima: Fractional ARIMA (and Other Long Memory) Time Series Modeling. R package version 1.3-4. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Xie, Yihui. 2015. Dynamic Documents with R and knitr, 2nd ed.Boca Raton: Chapman and Hall/CRC, ISBN 978-1498716963. [Google Scholar]
- Xie, Yihui. 2016. Bookdown: Authoring Books and Technical Documents with R Markdown. R package version 0.3. Vienna: R Foundation for Statistical Computing. [Google Scholar]

| Parameter | Value |
|---|---|
| atrLookback | 20 |
| atrMultiplier | 4 |
| fastLookback | 120 |
| slowLookback | 180 |
| longOnly | 0 |
| commissionPerShare | 0 |
| accountSize | 100,000 |
| fPercent | 0.01 |
| minRisk | 0.001 |
| stopTWR | 0.7 |
| nRowsScenario | 1250 |
| nPathsScenario | 1000 |
| S0 | 1 |
| T | 5 |
| xMean | −6.2146 |
| xSigma2 | 0.15 |
| randomSeed | 1,234,567 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nokes, D.; Fulton, L. Analysis of a Global Futures Trend-Following Strategy. J. Risk Financial Manag. 2019, 12, 111. https://doi.org/10.3390/jrfm12030111
Nokes D, Fulton L. Analysis of a Global Futures Trend-Following Strategy. Journal of Risk and Financial Management. 2019; 12(3):111. https://doi.org/10.3390/jrfm12030111
Chicago/Turabian StyleNokes, Derek, and Lawrence Fulton. 2019. "Analysis of a Global Futures Trend-Following Strategy" Journal of Risk and Financial Management 12, no. 3: 111. https://doi.org/10.3390/jrfm12030111
APA StyleNokes, D., & Fulton, L. (2019). Analysis of a Global Futures Trend-Following Strategy. Journal of Risk and Financial Management, 12(3), 111. https://doi.org/10.3390/jrfm12030111






