Abstract
We propose a novel approach that combines random forests and the wavelet transform to model the prediction of currency crises. Our classification model of random forests, built using both standard predictors and wavelet predictors, and obtained from the wavelet transform, achieves a demonstrably high level of predictive accuracy. We also use variable importance measures to find that wavelet predictors are key predictors of crises. In particular, we find that real exchange rate appreciation and overvaluation, which are measured over a horizon of 16–32 months, are the most important.
JEL Codes:
F31; F37; F47
1. Introduction
Severe economic collapse in developing countries often involves currency crises triggered by speculative attacks on the currency and sudden stops to capital inflows. An unexpectedly sharp exchange rate depreciation tends to have a contractionary effect on economic activities, owing to an extensive dollarization of liabilities in both bank and corporate balance sheets. Thus, preventing serious currency crises is considered a priority task of macroeconomic management in developing countries.
Having observed the severe economic consequences of emerging market currency crises during the 1990s, economists have searched for a reliable currency crisis prediction model. The seminal works include Frankel and Rose (1996) and Kaminsky et al. (1998). Frankel and Rose (1996) define a currency crash as the nominal depreciation of a currency’s value by at least 25%, which is also at least a 10% increase in the rate of depreciation. They estimate multivariate logistic regressions and find that a currency crash tends to occur when output growth is low, the growth of domestic credit is high, and the foreign interest level is high. Kaminsky et al. (1998) propose a signaling approach, which seeks to identify the threshold values for individual predictors. They find that exports, real exchange rate overvaluation, GDP growth, foreign exchange reserves, and equity prices are the most reliable predictors of crises. Berg and Pattillo (1999) use panel probit models and show that their forecasting ability outperforms the signaling approach. Bussiere and Fratzscher (2006) use multinomial logistic regressions, which distinguish between tranquil periods, crisis periods, and post-crisis periods. They use the exchange market pressure (EMP) index originally proposed by Eichengreen et al. (1995) to define a currency crisis and show that the multinomial logistic model predicts crises better than the binomial logistic model. In a similar vein, Abiad (2003) and Martinez-Peria (2002) use a Markov-switching model, which identifies and characterizes crisis periods endogenously. Shimpalee and Breuer (2006) focus on the role of institutional factors and use the probit model to show that corruption, de facto fixed exchange rates, weak government stability, and weak law and order increase the probability of crises.
The global financial crisis of 2008 has rekindled interest in this topic. Rose and Spiegel (2011, 2012) regressed the measure of crisis intensity on a set of potential predictors; however, they found few clear and reliable predictors for the cross-country incidence of severe recessions during the global financial crisis. Frankel and Saravelos (2012) investigated whether traditional indicators can help explain why some countries were badly impacted by the global financial crisis and found that foreign exchange reserves and real exchange rate overvaluation are the most useful predictors. Gourinchas and Obstfeld (2012) employed the methods of event studies and logit regressions and found that domestic credit expansion, real exchange rate appreciation, and foreign exchange reserves are useful predictors of crises in emerging market economies. Sevim et al. (2014) used decision trees and artificial neural networks to predict currency crises in Turkey and showed that results from these two methods are superior to those obtained by logistic regressions.
In this study, we propose a novel approach that combines a machine learning technique of random forests and a signal processing method of the wavelet transform to model the prediction of currency crises. We demonstrate that our model can achieve a high level of accuracy in predicting currency crises. Our contribution to the literature is two-fold. First, we use the wavelet transform to extract key features of exchange rate behavior that may signal the risk of currency crises. The existing studies tend to focus on a particular aspect of exchange rate behavior, such as overvaluation or volatility over a particular period of time. By applying the wavelet transform, we can systemically extract various features of exchange rate behavior across different time horizons. Recent literature in economics and finance makes extensive use of wavelet analysis, indicating its usefulness as a tool for feature extraction (Reboredo and Rivera-Castro 2013; Cai et al. 2017; Faria and Verona 2018). Second, we construct a prediction model by applying the random forests method, which is a variant of decision trees. The existing literature is generally more concerned with identifying the key predictors of crises than improving the predictive accuracy (Frankel and Saravelos 2012). We choose the random forests method to construct a prediction model because it can significantly improve predictive accuracy by building a large number of trees using random input selection (Breiman 2001). In addition, the random forests method provides variable importance measures that rank predictors according to their contribution to the prediction. Thus, the random forests method also addresses the traditional question of which predictors are most reliable. Owing to its superior performance, the random forests method has been increasingly employed in the area of economic and financial forecasting (Tanaka et al. 2018).
2. Methodology and Data
2.1. Discrete Wavelet Transformation
We applied the discrete wavelet transform (DWT) to a time series of monthly exchange rates and systemically extracted key features of exchange rate behavior over different time horizons. Specifically, we used a modified version of DWT known as the maximal overlap DWT (MODWT) because its sample size need not be restricted to a power of two. Existing studies typically measure the deviation from the trend and the volatility of exchange rates over an arbitrarily selected period of time. Our approach has an advantage over the existing methods because it evaluates various aspects of exchange rate behavior over different time horizons. The MODWT was computed using the pyramid algorithm proposed by Percival and Walden (2000)1.
The sample variance of the exchange rate series can be decomposed into parts corresponding to the variance of the series on different scales. For a partial DWT of level J0, the decomposition is given by:
where denotes the sample variance of the exchange rate series; denotes an N dimensional vector, whose element is the jth level wavelet coefficient corresponding to a scale of ; denotes an N dimensional column vector, whose element is the J0th level scaling coefficient corresponding to a scale of ; and denotes the sample average of the exchange rate series2. The jth level wavelet coefficients of and the scaling coefficients of are given by:
where and are matrices whose rows contain circularly shifted and up-sampled versions of the wavelet filter, , and scaling filter, , periodized to length N; N denotes the sample size; and denotes an N dimensional vector, whose element {Xt} is the exchange rate series3.
The multi-resolution analysis (MRA) decomposes a time series of exchange rates into parts corresponding to the variation of the series on different scales. For a partial DWT of level J0, the MRA is given by:
where denotes an N dimensional vector whose element is the jth level wavelet detail corresponding to a scale, , and denotes an N dimensional vector, whose element is the J0th level smooth function corresponding to a scale, . The jth level details of and the smooth function of are given by:
and
respectively, where and denote the transposers of and , respectively4.
A cascade of wavelet filters relating to Xt is an approximation to a band-pass filter with the pass-band given by , while a cascade of scaling filters relating to Xt is an approximation to a low-pass filter with the pass-band given by . Correspondingly, represents the variation of monthly exchange rates over months, while represents the trend obtained after the sum of , up to the jth level, is removed from the series.
We set J0 = 5 and computed each level of , , , and up to the fifth level. Our choice of MODWT wavelet and scaling filters are Harr filters5, which are given by:
We used a time series of , , , and as predictors for building a classification model of random forests. Specifically, we used the square of and to capture the scale-by-scale contribution to the volatility of nominal exchange rates, while we used to capture the variation of real exchange rates over various time horizons. In addition, we measured the overvaluation of real exchange rates by computing the difference between the actual value of the real exchange rates and the corresponding on each scale. The nominal exchange rate was the end-of-period monthly bilateral dollar exchange rate, while the real exchange rate is computed by deflating the nominal exchange rate with the consumer price index (CPI). Both nominal and real exchange rates were transformed into logarithmic terms.
2.2. The EMP Index
A currency crisis can be characterized as a situation in which a country’s currency is under a severe attack that leads to a sharp depreciation of exchange rates and/or a substantial loss in foreign exchange reserves. To measure the extent of downward pressures on exchange rates, many studies employ the EMP index originally proposed by Eichengreen et al. (1995). In this study, we used the modified version of the EMP index employed by Bussiere and Fratzscher (2006). The modified index is the weighted average of the annual changes of real exchange rates and foreign exchange reserves given by:6
where denotes the real exchange rate as defined above; denotes the foreign exchange reserves; and denote the inverse of the variance of change rates in exchange rates and foreign exchange reserves, respectively; and the subscripts i and t denote a specific country and time, respectively. Using this EMP index, a binary variable of currency crises is defined as follows:
where and denote the sample mean and the standard deviation of the EMP index, respectively, for each country.
Table 1 shows the number of currency crises obtained during the sample period by using Equation (9).

Table 1.
Number of currency crises.
2.3. Classification Model of Random Forests
In this paper, we built a classification model of random forests for predicting currency crises. An alternative method is to estimate a probit or a logistic regression, in which the probability of a crisis is regressed on a set of predictors, such as exchange rates, foreign exchange reserves, and domestic credit supply. In this study, we employed the method of random forests because it tends to perform better in terms of predictive accuracy. The random forests classification model is a variant of classification trees, which split the data at each node into smaller, more homogeneous groups. To achieve homogeneity, the classification trees search the predictor to split the data and the value at which they are split (Kuhn and Johnson 2013). The homogeneity is measured by the Gini index, which is defined for the two-class problem as:
where and are the probabilities for the classes. A smaller value of the Gini index implies a greater degree of homogeneity in the group.
Compared with a basic classification tree, the random forests method performs better in terms of classification accuracy for two main reasons. First, it seeks to reduce the prediction variance and, thus, to improve predictive performance over a single tree by so-called bagging, which is the building of many trees using different bootstrapped training data sets and averaging the resulting predictions. Second, it seeks to lessen correlation among trees by adding randomness to the selection of predictors at each split (Breiman 2001).
We followed Kuhn and Johnson’s (2013) method for building a random forests classification model and evaluated its performance 7. Our selection of predictors was guided by Frankel and Saravelos (2012), who conducted an extensive literature survey and concluded that the most reliable indicators for predicting crises include foreign exchange reserves, the real exchange rate, the growth rate of credit, GDP, and the current account. Hence, we used the annual series of the following indicators to predict whether a crisis occurs in the following year: (i) the ratio of total reserves to GDP (res_gdp); (ii) the growth rate of total reserves; (gr_res); (iii) the growth rate of real GDP (gr_gdp); (iv) the current account balance as a percentage of GDP (ca); (v) the growth rate of broad money (gr_bm); (vi) the ratio of broad money to GDP (bm_gdp); (vii) the ratio of broad money to total reserves (bm_res); (viii) for real exchange rates (dj_rer); (ix) real exchange rate overvaluation, measured by the difference between the actual value and (ovj_rer); (x) the square of for nominal exchange rates (wj_ner); and (xi) the square of for nominal exchange rates (v5_ner). Note that the annual data for the wavelet predictors corresponding to indicators (viii)–(xi) were constructed by averaging the monthly series obtained from the DWT for each year.
The sample for predictors covers 40 developing countries over the period 1991–2015. Thus, the corresponding sample of the EMP index covers the same countries over the period 1992–2016. The list of the sample countries is provided in the Appendix A. We selected countries for which the proportion of missing data of monthly exchange rates or CPI in the total sample was not more than 10%. The k-nearest-neighbor imputation was used to deal with the missing data. The data sources were the International Financial Statistics of the International Monetary Fund (IMF) and the World Development Indicators of the World Bank. Table 2 shows the summary statistics of the variables.

Table 2.
Summary statistics. EMP: exchange market pressure.
3. Results
3.1. Wavelet Predictors
Table 3 compares the mean and standard deviations of wavelet predictors between the crisis and non-crisis samples. The former includes the observations of wavelet predictors in the year immediately before a crisis, while the latter includes those in the year immediately before a year with no crisis.

Table 3.
Wavelet predictors (crisis vs. non-crisis).
There are three points worth noting here. First, the means for all levels of dj_rer in the crisis sample were negative, while those in the non-crisis sample were positive. The t-test rejects the null hypothesis that the mean is the same across the two samples for all levels of dj_rer. These results indicate that the appreciation of the real exchange rate over various time horizons was associated with a crisis in the following year. In other words, the appreciation of the real exchange rate signals the risk of a crisis. Second, the means for all levels of ovj_rer in the crisis sample were negative, while those in the non-crisis sample were positive. The corresponding t-test rejects the null hypothesis of the same mean for all levels of ovj_rer. The results indicate that the overvaluation of the real exchange rate over various time horizons signals the risk of a crisis. Third, the means of wj_ner (j = 1~5) and v5_ner in the crisis sample were larger than those in the non-crisis sample. However, the t-test rejects the null hypothesis of the same mean only for W5_ner at the 5% significance level. The results indicate that a greater volatility of the nominal exchange rate measured by the square of W5_ner signals the risk of a crisis.
Based on these analyses, we speculate that wavelet predictors will play an important role in constructing prediction models for currency crises.
3.2. Predictive Accuracy of the Random Forests Classification Model
We constructed a random forests classification model using both standard predictors and wavelet predictors, as discussed in Section 2.3. For the purpose of comparison, we also estimated a conventional logistic regression. We kept the subset of the predictor sample covering the period 2011–2015 as the test set for evaluating model performance. Thus, the training set used for building the model was the subset of the sample covering the period 1991–2010. To reduce model bias arising from the imbalance in sizes between the crisis and non-crisis samples, we truncated the non-crisis sample by selecting only those observations for crisis-hit countries corresponding to the two years prior to the crisis. Hence, if a country was hit by a crisis in 1997, the observation of the predictors for 1996 was included in the crisis sample and the observations of the predictors for 1994–1995 were included in the non-crisis sample. This represents an addition of three observations to the training set8.
Table 4 shows the evaluation of the predictive accuracy of the two models9. The results are shown for probability thresholds of 50% and 70%. In the former, we predicted a crisis if the probability of a crisis predicted by a model exceeds 50%, while in the latter we predicted a crisis only if the probability exceeds 70%.

Table 4.
Predictive accuracy of the models. AUC: area under the receiver operating characteristic curve.
The sensitivity is defined as the ratio that a crisis is predicted accurately for all samples having a crisis event, and is given by:
The sensitivity is synonymous with the true-positive rate. By contrast, the specificity is defined as the ratio that a non-crisis is predicted accurately for all samples without a crisis event, which is given by:
The false-positive rate is defined as one minus the specificity. Since there tends to be a trade-off between the sensitivity and the specificity, the balanced accuracy and the F-measure are often used to evaluate the overall accuracy. The former is the arithmetic mean of the sensitivity and the specificity, while the latter is the harmonic mean. As can be seen from the table, the levels of sensitivity, specificity, balanced accuracy, and the F-measure are fairly high for both the random forests method and the logistic regression. Overall, the random forests method performs better than the logistic regression in terms of classification accuracy. Note that both the balanced accuracy and the F-measure for the random forests method exceed 0.9 based on the 50% threshold.
We also used a receiver operating characteristic (ROC) curve to evaluate the predictive accuracy of the models. A ROC curve was constructed by plotting the true-positive rate and the false-positive rate against each other for each candidate threshold. The measure of the overall performance of the model was given by the area under the ROC curve (AUC). A larger value of AUC implies a better predictive performance of the model. The level of AUC was fairly high for both the random forests and the logistic regression, and the former performed better than the latter in terms of overall accuracy.
3.3. Variable Importance Measures
A valuable property of the random forests method is that it provides variable importance measures that rank predictors according to their contribution to the prediction. The variable importance measure was calculated by adding up the total reduction in the Gini index by splits over a given predictor, averaged over all bagged trees.
Figure 1 shows the variable importance measure for each predictor. Among the range of wavelet predictors, ov4_rer and d4_rer are the most important crisis predictors. The result is in line with the existing literature that emphasizes the importance of the real exchange rate overvaluation in signaling the risk of currency crises (see, for example, Kaminsky et al. 1998; Frankel and Saravelos 2012; Gourinchas and Obstfeld 2012). The remaining top five predictors include ov3_rer, d3_rer, and w5_ner. It is worth noting that the volatility of nominal exchange rates is also an important crisis predictor. In contrast to common perception, the level of foreign exchange reserves or the growth rate of domestic credit are less important crisis predictors in our model.
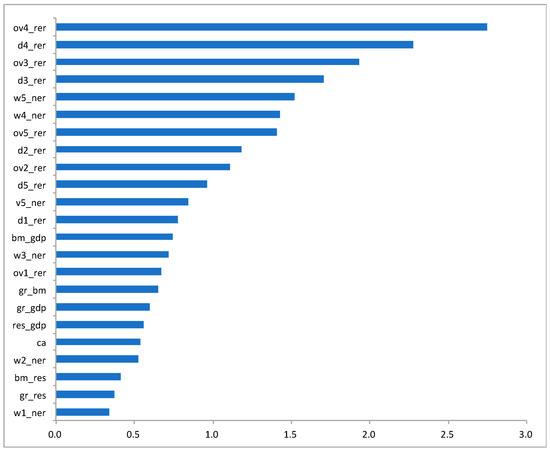
Figure 1.
Variable importance measures.
To summarize, we found that wavelet predictors, which capture the features of exchange rate behavior over various time horizons, are the key currency crisis predictors. In particular, we found that real exchange rate appreciation and overvaluation, which are measured over a horizon of 16–32 months, are the most important predictors. We also found that nominal exchange rate volatility, which was measured over a horizon of 32–64 months, is an important predictor.
4. Conclusions
In this study, we proposed a novel approach that combines a machine learning technique of random forests and a signal processing method of the wavelet transform to model the prediction of currency crises. In the first step, we used the wavelet transform to systemically extract key features of exchange rate behavior that may signal the risk of currency crises. Next, we built a random forests classification model using both standard predictors identified in the literature and wavelet predictors obtained from the wavelet transform. We demonstrated that the prediction model constructed by the random forests method can achieve a high level of predictive accuracy, presumably because the wavelet transform can better extract key features of exchange rate behavior while the random forests can improve accuracy by combining a large number of trees using random input selection. We also used the variable importance measures to find that wavelet predictors, which capture the features of exchange rate behavior over various time horizons, are key currency crisis predictors. In particular, we find that real exchange rate appreciation and overvaluation, which are measured over a horizon of 16–32 months, are the most important crisis predictors.
We believe that our novel approach to modeling the prediction of currency crises will prove useful in detecting the risk of crises and, thus, in taking preemptive action. One constraint on the practical use of our model is the limited availability of monthly data on exchange rates and price indices in developing countries. Future research may focus more on establishing an effective method of imputation that renders our approach more robust to missing data.
Author Contributions
S.H. and T.K. conceived and designed the experiments; L.X. performed the experiments, analyzed the data, and contributed reagents/materials/analysis tools; L.X., S.H., and T.K. wrote the paper.
Funding
This research was supported by JSPS KAKENHI Grant Number 17K18564, (A) 17H00983, and 18K01610.
Acknowledgments
We are grateful to two anonymous referees for their helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Appendix A. List of Sample Countries
Algeria, Bulgaria, Burundi, Cabo Verde, Central African Republic, Chad, Chile, China, Colombia, Dominican Republic, Egypt, Equatorial Guinea, Gabon, Gambia, Guatemala, Honduras, Hungary, Kenya, Madagascar, Malawi, Malaysia, Mauritius, Mexico, Namibia, Nigeria, Peru, Philippines, Poland, Romania, Seychelles, South Africa, Sri Lanka, Sudan, Thailand, Tunisia, Turkey, Uganda, Uruguay, Venezuela, Zambia.
References
- Abiad, Abdul. 2003. Early Warning Systems: A Survey and a Regime Switching Approach. IMF Working paper No. 03/23. Washington, DC, USA: International Monetary Fund. [Google Scholar]
- Berg, Andrew, and Catherine Pattillo. 1999. Predicting currency crises: The indicator approach and an alternative. Journal of International Money and Finance 18: 561–86. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Bussiere, Matthieu, and Marcel Fratzscher. 2006. Towards a new early warning system of financial crises. Journal of International Money and Finance 25: 953–73. [Google Scholar] [CrossRef]
- Cai, Xiao Jing, Shuairu Tian, Nannan Yuan, and Shigeyuki Hamori. 2017. Interdependence between Oil and East Asian Stock Markets: Evidence from Wavelet Coherence Analysis. Journal of International Financial Markets, Institutions and Money 48: 206–23. [Google Scholar] [CrossRef]
- Eichengreen, Barry, Andrew K. Rose, and Charles Wyplosz. 1995. Exchange market mayhem: The antecedents and aftermath of speculative arracks. Economic Policy 21: 249–312. [Google Scholar] [CrossRef]
- Faria, Gonçalo, and Fabio Verona. 2018. Forecasting stock market returns by summing the frequency decomposed parts. Journal of Empirical Finance 45: 228–42. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A., and Andrew K. Rose. 1996. Currency crashes in emerging markets: An empirical treatment. Journal of International Economics 41: 351–66. [Google Scholar] [CrossRef]
- Frankel, Jeffrey, and George Saravelos. 2012. Can leading indicators assess country vulnerability? Evidence from the 2008–2009 global financial crisis. Journal of International Economics 87: 216–31. [Google Scholar] [CrossRef]
- Gourinchas, Pierre-Olivier, and Maurice Obstfeld. 2012. Stories of the twentieth century for the twenty-first. American Economic Journal: Macroeconomics 4: 226–65. [Google Scholar] [CrossRef]
- Kaminsky, Graciela, Saul Lizondo, and Carmen M. Reinhart. 1998. The leading indicators of currency crises. IMF Staff Paper 45: 1–48. [Google Scholar] [CrossRef]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York: Springer. [Google Scholar]
- Percival, Donald B., and Andrew T. Walden. 2000. Wavelet Methods for Time Series Analysis. Cambridge: Cambridge University Press. [Google Scholar]
- Peria, Maria Soledad Martinez. 2002. A regime-switching approach to the study of speculative attacks: A focus on EMS crises. Empirical Economics 27: 299–334. [Google Scholar] [CrossRef]
- Reboredo, Juan C., and Miguel A. Rivera-Castro. 2013. A Wavelet decomposition approach to crude oil price and exchange rate dependence. Economic Modelling 32: 42–57. [Google Scholar] [CrossRef]
- Rose, Andrew K., and Mark M. Spiegel. 2011. Cross-country causes and consequences of the crisis: An update. European Economic Review 55: 309–24. [Google Scholar] [CrossRef]
- Rose, Andrew K., and Mark M. Spiegel. 2012. Cross-country causes and consequences of the 2008 crisis: Early warning. Japan and the World Economy 24: 1–16. [Google Scholar] [CrossRef]
- Sevim, Cuneyt, Asil Oztekin, Ozkan Bali, Serkan Gumus, and Erkam Guresen. 2014. Developing an early warning system to predict currency crises. European Journal of Operational Research 237: 1095–104. [Google Scholar] [CrossRef]
- Shimpalee, Pattama L., and Janice Boucher Breuer. 2006. Currency crises and institutions. Journal of International Money and Finance 25: 125–45. [Google Scholar] [CrossRef]
- Tanaka, Katsuyuki, Takuji Kinkyo, and Shigeyuki Hamori. 2018. Financial hazard map: Financial vulnerability predicted by a random forests classification model. Sustainability 10: 1530. [Google Scholar] [CrossRef]
| 1 | The computation of the MODWT is conducted using the “Wavelets” package in the R software package. |
| 2 | Equation (1) is derived from the energy preserving condition: . |
| 3 | While Fourier transform coefficients are associated with frequencies, wavelet coefficients are associated with a particular scale and set of times. |
| 4 | Using the orthonormality of DWT, the MRA is obtained by pre-multiplying both sides of Equations (2) and (3) by the transposer of and , respectively. |
| 5 | In addition to the Harr filter, we also used LA8 and D4 to derive wavelet predictors and evaluate the predictive accuracy. The reason we have chosen to use the Harr filter is because it is the only filter that produces consistent results. When we used LA8 and D4, the random forests method performed better than the logistic regression based on the balanced accuracy and the F-measure, while the latter performed better than the former based on AUC. By contrast, the random forests method consistently outperformed the logistic regression when the Harr filter was used. |
| 6 | Although the original index also includes interest rate differentials, Kaminsky and Reinhart (1998) removed it from their index because developing countries often adopt interest rate control. Since our sample includes many developing countries, we exclude interest rate differentials from the index. Note also that real exchange rates are used instead of nominal exchange rates to take into account differences in inflation rates across countries. |
| 7 | The computation is conducted using “caret”, “randomForest”, and “pROC” packages in the R software package. |
| 8 | As a result of the truncation, the number of observations in the training set is 53, of which the number of crisis and non-crisis is 19 and 34, respectively. The test set includes all 200 observations, of which the number of crises and non-crisis is 4 and 196, respectively. |
| 9 | We use the set.seed ( ) function in R to reproduce the results. Our results for predictive accuracy and variable importance measures are obtained when the function takes the value of 10. Regarding the choice of key parameters, notably, the number of tress to grow, the minimum size of terminal nodes, and the maximum number of terminal nodes, we use the default values given by “randomForests” package, which are 500, 1, and NULL (which implies that trees are grown to the maximum possible, subject to limits by the minimum size of terminal nodes), respectively. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).