Unconventional U.S. Monetary Policy: New Tools, Same Channels? †
Abstract
1. Introduction
2. Econometric Framework
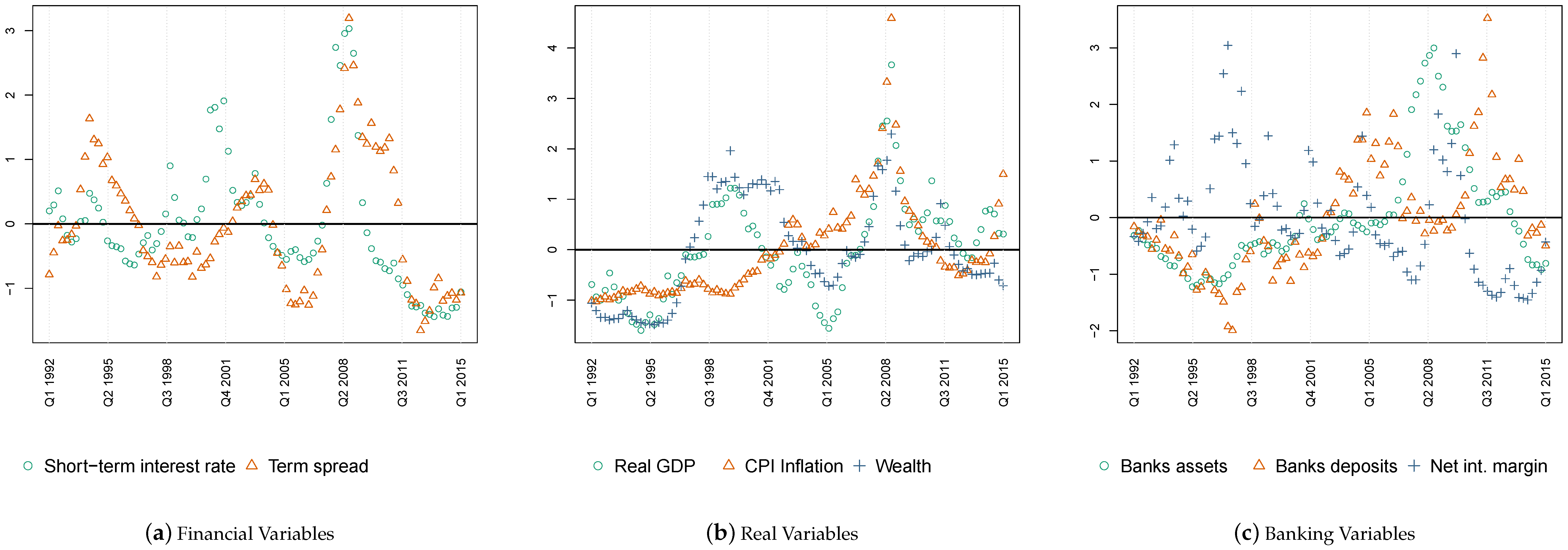
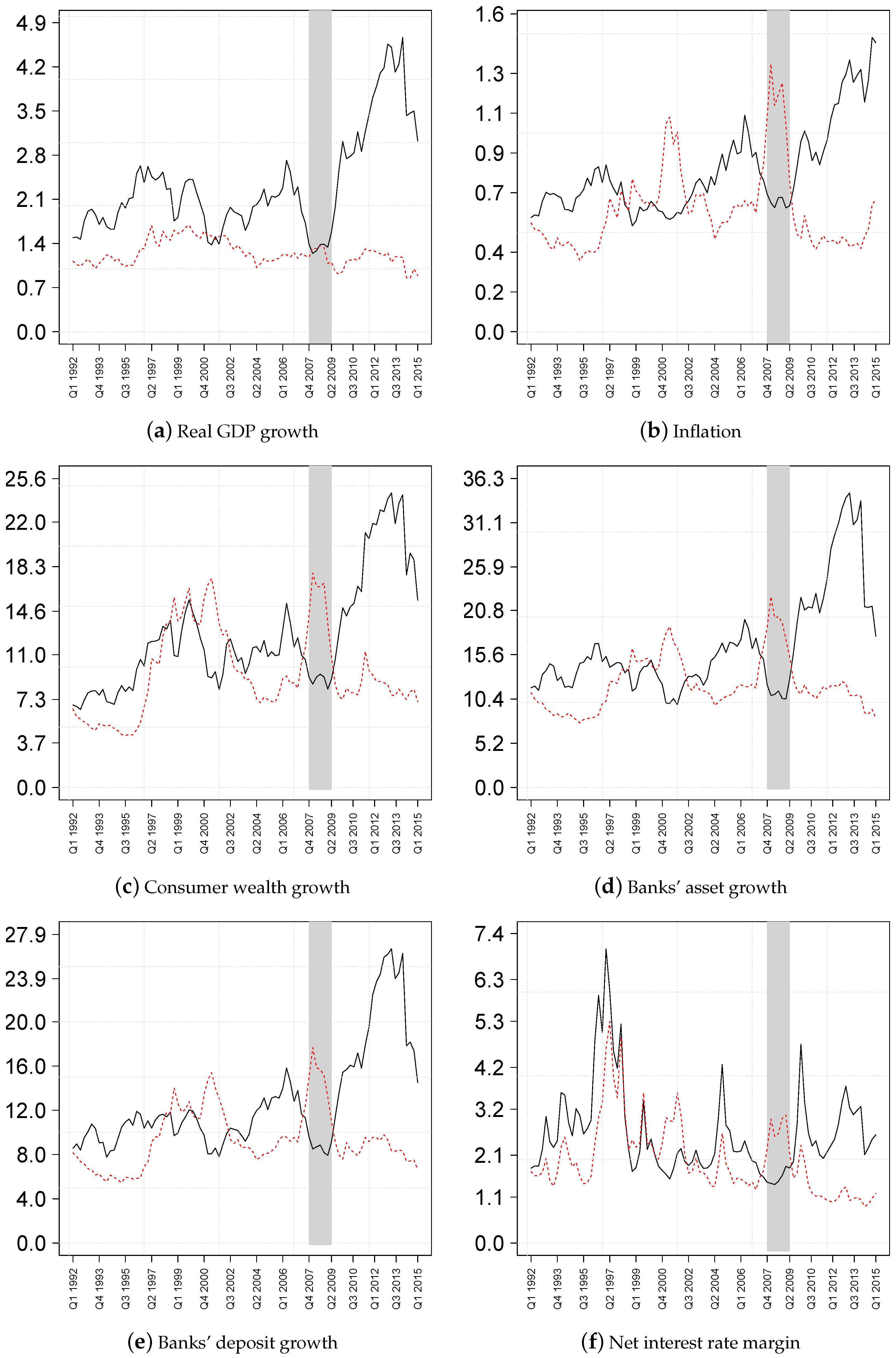
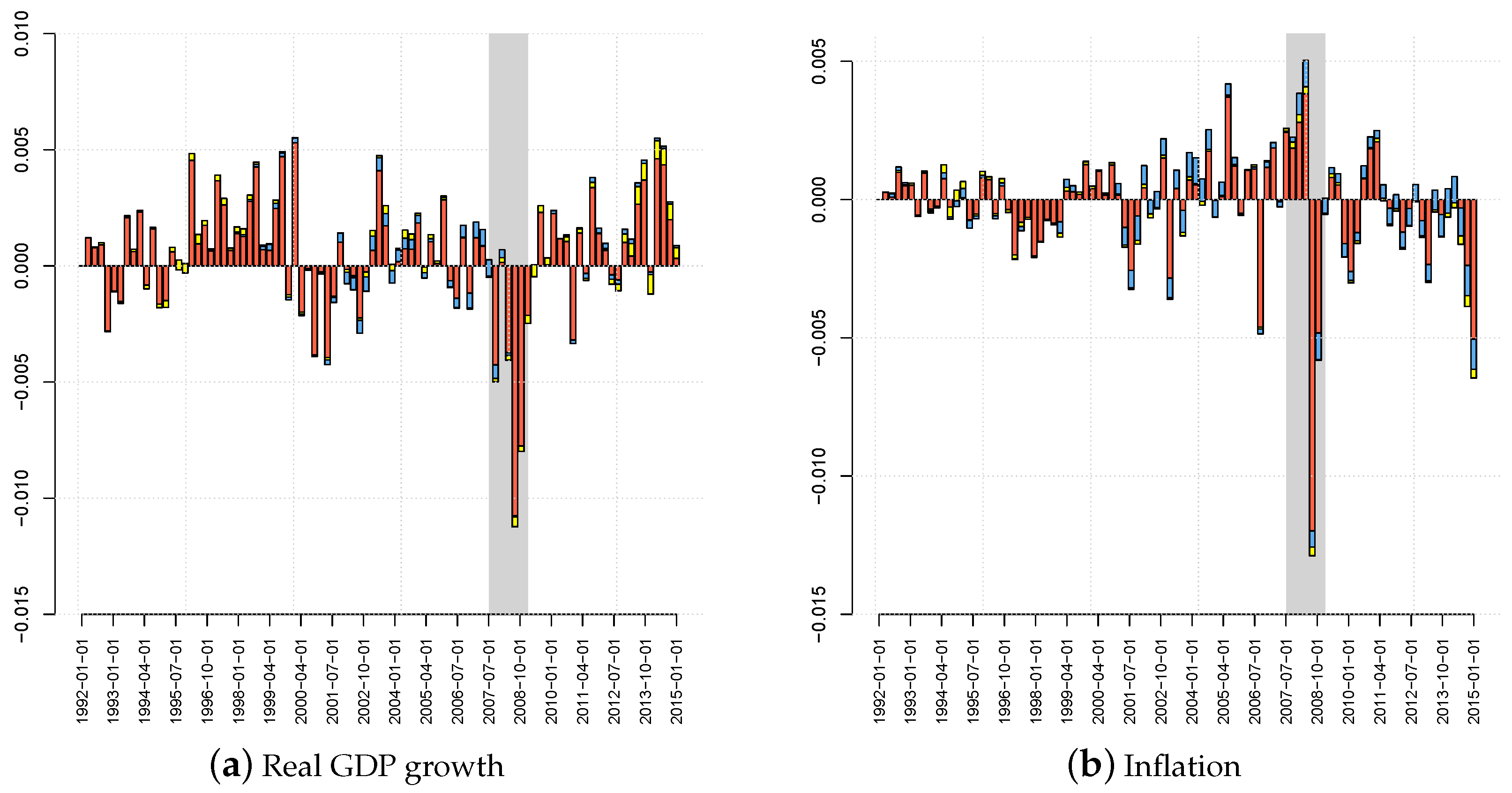
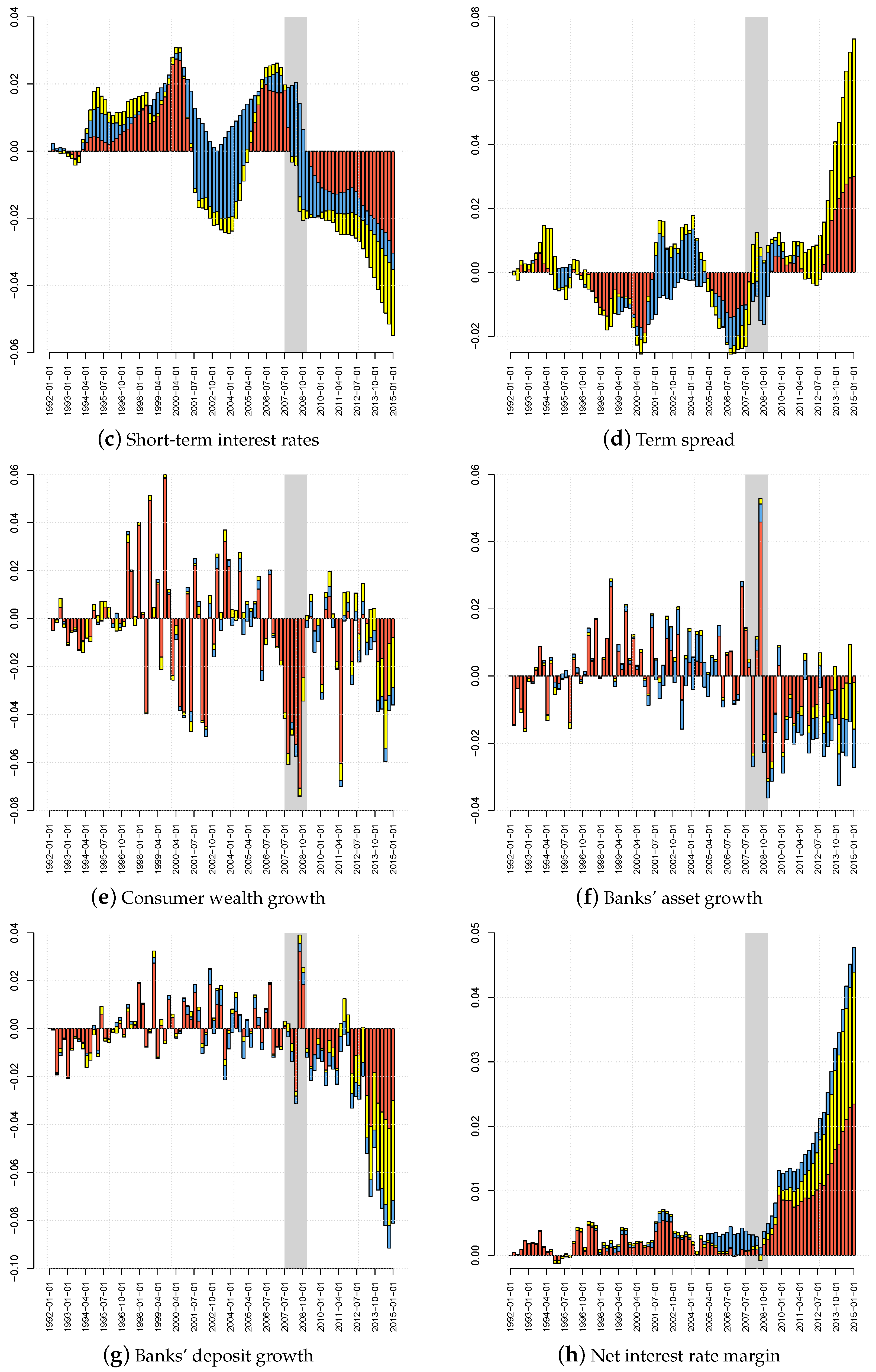
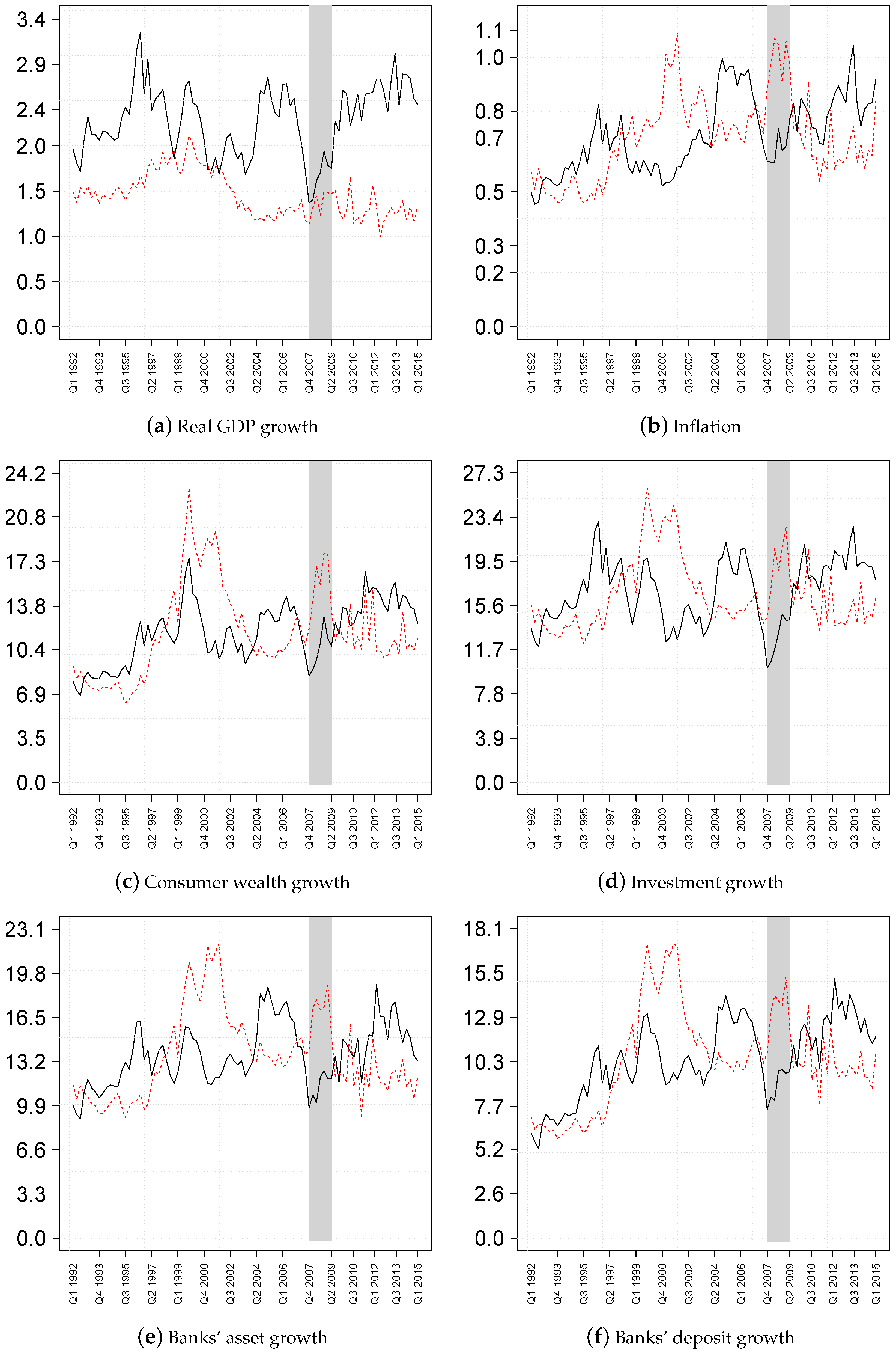
2.1. Data
2.2. The TVP-SV-VAR Model with a Cholesky Structure
2.3. Bayesian Inference
General Prior Setup and Implementation
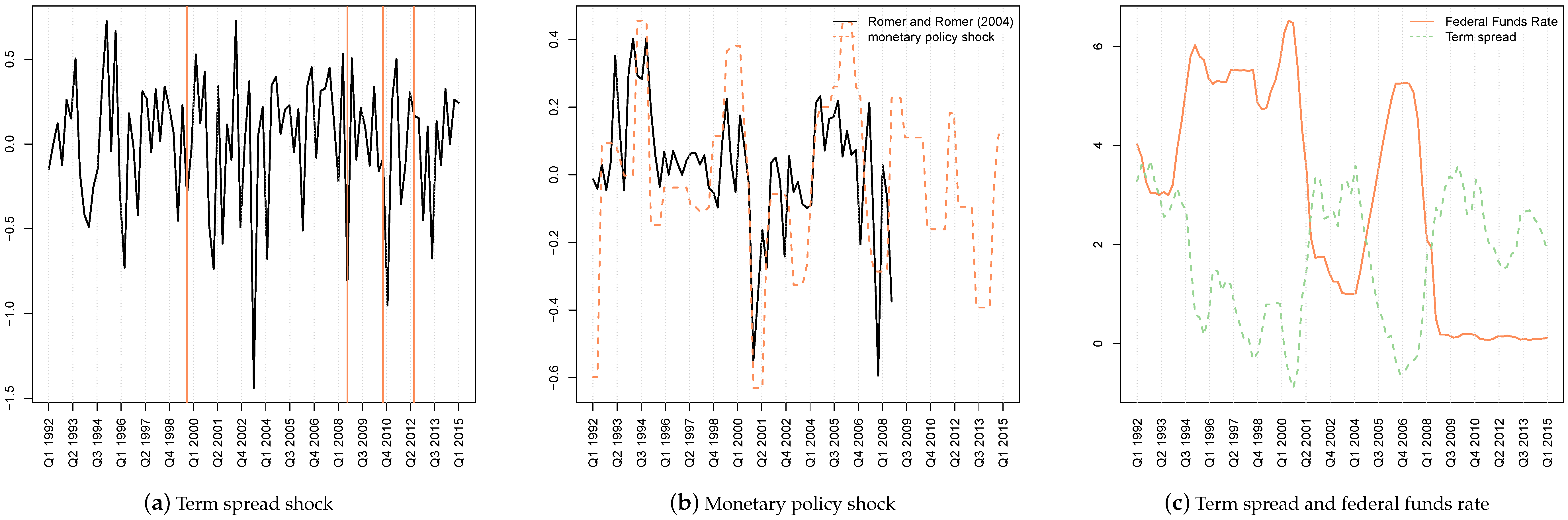
2.4. Structural Identification
3. Empirical Results
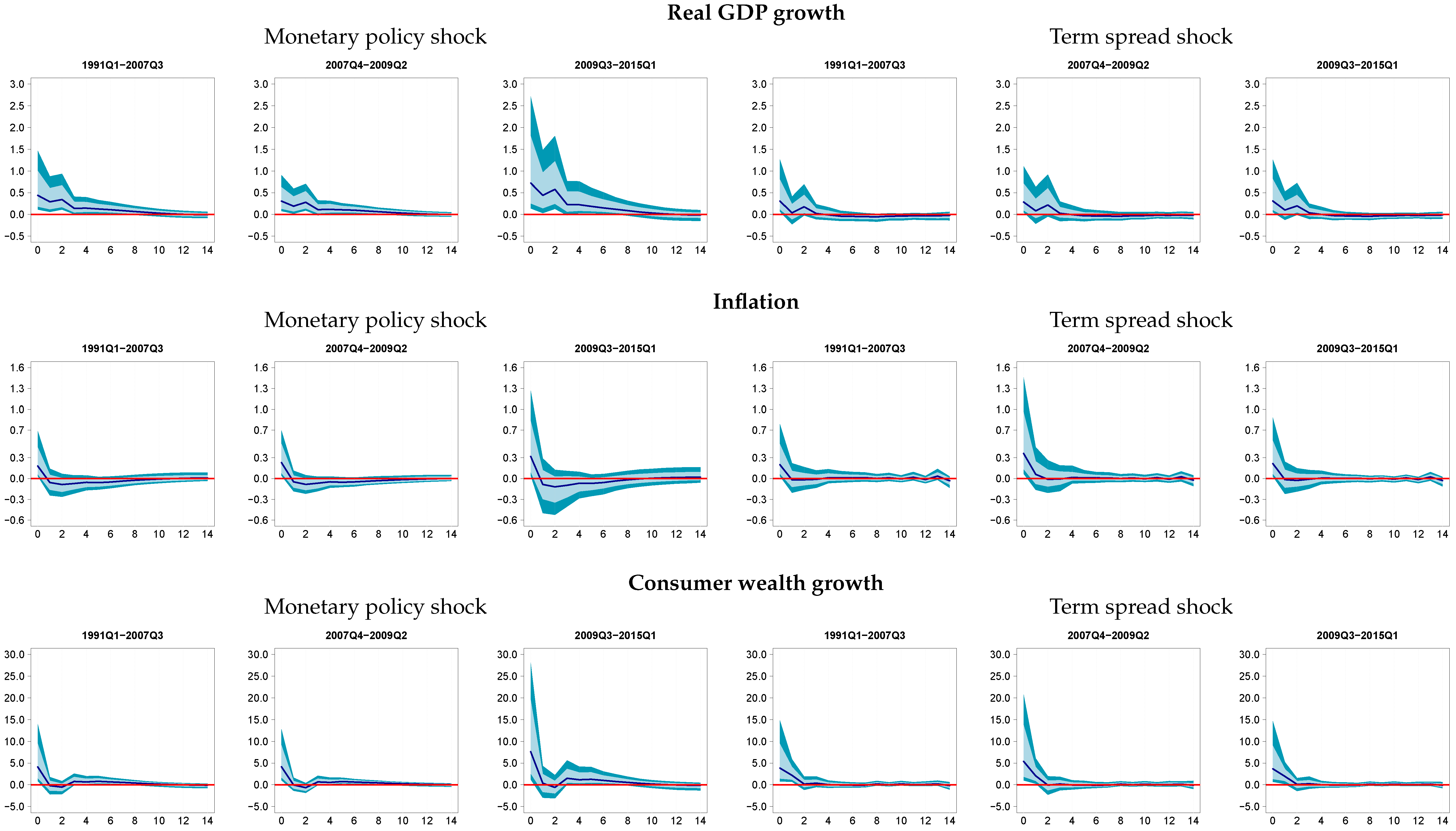
3.1. How Do Term Spread and Monetary Policy Shocks Affect Output Growth and Inflation?
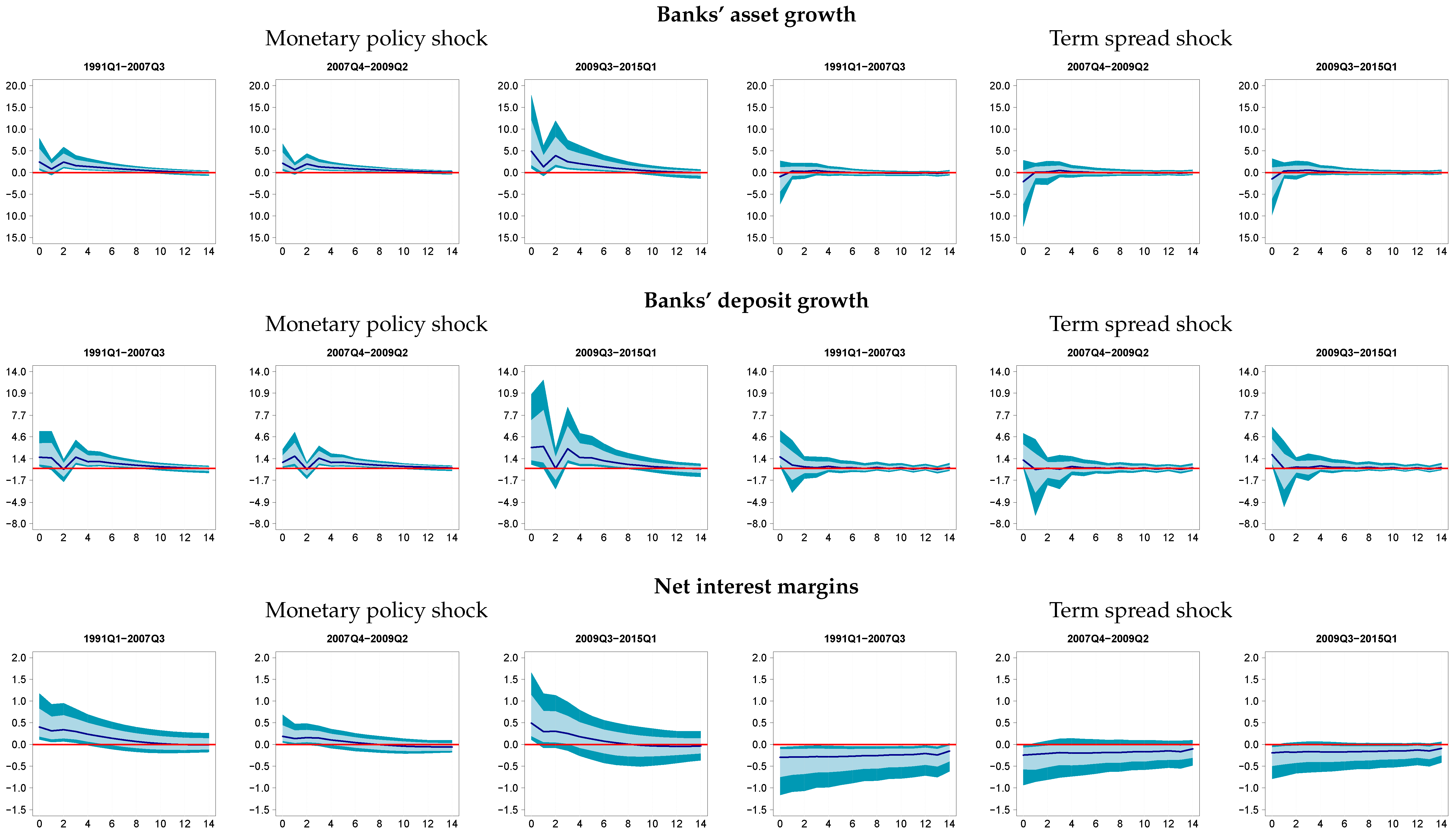
3.2. The Transmission of Monetary Policy and Term Spread Shocks
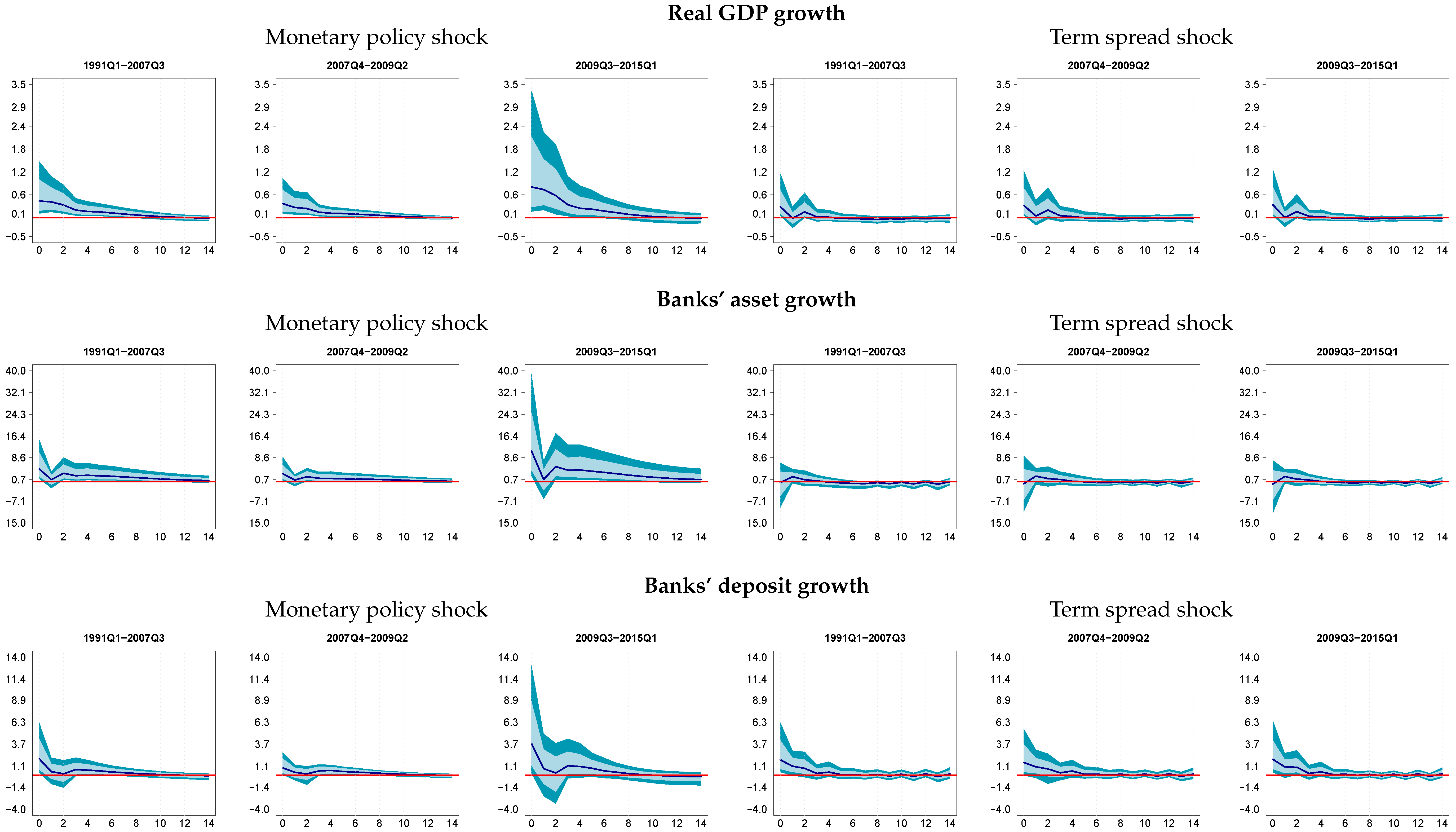
3.3. Do Effects Vary over Time?
3.4. Did Term Spread and Monetary Policy Shocks Matter Historically?
3.5. Robustness and Extensions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Structural Identification
Appendix B. A Brief Sketch of the Markov Chain Monte Carlo Algorithm
- Sample and using the algorithm of Carter and Kohn (1994).
- Sample and the corresponding parameters of Equation (7) through the algorithm put forth in Kastner and Frühwirth-Schnatter (2013). A brief description of this algorithm is provided in Appendix C.
Appendix C. Sampling Log-Volatilities
- Sample or , all without a loop (AWOL). Here, is a vector of stacked coefficients and . Following Rue (2001), can be written in terms of a multivariate normal distribution:Similarly, the normal distribution corresponding to the non-centered parameterization is given by:The corresponding posterior moments are:and:Multiplying by yields the moments for the non-centered parameterization: and . Finally, the initial states of , and are obtained from their respective stationary distributions.
- Obtain the parameters of Equation (7) and Equation (A8). Since we impose a non-conjugate Gamma prior on , we employ a Metropolis-within-Gibbs algorithm to sample and for both parameterizations. For the centered variant, we simulate and with a single Gibbs step, and is sampled through an MH step. For the non-centered parameterization, we sample with MH and the other parameters with Gibbs steps.
- Sample the mixture indicators with inverse transform sampling. Note that we can rewrite Equation (A8) as:This allows us to compute the posterior probabilities that , which are given by:where are the unnormalized weights associated with the c-th mixture component.
References
- Aastveit, Knut Are, Gisle James Natvik, and Sergio Sola. 2017. Economic uncertainty and the influence of monetary policy. Journal of International Money and Finance 76: 50–67. [Google Scholar] [CrossRef]
- Adrian, Tobias, Emanuel Moench, and Hyun Song Shin. 2010. Financial Intermediation, Asset Prices, and Macroeconomic Dynamics. Staff Reports 422. New York: Federal Reserve Bank of New York. [Google Scholar]
- Adrian, Tobias, and Hyun Song Shin. 2010. Financial Intermediaries and Monetary Economics. In Handbook of Monetary Economics. Edited by Benjamin. M. Friedman and Michael Woodford. Amsterdam: Elsevier, vol. 3, chp. 12. pp. 601–50. [Google Scholar]
- Baumeister, Christiane, and Luca Benati. 2013. Unconventional Monetary Policy and the Great Recession: Estimating the Macroeconomic Effects of a Spread Compression at the Zero Lower Bound. International Journal of Central Banking 9: 165–212. [Google Scholar]
- Baumeister, Christiane, and James D. Hamilton. 2015. Sign restrictions, structural vector autoregressions, and useful prior information. Econometrica 83: 1963–99. [Google Scholar] [CrossRef]
- Bech, Morten L., Leonardo Gambacorta, and Enisse Kharroubi. 2014. Monetary Policy in a Downturn: Are Financial Crises Special? International Finance 17: 99–119. [Google Scholar] [CrossRef]
- Benati, Luca, and Charles Goodhart. 2008. Investigating time-variation in the marginal predictive power of the yield spread. Journal of Economic Dynamics and Control 32: 1236–72. [Google Scholar] [CrossRef]
- Bernanke, Ben S., and Alan S. Blinder. 1988. Credit, Money, and Aggregate Demand. American Economic Review 78: 435–9. [Google Scholar]
- Bernanke, Ben S., and Mark Gertler. 1995. Inside the Black Box: The Credit Channel of Monetary Policy Transmission. Journal of Economic Perspectives 9: 27–48. [Google Scholar] [CrossRef]
- Bernanke, Ben S., Mark Gertler, and Mark Watson. 1997. Systematic Monetary Policy and the Effects of Oil Price Shocks. Brookings Papers on Economic Activity 28: 91–157. [Google Scholar] [CrossRef]
- Black, Lamont, Diana Hancock, and Waynee Passmore. 2007. Bank Core Deposits and the Mitigation of Monetary Policy; Technical Report 65; Federal Reserve Board Finance and Economics Discussion Series; Washington: Federal Reserve Board.
- Bloom, Nicholas. 2009. The Impact of Uncertainty Shocks. Econometrica 77: 623–85. [Google Scholar]
- Boivin, Jean, and Marc P. Giannoni. 2006. Has Monetary Policy Become More Effective? The Review of Economics and Statistics 88: 445–62. [Google Scholar] [CrossRef]
- Boivin, Jean, Michael T. Kiley, and Frederic S. Mishkin. 2010. How Has the Monetary Transmission Mechanism Evolved Over Time? In Handbook of Monetary Economics. Edited by Benjamin. M. Friedman and Michael Woodford. Amsterdam: Elsevier, vol. 3, chp. 8. pp. 369–422. [Google Scholar]
- Breitfuß, Sebastian, Martin Feldkircher, and Florian Huber. 2018. Changes in U.S. monetary policy and its transmission over the last century. German Economic Review. [Google Scholar] [CrossRef]
- Butt, Nick, Rohan Churm, Michael McMahon, Arpad Morotz, and Jochen Schanz. 2014. QE and the Bank Lending Channel in the United Kingdom. Working Paper 511. London: Bank of England. [Google Scholar]
- Carriero, Andrea, Todd E Clark, and Massimiliano Marcellino. 2015. Large Vector Autoregressions With Asymmetric Priors. Working Paper Series (2015/759); London: Queen Mary University of London. [Google Scholar]
- Carter, Chris K., and Robert Kohn. 1994. On gibbs sampling for state space models. Biometrika 81: 541–53. [Google Scholar] [CrossRef]
- Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans. 1996. The Effects of Monetary Policy Shocks: Evidence from the Flow of Funds. The Review of Economics and Statistics 78: 16–34. [Google Scholar] [CrossRef]
- Christiano, Lawrence J., Martin Eichenbaum, and Charles L. Evans. 2005. Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy 113: 1–45. [Google Scholar] [CrossRef]
- Cogley, Timothy, Sergei Morozov, and Thomas J. Sargent. 2005. Bayesian fan charts for uk inflation: Forecasting and sources of uncertainty in an evolving monetary system. Journal of Economic Dynamics and Control 29: 1893–925. [Google Scholar] [CrossRef]
- Cogley, Timothy, and Thomas J. Sargent. 2002. Evolving Post-World War II U.S. Inflation Dynamics. In NBER Macroeconomics Annual 2001. Cambridge: National Bureau of Economic Research, Inc., vol. 16, NBER Chapters. pp. 331–88. [Google Scholar]
- Cogley, Timothy, and Thomas J. Sargent. 2005. Drifts and volatilities: Monetary policies and outcomes in the post wwii us. Review of Economic Dynamics 8: 262–302. [Google Scholar] [CrossRef]
- Coibion, Olivier. 2012. Are the Effects of Monetary Policy Shocks Big or Small? American Economic Journal: Macroeconomics 4: 1–32. [Google Scholar] [CrossRef]
- Doh, Taeyoung. 2010. The efficacy of large-scale asset purchases at the zero lower bound. Economic Review 95: 5–34. [Google Scholar]
- Dunne, Peter, Mary Everett, and Rebecca Stuart. 2015. The Expanded Asset Purchase Programme—What, Why and How of Euro Area QE. Quarterly Bulletin Articles. Dublin: Central Bank of Ireland, pp. 61–71. [Google Scholar]
- Engen, Eric M., Thomas T. Laubach, and David Reifschneider. 2015. The Macroeconomic Effects of the Federal Reserve’s Unconventional Monetary Policies; Finance and Economic Discussion Series 2015-005; Washington: Board of Governors of the Federal Reserve System (U.S.).
- Fawley, Brett W., and Luciana Juvenal. 2012. Quantitative easing: Lessons we’ve learned. The Regional Economist 7: 8–9. [Google Scholar]
- Fernández-Villaverde, Jesús, Pablo Guerró-Quintana, Juan F. Rubio-Ramírez, and Martin Uribe. 2011. Risk matters: The real effects of volatility shocks. American Economic Review 101: 2530–61. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, Sylvia. 1994. Data augmentation and dynamic linear models. Journal of Time Series Analysis 15: 183–202. [Google Scholar] [CrossRef]
- Fry, Renée, and Adrian Pagan. 2011. Sign restrictions in structural vector autoregressions: A critical review. Journal of Economic Literature 49: 938–60. [Google Scholar] [CrossRef]
- Gagnon, Joseph, Matthew Raskin, Julie Remache, and Brian Sack. 2011. The Financial Market Effects of the Federal Reserve’s Large-Scale Asset Purchases. International Journal of Central Banking 7: 3–43. [Google Scholar]
- Gertler, Mark, and Peter Karadi. 2015. Monetary policy surprises, credit costs, and economic activity. American Economic Journal: Macroeconomics 7: 44–76. [Google Scholar] [CrossRef]
- Gorodnichenko, Yuriy. 2005. Reduced-Rank Identification of Structural Shocks in VARs. Macroeconomics 0512011. Germany: University Library of Munich. [Google Scholar]
- Greenwood, Robin, and Dimitri Vayanos. 2010. Price Pressure in the Government Bond Market. American Economic Review 100: 585–90. [Google Scholar] [CrossRef]
- Hamilton, James D. 2018. The Efficacy of Large-Scale Asset Purchases When the Short-term Interest Rate is at its Effective Lower Bound. Brookings Papers on Economic Activity. Washington: Brookings Press. [Google Scholar]
- Hamilton, James D., and Jing Cynthia Wu. 2012. The Effectiveness of Alternative Monetary Policy Tools in a Zero Lower Bound Environment. Journal of Money, Credit and Banking 44: 3–46. [Google Scholar] [CrossRef]
- Hubrich, Kirstin, and Robert J. Tetlow. 2015. Financial stress and economic dynamics: The transmission of crises. Journal of Monetary Economics 70: 100–15. [Google Scholar] [CrossRef]
- Inoue, Atsushi, and Barbara Rossi. 2018. The Effects of Conventional and Unconventional Monetary Policy on Exchange Rates. NBER Working Papers 25021. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Ireland, Peter N. 2005. The Monetary Transmission Mechanism. Working Papers 06-1. Boston: Federal Reserve Bank of Boston. [Google Scholar]
- Jannsen, Nils, Galina Potjagailo, and Maik H. Wolters. 2014. Monetary Policy during Financial Crises: Is the Transmission Mechanism Impaired? Kiel: Kiel Institute for the World Economy, mimeo. [Google Scholar]
- Joyce, Michael, David Miles, Andrew Scott, and Dimitri Vayanos. 2012. Quantitative easing and unconventional monetary policy—An introduction. The Economic Journal 122: F271–88. [Google Scholar] [CrossRef]
- Kastner, Gregor. 2013. Stochvol: Efficient Bayesian Inference for Stochastic Volatility (sv) Models. R Package Version 0.7-1. Available online: http://CRAN.R-project.org/package=stochvol (accessed on 25 October 2018).
- Kastner, Gregor, and Sylvia Frühwirth-Schnatter. 2013. Ancillarity-sufficiency interweaving strategy (asis) for boosting mcmc estimation of stochastic volatility models. Computational Statistics & Data Analysis 76: 408–23. [Google Scholar]
- Kastner, Gregor, Florian Huber, and Martin Feldkircher. 2018. Should I stay or should I go? A latent threshold approach to large-scale mixture innovation models. Journal of Applied Econometrics arXiv:1607.04532. [Google Scholar]
- Korobilis, Dimitris. 2013. Assessing the Transmission of Monetary Policy Using Time-varying Parameter Dynamic Factor Models. Oxford Bulletin of Economics and Statistics 75: 157–79. [Google Scholar] [CrossRef]
- Krishnamurthy, Arvind, and Annette Vissing-Jorgensen. 2011. The Effects of Quantitative Easing on Interest Rates: Channels and Implications for Policy. Brookings Papers on Economic Activity 43: 215–87. [Google Scholar] [CrossRef]
- Leeper, Eric M., Christopher A. Sims, and Tao Zha. 1996. What Does Monetary Policy Do? Brookings Papers on Economic Activity 27: 1–78. [Google Scholar] [CrossRef]
- Lopes, Hedibert F, Robert E. McCulloch, and Ruey S. Tsay. 2013. Cholesky Stochastic Volatility Models for High-Dimensional Time Series. Technical Report. Chicago: University of Chicago, mimeo. [Google Scholar]
- Ludvigson, Sydney, Charles Steindel, and Martin Lettau. 2002. Monetary policy transmission through the consumption-wealth channel. Economic Policy Review 8: 117–33. [Google Scholar]
- McKay, Alisdair, Emi Nakamura, and Jón Steinsson. 2016. The Power of Forward Guidance Revisited. American Economic Review 106: 3133–58. [Google Scholar] [CrossRef]
- Miranda-Agrippino, Silvia. 2016. Unsurprising Shocks: Information, Premia, and the Monetary Transmission. Technical Report 626, Bank of England Working Paper. London: Bank of England. [Google Scholar]
- Miranda-Agrippino, Silvia, and Giovanni Ricco. 2017. The Transmission of Monetary Policy Shocks. Technical Report 657, Bank of England Working Paper. London: Bank of England. [Google Scholar]
- Nakamura, Emi, and Jón Steinsson. 2018. High Frequency Identification of Monetary Non-Neutrality: The Information Effect. Quarterly Journal of Economics 133: 1283–330. [Google Scholar] [CrossRef]
- Nelson, Benjamin, Gabor Pinter, and Konstantinos Theodoridis. 2018. Do contractionary monetary policy shocks expand shadow banking? Journal of Applied Econometrics 33: 198–211. [Google Scholar] [CrossRef]
- Primiceri, Giorgio E. 2005. Time varying structural vector autoregressions and monetary policy. The Review of Economic Studies 72: 821–52. [Google Scholar] [CrossRef]
- Romer, Christina D., and David H. Romer. 2004. A New Measure of Monetary Shocks: Derivation and Implications. American Economic Review 94: 1055–84. [Google Scholar] [CrossRef]
- Rubio-Ramírez, Juan F., Daniel F. Waggoner, and Tao Zha. 2010. Structural vector autoregressions: Theory of identification and algorithms for inference. Review of Economic Studies 77: 665–96. [Google Scholar] [CrossRef]
- Rue, Håvard. 2001. Fast sampling of gaussian markov random fields. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63: 325–38. [Google Scholar] [CrossRef]
- Sims, Christopher A. 2001. Discussion of Cogley and Sargent ’Evolving Post World War II U.S. Inflation Dynamics’. NBER Macroeconomics Annual 16: 373–79. [Google Scholar]
- Sims, Christopher A., and Tao Zha. 1998. Bayesian Methods for Dynamic Multivariate Models. International Economic Review 39: 949–68. [Google Scholar] [CrossRef]
- Stein, Jeremy C. 2012. Evaluating Large-Scale Asset Purchases. Speech at the Brookings Institution. Washington, D.C.: Brookings Institution. [Google Scholar]
- Tenreyro, Silvana, and Gregory Thwaites. 2016. Pushing on a string: U.S. monetary policy is less powerful in recessions. American Economic Journal: Macroeconomics 8: 43–74. [Google Scholar] [CrossRef]
- Uhlig, Harald. 2005. What are the effects of monetary policy on output? Results from an agnostic identification procedure. Journal of Monetary Economics 52: 381–419. [Google Scholar] [CrossRef]
- Wu, Tao. 2014. Unconventional Monetary Policy and Long-Term Interest Rates. Technical Report WP/14/189, IMF Working Paper. Washington: International Monetary Fund (IMF). [Google Scholar]
| 1. | Data on real GDP growth (GDPC96), CPI inflation (CPALTT01USQ661S), the effective federal funds rate (FEDFUNDS) calculated as the quarterly average of daily rates, 10-year-government bond yields to proxy long-term interest rates (IRLTLT01USQ156N), net worth of households and nonprofit organizations resembling consumer wealth (TNWBSHNO) deflated by the personal income deflator (PCECTPI) and net interest rate margins for large U.S. banks (USG15NIM) are from the Fred database, https://research.stlouisfed.org/fred2/. Data on commercial banks’ assets (FL764090005.Q, FL474090005.Q), deposits (FL763127005.Q, FL764110005.Q FL763131005.Q, FL763135005.Q, FL762150005.Q) are from the financial accounts database of the Federal Reserve System, https://www.federalreserve.gov/releases/z1/current/. By and large, all transformed data are stationary according to an augmented Dickey–Fuller test. |
| 2. | See, for example, Cogley and Sargent (2005), who in response to the criticism raised by Sims (2001), extended their TVP framework put forward in Cogley and Sargent (2002) to allow for stochastic volatility. |
| 3. | In fact, experimenting with stationary state equations for and leaves our results qualitatively unchanged. |
| 4. | |
| 5. | Another strand of the literature proposes factor augmented VARs (FAVARs) with drifting parameters and stochastic volatility (Korobilis 2013). While FAVARs provide a flexible means of reducing the dimensionality of the estimation problem at hand, they could also lead to problems with respect to identification and structural interpretation of the underlying shocks. |
| 6. | Since we estimate the model on an equation-by-equation basis, and are block diagonal matrices. |
| 7. | There is a huge literature on the identification of conventional monetary policy shocks, but a consensus seems so far out of reach. Alternatively, one could use recursive identification, such as heavily used in the early literature; see, e.g., (Christiano et al. 2005). Recursive identification got criticized recently because of the stark underlying assumptions about the information set of the respective central bank and the unrealistic timing of the shocks, especially when also dealing with financial data. Since then, a number of authors proposed the use of external instruments, based on either the narrative approach (Romer and Romer 2004) or high frequency information (Gertler and Karadi 2015; Miranda-Agrippino and Ricco 2017). However, also, this literature came under criticism, since as pointed out by Hamilton (2018), Fed announcements provide not only information about a policy action, but about the Fed’s assessment of future economic conditions, and these effects are not easily separated. An approach to separate these effects is provided in Miranda-Agrippino (2016) and Nakamura and Steinsson (2018). |
| 8. | One aspect of monetary policy that we do not capture directly is forward guidance. There is a fast-growing literature assessing the effects of forward guidance; see, e.g., McKay et al. (2016), who present a theoretical model in which the power of forward guidance is highly sensitive to the assumption of complete markets. More recently, Nakamura and Steinsson (2018) provided an external instrument that measures also changes in the path of future interest rates in response to Fed announcements, which allows one to capture forward guidance effects empirically. |
| 9. | More specifically, an unexpected monetary expansion can be expected to drive up inflation and therefore inflation expectations. This in turn implies long-rates to decrease less strongly than short rates, causing a widening of the yield curve (Benati and Goodhart 2008). |
| 10. | In the case that the Fed purchases assets directly from the banking sector, the proceeds would be charged to the banks’ reserve balances with the Fed, leaving deposits untouched. The positive restriction on deposit growth is warranted since part of the Fed’s purchases directly concern the private non-banking sector. |
| 11. | To be precise, the narrative shock is transformed to quarterly frequency by simply averaging over the corresponding months. The monetary policy shock corresponds to the smoothed structural shocks. In general, residuals of the VAR are more volatile due to the inherent iid assumption, which is why we opted for smoothing the shocks, facilitating visual comparison to the more persistent narrative shocks. |
| 12. | All results are based on 500 draws from the full set of 15,000 posterior draws that have been collected after a burn-in phase of 15,000 draws. |
| 13. | These are based on the National Bureau of Economic Research (NBER) dating of recessions, available at http://www.nber.org/cycles.html. The full history of impulse responses over time and for all variables is available from the authors upon request. |
| 14. | Responses are to be interpreted as the reaction of a variable to a hypothetical 100-bp monetary policy/term spread shock independent of the actual value of the FFR during that period. |
| 15. | Data on shadow assets (FL504090005.Q, FL674090005.Q, FL614090005.Q) are from the financial accounts database of the Federal Reserve System, http://www.federalserver.gov/releases/z1/about.htm. |
| Shock | Channel | Aggregate Demand | ||||||
|---|---|---|---|---|---|---|---|---|
| sp | nim | |||||||
| Monetary Policy | ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ |
| Term Spread | 0 | ↓ | ↑ | ↓ | demand ↑/supply ↓ = ? | ↑ | ↑ | ↑ |
| Monetary Policy Shock | ||||
| 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | 1991Q1–2015Q1 | |
| Real GDP growth | 0.10 | 0.10 | 0.08 | 0.10 |
| Inflation | 0.06 | 0.04 | 0.04 | 0.06 |
| Consumer wealth growth | 0.07 | 0.08 | 0.07 | 0.07 |
| Short-term interest rate | 0.07 | 0.07 | 0.06 | 0.07 |
| Banks’ deposit growth | 0.10 | 0.10 | 0.09 | 0.10 |
| Banks’ asset growth | 0.13 | 0.11 | 0.10 | 0.12 |
| Term spread | 0.11 | 0.13 | 0.10 | 0.11 |
| Net interest rate margin | 0.08 | 0.09 | 0.07 | 0.08 |
| Term Spread Shock | ||||
| 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | 1991Q1–2015Q1 | |
| Real GDP growth | 0.08 | 0.07 | 0.07 | 0.08 |
| Inflation | 0.10 | 0.05 | 0.08 | 0.09 |
| Consumer wealth growth | 0.13 | 0.08 | 0.10 | 0.12 |
| Short-term interest rate | 0.12 | 0.06 | 0.09 | 0.11 |
| Banks’ deposits | 0.11 | 0.08 | 0.10 | 0.11 |
| Banks’ assets | 0.11 | 0.09 | 0.10 | 0.11 |
| Term spread | 0.12 | 0.06 | 0.09 | 0.11 |
| Net interest rate margin | 0.17 | 0.10 | 0.12 | 0.15 |
| Correlation of Shadow Assets with Baseline | ||||||
| Monetary policy shock | Term spread shock | |||||
| 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | |
| Real GDP growth | 0.976 | 0.969 | 0.968 | 0.984 | 0.979 | 0.948 |
| Inflation | 0.957 | 0.991 | 0.914 | 0.963 | 0.950 | 0.938 |
| Wealth | 0.996 | 0.998 | 0.997 | 0.995 | 0.996 | 0.994 |
| Short-term interest rate | 0.994 | 0.999 | 0.978 | 1.000 | 0.999 | 1.000 |
| Banks’ deposits | 0.775 | 0.658 | 0.768 | 0.930 | 0.694 | 0.810 |
| Banks’ assets | 0.934 | 0.956 | 0.926 | 0.497 | 0.457 | 0.625 |
| Term spread | 0.999 | 0.999 | 0.996 | 0.990 | 0.978 | 0.988 |
| Net interest rate margin | 0.996 | 0.994 | 0.994 | 0.930 | 0.694 | 0.786 |
| Average Correlation of Different Cholesky Orderings with Baseline | ||||||
| Monetary policy shock | Term spread shock | |||||
| 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | 1991Q1–2007Q3 | 2007Q4–2009Q2 | 2009Q3–2015Q1 | |
| Real GDP growth | 0.999 | 0.995 | 0.999 | 0.998 | 0.997 | 0.990 |
| Inflation | 0.998 | 0.998 | 0.995 | 0.996 | 0.998 | 0.995 |
| Wealth | 0.999 | 0.999 | 0.999 | 1.000 | 1.000 | 0.999 |
| Short-term interest rate | 0.999 | 0.989 | 1.000 | 1.000 | 1.000 | 1.000 |
| Banks’ deposits | 0.998 | 0.993 | 0.998 | 0.998 | 0.984 | 0.986 |
| Banks’ assets | 0.998 | 0.997 | 0.999 | 0.999 | 0.997 | 0.961 |
| Term spread | 1.000 | 0.996 | 1.000 | 0.999 | 0.997 | 1.000 |
| Net interest rate margin | 1.000 | 0.998 | 0.999 | 0.987 | 0.954 | 0.837 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldkircher, M.; Huber, F. Unconventional U.S. Monetary Policy: New Tools, Same Channels? J. Risk Financial Manag. 2018, 11, 71. https://doi.org/10.3390/jrfm11040071
Feldkircher M, Huber F. Unconventional U.S. Monetary Policy: New Tools, Same Channels? Journal of Risk and Financial Management. 2018; 11(4):71. https://doi.org/10.3390/jrfm11040071
Chicago/Turabian StyleFeldkircher, Martin, and Florian Huber. 2018. "Unconventional U.S. Monetary Policy: New Tools, Same Channels?" Journal of Risk and Financial Management 11, no. 4: 71. https://doi.org/10.3390/jrfm11040071
APA StyleFeldkircher, M., & Huber, F. (2018). Unconventional U.S. Monetary Policy: New Tools, Same Channels? Journal of Risk and Financial Management, 11(4), 71. https://doi.org/10.3390/jrfm11040071






