1. Introduction
Understanding bond risk premia remains one of the central issues in empirical finance. Much of this literature uses non-arbitrage affine term structure models (ATSM) to extract risk premium components from bond prices. The purpose of this paper is to analyze how apparently innocuous overidentifying restrictions imposed on ATSMs can lead to large differences in several measures of bond risk premia.
Long-term interest rates can be decomposed into expectations of average future short rates and a risk premium that investors demand for bearing long-term risk (the term premium). Forward interest rates can be split into an expected future interest rate and a risk premium component (the forward premium). Those are the measures of risk premia on which the literature has mostly focused. However, there are other definitions of risk premia that are arguably equally or more relevant from the point of view of market participants. An investor who buys a long-term bond financed by borrowing at a shorter interest rate is exposed to a risk premium (the bond holding risk premium). The return for an investor that writes a forward contract to buy a bond in the future, but closes the contract before the settlement date is also exposed to a risk premium (the holding forward risk premium). The contribution of this paper is to investigate to what extent different restrictions imposed on ATSMs, which often imply modest differences in the term and forward premiums, could lead to large differences in the bond holding and holding forward risk premiums.
1Since often the extracted factors, forward premiums and term premiums look similar across restricted ATSM models, researchers tend to choose their preferred models based on the parsimony or forecasting ability of future yields. Yet, overidentifying restrictions unsupported by the data can have a large impact on other measures of risk premia, such as the bond holding risk premium or the holding forward risk premium, particularly at longer horizons. The reason is that small errors compound and get amplified as the holding horizon increases. Therefore, if the objective of the analysis is to understand bond risk premia, researchers should be very careful in not imposing overidentifying restrictions unsupported by the data even though the more parsimonious model may produce similar factors or predict better than the unrestricted model. Those restrictions can be harmful.
The main, and perhaps only, reason to consider affine models of bond prices is to understand risk premia. As noted by
Joslin et al. (
2011) and
Duffee (
2011), if the objective of the analysis is to fit a yield curve or to forecast bond yields, little is gained by imposing non-arbitrage restrictions. However, to understand risk premia, non-arbitrage restrictions are of fundamental importance. Unfortunately, there is no clear guidance in the literature on how to impose restrictions on risk prices. This issue has been overlooked in the literature, and this paper is an attempt to fill this gap. To our knowledge,
Bauer (
2018) is the only paper that studied restrictions on risk prices. He did so from a Bayesian perspective and only focusing on the term premium and excess bond returns. This paper is complementary to Bauer’s in that we also analyze restrictions on risk prices, but from a different perspective. In particular, besides the term premium and excess returns, we analyze how restrictions on risk prices affect other measures of risk premia.
We first analyze to what extent usual restrictions imposed on risk prices or factor dynamics imply similar estimated term and forward premiums, but may lead to large differences in excess holding returns and holding forward premiums. The different concepts of risk premia are related among them, and small deviations in estimated forward premiums accumulate and can lead to large differences in expected excess returns of long-term bonds. For example, the bond holding risk premium is proportional to the forward risk premium, where the factor of proportionality increases with the maturity of the bond. Small differences in the estimated one-month forward risk premium, which may seem irrelevant if one focuses only on the forward premium, get amplified by about 120 times when we compute the risk premium associated with holding a 10-year bond financed by borrowing at the one-month interest rate.
Although the argument is general, we base our empirical investigation using the class of arbitrage-free Nelson and Siegel models. The work in
Nelson and Siegel (
1987) proposed a flexible, yet parsimonious functional form to model the cross-section of bond yields, which is widely used by practitioners and researchers.
2 The work in
Christensen et al. (
2011) showed that the Nelson and Siegel parametric representation of the yield curve can be made arbitrage-free by including a maturity-specific constant to the traditional Nelson and Siegel model. We use the Nelson and Siegel model because it is easy to estimate, and it is sufficiently general to make our point. We analyze several restrictions on risk prices and factor dynamics that are considered in the literature to analyze risk premia. Although the estimated factors are virtually identical across models, the estimates of risk premia that they produce often vary dramatically because the loadings on those factors change across models.
Using as a baseline the most general arbitrage-free Nelson and Siegel model, we evaluate to what extent the econometric rejections of the restrictions on risk prices are economically relevant (in terms of the estimated risk premia). For example, imposing a diagonal covariance matrix on the evolution of the risk factors is comfortably rejected using standard econometric tests, but the estimated risk premia are similar to those of the unrestricted model. On the other hand, imposing a diagonal matrix on the lagged values of the vector autoregression representation of the risk factors is also rejected, but with a much smaller likelihood ratio statistic. Yet, the estimated risk premiums in the restricted model are very different from those of the unrestricted model.
The main practical implication of these results is that, to analyze and forecast risk premia, it is advisable to consider the just identified model. Imposing restrictions that are unsupported by the data may lead to large errors in estimated and forecast measures of risk premia. These observations also have policy implications: to the extent that fluctuations in risk premia have macroeconomic consequences, a policy maker that reacts to spurious changes in risk premia may choose suboptimal policies.
Using an ex-ante empirical analysis,
Cochrane and Piazzesi (
2005,
2008) argued that excess returns are a function of a single factor and built an affine term structure model imposing this assumption on risk prices. Other papers used likelihood ratios to test whether certain risk prices are zero, e.g., (
Joslin et al. 2011). Some restrictions are often motivated on forecasting grounds. For example,
Christensen et al. (
2011) argued that imposing a diagonal structure on the factor dynamics outperforms a more general model in forecasting the yield curve. Even though this may be the correct procedure when the objective of the exercise is to forecast yields, it may be counterproductive when the objective is to understand risk premia. The reason is well known: even if the “true model” may contain many parameters, it may be outperformed out-of-sample by invalid reductions in the number of free parameters due to parameter uncertainty. When the issue is to understand the evolution and determinants of risk premia, restrictions that are not supported by the data using standard testing procedures may have damaging effects on the evaluation of risk compensation.
3The paper is organized as follows.
Section 2 describes a general affine term structure model and the four different concepts of risk premia that we consider.
Section 3 provides a Nelson–Siegel representation of the affine model that is used in the empirical section of the paper.
Section 4 shows the estimation results, and
Section 5 analyzes the impact of imposing restrictions on risk prices.
Section 6 concludes, and the Appendix contains some proofs.
2. An Affine Model of Bond Prices
Let
denote a
vector of unobserved risk factors that summarizes the information that investors use to price discount bonds. The risk factors evolve as a first order vector autoregression:
where
is lower triangular and
i.i.d.
.
Investors price nominal cash flows using the one-period stochastic discount factor:
The
vector
, referred to as the market price of risk, represents the compensation that investors demand to face shocks to the state vector
. The market price of risk is an affine function of the factors:
where
is a
vector and
is a
matrix of coefficients.
The principle of no-arbitrage implies that bond prices satisfy the recursion:
As shown by
Ang and Piazzesi (
2003), log bond prices,
, are also an affine function of the risk factors:
where the coefficients
and
satisfy the recursions:
with
,
and where
and
are defined as:
The continuously-compounded yield on an
n-period discount bond is thus:
with
and
.
We are also interested in the expected returns from holding forward contracts on discount bonds. Let
denote the settlement price of a forward contract entered into at time
t to buy an
-period discount bond at time
, with
. Since two different ways of moving one dollar from
t to
must cost the same, the law of one price implies:
The log forward rate is the implicit continuously-compounded interest rate of a forward contract with settlement price ,
In terms of bond prices, the log forward rate
is thus:
Therefore, the bond prices (
5) imply that forward rates are affine functions of the factors,
where
and
.
In what follows, we use different concepts of returns, all of which are measured on a monthly basis. The
h-period log holding return from buying an
n-period discount bond at time
t and selling it as an
-period bond at time
is:
Denote the
h-period log return from holding the
n-period bond in excess of the yield of an
h-period bond by:
Suppose now that, at time t, an investor enters into a forward contract to buy at time an -period discount bond, but closes the position at time . Closing the position is equivalent to writing a forward contract at time on an -period bond with settlement date . We define the h-period log holding return from holding the proposed forward as the difference between the log-forward rates associated with each of the contracts,
2.1. Bond Risk Premia
Our goal is to analyze how different restrictions on risk prices affect bond risk premia. However, what risk premium? Risk premia in bond markets are usually defined in terms of deviations from the expectational hypothesis. Four equivalent forms of the expectational hypothesis give rise to different, but related concepts of risk premia,
4The forward premium: The time
t forward rate for loans between times
and
is the expected
-period yield at time
plus a risk premium,
The bond holding risk premium: The expected
h-period log holding return of an
n-period bond measured on a monthly rate is the yield of an
h-period bond plus a risk premium:
The term premium: The
n-period yield is the average of expected one-period yields plus a risk premium,
The holding forward risk premium: Since buying or writing a forward contract costs zero, any expected return from holding a forward contract is a risk premium,
for all
h,
, and
.
The four definitions of risk premia are equivalent in the sense that if one of them is zero or constant, so are the other three (see the
Appendix A). For our purposes, it is useful to express the risk premiums
,
and
as a function of the forward premium
,
In particular, the bond holding risk premium is proportional to the forward premium , where the factor of proportionality increases with the maturity n of the bond for a given holding period h. Small differences in the estimated forward premium due to invalid parameter restrictions, which may seem irrelevant to the naked eye, accumulate and may drive large and economically meaningful differences in the bond holding risk premium. For example, a 10 basis point difference in the one-month forward premium () can lead to differences as large as 12 percentage points in the estimated one-month bond holding risk premium associated with holding a 10-year bond () financed by borrowing at the one-month rate. In this case, the factor of proportionality is .
The closed form expressions of the risk premiums using the structure of the affine model are the following,
where we define
;
; and
,
,
and
are time invariant Jensen inequality terms.
5 Note that with risk neutrality (when the physical and risk neutral measure coincide,
), risk premia collapse to the usual Jensen inequality terms.
Even though different restrictions on the parameters of the affine model usually deliver similar estimated risk factors
, the evolution of risk premia may vary across these models as long as the matrices
and
are different. Furthermore, for a given holding period
h, the bond holding risk premium
is more sensitive to differences between
and
than the forward risk premium the longer is the maturity of the bond
n. For example, when
, the loading of the holding bond risk premia on
is
, while that of the forward premium is
Thus, for the bond with the longest maturity in our sample,
, the loading of the forward premium on
is almost 120 times smaller than that of the bond holding risk premium. Therefore, small differences in the estimated coefficients may lead to very different estimates of bond holding risk premiums for long maturity bonds even though the forward premiums may look similar.
6 3. A Nelson–Siegel Representation of the Affine Model
General unrestricted affine models with unobserved factors are unidentified because the factors can be re-scaled, rotated and translated without affecting the empirical implications of the model. There are several representations of affine models that are identified. We follow
Christensen et al. (
2011) and use a representation of the arbitrage-free model in which the yield curve adopts an augmented Nelson–Siegel parametrization of the cross-section of bond yields. As noted by
Christensen et al. (
2011) and
Hamilton and Wu (
2012), the Nelson–Siegel model is a convenient representation that is econometrically identified (subject to minor identification restrictions) and that is easy to estimate using the method of maximum likelihood. This representation of the ATSM is sufficiently general to make our point that imposing invalid overidentifying restrictions on risk prices, which may look irrelevant from the point of view of some measures of risk premiums, could lead to large differences in other measures of risk premia.
The dynamic Nelson–Siegel model is a three-factor model that fits the cross-section and time series of yield remarkably well (
Diebold and Li 2006). Yet, in its traditional representation, the Nelson–Siegel model does not rule out arbitrage opportunities. The work in
Christensen et al. (
2011) showed that one can augment the Nelson–Siegel model with a maturity-specific constant to render it arbitrage-free. In particular, the yield
at any time
t as a function of the maturity of the bond
n is parametrized as:
where
are latent variables interpreted as level, slope and curvature factors; and the parameter
determines the shape of the loadings on the factors.
In the traditional Nelson–Siegel model,
for all
n. In the arbitrage-free Nelson–Siegel model, the vector of risk factors is
, and the factor loadings and constant
are chosen to satisfy the recursions (
6) and (
7). As shown by
Christensen et al. (
2011) in a continuous time setting, rendering the Nelson–Siegel model arbitrage-free requires imposing restrictions on the risk-neutral evolution of the state variables,
, where
,
and
. The conditions are as follows: consider any
vector
and a risk-neutral matrix on lagged values
defined as:
where
. Furthermore, let
be any number and
. Using these assumptions, the recursions (
6) imply:
precisely the factor loadings in the Nelson–Siegel representation (
19). The maturity-specific constant
is set to satisfy (
7). Given these values, the parameters of the market price of risk
and
are given by
and
.
Identification of the Nelson–Siegel model requires imposing simple restrictions on the parameter
and the risk-neutral intercept
. As in
Dai and Singleton (
2000), we set
. Furthermore, since in the recursion (
7),
is a scalar, we can identify a single parameter in
. We set
and estimate
as a free parameter along with the other parameters of the model.
Let
denote the set of yield maturities observed by the econometrician. Since there are more observed maturities than factors, the model is stochastically singular. One possibility is to assume that three yields, or three linear combinations of yields, are perfectly priced by the model and then to impose classical measurement errors into the remaining yields (see (
Hamilton and Wu 2012;
Joslin et al. 2011) among others). In contrast, the Nelson–Siegel literature, e.g., (
Christensen et al. 2011), assumes that all yields are measured with error, which is an appealing assumption to make since which yields are perfectly priced or measured without error is arbitrary. We follow the latter approach and assume that all yields are observed with uncorrelated measurement errors. Thus, for each yield
with
, the arbitrage-free Nelson–Siegel model is represented by the following system of equations:
where the state vector
is unobserved, the intercept
satisfies the recursion (
7) and
i.i.d.
.
Since the risk factors are unobserved, and it is not possible to recover from the observed yields, we use the Kalman filter to evaluate the prediction-error decomposition of the likelihood function. In the unrestricted Nelson–Siegel model, we maximize the log-likelihood function numerically choosing the free parameters , , , , and for . In restricted versions of the Nelson–Siegel model, we impose the appropriate restrictions on the free parameters.
4. Estimation Results
We used data on U.S. Treasury yields of fixed maturities of 3, 6, 12, 24, 36, 48, 60, 72, 84, 96, 108 and 120 months from January 1985 through December 2013. The shortest yield is the three-month treasury constant maturity rate obtained from the Federal Reserve Bank of St. Louis (Series DGS3MO). The remaining yields are from
Cochrane (
2015), who updated the data in
Joslin et al. (
2011) until December 2013.
We begin by estimating the unrestricted unobserved factor model imposing the arbitrage-free Nelson–Siegel parametrization discussed above. Using this model as a benchmark, we imposed restrictions commonly used in the literature on the parameters that determined the evolution of the risk factors under the physical measure. Those restrictions were often motivated in terms of forecasting performance or simplicity grounds. In particular, in the baseline case, we did not restrict any of the parameters of the model besides the aforementioned identifying restrictions. Since all the restricted models that we consider are nested, we next tested whether the restrictions were supported by the data using likelihood-ratio tests along with information criteria for in-sample comparisons. More importantly, we assessed the economic relevance of the restrictions by investigating their impact on estimated risk premia.
Table 1 shows the estimation results of the general model along with the log-likelihood value, information criteria and estimated parameter
of the different restricted models. The general model corresponds to the Nelson–Siegel parametrization without imposing any restriction on the evolution of the state variables. The restricted models impose different constraints on the state equation: we considered a model with a diagonal
matrix, as in
Christensen et al. (
2011); a model with a diagonal
matrix, as in
Gürkaynak and Wright (
2012); and a model in which only shocks that affect the market price of level risk
(the first element of
) are priced, in the spirit of
Cochrane and Piazzesi (
2005,
2008). Under this last parametrization, the matrix
had non-zeros only in the first row, and only the first element of the vector
was non-zero.
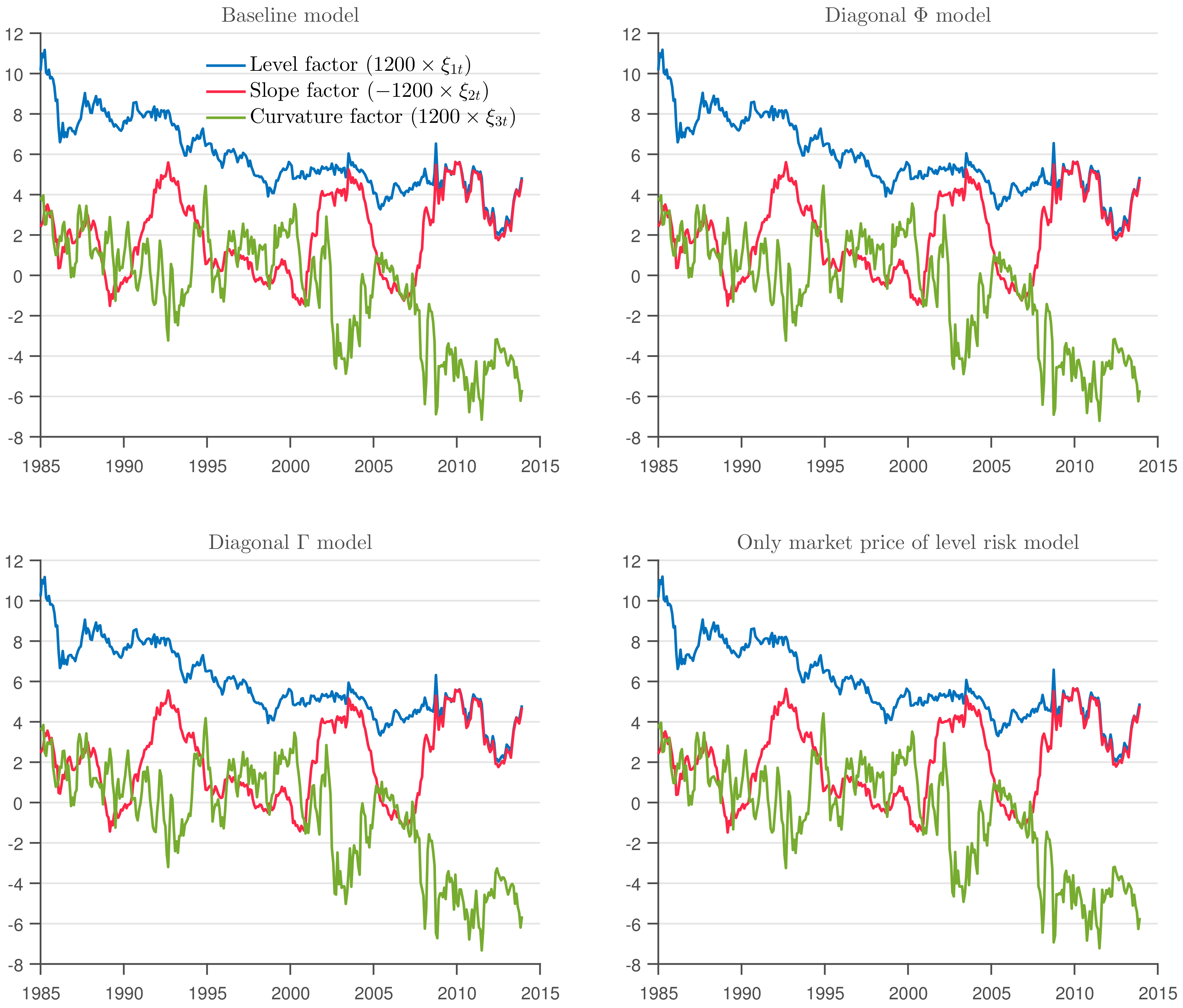
7 The likelihood ratio tests and the information criteria suggested that none of the models were valid restrictions of the general model. Yet, the estimated risk factors
and the parameter
, which governed the evolution of the risk factors under the risk-neutral measure, were virtually the same in all models (
Figure 1 and
Table 1). Since bond prices depend only on the parameters of the risk neutral measure (determined only by
and
in the Nelson–Siegel parametrization), the four models provided a virtually identical characterization of the cross-section of bond yields. Risk premiums, however, depend on the evolution of the risk factors under the physical measure, which did vary in the different models. Alternatively, the estimated values of the parameters
and
, displayed in
Table 2, differed substantially across models, often even with different signs.
5. Risk Premia and Restrictions on Risk Prices
In this section, we analyze how imposing different restrictions on the general model affects the four measures of risk premium discussed above.
5.1. The Forward Risk Premium
The forward risk premium can be computed from forecasts of the future yield curve (Equation (
11)). To the extent that these forecasts are similar to those obtained from reduced form vector autoregression, the forward risk premium would be almost model independent (see
Joslin et al. 2011,
Hamilton and Wu 2012 and
Duffee (
2011)).
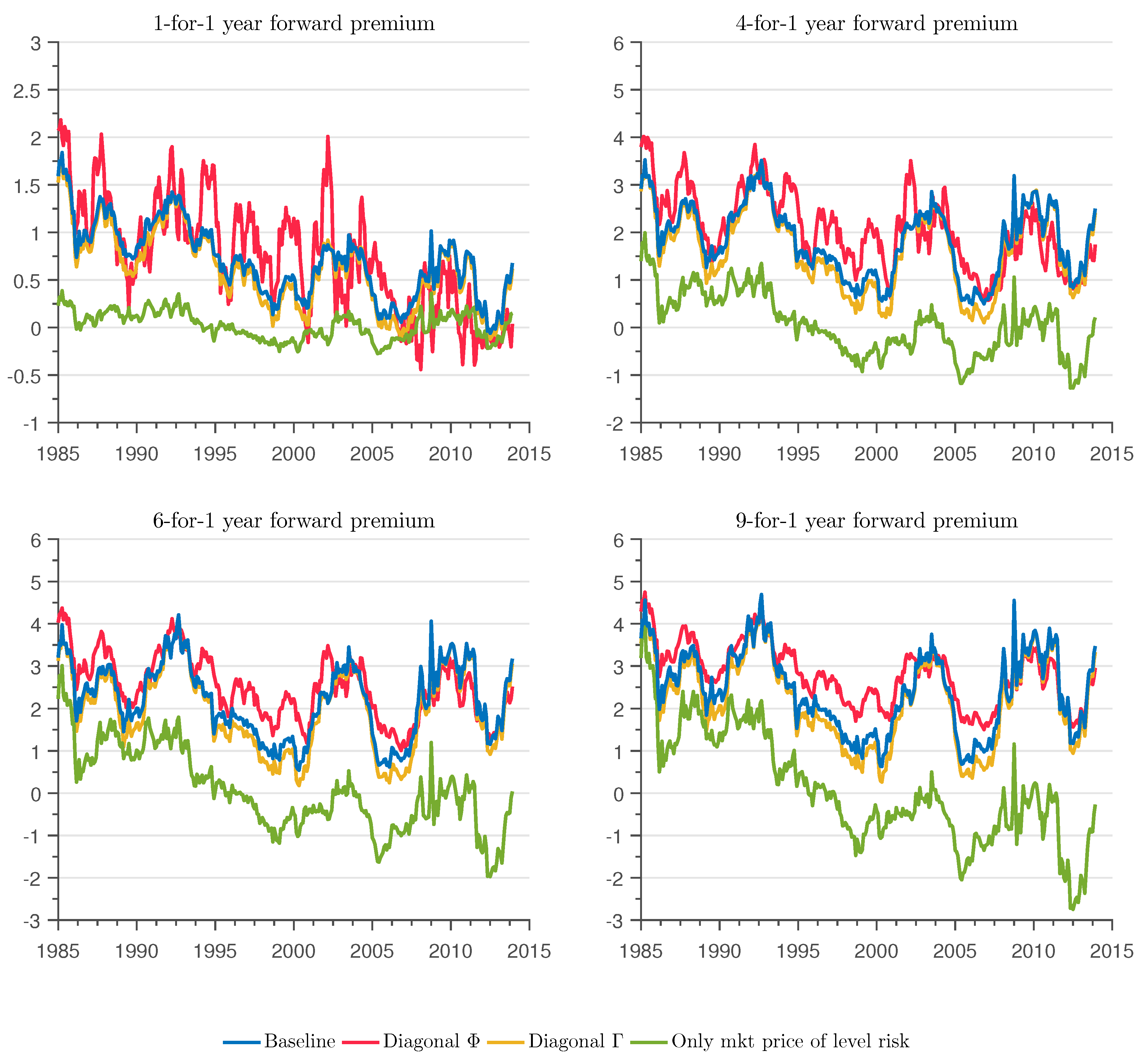
In
Figure 2, we show the estimated forward premiums in the four versions of the model. The upper left panel displays the premium associated with opening a forward contract with a settlement date one year ahead (
using our notation) on a bond that matures in one year (
). In general, the notation
s-for-
forward represents the premium associated with opening a forward contract with settlement date
s years ahead on a bond that matures in
years. Except for the factor model in which only the market price of level risk matters, the forward premium is roughly similar across models, particularly for longer term bonds. Although not shown in the figure, all forward premiums move almost one-to-one with the slope factor
of the yield curve. In the following subsections, we show how these small differences in the forward premium across models get amplified when considering other definitions of risk premium.
5.2. The Bond Holding Risk Premium
Given that the risk factors are virtually identical in the four models, differences in the estimated risk premiums come from differences in the factor loadings. Therefore, looking at factor loadings is a natural way to evaluate how sound the overidentifying restrictions are, we use Equation (
16) to analyze those factor loadings in the case of the bond holding risk premium for different bond maturities and holding periods. Results are expressed in annualized percentage terms.
The three plots on the left panel of
Figure 3 show the loadings on the factors
, respectively, of the one-month bond holding risk premium as a function the maturity of the bond (buy and hold for one month an
n period bond), for the four different models. The right panel displays the same loadings, but holding the position for one year.
The restrictions imposed on the models are economically relevant. In the baseline (unrestricted) model, and for both holding periods, the importance of the level factor increases with the maturity of the bond, while that of the slope factor is maximized (in absolute value) at about 84 months (seven years) when holding the bond for one month and is always decreasing in maturity when holding the bond for one year. The loading on the curvature factor is almost zero for bonds with maturities up to 40 months and then becomes negative and decreasing for bonds of longer maturities. In contrast, the model with a diagonal matrix works quite differently: the contribution of the level factor also increases (almost linearly) with the maturity of the bond, but by a much smaller rate than in the baseline model. On the other hand, the contribution of the curvature factor is now positive and increasing with the maturity of the bond for both holding periods. Those differences are economically relevant: a unit increase in the level factor leads to an increase in the one-month bond premium of over two percentage points for a 10-year bond in the baseline model, but of less than 0.5 percentage points in the diagonal model.
Perhaps surprisingly, the factor loadings of the model with a diagonal matrix are quite different from those of the baseline model. In the diagonal model, the loading on the level factor is half of that in the baseline model, the loading on the slope factor is twice as large and the loading on the curvature factor is mostly positive, while that in the baseline model is mostly negative. Yet, as we show below, those differences in the loadings tend to cancel out, and the evolution of the bond holding risk premium in the restricted model is similar to that in the baseline model.
The factor loadings of the model with only the market price of level risk (only the first row of is non-zero) are very different from those of the baseline model. The influence of the slope factor is virtually zero for all bond maturities and holding periods. This prediction is at odds with those of the other models, in which the slope factor has a significant impact on all measures of risk premia. Interestingly, for this restricted model, the importance of the level factor when holding long-term bonds is not only very similar to that in the baseline model, but also dominates quantitatively the influence of the other factors. This observation suggests that the evolution of the bond holding risk premium will be very different from that of the baseline model when considering short maturity bonds, but similar when considering longer term bonds.
We next evaluate the evolution over time of the bond holding risk premium derived from the four models. If a restricted model is statistically rejected, but it generates an estimated risk premium that is similar to that in the baseline model, one could claim that the statistical rejection is not economically relevant.
8 On the other hand, when a restricted model produces a risk premium that is substantially different from that in the baseline model, we say that the statistical rejection also has economic relevance.
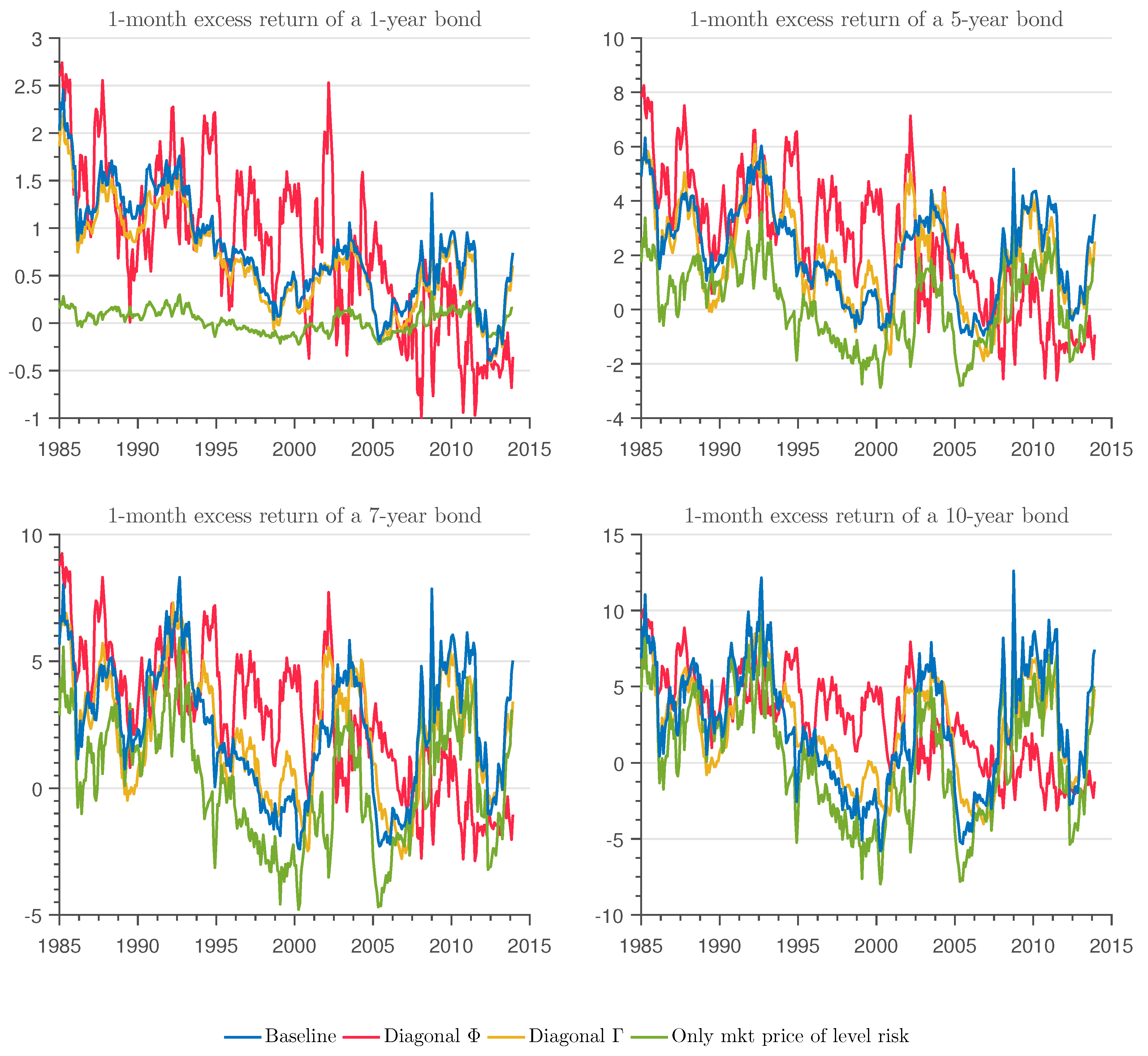
Figure 4 shows one-month bond holding excess returns for 1-year, 5-year, 7-year and 10-year bonds for the different models. Consistent with the information in
Figure 3, which shows that the loadings on the level and slope factors increase in absolute value with the maturity of the bond, we observe that the risk premia of long maturity bonds are substantially more volatile than those of shorter maturity bonds. The excess return from holding one-year bonds reaches a peak of around two percentage points, while those of the 5-, 7- and 10-year bonds are around six and 12 percentage points, respectively. Comparing this results with those presented in
Figure 1, it is apparent that excess holding returns move closely with the slope factor, especially for longer maturity bonds.
The model with a diagonal
matrix is the one that displays the smaller differences in the bond holding risk premium relative to the baseline model: the differences are centered on zero, and their magnitudes are smaller than those of the other restricted models. Which model differs the most relative to the baseline, however, depends on the maturity of the bond. For the one-year bond, the model with only the market price of level risk is, by far, the most different from the baseline, with differences reaching 100 percentage points of excess holding returns. This model, however, delivers risk premiums similar to those of the baseline model for long-term bonds. As
Figure 3 shows, in this model, the level factor dominates the contribution of the other two factors, and in that sense, it is similar to the baseline model. The second most different model is that with a diagonal
matrix. This model often produces differences of about 200 percentage points larger or smaller relative to the baseline (for example, in mid-2002).
Figure 5 displays the 6-month, 1-year, 5-year and 7-year excess returns from holding a 10-year bond. A pattern that emerges from the figure is that the risk premiums associated with longer maturity bonds are highly contemporaneously correlated with the slope factor
(see
Figure 1). As with the one-month excess holding returns, the model that is closest to the baseline is that with a diagonal
matrix.
5.3. The Term Premium
The
n-period term premium is difference between the yield on an
n-period zero coupon bond and the average of expected future short rates, where the average is taken between today and
periods ahead.
Figure 6 shows, in the different panels, the evolution of the term premium using 1-year, 4-year, 6-year and 10-year bonds for the baseline and the restricted models. Two messages follow from this plot. First, the term premium moves closely with the slope factor (
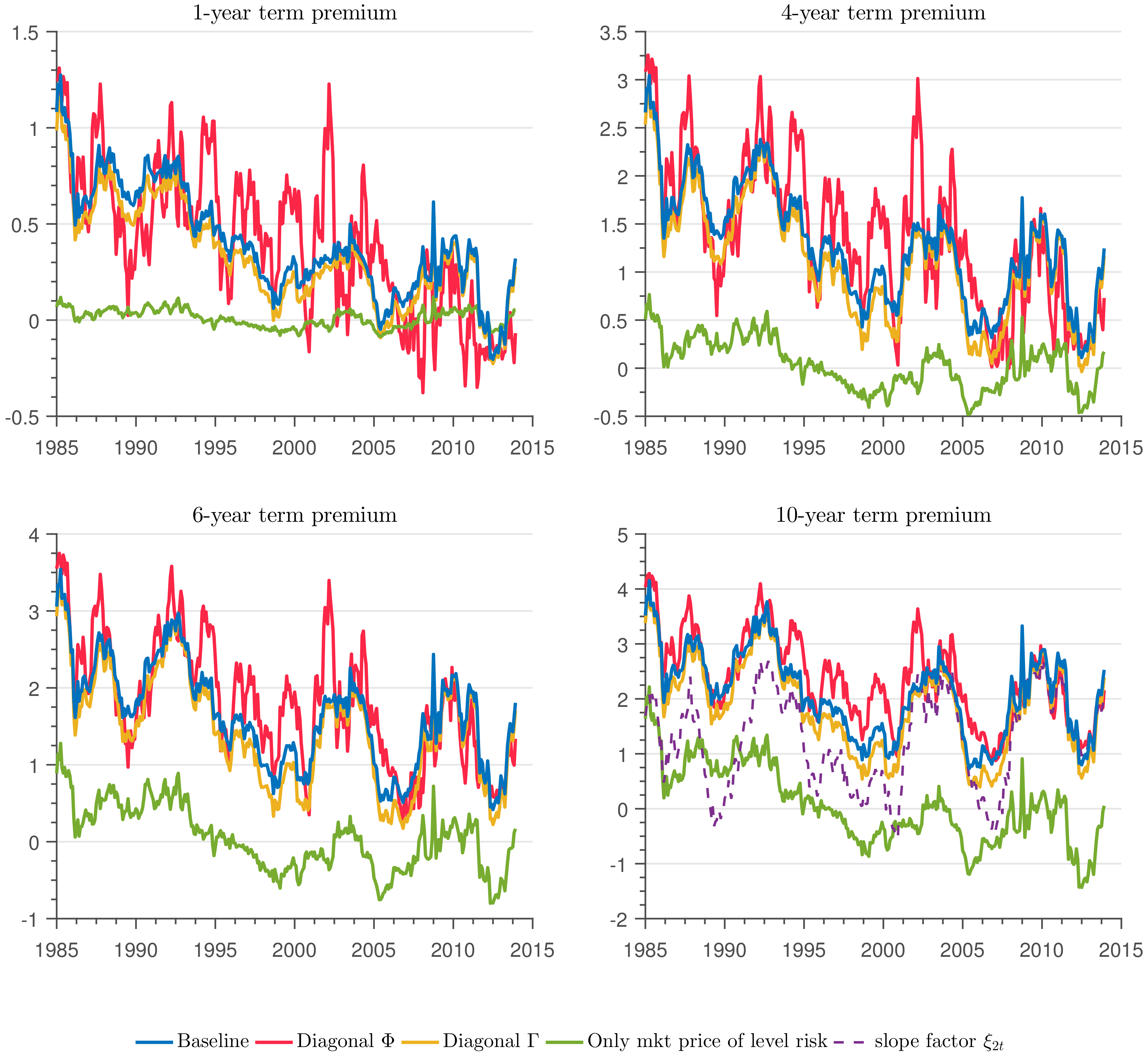
) especially for long maturity bonds. Second, the violations of the expectational hypothesis, as represented by the volatility of the term premium, become more apparent the longer the bond is under consideration. In particular, while the 10-year term premium can be as high as four percentage points and very volatile, the one-year term premium is smaller and less volatile, although it is far from constant and displays a decreasing trend over time. As for restrictions on risk prices, we still find that the model with a diagonal
matrix produces the term premium that is closest to the baseline.
5.4. The Holding Futures Risk Premium
Here, we consider the premium from holding a forward contract for a number of periods and selling it before the settlement date.
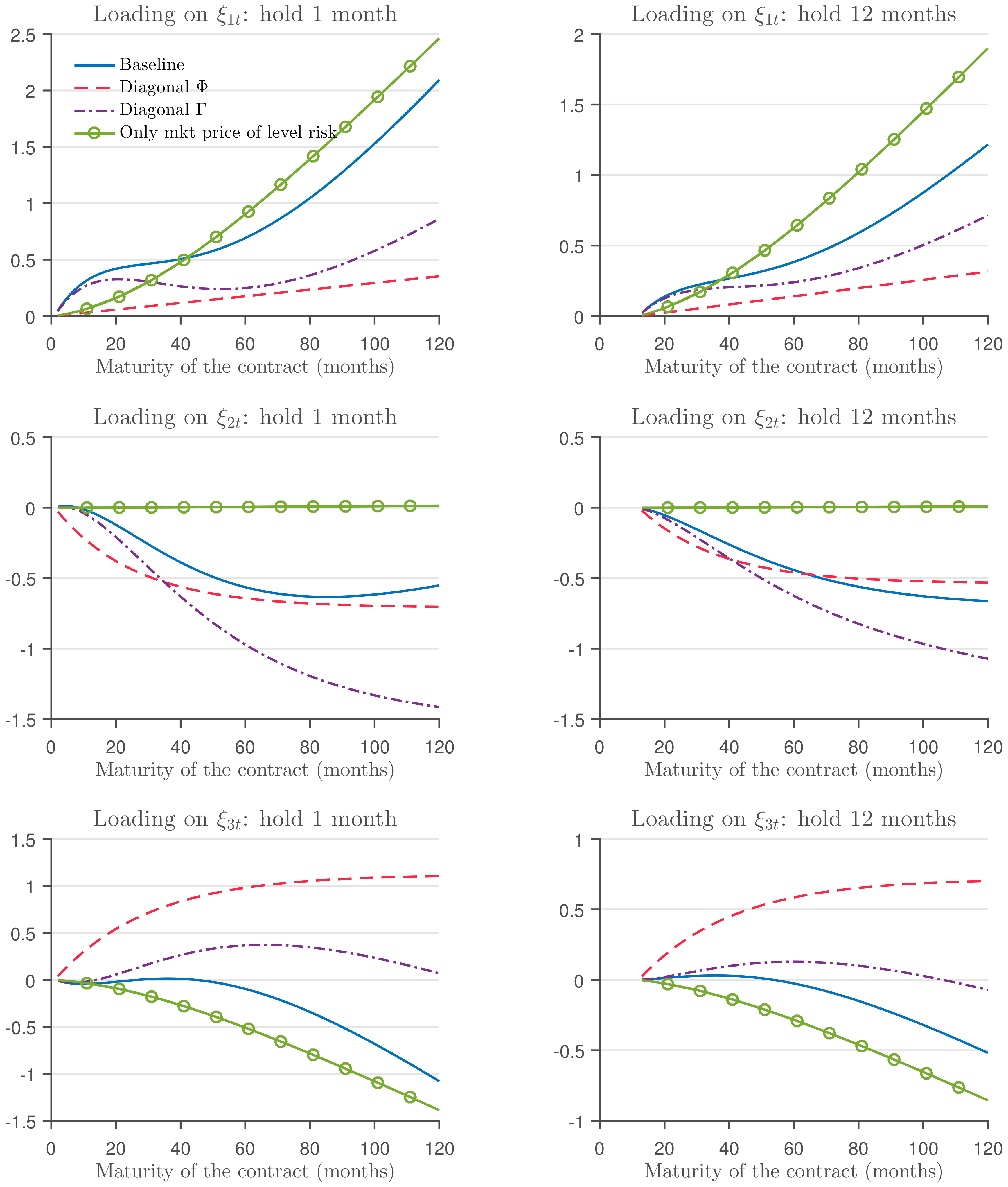
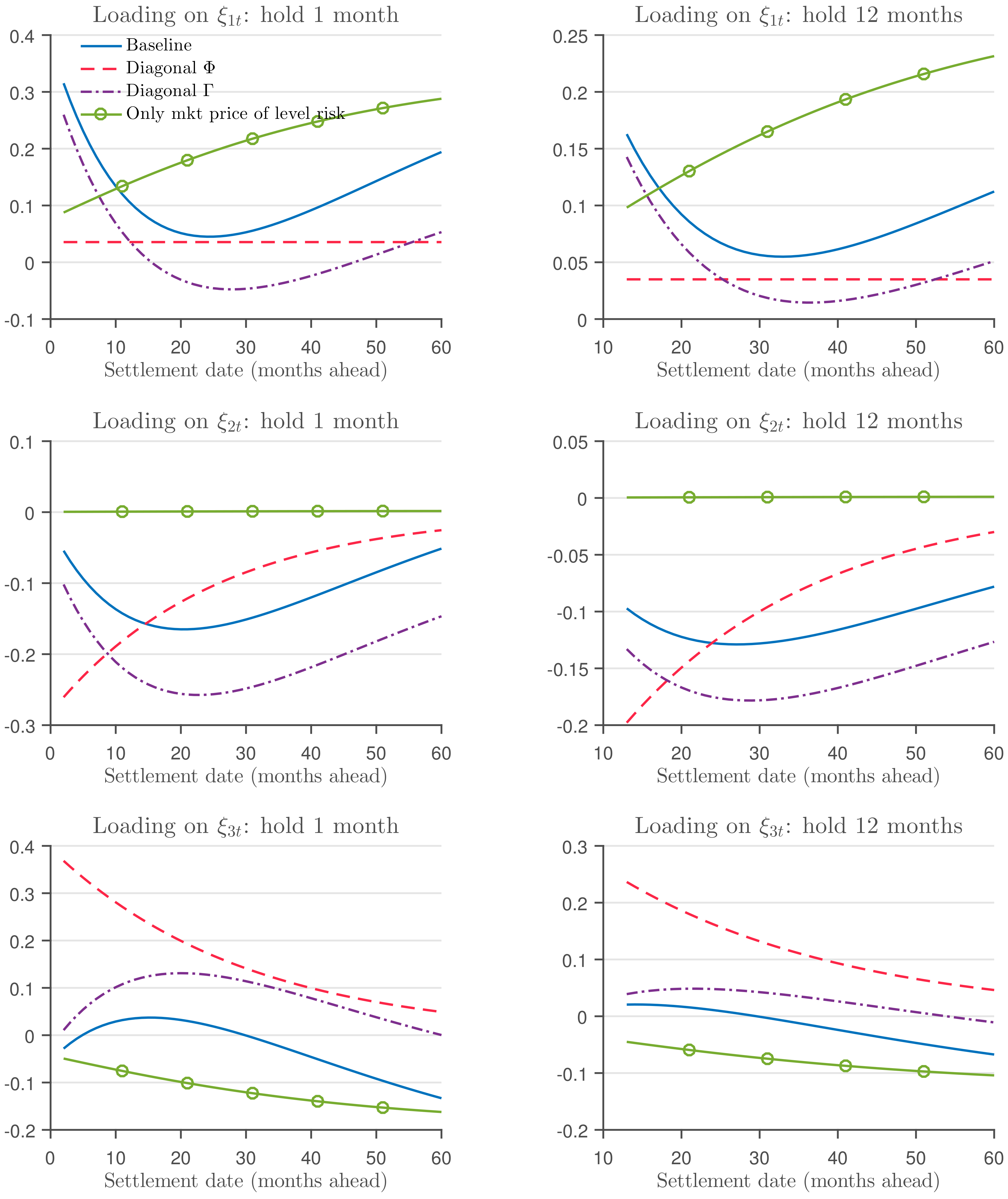
Figure 7 displays the factor loadings of the one-month (left panels) and one-year (right panels) holding forward risk premium as a function of the settlement date, for the different models. As in the case of the bond holding return, the shape of the loadings differ substantially depending on the restrictions that we impose on the models. While the loadings on the level and slope factors (
and
) have a U-shape in the baseline model, the loading on the level factor in the model with a diagonal
matrix is flat and close to zero, and the loading on the slope factor is negative and increases towards zero in the model with a diagonal
matrix. Likewise, in the model with only market price of level risk, the loading on the level factor increases with the settlement date, and that on the slope factor is virtually zero.
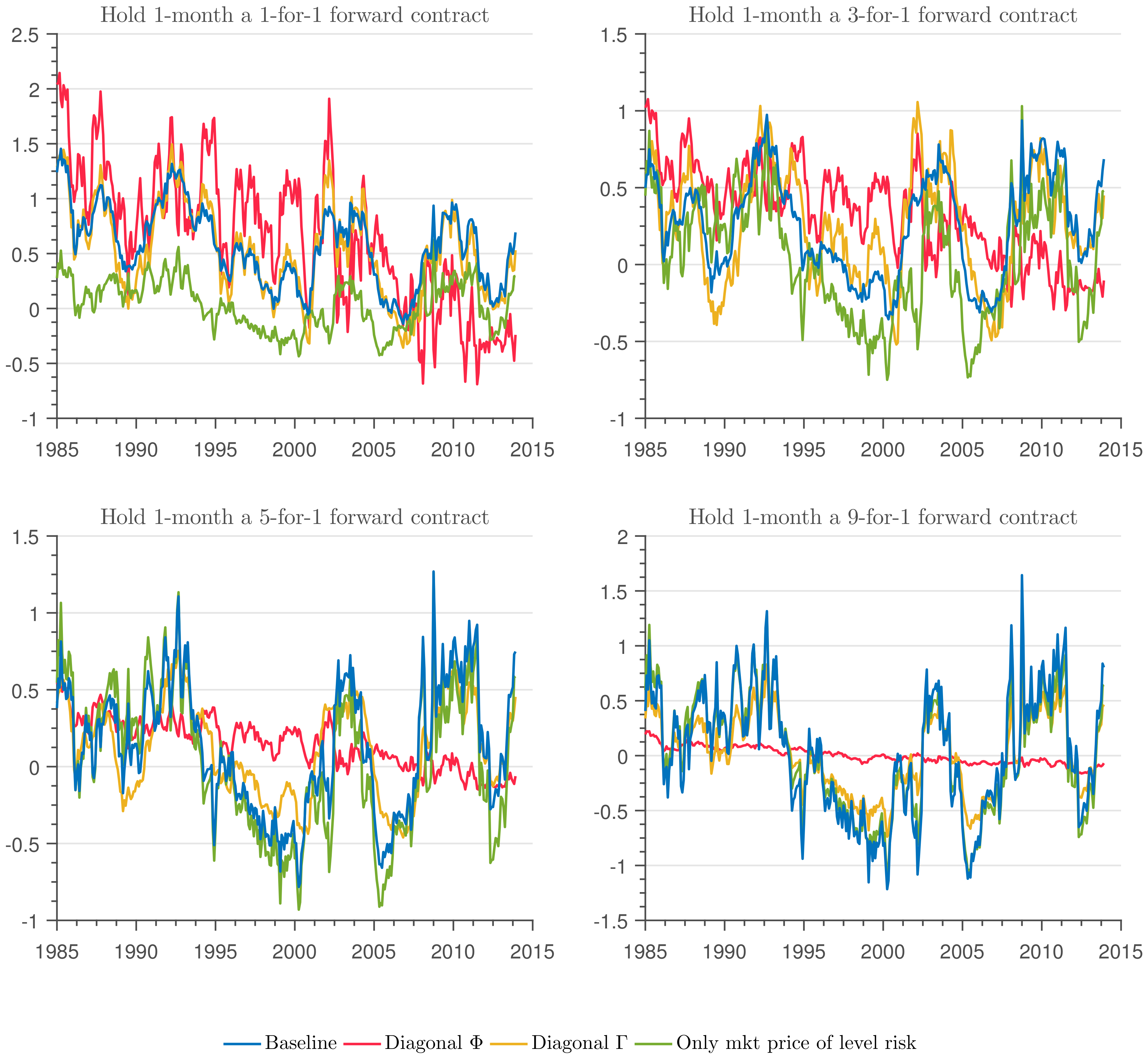
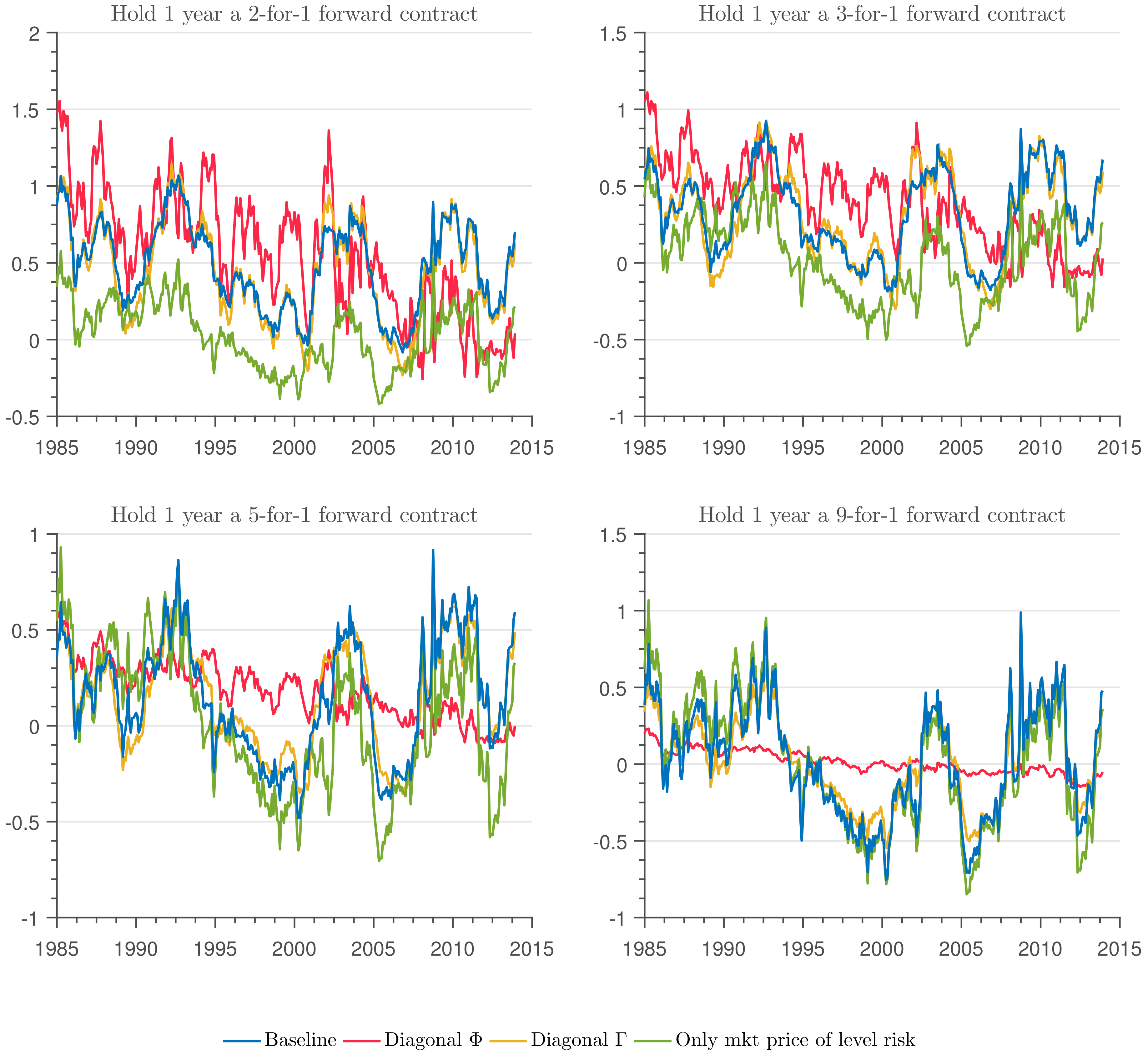
Figure 8 and
Figure 9 show the evolution of the one-month and one-year holding forward risk premiums. Three patterns emerge from the figures. First, the holding forward risk premiums are much smaller than the bond holding risk premiums (excess bond returns). Second, the holding forward premium is also highly contemporaneously correlated with the slope factor
. Third, the difference between the restricted models and the baseline tend to follow a pattern similar to the bond holding risk premium.
6. Final Remarks
In this paper, we analyzed how different restrictions on risk prices affect bond risk premia. The model that imposes a diagonal matrix and that with “only market price of level risk” are not only statistically rejected, but also produce measures of risk premia that are very different from those of the unrestricted model. Yet, there are models, such as that with a diagonal matrix, that are also rejected on statistical grounds, but that produce measures of risk premia very similar to those from the baseline model. This result follows because restrictions on have a minor impact on the market price of risk parameters. Any difference with the baseline model is of second order and comes from the indirect effect of the restrictions on the constants , and because the estimates of the remaining, common, parameters may be somewhat different.
In the baseline model, the forward premium is always positive, while the excess holding risk premium is often negative. We found that the slope factor moves almost one-to-one with several measures of risk premia, which suggests that looking at the empirical slope of the yield curve (which is highly correlated with the slope factor that we extract from the model) gives an accurate description of risk premia in bond markets. Furthermore, as has been documented many times, we find that the expectational hypothesis of the term of the structure of interest rates is at odds with the data.
In terms of how restrictions on risk prices affect risk premia, we found that the differences across models in the estimated forward premium are modest, but they get amplified when considering excess holding risk premiums. There are, however, cases in which the restricted models seem to work well. For example, the one-month excess return of a 10-year bond for the model with “only market price of level risk” is quite similar to that from the baseline model. This happens because the loading of the risk premium on the level factor increases with the maturity of the bond and dominates movements in risk premia relative to the contribution of the other factors, but only for long maturity bonds.
In sum, imposing overidentifying restrictions affect the evolution of risk premia dramatically in some cases (such as when is diagonal), but not so much in others (such as when is diagonal). Often, researchers impose overidentifying restrictions to reduce the number of parameters to estimate or for other reasons, such as forecasting performance, even though they are statistically rejected. Our exercises suggest that this practice is inappropriate, since it is difficult to know a priori when the restrictions will have a significant impact on estimated risk premia. Of course, there is no harm in imposing the restrictions if they are not statistically rejected. However, since there is no theoretical guidance on how to impose them and one gains at best a few degrees of freedom by finding the appropriate restrictions, we believe that it is advisable to focus on the just-identified case whenever the objective of the study is to understand risk premia.