Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence
Abstract
1. Introduction
2. The Model
2.1. Some Necessary Notations
2.2. The Insurance Risk Process
2.3. Description of Financial Market
2.4. Problem Formulation
3. The Closed-Form Solution to HJB Equation
4. Efficient Strategy and Efficient Frontier
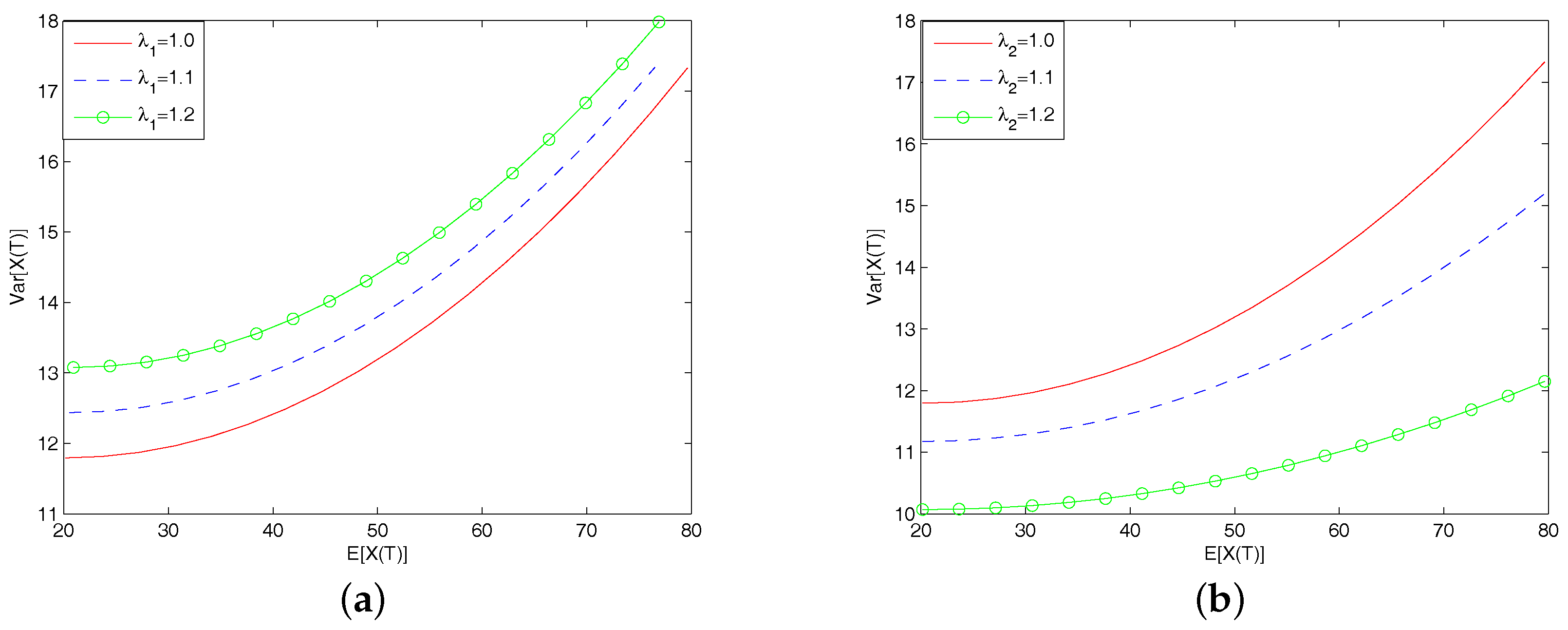
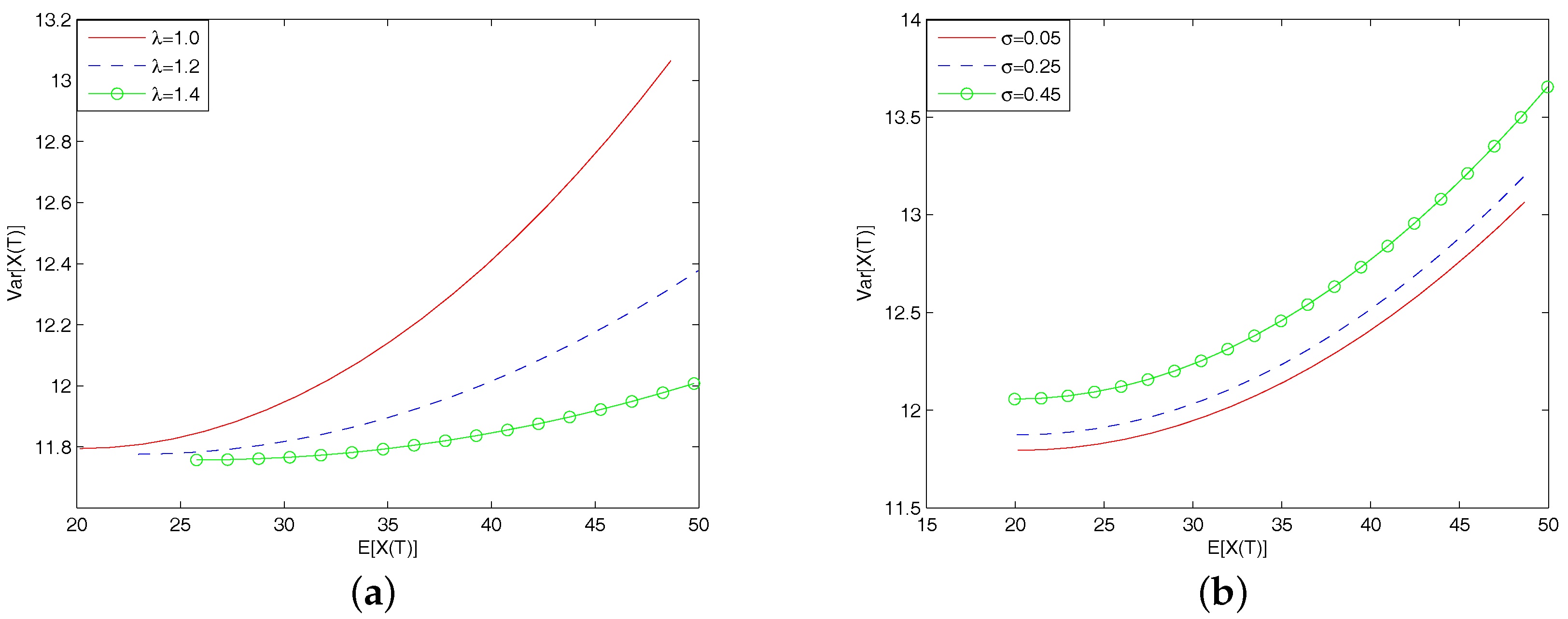
5. Sensitive Analysis
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Asmussen, Søren, Bjarne Højgaard, and Michael Taksar. 2000. Optimal risk control and dividend distribution policies. Example of excess-of loss reinsurance for an insurance corporation. Finance and Stochastics 4: 299–324. [Google Scholar] [CrossRef]
- Azcue, Pablo, and Nora Muler. 2005. Optimal reinsurance and dividend distribution policies in the Cramér-lundberg model. Mathematical Finance 15: 261–308. [Google Scholar] [CrossRef]
- Bäuerle, Nicole. 2005. Benchmark and mean-variance problems for insurers. Mathematical Methods of Operations Research 62: 159–65. [Google Scholar] [CrossRef]
- Bai, Lihua, and Huayue Zhang. 2008. Dynamic mean-variance problem with constranit risk control for the insurers. Mathematical Methods of Operations Research 68: 181–205. [Google Scholar] [CrossRef]
- Bai, Lihua, and Junyi Guo. 2010. Optimal dividend payments in the classical risk model when payments are subject to both transaction costs and taxes. Scandinavian Actuarial Journal 1: 36–55. [Google Scholar] [CrossRef]
- Bai, Lihua, Jun Cai, and Ming Zhou. 2013. Optimal reinsurance policies for an insurer with a bivariate reserve risk process in a dynamic setting. Insurance: Mathematics and Economics 53: 664–70. [Google Scholar] [CrossRef]
- Bi, Junna, and Junyi Guo. 2013. Optimal mean-variance problem with constrained controls in a jump-diffusion financial market for an insurer. Journal of Optimization Theory and Applications 157: 252–75. [Google Scholar] [CrossRef]
- Bi, Junna, Zhibin Liang, and Fangjun Xu. 2016. Optimal mean-variance investment and reinsurance problems for the risk model with common shock dependence. Insurance: Mathematics and Economics 70: 245–58. [Google Scholar] [CrossRef]
- Bielecki, T. R., H. Jin, S. R. Pliska, and X. Y. Zhou. 2005. Dynamic mean-variance with portfolio selection with bankruptcy prohibition. Mathematical Finance 15: 213–44. [Google Scholar] [CrossRef]
- Bouchard, Bruno, and Huyên Pham. 2004. Wealth-path dependent utility maximization in incomplete financial markets. Finance and Stochastics 8: 579–603. [Google Scholar] [CrossRef]
- Browne, Sid. 1995. Optimal investment policies for a firm with a random risk process: Exponentional utility and minimizing the probability of ruin. Mathematics of Operations Research 20: 937–58. [Google Scholar] [CrossRef]
- Cojocaru, Ionica. 2017. Ruin probabilities in multivariate risk models with periodic common shock. Scandinavian Actuarial Journal 2: 159–74. [Google Scholar] [CrossRef]
- Cossette, Hélene, and Etienne Marceau. 2000. The discrete-time risk model with correlated classes of business. Insurance: Mathematics and Economics 26: 133–49. [Google Scholar] [CrossRef]
- Delong, Łukasz. 2005. Optimal investment strategy for a non-life insurance company: Quadratic loss. Applications of Mathematics 32: 263–77. [Google Scholar] [CrossRef]
- Delong, Łukasz, and Russell Gerrard. 2007. Mean-variance portfolio selection for a non-life insurance company. Mathematical Methods of Operations Research 66: 339–67. [Google Scholar] [CrossRef]
- Fleming, Wendell H., and Halil Mete Soner. 2006. Controled Markov Processes and Viscosity Solutions. New York: Springer. [Google Scholar]
- Liang, Zhibin, and Kam Chuen Yuen. 2016. Optimal dynamic reinsurance with dependent risks: Variance premium principle. Scandinavian Actuarial Journal 1: 18–36. [Google Scholar] [CrossRef]
- Liang, Zhibin, Kam Chuen Yuen, and Caibin Zhang. 2017. Optimal reinsurance and investment in a jump-diffusion financial market with common shock dependence. Journal of Applied Mathematics and Computing 56: 637–64. [Google Scholar] [CrossRef]
- Liang, Zhibin, Junna Bi, Kam Chuen Yuen, and Caibin Zhang. 2016. Optimal mean-variance reinsurance and investment in a jump-diffusion financial market with common shock dependence. Mathematical Methods of Operations Research 84: 155–81. [Google Scholar] [CrossRef]
- Lim, Andrew EB. 2004. Quadratic hedging and mean-variance portfolio selection with random parameters in an incomplete market. Mathematics of Operations Research 29: 132–61. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. Journal of Finance 7: 77–91. [Google Scholar]
- Merton, Robert C. 1972. An analytical derivation of the efficient portfolio frontier. Journal of Financial and Quatative Analysis 7: 1851–72. [Google Scholar] [CrossRef]
- Ming, Zhiqin, Zhibin Liang, and Caibin Zhang. 2016. Optimal mean-variance reinsurance with common shock dependence. Anziam Journal 58: 162–81. [Google Scholar] [CrossRef]
- Protter, Philip E. 2004. Stochastic Integration and Differential Equations, 2nd ed. Berlin: Springer. [Google Scholar]
- Schmidli, Hanspeter. 2002. On minimizing the ruin probability by investment and reinsurance. Annals of Applied Probability 12: 890–907. [Google Scholar] [CrossRef]
- Yang, Hailiang, and Lihong Zhang. 2005. Optimal investment for an insurer with jump-diffusion risk process. Insurance: Mathematics and Economics 37: 615–34. [Google Scholar] [CrossRef]
- Yong, Jiongmin, and Xun Yu Zhou. 1999. Stochastic Controls: Hamilton Systems and HJB Equations. New York: Springer. [Google Scholar]
- Yuen, Kam Chuen, Zhibin Liang, and Ming Zhou. 2015. Optimal proportional reinsurance with common shock dependence. Insurance: Mathematics and Economics 64: 1–13. [Google Scholar] [CrossRef]
- Zhang, Caibin, and Zhibin Liang. 2017. Portfolio optimization for jump-diffusion risky asset with common shock dependence and state dependent risk aversion. Optimal Control Applications and Methods 38: 229–46. [Google Scholar] [CrossRef]
- Zhou, Xun Yu, and Duan Li. 2000. Continuous-time mean-variance portfolio selection: A stochastic LQ framework. Applied Mathematics and Optimization 42: 19–33. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Sun, Z. Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence. J. Risk Financial Manag. 2018, 11, 25. https://doi.org/10.3390/jrfm11020025
Tian Y, Sun Z. Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence. Journal of Risk and Financial Management. 2018; 11(2):25. https://doi.org/10.3390/jrfm11020025
Chicago/Turabian StyleTian, Yingxu, and Zhongyang Sun. 2018. "Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence" Journal of Risk and Financial Management 11, no. 2: 25. https://doi.org/10.3390/jrfm11020025
APA StyleTian, Y., & Sun, Z. (2018). Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence. Journal of Risk and Financial Management, 11(2), 25. https://doi.org/10.3390/jrfm11020025




