1. Introduction
While the reasons are limited, the subprime mortgage crisis (SMC) affected different aspects of the economy not only in the USA but also in other countries, from Europe to Asia, in terms of household net worth, employment, inflation, market capitalization, and GDP. Today, it is widely accepted that prior to the crisis, structured financial instruments and credit derivatives were utilized beyond their scope, mostly for speculation with high leverages rather than for hedging purposes. Directly after the housing bubble, high default rates in subprime mortgage credits had begun and financial institutions that either issued mortgage-based loans or invested in subprime asset-backed securities faced serious liquidity problems in their balance sheets. According to the statistics released by the International Monetary Fund (IMF) (
Dattels and Kodres 2009) as of April 2009, write-downs in global financial institutions reached
$4.1 trillion from the toxic assets. While some were saved by governments, most of them failed and proved catastrophic for the economy and investor expectations. As stated by
Adelson (
2013), depending on the way it is measured (for instance, market capitalization or world GDP), the cost of the financial crisis appears to fall between
$5 trillion and
$15 trillion, including the overseas effect.
Even though the Fed and other central banks took some steps to bail out, especially financial institutions, the crisis brought a disastrous decline in employment statistics worldwide. The effect of credit constraints on firms’ labor demand shifted the crisis from being a financial one to the real economy. According to the statistics released by OECD between 2007 and 2010, 10.2 million people lost their jobs in OECD countries (
Scarpetta 2008). The year 2009 witnessed another peak in the US economy with the highest deficit (12.8%—as a percentage of GDP) incurred in the general government budget (
OECD 2014). Despite of that, including 2014 and 2015, economic growth in the USA gained speed and with recovery in the labor market, earned support in private consumption. Although it originated in the US and later spilled over globally (
Gunay 2015;
Robertson 2016;
Yao et al. 2010;
Gunay 2016;
Puri et al. 2011;
Koy 2017), especially to some European countries in the form of sovereign debt crisis, the heaviest struggle has been witnessed in the US markets.
The Fed has taken many steps since the summer of 2007 and responded aggressively to the financial crisis through the execution of different monetary programs in order to support the financial and real industry. The tools the Fed employed can be summarized under three groups: the first group is related to the conventional role of the central banks as a lender of last resort (LOLR). During the crisis, with some discount window actions, such as term auction facility (TAF), primary dealer credit facility (PDCF), term securities lending facility (TSLF), and currency swap agreements, the Fed fulfilled its monetary goals. As stated by
Rosengren (
2009), while the discount window is employed only for depository institutions with PDCF, it is also extended to investment banks. In the second group, we observe the provision of funds to borrowers and investors who are in liquidity crunch in crucial markets. Commercial paper funding facility (CPFF), asset-backed commercial paper money market mutual fund liquidity facility (AMLF), money market investor funding facility (MMIFF), and the term asset-backed securities loan facility (TALF) can be categorized in this group. The third group of actions consists of open market operations. In this group, the Fed aimed to enhance the functioning of credit markets by putting pressure on them to lower longer-term interest rates. In addition to this, through the implementation of purchase agreements (the operation twist) for longer-term securities, the Fed has been more accommodative in its balance sheet (
Fed 2017a).
While the activities described above depict a wide variety of monetary policies, the Fed took the first action against the crisis in September 2007, and it consisted of a conventional monetary policy practice: lowering Federal funds rate (FFR). As of 18 September 2007, the FFR has been reduced from 5.25 to 4.75%. The downward trend in FFR has continued in 2007 and 2008. As of 16 December 2008, the lowest level (0.25%) has been observed and this rate remained consistent till 17 December 2015. Following this day, FFR increased continuously up to 1.25%. In October 2014, the Fed concluded the purchases of agency-guaranteed mortgage-backed securities (MBS) and longer-term Treasury securities. However, FFR changes have continued along with the financial crisis to achieve the following objectives: maximum employment and price stability (
Fed 2017b).
The aim of this paper is to investigate the effectiveness of FFR changes in the management of mortgage crisis. As discussed above, one of the most important monetary tools of the Central Bank of the USA is FFR. By changing the rate, the Fed signals the markets and other interest rates such as the Eurodollar rate and the LIBOR. Therefore, those actions are followed by all market players worldwide. In this study, through the application of the Markov switching regression (MRS-Regression) model, we analyze the effect of FFR across different parameters of the economy, such as employment level, inflation, housing, and personal savings. The variables used in empirical analysis can be summarized below with the respective notations:
| Variable | Notation |
| Fed Funds Rate | FFR |
| New Privately Owned Housing | HOUST |
| Consumer Price Index | CPI |
| Labour Market Conditions Index | LMCI |
| Personal Saving Rate | PSAVERT |
The contribution of this paper is that it introduces multiple perspectives regarding the crisis. Through the exploration of the different fields affected by the management of the crisis or policies of Fed, we analyze the effectiveness of the implemented policies. While most of the literature concentrates on the reasons that caused the crisis, only a limited number of papers investigate the effect of crisis in specific markets or parameters. To the best of our knowledge, this paper explains the reaction of multiple markets against the interest rate policy of Fed during the SMC for the first time.
The following sections of the paper are arranged as follows:
Section 2 contains econometrical methods employed in the analysis.
Section 3 discusses the results of the empirical tests.
Section 4 presents the conclusion.
3. Empirical Analysis
In this study, we analyze the interaction between different markets and interest rate policy of the Fed in the management of SMC. For this purpose, we examine this relationship through an MRS-Regression analysis. The model we determine consists of six variables: FFR, new privately-owned housing unit (HOUST), inflation rate (CPI), change in labor market conditions index (LMCI), personal savings index (PSAVERT), and dummy variable for the SMC period. The data for empirical analysis was obtained through the Federal Reserve Bank of St. Louis’ database. The period we study is August 1976–August 2016, and the data displays monthly frequency. In
Figure 1, we present the log-differences of the respective time series. As can be seen, while the HOUST variable is extremely volatile in each period, FFR exhibits fluctuation, especially between the years 2007 and 2016. Conversely, PSAVERT is highly variant in the years 1987, 2002, 2005, and 2008.
Unit root tests form one of the essential requirements in time series econometrics. As emphasized in the literature, working with non-stationary time series would bring on spurious results in empirical studies due to unstable representation of data. This is because it is evident that many financial time series exhibit trends that cause non-constant mean and variance over time. Apart from stationary, structural breaks in financial time series may also cause the results of the analysis to be artificial. ADF and PP unit root tests are conventionally applied in the literature. However, it is known that in the case of structural breaks in the data, these tests fail, as they present a bias in the rejection of null hypothesis. Based on these facts,
Kapetanios (
2005) introduced a unit root test against the occurrence of an unspecified number of breaks. In
Table 1, we present the results of Kapetanios multiple breaks unit root test for our variables.
By allowing up to five breaks, we executed the Kapetanios multiple breaks unit root test. The critical values of the test are as follows: −7.395, −6.717, and −6.417, for the confidence levels at 99, 95, and 90% respectively. The results provided in
Table 1 reveal that for the respective confidence levels, the null hypothesis is rejected, implying that the return series are stationary at level in the presence of structural breaks. Hence, in the following analysis, we employ the raw return series that do not have a difference, since they are
I(0). Before we move on to the MRS-Regression model, we need to determine whether our return series has non-linear features. As stated by
Broock et al. (
1996), a BDS test can be employed for a stochastic linearity analysis.
Brock and Sayers (
1988) implement the BDS test to the residuals of the estimated linear models. By following this approach here, we first estimate the ARMA structure of our return series. The results can be observed in
Table 2.
The results in
Table 2 indicate that the best linear model for the data is different in each return series. The residuals obtained from the ARMA models have been employed to conduct the BDS test. The BDS test requires the selection of two parameters nested in model itself:
e and
m. As stated by
Peel and Speight (
1995) in calculation of the BDS test statistic, for time series
a possible subset is created with overlapping entries that is
m-histories (m, embedding dimension). As for
e, it is the epsilon value in model to assign the distance (
e) between two
m-histories.
Hsieh and LeBaron (
1988) recommend the selection of an epsilon value between 0.5 and 1.5. Regarding the embedding dimension
m, we employed three values: 3, 5, and 7.
As observable in
Table 3, the estimated statistics at different dimensions and epsilon values are greater than the critical values of 1.96 and 2.575 at 0.95 and 0.99 confidence levels, implying that the null hypothesis is rejected at both confidence levels. The rejection of the null hypothesis indicates that the return series has non-linearity and is convenient for use in the MRS-Regression model.
As stated by
Balcilar et al. (
2015), the Markov regime switching models correspond with non-linear time series models that arise from non-linear dynamic processes for instance time-varying parameter, asymmetric business cycles, and structural breaks in a time series. Therefore, the determination of the non-linear structure of return series is essential for the Markov regime switching models. Rather than the linear models, the Markov regime switching models enable the analysis of the asymmetric relationship between the dependent and independent variables along with the business cycles or regimes. Markov regime switching model is more flexible due to the fact that parameters are allowed to be altered under different regimes over time. Since we examine the effect of Fed interest rate policy in different aspects of the economy, the consideration of varying policies during different business cycles is inevitable for the empirical analysis.
As can be observed from the results in
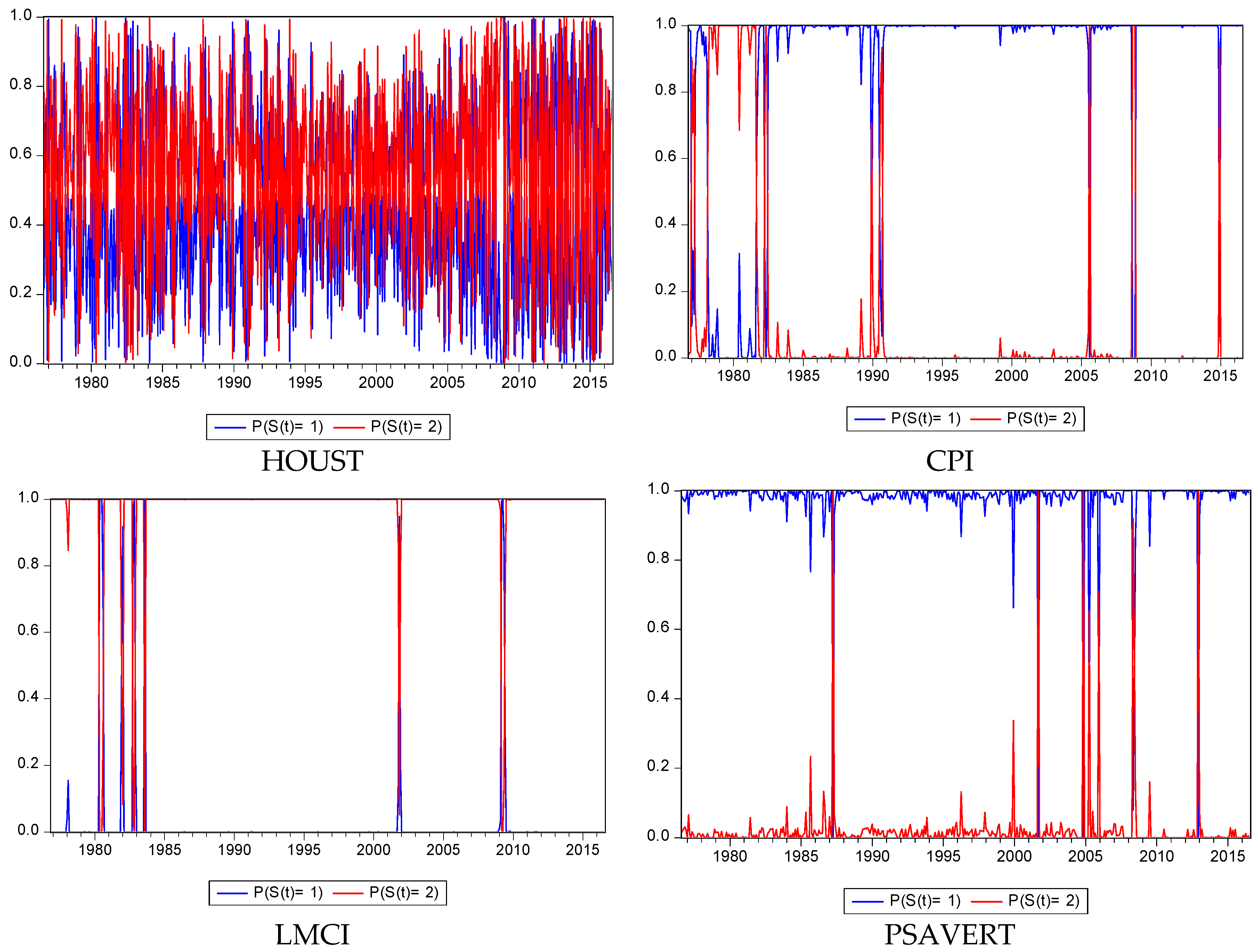
Table 4, we estimate four different MRS-Regression models, in each, the independent variable is FFR. We also present the filtered regime probabilities in
Figure 2. In order to identify the temporal effect of policy changes, in our analysis, we employ different lags for each variable. In addition to the lags, we also employ a common dummy variable in each model. This variable represents the SMC period in which the Fed exercise a loose monetary policy with very low interest rates. As the MRS-Regression model does not label the regimes, for this analysis we need to define and name the regimes for each model. Referring to the sign in the coefficient of constant variable we can assert that for all models, Regime 1 involves expansion and Regime 2 includes recession cycles. For instance, the positive sign in the constant variable of the first model indicates a positive value in housing statistics which is the indicator of expansion period. As for the dummy variable, it takes value of 1 in period of September 2007–December 2015 and 0 in remaining dates. By starting from 18 September 2007 until 17 December 2015 the Fed decreased the FFR continuously with following rates: 4.75, 4.50, 4.25, 3.50, 3.00, 2.25, 2.00, 1.50, 1.00, and 0.25%. Since in this period, the Fed implemented a loose monetary policy, significance of a dummy variable would be a success sign of the Fed for this specific period.
In our first model, we analyze the relationship between Fed interest rate policy and the housing market. In this model, the HOUST variable—which stands for New Privately Owned Housing Unit in the US—is the dependent variable, while the FFR and dummy form the independent variables. From the results, it is apparent that during an expansion period (Regime 1) once the FFR increases the value of HOUST decreases. Additionally, this influence emerges one period later (after one month on average) in the housing market, following the Fed’s action. During a period of recession, however, it is observed that the effect of Fed interest rate policy is not significant on the HOUST variable. According to the dummy variable, which measures the effectiveness of Fed policy (during 2008–2015), we observe that while in the expansion period, the Fed’s decisions significantly affect the housing market, in the recession period, this effect is not sufficient. According to the results for regime transition probabilities provided in
Table 5, for the housing market, the probability of remaining in the expansion regime is 0.14, while in the recession regime, it is 0.31. However, the transition probability from expansion to recession is 0.86, while the transition probability from recession to expansion is 0.68. These results indicate that the housing market in the period we analyzed tends to be in recession, though the transitions display an extremely high frequency according to the regime durations provided in
Table 4. Unlike other variables, the housing market displays an extremely short duration in each regime, while the recession period is longer on average.
Although the coefficient in inflation rate (CPI) is significant in both regimes, and the sign is consistent with our theoretical expectations, the value of the coefficient is nearly zero. Therefore, we omit this variable in the interpretation of results. It implies that even though the Fed interest rate policy exhibits an influence on the CPI, it is very low and systematically emerges after two months. Change in the Labor Market Conditions Index (LMCI) was introduced by Fed in 2014, which is responsible for tracking the changes in the labor market. The LMCI demonstrates a positive correlation with the employment rate. The model’s results indicate that the Fed interest rate increments during the recession period decrease the employment rate, but this effect emerges after three months on average. However, the statistically insignificant dummy variable indicates that this effect does not exist in the period of mortgage crisis and Fed policy changes are not effective in the labor market in this period. Transition probabilities also indicate that remaining in the recession period has a very high likelihood with the probability of 0.99 as against the probability for transition from recession to expansion period. In addition, regime durations also support this conclusion. Therefore, while the duration of the recession period is 79 months, for the expansion regime this time is 2.4 months.
Unlike the labor and housing markets, we have observed that the policy changes in FFR have a prompt influence on personal savings (PSAVERT). While during the expansion period, any increase in FFR leads to a decrease in the personal savings, during the recession regime, increases in FFR raise the personal savings tremendously. This conclusion reveals that personal savings are very sensitive to the actions taken by the Fed, especially in crisis periods. Furthermore, the reflection of the Fed policy is faster in personal savings than labor and housing markets. The statistically significant dummy variable also demonstrates a significant effect on personal savings in both phases of interest rate policy changes of the Fed. According to the transition statistics, if the present regime is expansion, the probability of remaining in this regime is 0.98, and even if the present regime is recession, the probability of the transition from recession to expansion is still extremely high with the ratio: 0.92. Therefore, we can say that individuals are liable to have less savings in the US. Regime durations also support this finding. According to
Table 4, the duration of the expansion regime is approximately eight times greater than that of the recession phase.
4. Conclusions
In this study, we discuss the effectiveness of Fed interest rates policy in different markets through the Markov regime switching regression analysis. In the empirical analysis, we examine this relationship for the labor market, housing market, inflation rate, and personal savings, especially during the SMC. Results indicate that the FFR affects the housing market only during the expansion period with one lag. With regard to inflation, while the effect of the policy changes is significant, the influence arises after two months, and the extent of the effect is very limited. It implies the likelihood of the application of alternative instruments of monetary policy other than the FFR by the Fed to control the inflation. In the labor market, while FFR changes have a significant effect, especially during the recession period, this interaction emerges after three months. However, we have observed that during the SMC, the Fed interest rate policies could not affect a recovery in employment rates. Surprisingly, results demonstrate that FFR has a prompt effect on personal savings, implying that personal savings and expenditures are very sensitive to the changes in FFR, and individuals react to the monetary policy of the Fed by investing less in savings during the expansion period and higher savings in recession period. Consequently, it can be said that the Fed interest rate policy is not sufficient to boost the economy in SMC period that is why the Fed has already used different tools and policies such as TAF, PDCF, TSLF, CPFF, AMLF, MMIFF, and TALF.