1. Introduction
A cryptocurrency can be defined as “a digital asset designed to work as a medium of exchange using cryptography to secure the transactions and to control the creation of additional units of the currency”. In recent years, the popularity and use of cryptocurrencies has increased dramatically. For example, the U.K. government is looking at Bitcoin technology (Bitcoin is the first and the most popular cryptocurrency) for tracking taxpayer money. The U.S. government is to sell over 44,000 Bitcoins.
Because of this increasing interest, there is a need to quantify the variation of cryptocurrencies. It is well known that cryptocurrencies are highly volatile compared to traditional currencies. Certainly, their exchange rates cannot be assumed to be independently and identically distributed. Perhaps the most popular models for the exchange rates of traditional currencies are based on Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models. However, there exists little work on fitting of GARCH-type models to the exchange rates of cryptocurrencies. The known work focuses on GARCH modelling of Bitcoin, the first and the most popular cryptocurrency.
Katsiampa (
2017) estimated the volatility of Bitcoin through a comparison of GARCH models, and the AR-CGARCH model was shown to give the optimal fit.
Urquhart (
2017) illustrated that HARmodels are more robust in modelling Bitcoin volatility than traditional GARCH models.
Stavroyiannis and Babalos (
2017) examined dynamic properties of Bitcoin modelling through univariate and multivariate GARCH models and vector autoregressive specifications.
Cermak (
2017) used a GARCH (1, 1) to model Bitcoin’s volatility with respect to macroeconomic variables, in countries where Bitcoin has the highest volume of trading. The results showed that Bitcoin behaves similarly to fiat currencies in China, the U.S. and Europe, but not in Japan. In particular, Bitcoin appeared to be an attractive asset for investment and store of value in China;
Bouoiyour and Selmi (
2015,
2016) analysed daily Bitcoin prices using an optimal-GARCH model and showed that the volatility has decreased when comparing data from 2010–2015 with data from the first half of 2015. The asymmetry in the Bitcoin market was still significant, suggesting that Bitcoin prices were driven more by negative than positive shocks;
Chen et al. (
2016) provided an econometric analysis of the CRIXindex family using data from 2014–2016. Using a variety of GARCH models, they found that the TGARCH (1, 1) model is the best fitting model for all sample data based on discrimination criteria such as the log likelihood, AIC and BIC. In addition, the DCC-GARCH (1, 1) was found to show volatility clustering and time varying covariances between three CRICindices;
Letra (
2016) used a GARCH (1, 1) model to analyse daily Bitcoin prices and search trends on Google, Wikipedia and tweets on Twitter. They found that Bitcoin prices were influenced by popularity, but also that web content and Bitcoin prices had some predictable power.
Dyhrberg (
2016a) applied the asymmetric GARCH methodology to explore the hedging capabilities of Bitcoin. It was shown that Bitcoin can be used as a hedge against stocks in the Financial Times Stock Exchange Index and against the American dollar in the short term.
Dyhrberg (
2016b) used GARCH models to explore the financial asset capabilities of Bitcoin. It was shown that Bitcoin has a place on the financial markets and in portfolio management as it can be classified as something in between gold and the American dollar, on a scale from pure medium of exchange advantages to pure store of value advantages.
Bouri et al. (
2017) used asymmetric GARCH models to investigate the relationship between price returns and volatility changes in the Bitcoin market around the price crash of 2013.
The aim of this paper is to provide GARCH-type modelling of the seven most popular cryptocurrencies. They are Bitcoin, Dash, Dogecoin, Litecoin, Maidsafecoin, Monero and Ripple. We fit twelve different GARCH-type models to the log returns of the exchange rates of each of these cryptocurrencies. The method of maximum likelihood was used for fitting. The goodness of fit was assessed in terms of five different criteria. Conclusions are drawn on the best fitting GARCH models, forecasts based on them and the ability of the models to estimate value at risk.
The contents of the paper are organized as follows.
Section 2 describes the data used and some summary statistics of the data described.
Section 3 describes the GARCH-type models fitted and the criteria used to assess their goodness of fit. The results of fitting the models and their discussion are given in
Section 4. Finally, some conclusions are noted in
Section 5.
2. Data
The data that we used in our analysis were the historical daily global price indices of particular cryptocurrencies and were extracted from the BNC2database from Quandl. In order to obtain the most accurate prices, the global indices were used as they are computed by using a weighted average of the price of each cryptocurrency, using prices from a number of different exchanges, as in
Chan et al. (
2017). Although our daily data begin only one day earlier than those in
Chan et al. (
2017), 22 June 2014, the end date is much later, on 17 May 2017. We obtained more up to date data for our analysis so that we could again analyse seven of the top fifteen cryptocurrencies, ranked by market capitalization, in May 2017. The most up to date (daily) market capitalization figures for all cryptocurrencies can be found online; see
CoinMarketCap (
2017). In May 2017, the top seven cryptocurrencies ranked by market capitalization were the same as those in February 2017 (
Chan et al. (
2017)) and include Bitcoin, Dash, LiteCoin, MaidSafeCoin, Monero, DogeCoin and Ripple. Other notable cryptocurrencies such as Ethereum, Ethereum Classic, Agur and NEMwere omitted due to the volume of available data. It should be noted that in May 2017, the seven cryptocurrencies represented 90 percent of the total market capitalization. However, due to the volatility of cryptocurrencies, the rankings of the respective cryptocurrencies has since changed. For a brief description of the seven cryptocurrencies, see
Chan et al. (
2017).
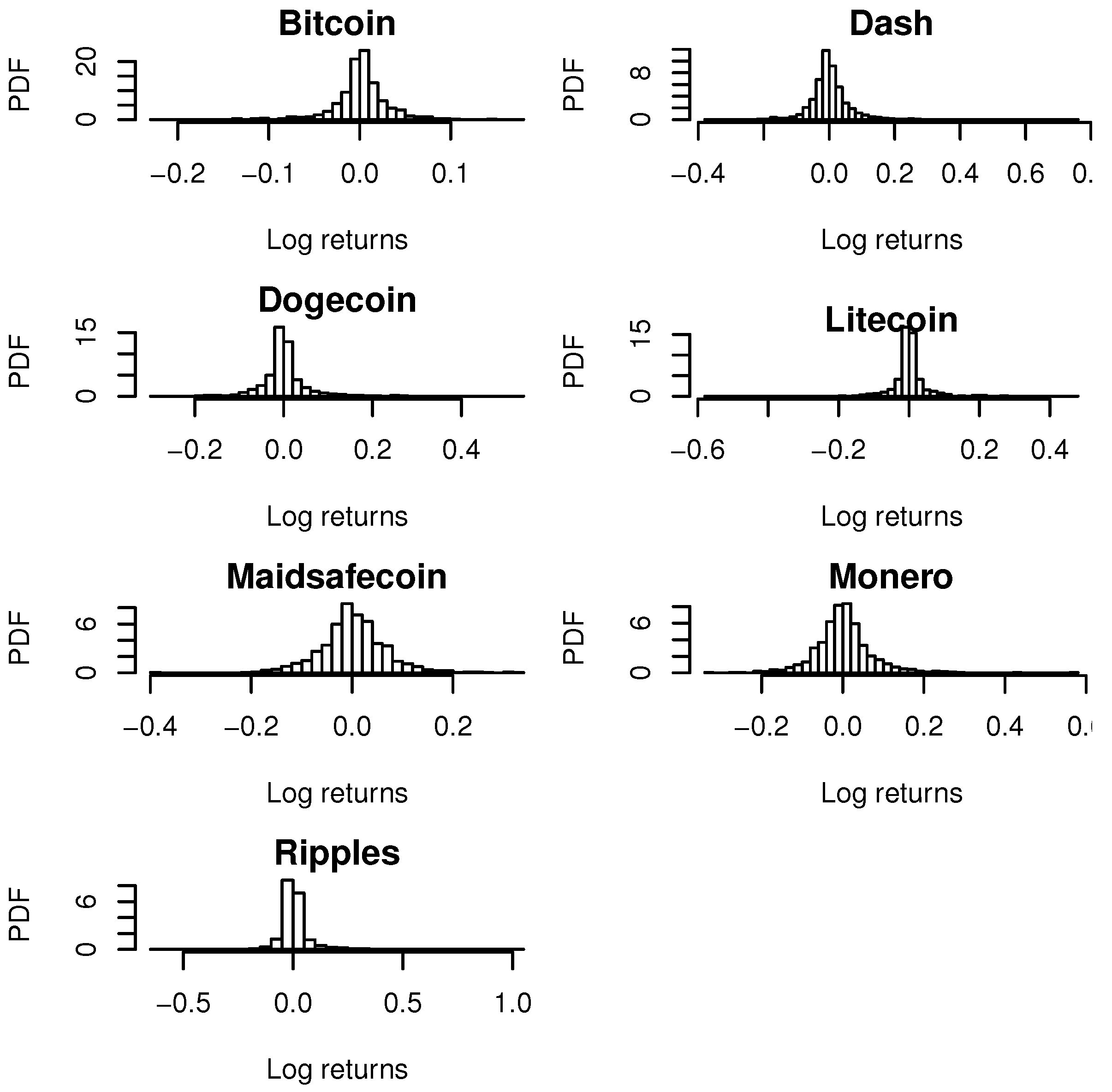
The summary statistics are the largest for Bitcoin, followed by Dash, Litecoin, Monero, Ripple, Maidsafecoin and Dogecoin (
Table 1). The log returns for each cryptocurrency are positively skewed. The log returns are heavy tailed with kurtosis greater than that of the normal distribution for Bitcoin, Dash, Litecoin and Ripple. The log returns are light tailed with kurtosis less than that of the normal distribution for Dogecoin, Maidsafecoin and Monero.
Figure 1 shows the histograms of the log returns of the daily market price indices for all exchanges trading in Bitcoin, Dash, Dogecoin, Litecoin, Maidsafecoin, Monero and Ripple. From the plots, we find that the log returns are more or less symmetrically distributed. Some histograms appear more peaked than others.
4. Results
We fitted SGARCH (1, 1), EGARCH (1, 1), GJRGARCH (1, 1), APARCH (1, 1), IGARCH (1, 1), CSGARCH (1, 1), GARCH (1, 1), TGARCH (1, 1), AVGARCH (1, 1), NGARCH (1, 1), NAGARCH (1, 1) and ALL GARCH (1, 1) models to the log returns of the exchange rates of Bitcoin, Dash, Dogecoin, Litecoin, Maidsafecoin, Monero and Ripple. The distribution of the innovation process were taken to be one of normal distribution, skew normal distribution, Student’s
t distribution, skew Student’s
t distribution, skew generalized error distribution, normal inverse Gaussian distribution, generalized hyperbolic distribution or Johnson’s SU distribution. The values of AIC, AICc, BIC, HQCand CAICare given in Tables 3–14 in
Chu et al. (
2017) for the fitted models.
The normal distribution gives the smallest values of AIC, AICc, BIC, HQC and CAIC for each cryptocurrency and each GARCH-type model. There are two exceptions however: for the TGARCH (1, 1) models fitted to Ripple, the skew normal distribution gives the smallest values of AIC, AICc, BIC, HQC and CAIC; for the AVGARCH (1, 1) models fitted to Ripple, the skew normal distribution gives the smallest values of AIC, AICc, BIC, HQC and CAIC.
Hence, the best fitting GARCH-type models are the ones with the innovation process following the normal distribution. The two exceptions are: the best of the TGARCH (1, 1) models fitted to Ripple is the one with the innovation process following the skew normal distribution; the best of the AVGARCH (1, 1) models fitted to Ripple is the one with the innovation process following the skew normal distribution.
Among the twelve best fitting GARCH type models, the IGARCH (1, 1) model with normal innovations gives the smallest values of AIC, AICc, BIC, HQC and CAIC for Bitcoin, Dash, Litecoin, Maidsafecoin and Monero. The GJRGARCH (1, 1) model with normal innovations gives the smallest values of AIC, AICc, BIC, HQC and CAIC for Dogecoin. The GARCH (1, 1) model with normal innovations gives the smallest values of AIC, AICc, BIC, HQC and CAIC for Ripple.
Hence, among all of the GARCH type models fitted, the IGARCH (1, 1) model gives the best fit for Bitcoin, Dash, Litecoin, Maidsafecoin and Monero; the GJRGARCH (1, 1) model gives the best fit for Dogecoin; the GARCH (1, 1) model gives the best fit for Ripple.
Figures 2–13 in
Chu et al. (
2017) show predicted values for the twenty five days following the end of each dataset. The predictions are given for each of the best fitting GARCH-type model. The predictions given are those based on the fitted model (red) and bootstrapping (black). The curves formed by the blue dots are the 5 percentiles, 25 percentiles, 75 percentiles and 95 percentiles of the bootstrap samples.
We see that the predictions based on the best fitting model and bootstrapping agree well. This is a sign of the goodness of fit of the models. The variation of the bootstrap-based percentile appears largest for Ripple for each GARCH-type model. The variation appears smallest for Bitcoin for each GARCH-type model.
We further checked the goodness of fit of the models by the one-sample Kolmogorov–Smirnov test. The p-values of this test for the seven best fitting SGARCH models were 0.238, 0.107, 0.290, 0.207, 0.228, 0.124 and 0.058. The corresponding p-values for the seven best fitting EGARCH models were 0.148, 0.333, 0.338, 0.116, 0.337, 0.369 and 0.229. The corresponding p-values for the seven best fitting GJRGARCH models were 0.345, 0.306, 0.352, 0.314, 0.286, 0.153 and 0.258. The corresponding p-values for the seven best fitting APARCH models were 0.091, 0.241, 0.109, 0.300, 0.394, 0.364 and 0.115. The corresponding p-values for the seven best fitting IGARCH models were 0.197, 0.118, 0.166, 0.207, 0.377, 0.238 and 0.370. The corresponding p-values for the seven best fitting CSGARCH models were 0.136, 0.298, 0.100, 0.073, 0.366, 0.167 and 0.279. The corresponding p-values for the seven best fitting GARCH models were 0.183, 0.217, 0.103, 0.236, 0.142, 0.392 and 0.129. The corresponding p-values for the seven best fitting TGARCH models were 0.087, 0.214, 0.280, 0.317, 0.219, 0.080 and 0.297. The corresponding p-values for the seven best fitting AVGARCH models were 0.071, 0.377, 0.210, 0.136, 0.120, 0.050 and 0.240. The corresponding p-values for the seven best fitting NGARCH models were 0.375, 0.231, 0.207, 0.139, 0.118, 0.236 and 0.341. The corresponding p-values for the seven best fitting NAGARCH models were 0.053, 0.267, 0.312, 0.281, 0.211, 0.051 and 0.335. The corresponding p-values for the seven best fitting ALLGARCH models were 0.241, 0.067, 0.304, 0.078, 0.155, 0.184 and 0.072. Hence, all of the best fitting models provide adequate fits at least at the five percent significance level.
Finally, we perform the unconditional and conditional coverage value at risk exceedances tests (
Christoffersen (
1998);
Christoffersen et al. (
2001)). The
p-values of the unconditional test for the best fitting models and various exceedance probabilities are given in
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8. The corresponding
p-values of the conditional test are given in the same tables. All of the
p-values are significant at the five percent level of significance. Hence, the best fitting models can be used to provide acceptable estimates of value at risk.
5. Conclusions
We find that the IGARCH and GJRGARCH models provide the best fits, in terms of modelling of the volatility in the most popular and largest cryptocurrencies. The IGARCH model falls within the standard GARCH framework and contains a conditional volatility process, which is highly persistent (with infinite memory), and this has been shown in the literature (
Caporale et al. (
2003)). However, although the IGARCH (1, 1) with normal innovations appears to give a good fit for numerous cryptocurrencies, it has been shown that this could stem from a structural change in the data, which may not be accounted for; i.e., a policy change (
Caporale et al. (
2003)). Therefore, more in depth analysis of the datasets may be required to confirm or deny possible structural change.
Due to the increasing demand and interest in cryptocurrencies, we believe that they should now be treated as more than just a novelty. Some cryptocurrencies have recently seen more growth than others, for example, Bitcoin, Ethereum, Litecoin and Ripple. However, there is still much discussion about whether cryptocurrencies, especially Bitcoin, should be classed as currencies, assets or investment vehicles, and this is a key topic in itself. Our analysis assumes that we are looking at cryptocurrencies in terms of financial assets, where most users are trading them for investment purposes: either as a long-term investment in new technology or looking to make a short-term profit. Investigating the volatility of cryptocurrencies is important in terms of financial investment like hedging or pricing instruments. Therefore, these results would be particularly useful in terms of portfolio and risk management and could help others make better informed decisions with regard to financial investments and the potential benefits and pitfalls of utilizing cryptocurrencies.
Our results show that cryptocurrencies such as Bitcoin, Ethereum, Litecoin and many others exhibit extreme volatility especially when we look at their inter-daily prices. This is suited for risk-seeking investors looking for a way to invest or enter into technology markets. Our results can also assist financial institutions.
Regulations and policies surrounding cryptocurrencies are being gradually tightened up by many countries; most recently, the U.S. Securities and Exchange Commission (SEC) has initiated plans to regulate the cryptocurrency exchange and all digital currencies. With the exponential growth of the initial coin offering to raise funds for start ups, we have seen China and South Korea (the biggest markets for cryptocurrencies) already regulating and banning such products. Overall, we believe in implementing more regulations and policy for cryptocurrencies as people are starting to see them as investment prospects.
A future work is to fit multivariate GARCH-type models to describe the joint behaviour of the exchange rates of Bitcoin, Dash, Dogecoin, Litecoin, Maidsafecoin, Monero and Ripple. This will require methodological, as well as empirical developments. Furthermore, we have used value at risk since it has been the most popular risk measure in finance. However, there is a shift of value at risk to stressed expected shortfall in the new Basel III regulation (see, for example,
Kinateder (
2016)). Therefore, another future work is to use expected shortfall instead of value at risk.