Portfolio Optimization and Mortgage Choice
Abstract
:1. Introduction
2. The Market Model
2.1. Realism and Limitations
3. Stylized Mortgage Products
3.1. A General Interest Rate Profile Design: The Fn-Loan
3.2. The Fixed Rate Mortgage
3.3. The Adjustable Rate Mortgage
4. Optimal Investment and Consumption
4.1. Solution to the Optimal Investment and Consumption Problem
4.2. Optimal Term Life Insurance
4.3. Optimal Consumption
5. Comparison between Optimization and Stylized Mortgage Products
5.1. The Investor Who Optimally Chooses the ARM
5.2. The Investor Who Optimally Chooses the FRM
5.3. A Moderate Investor
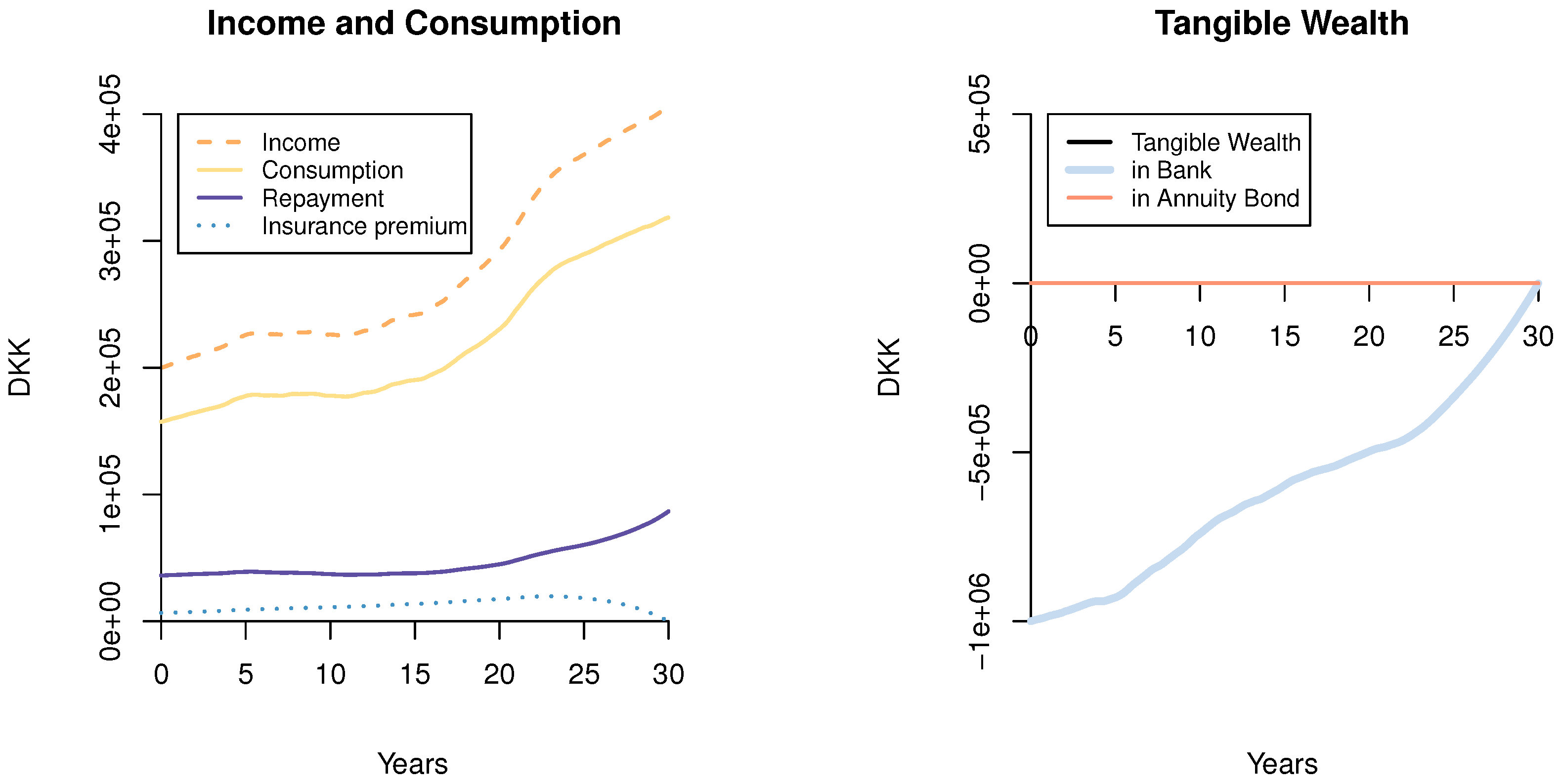
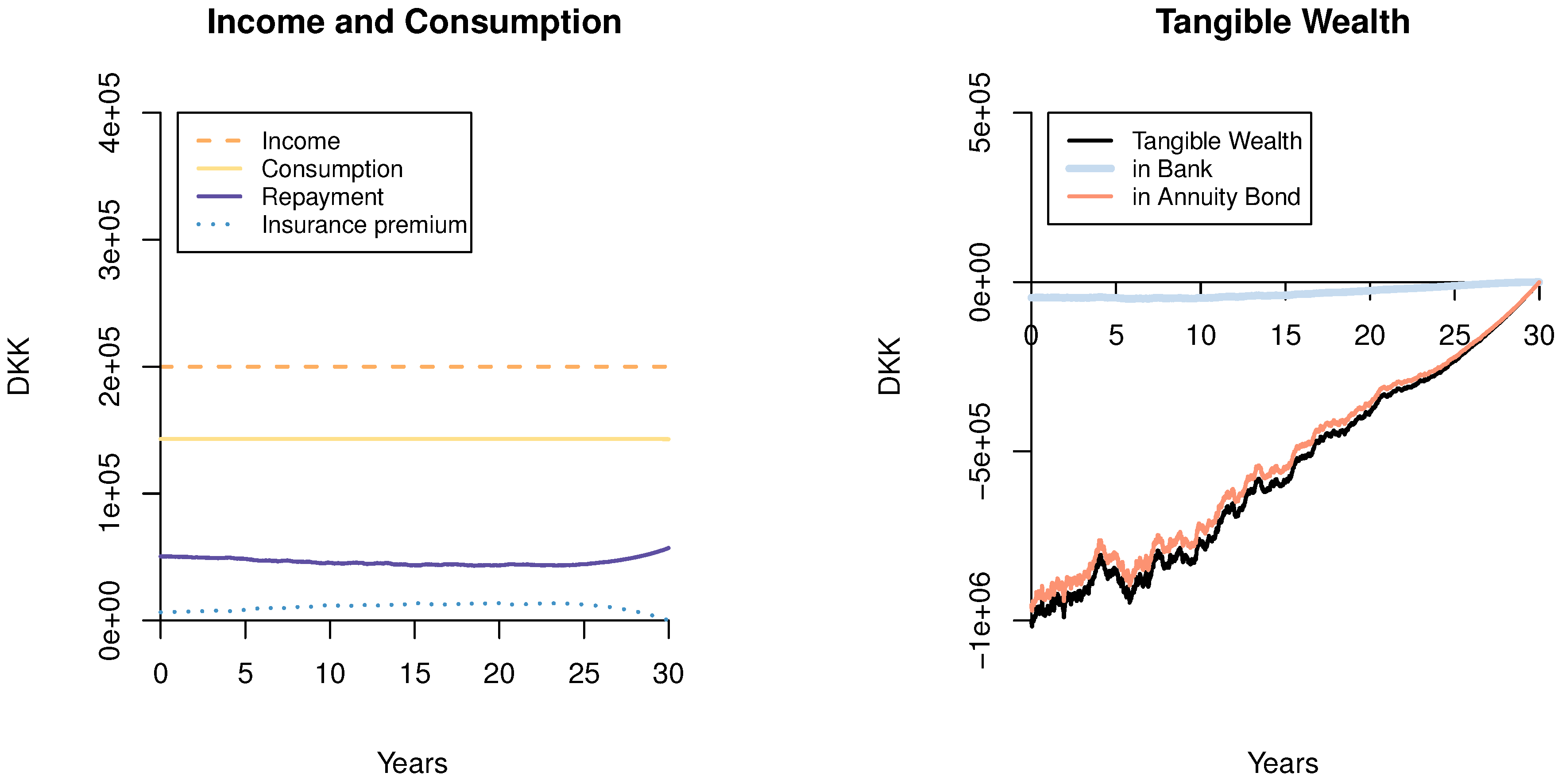
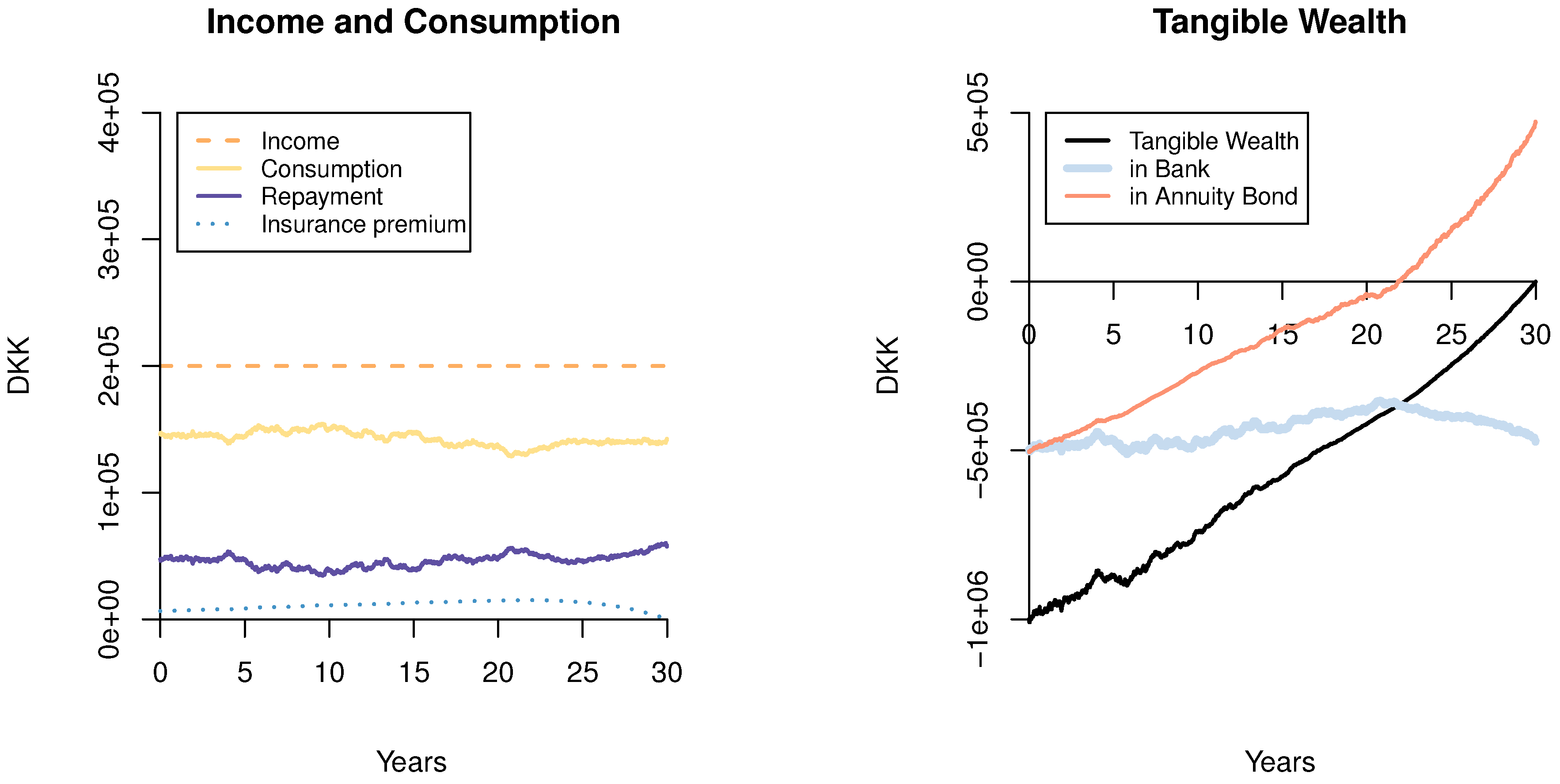
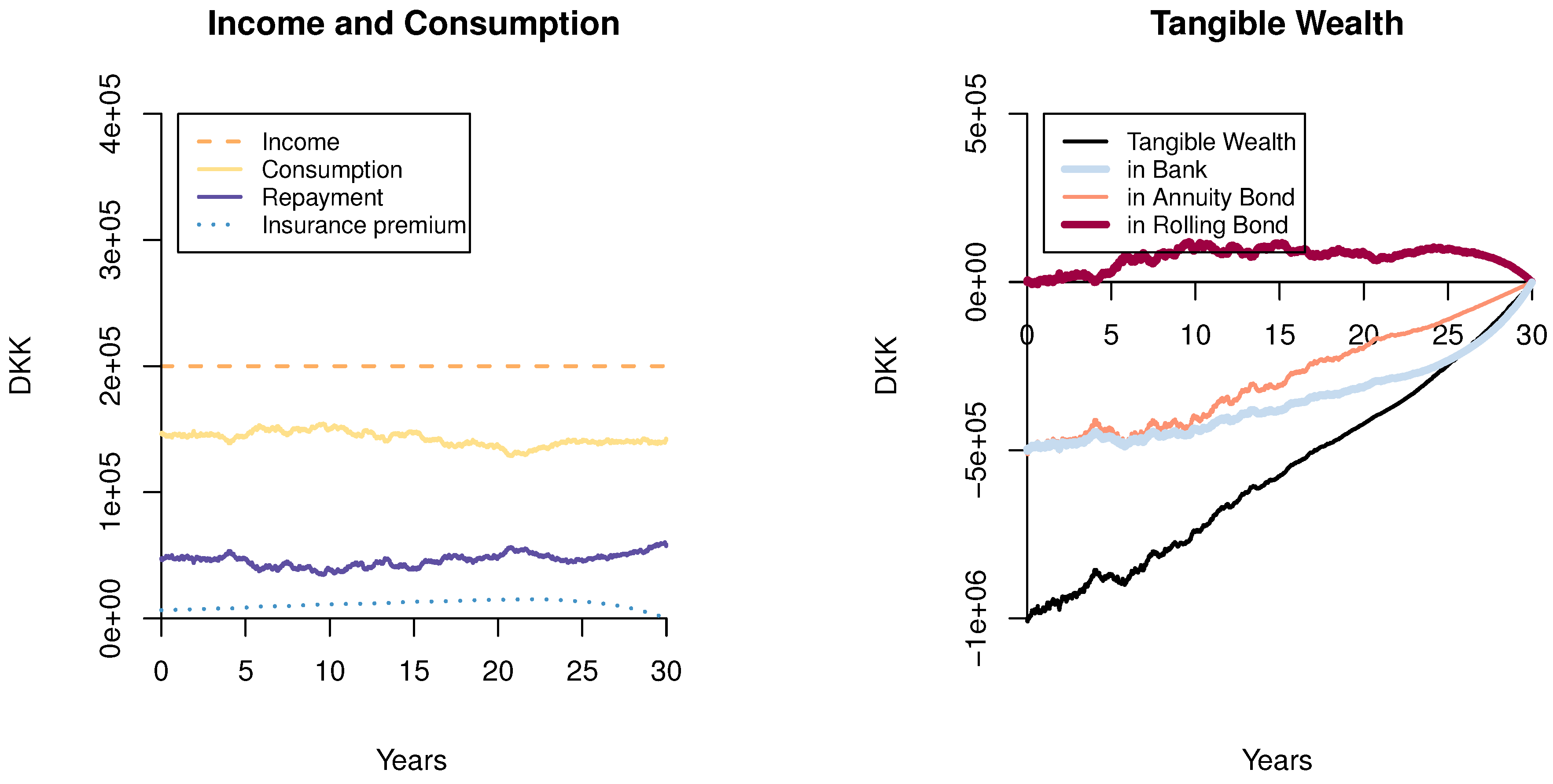
6. Numerical Examples
6.1. The ARM Investor with Mortality
6.2. The FRM Investor with Mortality
6.3. The Moderate FRM Investor
6.4. Effects of the Interest Rate Parameters
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ARM | Adjustable Rate Mortgage |
| FRM | Fixed Rate Mortgage |
| MLI | Mortgage Life Insurance |
| HJB | Hamilton–Jacobi–Bellman |
Appendix A. Solution to the HJB
- Step 1: Solve the optimization problem of the HJB equation
- Step 2: Insert the result from the optimization and derive the solution to the non-linear PDE (if possible)
- Step 3: Check that all of the assumptions made are able to apply a suitable verification theorem for the HJB applies. With the final step, it is ensured that it is in fact an optimal solution to the problem.
- Step 1:
- Given a solution V to the HJB-equation in (24), this would immediately lead to the optimal consumption:optimal investment:and optimal insurance:due to the restriction that at all times, .
- Step 2:
- Guessing the value function to be in the form of Equation (26) leads to the derivatives:giving optimal consumption:and optimal investment:which coincides perfectly with a simple version of Kraft and Munk [4], when . Determining the exact values of the function g is done by inserting the optimal strategies in the HJB equation in Equation (24). Substantial elimination, using among others the derivative structure of F, results in the following equation:Guessing g to be in the form of Equation (30) again allows deriving the functions and , and the results are given in Equations (32) and (31).
- Step 3:
- As mentioned in Korn and Kraft [25], the usual Lipschitz conditions and linear growth do not hold with the stochastic interest rate; that is why it is necessary to use an extension to the usual verification result of the HJB equation. Such an extension is provided in Kraft [3] and also applies with the addition of perfectly hedgeable labor income and mortality.
References
- R. Korn, and H. Kraft. “A stochastic control approach to portfolio problems with stochastic interest rates.” SIAM J. Control Optim. 40 (2002): 1250–1269. [Google Scholar] [CrossRef]
- C. Munk, and C. Sørensen. “Optimal consumption and investment strategies with stochastic interest rates.” J. Bank. Financ. 28 (2004): 1987–2013. [Google Scholar] [CrossRef]
- H. Kraft. “Optimal portfolios with stochastic short rate: Pitfalls when the short rate is non-Gaussian or the market price of risk is unbounded.” Int. J. Theor. Appl. Financ. 12 (2009): 767–796. [Google Scholar] [CrossRef]
- H. Kraft, and C. Munk. “Optimal housing, consumption, and investment decisions over the life cycle.” Manag. Sci. 57 (2011): 1025–1041. [Google Scholar] [CrossRef]
- J.Y. Campbell, and J.F. Cocco. “Household Risk Management and Optimal Mortgage Choice.” Q. J. Econ. 118 (2003): 1449–1494. [Google Scholar] [CrossRef] [Green Version]
- O. Van Hemert. “Household interest rate risk management.” Real Estate Econ. 38 (2010): 467–505. [Google Scholar] [CrossRef]
- A.M.B. Pedersen, A. Weissensteiner, and R. Poulsen. “Financial planning for young households.” Ann. Oper. Res. 205 (2013): 55–76. [Google Scholar] [CrossRef]
- Z. Bodie, R.C. Merton, and W.F. Samuelson. “Labor supply flexibility and portfolio choice in a life cycle model.” J. Econ. Dyn. Control 16 (1992): 427–449. [Google Scholar] [CrossRef]
- Nationalbanken. Fortsat Overvaegt af Rentefoelsomme Realkreditlaan. Technical Report; Copenhagen, Denmark: Nationalbanken, 2013. [Google Scholar]
- C. Badarinza, J.Y. Campbell, and T. Ramadorai. What Calls to Arms? International Evidence on Interest Rates and the Choice of Adjustable-Rate Mortgages. Technical Report; Cambridge, MA, USA: National Bureau of Economic Research, 2014. [Google Scholar]
- M. Svenstrup, and S. Willemann. “Reforming housing finance: Perspectives from Denmark.” J. Real Estate Res. 28 (2006): 105–130. [Google Scholar] [CrossRef]
- K. Haldrup. “On security of collateral in Danish mortgage finance: A formula of property rights, incentives and market mechanisms.” Eur. J. Law Econ., 2014, 1–29. [Google Scholar] [CrossRef]
- M.E. Yaari. “Uncertain lifetime, life insurance, and the theory of the consumer.” Rev. Econ. Stud. 22 (1965): 137–150. [Google Scholar] [CrossRef]
- S.F. Richard. “Optimal consumption, portfolio and life insurance rules for an uncertain lived individual in a continuous time model.” J. Financ. Econ. 2 (1975): 187–203. [Google Scholar] [CrossRef]
- S.J. Grossman, and G. Laroque. “Asset Pricing and Optimal Portfolio Choice in the Presence of Illiquid Durable Consumption Goods.” Econometrica 58 (1990): 25–51. [Google Scholar] [CrossRef]
- A. Damgaard, B. Fuglsbjerg, and C. Munk. “Optimal consumption and investment strategies with a perishable and an indivisible durable consumption good.” J. Econ. Dyn. Control 28 (2003): 209–253. [Google Scholar] [CrossRef]
- M. Flavin, and S. Nakagawa. “A Model of Housing in the Presence of Adjustment Costs: A Structural Interpretation of Habit Persistence.” Am. Econ. Rev. 98 (2008): 474–495. [Google Scholar] [CrossRef]
- S. Corradin, J.L. Fillat, and C. Vergara-Alert. “Optimal Portfolio Choice with Predictability in House Prices and Transaction Costs.” Rev. Financ. Stud. 27 (2014): 823–880. [Google Scholar] [CrossRef]
- J.B. Baesel, and N. Biger. “The Allocation of Risk: Some Implications of Fixed Versus Index-Linked Mortgages.” J. Financ. Quant. Anal. 15 (1980): 457–468. [Google Scholar] [CrossRef]
- M. Statman. “Fixed Rate or Index-Linked Mortgages from the Borrower’s Point of View: A Note.” J. Financ. Quant. Anal. 17 (1982): 451–457. [Google Scholar] [CrossRef]
- J. Alm, and J.R. Follain. “Alternative mortgage instruments, the tilt problem, and consumer welfare.” J. Financ. Quant. Anal. 19 (1984): 113–126. [Google Scholar] [CrossRef]
- J.K. Brueckner. “Borrower mobility, self-selection, and the relative prices of fixed- and adjustable-rate mortgages.” J. Financ. Int. 2 (1992): 401–421. [Google Scholar] [CrossRef]
- B. Villeneuve. “Mortgage life insurance: A rationale for a time limit in switching rights.” Math. Financ. Econ. 8 (2014): 473–487. [Google Scholar] [CrossRef]
- B. Coulibaly, and G. Li. “Choice of mortgage contracts: Evidence from the survey of consumer finances.” Real Estate Econ. 37 (2009): 659–673. [Google Scholar] [CrossRef]
- R. Korn, and H. Kraft. “On the stability of continuous-time portfolio problems with stochastic opportunity set.” Math. Financ. 14 (2004): 403–414. [Google Scholar] [CrossRef]
| Parameter | Variable | Value |
|---|---|---|
| Market parameters | ||
| Initial short rate | 0.02 | |
| Mean reversion rate | κ | 0.2 |
| Long-term mean level | 0.02 | |
| Interest volatility | 0.015 | |
| Volatility on rolling bond | 0.0736 | |
| Income parameters | ||
| Volatility | 0 | |
| Constant exponential rate | 0 | |
| Mortality parameters | ||
| Age-independent effect | ||
| Age effect (scale) | ||
| Age effect (exponential) | ||
| Investor parameters | ||
| Investment horizon | T | 30 |
| Age of investor | Age | 50 |
| Initial mortgage size (wealth) | million DKK |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordfang, M.-B.; Steffensen, M. Portfolio Optimization and Mortgage Choice. J. Risk Financial Manag. 2017, 10, 1. https://doi.org/10.3390/jrfm10010001
Nordfang M-B, Steffensen M. Portfolio Optimization and Mortgage Choice. Journal of Risk and Financial Management. 2017; 10(1):1. https://doi.org/10.3390/jrfm10010001
Chicago/Turabian StyleNordfang, Maj-Britt, and Mogens Steffensen. 2017. "Portfolio Optimization and Mortgage Choice" Journal of Risk and Financial Management 10, no. 1: 1. https://doi.org/10.3390/jrfm10010001
APA StyleNordfang, M.-B., & Steffensen, M. (2017). Portfolio Optimization and Mortgage Choice. Journal of Risk and Financial Management, 10(1), 1. https://doi.org/10.3390/jrfm10010001







