Lump Collision Phenomena to a Nonlinear Physical Model in Coastal Engineering
Abstract
:1. Introduction
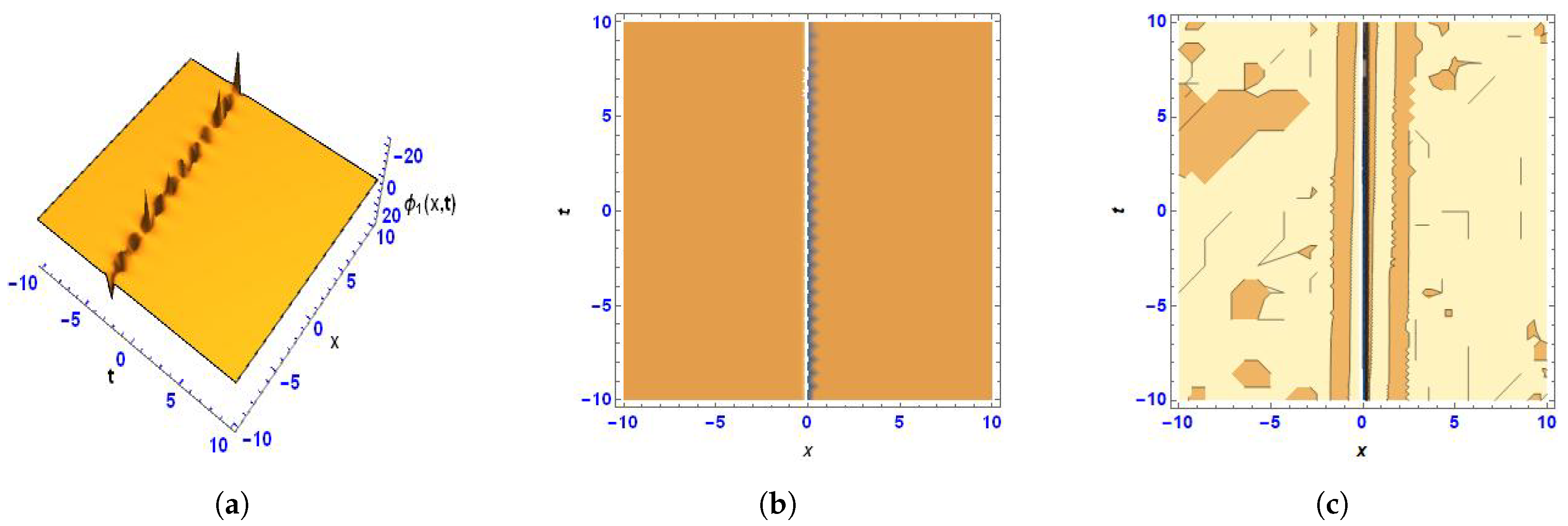
2. Breather Wave Solution
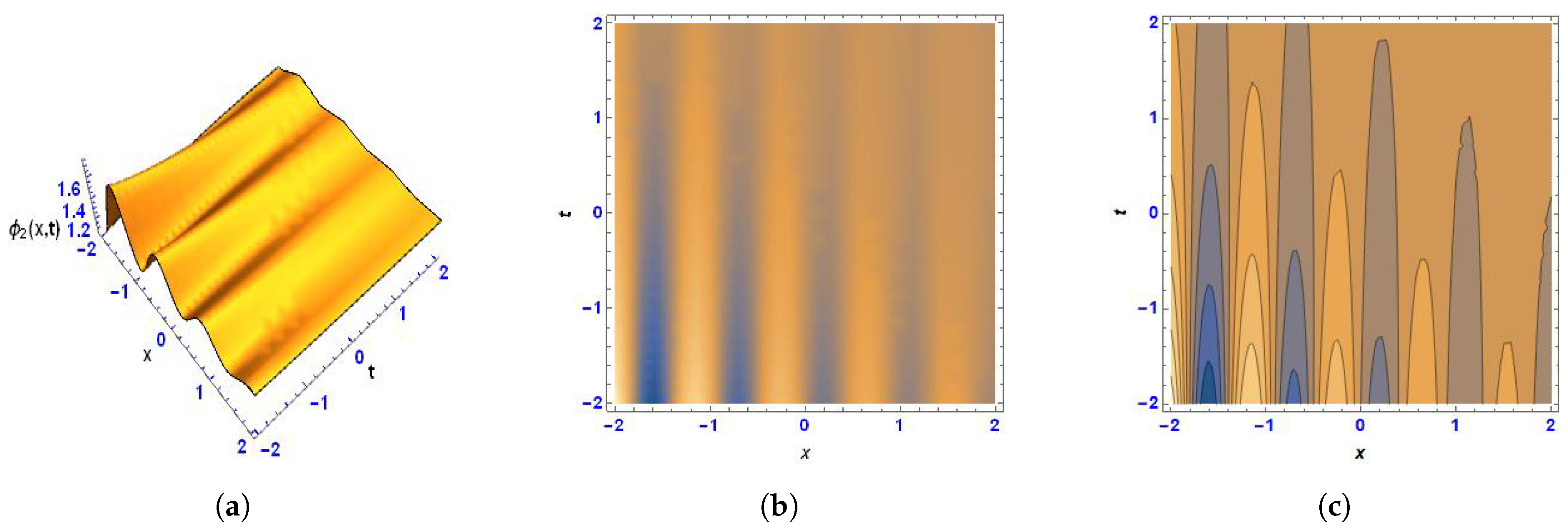
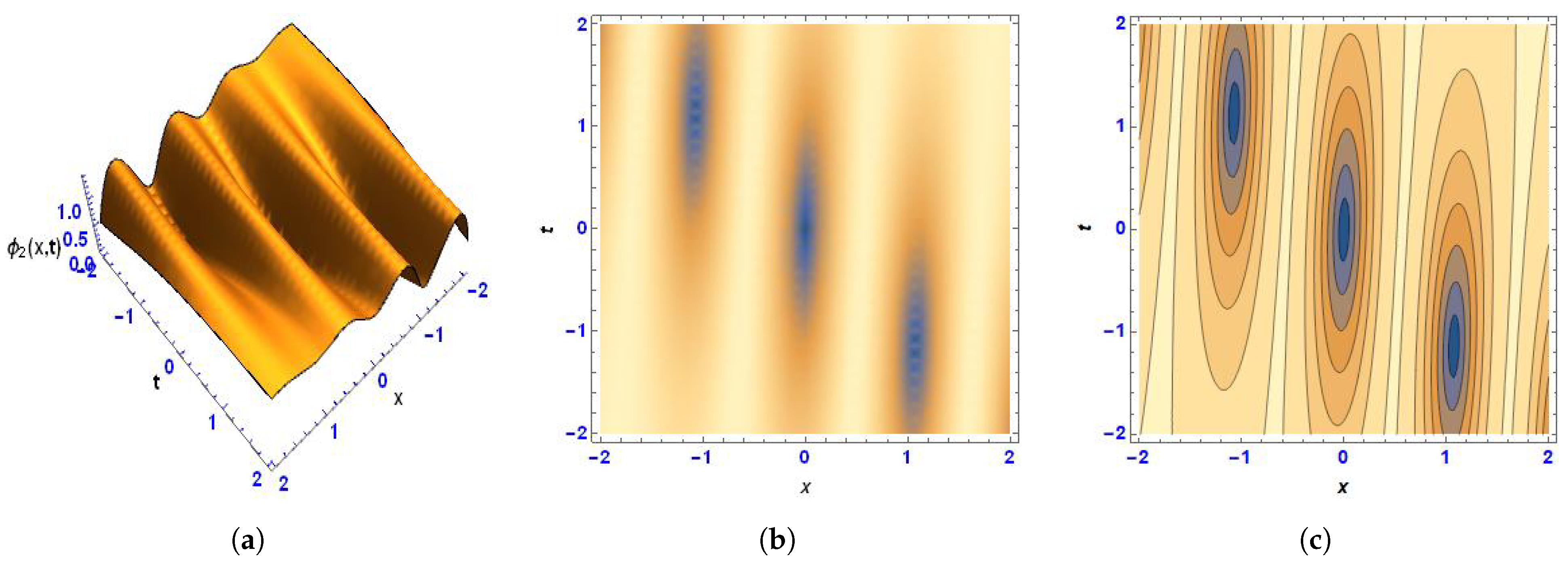
3. Lump-Periodic Solution
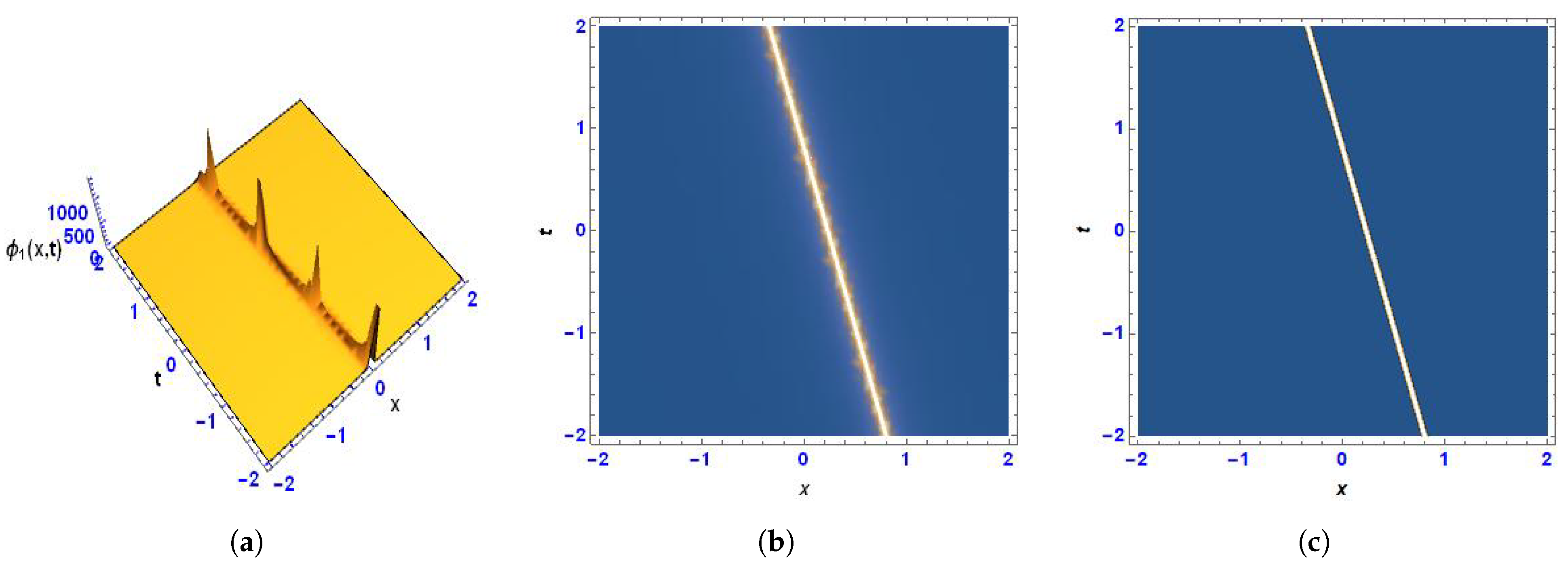
4. Two-Wave Solution
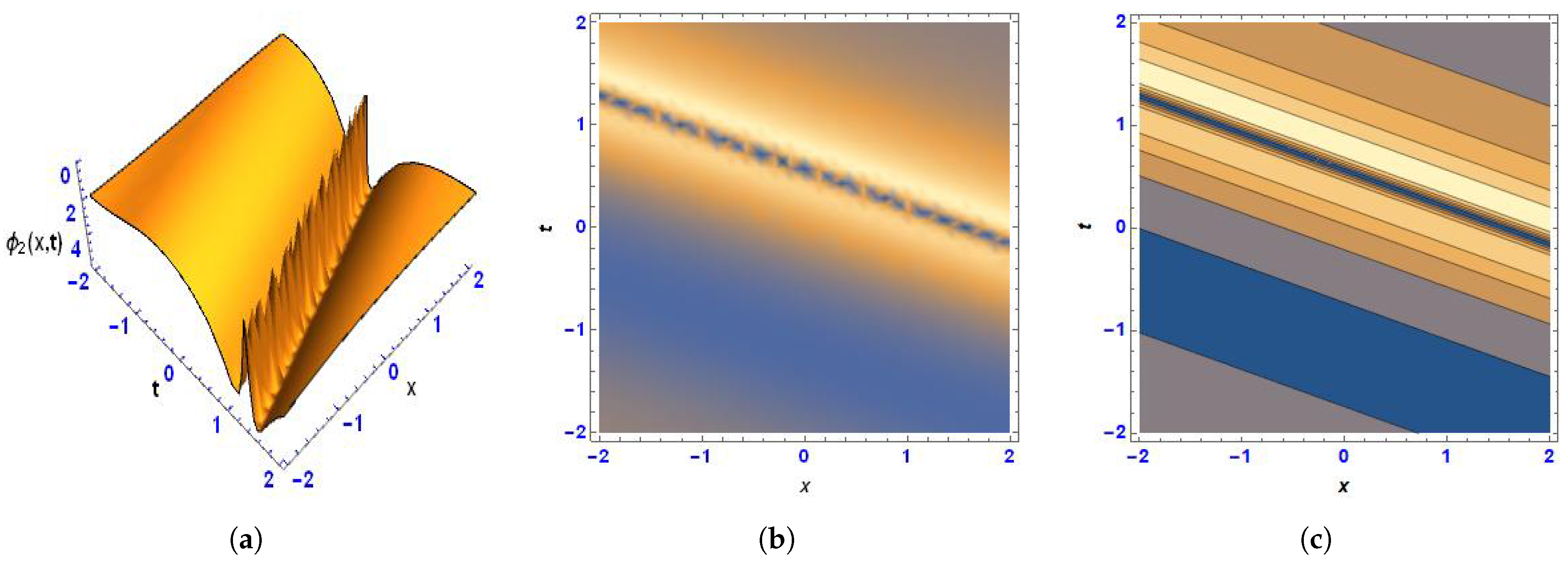
5. Physical Interpretation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdel-Khalek, S. Nonautonomous complex wave solutions to the (2+1)-dimensional variable-coefficients nonlinear Chiral Schrodinger equation. Results Phys. 2020, 19, 103604. [Google Scholar] [CrossRef]
- Yusuf, A.; Sulaiman, T.A.; Khalil, E.M. Construction of multi-wave complexiton solutions of the Kadomtsev-Petviashvili equation via two efficient analyzing techniques. Results Phys. 2021, 21, 103775. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.; Mohd, N.H. The modified simple equation method for exact and solitary wave solutions of nonlinear evolution equation. ISRN Math. Phys. 2013, 2013, 146704. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, N. Global well-posedness for the 2D Boussinesq equations with partial temperaturedependent dissipative terms. J. Math. Anal. Appl. 2018, 466, 351–372. [Google Scholar] [CrossRef]
- Gala, S.; Ragusa, M.A. Logarithmically improved regularity criterion for the Boussinesq equations in Besov spaces with negative indices. Appl. Anal. 2016, 95, 1271–1279. [Google Scholar] [CrossRef]
- Gala, S.; Guo, Z.; Ragusa, M.A. A remark on the regularity criterion of Boussinesq equations with zero heat conductivity. Appl. Math. Lett. 2014, 27, 70–73. [Google Scholar] [CrossRef]
- Bianca, C.; Pappalardo, F.; Motta, S.; Ragusa, M.A. Persistence analysis in a Kolmogorov-type model for cancer-immune system competition. AIP Conf. Proc. 2013, 1558, 1797–1800. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Alquran, A.; Syam, I. A reliable study of new nonlinear equation: Two-mode Kuramoto-Sivashinsky. Int. J. Appl. Comput. Math. 2018, 4, 64. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Ali, M. A numerical study on weak-dissipative two-mode perturbed Burgers’ and Ostrovsky models: Right-left moving waves. Eur. Phys. J. Plus 2018, 133, 164. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Momani, S.; Biswas, A. Dark and singular optical solutions with dual-mode nonlinear Schrodinger’s equation and Kerr-law nonlinearity. Optik 2018, 172, 822–825. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I. Multiplicative of dual-waves generated upon increasing the phase velocity parameter embedded in dual-mode Schrodinger with nonlinearity Kerr laws. Nonlinear Dyn. 2019, 96, 115–121. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Al-Shara, S.; Awawdeh, F.; Alquran, M. Variable coefficient equations of the Kadomtsev–Petviashvili hierarchy: Multiple soliton solutions and singular multiple soliton solutions. Phys. Scr. 2012, 85, 035001. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, H.M.; Al-Shara, S.; Awawdeh, F. A New Simplified Bilinear Method for the N-Soliton Solutions for a Generalized FmKdV Equation with Time-Dependent Variable Coefficients. IJNSN 2015, 16, 259–269. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Awawdeh, F.; Al-Shara, S.; Alquran, M.; Momani, S. Controllable dynamical behaviors and the analysis of fractal burgers hierarchy with the full effects of inhomogeneities of media. Rom. J. Phys. 2015, 60, 324–343. [Google Scholar]
- Ma, W.X.; Qin, Z.; Lu, X. Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn. 2016, 84, 923–931. [Google Scholar] [CrossRef]
- Yong, X.; Ma, W.X.; Huang, Y.; Liu, Y. Lump solutions to the Kadomtsev-Petviashvili I equation with a self-consistent source. Comput. Math. Appl. 2018, 75, 3414–3419. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X. Abundant lump-type solutions of the Jimbo-Miwa equation in (3+1)-dimensions. Comput. Math. Appl. 2017, 73, 220–225. [Google Scholar] [CrossRef]
- Tang, Y.; Tao, S.; Guan, Q. Lump solitons and the interaction phenomena of them for two classes of nonlinear evolution equations. Comput. Math. Appl. 2016, 72, 2334–2342. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X.; Qin, Z. Lump and lump-soliton solutions to the (2+1)dimensional Ito equation. Anal. Math. Phys. 2018, 8, 427–436. [Google Scholar] [CrossRef]
- Ma, W.X. Lump-type solutions to the (3+1)-dimensional Jimbo-Miwa equation. Int. J. Nonlinear Sci. Numer. Simul. 2017, 17, 355–359. [Google Scholar] [CrossRef]
- Ma, W.X. Lump solutions to the Kadomtsev-Petviashvili equation. Phys. Lett. A 2015, 379, 1975–1978. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X. Lump solutions to the BKP equation by symbolic computation. Int. J. Mod. Phys. B 2016, 30, 1640028. [Google Scholar] [CrossRef] [Green Version]
- Kauo, D.J. The lump solutions and the Backlund transformation for the three-dimensional three-wave resonant interaction. J. Math. Phys. 1981, 22, 1176–1181. [Google Scholar]
- Zhang, H.Q.; Ma, W.X. Lump solutions to the (2+1)-dimensional Sawada-Kotera equation. Nonlinear Dyn. 2017, 87, 2305–2310. [Google Scholar] [CrossRef]
- Chen, S.T.; Ma, W.X. Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation. Front. Math. China 2018, 13, 525–534. [Google Scholar] [CrossRef]
- Ma, W.X. A search for lump solutions to a combined fourth order nonlinear PDE in (2+1)-dimensions. J. Appl. Anal. Comput. 2019, 9, 1319–1332. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, Y.; Dougherty, R. Lump-type solutions to nonlinear differential equations derived from generalized bilinear equations. Int. J. Mod. Phys. B 2016, 30, 1640018. [Google Scholar] [CrossRef]
- Zhao, H.Q.; Ma, W.X. Mixed lump-kink solutions to the KP equation. Comput. Math. Appl. 2017, 74, 1399–1405. [Google Scholar] [CrossRef]
- Yusuf, A.; Sulaiman, T.A.; Inc, M.; Bayram, M. Breather wave, lump-periodic solutions and some other interaction phenomena to the Caudrey–Dodd–Gibbon equation. Eur. Phys. J. Plus 2020, 135, 563. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Atangana, A. New lump, lump-kink, breather waves and other interaction solutions to the (3+1)dimensional soliton equation. Commun. Theor. Phys. 2020, 72, 085004. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A. Dynamics of lump periodic and breather waves solutions with variable coefficients in liquid with gas bubbles. Waves Random Complex Media 2021, 1–14. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Alquran, M. Dynamics of optical solitons and nonautonomous complex wave solutions to the nonlinear Schrodinger equation with variable coefficients. Nonlinear Dyn. 2021, 104, 639–648. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. Investigation into the Explicit Solutions of the Integrable (2+1)—Dimensional Maccari System via the Variational Approach. Axioms 2022, 11, 234. [Google Scholar] [CrossRef]
- Wang, K.J. Traveling wave solutions of the Gardner equation in dusty plasmas. Results Phys. 2022, 33, 105207. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D. Exact traveling wave solutions for the system of the ion sound and Langmuir waves by using three effective methods. Results Phys. 2022, 35, 105390. [Google Scholar] [CrossRef]
- Wang, K.J. Abundant exact soliton solutions to the Fokas system. Optik 2022, 249, 168265. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D.; Shi, F. Abundant exact travelıng wave solutıons to the local fractıonal (3+1)-dimensional Boiti–Leon–Manna–pempinelli equation. Fractals 2022, 30, 2250064. [Google Scholar] [CrossRef]
- Wei, M.; Cai, J. The Exact Rational Solutions to a Shallow Water Wave-Like Equation by Generalized Bilinear Method. J. Appl. Math. Phys. 2017, 5, 715–721. [Google Scholar] [CrossRef] [Green Version]
- Vreugdenhil, C.B. Numerical Methods for Shallow-Water Flow, Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Method for solving the sine-Gordon equation. Phys. Rev. Lett. 1973, 30, 1262–1264. [Google Scholar] [CrossRef]
- Chakravorty, P. What Is a Signal? [Lecture Notes]. IEEE Signal Process. Mag. 1982, 35, 175–177. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sulaiman, T.A.; Yusuf, A.; Alshomrani, A.S.; Baleanu, D. Lump Collision Phenomena to a Nonlinear Physical Model in Coastal Engineering. Mathematics 2022, 10, 2805. https://doi.org/10.3390/math10152805
Sulaiman TA, Yusuf A, Alshomrani AS, Baleanu D. Lump Collision Phenomena to a Nonlinear Physical Model in Coastal Engineering. Mathematics. 2022; 10(15):2805. https://doi.org/10.3390/math10152805
Chicago/Turabian StyleSulaiman, Tukur Abdulkadir, Abdullahi Yusuf, Ali Saleh Alshomrani, and Dumitru Baleanu. 2022. "Lump Collision Phenomena to a Nonlinear Physical Model in Coastal Engineering" Mathematics 10, no. 15: 2805. https://doi.org/10.3390/math10152805






