Risk Assessment and Hierarchical Risk Management of Enterprises in Chemical Industrial Parks Based on Catastrophe Theory
Abstract
:1. Introduction
| Method | Study (year) | Detial |
|---|---|---|
| Material risk analysis approach | Cave et al. (1997) [4] | Defined the environmental hazard index (EHI) and applied it to the chemical industry for a case study of the degree of environmental impacts. |
| Gunasekera and Edwards (2003) [5] | Employed the atmospheric hazard index (AHI) for comparative analysis of environmental risks of the same chemical products. | |
| production process safety assessment approach | Shah et al. (2003) [6] | Constructed a hierarchy of safety, health and environment, which involves multiple layers of material, reaction, devices, and safety technology for comparison of inherent risks in different production processes. |
| Faisal et al. (2005) [7] | Proposed a comprehensive inherent safety index evaluation method that considers the economic evaluation and risk assessment for evaluation of the inherent level of risk associated with production processes. | |
| Wei et al. (2008) [8] | Suggested the use of a layer of protection analysis (LOPA) and applied it to risk assessment of chemical reactions during hydroxylamine production. | |
| Environmental risk index method | Achour et al. (2005) [9] | Established the material quantitative index of process flow and the inherent risk index of risk source for environmental risk assessment of production processes. |
| Jia et al. (2010) [10] | Constructed a comprehensive evaluation index of accidental environmental risks from petrochemical enterprises based on the hazardous materials present, production processes, and enterprise distribution. | |
| EU (1993) [11] (2003) [12] | Applyed a comprehensive risk assessment approach that considers environmental and human exposure and evaluates the risks caused by the exposure. | |
| Huang et al. (2011) [13] | Established a CIP risk assessment index system that considers risk at both the level of the CIP and relevant enterprises, and then conducted a case study in Jiangsu Province, China. |
2. Methods
2.1. Catastrophe Theory
| Category | Potential function | Bifurcation set | Normalization formula | Dimension of control variables |
|---|---|---|---|---|
| Fold model | f(x) = x3 + ax | a = −3x2 | 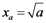 | 1 |
| Cusp model | f(x) = x4 + ax2 + bx | a = −6x2, b = 8x3 | 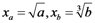 | 2 |
| Swallowtail model | f(x) = x5 + ax3 + bx2 + cx | a = −6x2, b = 8x3 | 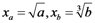 | 3 |
| Butterfly model | f(x) = x6 + ax4 + bx3 + cx2 + dx | a = −10x2, b = 20x3 | 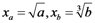 | 4 |
2.2. Establishment of A Catastrophe Model for Accidental Risk Assessment of Chemical Enterprises
2.2.1. Index System Establishment
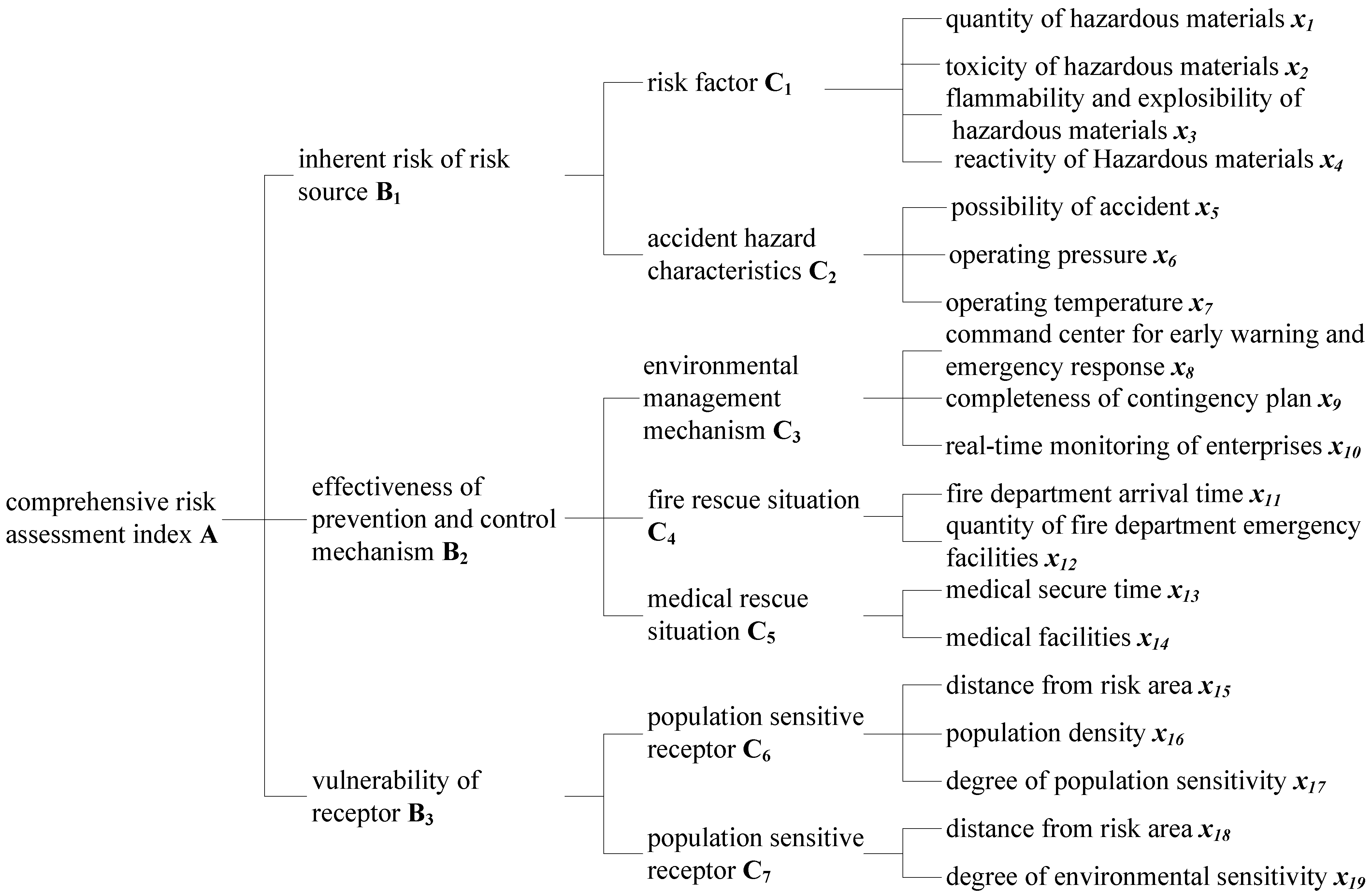
2.2.2. Determination of Primary and Secondary Status of Variable Indices in Each Layer
2.2.3. Control Variable Standardization


2.2.4. Risk Level Transformation
| Risk level | Relative degree of membership obtained by catastrophe model | Corresponding ordinary-use values |
|---|---|---|
| Very safe | >0.9884 | >0.8 |
| Safe | 0.9884–0.9738 | 0.8–0.6 |
| Generally recognized as safe (GRAS) | 0.9738–0.9539 | 0.6–0.4 |
| Unsafe | 0.9539–0.9213 | 0.4–0.2 |
| Very unsafe | <0.9213 | <0.2 |
3. Examples
3.1. Study Site

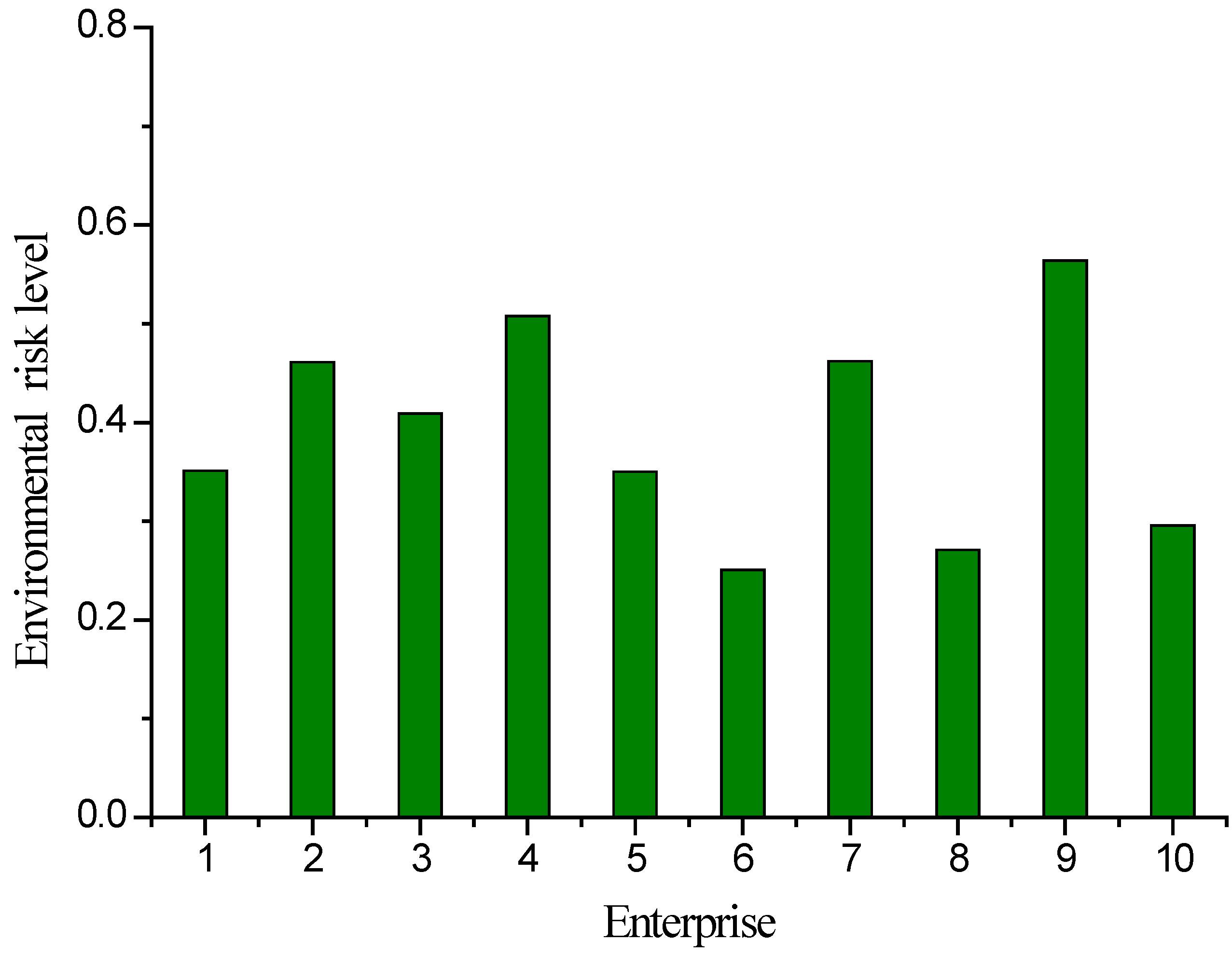
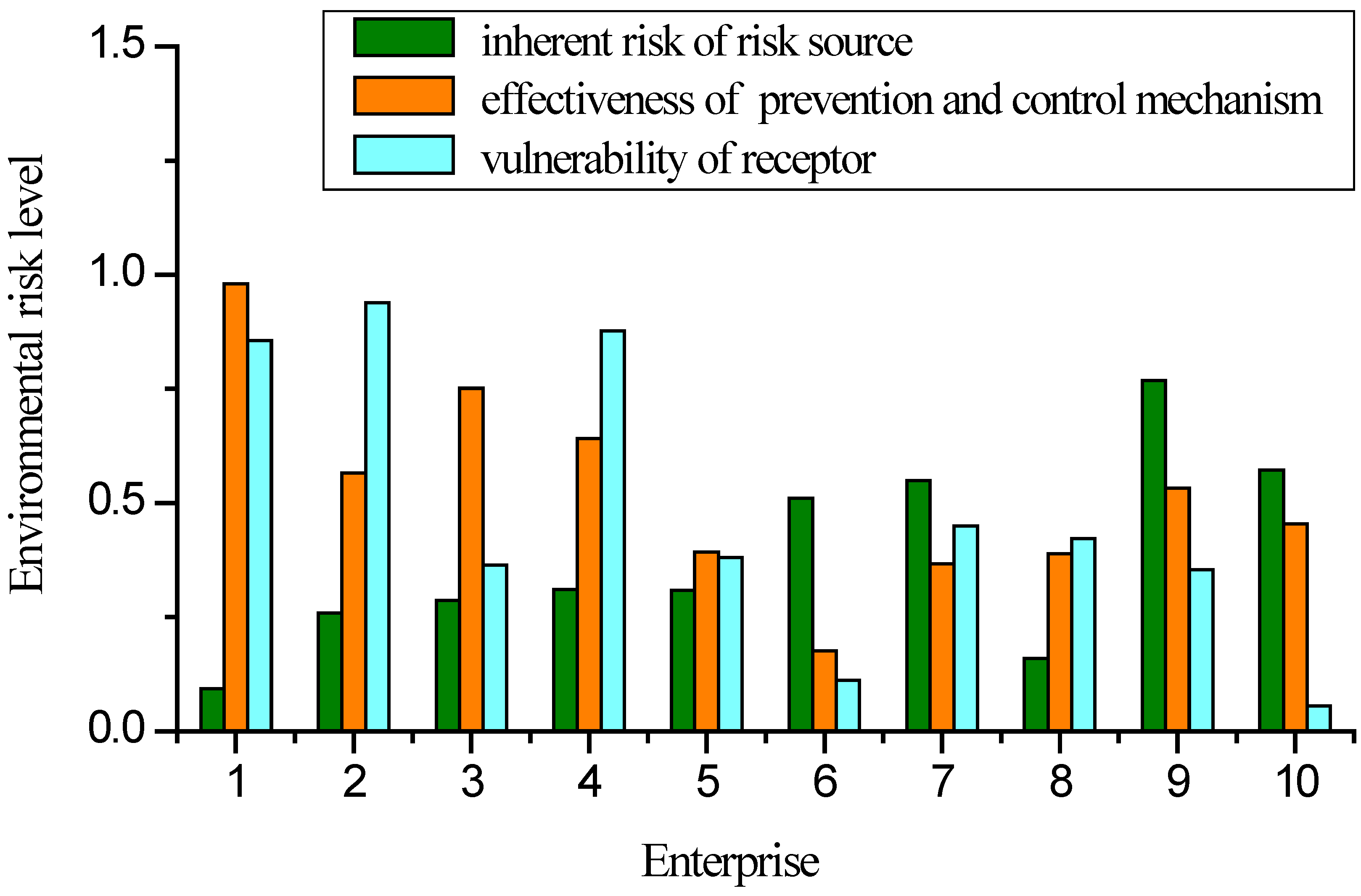
3.2. Catastrophe Theory Application
| NO. | Goal | Criteria | Sub-criteria | NO. | Goal | Criteria | Sub-criteria | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A = 0.9481 | B1 | 0.7256 | C1 | 0.6331 | 6 | A = 0.9322 | B1 | 0.9120 | C1 | 0.9075 |
| C2 | 0.2817 | C2 | 0.6614 | ||||||||
| B2 | 0.9961 | C3 | 0.9769 | B2 | 0.7874 | C3 | 0.7889 | ||||
| C4 | 1.0000 | C4 | 0.3150 | ||||||||
| C5 | 1.0000 | C5 | 0.3969 | ||||||||
| B3 | 0.9749 | C6 | 0.9710 | B3 | 0.7106 | C6 | 0.3333 | ||||
| C7 | 0.8969 | C7 | 0.6010 | ||||||||
| 2 | A = 0.9612 | B1 | 0.8324 | C1 | 0.6686 | 7 | A = 0.9613 | B1 | 0.9211 | C1 | 0.7093 |
| C2 | 0.6080 | C2 | 1.0000 | ||||||||
| B2 | 0.9239 | C3 | 0.8272 | B2 | 0.8706 | C3 | 0.7889 | ||||
| C4 | 0.8078 | C4 | 0.5650 | ||||||||
| C5 | 0.7504 | C5 | 0.6469 | ||||||||
| B3 | 0.9890 | C6 | 0.9564 | B3 | 0.8823 | C6 | 0.8476 | ||||
| C7 | 1.0000 | C7 | 0.6010 | ||||||||
| 3 | A = 0.9554 | B1 | 0.8436 | C1 | 0.7498 | 8 | A = 0.9357 | B1 | 0.7797 | C1 | 0.7500 |
| C2 | 0.5539 | C2 | 0.3333 | ||||||||
| B2 | 0.9605 | C3 | 0.9024 | B2 | 0.8777 | C3 | 0.8272 | ||||
| C4 | 0.8873 | C4 | 0.5650 | ||||||||
| C5 | 0.8873 | C5 | 0.6469 | ||||||||
| B3 | 0.8536 | C6 | 0.5003 | B3 | 0.8735 | C6 | 0.8155 | ||||
| C7 | 1.0000 | C7 | 0.2041 | ||||||||
| 4 | A = 0.9659 | B1 | 0.8531 | C1 | 0.7500 | 9 | A = 0.9710 | B1 | 0.9636 | C1 | 0.8595 |
| C2 | 0.5932 | C2 | 1.0000 | ||||||||
| B2 | 0.9399 | C3 | 0.8272 | B2 | 0.9163 | C3 | 0.8272 | ||||
| C4 | 0.8299 | C4 | 0.7504 | ||||||||
| C5 | 0.8873 | C5 | 0.7504 | ||||||||
| B3 | 0.9785 | C6 | 0.9855 | B3 | 0.8499 | C6 | 0.9312 | ||||
| C7 | 0.8969 | C7 | 0.0000 | ||||||||
| 5 | A = 0.9479 | B1 | 0.8519 | C1 | 0.7175 | 10 | A = 0.9400 | B1 | 0.9260 | C1 | 0.7259 |
| C2 | 0.6288 | C2 | 1.0000 | ||||||||
| B2 | 0.8788 | C3 | 0.8336 | B2 | 0.8968 | C3 | 0.8272 | ||||
| C4 | 0.5650 | C4 | 0.6469 | ||||||||
| C5 | 0.6469 | C5 | 0.7043 | ||||||||
| B3 | 0.8596 | C6 | 0.7662 | B3 | 0.6370 | C6 | 0.4694 | ||||
| C7 | 0.6010 | C7 | 0.2041 | ||||||||
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Li, F.Y.; Bi, J.; Huang, L.; Qu, C.S.; Yang, J.; Bu, Q.M. Mapping human vulnerability to chemical accidents in the vicinity of chemical industry parks. J. Hazard. Mater. 2010, 179, 247–255. [Google Scholar]
- Xu, M.; Wu, Z.Z. Three-stage optimal method of land-use safety planning for chemical industry park. Procedia Eng. 2011, 26, 1844–1850. [Google Scholar] [CrossRef]
- Ding, J.S.; Hua, W.Q. Featured chemical industrial parks in China: History, current status and outlook. Resour. Conserv. Recycl. 2012, 63, 43–53. [Google Scholar] [CrossRef]
- Cave, S.R.; Edwards, D.W. Chemical process route selection based on assessment of inherent environmental hazard. Comput. Chem. Eng. 1997, 21, S965–S970. [Google Scholar]
- Gunasekera, M.Y.; Edwards, D.W. Estimating the environmental impact of catastrophic chemical releases to the atmosphere an index method for ranking alternative chemical process route. Saf. Environ. Prot. 2003, 81, 463–474. [Google Scholar] [CrossRef]
- Shah, S.; Fischer, U.; Hungerbühler, K. A hierarchical approach for the evaluation of chemical process aspects from the perspective of inherent safety. Process Saf. Environ. Prot. 2003, 81, 430–443. [Google Scholar] [CrossRef]
- Faisal, I.K.; Paul, R.A. I2SI: A comprehensive quantitative tool for inherent safety and cost evaluation. J. Loss Prev. Process Ind. 2005, 18, 310–326. [Google Scholar] [CrossRef]
- Wei, C.Y.; Rogers, W.J.; Mannan, M.S. Layer of protection analysis for reactive chemical risk assessment. J. Hazard. Mater. 2008, 159, 19–24. [Google Scholar] [CrossRef]
- Achour, M.H.; Haroun, A.E.; Schult, C.J.; Gasem, K.A.M. A new method to assess the environmental risk of a chemical process. Chem. Eng. Process. 2005, 44, 901–909. [Google Scholar] [CrossRef]
- Jia, Q.; Huang, L.; Yuan, Z.W.; Zhang, X.F. Assessment and management of accidental environmental risks in the petrochemical industry. Acta. Sci. Circumst. 2010, 30, 1510–1517. [Google Scholar]
- European Council. Council regulation (EEC) No 793/93 of 23 March 1993 on the evaluation and control of the risks of existing substances. Off. J. 1993, L84, 1–75.
- European Commission, Technical Guidance Document on Risk Assessment in Support of Commission Directive 93/67/EEC on Risk Assessment for New Notified Substances and Commission Regulation (EC) No 1488/94 on Risk Assessment for Existing Substances, and Directive 98/8/EC of the European Parliament and of the Council Concerning the Placing of Biocidal Products on the Market—Part I; Institute for Health and Consumer Protection, European Chemicals Bureau, European Communities: Varese, Italy, 2003.
- Huang, L.; Wan, W.B.; Li, F.Y.; Li, B.; Yang, J.; Bi, J. A two-scale system to identify environmental risk of chemical industry clusters. J. Hazard. Mater. 2011, 186, 247–255. [Google Scholar] [CrossRef]
- Zeeman, E.C. Catastrophe theory. Sci. Am. 1976, 234, 65–83. [Google Scholar] [CrossRef]
- Zhang, T.J.; Ren, S.X.; Li, S.G.; Zhang, T.C.; Xu, H.J. Application of the catastrophe progression method in predicting coal and gas outburst. Min. Sci. Technol. 2009, 19, 430–434. [Google Scholar]
- Su, S.L.; Li, D.; Yu, X.; Zhang, Z.H.; Zhang, Q.; Xiao, R.; Zhi, J.J.; Wu, J.P. Assessing land ecological security in Shanghai (China) based on catastrophe theory. Stoch. Environ. Res. Risk. Assess. 2011, 25, 737–746. [Google Scholar] [CrossRef]
- Wang, W.J.; Liu, S.L.; Zhang, S.S.; Chen, J.W. Assessment of a model of pollution disaster in near-shore coastal waters based on catastrophe theory. Ecol. Model. 2011, 222, 307–312. [Google Scholar] [CrossRef]
- Poston, T.; Ian, S. Catastrophe Theory and Its Applications, 1st ed; Pitman Publishing Ltd.: London, UK, 1978. [Google Scholar]
- Bi, J.; Yang, J.; Li, Q.L. Regional Environmental Risk Analysis and Management, 1st ed; China Environmental Science Press: Beijing, China, 2006; pp. 22–30. (in Chinese) [Google Scholar]
- Chen, G.H.; Zhang, J.; Zhang, H.; Yan, W.W.; Chen, Q.G. Study on regional risk assessment methodology. China Saf. Sci. J. 2006, 16, 112–117. (in Chinese). [Google Scholar]
- Jiang, W.Y.; Tang, Q.H.; Li, H.Z.; Yu, W.X.; Liu, J.X. Development of composite environment risk evaluation method for chemical enterprises and its application. China Environ. Sci. 2010, 30, 133–138. (in Chinese). [Google Scholar]
- Standardization Administration of the People’s Republic of China. Identification of Major Hazard Installations for Dangerous Chemicals (GB18218–2009); Standards Press of China: Beijing, China, 2009. (in Chinese)
- The Administrative Centre for China’s Agenda 21. Guidelines on Emergency Response System for Chemical Industry Parks; Chemical industry press: Beijing, China, 2006. (in Chinese)
- Shi, Y.Q.; Liu, Y.L.; He, J.P. Further study on some questions of catastrophe evaluation method. Eng. J. Wuhan Univ. 2003, 36, 132–136. (in Chinese). [Google Scholar]
- Xiong, Y.; Zeng, G.M.; Chen, G.Q.; Tang, L.; Wang, K.L.; Huang, D.Y. Combining AHP with GIS in synthetic evaluation of eco-environment quality—A case study of Hunan Province, China. Ecol. Model. 2007, 209, 307–312. [Google Scholar]
Appendix
| Criteria | Sub-criteria | Alternative | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | C1 | x1 (t) | 351 | 105 | 5.69 | 0.5 | 4.56 | 20 | 200 | 0.5 | 2,000 | 2,800 |
| x5 | 3 | 3 | 1 | 4 | 1 | 2 | 2 | 4 | 1 | 1 | ||
| x3 | 1 | 0 | 3 | 0 | 3 | 2 | 3 | 0 | 1 | 1 | ||
| x4 | 2 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| C2 | x5 (10–6/y) | 5 | 1 | 5 | 5 | 5 | 5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| x6 (bar) | 20 | 7 | 13.5 | 11 | 5 | 1 | 1 | 20 | 1 | 1 | ||
| x7 (°C) | 500 | 1,000 | 160 | 20 | 160 | 80 | 20 | 20 | 20 | 20 | ||
| B2 | C3 | x8 | 1 | 0.75 | 1 | 0.75 | 1 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 |
| x9 | 1 | 0.75 | 1 | 0.75 | 0.5 | 0.5 | 0.5 | 0.75 | 0.75 | 0.75 | ||
| x10 | 0.75 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | ||
| C4 | x11 (min) | 10 | 20 | 15 | 15 | 25 | 30 | 25 | 25 | 20 | 25 | |
| x12 | 1 | 0.75 | 0.75 | 0.5 | 0.25 | 0.25 | 0.25 | 0.25 | 0.5 | 0.5 | ||
| C5 | x13 (min) | 10 | 15 | 10 | 10 | 15 | 10 | 10 | 10 | 15 | 10 | |
| x14 | 1 | 0.5 | 0.75 | 0.75 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.75 | ||
| B3 | C6 | x15 (m) | 1,000 | 1,000 | 800 | 1,100 | 700 | 500 | 1,000 | 900 | 1,100 | 600 |
| x16 (person/hm2) | 20 | 25 | 40 | 25 | 45 | 60 | 50 | 50 | 40 | 60 | ||
| x17 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||
| C7 | x18 (m) | 100 | 100 | 100 | 100 | 50 | 50 | 50 | 50 | 40 | 50 | |
| x19 | 4 | 5 | 5 | 4 | 4 | 4 | 4 | 3 | 3 | 3 |
| Criteria | Sub-criteria | Alternative | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | C1 | x1 | 0.8748 | 0.9627 | 0.9981 | 1.0000 | 0.9985 | 0.9930 | 0.9287 | 1.0000 | 0.2858 | 0.0000 |
| x2 | 0.3333 | 0.3333 | 1.0000 | 0.0000 | 1.0000 | 0.6667 | 0.6667 | 0.0000 | 1.0000 | 1.0000 | ||
| x3 | 0.6667 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 0.3333 | 0.0000 | 1.0000 | 0.6667 | 0.6667 | ||
| x4 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 0.5000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| C2 | x5 | 0.0000 | 0.8889 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | |
| x6 | 0.0000 | 0.6842 | 0.3421 | 0.4737 | 0.7895 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | ||
| x7 | 0.5102 | 0.0000 | 0.8571 | 1.0000 | 0.8571 | 0.9388 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| B2 | C3 | x8 | 1.0000 | 0.7500 | 1.0000 | 0.7500 | 1.0000 | 0.7500 | 0.7500 | 0.7500 | 0.7500 | 0.7500 |
| x9 | 1.0000 | 0.7500 | 1.0000 | 0.7500 | 0.5000 | 0.5000 | 0.5000 | 0.7500 | 0.7500 | 0.7500 | ||
| x10 | 0.7500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | ||
| C4 | x11 | 1.0000 | 0.5000 | 0.7500 | 0.7500 | 0.2500 | 0.0000 | 0.2500 | 0.2500 | 0.5000 | 0.2500 | |
| x12 | 1.0000 | 0.7500 | 0.7500 | 0.5000 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | 0.5000 | 0.5000 | ||
| C5 | x13 | 1.0000 | 0.5000 | 0.7500 | 0.7500 | 0.2500 | 0.0000 | 0.2500 | 0.2500 | 0.5000 | 0.2500 | |
| x14 | 1.0000 | 0.5000 | 0.7500 | 0.7500 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.7500 | ||
| B3 | C6 | x15 | 0.8333 | 0.8333 | 0.5000 | 1.0000 | 0.3333 | 0.0000 | 0.8333 | 0.6667 | 1.0000 | 0.1667 |
| x16 | 1.0000 | 0.8750 | 0.5000 | 0.8750 | 0.3750 | 0.0000 | 0.2500 | 0.2500 | 0.5000 | 0.0000 | ||
| x17 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| C7 | x18 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.0000 | 0.1667 | |
| x19 | 0.5000 | 1.0000 | 1.0000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.0000 |
Appendix 3. An Example of the calculation of total catastrophe membership degree.
Calculation of C-level Membership Degree Using x as the Control Variable

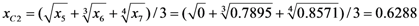
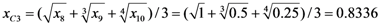
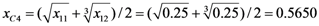

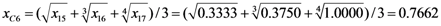
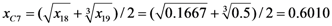
Calculation of B-level Membership Degree Using C-level Indices as Control Variables
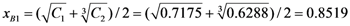
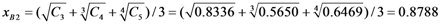
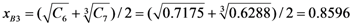
Calculation of Comprehensive Membership Values of Chemical Enterprise Environmental Risks
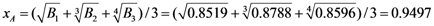
Comparison of the Calculation Results with the Assessment Levels Shown in Table 2 Indicated that the Risk Level of the Enterprise 5 was Unsafe.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Y.; Song, G.; Yang, F.; Zhang, S.; Zhang, Y.; Liu, Z. Risk Assessment and Hierarchical Risk Management of Enterprises in Chemical Industrial Parks Based on Catastrophe Theory. Int. J. Environ. Res. Public Health 2012, 9, 4386-4402. https://doi.org/10.3390/ijerph9124386
Chen Y, Song G, Yang F, Zhang S, Zhang Y, Liu Z. Risk Assessment and Hierarchical Risk Management of Enterprises in Chemical Industrial Parks Based on Catastrophe Theory. International Journal of Environmental Research and Public Health. 2012; 9(12):4386-4402. https://doi.org/10.3390/ijerph9124386
Chicago/Turabian StyleChen, Yu, Guobao Song, Fenglin Yang, Shushen Zhang, Yun Zhang, and Zhenyu Liu. 2012. "Risk Assessment and Hierarchical Risk Management of Enterprises in Chemical Industrial Parks Based on Catastrophe Theory" International Journal of Environmental Research and Public Health 9, no. 12: 4386-4402. https://doi.org/10.3390/ijerph9124386
APA StyleChen, Y., Song, G., Yang, F., Zhang, S., Zhang, Y., & Liu, Z. (2012). Risk Assessment and Hierarchical Risk Management of Enterprises in Chemical Industrial Parks Based on Catastrophe Theory. International Journal of Environmental Research and Public Health, 9(12), 4386-4402. https://doi.org/10.3390/ijerph9124386





