Abstract
Fine airborne particulate matter (PM2.5) has adverse effects on human health. Assessing the long-term effects of PM2.5 exposure on human health and ecology is often limited by a lack of reliable PM2.5 measurements. In Taipei, PM2.5 levels were not systematically measured until August, 2005. Due to the popularity of geographic information systems (GIS), the landuse regression method has been widely used in the spatial estimation of PM concentrations. This method accounts for the potential contributing factors of the local environment, such as traffic volume. Geostatistical methods, on other hand, account for the spatiotemporal dependence among the observations of ambient pollutants. This study assesses the performance of the landuse regression model for the spatiotemporal estimation of PM2.5 in the Taipei area. Specifically, this study integrates the landuse regression model with the geostatistical approach within the framework of the Bayesian maximum entropy (BME) method. The resulting epistemic framework can assimilate knowledge bases including: (a) empirical-based spatial trends of PM concentration based on landuse regression, (b) the spatio-temporal dependence among PM observation information, and (c) site-specific PM observations. The proposed approach performs the spatiotemporal estimation of PM2.5 levels in the Taipei area (Taiwan) from 2005–2007.
1. Introduction
Numerous studies over the last two decades indicate that the air quality measure of fine PM particles (PM2.5, particulate matter particles with an aerodynamic diameter ≤2.5 μm) can be more indicative of potential threats to human health than the commonly and long-used air quality measures of coarse particles, i.e., PM10 (particulate matter particles with an aerodynamic diameter ≤10 μm) and total suspended particles (TSP). An increase in long-term exposure to PM2.5 is closely associated with increased mortality and diseases, such as lung cancer and cardiopulmonary disease [1–4]. Despite the long history of air quality monitoring throughout the entire island of Taiwan from 1983, and much like many other countries, its PM2.5 monitoring network did not begin to operate systematically and regularly until August 2005. The lack of long-term PM2.5 measurements prevents epidemiologists from assessing the chronic health effects of long-term exposure to PM2.5. Geostatistical techniques have been applied to estimate the spatiotemporal distributions of PM2.5 before the establishment of PM2.5 monitoring networks [5–8]. The ratio of PM2.5/PM10 is often used as an important indicator to characterize the underlying atmospheric processes within the local environment [7,8]. However, PM2.5/PM10 ratios can vary with time and space, depending on the landuse and emission patterns of the space-time location. For example, these ratios are approximately 0.69 and 0.52, respectively, in the urban and suburb areas of Shanghai (China) [9], about 0.45 among five different Asian regions (Australia, Hong Kong, Korea, Philippines, Vietnam, and Japan) [10], and range from 0.39 to 0.69 in urban and semi-rural areas of the United States [11]. Previous research provides a summary of PM2.5/PM10 ratios in megacities around the world [12]. Intra-urban ratios change significantly in Taipei, with a PM2.5/PM10 ratio of approximately 0.82 around the Bei-tou incinerator [13], 0.68 in high traffic areas, and 0.57 in downtown areas [14].
The spatial and temporal variation of PM2.5, PM10, and other air quality levels in Taiwan are generally high due to their high association with local emission patterns and meteorological conditions. Recent developments have been focusing on quantifying the levels of PM2.5, PM10, and other air quality observations using the surrogates of local emissions [15,16]. The landuse regression technique (LUR) has been widely applied to determine the linear relationship between air quality measures and landuse information and generate air quality maps with high spatial resolution [17–21]. In general, LUR air quality maps can delineate the significant contributions of certain geographical objects, such as highways. However, due to changes in meteorological conditions and limited landuse information, the quantitative results of air quality levels by LUR can vary from time to time. Therefore, the LUR is generally used to quantify the long-term average air quality levels in space [20–23]. Studies show that landuse information also plays an important role in the variation of the PM2.5/PM10 levels due to traffic and road emissions [24,25]. This is because the influence degree to PM2.5 and PM10 varies across different local landuse patterns. In addition, the temporal variations of PM2.5/PM10 resulting from the change of meteorological conditions can be less significant than the direct observations of PM2.5 and PM10. These characteristics make the PM2.5/PM10 ratio a proper surrogate of air quality patterns, which quantify the contributions of spatial variations in landuse patterns. However, relatively few studies investigate the relationship between the PM2.5/PM10 ratios and landuse information.
This study investigates the spatiotemporal distribution of PM2.5 across the Taipei area from 2005–2007 by integrating the information of PM10 and landuse information. This study uses LUR to establish a quantitative relationship between PM2.5/PM10 and landuse information. The Bayesian maximum entropy (BME) method is then used to assimilate the PM2.5 and the secondary information from the LUR analysis. The comparison is made by assessing the improvement of PM2.5 prediction accuracy with the incorporation of the secondary information, i.e., geostatistical estimation by (1) only PM2.5, (2) both PM2.5 and PM10 and (3) PM2.5, PM10 and landuse information.
2. Materials
2.1. Study Area
Taipei, including Taipei city and Taipei county, is the largest metropolitan area in Taiwan, and has a vehicle density as high as 6,000 vehicles per km2. In addition to traffic emissions, three incineration plants are major sources of pollutants in the area [26].
The Taipei area is bounded by mountains, i.e., Yangming Mountains to the north, Linkou mesa to the west, and a ridge of the Snow Mountains to the southeast. These mountains form the second largest basin of the island (Figure 1). This basin topography increases the concentration level of ambient pollutants and creates a high contrast between the urbanization of the basin floor in Taipei and the surrounding mountain areas.
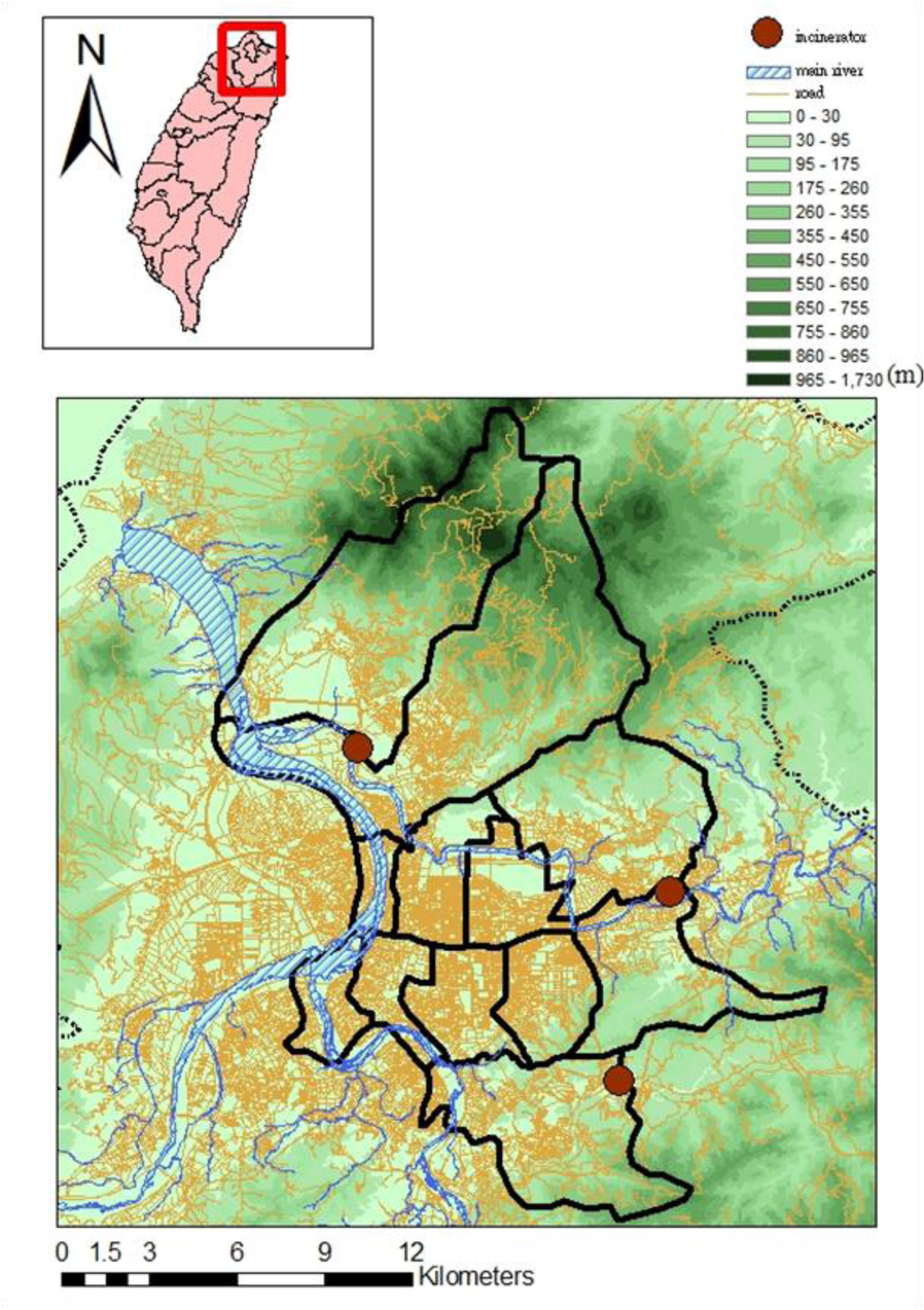
Figure 1.
The highways, rivers, and topography in the Taipei metropolitan area.
2.2. Ambient Pollutant Data
An island-wide monitoring network operated by Taiwan Environmental Protection Agency (TWEPA) regularly records ambient pollutants, i.e., criteria pollutants such as PM, ozone, NOx, CO, SO2 [27], and meteorological variables. There are 18 TWEPA stations within the Taipei metropolitan area, and these stations recorded both PM2.5 and PM10 from 2005–2007. Table 1 summarizes the PM2.5 and PM10 statistics.

Table 1.
Summary of statistics of hourly PM10 and PM2.5 observations from 2005–2007 (unit: μg/m3).
In addition, the Department of Environmental Protection and the local governments of Taipei city and Taipei county (TPEDEP) have independently collected PM data since 1970 and 1990, respectively. However, only the Taipei city government records PM10 on a daily basis at its eight stations. This study uses the PM2.5 and PM10 data from both central and local governments to estimate the monthly PM2.5/PM10 ratios at every PM station (Figure 2). This study aggregates the PM2.5 and PM10 data into monthly data following the procedure suggested by USEPA [28]. The monthly PM2.5 levels at the TPEDEP stations were estimated by the BME method as discussed below with only PM2.5 observations. The estimated monthly PM2.5 and PM10 were then used to obtain the spatiotemporal distribution of PM2.5/PM10 ratios for all stations from 2005–2007. The other observed ambient pollutants, i.e., CO, NO2, SO2, and O3, were used as the emission indicators, as discussed below.
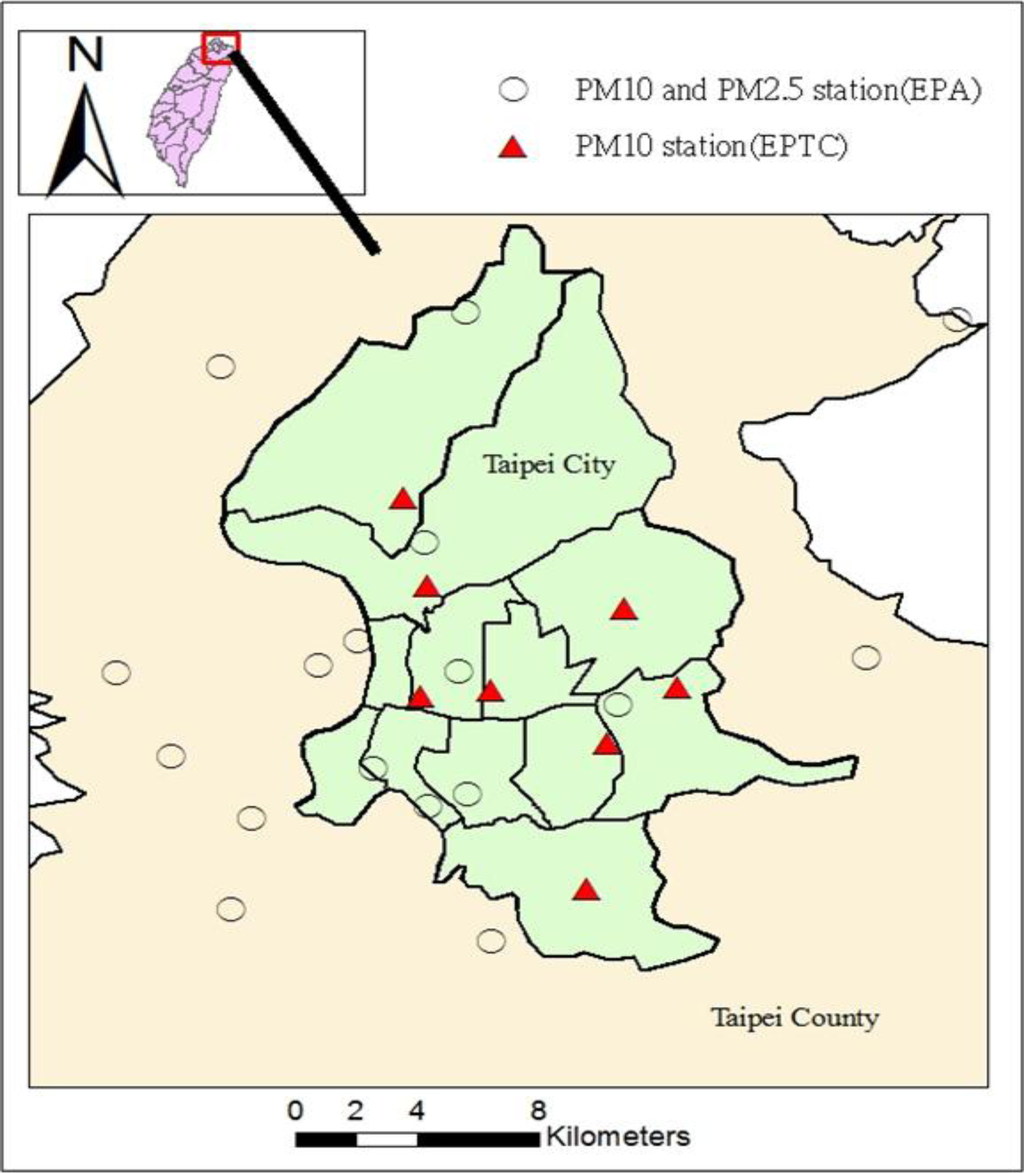
Figure 2.
Spatial distribution of PM10 and PM2.5 monitoring stations in Taipei.
2.3. Landuse Data
The National Land Surveying and Mapping Center (Taiwan) conducted a comprehensive landuse surveying of the entire Taipei area in 2007. This survey includes nine major classes of land usage, including agriculture, forest, traffic, water, buildings, utilities, recreation areas, mining areas, and others, i.e., transportation data discussed below. Each of the major landuse categories mentioned above includes more detailed classifications [29] This study analyzes the potential major or minor landuse classes that may have positive or negative effects on the air quality levels. The selection criteria include significant variables identified in previous studies, e.g., roads, and insights from local experts [30], e.g., motorcycles. The selected landuse classes include the areas of farms, forests, railroad, freeway, highway, roads, ports, government institutions, school, commerce, residence, industry, hospital, social welfare facilities, public utilities, and parks.
Figure 3 shows the spatial distribution of some landuse classes in Taipei. This figure clearly shows that city development is concentrated in the plains of the Taipei basin floor. In addition, this study generates spatiotemporal traffic information by uniformly assigning the recorded number of various registered vehicles [31,32] to the study area based on the road areas identified by the landuse data. The vehicle types of this analysis include motorcycle, bus, passenger car, and truck.
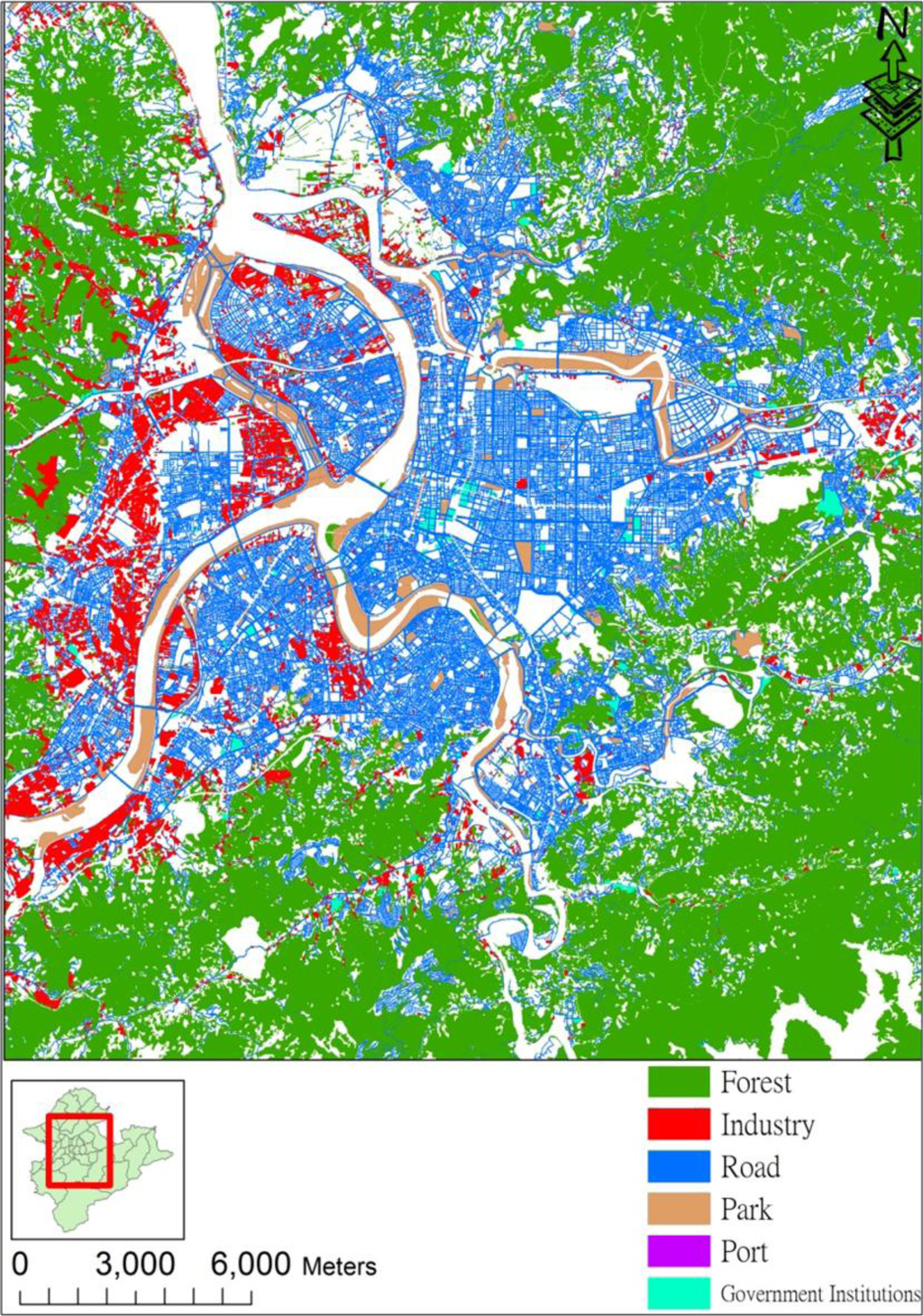
Figure 3.
Spatial distribution of landuse patterns in Taipei area.
3. Methods
This study uses a landuse regression method to determine the relationship between PM2.5/PM10 and local emission-related information. The emission-related information in this study includes non-PM ambient pollutants and landuse data. Local emission-related data are derived by GIS functions which estimate this size or area of selected indicators within the specified spatial buffers. Various spatial ranges of buffers are used for landuse information surrounding the PM2.5/PM10 data (i.e., 0–50 m, 50–100 m, 100–300 m, 300–500 m, and 500–1,000 m) to determine the different ranges of transport processes produced by different types of emissions. The relationship between the sizes/proximity of local emission-related data and PM2.5/PM10 ratios is assumed to be homogeneous over the entire study area, and can therefore be formulated in a linear form. Multivariate stepwise regression analysis was performed to select the most significant regressors and estimate their associated parameters. Due to the high linear dependencies among the selected emission-related variables in the landuse regression model, this study uses the variance inflation factor (VIF) to identify multicolinearity among the regressors and avoid potentially dubious results from the analysis [33]. This study uses SPSS software for landuse regression analysis.
The BME method mathematically represents air pollution attributes (i.e., PM measurements and ratios) in terms of spatiotemporal random fields (S/TRF; [34]). Let Xp = Xs,t denote a S/TRF of an air pollution attribute, where the vector p = (s,t)denotes a spatiotemporal point (s is the geographical location and t is the time). The S/TRF model is a collection of all physically possible realizations of the attribute to be represented mathematically. The S/TRF model is fully characterized by its probability density function (pdf), fKB, where the subscript KB denotes the ‘knowledge base’ used to construct the pdf. In particular, BME considers a distinction between: (a) the general KB, denoted by G-KB, and (b) the site-specific KB, S-KB. The total KB is denoted as K = G ∪ S, i.e., it includes both the general and the site-specific KB. The fundamental BME equations are as follows (for technical details, see [35,36]):
where g is a vector of gα -functions (α = 1,2,...) that stochastically represents the G-KB under consideration (the bar denotes statistical expectation), μ is a vector of μα -coefficients that depends on the space-time coordinates and is associated with g (i.e., μα expresses the relative significance of each gα -function in the composite solution sought), ξS represents the S-KB available, A is a normalization parameter, and fK is the pollutant pdf at each space-time point (the subscript K means that fK is based on the blending of the core and site-specific KB). The terms g and ξS the inputs in Equation (1), whereas the unknowns are the μ and fK across space-time.
The G-KB refers to the entire p -domain of interest, which consists of the space-time point vector pk, where attribute estimates are sought, and the point vector pdata, where site-specific information is available. The G-KB may include theoretical space-time dependence models (mean, covariance, variogram, generalized covariance, multiple-point statistics, and continuity orders) of the air pollution attribute Xp [37,38]. The S -KB includes physical data χdata obtained at points pi (i = 1,2,…, m) of the specified geographical area, i.e., the various kinds of PM measurements or ratios are considered part of the S -KB and are expressed by S :χdata = (χhard, χsoft) = (χ1,…, χm) where the χhard = (χ1,…, χmh) denote hard data at points pi (i = 1,2,…, mh) that are exact PM measurements (i.e., the hard χhard occur with probability one); and the χsoft = (χmh+1,.…, χm) denote soft data at points pi (i = mh +1,…, m) that may include uncertain evidence and secondary information. This study represents the soft PM data from landuse regression model in the interval, IS, i.e., χsoft : {χi ∈ Ii =[li, ui],i = mh + 1,…,m}; For other examples of soft data, see [39,40].
This study characterizes both PM2.5, Xs,t and PM10, Ys,t, concentrations by S/TRF. The PM2.5/PM10 ratio can be represented as rs,t = Xs,t/Ys,t, where t is the time in months during the period 2005–2007. The values of rs,t, can be estimated monthly at each PM monitor station based on the recorded or estimated PM data. The monthly rs,t, of PM2.5/PM10 ratios were calculated at the monitoring stations where daily PM2.5 and PM10 data are both available and the eight PM10 stations operated by TPEDEP where only daily PM10 data was observed. During the study period, the rp -values at the stations were assumed to be an empirical function of the emission-related indicators by LUR. The spatiotemporal distribution of the ratios across the study area is estimated based on this empirical relationship and the citywide emission information obtained using ArcGIS 9.2. Note that the uncertainty is prevalent in the estimation of spatiotemporal distribution of the ratios. The ratios at each space-time location are assumed to be uniform-distributed with intervals of ⌊r̂s,t – SD(r̂s,t), r̂s,t + SD(r̂s,t)⌋, where r̂s,t and SD(r̂s,t) represent the ratio estimation and its standard deviation from LUR, respectively. The multiplication of PM2.5/PM10 ratios and PM10 generates an uncertain spatiotemporal trend of PM2.5. To account for the uncertainty in the ratio estimation and subsequent trend estimation in space and time, this study uses the BME method for the spatiotemporal estimation of the PM2.5 with the uniform-distributed PM2.5 residuals which upper and lower bounds are derived from the intervals of trend estimations and the PM2.5 observations. In summary, this study applies the two-stage approach to integrate landuse regression and BME methods for spatiotemporal PM2.5 estimations, in which landuse regression is used to characterize the spatial variability of PM2.5, i.e., ratios, and BME performs later by assimilating the uncertainty by landuse regression and the spatiotemporal dependence for the modeling of spatiotemporal PM2.5 distribution.
4. Results
Table 2 lists the selected variables from the emission-related dataset in LUR model by the stepwise regression method. This table lists variables by the rank of their significance to the variation of PM2.5/PM10 ratios. Most of the selected variables can elevate the level of PM2.5/PM10 ratios. The road, forest, industrial area, and park landuse patterns has the greatest effect on increasing the PM2.5/PM10 ratios. Most selected ranges of the variables are 500 m–1,000 m.

Table 2.
Coefficients of selected variables of LUR model.
This implies that the level of PM2.5/PM10 represents the general air quality patterns of the area surrounding the monitoring stations rather than the direct emission impact from the short distances. The only selected variable that shows the ability to reduce PM2.5/PM10 values is the park landuse pattern, which ranges between 300 m and 500 m. Note that most traffic information is not included in the model due to multicollinearity with the spatial distribution of road area. The exception is the bus volume, which can increase the local ratio level within.
The spatiotemporal distribution of monthly PM2.5 can be obtained by multiplying the empirical functional of landuse information, i.e., the LUR model and PM10 variation in space and time. However, the spatiotemporal dependence among the PM2.5 is not considered. This study integrates the BME method with LUR to model the high frequency part of the PM2.5 variation in space and time, i.e., the unexplained PM2.5 noise in the LUR model. The high frequency part of spatiotemporal variation of PM2.5 is characterized by the stationary nested covariance shown below (see Figure 4):
where [c0,c1]=[10.5, 3.729], [ar1,ar2]=[11.092 km, 50 km] and [at1,at2]=[3 month, 50 month]. The BME method integrates the probabilistic data of PM2.5 residuals and spatiotemporal covariance model in Equation (2) to generate the monthly spatiotemporal distributions of PM2.5 from 2005–2007.
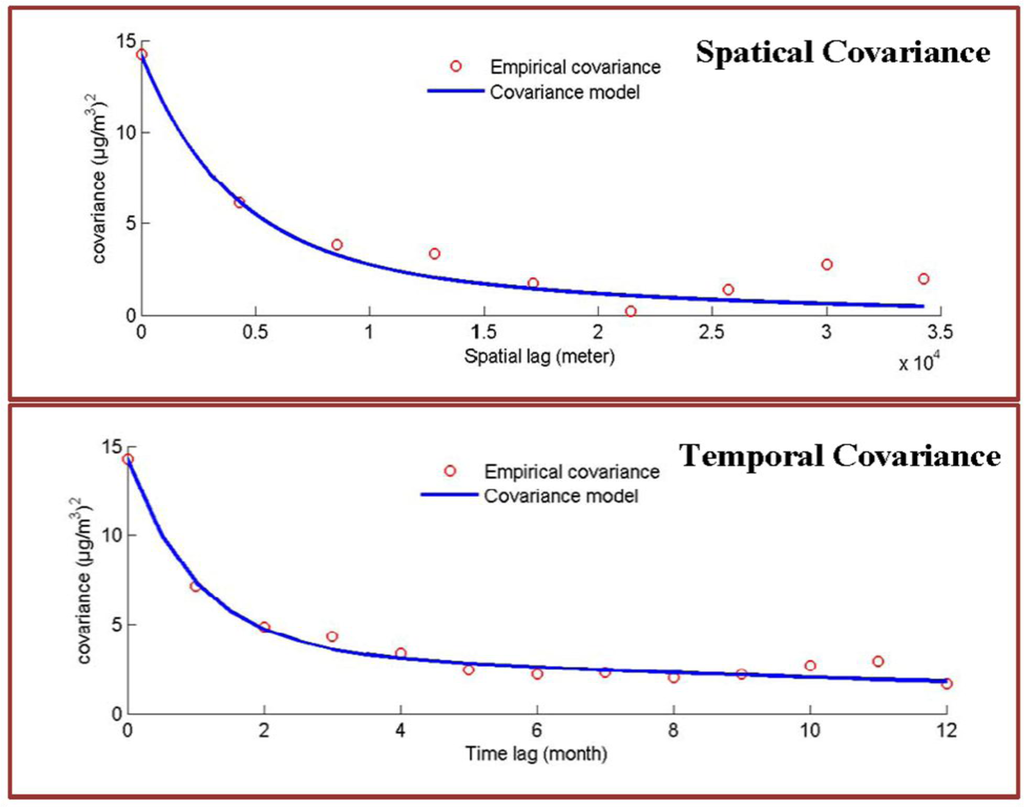
Figure 4.
Spatiotemporal covariance of PM2.5 (top) pure spatial covariance (bottom) pure temporal covariance.
This study compares the modeling of spatiotemporal PM2.5 distribution using the kriging method, LUR method, and the integration of LUR and BME methods, respectively (Table 3). The kriging estimation is based upon the modeling of PM2.5 observations directly, and ignores their uncertainty [35]. Leave-one cross-validation results show that the LUR model outperforms the kriging method in PM2.5 estimations. Furthermore, the BME method can improve the accuracy of PM2.5 estimation in this study. Figure 5 and Figure 6 show the spatial distribution of estimation performance at each PM2.5 observation location by the LUR model and BME method, respectively.

Table 3.
Results of cross validation.
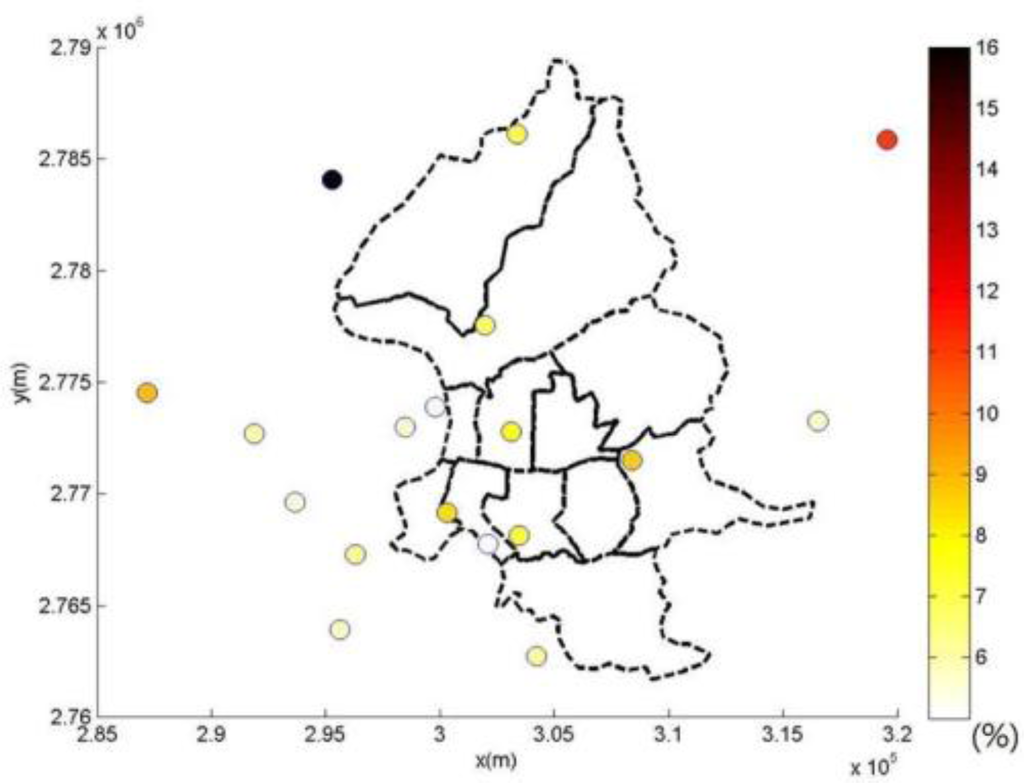
Figure 5.
Spatial distribution of relative error of PM2.5 estimations by LUR model.
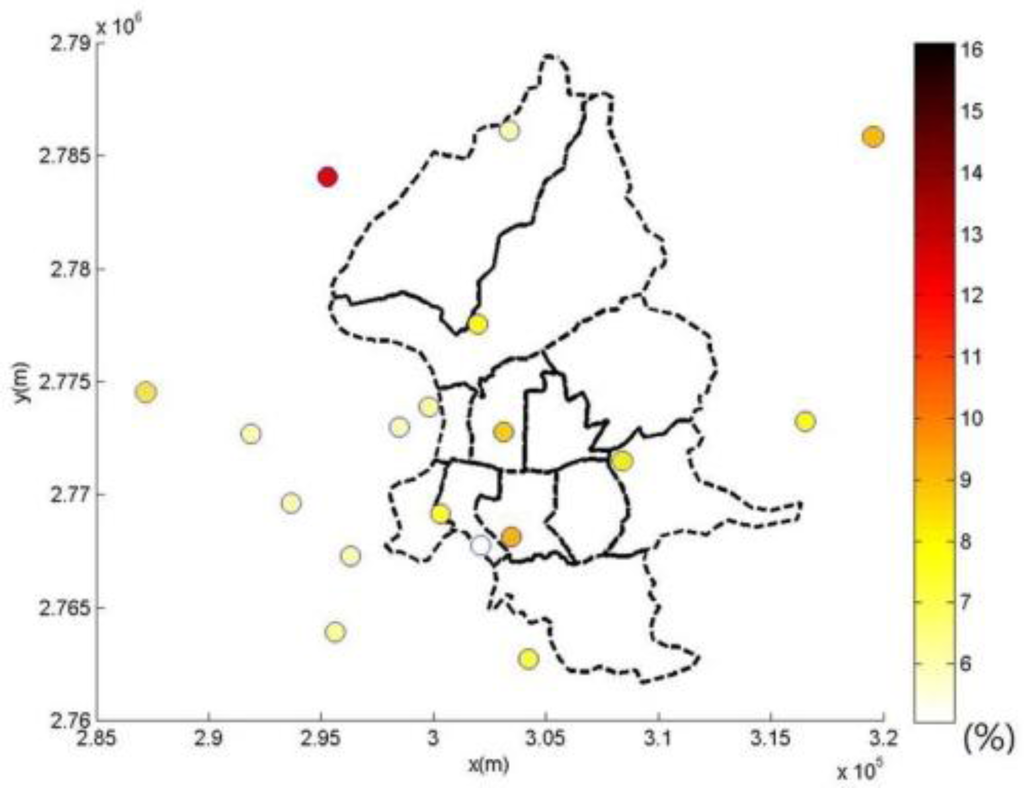
Figure 6.
Spatial distribution of relative error of PM2.5 estimations by the integration of LUR and BME methods.
Figure 7 shows the temporal variation of monthly PM2.5 observations and their estimations by BME method at the four selected locations, i.e., Yungho, Cailiao, Sijhih, and Yangming. The selected locations represent different parts of Taipei area.
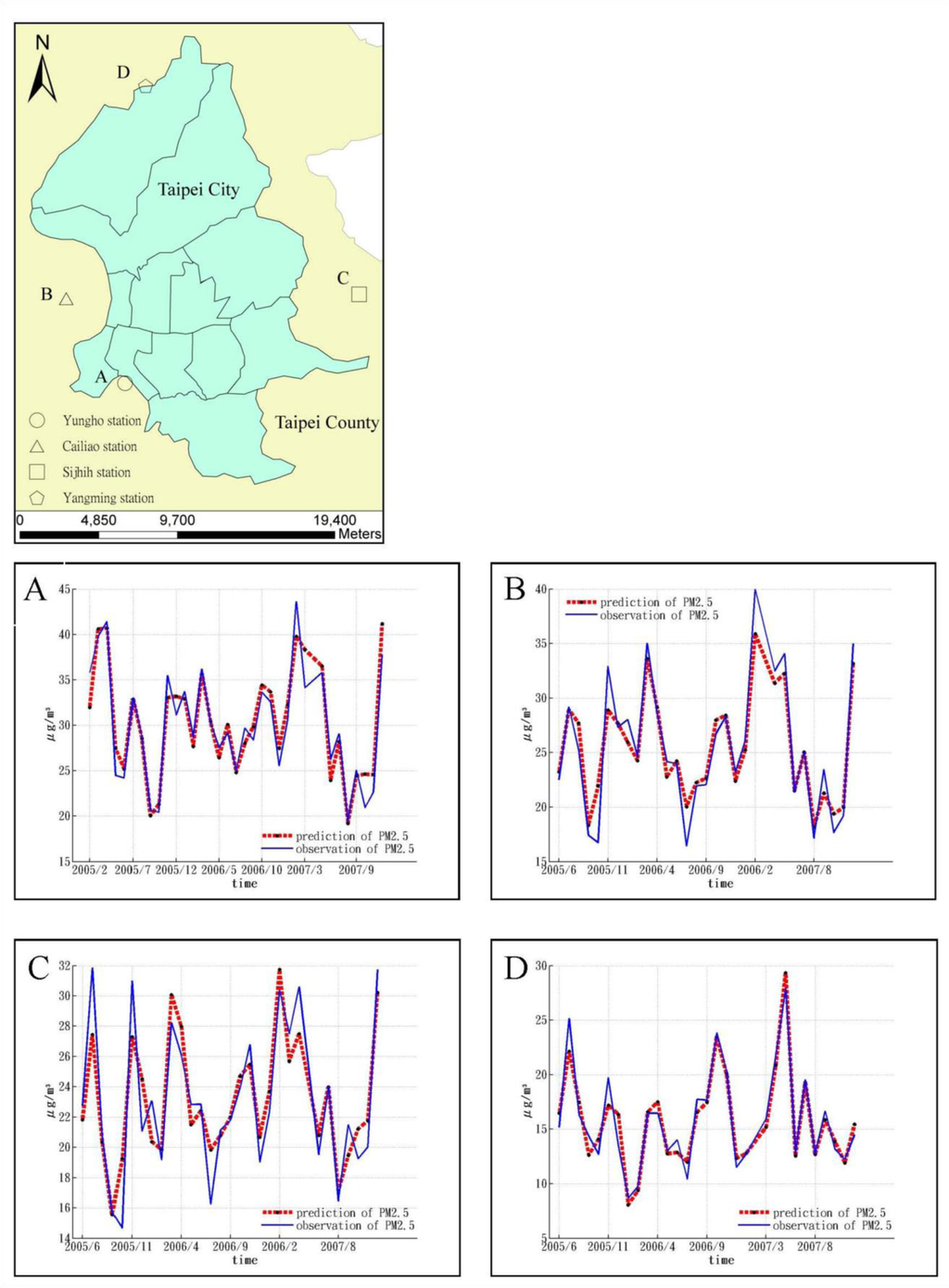
Figure 7.
A comparison of PM2.5 observations and estimations at four PM2.5 stations: (A) Yungho station, (B) Cailiao station, (C) Sijhih station, and (D) Yangming station.
5. Discussion
This study uses the BME method to integrate the LUR model in the prediction (estimation) of fine particulate matter concentrations across space-time in the Taipei metropolitan area. This implementation of BME theory allows this study to determine attribute distributions in a composite space-time domain without restrictive or unrealistic assumptions (such as linearity, normality, independency etc.). The general knowledge base of the BME method used to characterize the general pattern of PM2.5 is based on the empirical relationship between landuse information and the LUR model. Many studies [18,20,41] show that the LUR is able to produce high-resolution air quality maps and address the effects of each landuse pattern. However, updating a landuse database often requires tremendous efforts, making it difficult to update the information of landuse changes over time. To characterize the general pattern of PM2.5 in space and time, the emission-related database in this study includes the variables of non-PM ambient pollutants and traffic information, which change over time and are considered to be highly associated with the level of PM2.5. As a useful indicator of local emission patterns [7,8], this study determines PM2.5/PM10 ratios based on landuse distribution and some LUR model emission information mentioned above. As expected, most of the significant variables in the LUR model of ratios are pure spatial information, i.e., certain landuse patterns within the certain distances from the observation locations. This implies that the spatial variation of PM2.5/PM10 ratios exceeds its temporal variation, i.e., the effects of landuse data to PM2.5/PM10 ratios in Taipei are more important than other temporal factors, such as meteorological and seasonal effects. In addition, the monthly ratios mostly characterize the general emission pattern. Therefore, the ranges with greatest size of area at each neighborhood appear most frequently in this study. The factors included in this study are mostly variables which can increase the level of ratios. Some of the potential variable can significant reduce the level of ratios are selected, e.g., forest and park. Among them, the contradiction of the park effect from different ranges may be due to the common spatial distribution of the urban setting in Taipei, in which major parks are commonly located near high-density urbanized areas. Thus, only locations immediately next to parks can enjoy have the advantages of the park’s ability to improve air quality. As for areas situated further from the parks, the air quality levels can easily be elevated by other contributing factors. This is partially responsible for the high variability of PM2.5 levels, which can increase significantly based on local emissions and decrease significantly when emission sources are removed.
Covariance analysis shows that the PM2.5 exhibits two spatiotemporal interactions with different space-time ranges. These interactions represent the local and long-term transport patterns of fine particulate matter over the Taipei area with the two distinct space-time ranges: [11 km, 3 months] and [50 km, 50 months]. The dominant process of PM2.5 distribution is the local transport with spatial and temporal extents of 11 km and 3 months. The spatial extent considers the size of highly-urbanized areas, while the temporal range shows how seasonal effects play an important role in the concentration level of PM2.5. The variability of long-term process can result from the mass dispersion over the continents, such as dust storms, due to certain meteorological conditions [42–45].
Figure 4 and Figure 5 show the spatial distributions of performance assessment for the LUR and BME methods. Results show that both analyses obtain similar spatial patterns of accuracy distribution, and can perform relatively better in areas with better PM observations. The analysis of the LUR model assumes a homogenous relationship between landuse information and PM observations across space and time. However, the heterogeneity of the statistical relationship between the landuse and PM concentration may vary from location to location due to distinct causality between analysis attributes. This spatial unbalance of information support causes the homogeneous relationship address the area of abundant information better. This results in distinct performance differences between the central and boundary areas in spatial distribution of cross-validation results of the LUR and BME methods, especially in Figure 4. Though the BME method shares the same spatiotemporal patterns as the LUR model, the inclusion of spatiotemporal dependence in the BME method reduces the effects of unbalance information and improves the estimation accuracy, as Figure 5 shows.
Table 3 shows the advantages of integrating landuse information in spatiotemporal estimation in PM2.5. Cross-validation comparison shows that the LUR model offers greater improvement than the kriging method, i.e., the most-widely used geostatistical method. The LUR and kriging methods only consider landuse information and spatiotempral dependence among PM2.5, respectively. Table 3 shows that the BME method achieves the smallest mean square error, standard deviation, and other statistics in PM2.5 estimation errors. Figure 6 compares the temporal distribution of PM2.5 observations and BME estimations for four selected locations. The four locations were selected to represent the East, South, West, and North parts of the city, respectively. Results show that, for all locations, the BME estimations generally achieved good agreement with the PM2.5 observations.
6. Conclusions
This study discusses the application of spatiotemporal statistics to science-based PM2.5 mapping in Taipei. The main goals of the BME method are to generate PM2.5 maps in a composite space-time domain, in which the core knowledge in the form of empirical laws by LUR model with the informative secondary information derived from landuse data. Results show that incorporation of multi-sourced soft and hard information through BME analysis and mapping can effectively improve the accuracy of PM2.5 estimation across space-time. This analysis demonstrates the most influential landuse patterns elevating PM2.5 levels. In addition, the two dominant space-time mechanisms underlying PM2.5 space-time distributions in Taipei include local and long-term transport processes.
Acknowledgments
This research was supported by funds from the National Science Council of Taiwan (NSC 99-2625-M-002-007) and (NSC 98-2313-B-451-005).
References
- Pope, CA; Hansen, ML; Long, RW; Nielsen, KR; Eatough, NL; Wilson, WE; Eatough, DJ. Ambient particulate air pollution, heart rate variability, and blood markers of inflammation in a panel of elderly subjects. Environ. Health Perspect 2004, 112, 339–345. [Google Scholar]
- Pope, CA. Epidemiology of fine particulate air pollution and human health: Biologic mechanisms and who’s at risk? Environ. Health Perspect 2000, 108, 713–723. [Google Scholar]
- Pope, CA. Review: Epidemiological basis for particulate air pollution health standards. Aerosol Sci. Tech 2000, 32, 4–14. [Google Scholar]
- Dockery, DW; Pope, CA; Xu, XP; Spengler, JD; Ware, JH; Fay, ME; Ferris, BG; Speizer, FE. An association between air-pollution and mortality in 6 United-States cities. N. Engl. J. Med 1993, 329, 1753–1759. [Google Scholar]
- Yanosky, JD; Paciorek, CJ; Suh, HH. Predicting chronic fine and coarse particulate exposures using spatio-temporal models for the northeastern and midwestern US. Environ Health Perspect 2009, (in press).. [Google Scholar]
- Paciorek, CJ; Yanosky, JD; Puett, RC; Laden, F; Suh, HH. Practical large-scale spatio-temporal modeling of particulate matter concentrations. Ann. Appl. Stat 2009, 3, 370–397. [Google Scholar]
- Yu, HL; Wang, CH. Retrospective prediction of intraurban spatiotemporal distribution of PM2.5 in Taipei. Atmos Environ 2010. (submitted).. [Google Scholar]
- Yu, HL; Christakos, G; Chen, JC. Spatiotemporal Air Pollution Modeling and Prediction in Epidemiologic Research. In Air Pollution Research Trends; Columbus, F, Ed.; Nova Science Publishers, Inc: Hauppauge, NY, USA, 2007; pp. 57–75. [Google Scholar]
- Zhang, YX; Zhang, YM; Wang, YS; Li, DL. PIXE characterization of PM10 and PM2.5 particulate matter collected during the winter season in Shanghai city. J. Radioanal. Nucl. Chem 2006, 267, 497–499. [Google Scholar]
- Cohen, DD; Garton, D; Stilcer, E; Wang, T; Poon, S; Kim, JY; Oh, SN; Shin, H-J; Ko, MY; Santos, F; et al. Characterisation of PM2.5 and PM10 Fine Particle Pollution in Several Asian Regions. Proceedings of 16th Internatinal Clean Air Conference, Christchurch, New Zealand; 2005; pp. 18–22. [Google Scholar]
- Criterion Document on Particulate Matter; U.S. Environmental Protection Agency (USEPA): Washington, DC, USA, 2001.
- Das, M; Maiti, SK; Mukhopadhyay, U. Distribution of PM2.5 and PM10-2.5 in PM10 fraction in ambient air due to vehicular pollution in Kolkata megacity. Environ. Monit. Assess 2006, 122, 111–123. [Google Scholar]
- Mao, IF; Chen, CN; Lin, YC; Chen, ML. Airborne particle PM2.5/PM10 mass distribution and particle-bound PAH concentrations near a medical waste incinerator. Atmos. Environ 2007, 41, 2467–2475. [Google Scholar]
- Li, CS; Lin, CH. PM1/PM2.5/PM10 characteristics in the urban atmosphere of Taipei. Aerosol Sci. Tech 2002, 36, 469–473. [Google Scholar]
- Kumar, U; Jain, VK. ARIMA forecasting of ambient air pollutants (O3, NO, NO2 and CO). Stoch. Environ. Res. Risk Assess 2010, 24, 751–760. [Google Scholar]
- Li, HL; Huang, GH; Zou, Y. An integrated fuzzy-stochastic modeling approach for assessing health-impact risk from air pollution. Stoch. Environ. Res. Risk Assess 2008, 22, 789–803. [Google Scholar]
- Gilbert, NL; Goldberg, MS; Brook, JR; Jerrett, M. The influence of highway traffic on ambient nitrogen dioxide concentrations beyond the immediate vicinity of highways. Atmos. Environ 2007, 41, 2670–2673. [Google Scholar]
- Jerrett, M. On the use and interpretation of land use regression estimates in chronic air pollution epidemiology. Epidemiology 2008, 19, S38–S38. [Google Scholar]
- Jerrett, M; Arain, A; Kanaroglou, P; Beckerman, B; Potoglou, D; Sahsuvaroglu, T; Morrison, J; Giovis, C. A review and evaluation of intraurban air pollution exposure models. J. Expos. Anal. Environ. Epidem 2005, 15, 185–204. [Google Scholar]
- Sahsuvaroglu, T; Jerrett, M; Sears, MR; McConnell, R; Finkelstein, N; Arain, A; Newbold, B; Burnett, R. Spatial analysis of air pollution and childhood asthma in Hamilton, Canada: Comparing exposure methods in sensitive subgroups. Environ Health 2009, 8. [Google Scholar]
- Sangrador, JLT; Nunez, MCE; Villarreal, AB; Cadena, LH; Jerrett, M; Romieu, I. A land use regression model for predicting PM2.5 in Mexico City. Epidemiology 2008, 19, S259–S259. [Google Scholar]
- Gilbert, NL; Goldberg, MS; Beckerman, B; Brook, JR; Jerrett, M. Assessing spatial variability of ambient nitrogen dioxide in Montreal, Canada, with a land-use regression model. J. Air Waste Manage. Assoc 2005, 55, 1059–1063. [Google Scholar]
- Jerrett, M; Burnett, RT; Ma, RJ; Pope, CA; Krewski, D; Newbold, KB; Thurston, G; Shi, YL; Finkelstein, N; Calle, EE; et al. Spatial analysis of air pollution and mortality in Los Angeles. Epidemiology 2005, 16, 727–736. [Google Scholar]
- Gehrig, R; Buchmann, B. Characterising seasonal variations and spatial distribution of ambient PM10 and PM2.5 concentrations based on long-term Swiss monitoring data. Atmos. Environ 2003, 37, 2571–2580. [Google Scholar]
- Querol, X; Alastuey, A; Rodriguez, S; Plana, F; Ruiz, CR; Cots, N; Massague, G; Puig, O. PM10 and PM2.5 source apportionment in the Barcelona Metropolitan area, Catalonia, Spain. Atmos. Environ 2001, 35, 6407–6419. [Google Scholar]
- Chang, SC; Lee, CT. Evaluation of the trend of air quality in Taipei, Taiwan from 1994 to 2003. Environ. Monit. Assess 2007, 127, 87–96. [Google Scholar]
- Air Quality in Taiwan Annual Report; Taiwan Environmental Protection Agency (TWEPA): Taipei, Taiwan, 2006.
- AQS Raw Data Summary Formulas Draft; U.S. Environmental Protection Agency (USEPA): Washington, DC, USA, 2004.
- National Land Surveying Project; National Land Surveying and Mapping Center, Taiwan Ministry of Interior (TMI): Taipei, Taiwan, 2007.
- Hoek, G; Beelen, R; de Hoogh, K; Vienneau, D; Gulliver, J; Fischer, P; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ 2008, 42, 7561–7578. [Google Scholar]
- Annual Report of Registered Vehicles in Taipei City; Taipei City Government: Taipei, Taiwan, 2007.
- Annual Report of Registered Vehicles; Taiwan Ministry of Transportation and Communication: Taipei County, Taiwan, 2007.
- Graybill, FA; Iyer, HK. Regression Analysis: Concepts and Applications; Duxbury Press: Belmont, CA, USA, 1994. [Google Scholar]
- Christakos, G. Random Field Models in Earth Sciences; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Christakos, G. Modern Spatiotemporal Geostatistics; Oxford University Press: New York, NY, USA, 2000; p. 304. [Google Scholar]
- Christakos, G; Olea, RA; Serre, ML; Yu, HL; Wang, L. Interdisciplinary Public Health Reasoning and Epidemic Modelling: The Case of Black Death; Springer-Verlag: New York, NY, USA, 2005. [Google Scholar]
- Kolovos, A; Christakos, G; Serre, ML; Miller, CT. Computational Bayesian maximum entropy solution of a stochastic advection-reaction equation in the light of site-specific information. Water Resour Res 2002, 38. [Google Scholar]
- Porcu, E; Mateu, J; Saura, F. New classes of covariance and spectral density functions for spatio-temporal modelling. Stoch. Environ. Res. Risk Assess 2008, 22, S65–S79. [Google Scholar]
- Yu, HL; Kolovos, A; Christakos, G; Chen, JC; Warmerdam, S; Dev, B. Interactive spatiotemporal modelling of health systems: The SEKS-GUI framework. Stoch. Environ. Res. Risk Assess 2007, 21, 555–572. [Google Scholar]
- Wibrin, MA; Bogaert, P; Fasbender, D. Combining categorical and continuous spatial information within the Bayesian maximum entropy paradigm. Stoch. Environ. Res. Risk Assess 2006, 20, 423–433. [Google Scholar]
- Best, NG; Ickstadt, K; Wolpert, RL; Birggs, DJ. Combining Models of Health and Exposure Data: The Saviah Study. In Spatial Epidemiology: Methods and Applications; Elliott, P, Wakefield, JC, Best, NG, Briggs, D, Eds.; Oxford University Press: Oxford, UK, 2000; pp. 393–414. [Google Scholar]
- Hsu, SC; Liu, SC; Lin, CY; Hsu, RT; Huang, YT; Chen, YW. Metal compositions of PM10 and PM2.5 aerosols in Taipei during spring, 2002. Terr. Atmos. Ocean. Sci 2004, 15, 925–948. [Google Scholar]
- Lin, CY; Liu, SC; Chou, CCK; Huang, SJ; Liu, CM; Kuo, CH; Young, CY. Long-range transport of aerosols and their impact on the air quality of Taiwan. Atmos. Environ 2005, 39, 6066–6076. [Google Scholar]
- Tsai, YI; Chen, CL. Characterization of Asian dust storm and non-Asian dust storm PM2.5 aerosol in southern Taiwan. Atmos. Environ 2006, 40, 4734–4750. [Google Scholar]
- Kuo, HW; Shen, HY. Indoor and outdoor PM2.5 and PM10 concentrations in the air during a dust storm. Bldg. Environ 2010, 45, 610–614. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).