Distributional Benefit Analysis of a National Air Quality Rule
Abstract
:1. Introduction
- Are different socio-demographic population subgroups being exposed to different pollution levels before a rule is implemented (baseline scenario)?
- When a given rule is implemented, do different subgroups benefit differentially? That is, do some subgroups enjoy greater reductions in pollution levels than others?
- Do some subgroups enjoy greater reductions in health risks as a result of a given rule or regulation?
- As a result of a given rule, do the pollutant exposures (and associated health risks) experienced by different subgroups become less unequal?
2. Distributional Benefits Analysis of EPA’s Heavy Duty Diesel Rule in 2030
- The ambient PM2.5 concentrations to which they are expected to be exposed in the 2030 baseline (i.e., in the absence of the rule);
- The reductions in ambient PM2.5 concentrations they are expected to experience in 2030 as a result of the rule; and
- The corresponding reductions in all-cause mortality they are expected to experience as a result of the rule.
2.1. Estimating Baseline Pollutant Exposures and Reductions in Exposure as a Result of the HDD Rule
2.2. Estimating Reductions in Health Effect Incidence Rates Corresponding to Reductions in PM2.5
3. Discussion
4. Conclusions
Acknowledgments
References
- U.S. EPA. Regulatory Impact Analysis: Heavy-Duty Engine and Vehicle Standards and Highway Diesel Fuel Sulfur Control Requirements; EPA 420-R-00-026; U.S. EPA, Office of Air and Radiation: Washington, DC, USA, 2000. [Google Scholar]
- Stretesky, P; Lynch, M. Environmental justice and the prediction of distance to accidental chemical releases in Hillsborough county, Florida. Soc. Sci. Quart 1999, 80, 830–846. [Google Scholar]
- Davidson, P; Anderton, DL. Demographics of dumping II: A national environmental equity survey and the distribution of hazardous materials handlers. Demography 2000, 37, 461–466. [Google Scholar]
- Hite, D. A random utility model of environmental quality. Growth and Change 2000, 31, 40–58. [Google Scholar]
- Mantaay, J. Mapping environmental injustices: Pitfalls and potential of geographic information systems in assessing environmental health and equity. Environ. Health Perspect 2002, 110, 161–171. [Google Scholar]
- Gray, W; Shadbegian, R. Optimal pollution abatement—whose benefits matter, and how much? J. Environ. Econ. Manage 2004, 47, 510–534. [Google Scholar]
- Gwynn, RC; Burnett, RT; Thurston, GD. A time-series analysis of acidic particulate matter and daily mortality and morbidity in the Buffalo, New York, region. Environ. Health Perspect 2000, 108, 125–133. [Google Scholar]
- Apelberg, BJ; Buckley, TJ; White, RH. Socioeconomic and racial disparities in cancer risk from air toxics in Maryland. Environ. Health Perspect 2005, 113, 693–699. [Google Scholar]
- Morello-Frosch, R; Jesdale, BM. Separate and unequal: Residential segregation and estimated cancer risks associated with ambient air toxics in U.S. metropolitan areas. Environ. Health Perspect 2006, 114, 386–393. [Google Scholar]
- Levy, JI; Wilson, AM; Zwack, LM. Quantifying the efficiency and equity implications of power plant air pollution control strategies in the United States. Environ. Health Perspect 2007, 115, 743–750. [Google Scholar]
- Linder, SH; Marko, D; Sexton, K. Cumulative cancer risk from air pollution in houston: Disparities in risk burden and social disadvantage. Environ. Sci. Technol 2008, 42, 4312–4322. [Google Scholar]
- Gwynn, RC; Thurston, GD. The burden of air pollution: Impacts among racial minorities. Environ. Health Perspect 2001, 109, 501–506. [Google Scholar]
- Perlin, SA; Setzer, RW; Creason, J; Sexton, K. Distribution of industrial air emissions by income and race in the United States: An approach using the toxic release inventory. Environ. Sci. Technol 1995, 29, 69–80. [Google Scholar]
- Bowen, WM; Salling, MJ; Haynes, KE; Cyran, EJ. Toward environmental justice: Spatial equity in Ohio and Cleveland. Ann. Assoc. Am. Geogr 1995, 85, 641–663. [Google Scholar]
- Bullard, RD. The legacy of american apartheid and environmental racism. St. John’s J. Legal Comment 1994, 9, 445–474. [Google Scholar]
- Lejano, RP; Iseki, H. Environmental justice: Spatial distribution of hazardous waste treatment, storage and disposal facilities in Los Angeles. J. Urban Plann. Dev 2001, 127, 51–62. [Google Scholar]
- Levy, JI; Chemerynski, SM; Tuchmann, JL. Incorporating concepts of inequality and inequity into health benefits analysis. Int J Equity Health 2006, 5, 2. [Google Scholar] [CrossRef]
- Levy, JI; Greco, SL; Melly, SJ; Mukhi, N. Evaluating efficiency-equality tradeoffs for mobile source control strategies in an urban area. Risk Anal 2009, 29, 34–47. [Google Scholar]
- U.S. EPA. Regulatory Impact Analysis: Control of Emissions of Air Pollution from Locomotive Engines and Marine Compression Ignition Engines Less than 30 Liters Per Cylinder; EPA420-R-08-001; Office of Transportation and Air Quality, Assessment and Standards Division: Washington, DC, USA, 2008. [Google Scholar]
- Abt Associates Inc. Final Heavy Duty Engine/Diesel Fuel Rule: Air Quality Estimation, Selected Health and Welfare Benefits Methods, and Benefit Analysis Results; Prepared for US EPA, Office of Air Quality Planning and Standards: Research Triangle Park, NC, USA, 2000. [Google Scholar]
- Abt Associates Inc. Environmental Benefits Mapping and Analysis Program (BenMAP), 4.0; Prepared for US EPA, Office of Air Quality Planning and Standards: Research Triangle Park, NC, USA, 2010. [Google Scholar]
- Davidson, K; Hallberg, A; McCubbin, D; Hubbell, B. Analysis of PM2.5 using the environmental benefits mapping and analysis program (BenMAP). J. Toxicol. Environ. Health A 2007, 70, 332–346. [Google Scholar]
- Woods & Poole Economics Inc. Complete Demographic Database; Woods & Poole Economics Inc: Washington, DC, USA, 2007. [Google Scholar]
- U.S. EPA. Air Quality Criteria for Particulate Matter; EPA 600/P-99/002aF-bF; U.S. EPA, Office of Air and Radiation: Washington, DC, USA, 2004. [Google Scholar]
- Cowell, FA. Measuring Inequality, 1st ed; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Atkinson, AB. On the measurement of inequality. J. Econ. Theory 1970, 2, 244–263. [Google Scholar]
- Cowell, FA. On the structure of additive inequality measures. Rev. Econ. Stud 1980, 47, 521–531. [Google Scholar]
- Lasso de la Vega, M; Urrutia, A. A new factorial decomposition for the Atkinson measure. Econ. Bull 2003, 4, 1–12. [Google Scholar]
- Krewski, D; Burnett, R; Goldberg, M; Hoover, K; Siemiatycki, J; Jerrett, M; Abrahamowicz, M; White, M. Reanalysis of the Harvard Six Cities Study and the American Cancer Society Study of Particulate Air Pollution and Mortality; Health Effects Institute: Cambridge, MA, USA, 2000; p. 295. [Google Scholar]
- Samet, J; Zeger, S; Dominici, F; Curriero, F; Coursac, I; Dockery, D; Schwartz, J; Zanobetti, A. The National Morbidity, Mortality, and Air Pollution Study; Report No 94; Health Effects Institute: Cambridge, MA, USA, 2000. [Google Scholar]
- Sheppard, L; Levy, D; Norris, G; Larson, TV; Koenig, JQ. Effects of ambient air pollution on nonelderly asthma hospital admissions in Seattle, Washington, 1987–1994. Epidemiology 1999, 10, 23–30. [Google Scholar]
- Schwartz, J; Slater, D; Larson, TV; Pierson, WE; Koenig, JQ. particulate air pollution and hospital emergency room visits for asthma in Seattle. Am. Rev. Respir. Dis 1993, 147, 826–831. [Google Scholar]
- Woodruff, TJ; Parker, JD; Schoendorf, KC. Fine particulate matter (PM2.5) air pollution and selected causes of postneonatal infant mortality in California. Environ. Health Perspect 2006, 114, 786–790. [Google Scholar]
- Pope, CA, III; Burnett, RT; Thun, MJ; Calle, EE; Krewski, D; Ito, K; Thurston, GD. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA 2002, 287, 1132–1141. [Google Scholar]
- Banzhaf, HS; Walsh, RP. Do people vote with their feet? An empirical test of Tiebout’s mechanism. Am. Econ. Rev 2008, 98, 843–863. [Google Scholar]
- Li, W. Beyond Chinatown, beyond Enclave: Reconceptualizing contemporary Chinese settlements in the United States. GeoJournal 2005, 64, 31–40. [Google Scholar]
- Min, PG. Settlement Patterns and Diversity. In Asian Americans: Contemporary Trends and Issues, 2nd ed; Min, PG, Ed.; Sage Publications Ltd: London, UK, 2006; pp. 32–53. [Google Scholar]
- Li, W. Changing Asian immigration and settlement in the Pacific Rim. New Zealand Popul Rev 2008, 33/34, 69–93. [Google Scholar]
- Fullerton, D. Distributional Effects of Environmental and Energy Policy: An Introduction. In National Bureau of Economic Research Working Paper Series; National Bureau of Economic Research: Cambridge, MA, USA, 2008. [Google Scholar]
- Morello-Frosch, R; Pastor, M; Porras, C; Sadd, J. Environmental justice and regional inequality in Southern California: Implications for future research. Environ. Health Perspect 2002, 110, 149–154. [Google Scholar]
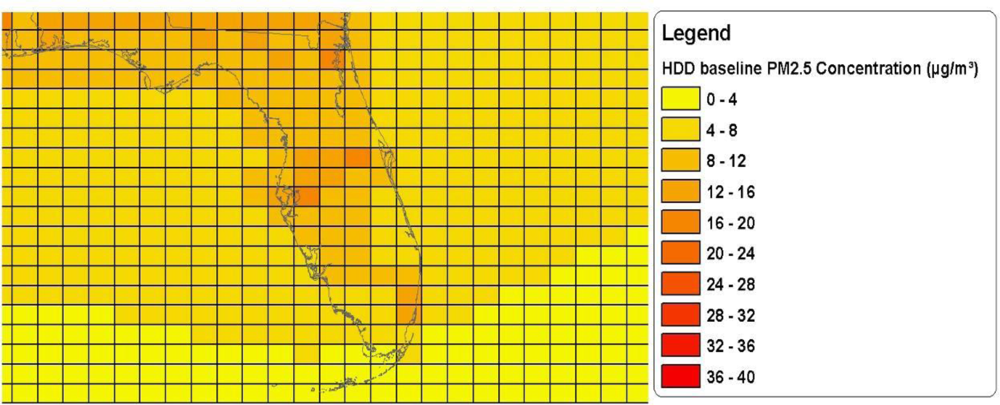
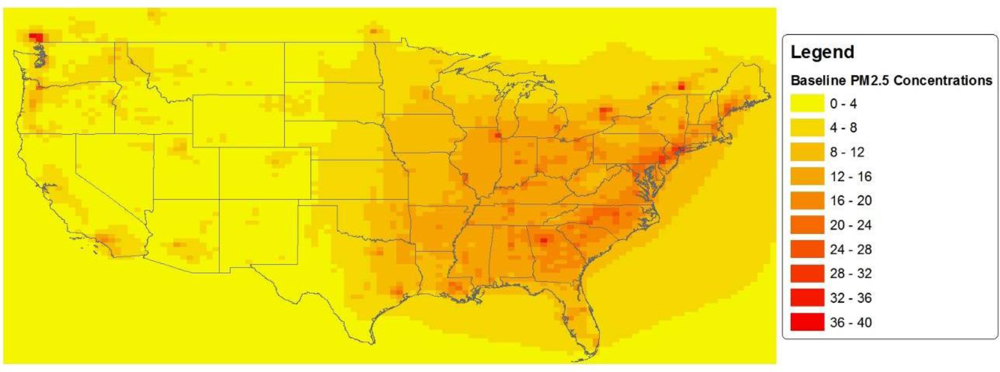
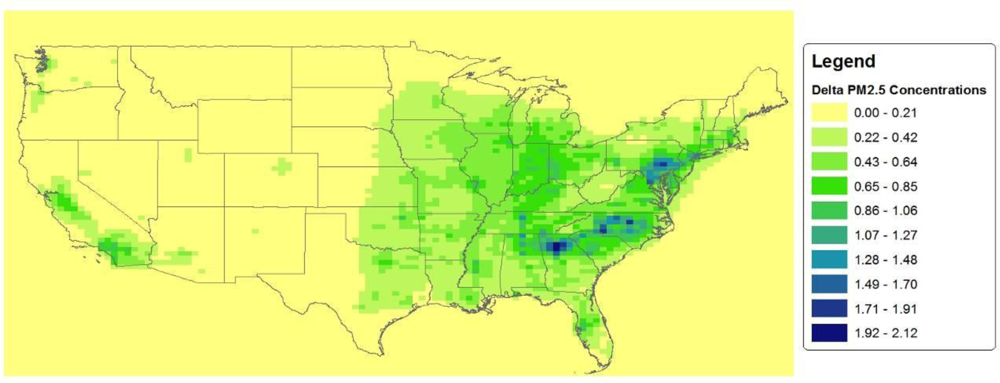


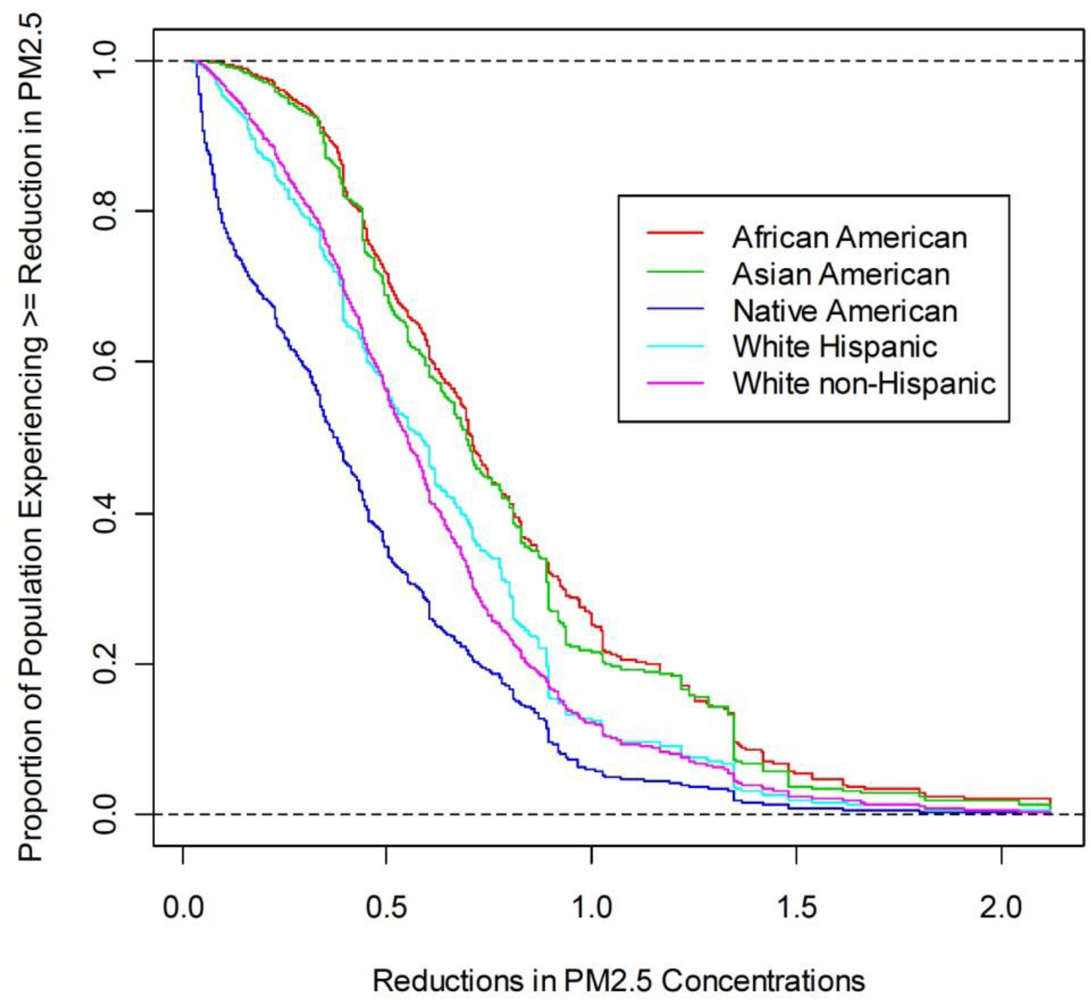
| Racial/Ethnic Subgroup | Mean (μg/m3) | SD (μg/m3) | Percentiles (μg/m3) | Atkinson Index | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5th | 25th | 50th | 75th | 95th | ɛ = 0.5 | ɛ = 1 | |||
| Baseline PM2.5 Exposures | |||||||||
| Total Population | 14.65 | 7.39 | 4.05 | 9.52 | 14.05 | 18.02 | 28.44 | 0.064 | 0.131 |
| Asian American | 16.71 | 9.13 | 5.64 | 9.53 | 15.03 | 21.31 | 39.59 | 0.072 | 0.144 |
| African American | 18.13 | 7.50 | 7.42 | 13.22 | 16.99 | 21.47 | 34.47 | 0.042 | 0.085 |
| Native American | 10.22 | 6.97 | 2.47 | 4.43 | 9.17 | 13.74 | 22.61 | 0.106 | 0.207 |
| White Hispanic | 13.39 | 8.21 | 3.38 | 6.78 | 12.40 | 17.28 | 29.32 | 0.088 | 0.176 |
| White non-Hispanic | 14.07 | 6.45 | 4.16 | 9.61 | 13.89 | 17.22 | 25.35 | 0.054 | 0.113 |
| Within-Group Inequality | 0.060 | 0.123 | |||||||
| Between-Group Inequality | 0.004 | 0.009 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 15.0 | 13.7 | |||||||
| Control Scenario PM2.5 Exposures | |||||||||
| Total Population | 14.01 | 7.07 | 3.84 | 9.15 | 13.52 | 17.22 | 27.41 | 0.063 | 0.131 |
| Asian American | 15.94 | 8.80 | 5.21 | 9.15 | 14.33 | 20.14 | 38.24 | 0.073 | 0.146 |
| African American | 17.34 | 7.17 | 7.05 | 12.75 | 16.34 | 20.61 | 32.35 | 0.042 | 0.085 |
| Native American | 9.78 | 6.66 | 2.42 | 4.24 | 8.70 | 13.15 | 21.38 | 0.104 | 0.205 |
| White Hispanic | 12.77 | 7.90 | 3.22 | 6.52 | 11.73 | 16.46 | 28.08 | 0.089 | 0.178 |
| White non-Hispanic | 13.46 | 6.15 | 4.01 | 9.25 | 13.43 | 16.45 | 23.87 | 0.054 | 0.112 |
| Within-Group Inequality | 0.060 | 0.123 | |||||||
| Between-Group Inequality | 0.004 | 0.009 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 15.0 | 13.7 | |||||||
| Racial/Ethnic Subgroup | Mean | SD | Percentiles | Atkinson Index | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5th | 25th | 50th | 75th | 95th | ɛ = 0.5 | ɛ = 1 | |||
| Absolute Reductions in PM2.5 Exposure (μg/m3) | |||||||||
| Total Population | 0.64 | 0.39 | 0.13 | 0.38 | 0.59 | 0.83 | 1.36 | 0.088 | 0.184 |
| Asian American | 0.77 | 0.41 | 0.25 | 0.45 | 0.69 | 0.93 | 1.48 | 0.068 | 0.137 |
| African American | 0.79 | 0.42 | 0.27 | 0.47 | 0.71 | 1.01 | 1.54 | 0.067 | 0.135 |
| Native American | 0.44 | 0.35 | 0.04 | 0.13 | 0.37 | 0.62 | 1.05 | 0.167 | 0.344 |
| White Hispanic | 0.62 | 0.37 | 0.11 | 0.34 | 0.59 | 0.83 | 1.35 | 0.096 | 0.202 |
| White non-Hispanic | 0.61 | 0.37 | 0.13 | 0.36 | 0.55 | 0.78 | 1.35 | 0.088 | 0.182 |
| Within-Group Inequality | 0.085 | 0.175 | |||||||
| Between-Group Inequality | 0.004 | 0.010 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 21.3 | 17.5 | |||||||
| Relative Reductions in PM2.5 Exposures (% of Baseline) | |||||||||
| Total Population | 4.39 | 1.55 | 2.25 | 3.40 | 4.15 | 5.12 | 7.16 | 0.030 | 0.060 |
| Asian American | 4.86 | 1.56 | 2.90 | 3.61 | 4.52 | 5.92 | 7.86 | 0.025 | 0.050 |
| African American | 4.33 | 1.38 | 2.55 | 3.40 | 4.09 | 5.12 | 6.90 | 0.024 | 0.048 |
| Native American | 3.97 | 1.87 | 1.44 | 2.68 | 3.77 | 4.89 | 7.68 | 0.054 | 0.108 |
| White Hispanic | 4.79 | 1.86 | 2.51 | 3.40 | 4.44 | 5.79 | 8.16 | 0.035 | 0.070 |
| White non-Hispanic | 4.22 | 1.43 | 2.08 | 3.34 | 4.10 | 4.89 | 6.90 | 0.028 | 0.058 |
| Within-Group Inequality | 0.029 | 0.059 | |||||||
| Between-Group Inequality | 0.001 | 0.002 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 29.0 | 29.5 | |||||||
| Age/Race | Baseline Incidence per Million Population | Absolute Reduction in PM2.5 Level (μg/m3) | Relative Reduction in PM2.5 Level * | Absolute Reduction in Incidence per Million Population | Relative Reduction in Incidence * |
|---|---|---|---|---|---|
| Infants (Age 0) ** | |||||
| Asian American | 2,907 | 0.71 | 1.2 | 13.7 | 0.7 |
| African American | 9,543 | 0.74 | 1.2 | 47.1 | 2.3 |
| Native American | 4,166 | 0.38 | 0.6 | 9.1 | 0.4 |
| White | 4,005 | 0.57 | 0.9 | 15.3 | 0.8 |
| Total Population | 4,816 | 0.61 | -- | 20.2 | -- |
| Adults (30 64) *** | |||||
| Asian American | 1,771 | 0.69 | 1.2 | 6.6 | 0.6 |
| African American | 5,183 | 0.73 | 1.2 | 21.7 | 2.0 |
| Native American | 2,587 | 0.40 | 0.7 | 4.7 | 0.4 |
| White | 3,027 | 0.55 | 0.9 | 9.7 | 0.9 |
| Total Population | 3,225 | 0.58 | -- | 11.1 | -- |
| Elderly (65 +) *** | |||||
| Asian American | 20,411 | 0.67 | 1.2 | 77.6 | 0.6 |
| African American | 39,783 | 0.74 | 1.3 | 170.2 | 1.4 |
| Native American | 25,344 | 0.39 | 0.7 | 52.9 | 0.4 |
| White | 37,945 | 0.54 | 1.0 | 119.7 | 1.0 |
| Total Population | 36,863 | 0.57 | -- | 121.4 | -- |
| Racial/Ethnic Subgroup | Mean | SD | Percentiles | Atkinson Index | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5th | 25th | 50th | 75th | 95th | ɛ = 0.5 | ɛ = 1 | |||
| Infants (Age 0) * | |||||||||
| Total Population | 20.2 | 14.7 | 2.8 | 9.6 | 17.0 | 26.5 | 50.1 | 0.158 | 0.305 |
| Asian American | 13.7 | 9.8 | 3.2 | 7.4 | 11.3 | 17.4 | 33.8 | 0.105 | 0.224 |
| African American | 47.1 | 26.6 | 11.3 | 26.2 | 41.4 | 67.2 | 97.0 | 0.084 | 0.175 |
| Native American | 9.1 | 8.4 | 1.3 | 3.0 | 6.8 | 12.2 | 25.4 | 0.170 | 0.343 |
| White | 15.3 | 10.2 | 2.3 | 7.8 | 13.6 | 20.1 | 35.3 | 0.111 | 0.230 |
| Within-Group Inequality | 0.101 | 0.210 | |||||||
| Between-Group Inequality | 0.064 | 0.121 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 1.6 | 1.7 | |||||||
| Adults (30 64) ** | |||||||||
| Total Population | 11.1 | 7.4 | 1.6 | 5.6 | 9.8 | 14.5 | 24.8 | 0.129 | 0.261 |
| Asian American | 6.6 | 3.8 | 1.6 | 4.0 | 5.9 | 8.8 | 12.4 | 0.078 | 0.159 |
| African American | 21.7 | 11.8 | 5.4 | 13.4 | 19.2 | 29.3 | 44.0 | 0.077 | 0.163 |
| Native American | 4.7 | 3.9 | 0.8 | 1.7 | 3.7 | 6.5 | 11.7 | 0.148 | 0.287 |
| White | 9.7 | 6.3 | 1.5 | 4.9 | 8.8 | 13.1 | 22.3 | 0.109 | 0.230 |
| Within-Group Inequality | 0.099 | 0.209 | |||||||
| Between-Group Inequality | 0.033 | 0.066 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 3.0 | 3.2 | |||||||
| Elderly (65+) ** | |||||||||
| Total Population | 121.4 | 79.7 | 18.1 | 62.2 | 107.9 | 160.4 | 278.6 | 0.115 | 0.239 |
| Asian American | 77.6 | 44.5 | 16.1 | 45.7 | 70.4 | 101.6 | 164.7 | 0.086 | 0.179 |
| African American | 170.2 | 92.9 | 41.3 | 97.9 | 157.8 | 231.3 | 328.9 | 0.079 | 0.164 |
| Native American | 52.9 | 47.9 | 6.2 | 14.7 | 40.3 | 75.5 | 158.2 | 0.185 | 0.362 |
| White | 119.7 | 80.7 | 17.3 | 57.9 | 105.5 | 160.1 | 283.5 | 0.114 | 0.238 |
| Within-Group Inequality | 0.109 | 0.226 | |||||||
| Between-Group Inequality | 0.008 | 0.018 | |||||||
| Ratio of Within-Group Inequality to Between-Group Inequality | 14.1 | 12.8 | |||||||
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Post, E.S.; Belova, A.; Huang, J. Distributional Benefit Analysis of a National Air Quality Rule. Int. J. Environ. Res. Public Health 2011, 8, 1872-1892. https://doi.org/10.3390/ijerph8061872
Post ES, Belova A, Huang J. Distributional Benefit Analysis of a National Air Quality Rule. International Journal of Environmental Research and Public Health. 2011; 8(6):1872-1892. https://doi.org/10.3390/ijerph8061872
Chicago/Turabian StylePost, Ellen S., Anna Belova, and Jin Huang. 2011. "Distributional Benefit Analysis of a National Air Quality Rule" International Journal of Environmental Research and Public Health 8, no. 6: 1872-1892. https://doi.org/10.3390/ijerph8061872
APA StylePost, E. S., Belova, A., & Huang, J. (2011). Distributional Benefit Analysis of a National Air Quality Rule. International Journal of Environmental Research and Public Health, 8(6), 1872-1892. https://doi.org/10.3390/ijerph8061872




