A Simple Model of Tetracycline Antibiotic Resistance in the Aquatic Environment (with Application to the Poudre River)
Abstract
:1. Introduction
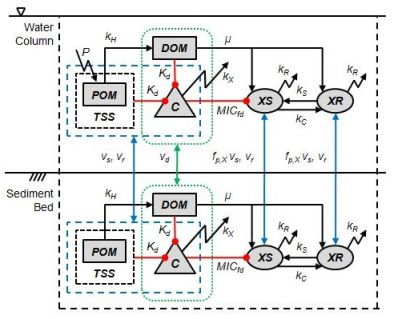
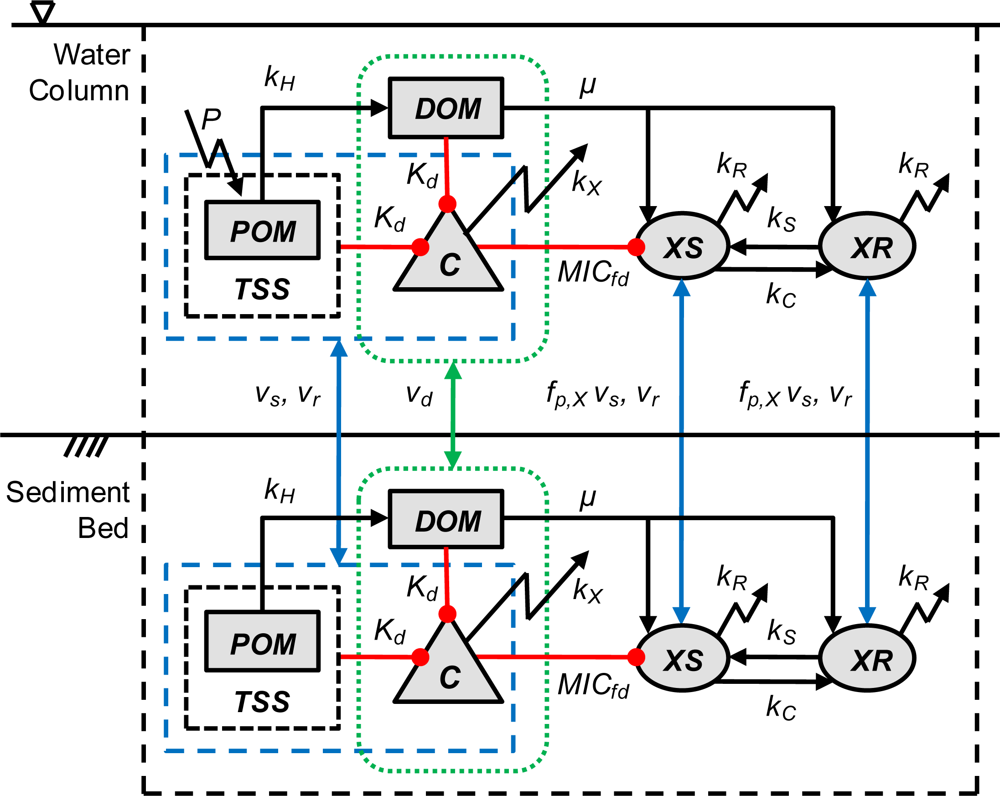
2. Model Description
2.1. Tetracycline
2.2. Bacteria
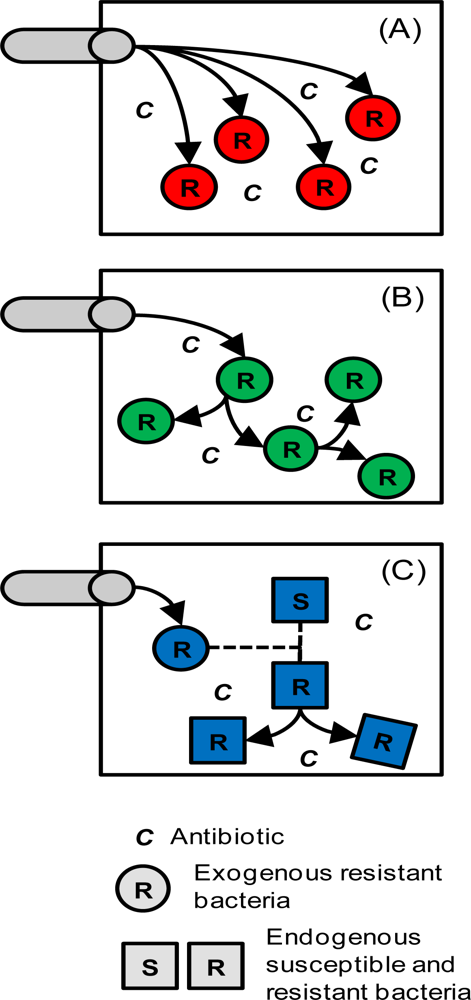
2.3. Tetracycline Action, Resistance, Cost of Resistance and Transfer of Resistance
2.4. Bioavailability of Tetracycline
2.5. Organic Matter
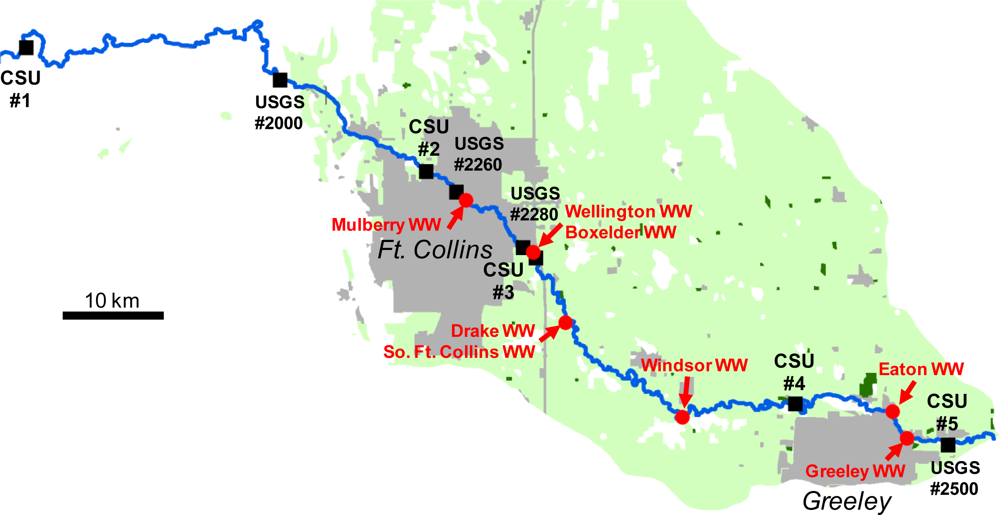
3. Poudre River Application
3.1. Model Input
3.2. Simulations Performed
4. Results & Discussion
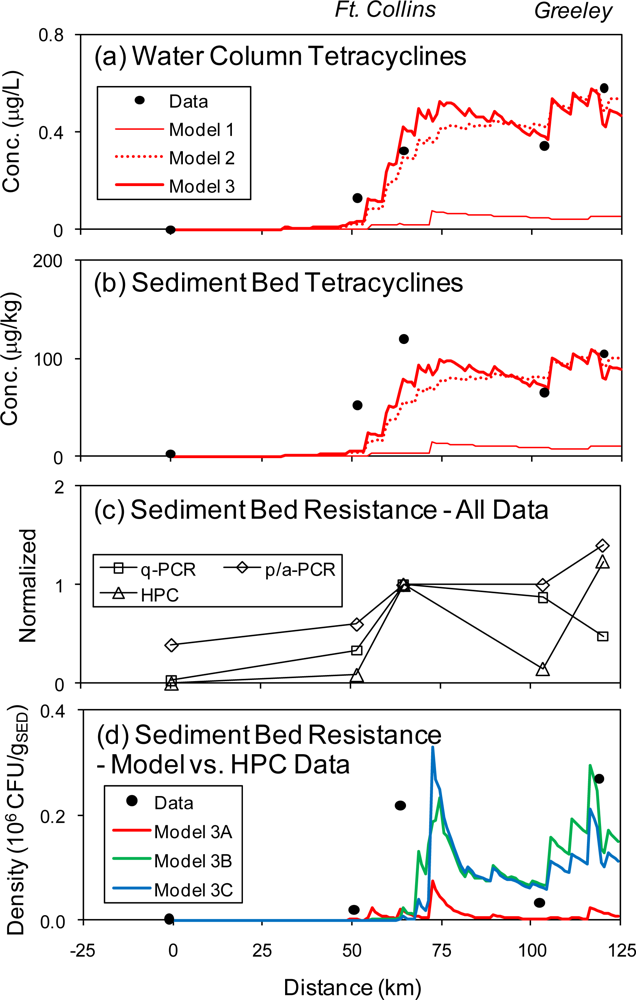
4.1. Tetracyclines Concentration
4.2. Tetracycline Resistance
5. Outlook
Supplementary Information
ijerph-08-00480-s001.doc ijerph-08-00480-s002.pdfAcknowledgments
- Supporting Information AvailableFull model equations, input data and discussion, and additional results.
References and Notes
- Levy, SB; Marshall, B. Antibacterial resistance worldwide: Causes, challenges and responses. Nat. Med 2004, 10, S122–S129. [Google Scholar]
- Webb, GF; D’Agata, EMC; Magal, P; Ruan, S. A model of antibiotic-resistant bacterial epidemics in hospitals. PNAS 2005, 102, 13343–13348. [Google Scholar]
- Kümmerer, K. Resistance in the environment. J. Antimicrob. Chemother 2004, 54, 311–320. [Google Scholar]
- Pruden, A; Pei, R; Storteboom, H; Carlson, KH. Antibiotic resistance genes as emerging contaminants: Studies in Northern Colorado. Environ. Sci. Tech 2006, 40, 7445–7450. [Google Scholar]
- Goñi-Urriza, M; Capdepuy, M; Arpin, C; Raymond, N; Caumette, P; Quentin, C. Impact of an urban effluent on antibiotic resistance of riverine Enterobacteriaceae and Aeromonas spp. Appl. Environ. Microbiol 2000, 66, 125–132. [Google Scholar]
- Tao, R; Ying, G-G; Su, H-C; Zhou, H-W; Sidhu, JPS. Detection of antibiotic resistance and tetracycline resistance genes in Enterobacteriaceae isolated from the Pearl rivers in South China. Environ. Poll 2010, 158, 2101–2109. [Google Scholar]
- Grabow, WOK; Prozesky, OW; Burger, JS. Behaviour in a river and dam of coliform bacteria with transferable or non-transferable drug resistance. Water Res 1975, 9, 777–782. [Google Scholar]
- Haack, BJ; Andrews, RE, Jr. Isolation of Tn916-like conjugal elements from swine lot effluent. Can. J. Microbiol 2000, 46, 542–549. [Google Scholar]
- Nygaard, K; Lunestad, BT; Hektoen, H; Berge, JA; Hormazabal, V. Resistance to oxytetracycline, oxolinic acid and furazolidone in bacteria from marine sediments. Aquaculture 1992, 104, 31–36. [Google Scholar]
- Muñoz-Aguayo, J; Lang, KS; LaPara, TM; González, G; Singer, RS. Evaluating the effects of chlortetracycline on the proliferation of antibiotic-resistant bacteria in a simulated river water ecosystem. Appl. Environ. Microbiol 2007, 73, 5421–5425. [Google Scholar]
- Knapp, CW; Engemann, CA; Hanson, ML; Keen, PL; Hall, KJ; Graham, DW. Indirect evidence of transposon-mediated selection of antibiotic resistance genes in aquatic systems at low-level oxytetracycline exposures. Environ. Sci. Technol 2008, 42, 5348–5353. [Google Scholar]
- Ashelford, KE; Fry, JC; Day, MJ; Hill, KE; Learner, MA; Marchesi, JR; Perkins, CD; Weightman, AJ. Using microcosms to study gene transfer in aquatic habitats. FEMS Microbiol. Eco 1997, 23, 81–94. [Google Scholar]
- Stewart, KR; Koditschek, L. Drug-resistance transfer in Escherichia coli in New York bight sediment. Mar. Poll. Bull 1980, 11, 130–133. [Google Scholar]
- Baker-Austin, C; Wright, MS; Stepanauskas, R; McArthur, JV. Co-selection of antibiotic and metal resistance. Trends Microbiol 2006, 14, 176–182. [Google Scholar]
- Rose, PE; Pedersen, JA. Fate of oxytetracycline in streams receiving aquaculture discharges: Model simulations. Environ. Toxicol. Chem 2005, 24, 40–50. [Google Scholar]
- Anderson, PD; D’Aco, VJ; Shanahan, P; Chapra, SC; Buzby, ME; Cunningham, VL; DuPlessie, BM; Hayes, EP; Mastrocco, FJ; Parke, NJ; Rader, JC; Samuelian, JH; Schwab, BW. Screening analysis of human pharmaceutical compounds in U.S. surface waters. Environ. Sci. Technol 2004, 38, 838–849. [Google Scholar]
- Connolly, JP; Coffin, RB; Landeck, RE. Modeling carbon utilization by bacteria in natural water systems. In Modeling the Metabolic and Physiologic Activities of Microorganisms; Hurst, CJ, Ed.; John Wiley & Sons. Inc: New York, NY, USA, 1992; pp. 249–276. [Google Scholar]
- Servais, P; Anzil, A; Ventresque, C. A simple method for the determination of biodegradable dissolved organic carbon in water. Appl. Environ. Microbiol 1989, 55, 2732–2734. [Google Scholar]
- Vital, M; Hammes, F; Egli, T. Escherichia coli O157 can grow in natural fresh water at low carbon concentrations. Environ. Microbiol 2008, 10, 2387–2396. [Google Scholar]
- Schnoor, JL. Environmental Modeling: Fate and Transport of Pollutants in Water, Air and Soil; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Chapra, SC. Surface Water-Quality Modeling; McGraw-Hill: Boston, MT, USA, 1997. [Google Scholar]
- Werner, JJ; Arnold, WA; McNeill, K. Water hardness as a photochemical parameter: Tetracycline photolysis as a function of calcium concentration, magnesium concentration, and pH. Environ. Sci. Tech 2006, 40, 7236–7241. [Google Scholar]
- Figueroa, RA; Leonard, A; MacKay, AA. Modeling tetracycline antibiotic sorption to clays. Environ. Sci. Technol 2004, 38, 476–483. [Google Scholar]
- Sithole, BB; Guy, RD. Models for tetracycline in aquatic environments. Water, Air, Soil Pollut 1987, 32, 303–314. [Google Scholar]
- Tolls, J. Sorption of veterinary pharmaceuticals in soils: A review. Environ. Sci. Technol 2001, 35, 3397–3406. [Google Scholar]
- Chopra, I; Roberts, M. Tetracycline antibiotics: Mode of action, applications, molecular biology, and epidemiology of bacterial resistance. Microbiol. Mol. Biol. Rev 2001, 65, 232–260. [Google Scholar]
- Garrett, ER; Miller, GH; Brown, MRW. Kinetics and mechanisms of action of antibiotics on microorganisms V chloramphenicol and tetracycline affected Escherichia coli generation rates. J. Pharm. Sci 1966, 55, 593–600. [Google Scholar]
- Björkman, J; Andersson, DI. The cost of antibiotic resistance from a bacterial perspective. Drug Resist. Updat 2000, 3, 237–245. [Google Scholar]
- Bouma, JE; Lenski, RE. Evolution of a bacterial/plasmid association. Nature 1988, 335, 351–352. [Google Scholar]
- Stewart, FM; Levin, BR. The population biology of bacterial plasmids: A priori conditions for the existence of conjugationally transmitted factors. Genetics 1977, 87, 209–228. [Google Scholar]
- Di Toro, DM; Zarba, CS; Hansen, DJ; Berry, WJ; Swartz, RC; Cowan, CE; Pavlou, SP; Allen, HE; Thomas, NA; Paquin, PR. Technical basis for establishing sediment quality criteria for nonionic organic chemicals using equilibrium partitioning. Environ. Toxicol. Chem 1991, 10, 1541–1583. [Google Scholar]
- Garrett, ER; Miller, GH. Kinetics and mechanisms of action of antibiotics on microorganisms III. Inhibitory action of tetracycline and chloramphenicol on Escherichia coli established by total and viable counts. J. Pharm. Sci 1965, 54, 427–431. [Google Scholar]
- Lunestad, BT; Goksoeyr, J. Reduction in the antibacterial effect of oxytetracycline in sea water by complex formation with magnesium and calcium. Dis. Aquat. Organ 1990, 9, 67–72. [Google Scholar]
- Halling-Sørensen, B; Sengeløv, G; Ingerslev, F; Jensen, LB. Reduced antimicrobial potencies of oxytetracycline, tylosin, sulfadiazin, streptomycin, ciprofloxacin, and olaquindox due to environmental processes. Arch. Environ. Cont. Toxicol 2003, 44, 7–16. [Google Scholar]
- Chander, Y; Kumar, K; Goyal, SM; Gupta, SC. Antibacterial activity of soil-bound antibiotics. J. Environ. Qual 2005, 34, 1952–1957. [Google Scholar]
- Kim, SC; Carlson, K. Temporal and spatial trends in the occurrence of human and veterinary antibiotics in aqueous and river sediment matrices. Environ. Sci. Tech 2007, 41, 50–57. [Google Scholar]
- Yang, S; Carlson, K. Evolution of antibiotic occurrence in a river through pristine, urban and agricultural landscapes. Water Res 2003, 37, 4645–4656. [Google Scholar]
- Yang, S; Carlson, K. Routine monitoring of antibiotics in water and wastewater with a radioimmunoassay technique. Water Res 2004, 38, 3155–3166. [Google Scholar]
- Yang, S; Cha, J; Carlson, K. Simultaneous extraction and analysis of 11 tetracycline and sulfonamide antibiotics in influent and effluent domestic wastewater by solid-phase extraction and liquid chromatography-electrospray ionization tandem mass spectrometry. J. Chrom. A 2005, 1097, 40–53. [Google Scholar]
- Kim, SC; Carlson, K. Quantification of human and veterinary antibiotics in water and sediment using SPE/LC/MS/MS. Anal. Bioanal. Chem 2007, 387, 1301–1315. [Google Scholar]
- Pei, R; Kim, S-C; Carlson, KH; Pruden, A. Effect of river landscape on the sediment concentrations of antibiotics and corresponding antibiotic resistance genes (ARG). Water Res 2006, 40, 2427–2435. [Google Scholar]
- Storteboom, H; Arabi, M; Davis, JG; Crimi, B; Pruden, A. Identification of antibiotic-resistance-gene molecular signatures suitable as tracers of pristine river, urban, and agricultural sources. Environ. Sci. Technol 2010, 44, 1947–1953. [Google Scholar]
- Handelsman, J. Metagenomics: Application of genomics to uncultured microorganisms. Microbiol. Mol. Biol. Rev 2004, 68, 669–685. [Google Scholar]
- Kolpin, DW; Furlong, ET; Meyer, MT; Thurman, EM; Zaugg, SD; Barber, LB; Buxton, HT. Pharmaceuticals, hormones, and other organic wastewater contaminants in U.S. streams, 1999−2000: A national reconnaissance. Environ. Sci. Tech 2002, 36, 1202–1211. [Google Scholar]
- Antimicrobial Agents: Antibacterials and Antifungals; Bryskier, A (Ed.) ASM Press: Washington, DC, USA, 2005.
- Lebek, G; Egger, R. R-selection of subbacteriostatic tetracyclin-concentrations. Zentralbl. Bakteriol. Mikrobiol. Hyg. A 1983, 255, 340–345. [Google Scholar]
- Thanassi, DG; Suh, GS; Nikaido, H. Role of outer membrane barrier in efflux-mediated tetracycline resistance of Escherichia coli. J. Bacteriol 1995, 177, 998–1007. [Google Scholar]
- Hellweger, FL. Resonating circadian clocks enhance fitness in cyanobacteria in silico. Ecol. Model 2010, 221, 1620–1629. [Google Scholar]
| symbol | units | value | literature(b) |
|---|---|---|---|
| Kd,solid | log L·kgS−1 | 2.3 | −0.52–5.5 |
| Kd,DOM | log L·kgC−1 | 4.2 | 3.2–5.4 |
| kX | d−1 | 0, 1.0(c) | 0.046–43 (d) |
| MICfd | μg·L−1 | 13 | 12–14 |
| α | % | 1.0, 100 (e) | −3.7–89 |
| kS | d−1 | 0, 4.0 × 10−3 (f) | 0–0.13 |
| kC | L·mgC−1·d−1 | 0, 1.0 × 10−5 (f) | 0–1.0 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hellweger, F.L.; Ruan, X.; Sanchez, S. A Simple Model of Tetracycline Antibiotic Resistance in the Aquatic Environment (with Application to the Poudre River). Int. J. Environ. Res. Public Health 2011, 8, 480-497. https://doi.org/10.3390/ijerph8020480
Hellweger FL, Ruan X, Sanchez S. A Simple Model of Tetracycline Antibiotic Resistance in the Aquatic Environment (with Application to the Poudre River). International Journal of Environmental Research and Public Health. 2011; 8(2):480-497. https://doi.org/10.3390/ijerph8020480
Chicago/Turabian StyleHellweger, Ferdi L., Xiaodan Ruan, and Sarah Sanchez. 2011. "A Simple Model of Tetracycline Antibiotic Resistance in the Aquatic Environment (with Application to the Poudre River)" International Journal of Environmental Research and Public Health 8, no. 2: 480-497. https://doi.org/10.3390/ijerph8020480
APA StyleHellweger, F. L., Ruan, X., & Sanchez, S. (2011). A Simple Model of Tetracycline Antibiotic Resistance in the Aquatic Environment (with Application to the Poudre River). International Journal of Environmental Research and Public Health, 8(2), 480-497. https://doi.org/10.3390/ijerph8020480