Hotspot Analysis of Spatial Environmental Pollutants Using Kernel Density Estimation and Geostatistical Techniques
Abstract
:1. Introduction
2. Methods and Materials
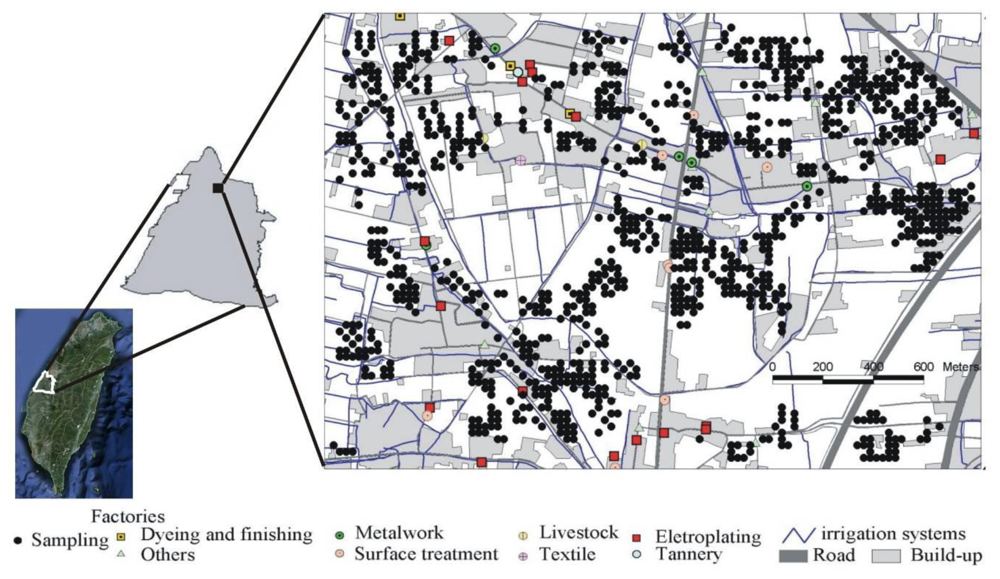
2.1. Study Area and Soil Sampling
2.2. Kernel Density Estimation (KDE)
2.3. Indicator Kriging (IK)
2.4. Sequential Indicator Simulation (SIS)
- Define a random path that visits each location of the domain once, in which all nodes {si, i = 1,N} ··· discretizing the interest domain. A random visiting sequence ensures that no spatial continuity artifact is introduced into the simulation by a specific path visiting N nodes.
- At the first visited nodes (s1):
- Model, using either a parametric or nonparametric approach, the local ccdf of z(s1) conditional on n original data {z(sα),α =1,···,n}:
- Generate, via the Monte Carlo drawing relation, a simulated value z(l) (s1) from this ccdf FZ (s1 ; z1 | (n)), and add it to the conditioning data set, now of dimension n +1, to be used for all subsequent local ccdf determinations.
- At the ith node si along the random path:
- Model the local ccdf of z(si) conditional on n original data and the i −1 near previously simulated values:
- Generate a simulated value z(l) (si) from this ccdf, and add it to the conditioning data set, now of dimension n + i.
- Repeat step 3 until all N nodes along the random path are visited.
3. Results and Discussion
3.1. Basic Statistics
3.2. Point Pattern Analysis Using Kernel Density Estimation (KDE)
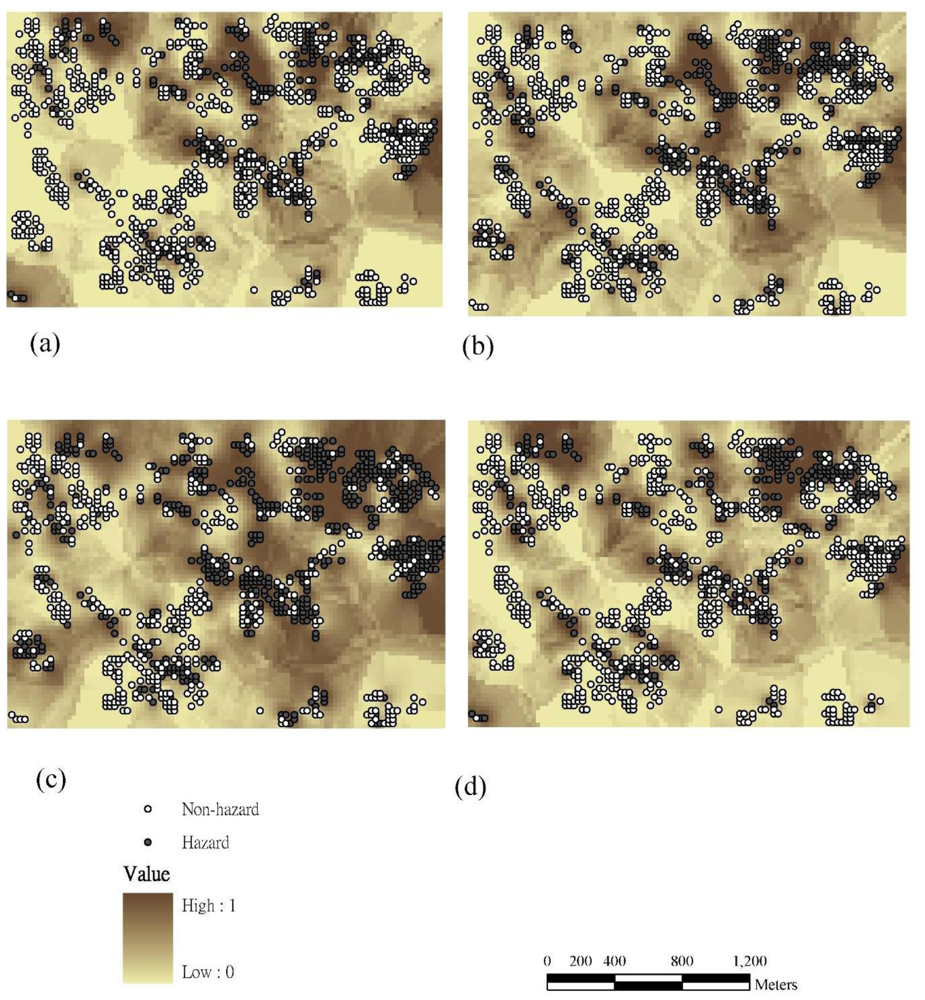
3.3. Sampling Density and Spatial Interpolation of Probability Exceeding Control Standards Using the IK and SIS Approaches
3.4. Comparisons of Hotspot Visualizations by Various Methods
4. Conclusions
Acknowledgements
References and Notes
- Yu, H; Wang, JL; Fang, W; Yuan, JG; Yang, ZY. Cadmium accumulation in different rice cultivars and screening for pollution-safe cultivars of rice. Sci. Total E 2006, 370, 302–309. [Google Scholar]
- Hossain, MF. Arsenic contamination in Bangladesh—an overview. Agr. Eco. Env 2006, 113, 1–16. [Google Scholar]
- Rehman, W; Zeb, A; Noor, N; Nawaz, M. Heavy metal pollution assessment in various industries of Pakistan. Envir. Geol 2008, 55, 353–358. [Google Scholar]
- Shomar, B. Sources and build up of Zn, Cd, Cr and Pb in the sludge of Gaza. Env. Mon. Ass 2009, 155, 51–62. [Google Scholar]
- Goovaerts, P. Geostatistical modelling of uncertainty in soil science. Geoderma 2001, 103, 3–26. [Google Scholar]
- van Meirvenne, M; Goovaerts, P. Evaluating the probability of exceeding a site-specific soil cadmium contamination threshold. Geoderma 2001, 102, 75–100. [Google Scholar]
- Amini, M. Mapping risk of cadmium and lead contamination to human health in soils of Central Iran. Sci. Total E 2005, 347, 64–77. [Google Scholar]
- Lin, YP. Multivariate geostatistical methods to identify and map spatial variations of soil heavy metals. Envir. Geol 2002, 42, 1–10. [Google Scholar]
- Hassan, MM; Atkins, PJ. Arsenic risk mapping in Bangladesh: a simulation technique of cokriging estimation from regional count data. J. Environ. Sci. Health A 2007, 42, 1719–1728. [Google Scholar]
- Goovaerts, P. Geostatistics in soil science: state-of-the-art and perspectives. Geoderma 1999, 89, 1–45. [Google Scholar]
- Goovaerts, P. Soares, A, Gómez-Hernández, J, Froidevaux, R, Eds.; Kriging vs. stochastic simulation for risk analysis in soil contamination. In geoENV I—Geostatistics for Environmental Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; pp. 247–258. [Google Scholar]
- Lin, YP; Chang, TK; Shih, CW; Tseng, CH. Factorial and indicator kriging methods using a geographic information system to delineate spatial variation and pollution sources of soil heavy metals. Envir. Geol 2002, 42, 900–909. [Google Scholar]
- Brus, DJ; de Gruijter, JJ; Walvoort, DJJ; de Vries, F; Bronswijk, JJB; Romkens, PFAM; de Vries, W. Mapping the probability of exceeding critical thresholds for cadmium concentrations in soils in the Netherlands. J. Envir. Q 2002, 31, 1875–1884. [Google Scholar]
- Huang, SS; Liao, QL; Hua, M; Wu, XM; Bi, KS; Yan, CY; Chen, B; Zhang, XY. Survey of heavy metal pollution and assessment of agricultural soil in Yangzhong district, Jiangsu Province, China. Chemosphere 2007, 67, 2148–2155. [Google Scholar]
- Lin, YP; Cheng, BY; Shyu, GS; Chang, TK. Combining a finite mixture distribution model with indicator kriging to delineate and map the spatial patterns of soil heavy metal pollution in Chunghua County, central Taiwan. Environ. Pollut 2010, 158, 235–244. [Google Scholar]
- Chu, HJ; Lin, YP; Jang, CS; Chang, TK. Delineating the hazard zone of multiple soil pollutants by multivariate indicator kriging and conditioned Latin hypercube sampling. Geoderma 2010, 158, 242–251. [Google Scholar]
- Deutsch, CV; Journel, AG. GSLIB, Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Juang, KW; Chen, YS; Lee, DY. Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils. Environ. Pollut 2004, 127, 229–238. [Google Scholar]
- Zhao, YC; Shi, XZ; Yu, DS; Wang, HJ; Sun, WX. Uncertainty assessment of spatial patterns of soil organic carbon density using sequential indicator simulation, a case study of Hebei province, China. Chemosphere 2005, 59, 1527–1535. [Google Scholar]
- Bailey, TC; Gatrell, AC. Interactive Spatial Data Analysis; Longman: Essex, UK, 1995. [Google Scholar]
- Silverman, BW. Density Estimation for Statistics and Data Analysis; Chapman Hall: London, UK, 1986. [Google Scholar]
- Xie, ZX; Yan, J. Kernel Density Estimation of traffic accidents in a network space. Comput. Environ. Urban 2008, 32, 396–406. [Google Scholar]
- Schnabel, U; Tietje, O. Explorative data analysis of heavy metal contaminated soil using multidimensional spatial regression. Envir. Geol 2003, 44, 893–904. [Google Scholar]
- Serra-Sogas, N; O’Hara, PD; Canessa, R; Keller, P; Pelot, R. Visualization of spatial patterns and temporal trends for aerial surveillance of illegal oil discharges in western Canadian marine waters. Mar. Pollut. Bull 2008, 56, 825–833. [Google Scholar]
- Lin, YP; Chu, HJ; Hwang, YL; Chen, BY; Chang, TK. Modeling spatial uncertainty of heavy metals content in soil by conditional latin hypercube sampling and geostatistical simulation. Environ. Earth Sciences 2010, (in press). [Google Scholar]
- Kyriakidis, PC. Hunsaker, CT, Goodchild, MF, Friedl, MA, Case, TJ, Eds.; Geostatistical models of uncertainty for spatial data. In Spatial Uncertainty in Ecology: Implications for Remote Sensing and GIS Applications; Springer-Verlag: New York, NY, USA, 2001; pp. 175–213. [Google Scholar]
- Zhang, C; Tang, Y; Luo, L; Xu, W. Outlier identification and visualization for Pb concentrations in urban soils and its implications for identification of potential contaminated land. Environ. Pollut 2009, 157, 3083–3090. [Google Scholar]
- Wang, XJ; Qi, F. The effects of sampling design on spatial structure analysis of contaminated soil. Sci. Total Environ 1998, 224, 29–41. [Google Scholar]
- Lin, YP; Chang, TK. Geostatistical simulation and estimation of the spatial variability of soil zinc. J. Environ. Sci. Health A 2000, 35, 327–347. [Google Scholar]
- Chang, LC; Chu, HJ; Hsiao, CT. Optimal planning of a dynamic pump-treat-inject groundwater remediation system. J. Hydrol 2007, 342, 295–304. [Google Scholar]
- Telesca, L; Caggiano, R; Lapenna, V; Lovallo, M; Trippetta, S; Macchiato, M. The Fisher information measure and Shannon entropy for particulate matter measurements. Phys. Stat. Mech. Appl 2008, 387, 4387–4392. [Google Scholar]
- Telesca, L; Caggiano, R; Lapenna, V; Lovallo, M; Trippetta, S; Macchiato, M. Analysis of dynamics in Cd, Fe and Pb particulate matter by using the Fisher-Shannon method. Water Air Soil Pollut 2009, 201, 33–41. [Google Scholar]
- Yu, HL; Chu, HJ. Understanding space-time patterns of groundwater systems by empirical orthogonal functions: a case study in the Choshui River Alluvial Fan, Taiwan. J. Hydrol 2010, 381, 239–247. [Google Scholar]


| Min (mg/kg) | Median (mg/kg) | Max (mg/kg) | Average (mg/kg) | SD (mg/kg) | Control standards (mg/kg) | Number of observances over control standards | |
|---|---|---|---|---|---|---|---|
| Cr | 22.6 | 119.0 | 3,070.0 | 194.0 | 212.5 | 250 | 286 |
| Cu | 11.0 | 116.0 | 3,810.0 | 194.7 | 222.7 | 200 | 395 |
| Ni | 21.3 | 189.2 | 4,020.0 | 271.3 | 259.0 | 200 | 622 |
| Zn | 60.5 | 337.0 | 7,850.0 | 526.4 | 549.6 | 600 | 336 |
| Threshold (mg/kg) | Model | C0 | C0+C | R (m) | RSS | r2 | |
|---|---|---|---|---|---|---|---|
| Cr | 250 | Exp. | 0.0237 | 0.1874 | 120 | 2.52E-04 | 0.859 |
| Cu | 200 | Exp. | 0.0251 | 0.2202 | 135 | 3.08E-04 | 0.904 |
| Ni | 200 | Exp. | 0.0206 | 0.2352 | 249 | 3.39E-03 | 0.723 |
| Zn | 600 | Exp. | 0.0221 | 0.2042 | 147 | 6.05E-04 | 0.808 |
| Heavy metal | Model | Parameters | RSS | r2 | |||
|---|---|---|---|---|---|---|---|
| C0 | C0+C | R (m) | |||||
| Cr | 25% | Exp. | 0.020 | 0.184 | 216 | 1.730E-03 | 0.722 |
| 50% | Exp. | 0.026 | 0.247 | 171 | 1.202E-03 | 0.807 | |
| 75% | Exp. | 0.025 | 0.190 | 120 | 2.075E-04 | 0.852 | |
| Cu | 25% | Exp. | 0.017 | 0.184 | 240 | 2.008E-03 | 0.737 |
| 50% | Exp. | 0.025 | 0.247 | 186 | 7.016E-04 | 0.899 | |
| 75% | Exp. | 0.024 | 0.190 | 108 | 5.293E-04 | 0.663 | |
| Ni | 25% | Exp. | 0.015 | 0.179 | 222 | 2.614E-03 | 0.634 |
| 50% | Exp. | 0.022 | 0.237 | 228 | 3.608E-03 | 0.671 | |
| 75% | Exp. | 0.018 | 0.183 | 159 | 5.723E-04 | 0.805 | |
| Zn | 25% | Exp. | 0.024 | 0.190 | 222 | 1.464E-03 | 0.768 |
| 50% | Exp. | 0.028 | 0.250 | 171 | 3.795E-04 | 0.936 | |
| 75% | Exp. | 0.021 | 0.189 | 144 | 8.077E-03 | 0.710 | |
| Critical probability(pc) | Number of grid which value is over pc | Density value (L/m2) | ||
|---|---|---|---|---|
| Mean | Range | |||
| Cr | 0.6 | 591 | 0.00028 | 0.00066 |
| 0.7 | 467 | 0.00031 | 0.00066 | |
| 0.8 | 373 | 0.00033 | 0.00066 | |
| 0.9 | 310 | 0.00034 | 0.00066 | |
| Cu | 0.6 | 851 | 0.00029 | 0.00082 |
| 0.7 | 643 | 0.00032 | 0.00081 | |
| 0.8 | 505 | 0.00034 | 0.00080 | |
| 0.9 | 403 | 0.00036 | 0.00080 | |
| Ni | 0.6 | 2,157 | 0.00023 | 0.00071 |
| 0.7 | 1,554 | 0.00027 | 0.00070 | |
| 0.8 | 1,099 | 0.00030 | 0.00067 | |
| 0.9 | 773 | 0.00032 | 0.00067 | |
| Zn | 0.6 | 709 | 0.00028 | 0.00079 |
| 0.7 | 560 | 0.00030 | 0.00079 | |
| 0.8 | 453 | 0.00032 | 0.00079 | |
| 0.9 | 379 | 0.00033 | 0.00079 | |
© 2011 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lin, Y.-P.; Chu, H.-J.; Wu, C.-F.; Chang, T.-K.; Chen, C.-Y. Hotspot Analysis of Spatial Environmental Pollutants Using Kernel Density Estimation and Geostatistical Techniques. Int. J. Environ. Res. Public Health 2011, 8, 75-88. https://doi.org/10.3390/ijerph8010075
Lin Y-P, Chu H-J, Wu C-F, Chang T-K, Chen C-Y. Hotspot Analysis of Spatial Environmental Pollutants Using Kernel Density Estimation and Geostatistical Techniques. International Journal of Environmental Research and Public Health. 2011; 8(1):75-88. https://doi.org/10.3390/ijerph8010075
Chicago/Turabian StyleLin, Yu-Pin, Hone-Jay Chu, Chen-Fa Wu, Tsun-Kuo Chang, and Chiu-Yang Chen. 2011. "Hotspot Analysis of Spatial Environmental Pollutants Using Kernel Density Estimation and Geostatistical Techniques" International Journal of Environmental Research and Public Health 8, no. 1: 75-88. https://doi.org/10.3390/ijerph8010075
APA StyleLin, Y.-P., Chu, H.-J., Wu, C.-F., Chang, T.-K., & Chen, C.-Y. (2011). Hotspot Analysis of Spatial Environmental Pollutants Using Kernel Density Estimation and Geostatistical Techniques. International Journal of Environmental Research and Public Health, 8(1), 75-88. https://doi.org/10.3390/ijerph8010075








