Application of Bayesian Methods to Exposure Assessment of Area Concentrations at a Rubber Factory
Abstract
:1. Introduction
2. Study Factory and Methods
2.1. Study Factory
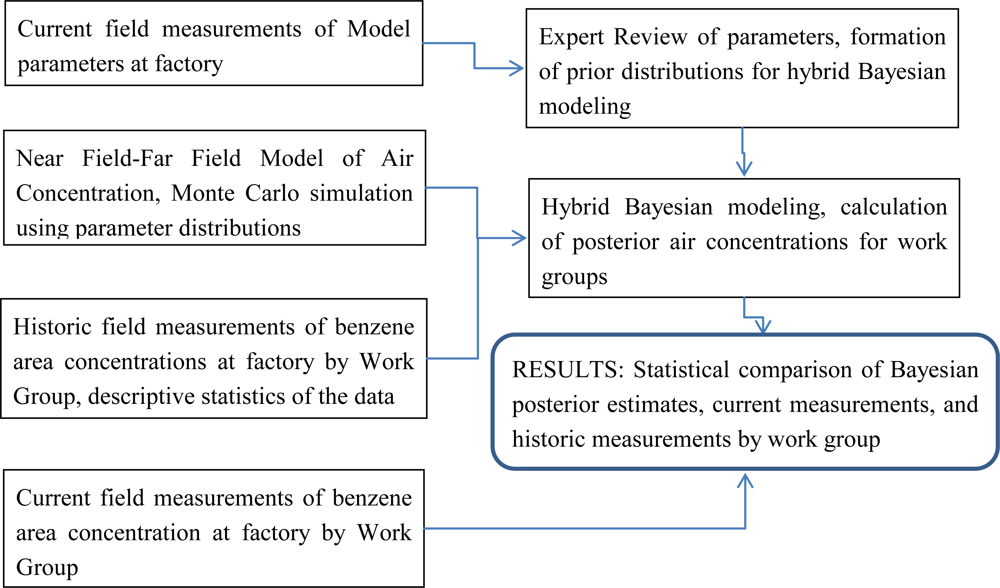
2.2. Bayesian Analysis Plan
- For mathematical modeling, parameters of evaporation surface area for pollutant production, air flow rate, work environment distance from source to workers, products and production made, working hours every year, and process technology were provided to a professional expert team. The experts were asked to provide their opinion on the distribution and errors of the parameters for the deterministic model. The resulting parameters from the expert review were used to predict air concentrations.
- Using parameters based on the expertise and historical working conditions, Monte Carlo simulation methods and the mathematical model were used to create the joint probability distributions and run for each sampled input parameters. These were the “prior” distributions, which characterized the uncertainty in the model output.
- The estimated variance of the available historical air concentration data (the “real world” observations) were applied to estimate the parameters for the Bayesian likelihood function, PL(M/e).
- Using WinBugs software [9] and Bayes rules, the prior was updated with the historical data to generate the posterior probability distribution of air concentrations Ppost(e/M).
2.3. Data Collection and Worksite Investigation
2.4. Data Selection for Deterministic Modeling
2.5. Current Worksite Benzene Air Sampling and Analysis
2.6. Estimation of Area Concentration with Bayesian Model
2.7. Quality Control
2.8. Statistical Analyses
3. Results
3.1. Benzene Levels by Current Field Survey
3.2. Benzene Levels of the Historical Measurements
3.3. Benzene Estimates by the Bayesian Model
4. Discussion
5. Conclusions Using the Hybrid Bayes Statistical Approach [6,8,9]
Acknowledgments
References
- Semple, S. Assessing occupational and environmental exposure. Occup. Med 2006, 55, 419–424. [Google Scholar]
- Esmen, N. Retrospective industrial hygiene surveys. Am. Ind. Hyg. Assoc. J 1979, 40, 58–65. [Google Scholar]
- Cherrie, JW; Schneider, T. Validation of a new method for structured subjective assessment of past concentrations. Ann. Occup. Hyg 1999, 43, 235–245. [Google Scholar]
- Burstyn, I; Kromhout, H. A critique of Bayesian methods for retrospective exposure assessment. Ann. Occup. Hyg 2002, 46, 429–431. [Google Scholar]
- Gurumurthy, R; James, HV. A Bayesian approach to retrospective exposure assessment. Appl. Occup. Envir. Hyg 1999, 14, 547–557. [Google Scholar]
- Gurumurthy, R. Retrospective exposure assessment using Bayesian methods. Ann. Occup. Hyg 2001, 45, 651–667. [Google Scholar]
- Spiegelhalter, DJ; Myles, JP; Jones, DR; Abrams, KR. Bayesian methods in health technology assessment: a review. Health Tech. Assess 2004, 4, 438–453. [Google Scholar]
- Burstyn, I; Teschke, K. Studying the determinants of exposure: a review of methods. Am. Ind. Hyg. Assoc. J 1999, 60, 57–72. [Google Scholar]
- Lunn, DJ; Thomas, A; Best, N; Spiegelhalter, D. WinBUGS--a Bayesian modelling framework: concepts, structure, and extensibility. Statistic. Comput 2000, 10, 325–337. [Google Scholar]
- Fong, Y; Wang, L. Maximum Allowable Concentration in the air of the workplace. Ind. Hyg. Occup. Dis 1992, 18, 315–319. [Google Scholar]
- Corn, M; Esmen, NA. Workplace exposure zones for classification of employee exposures to physical and chemical agents. Am. Ind. Hyg. Assoc. J 1979, 40, 47–57. [Google Scholar]
- Burdorf, A; Tongeren, M. Commentary: Variability in workplace exposures and the design of efficient measurement and control strategies. Ann. Occup. Hyg 2003, 47, 95–99. [Google Scholar]
- Collins, JJ; Ireland, BK; Easterday, PA; Nair, RS; Braun, J. Evaluation of lymphopenia among workers with low-level benzene exposure and the utility of routine data collection. Occup. Environ. Med 1979, 39, 232–237. [Google Scholar]
- Charles, BK. Two-Zone Steady State Model. In Mathematical models for estimating occupational exposure to chemicals, 1st Ed ed; AIHA Exposure Assessment Committee; AIHA Press: Fairfax, VA, USA, 2000; pp. 33–39. [Google Scholar]
- Shi, M; Zhang, M; Xu, Y; Zhu, Y. Experimental research on gas Chromatographic determination for o-chlorotoluene collected by activated charcoal in the workplace air. J. Environ. Occup. Med 2005, 22, 464–466. [Google Scholar]
- Greenland, S. Bayesian perspectives for epidemiological research: I. foundations and basic methods. Int. J. Epidemiol 2006, 35, 765–775. [Google Scholar]
- Hornung, RW; Reed, LD. Estimation of average concentration in the presence of nondetectable values. Appl. Occup. Environ. Hyg 1990, 5, 46–51. [Google Scholar]
- Bohong, X; Huifang, Y. Method of Sampling and Analysis in Workplace, 1st Ed, Press of People’s Public Safety University: Beijing, PR China, 2003; 223–229.
- Li, Y. Determination of benzene in the atmosphere of workshop by chromatography. Guizhou Chem. Ind 2000, 25, 35–36. [Google Scholar]
- Money, CD; Margary, SA. Improved use of workplace exposure data in the regulatory risk assessment of chemicals within Europe. Ann. Occup. Hyg 2002, 46, 279–285. [Google Scholar]
- Vocht, F; Straif, K; Szeszenia-Dabrowaka; Hagmar, L; Tom, S; Burstyn, I; Vermeulen, R; Kromhout, H. A database of exposures in the rubber manufacturing industry: design and quality control. Ann. Occup. Hyg 2005, 49, 691–701. [Google Scholar]
- Astrakianakis, G; Seixas, SN; Camp, JE; Christiani, CD; Feng, Z; Thomas, BD; Checkoway, H. Modeling, estimation and validation of cotton dust and endotoxin exposures in Chinese textile operations. Ann. Occup. Hyg 2006, 50, 573–582. [Google Scholar]
- Lavoué, J; Bégin, D; Beaudry, C; Gérin, M. Monte Carlo simulation to reconstruct formaldehyde exposure levels from summary parameters reported in the literature. Ann. Occup. Hyg 2007, 51, 161–172. [Google Scholar]
| Code | Workstation | Parameter | Number of measurements | AM or GM | Minimum | Maximum |
|---|---|---|---|---|---|---|
| 1.1 | Slurry applying | Pollutant production rate | 12 | 520 (515–524) | 353 | 1172 |
| General room ventilation | 6 | 629 (16–844) | 517 | 813 | ||
| NF interface ventilation | 6 | 25 (2.6–33.4) | 20 | 28.7 | ||
| 8.1 | Cloth-lining assembly | Pollutant production rate | 12 | 1302 (1293–1311) | 698 | 3903 |
| General room ventilation | 6 | 3501 (30–19832) | 210 | 29207 | ||
| NF interface ventilation | 6 | 71 (1–339) | 16 | 420 |
| Code | Workstation | Tasks | Workshop ventilation surface, m2 | Pollutant source | Distance between source to operator, m |
|---|---|---|---|---|---|
| 1.1 | Slurry making | slurry making | 4.2 | 4 mixer machines, the volatile surface was about 870 cm2 | 0.5 |
| 2.1 | Core assembly | similar with the cloth-lining assembly | 20.1 | Size of the containers were the same as the cloth-lining workshop, the number was a half of that workshop | 1.0 |
| 3.1 | East assembly | assembly | 181.4 | Size of the only container was that of the cloth-lining workshop | 1.2 |
| 3.2 | East assistant | vulcanizing, cutting cloth | 181.4 | Indirect exposure to the East Assembly | 5.0 |
| 4.1 | Steel weaving | steel weaving | 120.3 | Indirect exposure to Steel Weaving Assembly | 2.0 |
| 4.2 | Steel weaving assembly | steel weaving assembly | 120.3 | Sources were tubes of 2.5 cm radius and 25 cm length, surface was about 478 cm2 (about 1/15 of the cloth-lining workshop) | 1.0 |
| 4.3 | Steel weaving assistant | vulcanizing,, wrapping cloth | 120.3 | Indirect exposure to Steel Weaving Assembly | 4.0 |
| 5.1 | Line 3 assistant | feeding rubber mud | 180.5 | Indirect exposure to Line 3 Assembly | 3.0 |
| 5.2 | Line 3 assembly | assembly | 180.5 | 6 assembly machines, 2 times of the steel weaving assembly | 1.0 |
| 6.1 | Line 1–2 | assembly, feeding materials, cutting tubes | 79.6 | 1/3 of the line 3 | 2.0 |
| 7.1 | Slurry applying | slurry | 17.2 | 2 square boxes of 75×15 cm (surface about 2261 cm2) | 1.2 |
| 7.2 | Cotton tube weaving | applying weaving and applying slurring with machine | 26.5 | 15 slurry boxes of 50×25 cm | 4.5 |
| 7.3 | Cotton tube assistant | cutting cloth, staving tapes, vulcanizing | 26.5 | Indirect exposure to Cotton Tube Weaving | 6.4 |
| 8.1 | Cloth-lining assembly | cloth-lining assembly | 95.7 | 10 containers of 20×30 cm(volatile surface about 6,000 cm2) | 1.8 |
| 8.2 | Cloth-lining assistant | cutting cloth, staving tapes, vulcanizing | 62.9 | Indirect exposure to Cloth-lining Assembly | 4.0 |
| Code | Workstation | Pollutant production rate [AM(CI 90%), mg/min] | Workshop air flow [GM(CI 90%), m3/min] | Interface air flow [GM(CI 90%), m3/min] |
|---|---|---|---|---|
| 1.1 | Slurry making | 200(100–300) | 154(31–772) | 5(1–27) |
| 2.1 | Core assembly | 826(413–1239) | 735(147–3675) | 22(4–109) |
| 3.1 | East assembly | 165(83–248) | 6634(1327–33171) | 31(6–156) |
| 3.2 | East assistant | 165(83–248) | 6634(1327–33171) | 539(108–2696) |
| 4.1 | Steel weaving | 110(55–165) | 4403(881–22014) | 86(17–432) |
| 4.2 | Steel weaving assembly | 110(55–165) | 4403(881–22014) | 22(4–109) |
| 4.3 | Steel weaving assistant | 110(55–165) | 4403(881–22014) | 347(69–1736) |
| 5.1 | Line 3 assistant | 220(110–330) | 6634(1327–33171) | 194(39–972) |
| 5.2 | Line 3 assembly | 220(110–330) | 6634(1327–33171) | 22(4–109) |
| 6.1 | Line 1–2 | 73.2(37–110) | 2922(584–14610) | 86(17–432) |
| 7.1 | Slurry applying | 520(260–780) | 629(126–3145) | 25(5–125) |
| 7.2 | Cotton tube weaving | 4400(2200–6600) | 973(195–4863) | 437(87–2185) |
| 7.3 | Cotton tube assistant | 4400(2200–6600) | 973(187–4685) | 874(175–4370) |
| 8.1 | Cloth-lining assembly | 1302(651–1953) | 3501(700–17505) | 71(14–355) |
| 8.2 | Cloth-lining assistant | 1652(826–2478) | 2298(460–11492) | 347(69–1736) |
| Code | Workstation | Sampling day | Field Surveying | Historic Monitoring | Bayesian Estimating | ||
|---|---|---|---|---|---|---|---|
| Sample number (<LOD) | Geometric mean (CI 95%) | Sample number (<LOD) | Geometric mean (CI 95%) | Geometric mean (CI 95%) | |||
| 1.1 | Slurry making | 17 (1) | 152.2 (8.7–2662.3) − | 111.5 (46.6–266.6) | |||
| 2.1 | Core assembly | 12 (1) | 1.245 (0.1–18.9) − | 1.8 (1.4–2.5) | |||
| 3.1# | East assembly | 10 | 20 (3) | 3.0 (1.1–8.5)− | 11 (1) | 4.5 (1.1–18.9)− | 6.1 (1.2–30.1) |
| 3.2 | East assistant | 11 (2) | 0.9 (0.0–22.9) | 0.5 (0.4–0.6) | |||
| 4.1 | Steel weaving | 10 (2) | 20.7 (0.2–1958.0) − | 3.7 (2.1–6.6) | |||
| 4.2 | Steel weaving assembly | 13 (2) | 61.2 (1.6–2411.4) | 19.2 (15.1–24.4) | |||
| 4.3# | Steel weaving assistant | 10 | 20 (5) | 0.7 (0.1–6.3) + | 6 (1) | 1.3 (0.1–14.6) −,+ | 1.1 (0.6–1.9) |
| 5.1 | Line 3 assistant | 6 (1) | 4.8 (2.9–8.1) | 3.3 (1.4–7.6) | |||
| 5.2# | Line 3 assembly | 10 | 20 (2) | 17.3 (3.5–86.4) − | 5 (1) | 40.6 (20.4–80.7) | 21.4 (15.9–28.8) |
| 6.1# | Line 1–2 | 10 | 20 (7) | 0.5 (0.1–2.7) | 4 (1) | 2.0 (0.4–11.4) − | 0.9 (0.1–6.6) |
| 7.1# | Slurry applying | 9 | 18 (3) | 69.8 (62.2–78.2) − | 12 (1) | 60.9 (2.4–1573.2) − | 41.6 (13.5–128.9) |
| 7.2 | Cotton hose weaving | 7 (1) | 2.4 (0.4–14.4) − | 0.9 (0.6–1.6) | |||
| 7.3 | Cotton hose assistant | 8 (2) | 6.2 (1.5–26.2) | 10.9 (3.0–39.5) | |||
| 8.1# | Cloth-lining assembly | 9 | 18 (2) | 89.5 (34.8–230.5) − | 1 (0) | 409.4** | 125.7 (18.9–837.5) |
| 8.2# | Cloth-lining assistant | 10 | 20 (2) | 16.8 (2.5–114.) − | 1 (0) | 51 | 11. 9 (3.3–43.3) |
Share and Cite
He, Y.; Liang, Y.; Fu, H. Application of Bayesian Methods to Exposure Assessment of Area Concentrations at a Rubber Factory. Int. J. Environ. Res. Public Health 2009, 6, 622-634. https://doi.org/10.3390/ijerph6020622
He Y, Liang Y, Fu H. Application of Bayesian Methods to Exposure Assessment of Area Concentrations at a Rubber Factory. International Journal of Environmental Research and Public Health. 2009; 6(2):622-634. https://doi.org/10.3390/ijerph6020622
Chicago/Turabian StyleHe, Yonghua, Youxin Liang, and Hua Fu. 2009. "Application of Bayesian Methods to Exposure Assessment of Area Concentrations at a Rubber Factory" International Journal of Environmental Research and Public Health 6, no. 2: 622-634. https://doi.org/10.3390/ijerph6020622
APA StyleHe, Y., Liang, Y., & Fu, H. (2009). Application of Bayesian Methods to Exposure Assessment of Area Concentrations at a Rubber Factory. International Journal of Environmental Research and Public Health, 6(2), 622-634. https://doi.org/10.3390/ijerph6020622




