Examining the Dynamic Association of BMI and Mortality in the Framingham Heart Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Framingham Heart Study
2.2. Methods
2.2.1. Logistic Regression Models
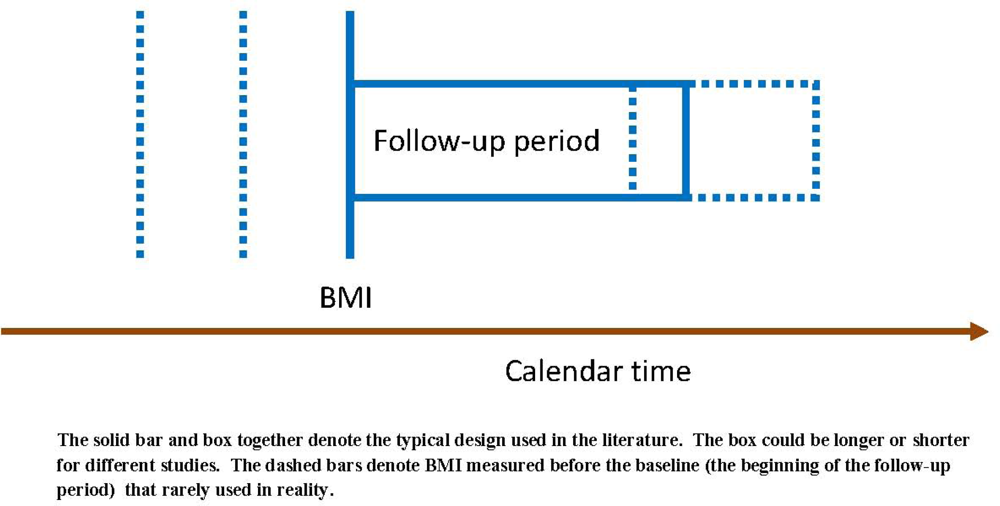
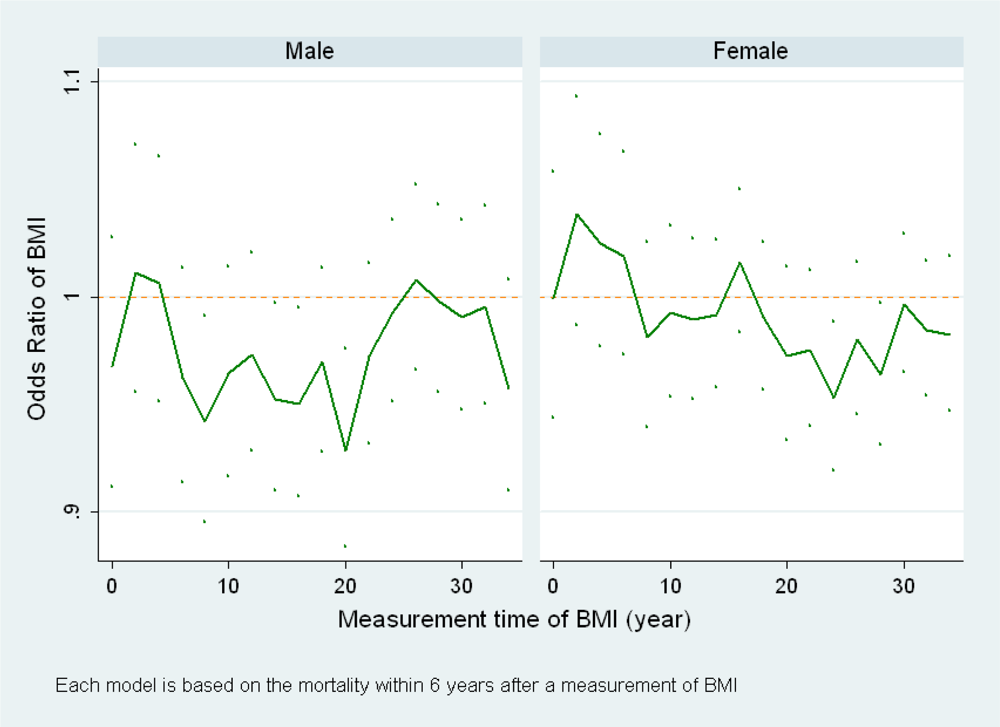
(a) When BMI at a different time point is used
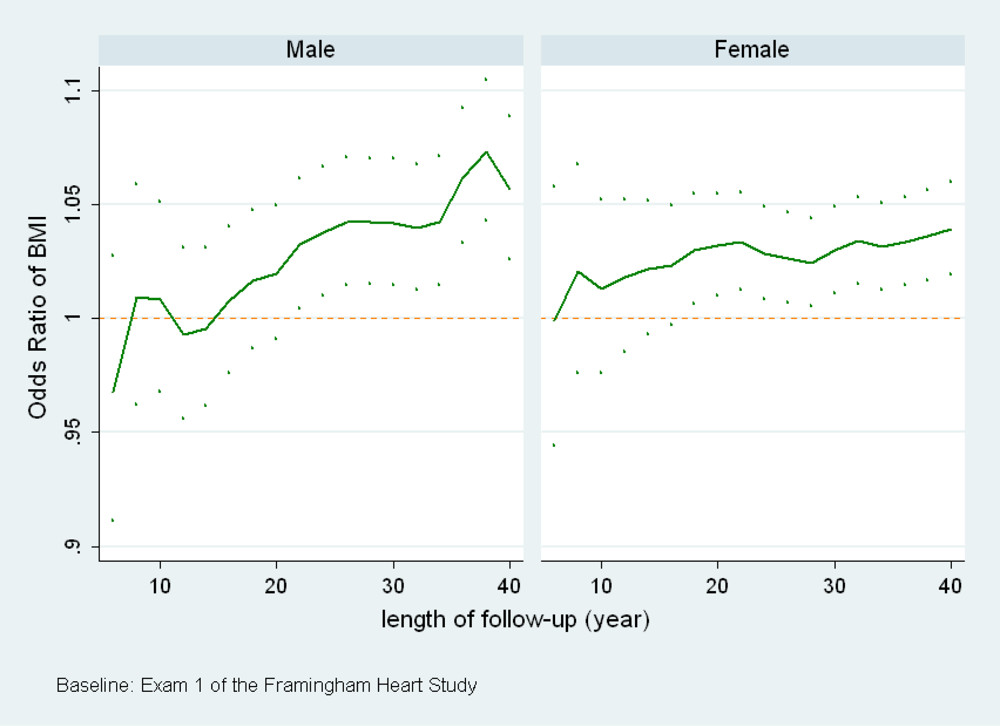
(b) When the length of follow-up changes
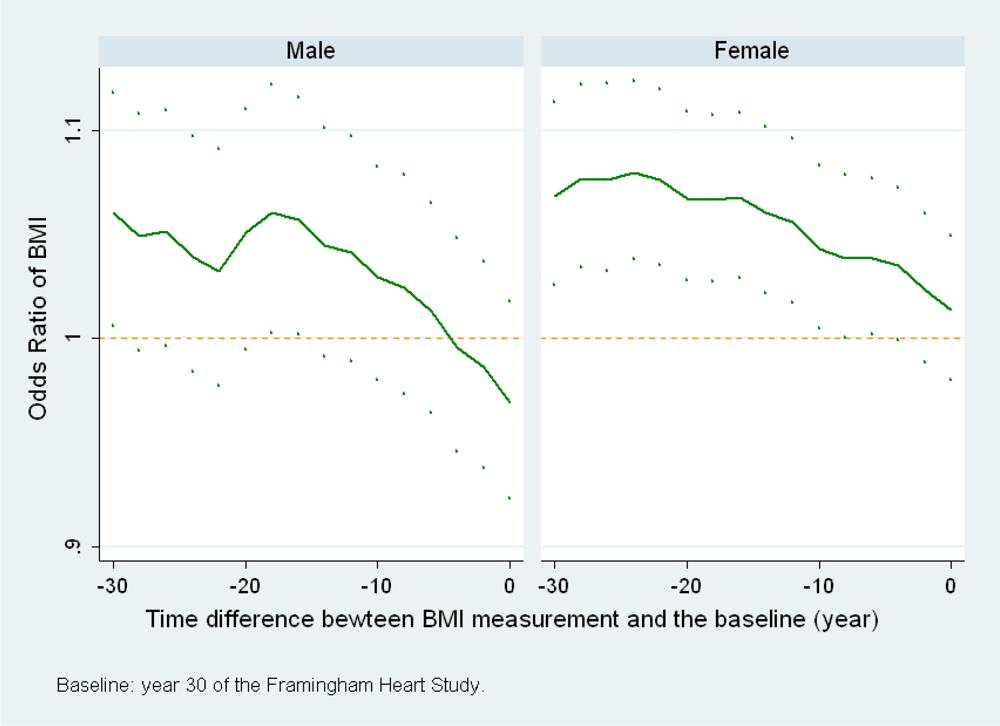
(c) When the calendar time of the baseline changes
2.2.2. Dynamic Survival Models
3. Results
3.1. Logistic Regression Models
(a) When BMI at a different time point is used
(b) When the length of follow-up changes
(c) When the calendar time of the baseline changes
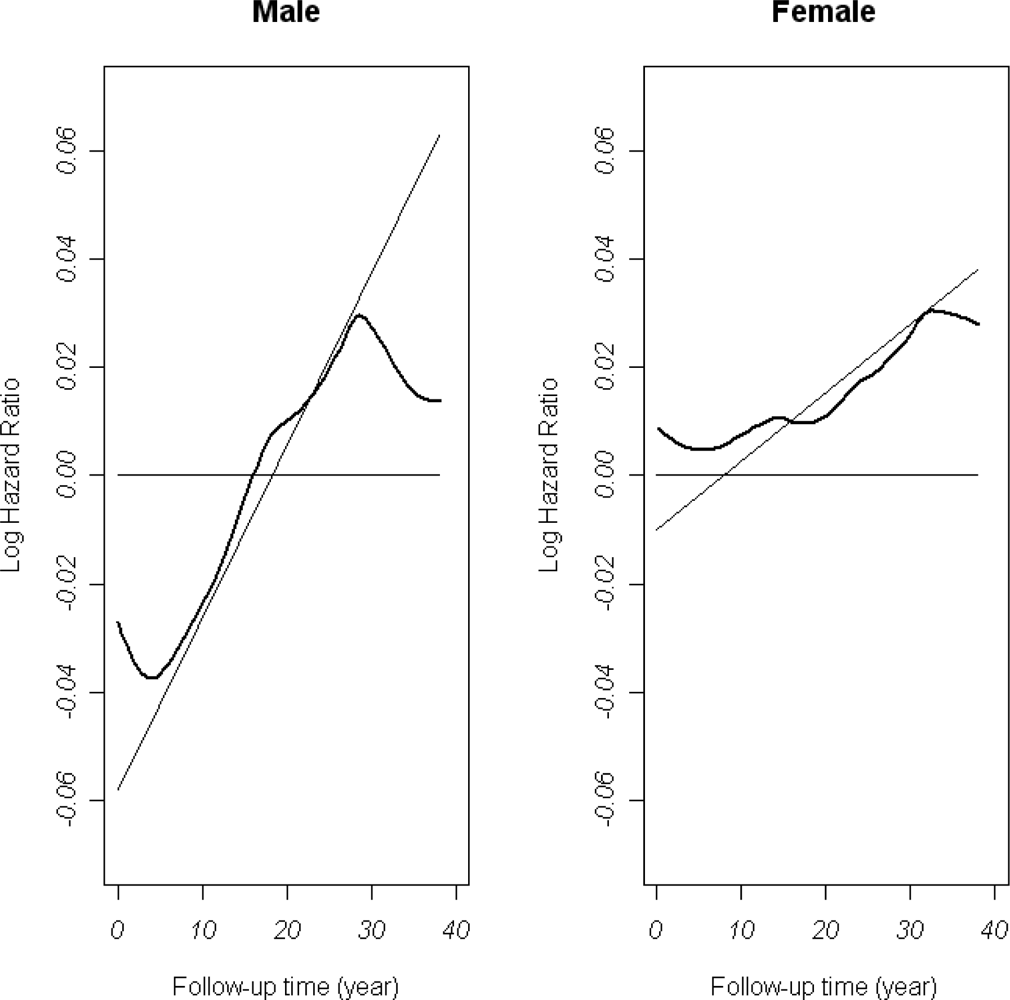
3.2. Dynamic Survival Models
4. Discussions
Acknowledgments
References
- Schroll, MA. Longitudinal epidemiological survey of relative weight at age 25, 50 and 60 in the Glostrup population of men and women born in 1914. Dan. Med. Bull 1981, 28, 106–116. [Google Scholar]
- Tuomilehto, J; Salonen, JT; Marti, B; Jalkanen, L; Puska, P; Nissinen, A; Wolf, E. Body weight and risk of myocardial infarction and death in the adult population of Eastern Finland. BMJ 1987, 295, 623–627. [Google Scholar]
- Vandenbroucke, JP; Mauritz, BJ; de Bruin, A; Verheesen, JHH; van der Heide-Wessel, C; van der Heide, RM. Weight, smoking, and mortality. JAMA 1984, 252, 2859–2860. [Google Scholar]
- Waaler, HT. Height, weight and mortality: the Norwegian experience. Acta. Med. Scan. Suppl 1984, 679, 1–56. [Google Scholar]
- Harris, T; Cook, EF; Garrison, R; Higgins, M; Kannel, W; Goldman, L. Body mass index and mortality among nonsmoking older persons: the Framingham Heart Study. JAMA 1998, 259, 1520–1524. [Google Scholar]
- Comstock, GW; Kendrick, MA; Livesay, VT. Subcutaneous fatness and mortality. Am. J. Epidemiol 1966, 83, 548–563. [Google Scholar]
- Lew, EA; Garfinkel, L. Variations in mortality by weight among 750,000 men and women. J. Chronic. Dis 1979, 32, 563–576. [Google Scholar]
- Folsom, AR; Kaye, SA; Sellers, TA; Hong, C; Cerhan, JR; Potter, JD; Prineas, RJ. Body fat distribution and 5-year risk of death in older women. JAMA 1993, 269, 483–487. [Google Scholar]
- Garrison, RJ; Feinleib, M; Castelli, WP; McNamara, PM. Cigarette smoking as a confounder of the relationship between relative weight and long-term mortality: the Framingham Heart Study. JAMA 1983, 249, 2199–2203. [Google Scholar]
- Linsted, K; Tonstad, S; Kuzma, JW. Body mass index and patterns of mortality among Seventh-day Adventist men. Int. J. Obes 1991, 15, 397–406. [Google Scholar]
- Lee, IM; Manson, JE; Hennekens, CH; Paffenbarger, RS. Body weight and mortality: a 27-year follow-up of middle-aged men. JAMA 1993, 270, 2823–2828. [Google Scholar]
- Wilcosky, T; Hyde, J; Anderson, JJ; Bangdiwala, S; Duncan, B. Obesity and mortality in the Lipid Research Clinics Program Follow-up Study. J. Clin. Epidemiol 1990, 43, 743–752. [Google Scholar]
- Cox, DR. Regression Models and Life-Tables. JRSS. Series B 1972, 34, 187–220. [Google Scholar]
- Gray, RJ. Flexible methods for analyzing survival data using splines, with applications to breast cancer prognosis. JASA 1992, 87, 942–951. [Google Scholar]
- Gray, RJ. Spline-based tests in survival analysis. Biometrics 1994, 50, 640–652. [Google Scholar]
- Grambsch, PM; Therneau, TM. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika 1994, 81, 515–526. [Google Scholar]
- Calle, EE; Thun, MJ; Petrelli, JM; Rodriguez, C; Heath, CW. Body-Mass Index and Mortality in a Prospective cohort of U.S. Adults. NEJM 1999, 341, 1097–1105. [Google Scholar]
- Manson, JE; Willett, WC; Stampfer, MJ; Colditz, GA; Hunter, DJ; Hankinson, SE; Hennekens, CH; Speizer, FE. Body Weight and Mortality among Women. NEJM 1995, 333, 677–685. [Google Scholar]
- Lawlor, DA; Hart, CL; Hole, DJ; Smith, GD. Reverse causality and confounding and the associations of overweight and obesity with mortality. Obesity 2006, 12, 2294–2304. [Google Scholar]
- Corrada, MM; Kawas, CH; Mozaffar, F; Paganini-Hill, A. Association of body mass index and weight change with all-cause mortality in the elderly. Am. J. Epidemiol 2006, 163, 938–949. [Google Scholar]
- Allison, DB; Faith, MS; Heo, M; Townsend-Butterworth, D; Williamson, D. Meta analysis of the effect of excluding early deaths on the estimated relationship between Body Mass Index and mortality. Obes. Res 1999, 7, 342–354. [Google Scholar]
- Greenberg, JA. Biases in the mortality risk versus body mass index relationship in the NHANES-1 epidemiological follow-up study. Int. J. Obes 2001, 25, 1071–1078. [Google Scholar]
| Analysis Result for Men | |||
| Variables | Hazards Ratio | p-value | Test of PH assumption (p-value) |
| Age (5 years) | 1.57 | < 0.001 | 0.034 |
| sbp (10 mmHg) | 1.15 | < 0.001 | 0.026 |
| Smoking | 1.42 | < 0.001 | < 0.0001 |
| BMI | 1.00 | 0.876 | 0.0001 |
| Analysis Result for Women | |||
| Variables | Hazards Ratio | p-value | Test of PH assumption (p-value) |
| Age (5 years) | 1.58 | < 0.001 | 0.001 |
| sbp (10 mmHg) | 1.12 | < 0.001 | 0.017 |
| Smoking | 1.42 | < 0.001 | 0.570 |
| BMI | 1.02 | 0.011 | 0.060 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
He, J.; McGee, D.; Niu, X.; Choi, W. Examining the Dynamic Association of BMI and Mortality in the Framingham Heart Study. Int. J. Environ. Res. Public Health 2009, 6, 3115-3126. https://doi.org/10.3390/ijerph6123115
He J, McGee D, Niu X, Choi W. Examining the Dynamic Association of BMI and Mortality in the Framingham Heart Study. International Journal of Environmental Research and Public Health. 2009; 6(12):3115-3126. https://doi.org/10.3390/ijerph6123115
Chicago/Turabian StyleHe, Jianghua, Daniel McGee, Xufeng Niu, and Won Choi. 2009. "Examining the Dynamic Association of BMI and Mortality in the Framingham Heart Study" International Journal of Environmental Research and Public Health 6, no. 12: 3115-3126. https://doi.org/10.3390/ijerph6123115
APA StyleHe, J., McGee, D., Niu, X., & Choi, W. (2009). Examining the Dynamic Association of BMI and Mortality in the Framingham Heart Study. International Journal of Environmental Research and Public Health, 6(12), 3115-3126. https://doi.org/10.3390/ijerph6123115




