Research on Seawater Intrusion Suppression Scheme of Minjiang River Estuary
Abstract
1. Introduction
2. Materials and Methods
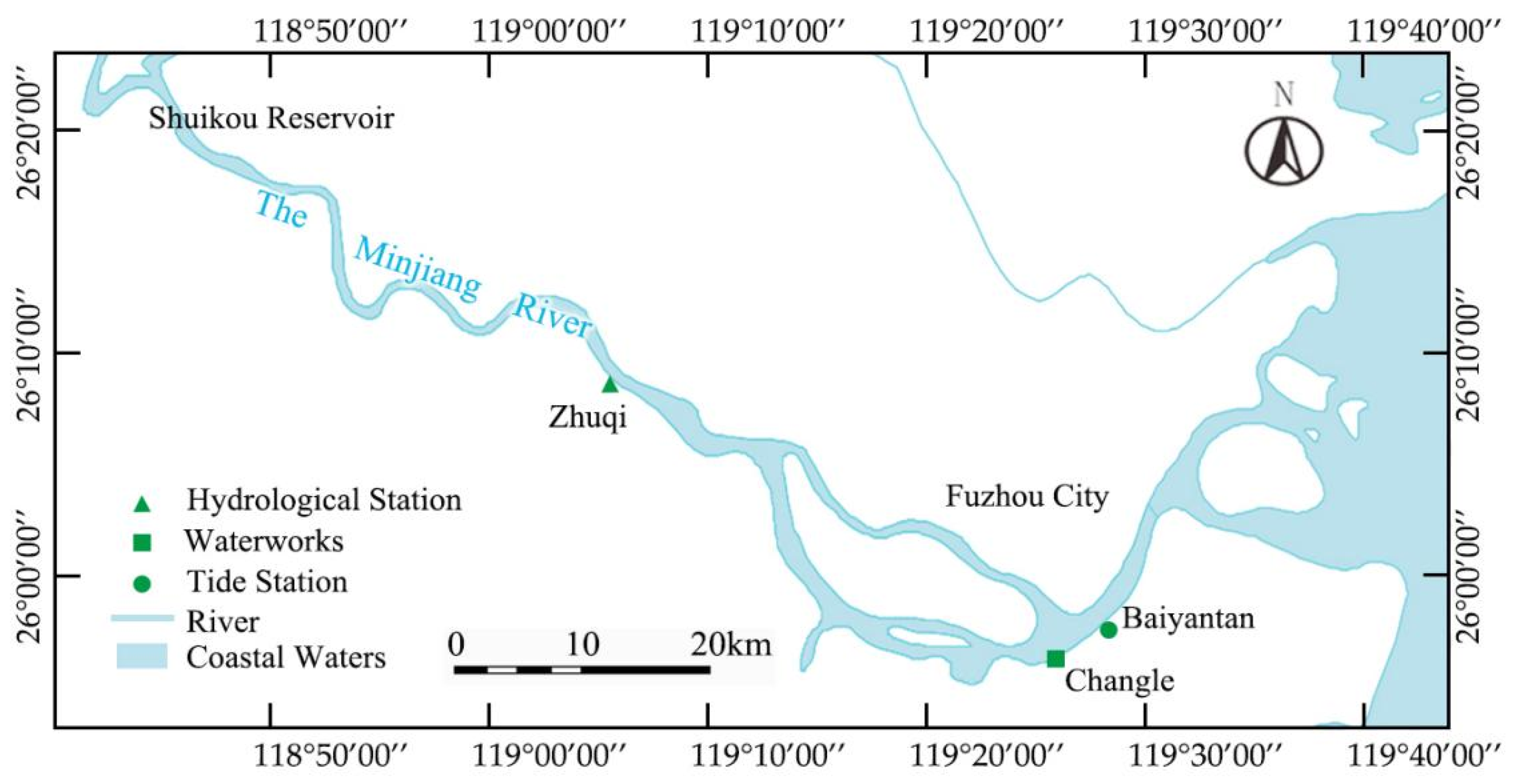
2.1. Study Area
2.2. Data Preparation
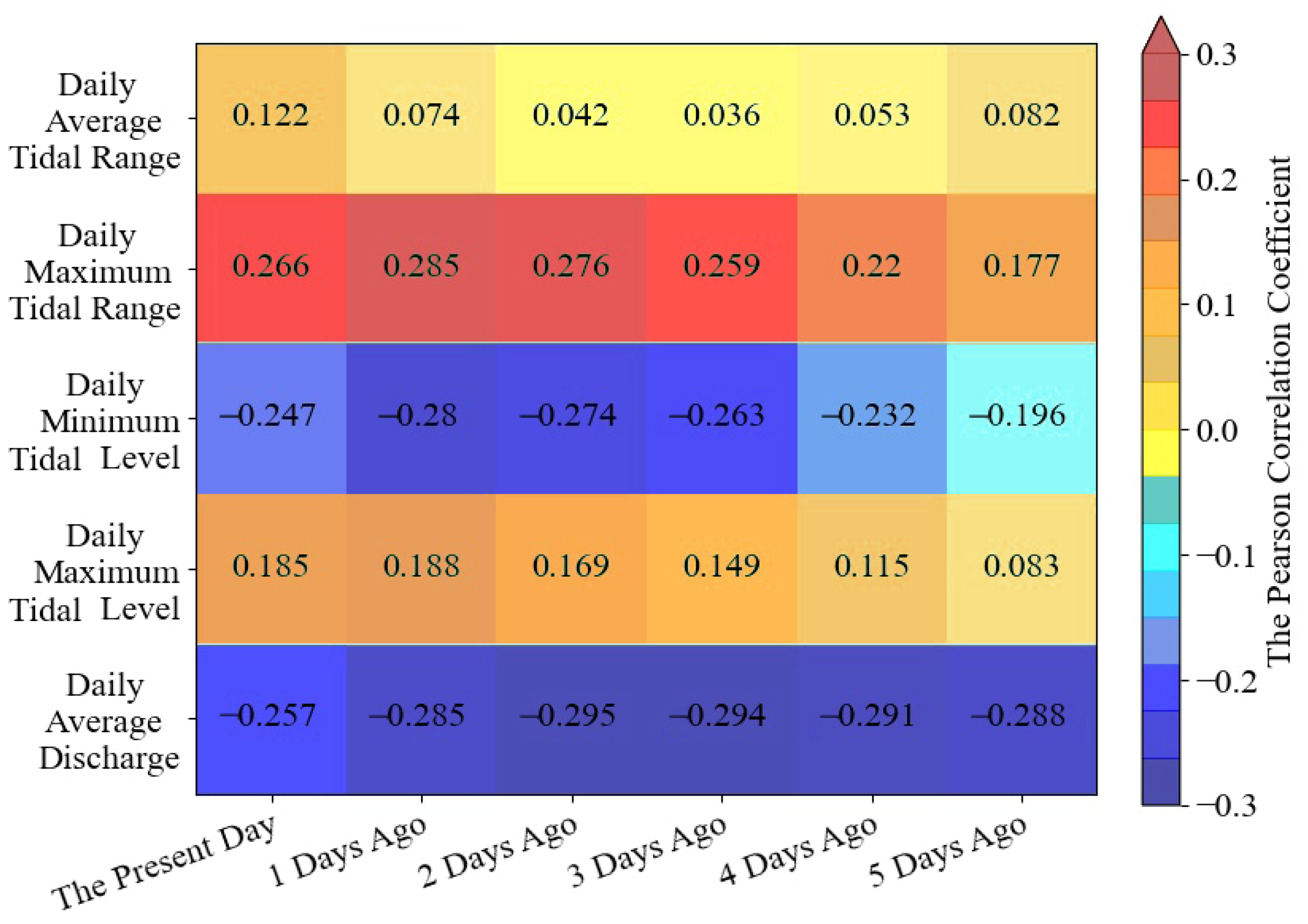
2.3. Factors Selection and Data Sources
2.4. Seawater Intrusion Suppression Model
2.4.1. Random Forest Algorithm
2.4.2. Chlorine Level Statistical Model
2.4.3. Seawater Intrusion Suppression Model
3. Results and Discussion
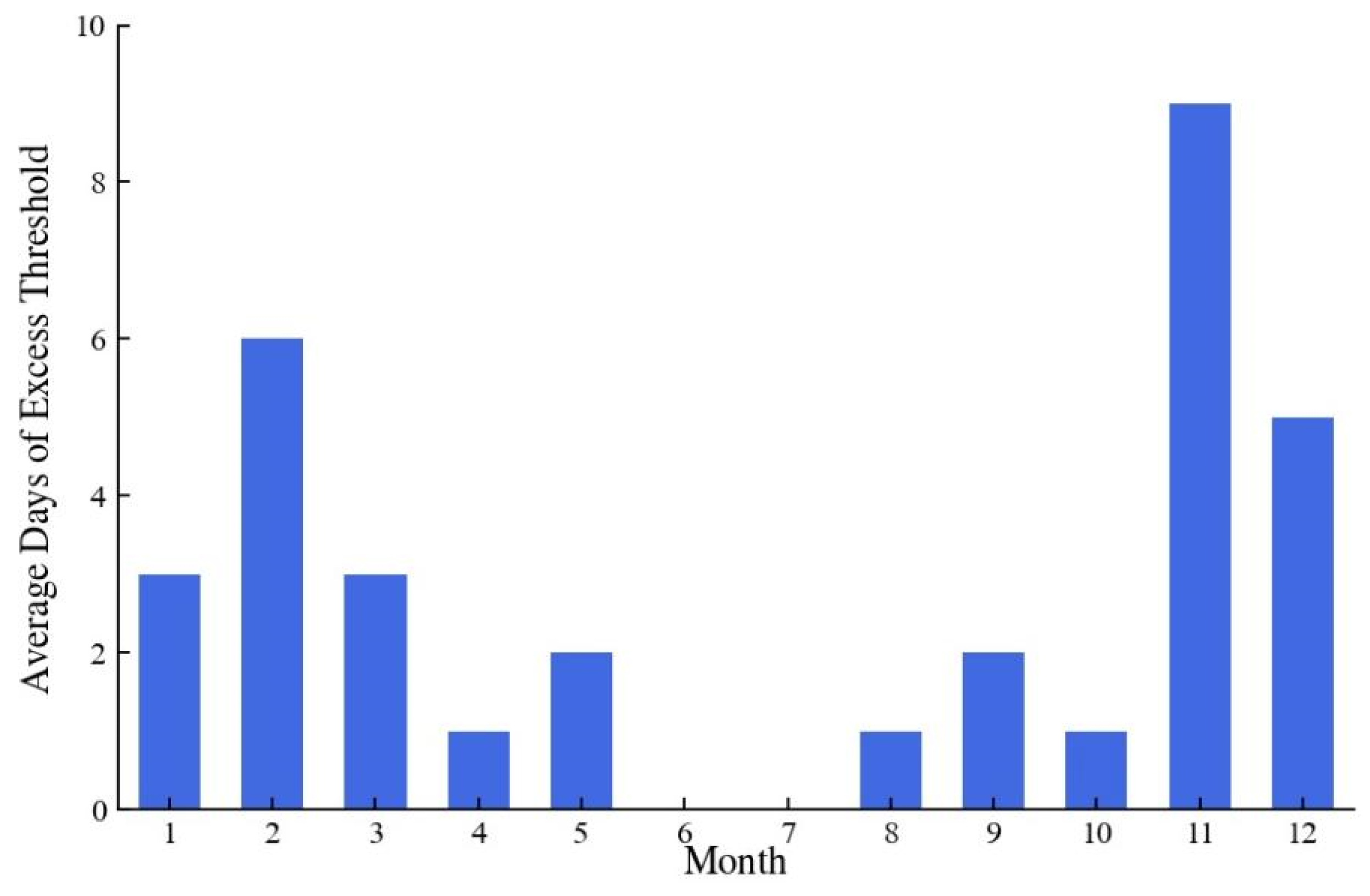
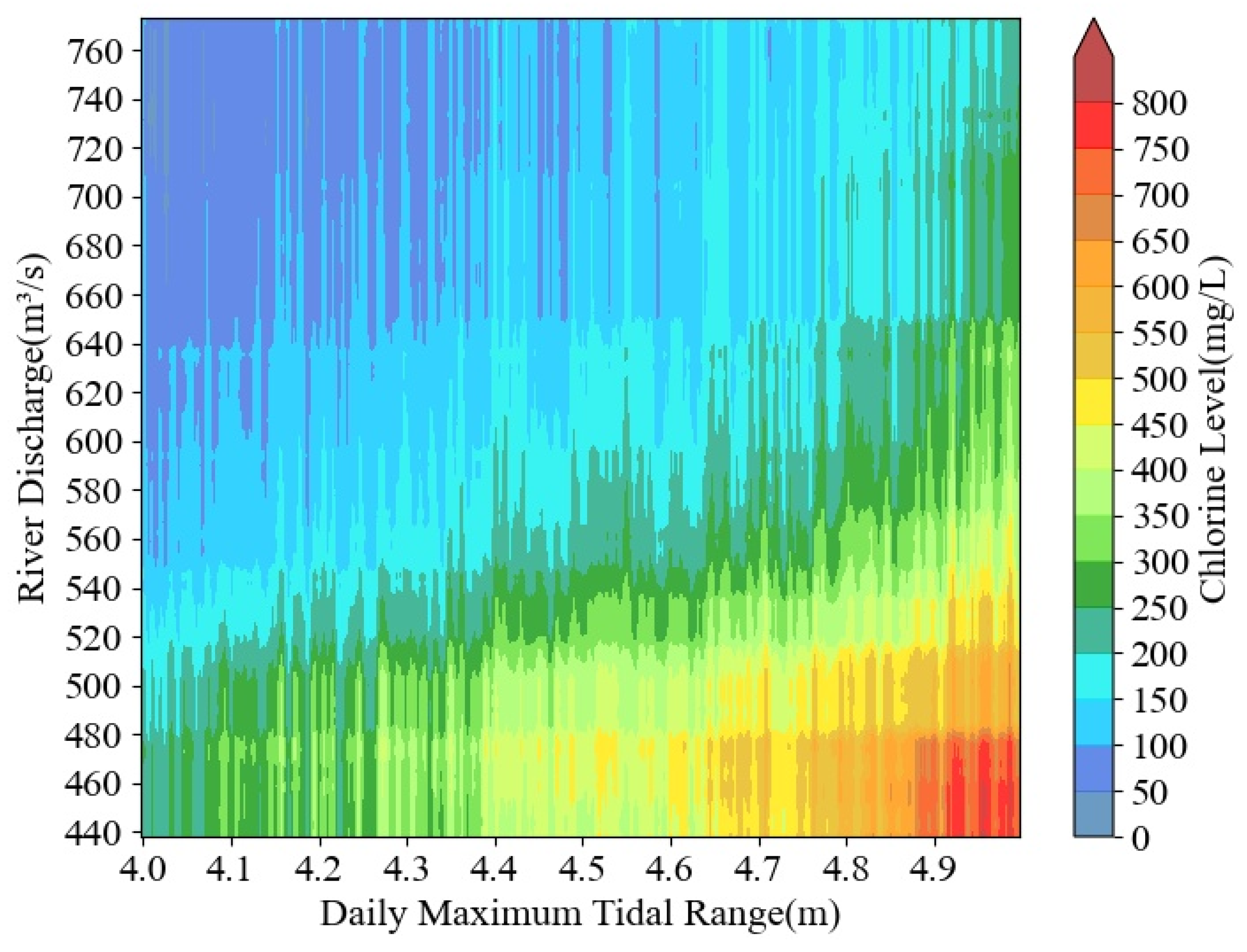
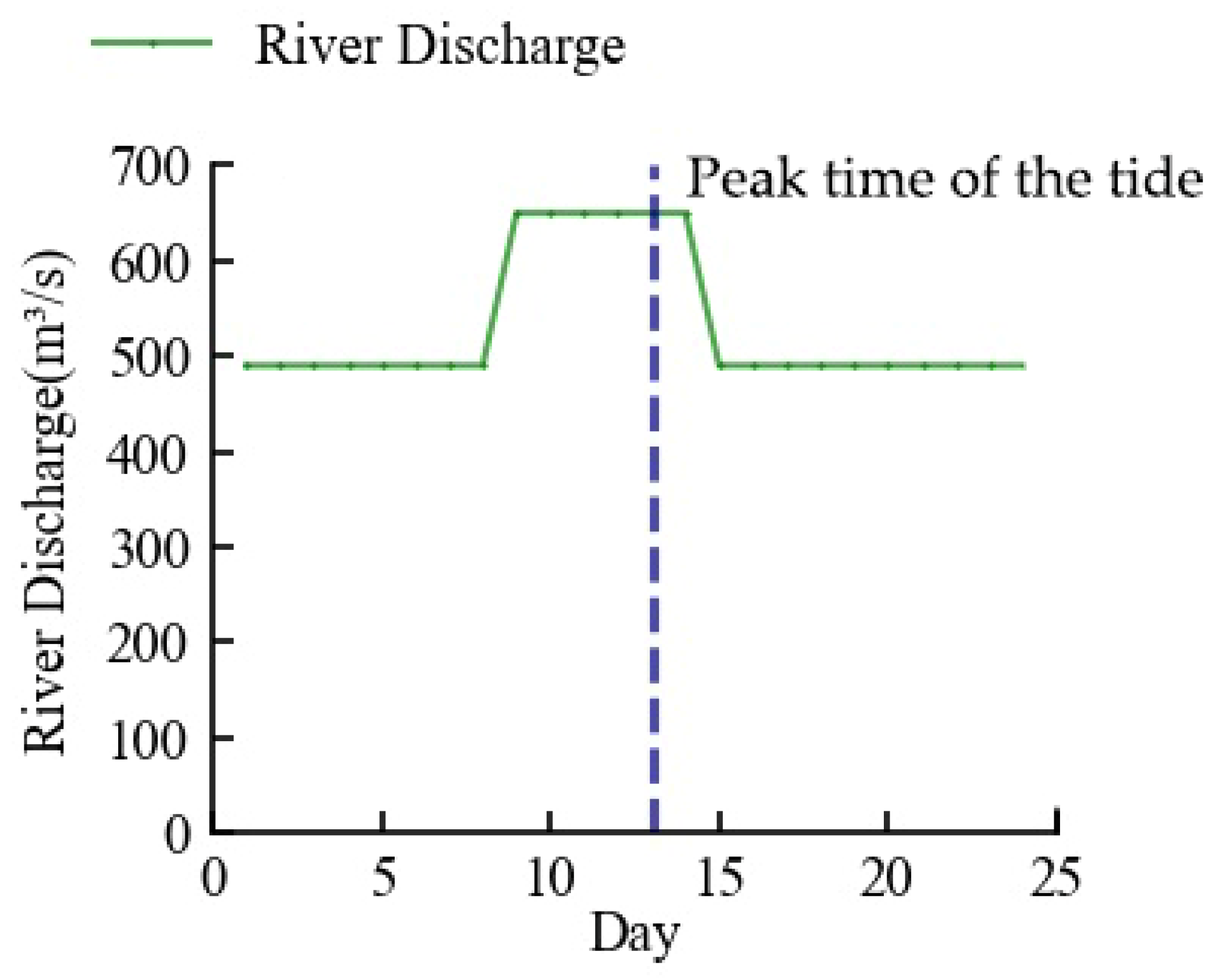
3.1. Effect of River Discharge
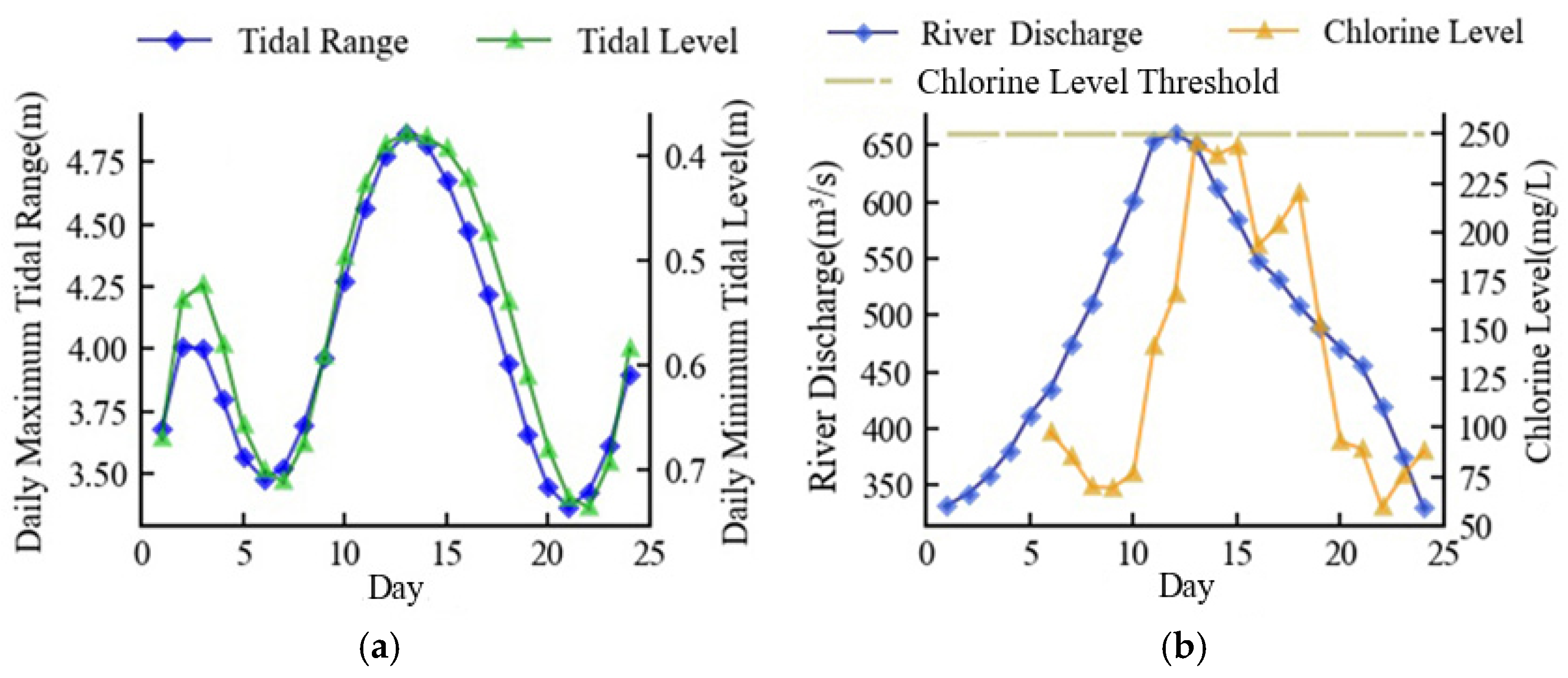
3.2. Minimum River Discharge for Seawater Suppression
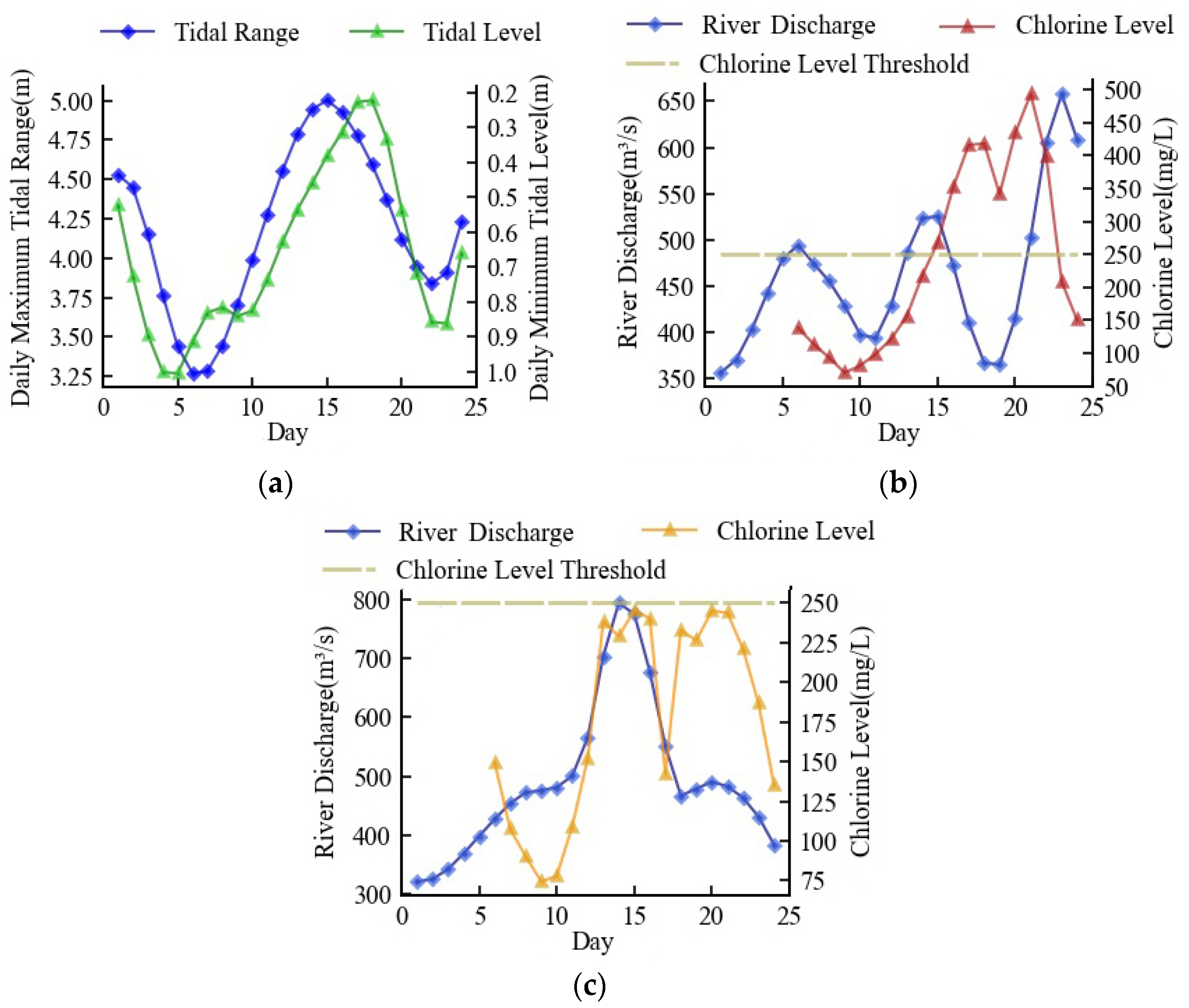
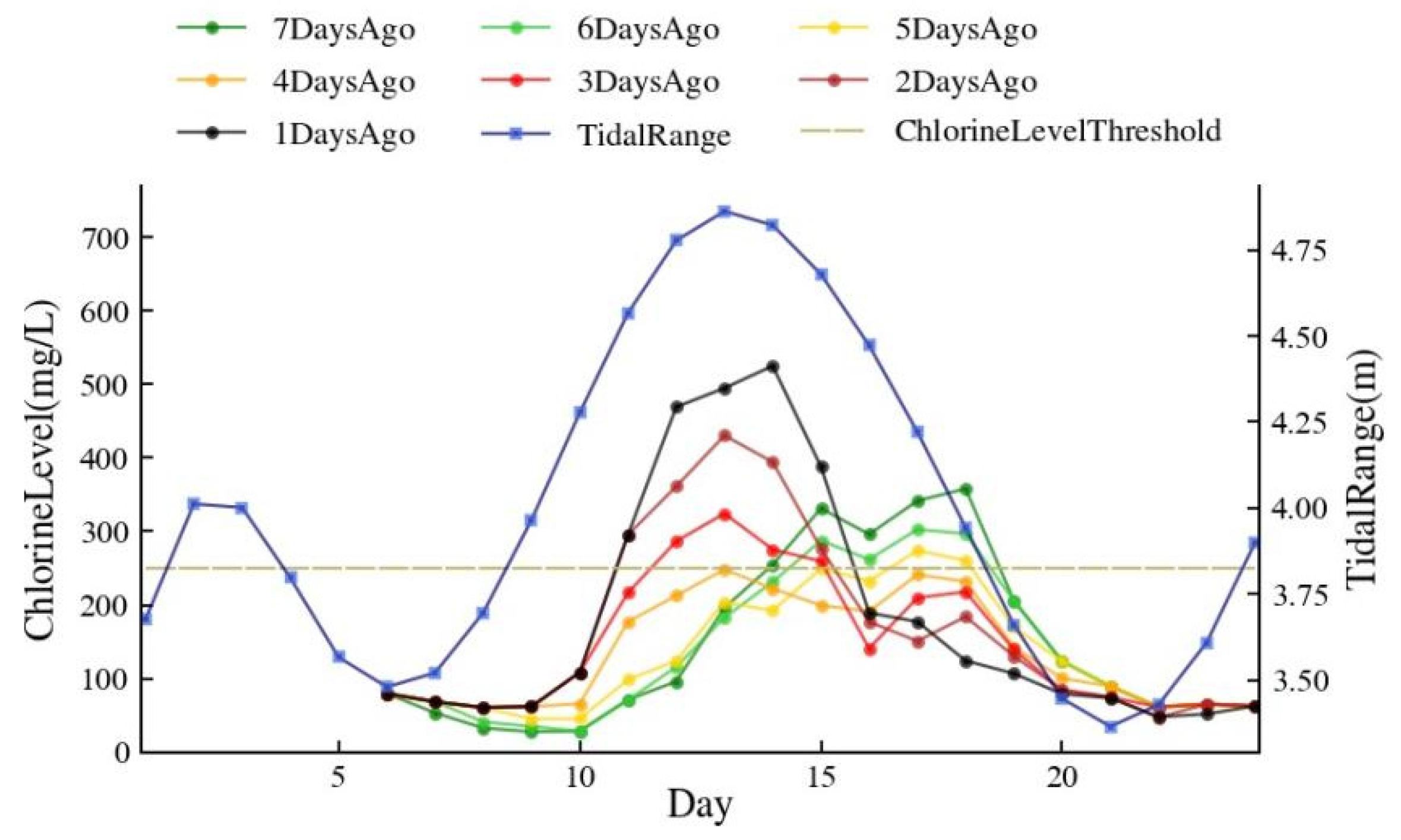
3.3. Practicable Seawater Suppression Scheme
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.Y. Preliminary Study of Yangtze River Estuary in 21st Century, 1st ed.; Ocean Press: Beijing, China, 2009; pp. 9–13. [Google Scholar]
- Mao, Z.C.; Shen, H.T.; Xiao, C.Y. Saltwater intrusion patterns in the Qingcaosha area Changjiang river estuary. Oceanol. Et Limnol. Sin. 2001, 32, 58–66. [Google Scholar]
- Werner, A.D.; Bakker, M.; Post, V.E.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation, and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Lin, J.; Snodsmith, J.B.; Zheng, C.; Wu, J. A modeling study of seawater intrusion in Alabama Gulf Coast, USA. Environ. Geol. 2009, 57, 119–130. [Google Scholar] [CrossRef]
- Izbicki, J.A. Chloride sources in a California coastal aquifer. Ground Water Pac. Rim Ctries. 1991, 7, 71–77. [Google Scholar]
- Alcérreca-Huerta, J.C.; Callejas-Jiménez, M.E.; Carrillo, L.; Castillo, M.M. Dam implications on salt-water intrusion and land use within a tropical estuarine environment of the Gulf of Mexico. Sci. Total Environ. 2019, 652, 1102–1112. [Google Scholar] [CrossRef] [PubMed]
- Werner, A.D. A review of seawater intrusion and its management in Australia. Hydrogeol. J. 2010, 18, 281–285. [Google Scholar] [CrossRef]
- Alfarrah, N.; Walraevens, K. Groundwater overexploitation and seawater intrusion in coastal areas of arid and semi-arid regions. Water 2018, 10, 143. [Google Scholar] [CrossRef]
- Mastrocicco, M.; Busico, G.; Colombani, N.; Vigliotti, M.; Ruberti, D. Modelling actual and future seawater intrusion in the Variconi coastal wetland (Italy) due to climate and landscape changes. Water 2019, 11, 1502. [Google Scholar] [CrossRef]
- Custodio, E. Coastal aquifers of Europe: An overview. Hydrogeol. J. 2010, 18, 269–280. [Google Scholar] [CrossRef]
- Xu, Z.; Ma, J.; Hu, Y. Saltwater intrusion function and preliminary application in the Yangtze River Estuary, China. Int. J. Environ. Res. Public Health 2019, 16, 118. [Google Scholar] [CrossRef]
- Jeen, S.W.; Kang, J.; Jung, H.; Lee, J. Review of seawater intrusion in western coastal regions of South Korea. Water 2021, 13, 761. [Google Scholar] [CrossRef]
- GB 3838-2002; Environmental Quality Standards for Surface Water. Standards Press of China: Beijing, China, 2009.
- Mohammed, R.; Scholz, M. Critical review of salinity intrusion in rivers and estuaries. J. Water Clim. Chang. 2018, 9, 1–16. [Google Scholar] [CrossRef]
- Xue, P.; Chen, C.; Ding, P.; Beardsley, R.C.; Lin, H.; Ge, J.; Kong, Y. Saltwater intrusion into the Changjiang River: A model-guided mechanism study. J. Geophys. Res. Ocean. 2009, 114, c2. [Google Scholar] [CrossRef]
- Xu, Z.; Ma, J.; Wang, H.; Zhao, J. Influence of River Discharge on the Transport of the Saltwater Group from the North Branch in the Yangtze River Estuary. Int. J. Environ. Res. Public Health 2020, 17, 9156. [Google Scholar] [CrossRef]
- Yin, X.L.; Zhao, X.F.; Huang, S.Q.; Lu, C. Basic response of saline water intrusion on combined action of runoff and tide in stratified estuary. Water Resour. Prot. 2020, 36, 68–74. [Google Scholar]
- Wang, Q.; Ye, R.H.; Wang, Y.P.; Zhang, M.R.; Kong, J. Statistical model for salinity prediction in Pearl River Estuary. Water Resour. Prot. 2018, 34, 82–87. [Google Scholar]
- Prandle, D. Saline intrusion in partially mixed estuaries. Estuar. Coast. Shelf Sci. 2004, 59, 385–397. [Google Scholar] [CrossRef]
- Sierra, J.P.; Sánchez-Arcilla, A.; Figueras, P.A.; Gonzalez Del Rio, J.; Rassmussen, E.K.; Mösso, C. Effects of discharge reductions on salt wedge dynamics of the Ebro River. River Res. Appl. 2004, 20, 61–77. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2011, 703, 152–162. [Google Scholar] [CrossRef]
- Tillman, F.D.; Anning, D.W.; Heilman, J.A.; Buto, S.G.; Miller, M.P. Managing salinity in Upper Colorado river basin streams: Selecting catchments for sediment control efforts using watershed characteristics and random forests models. Water 2018, 10, 676. [Google Scholar] [CrossRef]
- Li, W.S.; Zuo, C.S.; Wang, H.; Dong, J.S.; Gao, T.; Pan, S.; Jin, B.W. Salt tide intrusion characteristics in main estuaries of China. Mar. Sci. Bull. 2019, 38, 650–655. [Google Scholar]
- Yan, X.; Sun, Z.H.; Xie, C.S.; Xia, J.Q. Estimation of critical discharge for saltwater intrusion in the upper south branch of the Yangtze River Estuary using empirical models. Acta Geogr. Sin. 2019, 74, 935–947. [Google Scholar]
- Wen, P.; Qi, Z.M.; Liu, B. Research on Flow Capacity for Repelling Saltwater Intrusion in the North and West River Delta. J. China Hydrol. 2009, 29, 74–75+52. [Google Scholar]
- Al-Aesawi, Q.; Al-Nasrawi, A.K.; Jones, B.G.; Yang, S.Q. Geomatic freshwater discharge estimations and their effect on saltwater intrusion in alluvial systems: A case study in Shatt Al-Arab estuary. Environ. Earth Sci. 2021, 80, 643. [Google Scholar] [CrossRef]
- Liu, W.C.; Hsu, M.H.; Kuo, A.Y.; Kuo, J.T. The influence of river discharge on salinity intrusion in the Tanshui estuary, Taiwan. J. Coast. Res. 2001, 17, 544–552. [Google Scholar]
- Qiu, C.; Zhu, J.R. Influence of seasonal runoff regulation by the Three Gorges Reservoir on saltwater intrusion in the Changjiang River Estuary. Cont. Shelf Res. 2013, 71, 16–26. [Google Scholar] [CrossRef]
- Narvaez-Montoya, C.; Mahlknecht, J.; Torres-Martínez, J.A.; Mora, A.; Bertrand, G. Seawater intrusion pattern recognition supported by unsupervised learning: A systematic review and application. Sci. Total Environ. 2022, 864, 160933. [Google Scholar] [CrossRef]
- Lu, P.; Lin, K.; Xu, C.Y.; Lan, T.; Liu, Z.; He, Y. An integrated framework of input determination for ensemble forecasts of monthly estuarine saltwater intrusion. J. Hydrol. 2021, 598, 126–225. [Google Scholar] [CrossRef]
- Miao, T.; Guo, J. Application of artificial intelligence deep learning in numerical simulation of seawater intrusion. Environ. Sci. Pollut. Res. 2021, 28, 54096–54104. [Google Scholar] [CrossRef]
- Cao, T.; Han, D.; Song, X. Past, present, and future of global seawater intrusion research: A bibliometric analysis. J. Hydrol. 2021, 603, 126844. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Wu, J. Analysis of river evolution and impact in the downstream of Minjiang River. Hydraul. Sci. Technol. 2016, 4, 66–69. [Google Scholar]
- Zhao, J.; Zhang, Z.Y.; Xie, Z.Y.; Huang, J.L.; Huang, Z.Y. Water quality simulation of Minjiang estuary water plant based on BP artificial neural network. Environ. Sci. Technol. 2020, 43, 198–203. [Google Scholar]
- Chen, R.L.; Liu, C.; Gao, S.Y. Analysis of the mechanism on the saltwater intrusion in Modaomen estuary. Chin. J. Hydrodyn. 2011, 26, 312–317. [Google Scholar]
- Zhang, Y.; Liu, Y.; Wu, Y.; Ji, C.; Ma, Q. Short-term optimal operation of cascade reservoirs considering dynamic water flow hysteresis. Water 2019, 11, 2098. [Google Scholar] [CrossRef]
- Shawwash, Z.K.; Thomas, K.S.; Russel, S.O. The BC Hydro short term hydro scheduling optimization model. In Proceedings of the 21st International Conference on Power Industry Computer Applications (PICA 99), Santa Clara, CA, USA, 20–21 May 1999; pp. 183–189. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Hu, X.E. Effect of Cascade Hydropowers Peak Shaving on Navigation and Countermeasures Research. Ph.D. Thesis, Tianjin University, Tianjin, China, 2007. [Google Scholar]
- Lu, C.; Su, B.; Yuan, L.R.; Chen, R.L. Physical modeling experiments on the saltwater at Mill Gate—II Influence of runoff on the saltwater intrusion. Pearl River 2012, 33, 33–36. [Google Scholar]


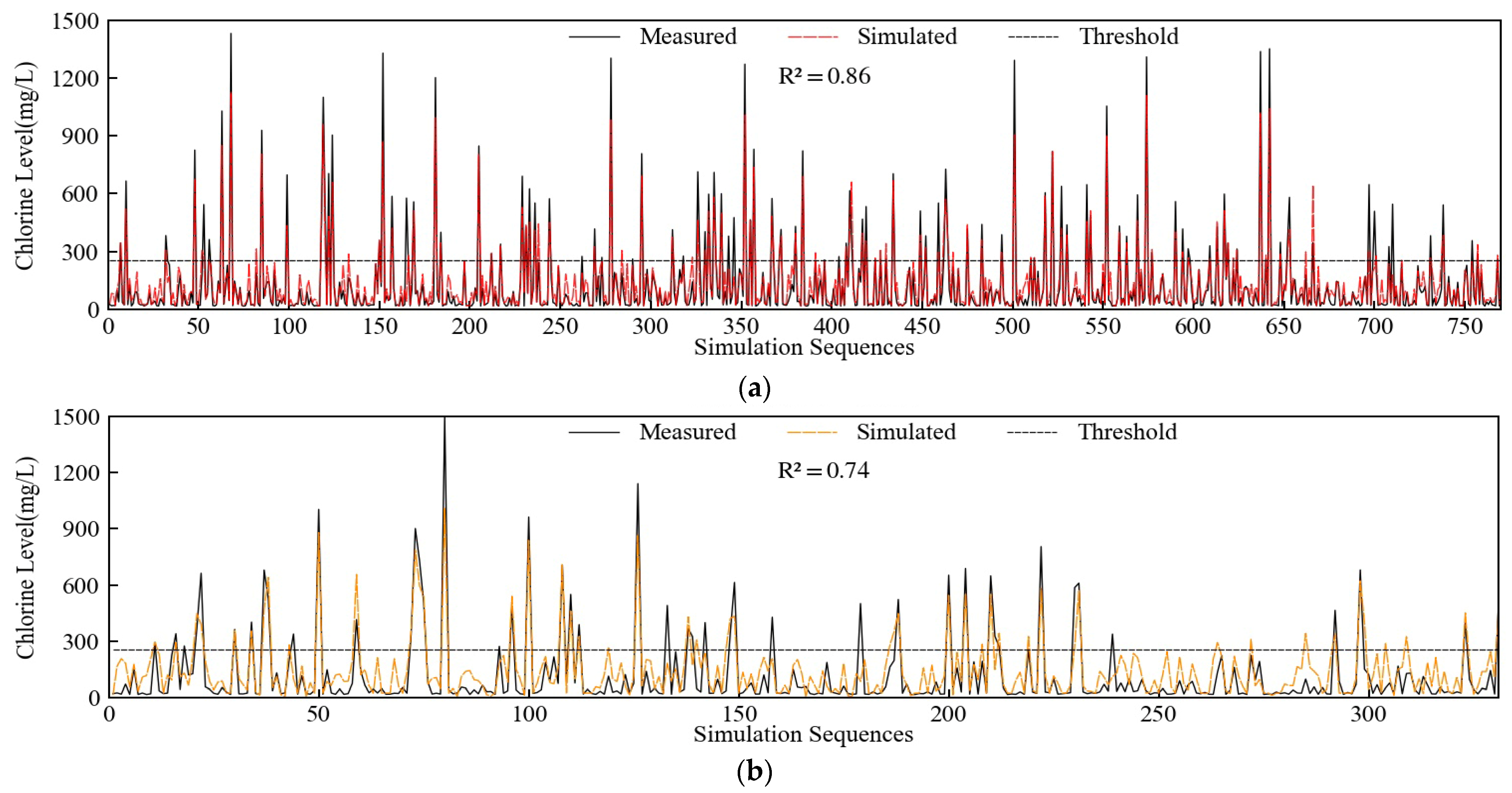

| No. | Occurrence Time | Measured Chlorine Level | Simulated Chlorine Level | ||
|---|---|---|---|---|---|
| Max. (mg/L) | Exceeded Time (Day) | Max. (mg/L) | Exceeded Time (Day) | ||
| 1 | Early January 2009 | 312.13 | 3 | 67.77 | 0 |
| 2 | Late January 2009 | 404.05 | 4 | 67.77 | 0 |
| 3 | Early February 2009 | 514.21 | 9 | 149.43 | 0 |
| 4 | Late February 2009 | 645.04 | 8 | 90.75 | 0 |
| 5 | Late September 2011 | 267.55 | 2 | 90.75 | 0 |
| 6 | Early October 2013 | 254.83 | 1 | 87.54 | 0 |
| 7 | Late October 2013 | 493.37 | 8 | 63.48 | 0 |
| 8 | Early November 2017 | 695.45 | 8 | 90.45 | 0 |
| 9 | Late November 2017 | 1457.17 | 19 | 70.22 | 0 |
| 10 | Early December 2017 | 917.13 | 11 | 495.52 | 5 |
| 11 | Late December 2017 | 814.79 | 15 | 208.57 | 0 |
| 12 | Early January 2018 | 1524.89 | 13 | 571.04 | 5 |
| 13 | Early February 2018 | 605.67 | 4 | 426.88 | 3 |
| 14 | Early March 2018 | 1332.31 | 13 | 431.94 | 5 |
| 15 | Late April 2018 | 722.41 | 9 | 241.72 | 0 |
| 16 | Early October 2018 | 913.91 | 10 | 149.89 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Guan, Y.; Zhang, D.; Niyongabo, A.; Ming, H.; Yu, Z.; Huang, Y. Research on Seawater Intrusion Suppression Scheme of Minjiang River Estuary. Int. J. Environ. Res. Public Health 2023, 20, 5211. https://doi.org/10.3390/ijerph20065211
Wang Z, Guan Y, Zhang D, Niyongabo A, Ming H, Yu Z, Huang Y. Research on Seawater Intrusion Suppression Scheme of Minjiang River Estuary. International Journal of Environmental Research and Public Health. 2023; 20(6):5211. https://doi.org/10.3390/ijerph20065211
Chicago/Turabian StyleWang, Ziyuan, Yiqing Guan, Danrong Zhang, Alain Niyongabo, Haowen Ming, Zhiming Yu, and Yihui Huang. 2023. "Research on Seawater Intrusion Suppression Scheme of Minjiang River Estuary" International Journal of Environmental Research and Public Health 20, no. 6: 5211. https://doi.org/10.3390/ijerph20065211
APA StyleWang, Z., Guan, Y., Zhang, D., Niyongabo, A., Ming, H., Yu, Z., & Huang, Y. (2023). Research on Seawater Intrusion Suppression Scheme of Minjiang River Estuary. International Journal of Environmental Research and Public Health, 20(6), 5211. https://doi.org/10.3390/ijerph20065211






