Predicting the Severity of Adverse Events on Osteoporosis Drugs Using Attribute Weighted Logistic Regression
Abstract
:1. Introduction
2. Related Work
3. Proposed Method
3.1. Weighted Logistic Regresion
3.2. Attribute Weight Based on Chi-Square
| Algorithm 1 Attribute weighted logistic regression |
| Input: training data 1: For each attribute xi in the training data - Compute following Equation (4) - Compute wi following Equation (6) 2: Incorporate attribute weights to train the weighted LR model (following Equation (3)) If wi = 0 then set aln(wi) = 1 × 10−10 Else if (βi > 0 and wi > 1) or (βi < 0 and wi < 1) then a = positive Else if (βi > 0 and wi < 1) or (βi < 0 and wi > 1) then a = negative |
4. Dataset and Evaluation Methods
4.1. Description of the Data
4.2. Data Preparation
4.3. Evaluation Methods
5. Experiments and Results
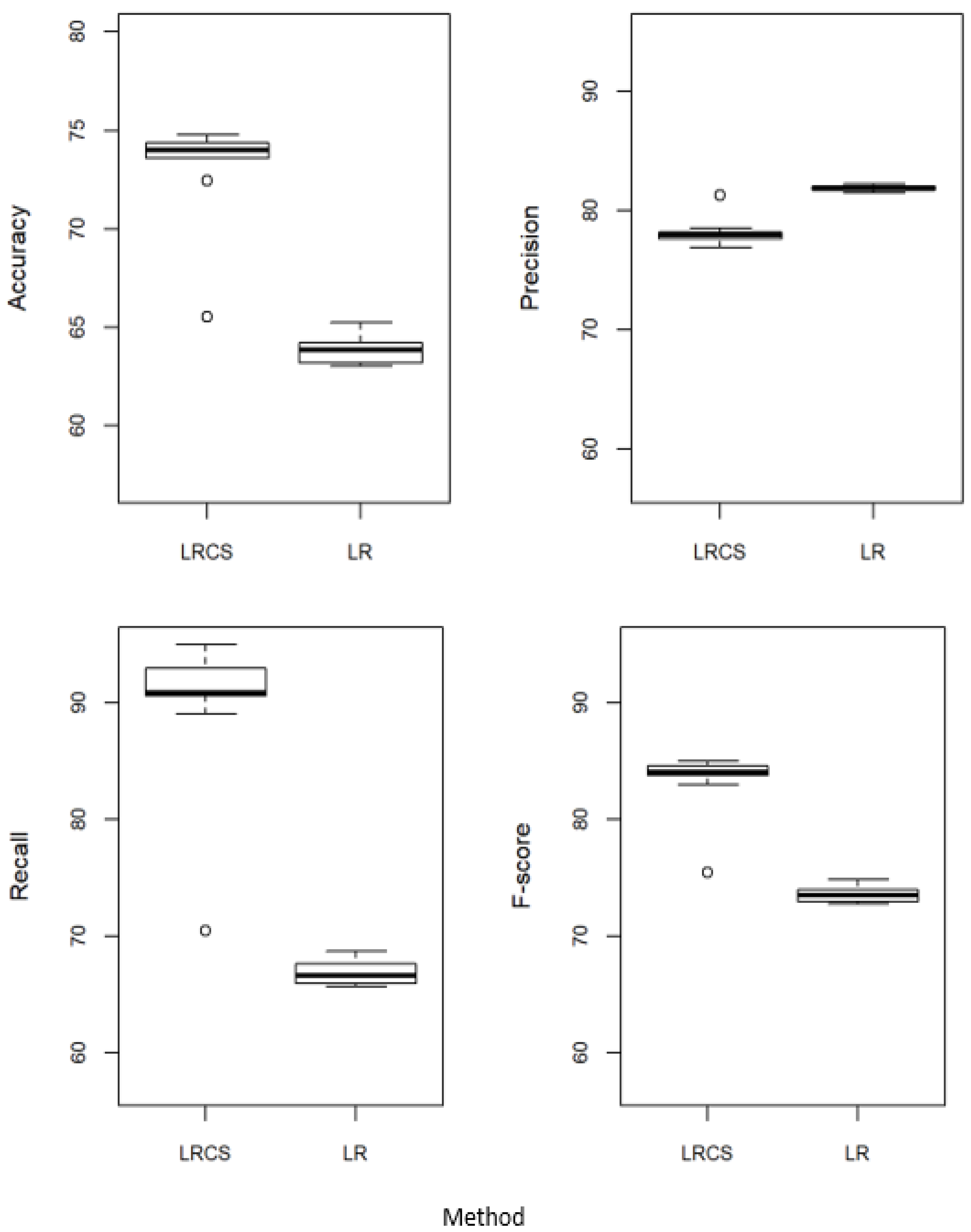
5.1. Proposed Method against the Standard Logistic Regression
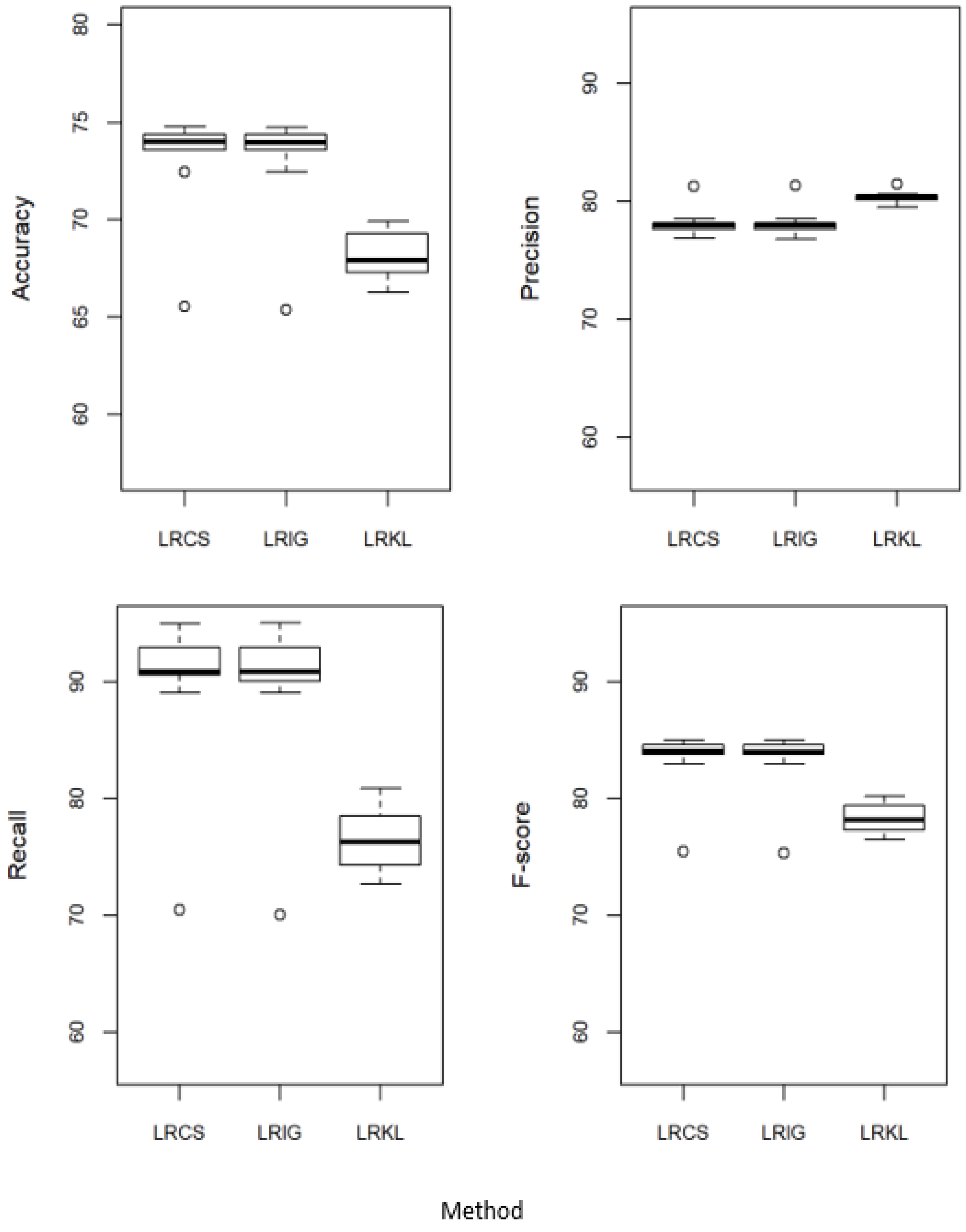
5.2. Proposed Method against the Baseline Attribute Weighing Methods
5.3. Proposed Method against the Baseline Classification Methods
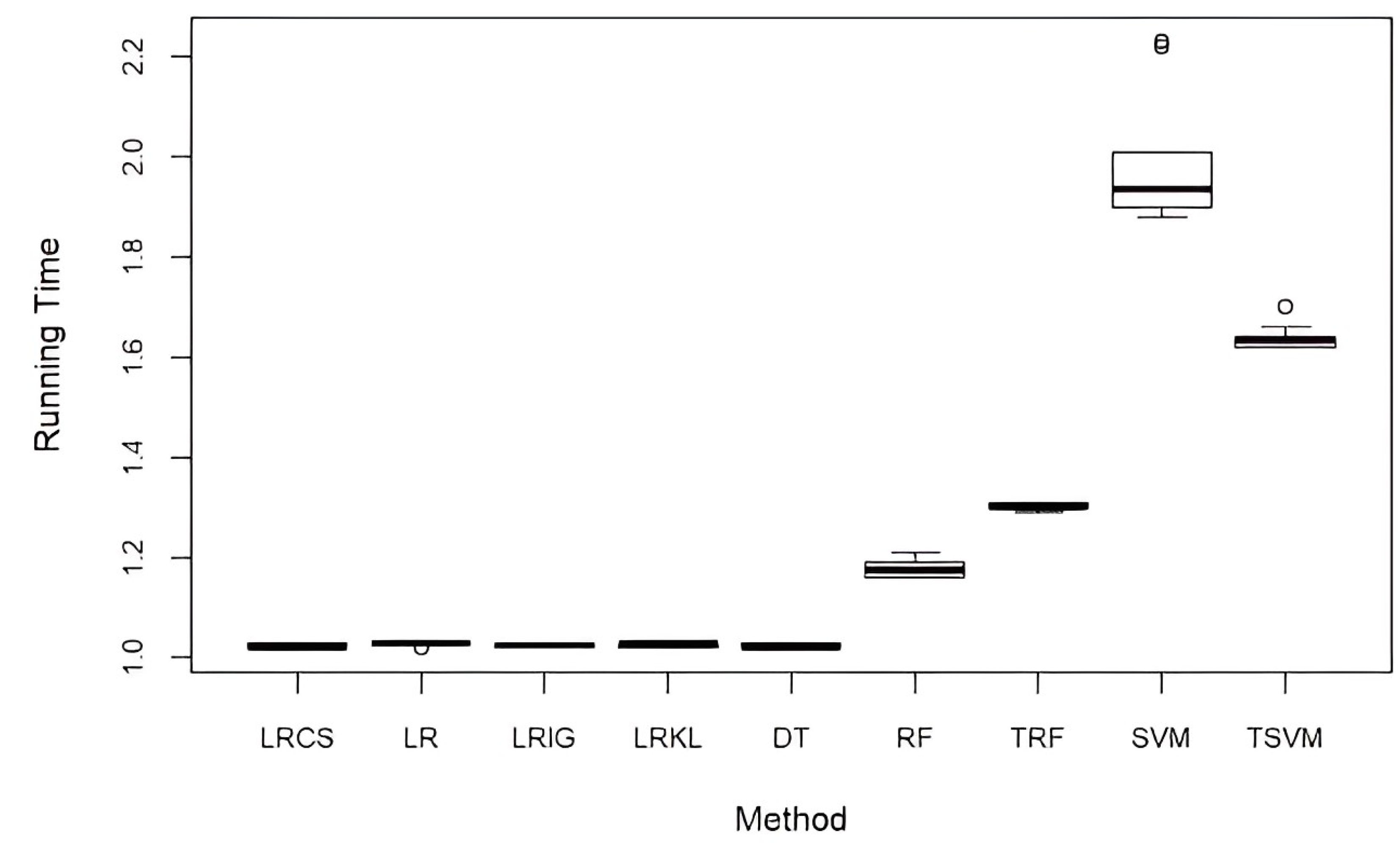
5.4. Computational Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Osteoporosis Foundation Website. Available online: www.iofbonehealth.org (accessed on 18 November 2022).
- Ibrahim, N.; Belal, N.; Badawy, O. Data mining model to predict Fosamax adverse events. Int. J. Comput. Inf. Technol. 2014, 3, 936–941. [Google Scholar]
- Yildirim, P.; Ekmekci, I.O.; Holzinger, A. On knowledge discovery in open medical data on the example of the FDA drug adverse event reporting system for alendronate (Fosamax). In International Workshop on Human-Computer Interaction and Knowledge Discovery in Complex, Unstructured, Big Data; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Lee, C.H.; Gutierrez, F.; Dou, D. Calculating feature weights in naive Bayes with Kullback-Leibler measure. In Proceedings of the 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011. [Google Scholar]
- Lee, C.H. An information-theoretic filter approach for value weighted classification learning in naive Bayes. Data Knowl. Eng. 2018, 113, 116–128. [Google Scholar] [CrossRef]
- Lee, C.H. A gradient approach for value weighted classification learning in naive Bayes. Knowl. Based Syst. 2015, 85, 71–79. [Google Scholar] [CrossRef]
- Foo, L.K.; Chua, S.L.; Ibrahim, N. Attribute weighted naïve Bayes classifier. Comput. Mater. Contin. 2022, 71, 1945–1957. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Duan, J.Z. Two Commonly Used Methods for Exposure—Adverse Events Analysis: Comparisons and Evaluations. J. Clin. Pharmacol. 2009, 49, 540–552. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Henderson, N.C.; Rohan, P.; Woo, E.J.; Russek-Cohen, E. Logistic regression likelihood ratio test analysis for detecting signals of adverse events in post-market safety surveillance. J. Biopharm. Stat. 2017, 27, 990–1008. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, L.; Li, C.; Kong, G. Two feature weighting approaches for naive Bayes text classifiers. Knowl. Based Syst. 2016, 100, 137–144. [Google Scholar] [CrossRef]
- Duan, W.; Lu, X.Y. Weighted naive Bayesian classifier model based on information gain. In Proceedings of the 2010 International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; Volume 2. [Google Scholar]
- Zhang, H.; Sheng, S. Learning weighted naive Bayes with accurate ranking. In Proceedings of the Fourth IEEE International Conference on Data Mining (ICDM’04), Brighton, UK, 1–4 November 2004. [Google Scholar]
- Korkmaz, S.A.; Korkmaz, M.F. A new method based cancer detection in mammogram textures by finding feature weights and using Kullback–Leibler measure with kernel estimation. Optik 2015, 126, 2576–2583. [Google Scholar] [CrossRef]
- Ouyed, O.; Allili, M.S. Feature weighting for multinomial kernel logistic regression and application to action recognition. Neurocomputing 2018, 275, 1752–1768. [Google Scholar] [CrossRef]
- Ouyed, O.; Allili, M.S. Group-of-features relevance in multinomial kernel logistic regression and application to human interaction recognition. Expert Syst. Appl. 2020, 148, 113247. [Google Scholar] [CrossRef]
- Krishnapuram, B.; Carin, L.; Figueiredo, M.A.; Hartemink, A.J. Sparse multinomial logistic regression: Fast algorithms and generalization bounds. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 957–968. [Google Scholar] [CrossRef]
- Ryali, S.; Supekar, K.; Abrams, D.A.; Menon, V. Sparse logistic regression for whole-brain classification of fMRI data. NeuroImage 2010, 51, 752–764. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Liu, C.; Luan, X.Z.; Leung, K.S.; Chan, T.M.; Xu, Z.B.; Zhang, H. Sparse logistic regression with a L 1/2 penalty for gene selection in cancer classification. BMC Bioinform. 2013, 14, 198. [Google Scholar] [CrossRef] [PubMed]
- Bertsimas, D.; Pauphilet, J.; Parys, B.V. Sparse classification: A scalable discrete optimization perspective. arXiv 2017, arXiv:1710.01352. [Google Scholar] [CrossRef]
- Bertsimas, D.; Parys, B.V. Sparse high-dimensional regression: Exact scalable algorithms and phase transitions. Ann. Stat. 2020, 48, 300–323. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pauphilet, J.; Parys, B.V. Sparse regression: Scalable algorithms and empirical performance. Stat. Sci. 2020, 35, 555–578. [Google Scholar] [CrossRef]
- Bach, F.R. Consistency of the group lasso and multiple kernel learning. J. Mach. Learn. Res. 2008, 9, 1179–1225. [Google Scholar] [CrossRef]
- Lin, Y.T.; Chu, C.Y.; Hung, K.S.; Lu, C.H.; Bednarczyk, E.M.; Chen, H.Y. Can machine learning predict pharmacotherapy outcomes? An application study in osteoporosis. Comput. Methods Programs Biomed. 2022, 225, 107028. [Google Scholar] [CrossRef]
- Jaganathan, K.; Tayara, H.; Chong, K.T. Prediction of drug-induced liver toxicity using SVM and optimal descriptor sets. Int. J. Mol. Sci. 2021, 22, 8073. [Google Scholar] [CrossRef]
- Cano, G.; Garcia-Rodriguez, J.; Garcia-Garcia, A.; Perez-Sanchez, H.; Benediktsson, J.A.; Thapa, A.; Barr, A. Automatic selection of molecular descriptors using random forest: Application to drug discovery. Expert Syst. Appl. 2017, 72, 151–159. [Google Scholar] [CrossRef]
- Peng, C.Y.J.; Lee, K.L.; Ingersoll, G.M. An introduction to logistic regression analysis and reporting. J. Educ. Res. 2002, 96, 3–14. [Google Scholar] [CrossRef]
- US FDA Database Website. Available online: https://fis.fda.gov/extensions/FPD-QDE-FAERS/FPD-QDE-FAERS.html (accessed on 18 November 2022).
- Taheri, S.; Yearwood, J.; Mammadov, M.; Seifollahi, S. Attribute weighted Naive Bayes classifier using a local optimization. Neural Comput. Appl. 2014, 24, 995–1002. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.; Pfahringer, B. Locally weighted naive bayes. In Proceedings of the Nineteenth Conference on Uncertainty in Artificial Intelligence. arXiv 2022, arXiv:1212.2487v1. [Google Scholar]
- Jiang, L.; Zhang, L.; Li, C.; Wu, J. A correlation-based feature weighting filter for naive Bayes. IEEE Trans. Knowl. Data Eng. 2018, 31, 201–213. [Google Scholar] [CrossRef]
- Jiang, L.; Li, C.; Wang, S.; Zhang, L. Deep feature weighting for naive Bayes and its application to text classification. Eng. Appl. Artif. Intell. 2016, 52, 26–39. [Google Scholar] [CrossRef]
- Fayyad, U.; Irani, K. Multi-interval discretization of continuous-valued attributes for classification learning. In Proceedings of the 13th International Joint Conference on Artificial Intelligence, Chambery, France, 1 September 1993; pp. 1022–1027. [Google Scholar]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 10 November 2022).

| (a) | ||||
|---|---|---|---|---|
| Study | Attribute Weighting Method | Classification Method | Dataset | Best Performing Model |
| Zhang et al. [11] | IG and χ2 statistic for words weighting | Multinomial NB and weighted NB | Benchmark textual data obtained from WEKA and Amazon website | IG weighted NB |
| Duan et al. [12] | IG | NB and weighted NB | Benchmark data from UCI database | IG weighted NB |
| Zhang and Sheng [13] | IG, hill climbing and Markov Chain Monte Carlo | NB, weighted NB and DT | Benchmark data from UCI database | IG with hill climbing weighted NB |
| Lee et al. [4] | KL | NB, KL weighted NB, Tree Augmented NB, NBTree and DT | Benchmark data from UCI database | KL weighted NB |
| Lee [5] | KL and DT | NB, KL feature weighted NB, KL value weighted NB, DT weighted NB, logistic, DT, Tree Augmented NB and RF | Benchmark data from UCI database | KL weighted NB |
| Foo et al. [7] | IG and KL | NB and weighted NB | Benchmark data from UCI and FDA databases | NA |
| Korkmaz and Korkmaz [14] | KL | KL weighted NB, Bayesian neural network, SVM and neural network | Breast cancer mammography | KL weighted NB |
| Ouyed and Allili [15] | Newton Raphson method | NB, Sparse multinomial LR, feature relevance multinomial kernel LR, kernel SVM and Lasso | Benchmark data from UCI database and simulated data | Multinominal kernel LR |
| Ouyed and Allili [16] | Gradient descent minimisation | Multinominal kernel LR, SVM and deep learning network | UT-interaction dataset | Multinominal kernel LR |
| (b) | ||||
| Study | Attribute Selection Method | Classification Method | Dataset | Best Performing Model |
| Krishnapuram et al. [17] | L1 regularization | SVM, relevance vector machine, sparse multinomial LR and ridge multinomial LR | Benchmark data from UCI database and online sources | Sparse multinomial LR |
| Ryali et al. [18] | Combination of L1 and L2 regularization | SVM based recursive feature elimination, LR based L1 and L2 | Whole brain dataset | L1 and L2 based LR |
| Liang et al. [19] | L1/2 regularization | k-nearest neighbor | Cancer datasets | NA |
| Lin et al. [24] | Genetic algorithm | LR, SVM, RF, ANN | Osteoporosis patients | LR and ANN |
| Jaganathan et al. [25] | Recursive feature elimination and cross-validation | SVM, LR, RF, DT, NB, MLP, XG boosting and k-nearest neighbor | Drug toxicity | Hyperparameter-tuned SVM |
| Cano et al. [26] | Random forest | RF, SVM and MLP | Drug activity | Hyperparameter-tuned RF |
| βi | Adding Attribute Weight | The Resulted Value | |
|---|---|---|---|
| wi < 1 | wi > 1 | ||
| Negative | +ln(wi) | −ln(wi) | Negative |
| Positive | −ln(wi) | +ln(wi) | Positive |
| Attribute | βi | Weight (wi) | ±ln(wi) | βi ± ln(wi) |
|---|---|---|---|---|
| x1 | −0.751 | 1.84 | −ln(1.84) | −1.36 |
| 0.86 | +ln(0.86) | −0.901 | ||
| x2 | 0.262 | 1.84 | +ln(1.84) | 0.871 |
| 0.86 | −ln(0.86) | 0.412 |
| xi | ||||||
| b1 | b2 | …. | bs | |||
| T | t1 | O11 | O12 | …. | O1s | MR1 |
| t2 | O21 | O22 | …. | O2s | MR2 | |
| . | . | . | ||||
| . | . | . | ||||
| . | . | . | ||||
| . | . | . | ||||
| tz | Oz1 | Oz2 | …. | Ozs | MRz | |
| MC1 | MC2 | …. | MCs | M | ||
| No | Attribute | Description | Attributes Values | Count | Severe Count | Non-Severe Count |
|---|---|---|---|---|---|---|
| 1 | Disease | A medical terminology based on medical dictionary for regulatory activities | Osteoporosis Osteopenia Osteoporosis prophylaxis | 19,622 789 165 | 11,536 342 78 | 8086 447 87 |
| 2 | Gender | Patient’s sex | Female | 18,522 | 10,633 | 7889 |
| Male | 2054 | 1323 | 731 | |||
| 3 | Drug name | The name of reported medicine | Forteo | 11,980 | 7929 | 4051 |
| Aclasta | 1633 | 863 | 770 | |||
| Zolendronic acid | 1270 | 522 | 748 | |||
| Prolia | 1221 | 508 | 713 | |||
| Reclast | 1179 | 580 | 599 | |||
| Fosamax | 1141 | 564 | 577 | |||
| Actonel | 824 | 441 | 383 | |||
| Evista | 544 | 267 | 277 | |||
| Boniva | 519 | 147 | 372 | |||
| Alendronate sodium | 265 | 135 | 130 | |||
| 4 | Dose frequency | The reported dosage frequency | Once | 349 | 185 | 164 |
| Every day | 12,788 | 8364 | 4424 | |||
| Every week | 1801 | 886 | 915 | |||
| Every month | 611 | 192 | 419 | |||
| Every 3 months | 74 | 28 | 46 | |||
| Every 6 months | 1043 | 443 | 600 | |||
| Every year | 3910 | 1858 | 2052 | |||
| 5 | Age | Patient’s age at event date | From 0 to 105 year | 20,576 | ||
| 6 | Duration | The period of using the drug until the event occurring | From 0 to 8677 day | 20,576 | ||
| 7 | Target attribute | The patient’s outcome of using the drug | Severe | 11,956 | ||
| Non-severe | 8620 |
| Attribute | Attribute Weights Using χ2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Fold 6 | Fold 7 | Fold 8 | Fold 9 | Fold 10 | |
| Disease | 0.19 | 0.14 | 0.15 | 0.16 | 0.18 | 0.17 | 0.17 | 0.18 | 0.17 | 0.18 |
| Gender | 0.07 | 0.06 | 0.07 | 0.09 | 0.09 | 0.08 | 0.05 | 0.08 | 0.07 | 0.07 |
| Drug name | 2.07 | 2.06 | 2.02 | 2.08 | 2.08 | 1.98 | 2.07 | 1.92 | 1.98 | 2.07 |
| Dose frequency | 1.87 | 1.83 | 1.78 | 1.84 | 1.89 | 1.82 | 1.82 | 1.71 | 1.84 | 1.81 |
| Age | 0.75 | 0.78 | 0.87 | 0.72 | 0.68 | 0.78 | 0.72 | 0.87 | 0.87 | 0.76 |
| Duration | 1.05 | 1.13 | 1.11 | 1.11 | 1.08 | 1.17 | 1.17 | 1.24 | 1.07 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, N.; Foo, L.K.; Chua, S.-L. Predicting the Severity of Adverse Events on Osteoporosis Drugs Using Attribute Weighted Logistic Regression. Int. J. Environ. Res. Public Health 2023, 20, 3289. https://doi.org/10.3390/ijerph20043289
Ibrahim N, Foo LK, Chua S-L. Predicting the Severity of Adverse Events on Osteoporosis Drugs Using Attribute Weighted Logistic Regression. International Journal of Environmental Research and Public Health. 2023; 20(4):3289. https://doi.org/10.3390/ijerph20043289
Chicago/Turabian StyleIbrahim, Neveen, Lee Kien Foo, and Sook-Ling Chua. 2023. "Predicting the Severity of Adverse Events on Osteoporosis Drugs Using Attribute Weighted Logistic Regression" International Journal of Environmental Research and Public Health 20, no. 4: 3289. https://doi.org/10.3390/ijerph20043289
APA StyleIbrahim, N., Foo, L. K., & Chua, S.-L. (2023). Predicting the Severity of Adverse Events on Osteoporosis Drugs Using Attribute Weighted Logistic Regression. International Journal of Environmental Research and Public Health, 20(4), 3289. https://doi.org/10.3390/ijerph20043289








