Research on Risk Assessment and Contamination Monitoring of Potential Toxic Elements in Mining Soils
Abstract
:1. Introduction
2. Materials and Methods
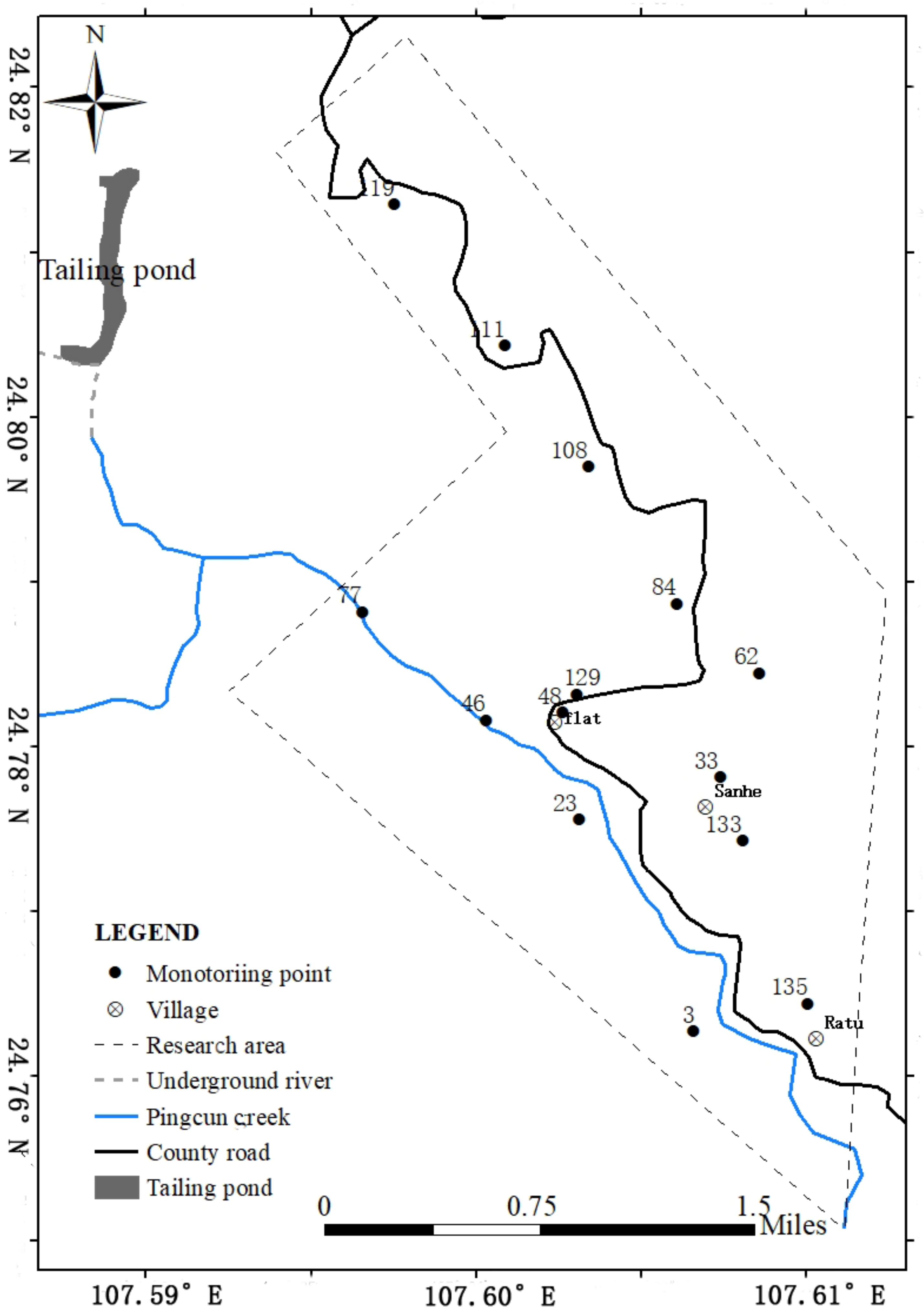
2.1. Sampling
2.2. Comprehensive Scoring Method
2.3. Analytical Hierarchy Process
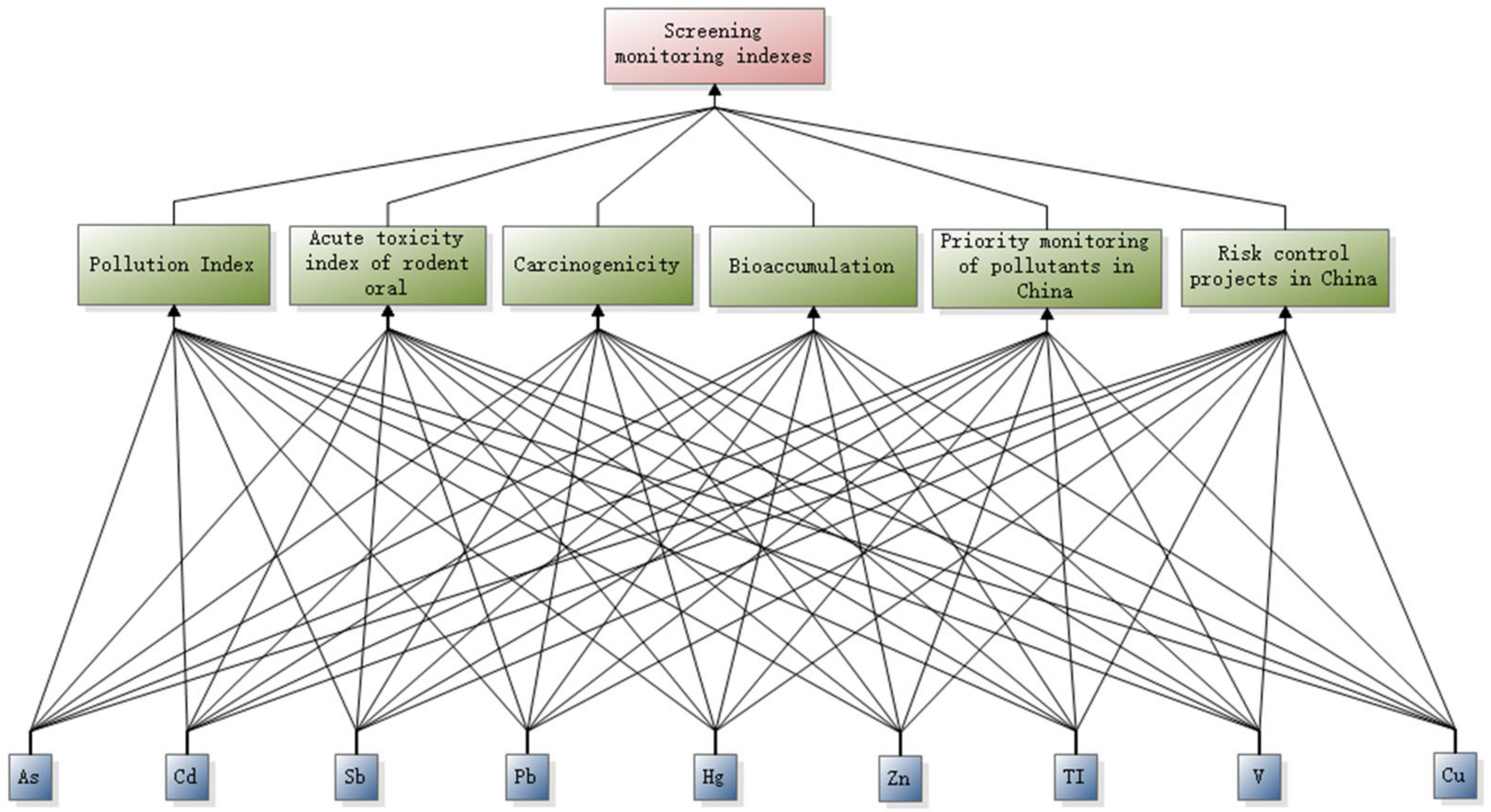
2.3.1. Establishment of Analytical Hierarchy Process
2.3.2. Judgment Function Structure
2.3.3. Calculation of the Matrix Feature Vector and Maximum Eigenvalue
2.3.4. Consistency Test
2.4. Potential Ecological Risk Index
2.5. Spatial Variability Analysis
2.6. OK Interpolation
2.7. RBF Interpolation
2.8. Principles of Optimizing Monitoring Sites
2.8.1. Representativeness
2.8.2. Comprehensiveness
3. Results and Discussion
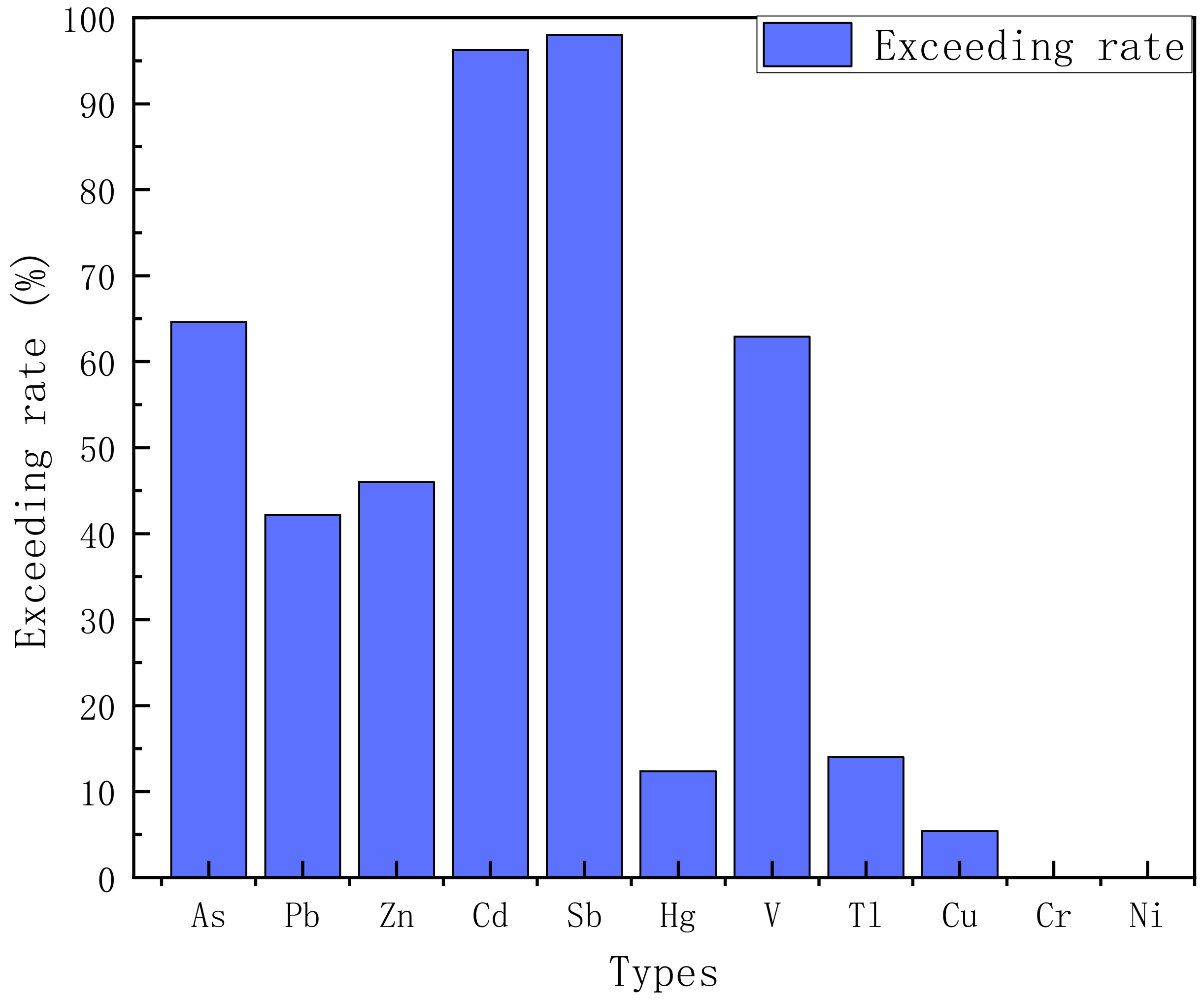
3.1. Screening of the Long-Term Monitoring Indicators
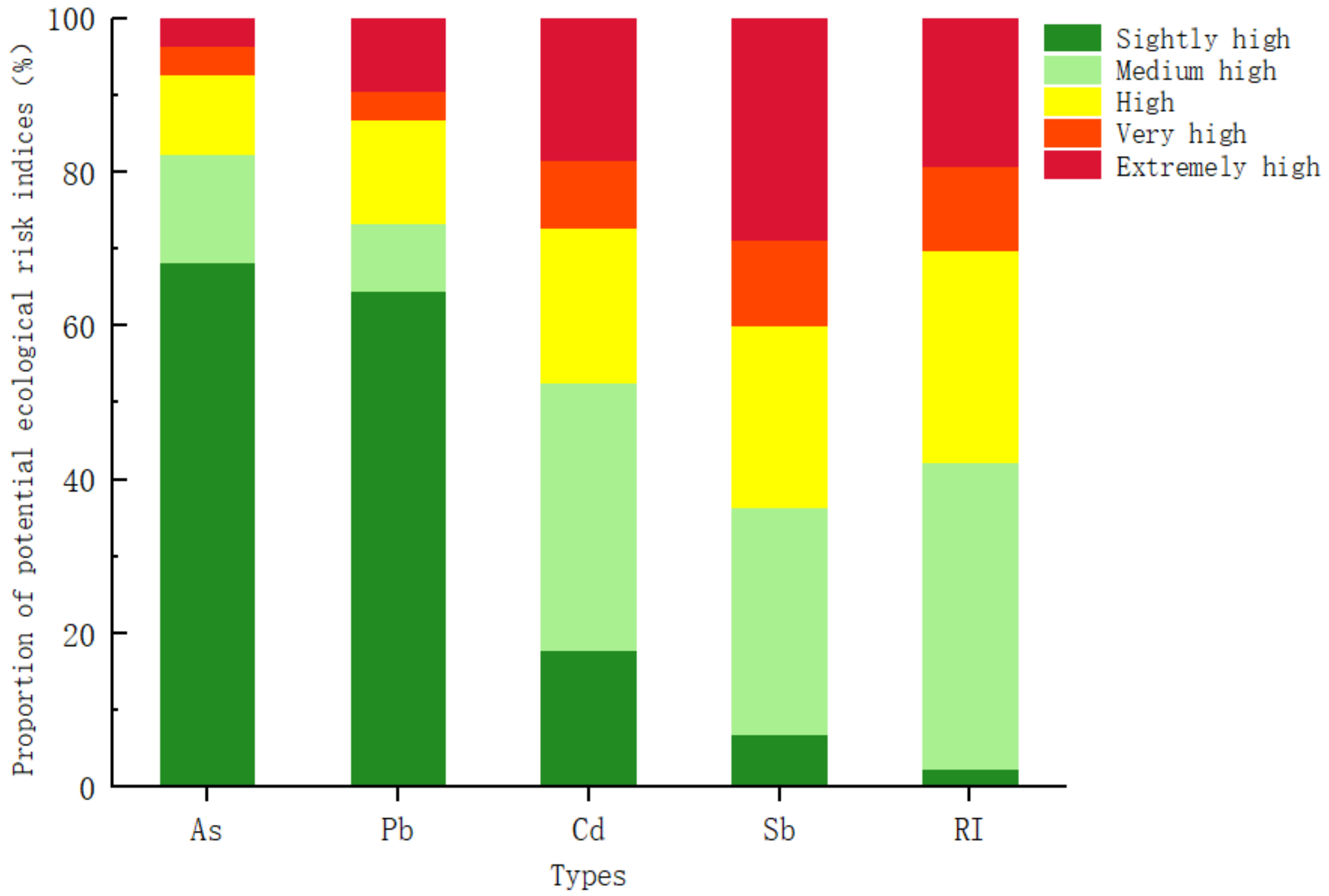
3.2. Potential Ecological Risk Assessment
3.2.1. Potential Ecological Risk Assessment of Monitoring Indicators
3.2.2. The Spatial Correlation Analysis of Potential Ecological Risks Index
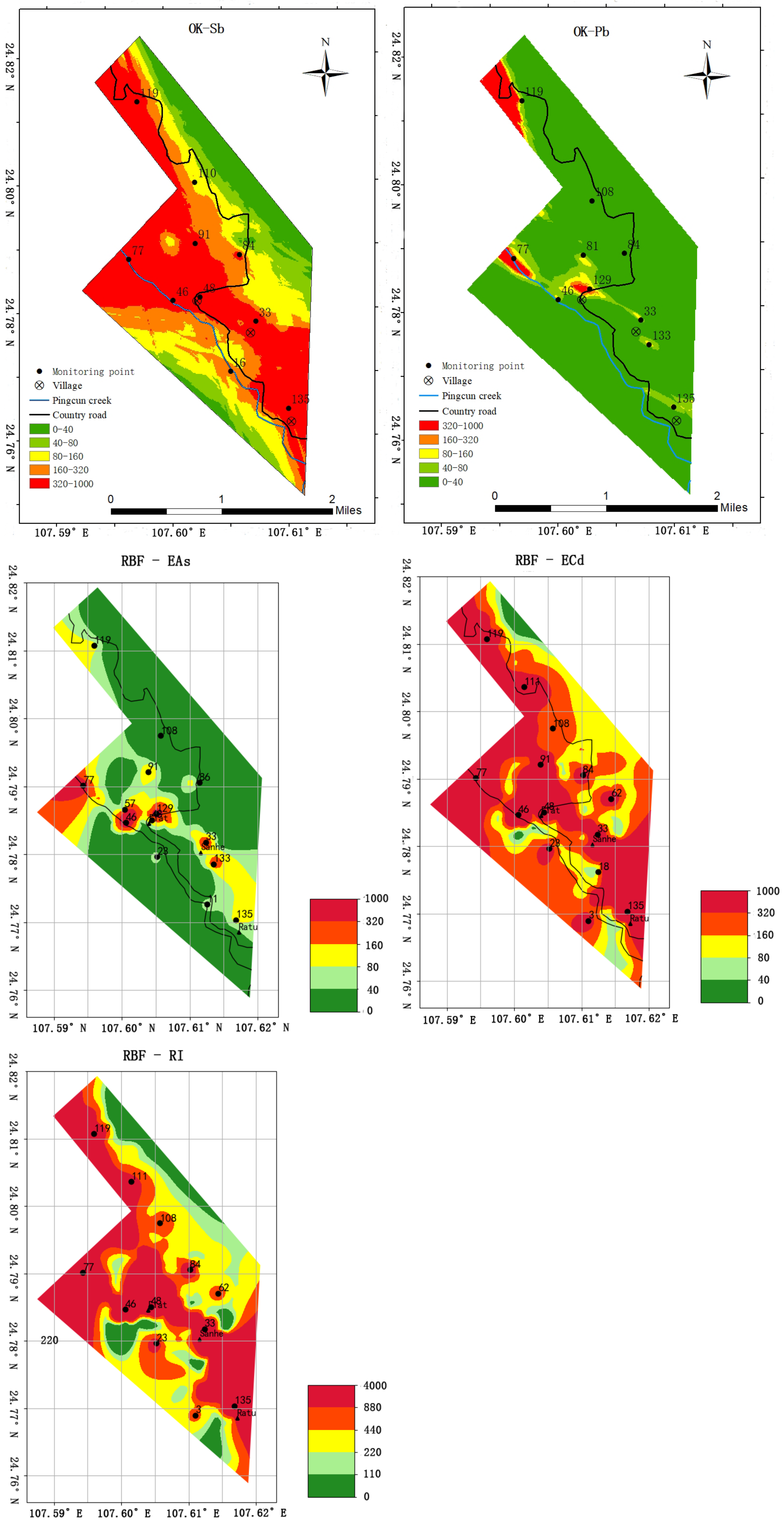
3.3. Comparison between OK and RBF Interpolation
3.4. The Spatial Distribution of Potential Ecological Risks of Monitoring Indicators
3.5. Optimize the Layout of Monitoring Points
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khanam, R.; Kumar, A.; Nayak, A.; Shahid, M.; Tripathi, R.; Vijayakumar, S.; Bhaduri, D.; Kumar, U.; Mohanty, S.; Panneerselvam, P.; et al. Metal(loid)s (As, Hg, Se, Pb and Cd) in paddy soil: Bioavailability and potential risk to human health. Sci. Total Environ. 2020, 699, 134330. [Google Scholar] [CrossRef] [PubMed]
- Mangla, D.; Sharma, A.; Ikram, S. Synthesis of ecological chitosan/PVP magnetic composite: Remediation of amoxicillin trihydrate from its aqueous solution, isotherm modelling, thermodynamic, and kinetic studies. React. Funct. Polym. 2022, 175, 105261. [Google Scholar] [CrossRef]
- Rahman, M.S.; Khan, M.; Jolly, Y.; Kabir, J.; Akter, S.; Salam, A. Assessing risk to human health for heavy metal contamination through street dust in the Southeast Asian Megacity: Dhaka, Bangladesh. Sci. Total Environ. 2019, 660, 1610–1622. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Choudhry, A.; Rathi, G.; Tara, N.; Abdulla, N.K.; Sajid, M.; Chaudhry, S.A. Chapter 30—Ferrite based magnetic nanocomposites for wastewater treatment through adsorption. In Contamination of Water; Ahamad, A., Siddiqui, S.I., Singh, P., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 449–460. [Google Scholar]
- Wu, W.; Wu, P.; Yang, F.; Sun, D.-L.; Zhang, D.-X.; Zhou, Y.-K. Assessment of heavy metal pollution and human health risks in urban soils around an electronics manufacturing facility. Sci. Total Environ. 2018, 630, 53–61. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, Q.; Yuan, Y.; Sun, W. Human health risk assessment of heavy metals in soil and food crops in the Pearl River Delta urban agglomeration of China. Food Chem. 2020, 316, 126213. [Google Scholar] [CrossRef]
- Sharma, A.; Mangla, D.; Choudhry, A.; Sajid, M.; Chaudhry, S.A. Facile synthesis, physico-chemical studies of Ocimum sanctum magnetic nanocomposite and its adsorptive application against Methylene blue. J. Mol. Liq. 2022, 362, 119752. [Google Scholar] [CrossRef]
- Chen, H.; Teng, Y.; Lu, S.; Wang, Y.; Wang, J. Contamination features and health risk of soil heavy metals in China. Sci. Total Environ. 2015, 512–513, 143–153. [Google Scholar] [CrossRef]
- MEP of China (Ministry of Environmental Protection of China). National Soil Pollution Survey Bulletin. 2014. Available online: https://www.mee.gov.cn/gkml/sthjbgw/qt/201404/t20140417_270670_wh.htm (accessed on 24 April 2014).
- Li, Z.Y.; Ma, Z.W.; van der Kuijp, T.J.; Yuan, Z.W.; Huang, L. A review of soil heavy metal pollution from mines in China: Pollution and health risk assessment. Sci. Total Environ. 2014, 468–469, 843–853. [Google Scholar] [CrossRef]
- Teng, Y.; Wu, J.; Lu, S.; Wang, Y.; Jiao, X.; Song, L. Soil and soil environmental quality monitoring in China: A review. Environ. Int. 2014, 69, 177–199. [Google Scholar] [CrossRef]
- Fang, Z. Heavy metal pollution comprehensive evaluation of contaminated soil in lead-zinc mining area based on the fuzzy mathematics. IOP Conf. Ser. Earth Environ. Sci. 2019, 300, 032114. [Google Scholar] [CrossRef]
- Sun, X.-T.; Zhou, Z.-F.; Zhang, S.-S. Optimization of Fuzzy Comprehensive Evaluation Model of Soil Heavy Metal Pollution Based on the Comprehensive Weight. In Proceedings of the 2016 International Conference on Environment, Climate Change and Sustainable Development (Eccsd 2016), Beijing, China, 28–29 May 2016; pp. 18–23. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, X.; Wang, Y.; Zhuang, D. Spatial characteristics of heavy metal pollution and the potential ecological risk of a typical mining area: A case study in China. Process. Saf. Environ. Prot. 2018, 113, 204–219. [Google Scholar] [CrossRef]
- Ding, X.; Chong, X.; Bao, Z.; Xue, Y.; Zhang, S. Fuzzy Comprehensive Assessment Method Based on the Entropy Weight Method and Its Application in the Water Environmental Safety Evaluation of the Heshangshan Drinking Water Source Area, Three Gorges Reservoir Area, China. Water 2017, 9, 329. [Google Scholar] [CrossRef]
- Saaty, T.L. Theory and Applications of the Analytic Network Process: Decision Making with Benefits, Opportunities, Costs, and Risks; RWS Publications: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, Y.; Wang, M.; Meng, H.; Ye, Z. Real-Time Detection Method for Heavy Metal Pollution in Soil of Mining Area. Glob. NEST: Int. J. 2020, 22, 570–578. [Google Scholar] [CrossRef]
- Yang, J.; Liu, H.; Yu, X.; Lv, Z.; Xiao, F. Entropy-Cloud Model of Heavy Metals Pollution Assessment in Farmland Soils of Mining Areas. Pol. J. Environ. Stud. 2016, 25, 1315–1322. [Google Scholar] [CrossRef]
- Islam, S.; Ahmed, K.; Mamun, H.A.; Masunaga, S. Potential ecological risk of hazardous elements in different land-use urban soils of Bangladesh. Sci. Total Environ. 2015, 512–513, 94–102. [Google Scholar] [CrossRef]
- Marrugo-Negrete, J.; Pinedo-Hernández, J.; Díez, S. Assessment of heavy metal pollution, spatial distribution and origin in agricultural soils along the Sinú River Basin, Colombia. Environ. Res. 2017, 154, 380–388. [Google Scholar] [CrossRef]
- He, J.; Yang, Y.; Christakos, G.; Liu, Y.; Yang, X. Assessment of soil heavy metal pollution using stochastic site indicators. Geoderma 2019, 337, 359–367. [Google Scholar] [CrossRef]
- Adimalla, N.; Chen, J.; Qian, H. Spatial characteristics of heavy metal contamination and potential human health risk assessment of urban soils: A case study from an urban region of South India. Ecotoxicol. Environ. Saf. 2020, 194, 110406. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.-L.; Zhu, J.-L.; Feng, Q.; Liu, W.; He, Y.-H.; Wang, X. Assessment of heavy metals in surface water, sediment and macrozoobenthos in inland rivers: A case study of the Heihe River, Northwest China. Environ. Sci. Pollut. Res. 2022, 29, 35253–35268. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Wang, S.; Huang, X. Influence of sampling scale and environmental factors on the spatial heterogeneity of soil organic carbon in a small Karst watershed. Fresenius Environ. Bull. 2018, 27, 1532–1544. [Google Scholar]
- Mottet, A.; Ladet, S.; Coqué, N.; Gibon, A. Agricultural land-use change and its drivers in mountain landscapes: A case study in the Pyrenees. Agric. Ecosyst. Environ. 2006, 114, 296–310. [Google Scholar] [CrossRef]
- Maas, S.; Scheifler, R.; Benslama, M.; Crini, N.; Lucot, E.; Brahmia, Z.; Benyacoub, S.; Giraudoux, P. Spatial distribution of heavy metal concentrations in urban, suburban and agricultural soils in a Mediterranean city of Algeria. Environ. Pollut. 2010, 158, 2294–2301. [Google Scholar] [CrossRef] [PubMed]
- Ding, Q.; Wang, Y.; Zhuang, D. Comparison of the common spatial interpolation methods used to analyze potentially toxic elements surrounding mining regions. J. Environ. Manag. 2018, 212, 23–31. [Google Scholar] [CrossRef]
- Elzwayie, A.; El-Shafie, A.; Yaseen, Z.M.; Afan, H.; Allawi, M.F. RBFNN-based model for heavy metal prediction for different climatic and pollution conditions. Neural Comput. Appl. 2017, 28, 1991–2003. [Google Scholar] [CrossRef]
- Winder, J. Soil Quality Monitoring Programs: A Literature Review: AESA; Agriculture, Food, and Rural Development: Edmonton, AB, Canada, 2003. [Google Scholar]
- Sun, Y.; Zhou, Q.; Xie, X.; Liu, R. Spatial, sources and risk assessment of heavy metal contamination of urban soils in typical regions of Shenyang, China. J. Hazard. Mater. 2010, 174, 455–462. [Google Scholar] [CrossRef]
- Tepanosyan, G.; Sahakyan, L.; Belyaeva, O.; Maghakyan, N.; Saghatelyan, A. Human health risk assessment and riskiest heavy metal origin identification in urban soils of Yerevan, Armenia. Chemosphere 2017, 184, 1230–1240. [Google Scholar] [CrossRef]
- Guangxi Institute of Environmental Science. Soil Background Value Research Method and Background Value of Guangxi Soil; Guangxi Science and Technology Press: Nanning, China, 1992; pp. 216–223. [Google Scholar]
- Technical Overview of Ecological Risk Assessment—Analysis Phase: Ecological Effects Characterization. Available online: http://www.epa.gov/pesticide-science-and-assessing-pesticide-risks/technical-overview-ecological-risk-assessment-0 (accessed on 2 February 2023).
- IARC Monographs on the Identification of Carcinogenic Hazards to Humans. Agents Classified by the IARC Monographs, Volumes 1–132—IARC Monographs on the Identification of Carcinogenic Hazards to Humans (who.int). Available online: https://monographs.iarc.who.int/agents-classified-by-the-iarc/ (accessed on 2 February 2023).
- Ibrahim, N.; El Afandi, G. Phytoremediation uptake model of heavy metals (Pb, Cd and Zn) in soil using Nerium oleander. Heliyon 2020, 6, e04445. [Google Scholar] [CrossRef]
- Zhang, S.; Yao, H.; Lu, Y.; Yu, X.; Wang, J.; Sun, S.; Liu, M.; Li, D.; Li, Y.-F.; Zhang, D. Uptake and translocation of polycyclic aromatic hydrocarbons (PAHs) and heavy metals by maize from soil irrigated with wastewater. Sci. Rep. 2017, 7, 12165. [Google Scholar] [CrossRef]
- Zhou, W.M.; Fu, D.Q.; Sun, Z.G. Determination of Black List of China’s Priority Pollutants in Water. Res. Environ. Sci. 1991, 4, 9–12. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment of the People’s Republic of China. Soil Environmental Quality Riskcontrol Standard for Soil Contamination of Agricultural Land; China Environmental Science Publishing House: Beijing, China, 2018; p. 3. [Google Scholar]
- Li, M.; Wang, Y.; Teng, Y. Application of comprehensive evaluation for screening of typical pollutants in groundwater of the LiaoRiver basin. J. Beijing Norm. Univ. 2015, 51, 64. [Google Scholar] [CrossRef]
- Hoseinie, S.; Ataei, M.; Osanloo, M. A new classification system for evaluating rock penetrability. Int. J. Rock Mech. Min. Sci. 2009, 46, 1329–1340. [Google Scholar] [CrossRef]
- Hayaty, M.; Mohammadi, M.R.T.; Rezaei, A.; Shayestehfar, M.R. Risk Assessment and Ranking of Metals Using FDAHP and TOPSIS. Mine Water Environ. 2014, 33, 157–164. [Google Scholar] [CrossRef]
- Amjad, H.; Hamid, S.; Niaz, Y.; Ashraf, M.; Yasir, U.; Chaudhary, A.; Arsalan, A.; Daud, M.W. Efficiency assessment of wastewater treatment plant: A case study of Pattoki, district Kasur, Pakistan. Earth Sci. Pak. 2019, 3, 01–04. [Google Scholar] [CrossRef]
- Wei, C.; Wei, J.; Kong, Q.; Fan, D.; Qiu, G.; Feng, C.; Li, F.; Preis, S.; Wei, C. Selection of optimum biological treatment for coking wastewater using analytic hierarchy process. Sci. Total Environ. 2020, 742, 140400. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, K.; Cai, Y.; Wang, Y.; Liu, Y. Distribution and ecological risk assessment of arsenic and some trace elements in soil of different land use types, Tianba Town, China. Environ. Technol. Innov. 2021, 24, 102041. [Google Scholar] [CrossRef]
- Iwegbue, C.M.; Martincigh, B.S. Ecological and human health risks arising from exposure to metals in urban soils under different land use in Nigeria. Environ. Sci. Pollut. Res. 2018, 25, 12373–12390. [Google Scholar] [CrossRef]
- Håkanson, L. An ecological risk index for aquatic pollution control. A sedimentological approach. Water Res. 1980, 14, 975–1001. [Google Scholar] [CrossRef]
- Zhuang, W.; Wang, Q.; Tang, L.; Liu, J.; Yue, W.; Liu, Y.; Zhou, F.; Chen, Q.; Wang, M. A new ecological risk assessment index for metal elements in sediments based on receptor model, speciation, and toxicity coefficient by taking the Nansihu Lake as an example. Ecol. Indic. 2018, 89, 725–737. [Google Scholar] [CrossRef]
- Trangmar, B.B.; Yost, R.S.; Uehara, G. Application of geostatistics to spatial studies of soil properties. Adv. Agron. 1986, 38, 45–94. [Google Scholar]
- Liu, X.; Wu, J.; Xu, J. Characterizing the risk assessment of heavy metals and sampling uncertainty analysis in paddy field by geostatistics and GIS. Environ. Pollut. 2006, 141, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Reza, S.K.; Baruah, U.; Singh, S.K.; Das, T.H. Geostatistical and multivariate analysis of soil heavy metal contamination near coal mining area, Northeastern India. Environ. Earth Sci. 2014, 73, 5425–5433. [Google Scholar] [CrossRef]
- Fei, X.; Christakos, G.; Xiao, R.; Ren, Z.; Liu, Y.; Lv, X. Improved heavy metal mapping and pollution source apportionment in Shanghai City soils using auxiliary information. Sci. Total Environ. 2019, 661, 168–177. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; O’Connor, D.; Nathanail, P.; Tian, L.; Ma, Y. Integrated GIS and multivariate statistical analysis for regional scale assessment of heavy metal soil contamination: A critical review. Environ. Pollut. 2017, 231, 1188–1200. [Google Scholar] [CrossRef]
- Holmström, K.; Quttineh, N.-H.; Edvall, M.M. An adaptive radial basis algorithm (ARBF) for expensive black-box mixed-integer constrained global optimization. Optim. Eng. 2008, 9, 311–339. [Google Scholar] [CrossRef]
- Björkman, M.; Holmström, K. Global Optimization of Costly Nonconvex Functions Using Radial Basis Functions. Optim. Eng. 2000, 1, 373–397. [Google Scholar] [CrossRef]
- Yokota, R.; Barba, L.; Knepley, M.G. PetRBF—A parallel O(N) algorithm for radial basis function interpolation with Gaussians. Comput. Methods Appl. Mech. Eng. 2010, 199, 1793–1804. [Google Scholar] [CrossRef]
- Van Duijvenbooden, W. Soil monitoring systems and their suitability for predicting delayed effects of diffuse pollutants. Agric. Ecosyst. Environ. 1998, 67, 189–196. [Google Scholar] [CrossRef]
- Li, X.-N.; Ding, S.-K.; Chen, W.-P.; Wang, X.-H.; Lü, S.-D.; Liu, R. Construction and Application of Early Warning System for Soil Environmental Quality. Huan Jing Ke Xue Huanjing Kexue 2020, 41, 2834–2841. [Google Scholar]


| Sort | As | Cr | Pb | V | Zn | Cd | Cu | Ni | Tl | Sb | Hg |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value (mg/kg) | 21.6 | 75.0 | 28.7 | 142.8 | 82.9 | 0.1 | 23.2 | 26.9 | 0.7 | 2.9 | 0.3 |
| Label | Screening Indicators | Weights Coefficients | Points | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| A | Pollution Inx | 25 | 1~1.2 | 1.2~1.4 | 1.4~1.6 | 1.6~1.8 | >1.8 |
| B | Acute toxicity index of rodent oral | 3 | no data | >5000 | 50~5000 | 5~50 | <5 |
| C | Carcinogenicity | 3 | no data | 4 | 3 | 2 | 1 |
| D | Bioaccumulation | 5 | no data | <3.5 | 3.5~4.2 | >4.2 | |
| E | Priority monitoring of pollutants in China | 12 | no | Yes | |||
| F | Risk control projects in China | 6 | no | Yes | |||
| Priority of Indicator Monitoring | Total Score | Significance |
|---|---|---|
| Level 1 | 210~240 | Priority monitoring |
| Level 2 | 160~210 | Secondary monitoring |
| Level 3 | 60~160 | Select monitoring |
| Matrix Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.90 | 1.21 | 1.24 | 1.32 | 1.41 | 1.45 |
| Ecological Risk Level | ||
|---|---|---|
| < 40 | < 110 | slight |
| 40 ≤ < 80 | 110 ≤ < 220 | medium |
| 80 ≤ < 160 | 220 ≤ < 440 | high |
| 160 ≤ < 320 | 440 ≤ < 880 | Very high |
| ≥ 320 | ≥ 880 | Extremely high |
| Index | Pollution Index | Acute Toxicity Index of Rodent Oral | Carcinogenicity | Bioaccumulation | Priority Monitoring of Pollutants in China | Risk Control Projects in China | Total |
|---|---|---|---|---|---|---|---|
| Cd | 5 | 3 | 3 | 2 | 3 | 5 | 219 |
| As | 4 | 3 | 4 | 4 | 3 | 5 | 207 |
| Sb | 5 | 2 | 5 | 4 | 1 | 1 | 184 |
| Pb | 3 | 3 | 4 | 1 | 3 | 5 | 167 |
| Hg | 2 | 4 | 1 | 4 | 3 | 5 | 151 |
| V | 4 | 1 | 1 | 3 | 1 | 1 | 139 |
| Zn | 3 | 3 | 1 | 2 | 1 | 5 | 139 |
| Tl | 2 | 4 | 5 | 1 | 3 | 1 | 124 |
| Cu | 1 | 3 | 1 | 1 | 3 | 5 | 108 |
| Arrangement | ||
|---|---|---|
| 6.0083 | 0.0013 | |
| 9.1423 | 0.0122 | |
| 9.1778 | 0.0152 | |
| 9.2095 | 0.0179 | |
| 9.0853 | 0.0073 | |
| 9.0000 | 0.0000 | |
| 9.1132 | 0.0097 |
| Sort | Cd | Sb | As | Pb | V | Hg | Zn | TI | Cu |
|---|---|---|---|---|---|---|---|---|---|
| Weight | 0.1622 | 0.1585 | 0.1451 | 0.1117 | 0.1007 | 0.0933 | 0.0899 | 0.0782 | 0.0605 |
| Project | MODEL | Nugget Value Co | Abutment Value Co + C | Nugget Coefficient Co/Co + C (%) | Variation A0 (m) | Decisive Factor r2 | Residual RSS |
|---|---|---|---|---|---|---|---|
| EAs | Spherical | 2.41 × 10−4 | 1.92 × 10−3 | 12.54 | 1470 | 0.817 | 6.82 × 10−7 |
| EPb | Spherical | 6.99 × 10−4 | 3.08 × 10−3 | 22.71 | 748 | 0.417 | 3.85 × 10−6 |
| ECd | index | 0.022 | 0.208 | 10.54 | 411 | 0.354 | 5.86 × 10−3 |
| ESb | Spherical | 0.149 | 0.440 | 33.87 | 891 | 0.563 | 4.10 × 10−2 |
| RI | Spherical | 0.102 | 0.257 | 39.50 | 681 | 0.438 | 1.33 × 10−2 |
| Heavy Metal | OK | RBF | |||||
|---|---|---|---|---|---|---|---|
| MAE | MSE | R2 | MAE | MSE | R2 | Kernel Function | |
| As | 0.0155 | 0.0005 | 0.6838 | 0.0152 | 0.0004 | 0.7125 | linear |
| Cd | 0.2610 | 0.1127 | 0.2880 | 0.2705 | 0.1009 | 0.3629 | linear |
| Pb | 0.0325 | 0.0018 | 0.3415 | 0.0341 | 0.0019 | 0.2801 | Inverse quadratic |
| Sb | 0.1320 | 0.0349 | 0.9080 | 0.3775 | 0.2325 | 0.3931 | linear |
| RI | 0.3694 | 0.2344 | 0.3281 | 0.3316 | 0.1917 | 0.4504 | thin plate |
| Serial Number | Sample Number | EAs | EPb | ECd | ESb | RI |
|---|---|---|---|---|---|---|
| 1 | 3 | √ | √ | |||
| 2 | 11 | √ | ||||
| 3 | 16 | √ | ||||
| 4 | 18 | √ | ||||
| 5 | 23 | √ | √ | √ | ||
| 6 | 33 | √ | √ | √ | √ | √ |
| 7 | 46 | √ | √ | √ | √ | √ |
| 8 | 48 | √ | √ | √ | √ | |
| 9 | 57 | √ | ||||
| 10 | 62 | √ | √ | |||
| 11 | 77 | √ | √ | √ | √ | √ |
| 12 | 81 | √ | ||||
| 13 | 84 | √ | √ | √ | √ | |
| 14 | 86 | √ | ||||
| 15 | 91 | √ | √ | √ | ||
| 17 | 108 | √ | √ | √ | √ | |
| 18 | 110 | √ | ||||
| 19 | 111 | √ | √ | |||
| 20 | 119 | √ | √ | √ | √ | √ |
| 21 | 129 | √ | √ | |||
| 22 | 133 | √ | √ | |||
| 23 | 135 | √ | √ | √ | √ | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wang, Y.; Zuo, R.; Zhang, K.; Li, C.; Song, Q.; Du, X. Research on Risk Assessment and Contamination Monitoring of Potential Toxic Elements in Mining Soils. Int. J. Environ. Res. Public Health 2023, 20, 3163. https://doi.org/10.3390/ijerph20043163
Yang J, Wang Y, Zuo R, Zhang K, Li C, Song Q, Du X. Research on Risk Assessment and Contamination Monitoring of Potential Toxic Elements in Mining Soils. International Journal of Environmental Research and Public Health. 2023; 20(4):3163. https://doi.org/10.3390/ijerph20043163
Chicago/Turabian StyleYang, Jie, Yunlong Wang, Rui Zuo, Kunfeng Zhang, Chunxing Li, Quanwei Song, and Xianyuan Du. 2023. "Research on Risk Assessment and Contamination Monitoring of Potential Toxic Elements in Mining Soils" International Journal of Environmental Research and Public Health 20, no. 4: 3163. https://doi.org/10.3390/ijerph20043163
APA StyleYang, J., Wang, Y., Zuo, R., Zhang, K., Li, C., Song, Q., & Du, X. (2023). Research on Risk Assessment and Contamination Monitoring of Potential Toxic Elements in Mining Soils. International Journal of Environmental Research and Public Health, 20(4), 3163. https://doi.org/10.3390/ijerph20043163






